1.
Introduction
Cancer, the disease that triggers the unregulated development of irregular cells in the human body, is one of the leading mortality factors among humankind. As the disorder causes the disease to go to the tissue level, precise detection at an early stage becomes challenging. Another obstacle faced at the treatment level is to decide the therapeutic effectiveness of the drugs to be administered. Therefore, many researchers worldwide are carrying out their research work to find out the cause of the origin of the disease and impart a patient-friendly, effective, and successful treatment method.
In cancer treatment, immunotherapies are used to enhance the host anti-tumour immune response by perturbing the tumor microenvironment. Over the past few years, different types of immunotherapies have been developed, spanning from Immune-Checkpoint Blockade (ICB) to strategies that boost the T cell activity [1,2]. But, a high dose of immunotherapy to a patient can induce negative responses such as fever, chills, weakness, nausea, etc. [3,4].
Chemotherapy is an effective method to fight against cancer [5]. However, it has a substantial adverse effect as induction of chemotherapeutic drugs depletes the immune system and makes the patients vulnerable to harmful infections. Thus, after the immune-depleting phase of chemotherapy, it becomes an absolute necessity to improve the patient's immune system. Therefore, it is a difficult challenge during the chemotherapy process to preserve a stable immune system and combat cancer successfully [6]. Cancer chemotherapy is usually administered on a cyclic basis. When an anti-cancer medicine is injected into the body, all harmless cells also get destroyed along with malignant cells. As a result, white blood cell counts decline to low rates, and life-threatening fever may occur [5]. Thus, control of the chemotherapy dosage becomes a very critical aspect in cancer chemotherapy design [7,8].
At the molecular level, cancer can be characterized as a genetic defect in the cell cycle. Gene therapy is a common form of immunotherapy that strengthens the body's immunity and aims to cure genetic conditions. By inserting a well-designed gene into the cells of the patients, correction can be carried out in the inborn inaccuracy of metabolism, inherited hereditary abnormality, etc.[9].
Ongoing research of clinical studies is now developing in cancer eradication policies by incorporating two or more drugs [10]. The application of chemotherapy and gene therapy is now in operation, which has demonstrated that this type of treatment reduces the primary tumor, avoids intra-peritoneal metastases, and restricts harmful side effects [11]. The application of TRAIL gene therapy and chemotherapy is also successful in the diagnosis of metastatic diseases [12]. Anti-cancer gene therapy under review is generally conducted in a two-phase cycle. The first step is a successful search for chemo-resistant cells during chemotherapy which results in an increased proportion of transfected cells. The population of the transfected cells must surpass that of the mutant cells to maintain the optimum relationship between the species necessary for the bystander effect. The second step consists of a negative selection step accomplished by ganciclovir injection. Such cells that are vulnerable to antiviral drug treatment through transfection or bystander effect will undergo activated apoptosis [13].
Mathematical modeling since a long time back has been used as a tool for finding out some solutions to the problems related to cancer and other dreaded diseases faced by the human population [14,15]. Kuznetsov et al. [16] proposed a model showing the reaction of the cytotoxic T lymphocyte to the development of the immunogenic tumor. Kirschner and Panetta [17] proposed a model to explore the effects of IL-2 therapy and ACI therapy on tumor-immune dynamics. Kolev et al. [18] presented a model that identified the early phases of a solid tumor or all phases of leukemia. A variety of clinical trials have been performed to investigate the impact of the immune system on the destruction of tumor cells in the body by inducing the host's immune response to destroy cancer cells [19,20]. As the tumor grows in the human body, the immune system seeks to recognize and destroy the tumor cells as soon as possible. In [21], Rihan et al. examined the interactions among tumor cells, immune-induced cells, and interleukin-2 (IL-2) cytokines. Very recently, in COVID-19 pandemic situation, Musa et al. [22] examined the dynamical feature of a deterministic COVID-19 model based on the data of Nigeria and also investigated the imapcts of awarness program and different hospitalization strategies in the society to effectively mitigate the epidemic. In the work [23], the authors formulated a model based on the data of Pakistan to investigate the role of quarantine and isolation in controlling the COVID-19 disease. Optimal control strategies have been proposed for a model in [24] to minimize the population number of infected and asymptotically infected people.
In the present day, researchers are interested in a combination of two or more therapies in the chemotherapeutic treatment protocols. Until now, several significant works have been carried out in the field of cancer chemotherapeutic modeling. De Pillis et al. [25] updated their previously proposed model [6] with the inclusion of NK cells, CD8+T cells, and IL-2 therapy. Their results revealed that while eliminating cancerous tissue in the presence of chemotherapy, immunotherapy is helpful for low immune efficacy patients. The effect of anti-angiogenic agents in controlling cancer with chemotherapy has been demonstrated in [26]. An appropriate optimal combination treatment of vaccine therapy and chemotherapy for controlling cancer dynamics has been presented in [27]. In consideration of radiotherapy as a treatment of cancer followed by chemotherapy, a periodic mathematical model has been proposed by Liu and Yang [28]. Guiraldello et al. [29] presented a mathematical model involving partial differential equations to show the behavior of tumor development in the presence of two chemotherapy protocols; Maximum Tolerated Dose (MTD) and metronomic, as well as two methods of drug delivery. They have also evaluated the effectiveness of both protocols. Pang et al. [30] explored the effect of a combination of immunotherapy and chemotherapy, single chemo, and single immunotherapy in their work. Rodrigues et al. [31] explored a model by considering chemo-immunotherapy as a treatment to reduce unwanted cytotoxic effects on immune cells of a cancer patient. In [32], the authors presented a model for the growth of the immune system during chemotherapy. Alqudah [33] introduced a new mathematical model for the treatment of cancer as a combination of chemotherapy and stem cell therapy. In 2013, Tsygvinsev et al. [34] proposed a mathematical model of gene therapy for cancer treatment by modifying an already investigated model [17]. We have considered a modified version of the model proposed by Tsygvintsev et al. [34] in which the authors studied the effects of gene therapy and immunotherapy. In contrast, in this paper we have introduced chemotherapy together with gene and immunotherapy as the treatment protocol.
Controlling drugs in the treatment of cancer patients is a big problem for researchers. Many researchers are working on optimal drug control for cancer treatment. Khajanchi and Ghosh [7] designed a model based on Kuznetsov et al. model [16] with two types of external treatments, one is ACI therapy for anti-tumor activity and another is IL-2 therapy for boosting the immune system to fight against tumor. Moreover, they have found the optimal combination treatment for tumor reduction. Sharma and Samanta [8] have carried out another optimal chemotherapeutic strategy for a tumor growth model and addressed that the administration of chemotherapy drug as control reduces the spread of the disease. Rihan et al. [35] established from their model that the performance of the combination therapy protocol of immuno-chemotherapy is better than the standard protocol of chemotherapy alone. d'Onofrio et al. [36] formulated a model for the optimal scheduling of angiogenic inhibitors in combination with a chemotherapeutic agent. In the work [37], the author explored the dynamical behavior of the glioma-immune interaction in conjunction with an optimally controlled immunotherapeutic drug ACI. By considering an abstract mathematical model of cancer chemotherapy, Leszczynski et al. [38] investigated an optimal control problem for a single drug remove and when various pharmacodynamic (PD) and pharmacokinetic (PK) models are included in the modeling. Recently, the authors of [39] designed an optimal model for chemotherapy treatment to find the best rate of drug injection during treatment. Najafi et al. [40] introduced an optimal control homotopy perturbation method to find better outcomes in drug controlling for therapeutic cancer model. Rihan et al. [41] studied an extended work of [17] to a delayed model of tumor-immune interactions and then find the optimal protocol of immuno-chemotherapy, which reduces the tumor load in a few months of therapy. In the work [42], the author performed a detailed analysis to find the optimal regimens of combined chemo-immunotherapy for a PKPD cancer evolution model. Das et al. [43] analyzed an optimal control problem of immuno-chemotherapeutic drugs for a delayed tumor-immune model. In this article, we propose a modified cancer gene therapy model following [34] in the presence of immunotherapy and chemotherapy. To control the immuno-chemo-drug toxicity effect on the patient, we also construct an optimal control problem for the proposed model which was not discussed in [34].
In section 2, we have described the model about which we have investigated in the subsequent sections.
2.
Model description
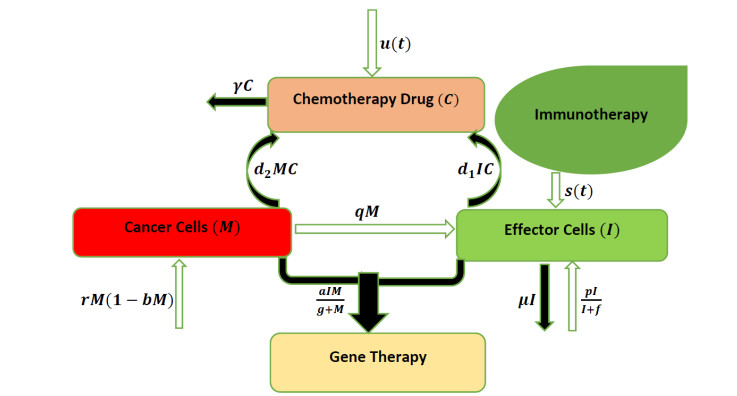
We already mentioned several research works to understand the effectiveness and side effects of chemotherapy and immunotherapy in cancer treatment. In work [34], the authors showed that high levels of immunotherapy and 'cancer clearance term' of gene therapy would be able to clear cancer optimally from patients' body. Lestari et al. [44] studied the local stability analysis of the proposed model in [34]. In [45], the authors estimated the external parameters of the model in [34] for which the growth of tumor cells remains under control. For further study on the applications of gene therapy in cancer treatment models, the authors would like to refer to the works [34,44] to the reader. In this work, we reconstruct the earlier proposed model [34] in combination with immuno-chemo-gene-therapy. The model is built based on interactions among tumor cells, effector immune cells, gene therapy, immunotherapy, and chemotherapeutic drugs. The assumptions imposed on the model are:
A1: Gene therapy detects how tumor cells are different from normal cells, and this can be described by the term qM with a fixed antigenicity q.
A2: Effector immune cells can proliferate themselves with proliferation rate p. However, effector immune cells also have a natural death rate μ.
A3: External source of immunotherapy s(t) (TIL-therapy) boosts the immune system, which is time-dependent.
A4: Cancer cells can grow logistically in the absence of immune cells and treatments.
A5: The interaction of effector cells and cancer cells during gene therapy is considered according to the Michaelis-Menten form −aIMg+M which is usually used for describing anti-tumor immune responses [17]. The term a represents the constant rate of cancer clearance during gene therapy.
A6: Chemotherapy can kill both the cell populations viz. cancer and effector immune cells with different constant rates.
The flowchart of the model is depicted in Figure 1.
Considering above mentioned assumptions and the flowchart, the model [34] can be reformulated as:
with initial conditions
The first equation represents the dynamics of the effector immune cells I(t). qM represents the cancer antigenicity during gene therapy, giving strong immunity to cancer. As the effector cells proliferate themselves, so it can be represented by the term pII+f. −μ represents the half-life of effector cells. The term s(t) is used for describing the dose of immunotherapy drug given, which boosts the immune system. −d1IC is the degradation of effector cells that get killed during chemotherapy.
The second equation describes the variability of the cancerous tumor cells M(t). The term rM(1−bM) represents the logistic growth of cancer cells. −aIMg+M describes the interaction between effector cells and cancer cells during gene therapy. The term −d2MC indicates the degradation of cancerous cells by chemotherapy.
The last equation is the continuous drug administration of chemotherapy, where u(t) represents the dose of the chemotherapeutic drug given, and γ is the per capita decay rate of the chemotherapeutic drug.
Due to bilogical meaning, all values of three state variables must be non-negative. In the following section, we will discuss the positiveness and boundedness of the solutions of the system (2.1).
3.
Basic characteristics of the solutions
In order to check the behavior of the solutions of the system (2.1), we have considered the dose of chemotherapeutic drug given u(t) as a constant with value u(t)=u0 and s(t)=s.
Theorem 3.1. Every solution of the system (2.1) with the non-neagtive initial conditions (2.2) are exists in IR3+, and are non-negative for all t≥0.
Proof. It is clear that the uniform continuity and locally Lipschitzian conditions hold for R.H.S of the system (2.1) on its domain. Hence, there exists an unique solution (I(t),M(t),C(t)) of (2.1) with initial conditions I(0)≥0, M(0)≥0, and C(0)≥0 on IR3+. Also, this unique solution is non-neagtive and it will be proved as follows:
We can write the system (2.1) as
Solving (3.1), we get
Therefore, the solution (I(t), M(t), C(t)) will be non-negative in IR3+ for all t≥0. This completes the proof.
Theorem 3.2. There exists bounded solutions for the model (2.1) subject to initial conditions I(0)≥0, M(0)≥0, and C(0)≥0.
Proof. From the second equation of system ({2.1}) and using the standard Kamke comparison theory [8] to it, we have
The third equation implies that
Now, using the bounds of M(t) (suppose supM(t)=Ms), the first equation implies that
By using the generalized Gronwall Lemma [35], we get
where, A is uniformly bounded. This completes the proof.
4.
Stability analysis
In this section, we will study the existence and stability behaviour of the system (2.1) at various equilibrium points. In order to investigate the dynamics of the system (2.1), we set u(t)=u0, s(t)=s, dIdt=0, dMdt=0, and dCdt=0. The equilibrium points of the system (2.1) are:
(1) The two equilibria E1(I1,0,u0γ) and E2(I2,0,u0γ), where cancerous tumor cells are not present, are termed as healthy equilibria. Here, I1 and I2 are the roots of the equation:
Solving above equation, we get the roots I1 and I2 as,
where
(2) The system exhibits the disease persistent equilibrium at E∗(I∗,M∗,u0γ), where both immune-effector cells and cancerous tumor cells will present. Here,
and
Now, let us study the existence and stability of two equilibria E1 and E2.
E1(I1,0,u0γ) exists only when I1>0 i.e., p+s+√(p+s−μf−d1fu0γ)2+4fs(μ+d1u0γ)>μf+d1fu0γ.
The variational matrix of system (2.1) at E1(I1,0,u0γ) is given by
The eigenvalues of V(E1) are: λ1,1=pf(I1+f)2−μ−d1u0γ, λ2,1=r−aI1g−d2u0γ, and λ3,1=−γ. Clearly, λ3,1<0. Now, E1 is stable if λ1,1<0 and λ2,1<0; this implies pf(I1+f)2−μ−d1u0γ<0 and r−aI1g−d2u0γ<0; which gives u0>γd1[pf(I1+f)2−μ] and r<aI1g+d2u0γ.
E2(I2,0,u0γ) exists only when I2>0 i.e., p+s>√(p+s−μf−d1fu0γ)2+4fs(μ+d1u0γ)+μf+d1fu0γ.
The variational matrix of the system (2.1) at E2(I2,0,u0γ) is given by
The eigenvalues of V(E2) are: λ1,2=pf(I2+f)2−μ−d1u0γ, λ2,2=r−aI2g−d2u0γ, and λ3,2=−γ. Clearly, λ3,2<0. Now, E2 is stable if λ1,2<0 and λ2,2<0; this implies pf(I2+f)2−μ−d1u0γ<0 and r−aI2g−d2u0γ<0; which gives u0>γd1[pf(I2+f)2−μ] and r<aI2g+d2u0γ. Thus, we have the following result.
Theorem 4.1. The healthy equilibrium E1 exists if
and it is locally asymptotically stable if
Other healthy equilibrium E2 exists if
and it is locally asymptotically stable if
Next, we will also study the existence and stability behaviour at the disease persistent equilibria E∗.
E∗(I∗,M∗,u0γ) exists only when I∗>0 and M∗>0 i.e, r(1−bM)>d2u0γ and μI∗+d1I∗u0γ>s+pI∗f+I∗.
The variational matrix of the system (2.1) at E∗(I∗,M∗,u0γ) is given by
One eigenvalue of V(E∗) is −γ and the other two eigenvalues of the matrix can be calculated from the follwing equation
where
Since −γ<0, hence, the equilibrium E∗ will be asymptotically stable if D1>0 and D2>0. Hence, we get the following result.
Theorem 4.2. The disease persistent equilibrium E∗ exists if
and it is locally asymptotically stable if
5.
The control problem
This section is related to the study of the control problem related to our proposed model (2.1), when we administer immunotherapy and chemotherapy treatments over a fixed period. For the biomedical perspective, we use the concept of optimal control for the model. This addresses how the combination of chemo-gene-immunotherapy may be an efficient treatment to assist the patient fighting against cancer.
To construct and analyze the optimal control problem for our proposed model, we follow the previous works [7,8,43]. As a higher dose of immunotherapy and chemotherapy causes many side effects, the total amount of immuno-chemotherapy agents must be minimized to minimize the tumor size. For that, we assume the immunotherapy and chemotherapeutic drugs are given as the functions s(t) and u(t), which are time-dependent. For the control variables s(t) and u(t), we consider quadratic controls to reflect the extremity of the imposed immunotherapy and chemotherapeutic drugs' side effects. Therefore, the objective functional which is to be minimized is defined as:
where the constants ξ1,ξ2, and ξ3 represent the weight factors of the respective terms which are used for balancing the size of the terms. The first term of the integrand signifies the number of cancerous cells while the second and third reflect the effectiveness of the drugs. Here, we establish an optimal control (s∗,u∗) such that
where Ω={(s,u):sanduare measurable, 50≤s≤100,0≤u≤1,andt∈[0,tf]} is the admissible control set. Hence, the problem with the control (s(t),u(t)) becomes
with initial conditions,
and the objective functional
5.1. The existence of optimal control
In this subsection, we will discuss the existence of the optimal control of our system (5.3). The solutions of the system (5.3) are bounded in a finite time interval. For proving this, we assume that
where →W=(IMC)T. Using the boundedness of the solutions, we get
As the above system is linear having bounded coefficients in a finite time interval, hence, we conclude that the solutions of the system (5.3) are bounded. Using the theorem proposed by Lukes [46], we get the admissible control class and the corresponding state equations with initial conditions (5.4) are found to be non-empty. Moreover, by deffinition of the set Ω, it is clear that the control set Ω is convex and closed. Since the state solutions are bounded, hence, the continuity of R.H.S of the state system (5.3) holds and is bounded above by a sum of the bounded control and state.
If π(s,u) denotes the integrand of Π(s,u), to prove the convexity of π(s,u) on Ω, we need to show
where v=(s1,u1) and w=(s2,u2) are two distinct elements of Ω and 0≤ϕ≤1. Now
which implies that the integrand of π(s,u) is convex on Ω. Again,
where η1=min{ξ22,ξ32}. Therefore, the integrand Π(s,u) is bounded below by η1(s2(t)+u2(t))−η2. Hence, there exists an optimal control (s∗,u∗) for which Π(s,u) is minimized. From the above analysis, we established the following theorem.
Theorem 5.1. There exists an optimal control (s∗,u∗) for a given objective functional
such that Π(s∗,u∗)=min{Π(s,u):(s,u)∈Ω}, where Ω={(s,u):s and uare measurable,50≤s(t)≤100,0≤u(t)≤1, and t∈[0,tf]} subject to the system (5.3) with initial conditions (5.4).
5.2. Characterization of optimal control
Pontryagins Maximum Principle [47] is invoked on the system (5.3) to derive the conditions for optimal control. For the system (5.3) the Hamiltonian is defined as follows:
where θ1,θ2, and θ3 are the adjoint functions which are to be determined.
Using Pontryagins Maximum Principle [47], the adjoint system and the transversality conditions can be obtained as follows:
The transversality conditions are
From the optimality conditions of sandu, we have
Using the bounds of control s(t)andu(t), we get
Hence, from the above discussion, we get the following result:
Theorem 5.2. For a given optimal control (s∗,u∗) with the corresponding state variables (I∗(t),M∗(t),C∗(t)), there exist co-states or adjoint variables θ1, θ2, and θ3 satisfying the following system:
with transversality conditions
Moreover,
In the next section, we have solved our uncontrolled system (2.1) by setting s(t)=s and u(t)=u0, and controlled system (5.3) alongwith adjoint system (5.17) both numerically and graphically.
6.
Numerical simulation
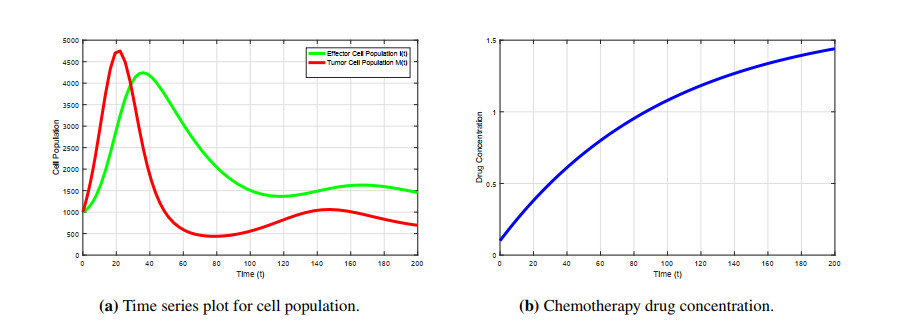
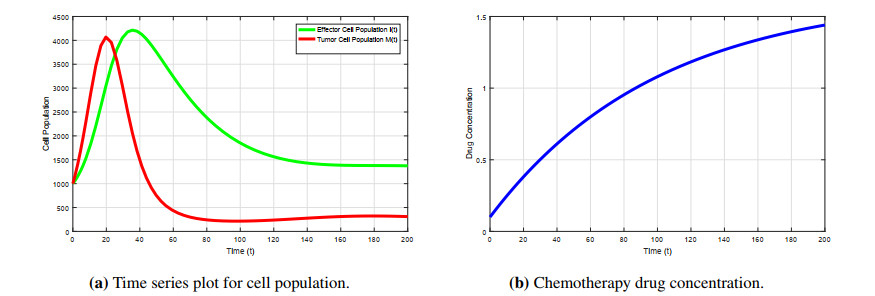
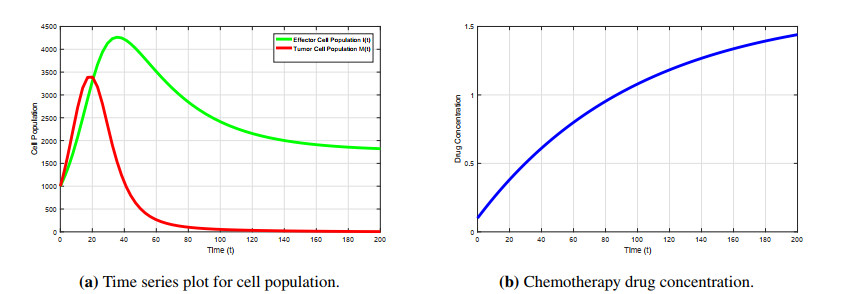
The following simulations have been done using the parameters of Table 1. For checking local behaviour of the system (2.1), we set the external immunotherapy s(t) as the key parameter and u(t)=u0. The time series diagrams of effector cells, tumor cells, and without control of drug administration for different values of s(t) but with the same cancer clearance term a have been presented in Figures 2–4. In Figure 2, it is seen that while the cancer clearance term is a=5 (1/time) during gene therapy with external immunotherapy s(t)=1 (cells/time), both effector and tumor cells go in tandem in the presence of chemotherapy. In this situation, there are two biologically feasible solutions E1(37.48,0,1.65) and E∗(965.34,556.72,1.65) (assuming u0=0.01650) having unstable behavior. In our second observation in Figure 3 with a=5 (1/time) and immunotherapy s(t)=25 (cells/time), the system has two feasible equilibrium points E2(837.483,0,1.65) and E∗(960.709,73.935,1.65) (assuming u0=0.01650) which are again found to be unstable. In Figure 4, we have observed that with external immunity strength s(t)=53 (cells/time), the cancer clearance term of gene therapy a=5 (1/time), and in the presence of chemo-drug, the tumor cell goes to zero rather than oscillating about zero in time around t=120 and the effector cells converge to a stable position. This scenario implies that there are only one biologically valid equilibrium E2(1770.82,0,1.65) (assuming u0=0.01650), which is locally stable in nature.
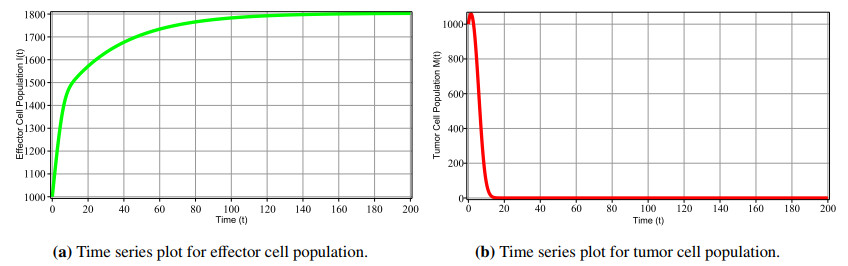
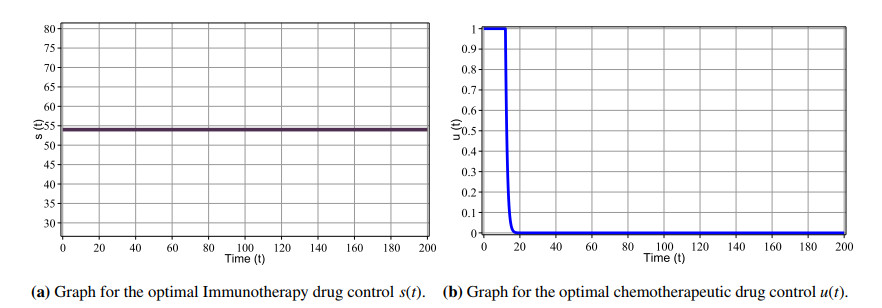
The optimal system (5.3) associated with the adjoint system (5.17) and the separated boundary conditions at time t=0 and t=tf are solved. Forward method is used to solve the original optimal system (5.3) and the backward method for the respective adjoint system (5.17) with tf=200. Here, we consider the treatment parameter a=5 and the drug administration s(t) and u(t) which will be controlled. As the variables associated with the optimal system (5.3) and in the objective functional (5.1) have different scales, hence, to balance the objective functional, we have chosen the weight constants ξ1=5, ξ2=10, and ξ3=10 in (5.1). In Figure 5(a), (b), we have presented the time series plots of effector cells and tumor cells with drug control. We have seen that the tumor cells vanish around time 15<tf<20. From Figure 6(a), it can be observed that the optimal drug dose for immunotherapy is s(t)=53 (cells/time) for which immune cell population becomes stable at a sufficient level and tumor cell vanishes. Figure 6(b) shows that the chemo-drug concentration reduces gradually depending upon the size of the tumor and hence it also goes to zero as the tumor vanishes from the body.
7.
Conclusions
We have developed an ODE mathematical model for tumor growth under the action of effector immune cells in the presence of gene therapy, immunotherapy and chemotherapy. We established the basic characteristics of the dependent variables of the model. We presented the stability analysis of the system, revealing the conditions that must hold well for the cure equilibrium to be attained. For the numerical solution, we set up s(t) as the key parameter. We investigated the dynamics of the model for the values (i) s(t)=1 (cells/time), (ii) s(t)=25 (cells/time), and (iii) s(t)=53 (cells/time), respectively. From the numerical simulation, it can be concluded that for the value of immunotherapy term s(t)=53 (cells/time), in the presence of gene and chemotherapy, tumor cells may eradicate from the body. In [34], the authors found the values of treatment term for the two cases:
Case (i): s(t)=100 and a(t)=2 for tumor clearence at a slower rate (where global stability conditions of the tumor-free state are not satisified).
Case (ii): s(t)=764.5072 and a(t)=38.0040 for tumor clearence at a faster rate (where global stability conditions of the tumor-free state are satisified).
However, our results reveal that when chemotherapy is applied, the patient requires less amount of external source of immunotherapy to fight against cancer. This conclusion can be drawn by comparing our results with those of [34].
We also have constructed an optimal control problem associated with the system to minimize the tumor cell population, immunotherapy and the chemotherapeutic drug within a finite time interval [0,200]. According to our results, the tumor cells can be eliminated from the body in a shorter period in the presence of chemo-immuno-gene therapy with the control of immuno-chemotherapy drug parameter s(t) and u(t). From optimal control problem, it can be also verified that the optimum amount of immunotherapy for which tumor is eradicated is 53 (cells/time). Our model is probably one of the very few models in which gene therapy is combined with chemo-immunotherapy for finding optimal cancer treatment. Also, our discussion and results are on the basis of a modified mathematical model and hence it is a theoretical one. The results of the work can be a guiding factor for clinicians and the usefulness of our theoretical prediction will depend on the practical results found by the experiment of the clinicians.
Numerical results of our paper are dervied using the inbuilt functions of MATLAB as we are more interested in discussing the qualitative dynamical behaviours of the considered model rather than the precision, rate of convergence etc. of the derived numerical solutions. Researchers who are interested in those issues are reffered to [48,49,50]. Qureshi and Yusuf [48] proposed a third order convergence numerical solver for continuous dynamical systems. The authors performed the error analysis of the proposed solver and found to contain the smallest errors when it is compared with two well-known solvers (Heun and RK3HM) having the same order of convergence. Odibat and Baleanu [49] derived a generalized Caputo-type fractional derivative. In addition to generalised Caputo-type fractional derivatives, they successfully implemented the adaptive P-C algorithm for finding numerical solution of some fractional order dynamical systems. In the work [50], the authors applied Mohand integral transform for finding the exact solutions of fractional-order ordinary differential equations under the Caputo type operator. Upon comparison, the obtained results were in agreement with results produced by other existing well-known integral transforms. Our future work is to see the more realistic scenarios using the fractional derivative to the model and investigate the related control problem. Interested reader may also see the references [1,2] for finding various treatment combinations along with optimal immunotherapy.
Conflict of interest
The authors declare that they have no competing interests.









 DownLoad:
DownLoad: