A new method based on semi-tensor product of matrices for solving reduced biquaternion matrix equation $\sum\limits_{p = 1}^l A_pXB_p = C$ and its application in color image restoration

1.   Introduction

In 1843, Irish mathematician Hamilton proposed the concept of quaternion, which is one of his greatest contributions to mathematical science. This discovery expanded the complex number field to higher dimensional space. Quaternion has been widely used in many fields, such as color image processing, modern physics, geostatics and so on ^[1,2,3,4]. However, processing some complex discrete-time signals requires some complex number systems of higher order. As a generalization of complex numbers, quaternion is easy to be thought of. Because of its non-commutative structure, quaternion is not suitable for digital signal processing. To solve this problem, Sch$\ddot{u}$tte and Wenzel introduced the reduced biquaternion and proposed their applications for the implementation of a digital filter in 1990 ^[5]. Reduced biquaternion is a kind of commutative quaternion. Using commutativity, reduced biquaternion and reduced biquaternion matrix have great achievements in many practical problems. For example, ^[6] applied reduced biquaternion in digital signal and image processing; ^[7] investigated two types of multistate Hopfield neural networks based on reduced biquaternion; ^[8] defined the reduced biquaternion canonical transform that can be used in color image processing; ^[9] proposed an algorithm for computing eigenvalues, eigenvectors, and singular value decomposition of reduced biquaternion matrices, and applied it in color image processing.

Matrix equation is an important branch of matrix theory, and many engineering application problems are modeled as matrix equation problems ^[10]. A linear matrix equation plays an important role in stability analysis of linear dynamic systems and theoretical development of nonlinear systems. For example, the Sylvester matrix equation is widely used in control theory ^[11,12], model reduction ^[13], image processing ^[14] and so on. The Lyapunov matrix equation is closely related to the $H_2$ norm of discrete-time linear systems ^[15], and plays an important role in studying the stability and accurate observability of the systems ^[16]. With the applications of reduced biquaternion and reduced biquaternion matrix becoming more and more extensive, many scholars are more and more interested in solving reduced biquaternion matrix equations. ^[17] studied the minimal norm least squares solution of the reduced biquaternion matrix equation $AX = B$ using $e_1-e_2$ representation, and applied it to color image restoration; ^[18] studied Hermitian solution of reduced biquaternion matrix equation $(AXB, CXD) = (E, G)$ by complex representation; ^[19] proposed the real vector representation method of reduced biquaternion using the semi-tensor product of real matrices to solve the least squares (anti)-Hermitian solution of reduced biquaternion matrix equation $\sum\limits_{i = 1}^k A_iXB_i = C$. In this paper, we will also use semi-tensor product as a basic tool to study matrix equation problems.

The semi-tensor product of real matrices was proposed by Cheng ^[20], which is a generalization of ordinary matrix multiplication and has quasi-commutativity under certain conditions. In this paper, we extend the semi-tensor product of real matrices to reduced biquaternion matrices, and then some new conclusions of reduced biquaternion matrix under vector operator are proposed by using semi-tensor product of reduced biquaternion matrices. Using these new conclusions, we study the reduced biquaternion matrix equation

Some contributions are summarized as follows:

1. Semi-tensor product of real matrices is generalized to reduced biquaternion matrices, and then some new results of reduced biquaternion matrices under vector operator are proposed, so that the reduced biquaternion matrix equation is directly transformed into reduced biquaternion linear equations.

2. Inspired by the $\mathcal{H}$-representation method, we define the $\mathcal{GH}$-representation method to eliminate redundant elements in reduced biquaternion matrices with special structure, so as to improve operation efficiency. We give the $\mathcal{GH}$-representation of anti-Hermitian matrix, Skew-Persymmetric matrix and Skew-Bisymmetric matrix, respectively.

3. Using semi-tensor product of matrices and the structure matrix of multiplication of reduced biquaternion, a more widely defined complex representation matrix of reduced biquaternion matrix is defined, which is called $\mathcal{L}_\mathcal{C}$-representation.

4. Compared with the real vector representation method in ^[19], the method proposed in this paper is superior in time. The method which we proposed is applied to color image restoration.

The remainder of this paper is organized as follows: Section 2 introduces the basic knowledge of reduced biquaternion, reduced biquaternion matrix and semi-tensor product of the reduced biquaternion matrices. Some new results are stated and proved in Section 3, including the vector operator of reduced biquaternion matrix, $\mathcal{L}_\mathcal{C}$-representation and $\mathcal{GH}$-representation; Section 4 gives the expression of the least squares solution of Problems 1, 2 and 3, the necessary and sufficient conditions for the compatibility and the expression of general solutions are obtained in corollary; In Section 5, corresponding algorithms are given, the effectiveness of the algorithms is verified by the corresponding numerical examples and a comparison between the method in this paper and the existed is made; Section 6 applies the proposed method to color image restoration; Section 7 summarizes the content of this paper.

Notations: $R/C/Q_{RB}$ represent the set of real number/complex number/reduced biquaternion, respectively. $R^n/C^n$ represent the set of all real/complex column vectors with order $n$, respectively. $R^{m\times n}/C^{m\times n}/Q_{RB}^{m\times n}$ represent the set of all $m\times n$ real matrices/complex matrices/reduced biquaternion matrices, respectively. $\bar{A}/A^T/A^H/A^\dagger$ represent the conjugate/the transpose/the conjugate transpose/Moore-Penrose inverse of matrix $A$, respectively. $\mathrm{Re}(A)$ and $\mathrm{Im}(A)$ represent the real and imaginary parts of matrix $A$, respectively. $\bar{a}_{ij}$ represents the conjugate of $a_{ij}$. $\delta_n^i$ is the $i$th column of identity matrix $I_n$. $\otimes$ represents the Kronecker product of matrices. $\ltimes/ \rtimes$ represent left semi-tensor product of matrices and right semi-tensor product of matrices, respectively. $\left \|\cdot\right \|_F$ represents the Frobenius norm of a matrix or Eucliden norm of a vector.

2.   Preliminaries

In this section, we give some necessary preliminaries, which will be used throughout this paper.

2.1.   Reduced biquaternion and reduced biquaternion matrix

Definition 2.1. ^[6] The set of reduced biquaternion is expressed as

where $\mathbf{i, j, k}$ satisfy

A reduced biquaternion $q$ can be uniquely represented as $q = q_1+q_2\mathbf{j}$, where $q_1 = q_{11}+q_{12}\mathbf{i}, \ q_2 = q_{13}+q_{14}\mathbf{i}\in C.$ The modulus of $q$ is defined as $|q| = \sqrt {\mid q_{11}\mid^2+\mid q_{12}\mid^2+\mid q_{13}\mid^2+\mid q_{14}\mid^2}.$ Similarly, a reduced biquaternion matrix $A = A_{11}+A_{12}\mathbf{i}+A_{13}\mathbf{j}+A_{14}\mathbf{k}$ can also be uniquely represented as $A = A_1+A_2\mathbf{j}$, where $A_1 = A_{11}+A_{12}\mathbf{i}, \ A_2 = A_{13}+A_{14}\mathbf{i}\in C^{m\times n}$. The norm of $A$ is defined as $\| A\|_{(F)} = \sqrt {\| A_{11}\|_F^2+\| A_{12}\|_F^2+\| A_{13}\|_F^2+\| A_{14}\|_F^2}$.

2.2.   Semi-tensor product of reduced biquaternion matrices

For semi-tensor product of real matrices, please refer to ^[21,22] for details. Now, we generalize semi-tensor product of real matrices to reduced biquaternion matrices.

Definition 2.2. Suppose $A\in Q_{RB}^{m\times n}, \ B\in Q_{RB}^{p\times q}$, left semi-tensor product of $A$ and $B$ is defined as

and right semi-tensor product of $A$ and $B$ is defined as

where $t = lcm(n, p)$ is the least common multiple of $n$ and $p$.

Remark 2.1. Left semi-tensor product of reduced biquaternion matrices and right semi-tensor product of reduced biquaternion matrices are collectively called semi-tensor product of reduced biquaternion matrices. When $n = p$, semi-tensor product of reduced biquaternion matrices is ordinarily reduced biquaternion matrix multiplication.

Example 2.1. Let $A = (1+\mathbf{i}\quad 2-\mathbf{j}\quad 3\mathbf{k}\quad \mathbf{i}+\mathbf{j}), B = (\mathbf{i}\quad \mathbf{k})^T$. Then

It can be seen from Example 2.1 that left semi-tensor product of reduced biquaternion matrices satisfies the multiplication of block matrices while right semi-tensor product of reduced biquaternion matrices does not. This is also the biggest difference between these two matrix multiplications, which makes the application range of left semi-tensor product of reduced biquaternion matrices wider than that of right semi-tensor product of reduced biquaternion matrices.

Since the left semi-tensor product of reduced biquaternion matrices is used more widely, the semi-tensor product of reduced biquaternion matrices mentioned below refers to left semi-tensor product of reduced biquaternion matrices.

Definition 2.3. Suppose $A = (a_{ij})\in Q_{RB}^{m\times n}$, denote

Theorem 2.1. Suppose $A = (a_{ij})\in Q_{RB}^{m\times n}, B = (b_{ij})\in Q_{RB}^{s\times t}$, and for any positive integer $p$, then

(1) $W_{[m, n]}V_r(A) = V_c(A), \quad W_{[n, m]}V_c(A) = V_r(A),$

(2) $W_{[s, p]}\ltimes B\ltimes W_{[p, t]}\ltimes A = (I_p \otimes B)\ltimes A,$

where $W_{[m, n]} = (I_n\otimes\delta_m^1, I_n\otimes\delta_m^2, \cdots, I_n\otimes\delta_m^m)$ is called swap matrix.

The above equations are easily obtained by direct calculation.

2.3.   Problem formulation

First, several kinds of reduced biquaternion matrices with symmetric structure are introduced.

Definition 2.4. Let $A = (a_{ij})\in {Q}_{RB}^{n\times n}$, denote $A^H = (\bar{a}_{ji})\in {Q}_{RB}^{n\times n}$, $A^{(H)} = (\bar{a}_{n-j+1, n-i+1})\in{Q}_{RB}^{n\times n}$, and $A^{(H)} = V_n A^H V_n$. $V_n$ has the following form, $V_n = \left(\begin{matrix} & & & 1\\ & & 1 & \\ & {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} & & \\ 1 & & & \end{matrix} \right)$, in which the other elements are zero.

(1) $A\in Q_{RB}^{n\times n}$ is called anti-Hermitian matrix if $A = -A^H$, denoted by $AH_{RB}^{n\times n}$.

(2) $A\in Q_{RB}^{n\times n}$ is called Skew-Persymmetric matrix if $A = -A^{(H)}$, denoted by $AP_{RB}^{n\times n}$.

(3) $A\in Q_{RB}^{n\times n}$ is called Skew-Bisymmetric matrix if $a_{ij} = a_{n-i+1, n-j+1} = -\bar{a}_{ji}$, denoted by $AB_{RB}^{n\times n}$.

For the above-mentioned special symmetric matrices, this paper studies the following problems.

Problem 1 Suppose $A_p\in{Q}_{RB}^{m\times n}, B_p\in{Q}_{RB}^{n\times q} (p = 1, \cdots, l), C\in{Q}_{RB}^{m\times q}$, and

find out $X_{AH}\in S_{AH}$ such that

Problem 2 Suppose $A_p\in{Q}_{RB}^{m\times n}, \ B_p\in{Q}_{RB}^{n\times q}\ (p = 1, \cdots, l), \ C\in{Q}_{RB}^{m\times q}$, and

find out $X_{AP}\in S_{AP}$ such that

Problem 3 Suppose $A_p\in{Q}_{RB}^{m\times n}, \ B_p\in{Q}_{RB}^{n\times q}\ (p = 1, \cdots, l), \ C\in{Q}_{RB}^{m\times q}$, and

find out $X_{AB}\in S_{AB}$ such that

3.   Some new properties of vector operators, $\mathcal{L}_\mathcal{C}$-representation and $\mathcal{GH}$-representation

3.1.   The properties of vector operator of reduced biquaternion matrix

Using the semi-tensor product of reduced biquaternion matrices, we can obtain some new properties of vector operators.

Theorem 3.1. Suppose $A\in Q_{RB}^{m\times n}, \ X\in Q_{RB}^{n\times q}, \ Y\in Q_{RB}^{p\times m}$, then

(1) $V_c(AX) = A\rtimes V_c(X), \ V_r(AX) = A\ltimes V_r(X);$

(2) $V_c(YA) = A^T\ltimes V_c(Y), \ V_r(YA) = A^T\rtimes V_r(Y).$

Proof. (1) For the equation $V_r(AX) = A\ltimes V_r(X)$, let $C = AX$, $a_i\ (i = 1, 2, \cdots, m)$ is the $i$-th row of $A$, $x_k\ (k = 1, 2, \cdots, n)$ is the $k$-th row of $X$, $c_i\ (i = 1, 2, \cdots, m)$ is the $i$-th row of $C$, then the $i$-th block of $A\ltimes V_r(X)$ is

therefore $V_r(AX) = A\ltimes V_r(X)$.

Applying Theorem 2.1, we have

(2) By $V_r(AX) = A\ltimes V_r(X)$, then

Applying Theorem 2.1, we have

Yuan et al. ^[18] pointed out that $V_c(ABC) = (C^T\otimes A)V_c(B)$ cannot hold in the reduced biquaternion algebra. However, the new conclusion of the reduced biquaternion matrix under the vector operator obtained using the semi-tensor product of reduced biquaternion matrices can prove that the conclusion in ^[18] is wrong.

Proposition 3.1. Let $A\in Q_{RB}^{m\times n}, \ B\in Q_{RB}^{n\times n}, \ C\in Q_{RB}^{n\times p}$, then

Proof: Using Theorem 3.1, then

3.2.   $\mathcal{L}_{\mathcal{C}}$-representation of reduced biquaternion matrix

Using semi-tensor product of matrices, we can find the isomorphism between the set of $m\times n$ reduced biquaternion matrices and the corresponding set of $2m\times 2n$ complex matrices, and give the computable algebraic expression of this isomorphism.

Definition 3.1. ^[22] Let $W_i(i = 0, 1, \cdots, n)$ be vector spaces. The mapping $F: \prod_{i = 1}^n W_i\rightarrow W_0$ is called a multilinear mapping, if for any $1\leq i\leq n, \alpha, \beta \in R,$

in which $x_i, y_i\in W_i, (1\leq i\leq n)$. If $dim(W_i) = k_i, (i = 0, 1, \cdots, n),$ and $(\delta_{k_i}^1, \delta_{k_i}^2, \cdots, \delta_{k_i}^{k_i})$ is the basis of $W_i$. Denote

then

which is called structure constant set of $F$. Arranging these structure constants in the following form

$M_F$ is called structure matrix of $F$.

Let $1\sim \delta_2^1, \mathbf{j}\sim \delta_2^2$ and define symbol $\times$ to represent the reduced biquaternion multiplication. The multiplication rule of the basis satisfies Definition 2.1. According to Definition 3.1, we can obtain the structure matrix of reduced biquaternion multiplication, denoted by $M$ as

Example 3.1. Suppose $a, b\in Q_{RB}$, it can also be representd as $a = a_1+a_2\mathbf{j}\sim \left(\begin{matrix}a_1\\a_2\end{matrix}\right), b = b_1+b_2\mathbf{j}\sim \left(\begin{matrix}b_1\\b_2\end{matrix}\right)$, where $a_1 = a_{11}+a_{12}\mathbf{i}, \ a_2 = a_{21}+a_{22}\mathbf{i}, \ b_1 = b_{11}+b_{12}\mathbf{i}, \ b_2 = b_{21}+b_{22}\mathbf{i}\in C$. Consider the multiplication $a\times b$ on $Q_{RB}$, we can obtain

Suppose $A = A_1+A_2\mathbf{j}$, we denote

Definition 3.2. Let $A = A_1+A_2\mathbf{j}\in Q_{RB}^{m\times n}$, where $A_1, A_2\in C^{m\times n}$, define a mapping from $Q_{RB}^{m\times n}$ to subspace of $C^{2m\times 2n}$

is called the complex matrix representation of reduced biquaternion matrix, if for $A\in Q_{RB}^{m\times n}, B\in Q_{RB}^{n\times p}$, $\chi$ satisfies

(1) $\chi(AB) = \chi(A)\chi(B),$

(2) $\chi^c(AB) = \chi(A)\chi^c(B),$

where $\chi^c(A) = \chi(A)\ltimes \delta_2^1$, then $\chi$ is called $\mathcal{L}_\mathcal{C}$-representation of reduced biquaternion matrix.

Next, using the semi-tensor product of reduced biquaternion matrices, we give the algebraic form of $\mathcal{L}_\mathcal{C}$-representation of reduced biquaternion matrix.

Proposition 3.2. Let $A\in Q_{RB}^{m\times n}, \ B\in Q_{RB}^{n\times p}$, then $\chi$ is $\mathcal{L}_\mathcal{C}$-representation of reduced biquaternion matrix if and only if

(1) $(M\otimes I_m)(I_2\otimes (\dot{E}_2\ltimes \overleftarrow{AB}))$

(2) $(M\otimes I_m)(\delta_2^1\otimes (\dot{E}_2\ltimes \overleftarrow{AB}))$

Proof. The proof is straightforward. For instance, we can prove each equation in Proposition 3.2 is equivalent to each equation in Dedinition 3.2. Consider the first one. Using the $\mathcal{L}_\mathcal{C}$-representation of reduced biquaternion matrix, we know $\chi(AB) = \chi(A)\chi(B)$ holds if and only if

which is equivalent to

Remark 3.1. The $\mathcal{L}_\mathcal{C}$-representation of reduced biquaternion matrix is not unique in sense that the structure matrix may be different due to the different vectorization choices of $1$ and $\mathbf{j}$ or the choices of $\dot{E}_2.$

Let us take a simple example to illustrate Remark 3.1.

Example 3.2. Fix $M = \left(\begin{matrix}1 & 0 & 0 & 1\\0 & 1 & 1 & 0\end{matrix}\right)$, if we select $\dot{E}_2 = \left(\begin{matrix}1 & 0\\0 & 1\end{matrix}\right)$, we can obtain

if we select $\dot{E}_2 = \left(\begin{matrix}1 & 0\\0 & -1\end{matrix}\right)$, we can obtain

Test the equations in Proposition 3.2 for $\chi^1(A)$ and $\chi^2(A)$, respectively, it can be found that $\chi^1$ and $\chi^2$ are all $\mathcal{L}_\mathcal{C}$-representation.

Remark 3.2. For convenience, $\chi$ used below is $\chi^1$.

3.3.   $\mathcal{G}{\mathcal{H}}$-representation of reduced biquaternion matrix with special structures

The $\mathcal{GH}$-representation method can represent a matrix with a special structure by its independent elements. This method is a generalization of the $\mathcal{H}$-representation method proposed by Zhang ^[23].

Definition 3.3. ^[23] Let $L\subset R^{n\times n}$ be a $p$-dimensional matrix subspace, where $(p\leq n^2)$, $e_1, \ e_2, \cdots, e_p$ are its basis, and define $H = [V_c(e_1), \ V_c(e_2), \cdots, V_c(e_p)]$, $\forall X\in L$, there exists unique $l_1, \ l_2, \cdots, l_p\in R$, such that $X = \sum\limits_{i = 1}^pl_ie_i$. There is a mapping $\varphi$: $X\in L\mapsto V_c(X)$, and

where $\widetilde X = [l_1, \ l_2, \cdots, l_p]^T\in R^p$, $H\widetilde X$ is called the $\mathcal{H}$-representation of $\varphi(X)$, $H$ is called the $\mathcal{H}$-representation matrix of $\varphi(X)$.

The $\mathcal{H}$-representation method can transform a matrix-valued equation into a standard vector-valued equation with independent coordinates. ^[23] used the $\mathcal{H}$-representation method to research the properties of a class of generalized Lyapunov equations, observability of linear stochastic time-varying systems, stochastic stability and stabilization. Reduced biquaternion matrix has one real part and three imaginary parts. The real matrix of different parts may not have the same structural characteristics, so the $\mathcal{H}$-representation method cannot be directly applied. We extend it to the $\mathcal{GH}$-representation method suitable for reduced biquaternion matrix.

Definition 3.4. Consider a reduced biquaternion matrices subspace $L\subset Q_{RB}^{n\times n}$. For each $X = X_{11}+X_{12}\mathbf{i}+X_{13}\mathbf{j}+X_{14}\mathbf{k}\in L$, let $\overrightarrow{X} = [X_{11}\ X_{12}\ X_{13}\ X_{14}]$, if we express

where $\bar{\bar{X}} = \left(\begin{matrix}\widetilde{X_{11}}\\\widetilde{X_{12}}\\\widetilde{X_{13}}\\\widetilde{X_{14}}\end{matrix}\right)$, then $G_H\bar{\bar{X}}$ is called the $\mathcal{GH}$-representation of $\phi(X)$, and $G_H$ is called the $\mathcal{GH}$-representation matrix of $\phi(X),$ where $G_H = \left(\begin{matrix}H_{X_1} & 0 & 0 & 0\\0&H_{X_2} & 0 & 0\\0 & 0&H_{X_3} & 0\\0 & 0 & 0&H_{X_4}\end{matrix}\right)$, $H_{X_i}$ represents the $\mathcal{H}$-representation matrix of real matrix $X_i, \ i = 1, 2, 3, 4.$

It is easy to see that the key to construct $\mathcal{GH}$-representation matrix is to find the $\mathcal{H}$-representation matrix of real matrix corresponding to four parts of reduced biquaternion matrix. Next, we give the $\mathcal{GH}$-representation matrix of anti-Hermitian matrix, Skew-Persymmetric matrix and Skew-Bisymmetric matrix, respectively.

First we consider anti-Hermitian matrix.

When $X = X_{11}+X_{12}\mathbf{i}+X_{13}\mathbf{j}+X_{14}\mathbf{k}\in AH_{RB}^{n\times n}$, $X_{11}$ is anti-symmetric matrix and $X_{12}, X_{13}, X_{14}$ are symmetric matrices. Denote $S_R^{n\times n}$ be the set of symmetric matrices and $AS_R^{n\times n}$ be the set of anti-symmetric matrices. For $L = S_R^{n\times n}$, we select a set of basis

where $E_{ij} = (e_{ij})_{n\times n}, \ e_{ij} = e_{ji} = 1$, the other elements are zeros.

Similarly, for $L = AS_R^{n\times n}$, we select a set of basis

where $F_{ij} = (f_{ij})_{n\times n}, \ f_{ij} = -f_{ji} = 1$, the other elements are zeros.

After the basis is determined above, for $L = S_R^{n\times n}/ AS_R^{n\times n}$, we have

$H_{S}/H_{AS}$ is used to represent the $\mathcal{H}$-representation matrix of $L = S_R^{n\times n}/ AS_R^{n\times n}$, respectively.

Theorem 3.2. For $X = X_{11}+X_{12}\mathbf{i}+X_{13}\mathbf{j}+X_{14}\mathbf{k}\in AH_{RB}^{n\times n}$, the $\mathcal{GH}$-representation of $X$ is expressed as

Similarly, we use the above idea to consider the other two classes of special matrices.

$P_R^{n\times n}$ represents the set of real matrices whose elements satisfy $a_{ij} = a_{n-j+1, n-i+1}$. $AP_R^{n\times n}$ represents the set of real matrices whose elements satisfy $a_{ij} = -a_{n-j+1, n-i+1}$. When $X = X_{11}+X_{12}\mathbf{i}+X_{13}\mathbf{j}+X_{14}\mathbf{k}\in AP_{RB}^{n\times n}$, $X_{11}\in AP_R^{n\times n}, X_{12}, X_{13}, X_{14}\in P_R^{n\times n}.$ For $L = P_R^{n\times n}$, we can select a set of basis

where $M_{ij} = (m_{ij})_{n\times n}, \ m_{ij} = m_{n+1-j, n+1-i} = 1$, the other elements are zeros.

For $L = AP_R^{n\times n}$, we take a set of basis

where $Z_{ij} = (z_{ij})_{n\times n}, \ z_{ij} = -z_{n+1-j, n+1-i} = 1$, the other elements are zeros.

After the basis is determined above, for $L = P_R^{n\times n}/AP_R^{n\times n}$, we have

In the same way, we denote the $\mathcal{H}$-representation matrix corresponding to $L = P_R^{n\times n}$ by $H_P$ and $H_{AP}$ refers to $\mathcal{H}$-representation matrix corresponding to $L = AP_R^{n\times n}$.

Theorem 3.3. For $X = X_{11}+X_{12}\mathbf{i}+X_{13}\mathbf{j}+X_{14}\mathbf{k}\in AP_{RB}^{n\times n}$, the $\mathcal{GH}$-representation of $X$ is expressed as

$B_R^{n\times n}$ represents the set of real matrices whose elements satisfy $a_{ij} = a_{n-i+1, n-j+1} = a_{ji}$. $AB_R^{n\times n}$ represents the set of real matrices whose elements satisfy $a_{ij} = a_{n-i+1, n-j+1} = -a_{ji}$. When $X = X_{11}+X_{12}\mathbf{i}+X_{13}\mathbf{j}+X_{14}\mathbf{k}\in AB_{RB}^{n\times n}$, $X_{11}\in AB_R^{n\times n}, X_{12}, X_{13}, X_{14}\in B_R^{n\times n},$ for $L = B_R^{n\times n}$, when $n$ is even, we can select a set of basis

when $n$ is odd, we can select a set of basis

where $S_{ij} = (s_{ij})_{n\times n}, \ s_{ij} = s_{n-i+1, n-j+1} = s_{ji} = 1$, the other elements are zeros. After the basis is determined above, when $n$ is even, we have

when $n$ is odd,

For $L = AB_R^{n\times n}$, when $n$ is even, we can select a set of basis

when $n$ is odd, we can select a set of basis

where $T_{ij} = (t_{ij})_{n\times n}, \ t_{ij} = t_{n-i+1, n-j+1} = -t_{ji} = 1$, the other elements are zeros. After the basis is determined above, when $n$ is even, we have

when $n$ is odd,

When $n$ is even, we denote the $\mathcal{H}$-representation matrix corresponding to $L = B_R^{n\times n}$ by $H_{B_1}$, and denote the $\mathcal{H}$-representation matrix corresponding to $L = AB_R^{n\times n}$ by $H_{AB_1}$.

When $n$ is odd, we denote the $\mathcal{H}$-representation matrix corresponding to $L = B_R^{n\times n}$ by $H_{B_2}$, and denote the $\mathcal{H}$-representation matrix corresponding to $L = AB_R^{n\times n}$ by $H_{AB_2}$.

Theorem 3.4. For $X = X_{11}+X_{12}\mathbf{i}+X_{13}\mathbf{j}+X_{14}\mathbf{k}\in AB_{RB}^{n\times n}$, when $n$ is even, the $\mathcal{GH}$-representation of $X$ is expressed as

when $n$ is odd, the $\mathcal{GH}$-representation of $X$ is expressed as

4.   Algebra solutions of problem 1, 2, 3

Using the semi-tensor product of reduced biquaternion matrices and $\mathcal{L}_\mathcal{C}$-representation method, we can transform the reduced biquaternion matrix equation into complex linear equations, and then, according to the special structure of the solution, the redundant elements are eliminated using the $\mathcal{GH}$-representation method, so as to simplify the operation. Finally, we can use the following existing classical results of matrix equations to solve the equation.

Lemma 4.1. ^[24] The least squares solutions of the matrix equation $Ax = b$ with $A\in R^{m\times n}$ and $b\in R^m$ can be represented as

where $y\in R^n$ is an arbitrary vector. The minimal norm least squares solution of the matrix equation $Ax = b$ is $A^\dagger b$.

Lemma 4.2. ^[24] The matrix equation $Ax = b$ with $A\in R^{m\times n}$ and $b\in R^m$ has a solution $x\in R^n$ if and only if

In that case it has the general solution

where $y\in R^n$ is an arbitrary vector. The minimal norm solution of the matrix equation $Ax = b$ is $A^\dagger b$.

For the convenience of narration, we introduce the following notation:

Let

Theorem 4.1. Suppose $A_p\in Q_{RB}^{m\times n}, \ B_p\in Q_{RB}^{n\times q}\ (p = 1, \cdots, l), \ C\in Q_{RB}^{m\times q}$. Then the set $S_{AH}$ of Problem 1 can be represented as

where $\forall y\in R^{2n^2+n}$, and the minimal norm least squares anti-Hermitian solution $X_{AH}$ satisfies

Proof.

From the $\mathcal{GH}$-representatian matrix of anti-Hermitian matrix, we can obtain

Then

thus

if and only if

For real linear equations

according to Lemma 4.1, its least squares solution is

where $\forall y\in R^{2n^2+n}$, (4.1) can be obtained by multiplying both sides of (4.3) by $V_{AH}$. Notice

then, we can obtain the minimal norm least squares anti-Hermitian solution $X_{AH}$ of reduced biquaternion matrix equation (1.1) satisfies

From the above proof process, we can obtain the compatible condition for the anti-Hermitian solution of reduced biquaternion matrix equation (1.1).

Corollary 4.1. Suppose $A_p\in Q_{RB}^{m\times n}, \ B_p\in Q_{RB}^{n\times q}\ (p = 1, \cdots, l), \ C\in Q_{RB}^{m\times q},$ $\breve{H}$ is in the form of Theorem 4.1. Then, equation (1.1) has a solution $X\in AH_{RB}^{n\times n}$ if and only if

In this case, the general solution of equation (1.1) can be expressed as

and the minimal norm anti-Hermitian solution $\ddot{X}_{AH}$ satisfies

Proof. Since

thus

thus (4.5) can be obtained. Moreover, using Lemma 4.2, we can obtain the expression of general solutions and the minimal norm solution.

Through the proof of Theorem 4.1, we can see that the main difference between Problem 1, 2 and 3 is that the $\mathcal{GH}$-representation matrix of the solution. Therefore, for Problem 2 and 3, we can easily get the following conclusions:

Theorem 4.2. Suppose $A_p\in Q_{RB}^{m\times n}, \ B_p\in Q_{RB}^{n\times q}\ (p = 1, \cdots, l), \ C\in Q_{RB}^{m\times q}$. Then the set $S_{AP}$ of Problem 2 can be represented as

where $\forall y\in R^{2n^2+n}$, and the minimal norm least squares Skew-Persymmetric solution $X_{AP}$ satisfies

Corollary 4.2. Suppose $A_p\in Q_{RB}^{m\times n}, \ B_p\in Q_{RB}^{n\times q}\ (p = 1, \cdots, l), \ C\in Q_{RB}^{m\times q},$ $\breve{P}$ is in the form of Theorem 4.2. Then, equation (1.1) has a solution $X\in AP_{RB}^{n\times n}$ if and only if

In this case, the general solution of equation (1.1) can be expressed as

and the minimal norm Skew-Persymmetric solution $\ddot{X}_{AP}$ satisfies

Theorem 4.3. Suppose $A_p\in Q_{RB}^{m\times n}, \ B_p\in Q_{RB}^{n\times q}\ (p = 1, \cdots, l), \ C\in Q_{RB}^{m\times q}$. When $n$ is even, then the set $S_{AB}$ of Problem 3 can be represented as

where $\forall y\in R^{n^2+n}$, and the minimal norm least squares Skew-Bisymmetric solution $X_{AB}$ satisfies

When $n$ is odd, the set $S_{AB}$ of Problem 3 can be represented as

where $\forall y\in R^{n^2+n+1}$, and the minimal norm least squares Skew-Bisymmetric solution $X_{AB}$ satisfies

Corollary 4.3. Suppose $A_p\in Q_{RB}^{m\times n}, \ B_p\in Q_{RB}^{n\times q}\ (p = 1, \cdots, l), \ C\in Q_{RB}^{m\times q}.$ When $n$ is even, $\breve{Be}$ is in the form of Theorem 4.4, then equation (1.1) has a solution $X\in AB_{RB}^{n\times n}$ if and only if

In this case, the general solution of equation (1.1) can be expressed as

and the minimal norm Skew-Bisymmetric solution $\ddot{X}_{AB}$ satisfies

When $n$ is odd, $\breve{Bo}$ is in the form of Theorem 4.4, then equation (1.1) has a solution $X\in AB_{RB}^{n\times n}$ if and only if

In this case, the general solution of equation (1.1) can be expressed as

and the minimal norm Skew-Bisymmetric solution $\ddot{X}_{AB}$ satisfies

5.   Algorithm and numerical example

In this section, we give an algorithm for calculating the minimal norm least squares anti-Hermitian/Skew-Persymmetric/Skew-Bisymmetric solution of reduced biquaternion matrix equation (1.1), and verify the effectiveness of the method proposed in this paper through numerical examples. Then, we compare the posed method with the real vector representation method in ^[19] to illustrate the improvement of our algorithm.

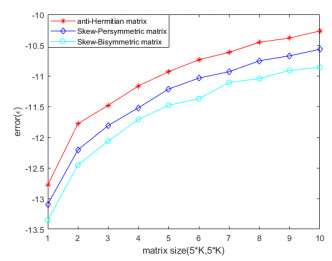
Example 5.1. Let $m = n = p = 5K, K = 1:10$, for fixed $A\in {Q}_{RB}^{m\times n}, \ B\in {Q}_{RB}^{n\times p}$, $X^*\in AH_{RB}^{n\times n}/AP_{RB}^{n\times n}/AB_{RB}^{n\times n}$, compute

For $AXB = C$ with unknown $X$, by Algorithm 1, we can obtain the numerical solution $X$. Denote the error between calculated solution $X$ and the exact solution $X^*$ as $\varepsilon = log_{10}\|X-X^*\|_{(F)}$ and $\varepsilon$ is recorded in Figure 1.

It can be seen from the error analysis charts that the method proposed in this paper is effective.

Next, we will make a comparison between the method in this paper and the real vector representation method ^[19].

Example 5.2. Let $m = n = p = K, K = 1:14$, for fixed $A\in {Q}_{RB}^{m\times n}, \ B\in {Q}_{RB}^{n\times p}$, $X^*\in AH_{RB}^{n\times n}$, compute

For $AXB = C$ with unknown $X$, numerical solution $X$ is obtained by using the method in this paper and the method in ^[19], respectively. Note down the CPU times of two methods. Detailed results are shown in Figure 2.

From Figure 2, we observe that the operation time of our method is significantly better than that of the method in ^[19].

6.   Application to color image restoration

With the increasing role of color images in daily life, color image restoration has become a hot research field. In recent years, reduced biquaternion has been widely used in color image processing because of its good structural characteristics ^[6,9,17,25].

In 2004, Pei ^[6] applied the reducd biquaternion model to image processing. A reduced biquaternion consists of one real part and three imaginary parts, however each pixel of a color image consists of three basic pixels: red, green and blue. Therefore, image processing is usually modeled as a pure imaginary reduce biquaternion, that is

where $r(x, y), g(x, y)$ and $b(x, y)$ are the red, green and blue values of the pixel $(x, y)$, respectively. Thus a color image with $m$ rows and $n$ columns can be represented by a pure imaginary reduced biquaternion matrix

The field of image restoration is required to retrieve the information from degraded images. Image restoration is to remove or reduce the degradation caused by noise, out of focus blurring and other factors in the process of image acquisition. A linear discrete model of image restoration is the matrix-vector equation

where $g$ is an observed image, $m$ is the true or ideal image, $n$ is additive noise, and $K$ is a matrix that represents the blurring phenomena. Given $g$, $K$, and in some cases, statistical information about the noise, the methods used in image restoration aim to construct an approximation to $m$. However, in most cases, the noise $n$ is unknown. We wish to find $m'$ such that

The problem described by the above model is the problem of the minimal norm least squares solution of reduced biquaternion matrix equation $\sum\limits_{p = 1}^l A_pXB_p = C$, when $p = 1$ and $B$ is the identity matrix.

Example 6.1. Given three $64\times 64$ ideal color images. $m = (m_r, m_g, m_b)$ is the image matrix, $m$ can be represented as the pure imaginary matrix $m = m_r\mathbf{i}+m_g\mathbf{j}+m_b\mathbf{k}$. By using $LEN = 15;\ THETA = 30;\ PSF = fspecial('motion', LEN, THETA)$ disturb the image $m_r$, and get the disturb image matrix $g_r$. Obviously, $K = g_rm_r^\dagger$. By using the matrix $K$, we can get the disturb image $g = (g_r, g_g, g_b) = Km = K(m_r, m_g, m_b)$. Through the "reshape" command of MATLAB, we can get the corresponding color restored image $m' = (m_r', m_g', m_b')$. The error of each channel is represented by $\epsilon_r, \ \epsilon_g, \ \epsilon_b$, respectively, and the results are shown in Table 1.

7.   Conclusions

In this paper, we use the semi-tensor product of reduced biquaternion matrices to obtain the algebraic expression of the isomorphism between the set of reduced biquaternion matrices and the corresponding set of complex representation matrices, and obtain some new conclusions of reduced biquaternion matrix under the vector operator, so that the problem of the reduced biquaternion matrix equation can be equivalently transformed into the problem of the reduced biquaternion linear equations, further transformed into real linear equations. Through the $\mathcal{GH}$-representation method we proposed, the number of variables in the real linear equations can be reduced, and the operation can be simplified. Finally, the proposed method is applied to color image restoration.

Acknowledgment

This work is supported by the National Natural Science Foundation of China under grant 62176112, the Natural Science Foundation of Shandong Province under grants ZR2020MA053, ZR2022MA030, and the Discipline with Strong Characteristics of Liaocheng University–Intelligent Science and Technology under grant 319462208. The authors are grateful to the referees for their careful reading and helpful suggestion, which have led to considerable improvement of the presentation of this paper.

Conflict of interest

The authors declare that there is no conflict of interest.