Sensor fault estimation for hydraulic servo actuator based on sliding mode observer

1.   Introduction

Important properties of the HSA, such as fast and accurate responses, high force/mass ratio, and relatively good stiffness, have attracted the great interest on the HSA and their applications. In the last two decades, high-performance controller design of the HSA has attracted increasing attention due to the expanded performance requirements of technical systems in industry ^[1,2,3].

Modern control systems are prone to faults, which can damage the systems themselves or the environments in which they operate. For this reason, fault detection and isolation (FDI) algotihms become essential, since they enable fault-tolerant actions that minimize the effect of faults and improve the overall system's reliability and safety. The research on FDI has received considerable attention during the last two decades due to the increasing demand for safety and reliability of automatic control systems ^[4,5]. Naturally, the nonlinear control problem for different dynamics systems is always a hot topic and has attracted compelling attention from scholars, see ^[6,7,8]. With the development of modern technology, autonomous systems are more and more dependent on sensors which often carry the most important information in automated/feedback control systems. Faults occurring in sensors may lead to poor regulation or tracking performance, or even affect the stability of the control system. On the other side, the stability analysis in dynamical systems has attracted widespread interests on both theoretical and practical fronts in recent years ^{[9,10,11,12,13]}. Therefore, the study of sensor fault diagnosis is becoming increasingly important.

The approaches of FDI developed in the past can be grouped into three fundamental categories: knowledge-based FDI methods, signal-based FDI and model-based FDI ^[14]. Among the possible approaches, the model-based FDI ones have been recognized as a handy tool by the scientific community and have been applied successfully to many physical systems, for example, lateral dynamics of a vehicle ^[15], aircraft ^[16], satellites ^[17], unmanned aerial vehicles (UAVs) ^[18], and wind turbines ^[19], among others. The basic idea of the observer-based FDI approaches, which fall into the category of model-based FDI, is to generally compare the actual system's behavior with the predicted or estimated behavior based on its mathematical model. Hence, the success of this type of technique directly relates to the mathematical model, which in reality is not a perfect representation. As a consequence, any discrepancies between the system and the model, which appear in the form of system uncertainties in the model, can cause a misleading alarm and make the FDI ineffective. Therefore, there is a need for a robust FDI which is sensitive to faults but insensitive to model uncertainties ^[20].

On the other side, fault estiamtion (FE) is different from the majority of fault detection and isolation (FDI) in the sense that it not only detects and isolates the fault, but also provides details of the fault, such as the location, size, and duration. Thus, it is especially useful for incipient faults and slow drifts, which are very difficult to detect. Also FE is vital in fault-tolerant control (FTC) systems which improve the system's performance. During the last two decades, considerable research results have been reported on sensor FE. In ^[21], an online estimation approach based on adaptive observer technique was adopted to reconstruct the sensor fault with an incipient time profile. A descriptor system approach was introduced to investigate sensor fault diagnosis for nonlinear systems in ^[22], which is applicable for sensor faults of any forms. Most physical systems are nonlinear, and therefore FDI should employ nonlinear algorithms, which are difficult to generalize and apply in many cases. It is well known that sliding mode techniques offer good potential for increasing the robustness of FDI by including a nonlinear discontinuous term that depends on the output estimation error into the observer ^[23,24]. During the last two decades, the research on sliding-mode observers (SMO)-based FE has received considerable attention. Several results have been reported on this topic ^{[25,26,27,28]}.

In this paper, a sensor FE scheme is proposed for uncertain Lipschitz nonlinear systems. By applying coordinate transformations, we first transform the the original system into two subsystems (subsystem-1 and 2) where subsystem-1 includes the effects of system uncertainties but is free from sensor faults and subsystem-2 has sensor faults but without any uncertainties. Therefore, the FE can be carried out independently and is not affected in the presence of uncertainties. This offers a significant advantage over some of the existing methods. For example in ^[22,29,30] the effects of uncertainties on the estimation of faults can only be minimized. The proposed method extends the results of ^[31,32] in which actuator FE of linear systems was studied to sensor FE for uncertain Lipschitz nonlinear systems. Moreover, most of the existing FE methods such as those reported in ^[22,33,34] assume that the value of the Lipschitz constant $\mathcal{L}_f$ is known and they incorporate this knowledge to obtain feasible LMI solutions. However, determining the value of $\mathcal{L}_f$ of a nonlinear system is often difficult. Further, if the value of $\mathcal{L}_f$ exceeds the admissible value, those methods often fail to find feasible LMI solutions. In this paper, the value of $\mathcal{L}_f$ is assumed to be unknown and adaptation laws are integrated into the proposed schemes such that $\mathcal{L}_f$ does not appear in the LMI formulation and the feasibility of LMIs is not dependent on the knowledge of this parameter. Therefore, the proposed method offer distinct advantages over some of the existing methods.

The remainder of the paper is organized as follows: Section 2 briefly describe model of the hydraulic servo actuator. Section 3 describes the mathematical preliminaries required for developing the FDI method and design procedure of the implemented SMO. The results of the simulation are shown in Section 4 and conclusions are given in Section 5.

2.   Description of the HSA

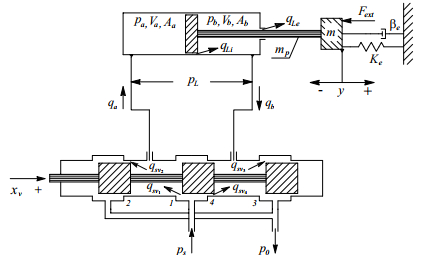
The HSA under study is shown in Fig. 1, which consists of the servo valve and the hydraulic cylinder. The analysis of the properties of the HSA comes out from dynamics of its components that involves the piston motion dynamics, pressure dynamics at the cylinder, and servo valve dynamics. Hence, the model of the HSA is derived from complex nonlinear equations that depend on many parameters which cannot be accurately obtained ^[35].

See Table 1 for the description of the HSA parameters. Using the notation in Figure 1, and defining the area ratio of the piston $\alpha = A_b / A_a$, $V_a = V_{a0} + y A_a$, $V_b = V_{b0} + (L - y)\alpha A_a$, $q_{Li} = c_{Li} (p_a - p_b)$, where $c_{Li}$ is the internal leakage flow coefficient, $c_{vi} > 0$ are discharge coefficients, the sign function $sg(x) = \left\{ \begin{matrix} x, \, \, \, x\ge 0 \\ 0, \, \, \, x < 0 \\ \end{matrix} \right.$, and assuming an external leakage negligible, the considered model can be described by the following equations:

According to Eqs (2.1)-(2.5) and defining the state and input variables as

the governing nonlinear continuous-time dynamics of the HSA can be expressed in a state-space form as follows

where $f(x(t))$ and $g(x(t), u(t))$ are the state dynamics and the input function, respectively

and output function $\eta (x(t)) = x_1(t)$, and disturbance function $h(t) = \begin{bmatrix} h_1(t) & -F_{ext}/m_t + h_2(t) & h_3(t) & h_4(t) \end{bmatrix}$ includes loads, unmodelled dynamics and parameter uncertainties, $f_S(t)$ includes sensor faults.

3.   SMO-based sensor fault estimation

Consider a non-linear system described by

where the state vector is $x \in \mathbb{R}^n$, the input vector is $u \in \mathbb{R}^m$, the output vector is $y \in \mathbb{R}^p$, the sensor fault is denoted as $f_s \in \mathbb{R}^q$. The known constant matrices are $A \in \mathbb{R}^{n\times n}$, $B \in \mathbb{R}^{n\times m}$, $C \in \mathbb{R}^{p\times n}$, $D \in \mathbb{R}^{p\times q}$, $E \in \mathbb{R}^{n\times r}$ $(p \geq q + r)$ and $W \in \mathbb{R}^{n\times j}$ with $D$ and $E$ both being of full rank.

Remark 1. It should be noted that the system uncertainty under consideration is unstructured, which is more general than the type of structured uncertainty that has been considered for fault diagnosis of Lipschitz nonlinear systems in the literature ^[33,36]. In the case of structured system uncertainty, certain rank conditions of the uncertainty distribution matrix are assumed to be satisfied such that the fault can be completely decoupled from the uncertainty.

For the objective of achieving sensor fault diagnosis, the following assumptions and Lemmas are intoduced. The nonlinear term $f(x, t) \in \mathbb{R}^j$ is assumed to be known and Lipschitz about $x$ uniformly $\forall x, \hat{x} \in \mathbb{R}^n$

where $\mathcal{L}_f$ is the known Lipschitz constant.

The unknown nonlinear term $\Delta \psi (t)$ is structured modelling uncertainty, but bounded, and satisfies $\Delta \psi (t)\le \xi$. Also, the unknown sensor fault and its derivative are norm bounded, i.e. $f_s(t) \le \rho$ and $\dot{f}_(t) \le \rho_s$.

Lemma 3.1. Let's assume ${\rm{rank}}(CE) = {\rm{rank}}(E)$. There exist linear transformations of coordinates

such that in the new coordinates, the system matrices become

where $T \in \mathbb{R}^{n \times n}$, $S \in \mathbb{R}^{p \times p}$, $T_1 \in \mathbb{R}^{r\times n}$, $S_1 \in \mathbb{R}^{r\times p}$, $z_1 \in \mathbb{R}^r$, $w_1 \in \mathbb{R}^r$, $A_1 \in \mathbb{R}^{r\times r}$, $A_4 \in \mathbb{R}^{(n-r)\times (n-r)}$, $B_1 \in \mathbb{R}^{r\times m}$, $E_1 \in \mathbb{R}^{r\times r}$, $W_1 \in \mathbb{R}^{r\times j}$, $C_1 \in \mathbb{R}^{r\times r}$, $C_4 \in \mathbb{R}^{(p-r)\times (n-r)}$ and $D_2 \in \mathbb{R}^{(p-r)\times q}$. $C_1$ is invertible.

After introducing the state and output transformations (3.3), the original system is converted into two subsystems:

For Subsystem 1, we define a new state $z_3 = \int\limits_0^t w_2(\tau)d\tau$ so that $\dot{z}_3 = C_4 z_2 + D_2 f_s$. An augmented system with the new state $z_3$ is therefore given as:

Subsystem (3.5) can be rewriten as in a more compact form as

where $z_0 \in \mathbb{R}^{n+p-2r}$, $\bar{A}_2 = \begin{bmatrix} A_2 & 0 \end{bmatrix} \in \mathbb{R}^{r\times (n+p-2r)}$. Also, Subsystem (3.6) can be stated as

in which $w_3 \in \mathbb{R}^{p-r}$, $A_0 = \begin{bmatrix} A_4 & 0 \\ C_4 & 0 \end{bmatrix} \in \mathbb{R}^{(n+p-2r)\times (n+p-2r)}$, $\bar{A}_3 = \begin{bmatrix} A_3 \\ 0 \end{bmatrix} \in \mathbb{R}^{(n+p-2r)\times r}$, $B_0 = \begin{bmatrix} B_2 \\ 0 \end{bmatrix} \in \mathbb{R}^{(n+p-2r)\times m}$, $D_0 = \begin{bmatrix} 0 \\ D_2 \end{bmatrix} \in \mathbb{R}^{(n+p-2r)\times q}$, $C_0 = \begin{bmatrix} 0 & I_{p-r} \end{bmatrix} \in \mathbb{R}^{(p-r)\times (n+p-2r)}$, $\bar{W}_2 = \begin{bmatrix} W_2 \\ 0 \end{bmatrix}$.

Lemma 3.2. ^[37,38] The pair $\left(A_0, C_0 \right)$ is detectable if and only if the minimum phase condition holds

for every complex number $s$ with nonnegative real part.

Now, a scheme which consists of two SMOs to estimate sensor faults is develepod. One of the SMOs is designed for subsystem (3.8) to estimate sensor faults, while other one is designed for subsystem (3.9) to eliminate the effects of system uncertainties.

For subsystem (3.8), the proposed SMO has the following form:

where $A_1^s \in \mathbb{R}^{r\times r}$ is a stable matrix which needs to be determined, $P_1$ is the Lyapunov matrix of $A_1^s$, $\hat{z} : = \begin{bmatrix} \left(C_1^{-1} S_1 y \right)^T & \left(\begin{bmatrix} I_{n-r} & 0 \end{bmatrix} \hat{z}_0 \right)^T \end{bmatrix} ^T$. The discontinuous output error injection term $v_1$, which is used to eliminate the effects of uncertainties, is defined by

where $\eta_1$ is a positive scalar to be determined. It should be noted that state $z_1$ can be obtained by the measured output $y$ as $z_1 = C_1^{-1} S_1 y$. $\hat{k}_1$ satisfies the following adaption law:

where $l_{k_1}$ is a positive constant. For subsystem (3.9), the proposed SMO has the following form:

where the observer gain $L_0 = \begin{bmatrix} L_{01} \\ L_{02} \end{bmatrix} \in \mathbb{R}^{(n+p-2r)\times (p-r)}$, in which $L_{01} \in \mathbb{R}^{(n-r)\times (p-r)}$, $H_0 \in \mathbb{R}^{j\times (p-r)}$, $P_0 = P_0^T \in \mathbb{R}^{(n+p-2r)\times (n+p-2r)}$. The discontinuous output error injection term $v_2$ is defined by

where $F_0 \in \mathbb{R}^{q\times (p-r)}$ is a matrix to be determined and $\eta_2$ is a positive scalar. $\hat{k}_2$ satisfies the following adaption law:

where $l_{k_1}$ is a positive constant.

We now present the following theorem which provides sufficient conditions for the existence of the proposed SMOs.

Theorem 3.3. Let's consider system (3.1) with introduced assumptions and lemmas. If there exist matrices $A_1^s$, $L_0$, $F_0$, $H_0$, $P_0 = P_0^T > 0$, $P_1 = P_1^T > 0$ such that

where $\Pi_1 = {A_1^s}^T P_1 + P_1 A_1^s$, $\Pi_2 = \left(A_0 - L_0 C_0 \right)^T P_0 + P_0 \left(A_0 - L_0 C_0 \right)$ then the error dynamics, after the occurrence of sensor faults

are assymtoticaly stable, in which the state estimation errors are defined as $e_1 = z_1 - \hat{z}_1$ and $e_0 = z_0 - \hat{z}_0$. The Proof of Theorem 3.3 can be seen in ^[39].

In practice, it is often difficult to know precisely the value of the Lipschitz constant in (3.2). This parameter plays an important role in the design of observers for nonlinear systems. It should be noted that in ^{[22,33,36,40]} the Lipschitz constant $\mathcal{L}_f$ is assumed to be known and is one of the parameters in the LMI formulation. This can be considered as one of the limitations of those methods. We have observed that it often fails to solve LMI if the value of $\mathcal{L}_f$ is too large. In order to find a feasible solution of LMI, the value of $\mathcal{L}_f$ may be reduced by introducing coordinate transformations for certain structures of the Lipshcitz function ^[41]. However, this may bring in an extra difficulty in the design of observers. In contrast to some of the existing methods, the Lipschitz constant $\mathcal{L}_f$ in this paper is assumed to be unknown and adaptive SMOs are proposed to deal with this situation. Specifically, the Lipschitz constants $\mathcal{L}_{f_1}$ and $\mathcal{L}_f$ are injected into the constants $k_1$ and $k_2$ which can be adjusted by the adaptation laws (3.13) and (3.16). Note that the asymptotic estimation of states can be guaranteed even if the estimates of k1 and k2 do not approach to their actual values ^[39].

Theorem 3.3 has shown that the error dynamics (3.20) and (3.21) are asymptotically stable. The objective now is to choose constants $\eta_1$ and $\eta_2$ such that the error dynamics can be driven to the sliding surface in finite time and a sliding motion can be maintained on it thereafter. For error dynamics (3.20) and (3.21), we define the sliding-mode surface as

The problem of finding matrices $A_1^s$, $L_0$, $F_0$, $H_0$, $P_0 = P_0^T > 0$, $P_1 = P_1^T > 0$ to simultaneously satisfy the Inequality (3.19) and Equalities (3.17) and (3.18) can be transformed into the following LMI optimization problem:

Minimize $\gamma_1 + \gamma_2$

subject to

$P_0 > 0$, $P_1 > 0$

and

where $X = P_1 A_1^s$ and $Y_0 = P_0 L_0$.

Theorem 3.4. Let's consider system (3.1) with introduced assumptions, lemmas and the proposed observers (3.11) and (3.14). Then the error dynamics (3.20) and (3.21) can be driven to the sliding surface (3.22) in finite time and remain on it if LMIs (3.23)-(3.25) are solvable and the gains $\eta_1$ and $\eta _2$ satisfy

where $\eta_3$ and $\eta_4$ are positive scalars. The Proof of Theorem 3.4 can be seen in ^[39].

After reaching the sliding surface, the sliding motion will be maintained thereafter, i.e., $C_0 e_0 = 0$. It follows from (3.21) that

where $v_{2eq}$ is the equivalent output error injection signal representing the average behavior of the discontinuous function $v_2$. Since $\lim\limits_{t\to \infty}e_0 = 0$ according to Theorem 3.3, it also holds that $\lim\limits_{t\to \infty} f(T^{-1} z, t) - f(T^{-1} \hat{z}, t) = 0$. From (3.28) it follows that the sensor fault can be approximated as

in which the equivalent output error injection signal $v_{2eq}$ can be obtained as

where $\delta$ is a small positive scalar to reduce the chattering effect.

4.   Simulation results

Effectiveness of the sensor FE approach will be considered on HSA model with following parameters: the viscous friction $B_C = \rm{200}\, \frac{\rm{N s}}{\rm{m}}$, the supply pressure $p_S = \rm{45}\, \rm{bar}$, the tank pressure $p_0 = \rm{1.6}\, \rm{bar}$, the bulk modulus of the fluid $\beta_e = \rm{2}\cdot\rm{10}^{\rm{8}}\, \rm{Pa}$, the total mass $m = \rm{25}\, \rm{kg}$, the initial chamber volumes $V_{a0} = V_{b0} = \rm{8.2}\cdot\rm{10}^{-\rm{6}}\, \rm{m}^{\rm{3}}$, the load spring gradient $K_e = \rm{10}^{-\rm{1}}$, the effective area of the head side of the piston $A_a = \rm{4.91}\cdot\rm{10}^{-\rm{4}}\, \rm{m}^{\rm{2}}$, the effective area of the rod side of the piston $A_b = \rm{2.43}\cdot\rm{10}^{-\rm{4}}\, \rm{m}^{\rm{2}}$, the internal leakage coefficient $c_{Li} = \rm{5}\cdot\rm{10}^{-\rm{14}}$, the piston stroke $L = \rm{1}\, \rm{m}$, discharge coefficients of valve orifices $c_{vi} = \rm{1.15}$, $i = \overline{1, 4}$.

It is assumed that there is an complex sensor fault composed of a combination of abrupt, ramp, and sine-type faults, which is represented as:

For simulation purposes, we set the control input $u(t)$ as sinus function $\sin (\pi t)$ and the system uncertainty $\Delta \psi (t)$ as

The results of fault estimation are illustrated in Figure 2. This figure clearly demonstrate that the proposed observer is able to estimate the sensor faults successfully, irrespective of uncertainties in the system. In addition to gradual and slow faults, such as a ramp and sinusoidal faults, it should be noted that fs changes abruptly at time instants $\rm{150}\, \rm{s}$ and $\rm{180}\, \rm{s}$, which indicates that the proposed observer has the ability to track abrupt faults.

Figure 3 shows the trajectories of the actual states and their estimates. It can be seen from the figures that the proposed observer can estimate the states accurately, before and after the occurrence of any fault.

It can be seen that despite the presence of system uncertainties and measurement noises, the tracking performances of states $x$ and sensor fault $f_s$ have achieved an ideal performance.

5.   Conclusions

In this paper, a new sensor FE scheme for uncertain Lipschitz nonlinear systems is developed. The proposed FE scheme essentially transforms the original system into two subsystems where the first one includes system uncertainties, but is free from sensor faults and the second one has sensor faults but without uncertainties. Using the integral observer based approach, sensor faults in the second subsystem are transformed into actuator faults. In the proposed scheme, two SMOs are designed. One of which is used to eliminate the effect of system uncertainties, while the other one is used to estimate sensor faults. Adaptation laws are integrated into the scheme to deal with the situation when the Lipschitz constant is unknown or too large. The observer design parameters can be obtained using LMI techniques in a systematic way. Effectiveness of the proposed FE scheme has been demonstrated considering the example of hydraulic servo actuator. Simulation results have shown that the proposed FE scheme is effective and feasible in the presence of system uncertainties. Future research may include extending the proposed methodology to a single link robotic arm with a revolute elastic joint.

Acknowledgment

This research has been supported by the Serbian Ministry of Education, Science and Technological Development under grant 451-03-68/2022-14/200108, and CNPq under grant 304032/2019-0.

Conflict of interest

The authors declare that there is no conflict of interest.