Normal form for lower dimensional elliptic tori in Hamiltonian systems

1.   Introduction

A rumor is unverified or false information that is often spread through word of mouth or social media. For instance, during the COVID-19 pandemic, a number of false claims, such as the idea that the virus could be cured by drinking bleach or that certain groups were immune to it, were widely circulated. Such false claims may lead to public panic and undermine social cohesion^[1,2]. Therefore, identifying and resisting rumors is crucial for maintaining social stability and national security^[3].

Daley and Kendall conducted a dynamic analysis of rumor propagation in the 1960s and proposed the DK (Daley—Kendall) model. This model primarily studies the spreading process of rumors in social networks, where individuals are treated as nodes and interact with each other to spread rumors^[4,5]. In 1973, Maki and Thompson extended the DK model and proposed the MT (Maki—Thompson) model, which primarily focuses on the individual behaviors and network structures' impact on rumor propagation^[6,7]. The MT model introduces the concepts of "susceptible", "infected", and "recovered" individuals, emphasizing that individuals may go through different stages in the process of rumor propagation. Furthermore, the model takes into account the different transmission probabilities and contact frequencies among individuals, thus providing a more complex analysis of transmission dynamics. With these extensions, the MT model provides a deeper understanding of how rumors spread and evolve in social networks^[8]. Based on this, subsequent researchers have studied and expanded on these two models from both external environmental and individual psychological perspectives, considering more factors that influence rumor propagation.

In tense or anxious external environments, media and sudden situations (such as disasters, crises, etc.) can all affect the speed of rumor propagation. People tend to seek information in times of uncertainty, and may be more likely to believe rumors^[9]. Based on the classic SIR model^[10,11], Sejeong et al. discussed the importance of identifying rumors in social media. Due to the fact that rumors propagate much faster in online than offline environments, researchers have studied the three aspects of rumor diffusion (temporal characteristics, structural characteristics, and linguistic characteristics; ) in order to identify the characteristics of rumors^[12]. Ozturk et al. explored the dual role of social media in information dissemination: It can quickly be used to share useful information but also to easily spread unverified rumors. Several design solutions have been proposed to reduce the spread of health-related rumors. Results show that providing users with information to refute rumors or warning them about the source of the rumors on a website can effectively reduce their spread^[13].

Pan et al. considered the impact of the number of media reports and rumors on media dissemination and established the SIDRW rumor propagation model, which found that positive media coverage can effectively reduce but not stop the spread of rumors^[14,15]. Guo et al. considered the impact of media coverage and time delay on rumor propagation and proposed a SEIMR rumor model with media coverage and time delay. The results showed that media coverage plays a crucial role in reducing the scale of rumor propagation. The greater the media penetration rate, the smaller the scale of rumor propagation^[16,17]. Yang et al. collected basic information data on internet rumors and highly topical public opinions; and used an improved SCIR model to analyze the propagation characteristics of internet rumors in different stages of suspicion under a suspicion mechanism. They also analyzed the stability of rumor propagation evolution by using time delay differential equations and punishment mechanisms. Researchers have found that increasing recovery rates is more effective than reducing fraud rates, and increasing eviction rates is more important than improving detection rates^[18]. Yong et al. explored the rumor dynamics in social networks during sudden situations and proposed a new rumor propagation model called ILRDS, which takes into account that ignorant individuals may enter a latent state based on their three different attitudes towards rumors or counter-rumors after coming into contact with them^[19].

In addition to external environmental factors, internal emotions, hesitation, and forgetfulness also have a certain impact on the propagation of rumors. Strong emotional drive makes it easier for people to share rumors related to emotions. Based on the theory of emotions, Zhang et al. proposed an online rumor propagation model to explore the impact of emotions embedded in online rumors on the audience's intent to spread rumors. The model was verified through quasi-experiments and specifically focused on online rumors with positive, neutral, and negative emotional expressions. The study provided new insights into the field of rumor research, emphasizing the importance of individual emotions in the propagation of rumors^[20]. Based on this, Li et al. proposed a new SVIR model. In this model, an alert emotional state is added to describe an individual's reaction to rumors. Researchers found that individuals are more likely to spread rumors when these are closely related to their own lives. Increasing individuals' awareness can effectively reduce the impact of rumors^[21]. Zeng et al. discussed the importance of individual emotional contagion in rumor propagation and debunking and studied the transformation of individual emotions into group emotions by improving the emotional model and simulating it. The results show that the emotional changes of netizens have different cycles and trends, but the ultimate distribution is relatively stable^[22].

Furthermore, researchers have discovered that the hesitation mechanism can increase the contagion threshold and influence individual behavior, thereby changing the speed of rumor diffusion and its ultimate impact. Xia et al. incorporated a hesitation mechanism into the SEIR model to propose an improved model, taking into account the attractiveness and ambiguity of rumor content. The results show that reducing ambiguity can effectively increase the transmission threshold of the SEIR model and reduce the maximum impact of rumors, while the transmission threshold is not related to the attractiveness of rumors^[23,24]. Chen et al. introduced the role of hesitators and rumor debunkers, and proposed the SEIOR rumor propagation model, which combines different rumor debunking methods, overcoming the limitations of existing models that are mostly based on a single propagation mechanism and a single debunking method^[25]. Meanwhile, the forgetting mechanism can also lead to misunderstandings and the spread of rumors, as individuals are prone to confuse information sources and cause inaccurate information to spread rapidly in social networks. Therefore, based on the classic SIR model, Zhao et al. proposed a rumor propagation model that takes into account the forgetting mechanism and studied the effects of average connectivity, forgetting rate, and suppression rate on rumor propagation. The results show that the network topology has a significant impact on the propagation of rumors: compared with the ER network, rumors spread faster in the BA scale-free network, and the final rumor size is smaller; the forgetting and memory mechanisms have a greater impact on the final size of the rumor^[26,27,28]. Subsequently, Ding et al. proposed the conceptual model of rumor propagation and countermeasures considering forgetfulness and constructed an individual-level mathematical model from the perspective of competitive innovation diffusion. The results show that counterargument strategies and counterargument forgetfulness both affect the process and outcomes of rumor propagation and control, with complex interactions among the various factors^[29].

Sha et al. studied the spread of rumors in information dissemination and explored the influence of network structure and government control. The rationality of the model was verified by numerical simulations and epidemic data fitting, emphasizing the importance of government intervention and improving individual discrimination in information control ^[30]. Li et al. studied the mechanism of online rumor propagation, analyzed the Turing instability combined with time delay and network structure, and proposed a strategy to manage rumor propagation by adjusting network structure and controlling propagation factors^[31]. Yuan et al. established a 2SIR rumor propagation model with a nonlinear suppression mechanism and time delay in a bilingual environment, analyzed the stability of the equilibrium point, basic propagation number, and optimal control in homogeneous and heterogeneous networks, and verified the theoretical results through numerical simulations^[32].

The studies on the external environmental factors, inner emotions, hesitation, and forgetfulness that contribute to the propagation of rumors have been quite comprehensive and extensive. However, considering the differences in individuals' ability to identify information, studies on rumor propagation from an information recognition perspective are relatively rare. Based on the classical SIR model, this paper adds a class of individuals: the truth communicators. Truth communicators have good discernment ability, can access information in a timely and effective manner, can distinguish truth from falsehood, identify rumors, and choose to spread the truth. People who lack discernment are easily misled and quickly spread false information, leading to the spread of rumors. Therefore, improving the public's discernment ability can help reduce the spread of false information and build a more rational information environment. This paper will study the problem of rumor propagation from the perspective of individuals' ability to identify information, thereby expanding our understanding of the issue.

The organization of the rest of this paper is as follows: Section 2 establishes the rumor propagation model; Section 3 determines the existence of equilibrium points, calculates the basic reproduction number, and analyzes the stability of the rumor equilibrium point. Section 4 utilizes Pontryagin's maximum principle to propose an optimal control strategy; Section 5 verifies the feasibility of the above conditions through numerical simulation; Section 6 conducts a sensitivity analysis of the model parameters; and Section 7 is the conclusion of this paper.

2.   Model building

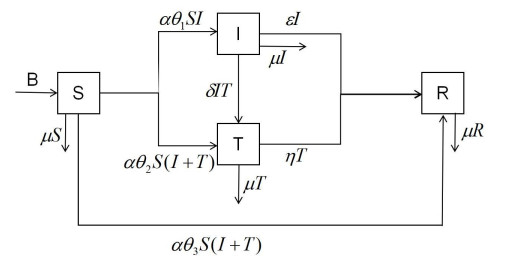
We discuss how the total number of people in this virtual community changes over time. The total number of people in the system at time t is represented by $N(t)$. Based on the classical SIR model, we divide the total population into four categories. The first category is the ignorant, representing individuals who have never heard rumors. The second category is the rumor disseminator, those whose information discrimination ability is not strong, who choose to believe in and spread rumors. The third category is the truth disseminator, which represents individuals with good information processing ability that can identify the inaccuracies in rumors and choose to disseminate true information. The fourth type is rumor immunity, indicating individuals who have encountered rumors, learned and reflected from them, enhanced their ability to identify them, and rejected such rumors. They are denoted by $S(t)$, $I(t)$, $T(t)$, and $R(t)$, respectively.

The number of people entering the system per unit of time is $B$, assuming that these people are ignorant people who have not heard the rumor, so $B$ is a constant. Suppose that the contact rate between the ignorant person and the rumor spreader is $\alpha$, that is, three phenomena will occur when the ignorant person hears the rumor: 1) Some people tend to believe unconfirmed news and thus become the disseminators of rumors. The probability is $\theta_1, \, \theta_1 \in (0, 1)$. 2) Some individuals have good information processing ability and can identify the truth more accurately and pass it on to others, the probability is $\theta_2, \, \theta_2 \in (0, 1)$. 3) The rest of the individuals exposed to the rumor are not interested in the rumor, and turn into rumor-immune with the probability of $\theta_3, \, \theta_3 \in (0, 1)$; where $\theta_1 + \theta_2 + \theta_3 = 1.$

After a period of rumor contact and spread, the rumor spreader encounters truth broadcasters with a $\delta$ contact rate, and transforms into immunizers with a $\epsilon$ probability. At the same time, the truth transmitter will also turn into an immune with a probability of $\eta$.

Due to factors such as population deaths, it is possible for each group to exit in the same proportion, i.e., the population migration rate is expressed by $\mu$.

In the above analysis, all parameters are positive. Based on the above assumptions and analysis, the flowchart of the rumor propagation model considering individual identification ability is shown in Figure 1:

We discussed the impact of individual identification abilities on the propagation of rumors.

As shown in Figure 1, the number of individuals belonging to the groups rumor ignorant, rumor spreader, truth spreader, and rumor immunity changes as follows:

(1) In unit time, the total number of people entering the system is $B$, and these people are ignorant who have not heard the rumors. When the ignorant person come into contact with the rumor spreader, the number of rumor spreader is $\theta _1\alpha SI$, the number of truth spreader is $\theta_2 \alpha S (I + T)$, and the number of rumor immune person is $\theta_3 \alpha S (I + T)$. The number of ignorant who move out of the social group at a $\mu$ removal rate due to reasons such as death or migration is $\mu S$. Therefore, the change of the ignorant in unit time is $B - \alpha \theta_1 S I - \alpha \theta_2 S (I + T) - \alpha \theta_3 S (I + T) - \mu S$.

(2) In unit time, after some ignorant person come into contact with a rumor spreader, the ignorant transforms into a rumor spreader with a probability of $\theta_1$, and the number of these is $\theta _1\alpha SI$. The rumor spreader contacts with the probability of $\delta$ and turns into the truth spreader, and the number of these is $\delta IT$. Since time-sensitive spreaders lose interest in rumor spreading, rumor spreaders are converted into immune people with a probability of $\epsilon$, whose number is $\epsilon I$. The number of rumor spreaders who move out of the social group at a $\mu$ removal rate due to reasons, such as death or migration is $\mu I$. Therefore, the change of rumor spreader in unit time is $\alpha \theta_1 \, SI - \delta IT - \epsilon I - \mu I$.

(3) In unit time, after some ignorant people come into contact with rumor spreaders and truth spreaders, the ignorant people turn into truth spreaders with the probability of $\theta_2$, and the number of these is $\theta_2 \alpha S (I + T)$. The rumor spreader contacts with the probability of $\delta$ and turns into the truth spreader, and the number of these people is $\delta IT$. Since time-sensitive spreaders lose interest in rumor spreading, rumor spreaders are converted into immune people with a probability of $\epsilon$, whose number is $\epsilon I$. The number of truth communicators who move out of social groups at a $\mu$ removal rate due to reasons, such as death or migration, is $\mu T$. Therefore, the change of the truth spreader per unit time is $\alpha \theta_2 S(I+T) + \delta I T - \eta T - \mu T$.

(4) In unit time, the proportion of ignorant people who were exposed to rumors and turned into immune is $\theta_3$, and the number of these people is $\theta_3 \alpha S (I + T)$. Because timeliness spreaders lose interest in rumor spreading, the number of some rumor spreaders converted to immunizers is $\epsilon I$, and the number of truth spreaders converted to immunizers is $\eta T$. Rumor immune persons move out of the social group for several reasons at a $\mu$ rate, the number of which is $\mu R$. Therefore, the immune change per unit time is $\epsilon I + \eta T + \alpha \theta_3 S(I+T) - \mu R$.

The meaning of each symbol in Figure 1 is shown in Table 1.

Based on this, we drew a flowchart of the model, as shown in Figure 1, and constructed dynamic equations such as (2.1).

Where, $B > 0, \, \alpha > 0, \, \theta_1 > 0, \, \theta_2 > 0, \, \theta_3 > 0, \, \epsilon > 0$, $\delta > 0, \, \eta > 0, \, \mu > 0$. $S(0) = S_0 \geq 0, \, I(0) = I_0 \geq 0, \, T(0) = T_0 \geq 0$, $R(0) = R_0 \geq 0.$

3.   Model analysis

Lemma 1. The closed set $\Omega = \left\{ (S, I, T, R) \in \mathbb{R}^4 \mid N \leq \frac{B}{\mu} \right\}$ is the positive invariant set of the model dynamics equation (2.1).

Proof. We can get $N = S + I + T + R$, so

It is easily shown that

and then

Thus, the positive invariant set of the model dynamics equation (2.1) is

3.1.   Basic reproductive number $R_0$

In epidemiology, $R_0$ refers to the number of susceptible individuals in a population that are successfully infected by an infectious agent during the entire duration of their infectious period when placed in an environment composed of susceptible individuals. Similarly, this paper uses this concept to indicate the number of ignorant individuals successfully infected by a rumor propagator while they are in a healthy group during the period of rumor spreading. That is, when $R_0 < 1$, the average number of infected people per transmission cycle is less than 1, which means that the rumor will disappear over time in the future. Instead, when $R_0 > 1$, the rumor will not disappear over time and will persist. Therefore, improving individual identification ability, enabling more people to realize the truth and falsity of information, and avoiding the spread of false news will also help effectively reduce $R_0$ and prevent the spread of rumors. This paper will use the next-generation production matrix method to calculate the basic reproduction number.

Let ${\mathbf X} = \begin{pmatrix} I & T & R & S \end{pmatrix}^T$, the model dynamics equation (2.1) can be written as

Where,

Calculate the Jacobian matrices of $F(X)$ and $V(X)$ in Eq (3.1) separately.

Thus, we can get

Let $\lambda$ be a characteristic value, then

Thus, the basic reproductive number $R_0 = \max\{ R_1, R_2 \}$, where,

Define$\quad R_0 = \max\{ R_1, R_2 \}$ to ensure that the maximum extent and speed of the spread can be predicted and controlled in the worst case scenario, so that effective response measures can be taken.

3.2.   The existence of equilibrium points

According to the dynamic equations, the model's equilibrium point without rumors is

Theorem 1. If

the equilibrium point $E^* = (S^*, I^*, T^*, R^*)$ exists.

Proof. Let N = 0 in the model dynamics equation (2.1), and the right side is 0.

We can get,

And the solution of T satisfies

Where,

In the above formula, $A_1 = \mu + \epsilon, \quad A_2 = 1 - \theta_1$. Dividing both sides of Eq (3.9) by $a$ yields:

Let the following formula be true $T^{*} = x - \frac{b}{3a}$, we can get

among

The solution is

Among

Discarding the imaginary numbers yields the final result:

To achieve $T^* > 0$, one must fulfill$-\frac{q}{2} > 0, -\frac{q}{2} > \sqrt{\left(\frac{q}{2} \right)^2 + \left(\frac{p}{3} \right)^3}, \frac{b}{3a} < 0.$ When $a > 0, b < 0, c < 0, d < 0, b > ac$, we can get $b^2 < abc, \quad 2b^2 < 9abc, \quad 27a^2 d - 9abc + 2b^2 < 0.$ Thus, $-\frac{q}{2} > 0.$ When $b^2 > 3ac, p < 0,$ we can get $-\frac{q}{2} > \sqrt{\left(\frac{q}{2} \right)^2 + \left(\frac{p}{3} \right)^3}.$

Upon summarizing, we can conclude that when

is ture, the equilibrium point $E^* = (S^*, I^*, T^*, R^*)$ exists.

3.3.   Stability of equilibrium points

Theorem 2. When $R_1 < 1, \quad R_2 < 1$ is true, the equilibrium point $E_0$ of the system is locally asymptotically stable.

Proof. The calculations show that the Jacobian matrix at the equilibrium point $E_0$ of the model 1 without rumors is:

Then the characteristic equation of matrix $J(E_0)$ can be expressed as

Based on the characteristic equation, the eigenvalues of the matrix $J(E_0)$ are found to be

If

then

leads to

Therefore, according to the Routh—Hurwitz (RH) criterion, when

is true, the equilibrium point

of the system is locally asymptotically stable.

Theorem 3. When $\mu \geq \alpha S, \quad \mu \geq \alpha (\theta_2 + \theta_3) S$, $E_0$ is globally asymptotically stable.

Proof. We can construct a Lyapunov function $L(t) = I(t)+T(t)+R(t)$, such that

Therefore, when $\mu \geq \alpha S, \quad \mu \geq \alpha (\theta_2 + \theta_3) S$ is true, $L'(t)$ is also true.

Theorem 4. When $A_3 C_2 - B_4 > 0, \ C_1 - B_5 > 0, \ A_1 + B_3 > \theta_1 B_1, \ \mu + \eta - \theta_2 B_1 - B_4 > 0$ is true, $E^*$ is locally asymptotically stable.

Proof. The Jacobian matrix of $E^*$

Let

then the characteristic equation of $J(E^*)$ is

It is known that $\lambda_1 = -\mu < 0$, let

then

The remaining eigenvalues satisfy the equation:

Where

When the conditions $A_3 C_2 - B_4 > 0$, $C_1 - B_5 > 0$, $A_1 + B_3 > \theta_1 B_1$, $\mu + \eta - \theta_2 B_1 - B_4 > 0$ are satisfied, then the following must also be true: $a_0 > 0$, $a_1 a_2 - a_3 a_0 > 0$. According to the Routh—Hurwitz criterion, the equilibrium point $E^*$ where rumors spread is locally asymptotically stable.

Theorem 5. If $R_0 > 1$, the equilibrium point of system $E^*$ is globally asymptotically stable.

Proof. Create the Lyapunov function.

Because $E^*$ exists, and $B - \mu S - \mu I - \mu T - \mu R = 0$ is equal to $B = \mu S^* - \mu I^* - \mu T^* - \mu R^* = 0,$ thus,

Therefore, according to the Lyapunov—Lasalle invariant set principle, $E^*$ is globally asymptotically stable.

4.   Optimal control analysis

The main role of optimal control in rumor propagation is to effectively reduce the spread speed and influence of rumors through means such as monitoring, information intervention, and public education, thereby maintaining social stability and information accuracy.

Based on the above-mentioned rumor-spreading model, three control objectives were proposed. That is, within a certain control time interval, on the one hand, the contact rate between the ignorant and the rumor spreaders should be controlled so that the number of rumor spreaders decreases gradually. Increasing the contact rate between rumor spreaders and truth spreaders makes the number of truth spreaders grow larger. On the other hand, the number of rumor spreaders who are transforming into truth spreaders is increasing; the research institute is studying the corresponding optimal control problem.

Therefore, the three proportional constants $\alpha, \epsilon, \delta$ in the model are replaced with the control variable $\alpha(t), \epsilon(t), \delta(t)$. Use control parameter $\alpha(t)$ to control the proportion of naive individuals who are transformed into rumor spreaders. When rumors spread, ordinary individuals lack good information discrimination ability and find it difficult to effectively identify the authenticity of information. Therefore, through education, people's ability to identify rumors should be enhanced, and they should be trained to effectively recognize false information, thereby reducing the spread of misleading information. Control parameter $\epsilon(t)$ will reduce the number of rumor spreaders and increase the number of immune individuals. Because individuals pay more attention to and identify with the rumors they are interested in, these rumors spread at a higher speed and to a wider extent in social networks. Therefore, the government and relevant institutions should proactively release transparent information and respond promptly to public concerns. As a result, the proportion of rumor spreaders will decrease. Control parameter $\delta(t)$ can make rumor spreaders more likely to become truth spreaders. In an environment with an abundance of information, individuals may selectively receive information that conforms to their preconceived notions, while ignoring or rejecting facts that refute rumors, leading to the continued spread of rumors on social networks. Therefore, the government can set up a reward system to encourage those who actively spread the truth, enhancing their sense of participation and enthusiasm.

Based on the above analysis, the definition of the objective function is as follows:

Seeking the optimal control strategy to minimize the objective functional within the control period, while satisfying the following state equation:

And the initial conditions

Therefore, $\alpha(t), \epsilon(t), \delta(t)$ is a measurable function, where $\alpha(t), \epsilon(t), \delta(t) \in U$ and $0 \leq \alpha(t), \epsilon(t), \delta(t) \leq 1, \quad \forall t \in [0, t_f]$, $t_f$ frepresents the end of the time interval being controlled, assuming that the starting point of the controlled time interval is the zero hour. $U$ represents the allowable set, while $c_1$ and $c_2, c_3$ represent the control strength and importance of the two control measures.

4.1.   The existence of optimal control

Theorem 6. Under the condition that the model dynamics equation (2.1) and initial conditions are satisfied, there exists an optimal control $\mu^* = (\alpha^*, \epsilon^*, \delta^*) \in U$ such that the following equation holds:

Proof. According to the classical optimal control literature, in order to prove the existence of optimal control, it is sufficient to verify the following five conditions:

$(1)$ Both the control variable and the state variable are nonnegative.

$(2)$ The set of admissible sets $U$ is a convex set and a closed set.

$(3)$ The integrand in the objective functional is a convex function defined on the admissible set $U$.

$(4)$ The right-hand side of the state system is a linearly bounded function of the control variables and state variables.

$(5)$ There are constants $d_1, d_2 > 0$ and $g > 1$ such that the integrand in the objective functional is:

And satisfies:

Only when all five of the above conditions are met can the existence of optimal control be proven. Conditions (1)–(3) are clearly met, and now we only need to prove conditions (4) and (5).

Given $N(t) = S(t) + I(t) + T(t) + R(t)$ and upper bounds $N(t)$ for the state variables, the following equation holds:

Then, condition (4) holds. For the final condition: $L(t; \alpha; \epsilon; \delta) \geq d_1 \left(|\alpha|^2 + |\epsilon|^2 + |\delta|^2 \right)^{\frac{g}{2}} - d_2$. Take $d_1 = \min \left\{ \frac{c_1}{2}, \frac{c_2}{2}, \frac{c_3}{2} \right\}$ and any $d_2 \in \mathbb{R}^+, \quad g = 2$ and it also satisfies the condition.

4.2.   Optimal control strategy

In order to better control rumor propagation, optimal control will be implemented. We can define a Hamiltonian function with a penalty term as follows:

Where $\omega_{ij}(t) \geq 0$ is the punishment operator that satisfies:

Theorem 7. There exists a consistent variable $\lambda_i \quad (i = 1, 2, 3, 4)$ that satisfies:

Furthermore, the expression for optimal control is given by $(\alpha^*, \epsilon^*, \delta^*)$.

Proof. According to Pontryagin's maximum principle, by calculating the reciprocal of each state variable to the Hamiltonian operator, a system of covariates can be obtained. The covariate system is:

The definite solution condition for a cooperative system is $\lambda_i(t_f) = 0, \quad i = 1, 2, 3, 4$. Let us now discuss how to obtain the optimal conditions. Taking the partial derivative of the Hamiltonian operator $H$ with respect to the state variable $U = (\alpha, \epsilon, \delta)$ and setting the derivative equal to zero yields:

Find the optimal control expression from this:

To obtain the optimal control without the punishment term $\omega_{11}, \omega_{12}$, the final expressions of the three optimal controls will be considered separately.

First, consider option $\alpha^*$, considering the following three scenarios:

(1) On set$0 < \alpha^*(t) < 1$, let $\omega_{11}(t) = \omega_{12}(t) = 0$, so the optimal control is

(2) On set $\alpha^*(t) = 1$, let $\omega_{11}(t) = 0$ have

(3) On set $\alpha^*(t) = 0$, let $\omega_{12}(t) = 0$ have

Therefore, the final expression for the optimal control $\alpha^*(t)$ is:

Similarly, the final expression of the optimal control $\epsilon^*(t)$, $\delta^*(t)$ is:

Therefore, the optimal control system is

and

5.   Numerical simulation

To analyze the stability and periodicity of the model dynamics equation (2.1), numerical simulations were conducted using optimization algorithms. Suppose we are analyzing the spread of rumors on a social media platform. Every day, many new users join this platform, and some of them post and spread rumors. Suppose that 2,000 new users join the platform every day, and they have no idea about its content. Some users began to spread false information on the platform by forwarding rumors, commenting, and giving likes. Each rumor spreader can come into contact with 10 ignorant people every day, and there is a 1% probability of converting these ignorant people into new spreaders. Meanwhile, 5% of the rumor spreaders no longer participate in spreading rumors or stop using social media every day, resulting in a decrease in their number. During this process, 2,000 new users join the platform every day, which is the number of people entering the system per unit time, B. If 5% of the rumor spreaders no longer participate in spreading or stop using social media every day, this is the exit rate of the social group within a unit of time. The statement that each rumor spreader can come into contact with 10 ignorant people every day indicates the probability of contact between ignorant people and rumor spreaders. In this paper, the numerical simulation of the model dynamics equation (2.1) was carried out based on the parameter values from relevant similar literature, and the rationality of the theoretical analysis results and conclusions mentioned above was verified.

5.1.   Numerical simulation of system stability

In the relevant literature, there is no uniform standard for the range of values of model parameters, and in most cases, these parameters are limited to positive numbers. Therefore, we referred to the numerical values in the existing literature and combined the requirements of stability conditions to set the parameter values in the numerical simulation. Through numerical simulations, we verified the rationality of the theoretical results. Meanwhile, we simulated the parameter values and optimal control, and the simulation results further supported our conclusions.

First, the stability of the equilibrium point is analyzed, as shown in Figures 2 and 3. Then, the effects of various parameters in the model dynamics equation (2.1) on the model were discussed, as shown in Figures 4–6.

Let $B = 1, \quad \alpha = 0.7, \quad \theta_1 = 0.5, \quad \theta_2 = 0.3, \quad \theta_3 = 0.2, \quad \epsilon = 0.3$, $\delta = 0.6, \quad \eta = 0.2, \quad \mu = 0.7$ and calculate the following: $R_1 = 0.5 < 1, R_2 = 0.3 < 1$. As shown in Figure 2, it can be seen that the number of $I(t), T(t), R(t)$ tends to approach 0 while the number of $S(t)$ tends to approach 1. In other words, in an idealized rumor propagation model, as time goes on, the number of rumor spreaders will eventually disappear, $S(t)$ will ultimately equal the total number of individuals in the rumor system, and individuals in the system will tend to stabilize. This means that rumors have a limited lifespan, and they eventually die out as the group's perception changes and the transmission channels break down.

Similarly, let $B = 1, \, \alpha = 0.6, \, \theta_1 = 0.6, \, \theta_2 = 0.1$, $\theta_3 = 0.3, \, \varepsilon = 0.4, \, \delta = 0.2, \, \eta = 0.2, \, \mu = 0.3$, and calculate $A_3 C_2 - B_4 > 0, \quad C_1 - B_5 > 0$, $A_1 + B_3 > \theta_1 B_1, \quad \mu + \eta - \theta_2 B_1 - B_4 > 0$, where the parameter values are set to satisfy the conditions of Theorem 4. At this point, Figure 3 clearly shows that the equilibrium point $E^*$ where rumor spreads is locally asymptotically stable under these parameters.

From Figure 3, it can be seen that in the early stages of rumor propagation, individuals with different levels of awareness have different perceptions of the rumor. Therefore, the number of $I(t), T(t)$ will drop sharply in a short period of time and then stabilize, while the number of $R(t)$ will rise sharply in a short period of time and reach a peak, then start to decline and eventually stabilize. The above trends indicate that rumors are manageable over time, but they will not disappear and will continue to exist.

To investigate the impact of different parameter values on rumor propagation in the model dynamics equation (2.1), we plotted the relationship between parameter changes and changes in the number of cabins, and drew conclusions from the resulting graph.

The following Figure 4 shows the variation of the number of $I(t)$ with different values of parameters $\alpha, \, \delta, \, \varepsilon, \, \theta_1$. As shown in the chart, $\alpha, \, \theta_1$ is positively correlated with $I(t)$, while $\delta, \, \varepsilon$ is negatively correlated with $I(t)$. Therefore, in order to reduce the number of $I(t)$, the value of $\alpha, \, \theta_1$ needs to be reduced and the value of $\delta, \, \varepsilon$ needs to be increased.

The following Figure 5 shows the variation of the number of $T(t)$ with different values of $\alpha$, $\delta$, $\eta$, and $\theta_2$. As shown in the chart, $\alpha$, $\delta$, and $\theta_2$ are positively correlated with $T(t)$, while $\eta$ is negatively correlated with $T(t)$. Therefore, to increase $T(t)$, the values of $\alpha$, $\delta$, and $\theta_2$ need to be increased, and the value of $\eta$ needs to be reduced.

The following Figure 6 shows the variation trend of the number of $R(t)$ with different values of $\alpha$, $\varepsilon$, $\eta$, and $\theta_3$. As shown in the figure, $\alpha$, $\varepsilon$, $\eta$, and $\theta_3$ are positively correlated with $R(t)$. Therefore, in order to increase $R(t)$, the values of $\alpha$, $\varepsilon$, $\eta$, and $\theta_3$ need to be increased.

In summary, to reduce the spread of rumors in society, it is necessary to reduce the contact rate between ignorant people and rumor spreaders, increase the probability of rumor spreaders transforming into truth spreaders, and raise the immunity rate. Therefore, to reduce the spread of rumors, we will control the spread of rumors by controlling the value of parameter $\alpha$, $\varepsilon$, $\delta$.

5.2.   Optimal control analysis

Figure 7 was created by varying the values of $\alpha$, $\varepsilon$, and $\delta$.

Because optimal control primarily controls the population density of rumor spreaders and truth spreaders, Figure 7 shows $I(t)$, $T(t)$. It is clearly evident that the optimal control outperforms the intermediate control and the single control. Under optimal control, the number of rumor spreaders eventually decreases to zero, while the number of truth spreaders gradually increases, effectively controlling the spread of rumors.

In real life, we can take specific measures to control parameters and the spread of rumors. Therefore, the government should promote the use of information verification websites and tools, so that the public can easily verify information they receive. Meanwhile, the government can strengthen the rumor reporting mechanism, encourage users to report false information, and promptly handle and delete false content, thus effectively suppressing the spread of rumors.

6.   Sensitivity analysis

To discuss the impact of parameters $\alpha$, $\varepsilon$, $\beta$, and $\eta$ on $R_1$ and $R_2$, we analyzed the basic reproductive numbers

and created a three-dimensional relationship graph, as shown in Figures 8 and 9.

We can calculate

The above formula shows that when $\alpha$ increases, the basic reproduction number $R_1$ also increases, indicating that as the contact rate between ignorants and rumor spreaders increases, the number of rumor spreaders will also increase. On the other hand, when $\epsilon$ increases, $R_1$ decreases, which indicates that the probability of rumor spreaders becoming immune is higher, and the number of rumors in the system will be fewer. Therefore, reducing the contact rate between ignorant people and rumor spreaders, and increasing the probability of transforming spreaders into immune individuals, can effectively reduce the spread of rumors and control them.

The above formula shows that when $\alpha$ increases, the basic reproduction number $R_2$ also increases, indicating that as the rate of contact between ignorants and truth spreaders increases, the number of truth spreaders will also increase. On the other hand, when $\eta$ increases, $R_2$ decreases, which indicates that the probability of truth spreaders becoming immune increases, and the number of immune individuals increases accordingly. Therefore, increasing the exposure rate of uninformed individuals to truth spreaders and increasing the probability of transforming spreaders into immunized individuals can effectively reduce the spread of rumors and control them.

7.   Conclusions

This paper builds on the classic SIR model and takes into account the individual's ability to process information in rumor spreading, establishing the SITR model. It analyzes the basic reproduction number, equilibrium point, and stability of rumors, and takes optimal control strategies. Through numerical simulations, the theoretical results are verified.

The main conclusions of this paper are as follows:

(1) When the basic reproduction number $R < 1$ is reached, rumors in the system will disappear over time; when the basic reproduction number $R > 1$ is reached, rumors in the system will not disappear and will eventually reach a stable state.

(2) Reducing the contact rate between $S(t)$ and $I(t)$ increasing the probability of $I(t)$ converting to $T(t)$ and raising the probability of spreaders becoming immune can all help to suppress the spread of rumors to varying degrees.

(3) While effective measures such as market regulation and dissemination of correct knowledge can control the spread of rumors, they cannot completely prevent them.

Rumors are a complex social phenomenon that involves various environments and factors, and further research on the subject is needed. This article conducted a preliminary exploration of the impact of individual differences in discernment ability on rumor propagation. In addition to the changes in different compartments considered in this paper, the influence of hesitant individuals on rumor spreading or the effect of the interaction between external environment and individual psychology on rumor spreading can also be introduced. Besides, the model in this paper assumes that everyone acts in the same way, which has certain limitations, because an individual's behavior may be influenced by various factors such as cultural background and social roles. It is expected that future research can further refine model building and validation, provide more effective strategies for suppressing rumor propagation, and provide a healthy information environment for society.

Author contributions

Xingtong Wang: Writing – original draft, Writing – review & editing; Sida Kang: Writing – original draft; Yuhan Hu: Supervision, Writing – review & editing.

Use of Generative-AI tools declaration

The authors declare they have not use Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Social Science Planning Fund of Liaoning Province China (No. L22AGL015).

Conflict of interest

All authors declare no conflicts of interest in this paper.