Heat diffusion in a channel under white noise modeling of turbulence

1.   Introduction

In the last four years, a new understanding of heat diffusion in a turbulant fluid modeled by white noise has been developed. The equation for the heat diffusion and transport, with a heat source $q$, is

where $\theta = \theta\left(t, x\right)$ is the temperature, $\kappa$ is the diffusion constant and $u = u\left(t, x\right)$ is the velocity field of the fluid. By turbulent fluid modeled by white noise we mean the case when, instead of considering true equations of motion of the fluid (which should also include the effect of the temperature on the motion), we assume that $u$ is a random field, Gaussian and white in time, with covariance structure give a priori (hence the temperature is a passive scalar). In this paper we choose the following description for $u$:

where $\sigma_{k}$ are vector fields and $W_{t}^{k}$ are independent Brownian motions on a filtered probability space $\left(\Omega, \mathcal{F}, \left(\mathcal{F}_{t}\right) _{t\geq0}, \mathbb{P}\right)$; for simplicity, assume $K$ is a finite set, but the case of a countable set can be studied without troubles at the price of additional summability assumptions. As expained in a number of classical or more modern works ^{[4,5,19,20,30,34,35]}, which extend to SPDE the remarkable principle of Wong-Zakai ^[36], the correct interpretation of Eq (1.1) when $u$ has the form (1.2) is the Stratonovich equation

or equivalently the Itô equation with corrector $\mathcal{L}\theta$ given by the second order differential operator (2.1) below:

This is the equation we shall investigate below.

Diffusion in a white noise velocity field is a classical subject, see for instance ^{[6,15,17,24,25,28,33]}. The new approach mentioned at the beginning of the introduction started with ^[16], and was interpreted initially as a scaling limit, for a suitable parametrization of the coefficients $\sigma_{k}\left(x\right)$ of the noise, such that in the limit the solution of Eq (1.4) converges (in a suitable topology) to the solution of the deterministic parabolic equation

where for simplicity of exposition we assume that the source $q$ is deterministic. Assuming that also the initial temperature $\theta_{0}$ is deterministic, the solution $\Theta$ is the average of $\theta$:

where $\mathbb{E}$ denotes the mathematical expectation on $\left(\Omega, \mathcal{F}, \mathbb{P}\right)$. That the mean temperature $\Theta\left(t, x\right)$ has enhanced dissipative properties (due to $\mathcal{L}$) was obviously well known, see for instance ^[28] Chapter 4, but the fact that in a suitable scaling limit the solution $\theta\left(t, x\right)$ was close to its average $\Theta\left(t, x\right)$ is a new information provided by ^[16]. Later on this result was perfectioned into quantitative estimates on the difference $\theta-\Theta$, in ^[11] and ^[12]; the present note is a continuation of these works. Let us mention the very important fact that both the scaling limit framework of ^[16] and the quantitative estimates extend to nonlinear problems, like the Navier-Stokes equations and others, as well as Wong-Zakai type results which motivate the Stratonovich operation, see ^{[9,10,12,13,14,21,22,23,26,27]}.

As already said, the present work is a continuation of ^[11,12]. The main novelty, beside the fact that we work in an infinite 2D channel, is the presence of a heat source $q$, neglected in previous works. This detail has an important consequence, not investigated before: that the deterministic Eq (1.5) has a unique non trivial stationary solution $\Theta_{st}$ and it becomes interesting to understand whether the solution $\theta$ of the stochastic problem (1.4) is close to $\Theta_{st}$, for large times. One of our main results, Theorem 7 below, gives sufficient conditions on the noise to have that $\theta$ is close to $\Theta_{st}$.

In Section 2 we define precisely the problem and state the main results, including the numerical ones. In Section 3 we prove the well posedness of the equations and in Section 4 we prove the main result on the link between $\theta\left(t, x\right)$ and $\Theta_{st}$.

Remark 1. We only focused our attention on an infinite 2d channel, to avoid the potential confusion of mixing different set-ups. However, all the results can be extended to $\mathbb{R}^d \times (-1, 1)$ and $\mathbb{T}^d\times (-1, 1)$ ($\mathbb{T}^d$ being the torus in dimension d), for both $d = 1, 2$, without any change or addition of stronger assumptions on the coefficients $\sigma_k$, the heat source $q$ and the initial condition $\theta_0$. To this purpose two key remarks are the validity of Poincaré inequality in these domains as well as the embedding of $W^{2, 2}$ into $L^{\infty}$.

2.   Main results

2.1.   Notations and definitions

Consider the 2D domain $D = \mathbb{R}\times\left(-1, 1\right)$, namely an infinite channel. We write the coordinates using the notation

because the global notation $x$ appears very often but also the vertical coordinate $z$ will play a basic role. Let $Z$ be a separable Hilbert space, denote by $L^2(\mathcal{F}_{t_0}, Z)$ the space of square integrable random variables with values in $Z$, measurable with respect to $\mathcal{F}_{t_0}$. Moreover, denote by $C_{\mathcal{F}}\left(\left[0, T\right]; Z\right)$ the space of continuous adapted processes $\left(X_{t}\right) _{t\in\left[0, T\right] }$ with values in $Z$ such that

and by $L_{\mathcal{F}}^{2}\left(0, T; Z\right)$ the space of progressively measurable processes $\left(X_{t}\right) _{t\in\left[0, T\right] }$ with values in $Z$ such that

Denote by $L^{2}\left(D\right)$ and $W^{k, 2}\left(D\right)$ the usual Lebesgue and Sobolev spaces and by $W_{0}^{k, 2}\left(D\right)$ the closure in $W^{k, 2}\left(D\right)$ of smooth compact support functions. Set $H = L^{2}\left(D\right)$, $V = W_{0}^{1, 2}\left(D\right)$, $D\left(A\right) = W^{2, 2}\left(D\right) \cap V$. We denote by $\langle\cdot, \cdot\rangle$ and $\lVert\cdot\rVert$ the inner product and the norm in $H$ respectively.

Assume that $K$ is a finite set and $\sigma_{k}\in \left(D\left(A\right)\cap C_{b}^{\infty}\left(D\right)\right)^2, \ \operatorname{div}\sigma_k = 0$, $k\in K$ (less is sufficient but we do not stress this level of generality). Define the matrix-valued function

If we denote by $W\left(t, x\right)$ the vector valued random field

(the velocity field $u$ given by (1.2) is the distributional time derivative of $W$) then we see that $Q\left(x, y\right)$ is the space-covarance of $W\left(1, x\right)$:

The matrix-function $Q\left(x, x\right)$ is elliptic:

for all $\xi = \left(\xi_{1}, ..., \xi_{d}\right) \in\mathbb{R}^{d}$. Consider the divergence form elliptic operator $\mathcal{L}$ defined as

for $\theta\in W^{2, 2}\left(D\right)$. Define the linear operator $A:D\left(A\right) \subset H\rightarrow H$ as

It is the infinitesimal generator of an analytic semigroup, see Section 3 and ^[31], that we denote by $e^{tA}$, $t\geq0$. Moreover, we denote by $V_{\alpha}$ the Hilbert space $D((-A)^{\frac{\alpha}{2}})$, see Section 3.

Definition 2. Given $\theta_{0}\in L^{2}(\mathcal{F}_{0}, H)$ and $q\in L^2(0, T; H)$, a stochastic process

is a mild solution of equation (1.4) if the following identity holds

for every $t\in\left[0, T\right]$, $\mathbb{P}$-a.s.

2.2.   Existence, uniqueness and regularity

Definition 3. Let $\alpha\in\mathbb{R}$. Problem (1.4) is well posed in $V_{\alpha}$, if for every $\theta_{0}\in L^{2}(\mathcal{F} _0, V_{\alpha})$ and $q\in L^2(0, T; V_{\alpha})$ there exists a unique $\theta$ mild solution of Eq (1.4) in $C_{\mathcal{F}} ([0, T]; V_{\alpha})\cap L_{\mathcal{F}}^{2}(0, T; V_{\alpha+1})$. Moreover $\theta$ depends continuously on $\theta_0$ and $q$.

Theorem 4. Equation (1.4) is well posed in $H$ in the sense of definition 3.

Theorem 5. Equation (1.4) is well posed in $V_{\alpha}$ for $0\leq\alpha\leq2$ in the sense of definition 3.

Moreover, if we assume only $\theta_0\in L^2(\mathcal{F}_0, H)$ and $q\in L^2(0, T; V_{\alpha})$ for some $0\leq\alpha\leq2$, then for every $\epsilon\in (0, T)$ we have $\theta|_{[\epsilon, T]}\in C_{\mathcal{F}}(\epsilon, T; V_{\alpha})\cap L^2_{\mathcal{F}}(\epsilon, T; V_{\alpha+1})$ and this restriction depends continuously on $\theta_0$ and $q$.

It is possible to get stronger regularity results adding further assumputions on the coefficients $\sigma_k$, see ^[8] for similar results in bounded domains. We do not stress these assumptions because in the following sections we need just the estimate guaranteed by the following corollary.

Corollary 6. If $\theta_0\in L^2(\mathcal{F}_0;D(A)), \ q(t)\equiv q\in D(A)$, then

for some $C$ independent from $T$.

2.3.   Link between $\theta\left(t, x\right)$ and the stationary solution $\Theta_{st}$

In this section we state our main result about the behavior of $\theta\left(t\right)$ for large times. Assume that $q$ is independent of time and introduce the stationary solution of Eq (1.5):

Define $\epsilon_{Q}\geq0$ as the smallest number such that

for all $v\in L^{2}\left(D, \mathbb{R}^{d}\right)$. Call $C_{\infty}\left(\theta_{0}, q\right) > 0$ a constant such that

Theorem 7. For every $\phi\in H$,

The theorem is proved in Section 4 below. The existence of a constant $C_{\infty}\left(\theta_{0}, q\right)$ is provided by Corollary 6 above. In order to be of interest for applications, this theorem requires two conditions:

$1).$ that $\epsilon_{Q}$ is small.

$2).$ that $\Theta_{st}$ is significantly affected by the noise.

In this section we discuss the first problem, the size of $\epsilon_{Q}$. In the next section we give numerical simulations which show the great difference between the prensence or absence of noise in the shape of $\Theta_{st}$.

Proposition 8. Assume that the family of coefficients $\left(\sigma_{k}\left( \cdot\right) \right) _{k\in K}$ has the following approximate orthogonality property: there exists a finite number $M\in\mathbb{N}$ and a partition $K = K_{1}\cup...\cup K_{M}$ such that

for all $i = 1, ..., M$. Then

Proof.

The approximate orthogonality property imposed in the previous proposition is a consequence, in examples, of the fact that the supports of elements of $K_{i}$ are disjoint, for all $i = 1, ..., M$. Therefore the approximation between $\theta\left(t\right)$ and $\Theta_{st}$ is good if the coefficients $\sigma_{k}$ have sufficiently disjoint supports and have sufficiently small size $\left\Vert \sigma_{k}\right\Vert^{2}$.

These conditions are compatible with a strong modification of the profile $\Theta_{st}$, with respect to the case of the parabolic profile given by the solution of $\kappa\Delta\theta = -q$. For other domains, in ^[11], a theoretical investigation of the difference is made; the theoretical result requires strong conditions; for instance the cardinality of $K$ must be very large and a finite but not small $M$ is required: certain supports have to overlap so that the noise acts everywhere. In the present work we show numerically, in the next section, that $\Theta_{st}$ differs significantly from the parabolic profile even for relatively modest sets $K$ and for $M = 1$.

2.4.   Numerical results

As announced in the previous section, the purpose of this numerical section is to show that the presence of the correction $\mathcal{L}\theta$, due to the noise, in the deterministic Eq (1.5), modifies the asymptotic profile, even when the noise is weak in intensity, as described in the previous section, in order to have a small constant $\epsilon_{Q}$.

We explain here this fact in two ways. The first one is theoretical, based on a very ideal noise. The second one is numerical.

2.4.1.   An ideal computation

In this subsection we suspend the requirement that $q, \Theta$ have to decay at infinity and accept a geometrically simpler case, although not strictly covered by the previous theory. We assume that the function $q\left(x\right)$ is equal to a constant $q$, and both the stationary solution $\Theta_{st}\left(x\right)$ and $Q\left(x, x\right)$ depend only on the vertical direction $z\in\left[-1, 1\right]$ and they are symmetric with respect to $z = 0$; and smooth. The equation

becomes

It gives us

without constants, since both sides of the identity should vanish at $z = 0$ (the function $\Theta_{st}$ is symmetric with respect to $z = 0$ and smooth, hence $\partial_{z}\Theta_{st}\left(0\right) = 0$). Therefore we have to solve

The solution of the previous equation is

Without noise the solution is

so the curvature $\frac{q}{\kappa}$ is large (for $\kappa$ small) and also the maximum is large:

Assume

with large $\sigma^{2}$ and small $\delta$. Then

If $z\in\left[-1, -1+\delta\right]$ we have

like in the case without noise but, for $z\in\left[-1+\delta, 0\right]$ we have

The curvature $\frac{q}{\kappa+c_{1}\sigma^{2}}$ is much smaller than $\frac{q}{\kappa}$ and the maximum

is very small for large $\sigma^{2}$ and small $\delta$.

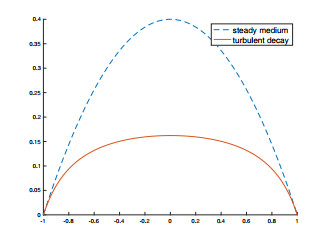
Figure 1 illustrates the modification of profile, from the standard parabolic one of free diffusion in a steady medium, to the case of turbulent decay. The reduction in heat content can be dramatic, due to turbulence, creating a fundamental engineering problem.

2.4.2.   2d numerical simulation of stationary solutions

The purpose of this subsection is the numerical simulation of the effects of an operator $\mathcal{L}$, based on the idea of vortex structures, to the solution of the problem

More details on the construction of this operator $\mathcal{L}$ can be found in ^[11]. In this subsection we continue to suspend the requirement that $q, \Theta$ have to decay at infinity and accept that the function $q\left(x\right)$ is equal to a constant $q$.

Recalling that

the $\sigma_k$'s are chosen in order to be a rescaled and shifted version of a vector field $w$ which satisfies several conditions:

$1).$ $w$ is smooth and $\operatorname{div} w = 0$;

$2).$ $w$ has compact support contained in $\overline{B(0, 1)}$;

$3).$ $w$ is close to $\frac{1}{2\pi}\frac{x^{\perp}}{|x|^2}$ near $x = 0$.

The first two properties are useful in order to have that the $\sigma_k$'s model the velocity of an incompressible fluid at rest. The third one is close to our idea of vortex structures. In particular, for $r > 0$ and $\{x_k\}_{k\in K}\subseteq \mathbb{R}^{2|K|}$ fixed, then

where $\Gamma$ is another parameter larger than $0$. It remains to describe how to choose $w$. We construct it as $w = \nabla^{\perp}\psi$ so that it is divergence free. It remains to fix $\psi$ compactly supported in $\overline{B(0, 1)}$ such that it is close to $\frac{log|x|}{2\pi}$ near $x = 0$.

where $f_{\epsilon}$ is a mollifier with support in $B(0, \epsilon)$ and $\psi_0$ is a $C^{\infty}(\mathbb{R}^2 \setminus \{0\})$ radial function such that

For numerical reasons we consider the problem in the bounded domain

In order to have that the $\sigma_k$'s model a fluid at rest, we can take

These are the real constraints on the parameters of our numerical simulation. The other parameters $\Gamma, \ K, \ \{x_k\}_{k\in K}$ can be chosen more arbitrarily in order to have satisfactory results. In fact, even if we do not examine the other constraints described in ^[11] the profile changes considerably in the region where the vortex structures have an impact.

The centers of the vortex structures $\{x_k\}$ have been chosen on a grid equally spaced in both directions. In particular we have chosen to take $10$ points in the $x_1$ direction between $-0.5$ and $0.5$ and $3$ points in the $z$ direction between $-0.05$ and $0.05$. Moreover, we take $r = 0.04, \ \epsilon = 0.1$ and $\Gamma = 0.02\sqrt{2}$. The other parameters of the problem are $\kappa = 0.05$ and $q\equiv1$. In this way the impact of the operator $\mathcal{L}$ is related to a small portion of the domain $\tilde{D}$ and we can completely appreciate how it changes the profile of the solution.

Figures 2 and 3 illustrate the modification of the profile, from the standard parabolic one of free diffusion in a steady medium, to the case of turbulent decay. Even if we use just a really reduced number of vortices we can observe a significant decay modification of the profile due to turbulence.

3.   Proof of Theorems 4, 5 and Corollary 6

3.1.   Abstract results

The following abstract results are taken from ^[8]. The regularity theory of these equations has been recently raised and improved by ^[2,3,29], where the reader may find additional results.

Let $H$ be a separable Hilbert space, $A:D(A)\subseteq H\rightarrow H$ the infinitesimal generator of a strongly continuous semigroup of negative type. Under these assumptions the family

forms a Hilbert scale with inner product $\langle\cdot, \cdot\rangle_{V_{\alpha}}$ and norm $\lVert\cdot\rVert_{V_{\alpha}}$, see ^[32]. We note that

are linear bounded operators. For $\alpha > 0$ we mean the restriction of $A$ to $V_{\alpha+2}$ and for $\alpha < 0$ there exists a unique linear bounded extension of $A$ from $V_{\alpha+2}$ and $V_{\alpha}$. Moreover, $\forall\alpha\in\mathbb{R}$, $A$ generates an analytic semigroup of negative type in $V_{\alpha}$ denoted by $e^{At}\in L(V_{\alpha}), \ t\geq 0$.

Consider the stochastic evolution equation

interpreted in mild sense

Definition 9. Let $\alpha\in\mathbb{R}, \ B^{k}\in L(V_{\alpha+1}, V_{\alpha})$, problem (3.1) is well posed in $V_{\alpha}$, if for every $u_{0}\in L^{2}(\mathcal{F} _{t_0}, V_{\alpha})$ and $q\in L^2(t_0, T; V_{\alpha})$ there exists a unique $u$ mild solution of Eq (3.2) in $C_{\mathcal{F}} ([0, T]; V_{\alpha})\cap L_{\mathcal{F}}^{2}(0, T; V_{\alpha+1})$. Moreover $u$ depends continuously on $u_0$ and $q$.

Theorem 10. Let $\alpha\in \mathbb{R}$ be fixed. Let $B^{k}\in L(V_{\alpha+1}, V_{\alpha})$ such that

and

for some constants $\eta\in(0, 1)$ $\lambda\geq0$ and $c > 0$. Then Eq (3.1) is well posed in $V_{\alpha}$. Moreover

for $\phi(t) = e^{At}u_0+\int_{t_0}^t e^{A(t-s)}q(s)\ ds$ and some constant $c > 0$ independent of $u_0$ and $q$.

Theorem 11. Let $\alpha < \beta$ be given real numbers. If Eq (3.1) is well posed in $V_{\alpha}$ and $V_{\beta}$, then it is well posed in $V_{\gamma}$ for all $\gamma\in[\alpha, \beta]$. Moreover, for every $u_0\in L^2_{\mathcal{F}}(V_{\alpha})$, $q \in L^2(t_0, T; V_{\beta})$ and $\epsilon\in (t_0, T)$, then $u|_{[\epsilon, T]}\in C_{\mathcal{F}}(\epsilon, T; V_{\beta})\cap L^2_{\mathcal{F}}(\epsilon, T; V_{\beta+1})$ and depends continuously from $u_0$ and $q$.

Theorem 12. Fixed $\alpha\in\mathbb{R}$, if the assumptions of theorem 10 hold true and

● $B^{k}\in L(V_{\alpha+3}, V_{\alpha+2})$;

● $L^{k}: = AB^{k}-B^{k}A\in L(V_{\alpha+3}, V_{\alpha})$ and

for some $c_{2} > 0$

then

for some $\tilde{\eta}\in(0, 1)$, $\tilde{\lambda}\geq0$ and $c > 0$. In particular Eq (3.1) is well posed in $V_{\alpha+2}$.

3.2.   Some results on elliptic operators

Let $A, \ H, \ V, \ D(A)$ and $D$ as described in Section 2.1. In particular $A$ is an elliptic operator. In fact $\forall x\in D$ and $\xi\in\mathbb{R}^2$

Moreover from the boundedness of $D$ in the second direction the Poincaré inequality holds, namely

For the operator $A$ the following results hold, see for example ^[1,7,18].

Proposition 13. -A is self-adjoint.

Proposition 14. A is the infinitesimal generator of an analytic semigroup of negative type.

Under these assumptions, as described in Section 3.1, the family

form a Hilbert scale with inner product $\langle\cdot, \cdot\rangle_{V_{\alpha}}$ and norm $\lVert\cdot\rVert_{V_{\alpha}}$. We note that

are linear bounder operators. For $\alpha > 0$ we mean the restriction of $A$ to $V_{\alpha+2}$ and for $\alpha < 0$ there exists a unique linear bounded extension of $A$ from $V_{\alpha+2}$ and $V_{\alpha}$. Moreover, $\forall\alpha\in\mathbb{R}$, $A$ generates an analytic semigroup of negative type in $V_{\alpha}$ denoted by $e^{At}\in L(V_{\alpha}), \ t\geq 0$.

Proposition 15.

● $D((-A)^{\theta}) = H^{2\theta}(D)\ \ \ if\ \theta\in(0, \frac {1}{4})$;

● $D((-A)^{\theta}) = \{u\in H^{2\theta}(D):\ u|_{\partial D} = 0\}\ \ \ if\ \theta\in(\frac{1}{4}, 1)$.

In particular, $H = V_0, \ V = V_1, \ D(A) = V_2$.

3.3.   Well posedness

3.3.1.   Reformulation of the problem

Equation (1.4) can be rewritten as

where $B^{k}u: = -\sum_{j = 1} ^{2}\sigma_{k}^{j}\frac{\partial u}{\partial x_{j}}$. $B^{k}\in L(V_{1}, H)$ without any further assumption on $\{\sigma_k\}_{k\in K}$. The linearity is obvious, the continuity follows from the boundedness of $\sigma_k$.

Definition 16. Given $\theta_{0}\in L^{2}(\mathcal{F}_{0}, H)$ and $q\in L^2(0, T; H)$, we say that a stochastic process $\theta$ is a weak solution of Eq (1.4) if

and for every $\phi\in D(A)$, we have

for every $t \in[0, T], \ \mathbb{P}-a.s.$

Proposition 17. $\theta$ is a weak solution of problem (1.4) if and only if is a mild solution of problem (1.4).

Proof. Let $\theta(t)$ be a weak solution and $\phi(t)\in C^{1}([0, T]; H)\cap C([0, T]; D(A))$. Let, moreover, $\pi = \{0 = t_{0} < t_{1} < \dots < T_{n} = T\}$ be a partition of $[0, T]$. Thus, using the identity

we get

It implies

where $s_{\pi}^{-}(s) = t_{i}$ if $s\in[t_{i}, t_{i+1}]$ and $s_{\pi}^{+}(s) = t_{i+1}$ if $s\in[t_{i}, t_{i+1}]$. Taking the limit over a sequence of partitions $\pi_N$ with size going to zero, we get

(thanks to the regularity of $\theta, \ \phi, \ q$, dominated convergence theorem and Itô isometry). The argument applies to a generic $t\in[0, T]$, hence we have

For such value of $t$, take the function $\phi_{t}(s) = e^{(t-s)A}\psi$ with $\psi\in D(A)$. This function is of class $\phi _{t}\in C^{1}([0, t]; H)\cap C([0, t]; D(A))$. Hence from previous identity we get

Recalling that $B^{k}v = -\sigma_{k}\cdot\nabla v, \ \operatorname{div}(\sigma_{k}) = 0$, integrating by parts and using the fact that $A$ is selfadjoint we get

By the arbitrarity of $\psi$ we get that $\theta$ is a mild solution, namely

Let now $\theta(t)$ be a mild solution and $\phi\in D(A)$. Doing the scalar product between $\theta(t)$ and $\phi$ we get

Let us analyze the quantity $\langle e^{tA}\theta_{0}, \phi\rangle$. Using the fact that $A$ is selfadjoint and integrating by parts backwards we get

Now thanks to the regularity of $\phi\in D(A)$ and the fact that $A$ is selfadjoint, exploiting the definition of mild solution we get

Let us note that

Thus we can apply the stochastic Fubini theorem to the stochastic integrals and, exploiting arguments analogous to the previous ones, we get

Applying Fubini theorem to $-\int_0^t ds\int_0^s \ du \langle e^{(s-u)A}q(u), A\phi\rangle$ we get

Putting together all these relations we get the weak formulation.

Remark 18. From the weak formulation we can obtain easily the Itô formula

Thanks to the results of Section 3.2 we know that $A$ is the infinitesimal generator of an analytic semigroup of negative type, hence we can apply the abstract results of Section 3.1.

3.3.2.   Proof of Theorem 4

Thanks to theorem 10 it is enough to show that there exist $\eta\in(0, 1), \lambda\geq0, \ c > 0$ such that:

$1).$ $\frac{1}{2}\sum_{k\in K}\lVert\sum_{j = 1}^{2} \sigma_{k}^{j}\frac{\partial u}{\partial x_{j}}\rVert^{2}\leq-\eta\langle Au, u\rangle+\lambda\lVert u\rVert^{2}\ \ \forall u\in D(A)$.

$2).$ $\sum_{k\in K}\lVert \sum_{j = 1}^{2} \sigma_{k}^{j}\frac{\partial u}{\partial x_{j}}\rVert^{2}\leq c\lVert u\rVert_{V}^{2}\ \ \forall u\in V$.

$1).$ Calling $M: = \lVert Q\rVert _{L^{\infty}(D)}$, the first inequality holds taking $\lambda\geq0, \ \eta\in[\frac{M}{2\kappa+M}, 1)$. In fact

and

Under previous assumptions on $\lambda$ and $\eta$

In particular, if we choose $\eta = \frac{M}{2\kappa+M}$ and $\lambda = 0$ we get

$2).$ The second inequality is satisfied taking $c = M: = \lVert Q\rVert_{L^{\infty}(D)}$. In fact, as above,

The assumptions of theorem 10 are satisfied for $\alpha = 0$. In particular, Eq (1.4) is well posed in $H$ and the thesis follows.

Remark 19. As a corollary one gets existence and uniqueness of the weak solution in the sense of definition 16.

3.3.3.   Proof of Theorem 5 and Corollary 6

$1).$ Theorem 5. Since Theorem 4 was proved verifying the assumptions of Theorem 10, we can exploit a bootstrapping procedure thanks to Theorem 11 and 12. Regardless of the other hypotheses, if $B^{k}\in L(V_{3}, D(A))$ then

In particular, if $u\in V_{3}$ thanks to the regularity of $\sigma_{k}$, then

Moreover, thanks to the assumptions on $\sigma_k$, $B^{k}\in L(V_{3}, D(A))$. The linearity is obvious. If $u\in V_{3}$, then $B^{k}u\in D(A)$ which means in particular that $B^{k}u|_{\{x_{2} = \pm 1\}} = 0.$ In fact

The continuity follows from the boundedness of the derivatives of $\sigma_k$ and by the equivalence between the norm of $H^{3}(D)$ and $V_{3}$ for $u\in V_{3}$. Then we get the first part of the thesis applying Theorem 12 and Theorem 11. The second part follows by the first one and Theorem 11.

$2).$ Corollary 6. Under these assumptions

thus from the Itô formula described in Remark 18, with starting time $t_0 = t$ and ending time $t+h$ we get

Looking carefully at the proof of Theorem 4 we know that $\exists\eta\in (0, 1)$ such that

Thus, taking the expected value and exploiting this relation, Young and Poincaré inequalities we get

namely there exist $C_1, \ C_2$ depending on $\eta, \ \kappa$ and $C_p$ such that

From Eq (3.4), exploiting the arbitrariness of $t$ and $h$ and the regularity of $\theta$, we can apply Gronwall's lemma in differential form proving that

Moreover we can apply the second part of Theorem 5 with parameters

$t_0 = t, \ T = t+2$. From the regularity of $\theta$ we get that

thus thanks to previous inequality

From the arbitrariness of $t$

It remains to show that

This inequality can be obtained directly from the well-posedness in $D(A)$ and we omit the details. Lastly by Sobolev embedding theorem, recalling that

we get the thesis.

4.   Proof of Theorem 7

Recall the identity

Set

Then

If $\phi\in H$,

Then (here we take advantage of the cancellations of Itô integrals)

Write $\phi_{t, s}: = e^{\left(t-s\right) A}\phi$. Then

Therefore

Now we use the fact that

Indeed,

For every $\epsilon > 0$, from the inequality $\left(a+b\right) ^{2} \leq\left(1+\epsilon\right) a^{2}+\left(1+\frac{4}{\epsilon}\right) b^{2}$ we have

This implies the result of the theorem.

Conflict of interest

The authors declare no conflict of interest.