Elevated ADAR expression is significantly linked to shorter overall survival and immune infiltration in patients with lung adenocarcinoma

1.   Introduction

The general fifth-order KdV equation is dedicated in a variety of scientific fields which is expressed by in the form of

where $a, b$ and $c$ are unknown constants. Many researchers have been studied symmetry reductions, consevation laws by using Lie symmetry analysis and exact traveling wave solutions of Eq (1.1) ^{[1,2,3,4,5,6]}.

Highly motivated by Eq (1.1), we consider the stochastic Wick-type fractional CDGSK equation in the form of

where "$\diamond$" is Wick product and $A(t)$ and $C(t)$ are white noise functionals defined in the Kondratiev distribution space. In particular, by choosing suitable $a, b$ and $c$ with $b = a$ and $c = a^2/5$, Eq (1.1) can be reduced to the SK and CDG equations as follows; when we take $a = b = c = 5$ and apply fractional order in Eq (1.1), the fractional SK equation is expressed by in the form of

and additionally, by taking $a = b = 30$, $c = 180$ in Eq (1.1) and applying fractional order, the fractional CDG equation is given by

Recently, periodic and rational solutions of the SK and CDG equations have been studied by using the conformable dreivative and $(G'/G)$-expansion method and so on ^[16,17,18]. M. Arshad et al. have been applied the generalized $\exp(-\Phi(\xi))$-expansion method and the improved sub-equation method for exact solutions of the SK equation ^[9]. M. Safari has been used to variational iteration method and Adomian decomposition method to find numerical solutions of the CDG equation ^[7] and $(G'/G)$-expansion method is used to find exact traveling wave solutions of the CDG equation ^[8]. In addition, several powerful techniques are available in the literature to find exact and numerical solutions of nonlinear partial diffrential equations (NPDEs) such as predictor-corrector method ^[10], Jacobi elliptic function method ^[11,12], Kudrayshov method ^[13,14], homogeneous balance method ^[15], and so on. Painlevé test is a powerful approach for investigating the integrability properties of many nonlinear evolution equations. It is important to note about the integrability of NPDEs before finding exact solutions of them. So we can determine appropriate conditions when there is the general solution of NPDE or when we can find some exact solutions of NPDE or when we cannot find any exact solution of NPDE ^[19]. Fractional calculus is utilized to the study of fractional integrals and fractional derivatives for bounded measurable functions ^[20]. So, the fractional nonlinear evolution models are an interest issue in mathematical physics and engineering ^{[21,22,23,24,25]}. It should be mentioned that deriving exact and numerical solutions of the fractional NPDEs (FNPDEs) can describe physical phenomena better than the generalized NPDEs arising in the various fields ^{[26,27,28,29,30,31,32]}. In addition, we believe that finding Wick-type versions of exact traveling wave solutions of the stochastic Wick-type FNPDEs plays a significant role in the description of physical phenomena of their equations.

This paper is organized as follows; in Section 2, we give the definitions of the Wick product, the Hermite transformation and the conformable fractional derivative and steps of finding exact traveling wave solutions of the stochastic Wick-type FNPDEs. In Section 3, we investigate the integrability of Eq (1.2) by using the Painlevé test and we obtain new Wick-type and non-Wick-type versions of exact traveling wave solutions of Eq (1.2). Section 4 consists of exact traveling wave solutions of the FNPDEs such as Eq (1.3) and Eq (1.4). Finally, some conclusions give in the end of this work.

2.   Preliminaries

In this section, we introduce the Wick product, the Hermite transform that can convert the FNPDEs into the stochastic Wick-type FNPDEs and the conformable fractional derivative to convert the orinary nonlinear differential equations into FNPDEs ^[33,34]. And we also introduce the steps of finding exact traveling wave solutions of the stochastic Wick-type FNPDEs. Let's see the basic definitions firstly.

2.1.   The basic definitions

Assume $S \left(\mathbb{R}^d \right)$ and $\left(S \left(\mathbb{R}^d \right)\right)^{*}$ are the Hida test function space and the Hida disturbance space on $\mathbb{R}^{d}$, respectively. Fixed $n \in \mathbb{R}$, $(S)_1^n$ consists of elements

where $c_{\alpha} \in \mathbb{R}^n, || x||_{1, k}^2 \equiv \sum_{\alpha} c_{\alpha}^2 (\alpha!)^2 (2 \mathbb{N})^{k\alpha} < \infty$ for all $k \in \mathbb{N}$ with $c_{\alpha}^2 = |c_{\alpha}|^2 = \sum_{k = 1}^{n} (c_{\alpha}^{(k)})^2, c_{\alpha} = (c_{\alpha}^{(1)}, \cdots, c_{\alpha}^{(n)}) \in \mathbb{R}^n, \alpha! = \prod_{k = 1}^{\infty} \alpha_k!$ and $(2\mathbb{N})^{\alpha} = \prod_j (2j)^{\alpha_j}$, and $H_{\alpha}(w) = \prod_{i = 1}^{\infty} H_{\alpha_i} (\left < x, \eta_i \right > ), w \in \left(S \left(\mathbb{R}^d \right)\right)^{*}, \alpha = (\alpha_1, \alpha_2, \cdots) \in J$.

The space $\left(\it{S} \right)_{-1}^{n}$ consisit of all formal expansions

where $a_{\alpha} \in \mathbb{R}^{n}, || X ||_{-1, -q} \equiv \sum_{\alpha} a_{\alpha}^2 \left(2 \mathbb{N} \right)^{-q\alpha} < \infty$, for all $n, q \in \mathbb{N}$. The family of seminorms $||x||_{1, k}, k \in \mathbb{N}$ gives rise to a topology on $\left(S \right)_{1}^{n}$, we can regard $\left(S \right)_{-1}^{n}$ as the dual of $\left(S \right)_{1}^{n}$ by the action

where $\left(a_{\alpha}, c_{\alpha} \right)$ is the usual inner product in $\mathbb{R}^n$.

Definition 2.1. Let $X = \sum_{\alpha} a_{\alpha} H_{\alpha}$ and $Y = \sum_{\beta} b_{\beta} H_{\beta}$ be two elements of $\left(\it{S} \right)_{-1}^{n}$ with $a_{\alpha}, b_{\beta} \in \mathbb{R}^{n}$. The Wick product of $X$ and $Y$ is the element $X \diamond Y$ given by

Definition 2.2. Let $X = \sum_{\alpha} a_{\alpha} H_{\alpha} \in (S)_{-1}^{n}$ and $a_{\alpha} \in \mathbb{R}^{n}$. The Hermite transform of $X$, denoted by $\tilde{X}(z)$, is defined by

where $z = (z_1, z_2, \ldots) \in \mathbb{C}^{n}$ and $z^{\alpha} = z_1^{\alpha_1} z_2^{\alpha_2} \cdots$ if $\alpha = (\alpha_1, \alpha_2, \ldots) \in J,$ where $z_j^0 = 1$.

Note that if $X, Y \in (S)_{-1}^{n}$, then the Hermite transform of $X \diamond Y$ is

for all $z$ such that $\tilde{X}(z)$ and $\tilde{Y}(z)$ exist, where $\tilde{X}(z) \cdot \tilde{Y}(z)$ is complex bilinear product between two elements of $\mathbb{C}^{n}$ defined by $(\nu_1, \nu_2, \ldots, \nu_{n}) \cdot (w_1, w_2, \ldots\, w_{n}) = \sum_{i = 1}^{n} \nu_i w_i$, where $\nu_i, w_i \in \mathbb{C}$.

Let $X = \sum_{\alpha} a_{\alpha} H_{\alpha} \in (S)_{-1}^{n}$. Then the vector $c_0 = \tilde{X}(0) \in \mathbb{R}^n$ is called the generalized expectation of $X$ and is denoted by $E(X)$. Suppose that $f : V \rightarrow \mathbb{C}^m$ is an analytic function, where $V$ is a neighborhood of $E(X)$. Assume that the Taylor series of $f$ around $E(X)$ has some coefficients in $\mathbb{R}^n$, then the Wick version $f^{\diamond}(X) = \mathcal{H}^{-1} \left(f \circ \tilde{X} \right) \in \left(S\right)_{-1}^{n}$.

The Wick exponent of $X \in (S)_{-1}^{n}$ is defined by $\exp^{\diamond} \{X\} = \sum_{n = 0}^{\infty} X^{\diamond n}/n!$. With the Hermite transformation, the Wick exponent shows the same algebra properties as the usual one. For example, $\exp^{\diamond} \{ X+Y\} = \exp^{\diamond} \{X\} \diamond \exp^{\diamond} \{Y\}$.

Now we introduce the conformable fractional derivative as below ^[39].

Definition 2.3. Given a function $g : (0, +\infty) \rightarrow \mathbb{R}$, then the conformable fractional derivative of a function $g$ is defined by

where $t > 0$ and $\alpha \in (0, 1]$.

We have some important rules of the conformable fractional derivatives for some familiar functions as follows;

2.2.   Steps for finding exact traveling wave solutions of the stochastic Wick-type FNPDEs

We will present steps for finding exact traveling wave solutions of the stochastic Wick-type FNPDEs. Consider the stochastic Wick-type FNPDE with respect to $x$ and $t$ as

where $U = U(x, t)$ is unknown solution. Eq (2.1) is a polynomial in $U$ and its various partial derivatives. We take the Hermite transformation of Eq (2.1). This turns the Wick product into the ordinary products and the equation takes the following form

where $\mathcal{ H}(U) = \tilde{U} = \tilde{U}(x, t, z)$ and $z = (z_1, z_2, \ldots) \in \mathbb{K}_q(r)$, for some $q, r$, where $\mathbb{K}_q (r) = \{z = (z_1, z_2, \ldots) \in \mathbb{C}^{\mathbb{N}} \rm{and} \sum_{\alpha \ne0} |z^{\alpha}|^2 (2\mathbb{N})^{q\alpha} < r^2 \}$. Then, under certain conditions, we can take the inverse Hermite transformation $U = \mathcal{H}^{-1} \left(\tilde{U} \right) \in (S)_{-1}$. and thereby obtain the solution $U$ of the original Wick equation (2.1). We have the following theorem ^[35].

Theorem 2.1. Suppose $\tilde{U}(x, t, z)$ is a solution $\rm($in the usual strong pointwise sense$)$ of Eq. (2.4) for $(x, t)$ in some bounded open set $\mathbf{G} \subset \mathbb{R}^d \times \mathbb{R}$, and for each $z \in \mathbb{K}_q(R)$, for some $q, R$. Moreover, suppose that $\tilde{U}(x, t, z)$ and all its partial derivatives involved in (2.4) are (uniformly) bounded for $(x, t, z) \in \mathbf{G} \times \mathbb{K}_q(R)$, continuous with respect to $(x, t) \in \mathbf{G}$ for all $z \in \mathbb{K}_q(R)$ and analytic with respect to $z \in \mathbb{K}_q(R)$, for all $(x, t) \in \mathbf{G}$. Then there exists $U(x, t) \in (S)_{-1}$ such that $\tilde{U}(x, t, z) = ( \mathcal{H}U(x, t))(z)$ for all $(x, t, z) \in \mathbf{G} \times \mathbb{K}_q(R)$ and $U(x, t)$ solves $\rm($in the strong sense in $(S)_{-1}$) Eq (2.1 $\rm)$ in $(S)_{-1}$ .

Next we introduce some steps to obtain the solution of Eq (2.2) in detail.

Step 1. Traveling wave variable is supposed by

where $X = \frac{ x^{\alpha}}{\alpha}, T = \frac{ t^{\alpha}}{\alpha}$, $k$ is unknown constant and $\tilde{\omega}(s, z)$ is unknown integrable function. By applying the conformable fractional derivative and traveling wave variable (2.3), Eq. (2.2) can be reduced into the following ordinary differential equation with respect to $\zeta$;

where $\tilde{\zeta} = \zeta$, $\tilde{\omega} = \omega$, $\tilde{U}(\zeta) = \tilde{U}(x, t, z)$ and $\tilde{U}_{\zeta} = d\tilde{U}/d{\zeta}, \tilde{U}_{\zeta\zeta} = d^2\tilde{U}/{\zeta}^2,$ and so on.

Step 2. Let's test the integrability of Eq. (2.4) by using Painlevé test. If Eq (2.4) passes Painlevé test by appropriate conditions of the integrability of Eq (2.4), it can move on next step to find exact solutions of Eq (2.4). If not, Eq (2.4) cannot give any exact solution.

Step 3. By homogeneous balance method, we take exact solution of Eq. (2.4) in the form of

where

that is satisfied the sub-equations

where $\tilde{p}(t, z)$ and $\tilde{q}(t, z)$ are integrable functions on $\mathbb{R}$ and $\left \{\tilde{A}_{j}(t, z) \right \}_{ j = 0}^{N}$ are unknown coefficients to be computed later, with $\tilde{A}_{N}(t, z) \neq 0$. The pole-order $N$ of exact solution (2.5) can be determined from the highest order linear term and the highest order nonlinear term in Eq (2.4) by homogeneous balance method ^[15].

Step 4. Equating each coefficient of the same order of $\left\{ \Psi(\zeta)/\Phi(\zeta)\right\}$ to zero by substituting exact solution (2.5) into Eq (2.4) and then the required relations of cofficients and physical parameters are found by solving the algebraic equations in terms of $\left\{ \tilde{A}_j(t, z) \right\}_{j = 0}^{N}, \tilde{p}(t, z)$, $\tilde{q}(t, z), k, \tilde{\omega}(t, z)$ with the aid of computer package programs. Replacing exact solution (2.5) by the traveling wave variable (2.3) and $\left\{ \tilde{A}_j(t, z) \right\}_{j = 0}^{N}$, we can construct the Wick-type exact traveling wave solutions of Eq (2.1) by using the inverse Hermite transform in Theorem 2.1.

3.   The stochastic Wick-type fractional CDGSK equaion (1.2)

In this section, we will obtain the conditions of integrability of Eq (1.2) by employing the Painlevé test. And then we can find the Wick-type and non-Wick-type versions of exact traveling wave solutions of Eq (1.2) by the sub-equations method if it passes the Painlevé test.

Now, by the definitions of the Wick product and the Hermite transformation, first of all, we change the non-Wick-type version of Eq (1.2) that is rewritten by in the form of

where $z = (z_1, z_2, \ldots) \in \mathbb{C}^{\mathbb{N}}$ is a vector parameter. Let $\tilde{U} = \tilde{U}(x, t, z) = \textsf{u}(\zeta(x, t, z))$ be the solution of Eq (3.1). With the use of traveling wave variable

where $X = \frac{x^{\alpha}}{\alpha}$ and $T = \frac{t^{\alpha}}{\alpha},$ and by the properties of the conformable fractional derivative, Eq (3.1) is rewritten by in the form of

where $\textsf{u}_{\zeta} = d \textsf{u}/d \zeta, \textsf{u}_{\zeta\zeta} = d^2 \textsf{u}d \zeta^2, \ldots$ and $a(t, z) = \tilde{A}(t, z), c(t, z) = \tilde{C}(t, z)$.

3.1.   The Painlevé test of Eq (3.3)

Let us test the integrability of Eq (3.3) on the Painlevé test ^[36,37,38]. First, to determine the pole order of the solution expansion of Eq (3.3), the equation with the leading members corresponding to Eq (3.3) is

Substituting $\textsf{u}(\zeta) = \frac{B_{-r}(t, z)}{\zeta^r}$ into Eq (3.4), we get

So, we have the first member of the solution expansion in Laurent series as follows;

Now we have to find Fuchs indices ^[37,38]. For this idea we substitute

into Eq (3.4) and equate the equation at $B_j(t, z)$ to zero, we have the equation for Fuchs indices in the following form of

In order to Eq (3.3) passes the Painlevé test, we have to obtain the integer values for Fuchs indices as follows;

Now, to find the conditions of the integrability of Eq (3.3), we consider Laurent series for general solution expansion of Eq (3.3) in the form of

where $B_2(t, z)$ and $B_6(t, z)$ are arbitrary functions corresponding to $j_2 = 2, j_3 = 6$, respectively.

We substitute Laurent series (3.10) into Eq (3.3) and equate coefficients at different powers of $\zeta$ to zero, we have special relations on coefficients and parameters of Eq (3.3) corresponding to Fuchs indices $j_2 = 2, j_3 = 6$ as follows;

where ${\mathbf B}_{51}(t, z) = k(a^{10} -20 a^8 c +600 a^6 c^2 -12 \times 10^4a^4 c^3$+$432 \times 10^4 a^2 c^4 -297 \times 10^5 c^5) B_2^2(t, z)$+$(30 a^8-1650 a^6 c +135 \times 10^2 a^4 c^2 +405 \times 10^3 a^2 c^3$-$405 \times 10^4 c^4)\omega, {\mathbf B}_{52}(t, z) = 2 a^{10}-165a^8 c+4825 a^6 c^2-60750 a^4c^3$+$3.375 \times 10^5 a^2 c^4-675 \times 10^3 c^5, {\mathbf B}_{61}(t, z)$ = $a^{10} -20 a^8 c +600 a^6c^2 -12 \times 10^4 a^4 c^3 +432 \times 10^4 a^2c^4 -297 \times 10^5 c^5, {\mathbf B}_{62}(t, z)$=$30 a^8 -1650 a^6c +135 \times 10^2 a^4c^2 +405 \times 10^3 a^2c^3-405 \times 10^4 c^4, {\mathbf B}_{63}(t, z)$=$2 a^{10}-165 a^8c +4825 a^6c^2-60750a^4c^3+3.375 \times 10^5a^2c^4-675 \times 10^3 c^5$, letting $a = a(t, z), c = c(t, z)$, $\omega = \tilde{\omega}(T, z)$ and $T = t^{\alpha}/\Gamma(1+\alpha)$.

Equation (3.3) would passes the Painlevé test if Eqs (3.12) and (3.16) were identically equal to zero. As the consequence of this expansion, there is the solution expansion of Eq (3.3) in Laurent series with two arbitrary functions $B_2(t, z)$ and $B_6(t, z)$. Then we can obtain exact solutions of Eq (3.3).

Remark 3.1. From the compatibilty conditions (3.12) and (3.16) at Fuchs indices $j_2 = 2$ and $j_3 = 6$, we have a relation of $c(t, z) = \frac{19 }{150}a^2(t, z), a(t, z) \ne 0$ and

respectively. By the traveling wave variable (3.2) and Laurent series (3.10), the solution expansion $\textsf{u}(\zeta)$ is expressed by in the form of

where $\zeta = kX + \int_0^T \tilde{\omega}(\tau, z) ds$, $X = \frac{x^{\alpha}}{\alpha}, T = \frac{t^{\alpha}}{\alpha}, \tau = \left[\alpha s \right]^{1/\alpha}, a = a(t, z)$.

If we take $c(t, z) = \frac{1}{5} a^2(t, z)$ and $B_2(t, z) = 0$, the solution expansion $\textsf{u}(\zeta)$ is expressed by in the form of

where $\zeta = kX +\int_0^T \tilde{\omega}(\tau, z) ds$, $X = \frac{x^{\alpha}}{\alpha}, T = \frac{t^{\alpha}}{\alpha}, \tau = \left[\alpha s \right]^{1/\alpha}$.

3.2.   Exact traveling wave solutions of Eq (1.2)

Now, let us find Wick-type and non-Wick-type versions of exact traveling wave solutions of Eq (1.2). First, to determine the pole-order $N$ of exact solution of Eq (3.3), we take the highest order linear term $\textsf{u}_{\zeta\zeta\zeta\zeta\zeta}$ and the highest order nonlinear term $\textsf{u}_{\zeta}\textsf{u}_{\zeta\zeta}$ in Eq (3.3) and so we obtain $N+5 = 2N+3$ which gives $N = 2$ by the homogeneous balance method ^[15]. Now, we take exact solution of Eq (3.3) in the form of

where $\{ \Psi(\zeta)/\Phi(\zeta)\}$ is given in Section 2. We substitute exact solution (3.19) and $\{ \Psi(\zeta)/\Phi(\zeta)\}$ into Eq (3.3) and then we can yield the algebraic equations by equating to zero the expressions with the same degree of $\{ \Psi(\zeta)/\Phi(\zeta)\}$. Solving the algebraic equations with respect to the unknowns $\tilde{A}_2(t, z), \tilde{A}_1(t, z), \tilde{A}_0(t, z)$ and $\tilde{\omega}(T, z)$ by the help of computer package programs, we obtain three nontrivial solution sets as follows;

In order to obtain the Wick-type versions of exact traveling wave solutions of Eq (1.2), we replace exact solution (3.19) by nontrivial solution sets (3.20)–(3.22) and Eq (2.6), and by using the inverse Hermite transformation $U = \mathcal{H}^{-1}(\tilde{U})$, we have the Wick-type exact traveling wave solutions of Eq (1.2) in the followings. Based on (3.20), we get the first Wick-type exact traveling wave solution of Eq. (1.2) in the following form

where

$\tau = [\alpha s]^{1/\alpha}$, $T = t^{\alpha}/\alpha$, and with a relation of $p(t) = -q(t)$,

$\mathbf{M}_1(t) = \sqrt{9 A^{\diamond 2}(t) -40 C(t)}\pm 3 A(t), \mathbf{M}_2(t)$= $27 A^{\diamond 5}(t) -144 A^{\diamond 3}(t) \diamond C(t) +320 A(t) \diamond C^{\diamond 2}(t), \mathbf{M}_3(t)$=$-760 A^{\diamond 2}(t) \diamond C^{\diamond2}(t) +1600 C^{\diamond3}(t), \mathbf{M}_4(t)$=$(3 A^{\diamond3}(t)-10 A(t) \diamond C(t)) \diamond \mathbf{M}_1(t) +20 A^{\diamond2}(t) \diamond C(t) -50 C^{\diamond 2}(t).$

Subsequently, from (3.21) and (3.22), we obtain the following Wick-type exact traveling wave solutions of Eq (1.2):

where

$\tau = [\alpha s]^{1/\alpha}$, $T = t^{\alpha}/\alpha$ and with the relations of $p(t) = -11.4244q(t)$ and $C(t) = 0.053 A^{\diamond 2}(t)$, and

where

$\tau = [\alpha s]^{1/\alpha}$, $T = t^{\alpha}/\alpha$ and with the relations of $p(t) = 3.7321 q(t)$ and $C(t) = -0.175 A^{\diamond 2}(t)$, and

where

$\tau = [\alpha s]^{1/\alpha}$, $T = t^{\alpha}/\alpha$ and with the relations of $p(t) = 0.2679 q(t)$ and $C(t) = -0.175 A^{\diamond 2}(t)$.

In white noise analysis, a version of Brownian motion $B(t)$ expresses informally $B(t) = \int_0^t W(\tau) d\tau$ and in a generalized sense, $W(t) = dB(t)/dt$, which is white noise defined in $\mathbb{R}$. Let's take $A(t) = f_1(t) + W(t)$ and $C(t) = f_2(t) + W(t)$ where $f_1(t)$ and $f_2(t)$ be integrable functions on $\mathbb{R}$. Based on the Wick-type exact traveling wave solutions (3.23)–(3.26), the non-Wick-type exact traveling wave solutions can be expressed by in the forms of

where

$\tau = [\alpha s]^{1/\alpha}$, $T = t^{\alpha}/\alpha$, and with a relation of $p(t) = -q(t)$,

$\mathbf{M}_1(t) = \pm 3 (f_1(t)+W(t)) + \sqrt{9 (f_1(t)+W(t))^2 -40 (f_2(t)+W(t)) },$

$\mathbf{M}_2(t) = 27 (f_1(t)+W(t))^5 -144 (f_1(t)+W(t))^3 (f_2(t)+W(t)) +320 (f_1(t)+W(t)) (f_2(t)+W(t))^2,$

$\mathbf{M}_3(t) = -760 (f_1(t)+W(t))^2 (f_1(t)+W(t))^2 +1600 (f_2(t)+W(t))^3,$

$\mathbf{M}_4(t) = (3 (f_1(t)+ W(t))^3 -10 (f_1(t)+W(t)) (f_2(t)+W(t))) \mathbf{M}_1(t) +20 (f_1(t)+W(t))^2 (f_2(t)+W(t)) -50 (f_2(t)+W(t))^2$.

where

$\tau = [\alpha s]^{1/\alpha}$, $T = t^{\alpha}/\alpha$ and with relations of $p(t) = -11.4244q(t)$ and $C(t) = 0.053 A^{ 2}(t)$, and

where

$\tau = [\alpha s]^{1/\alpha}$, $T = t^{\alpha}/\alpha$ and with relations of $p(t) = 2.7321 q(t)$ and $C(t) = -0.175 A^{2}(t)$, and

where

$\tau = [\alpha s]^{1/\alpha}$, $T = t^{\alpha}/\alpha$ and with relations of $p(t) = 0.2679 q(t)$ and $C(t) = - 0.175 A^{2}(t)$.

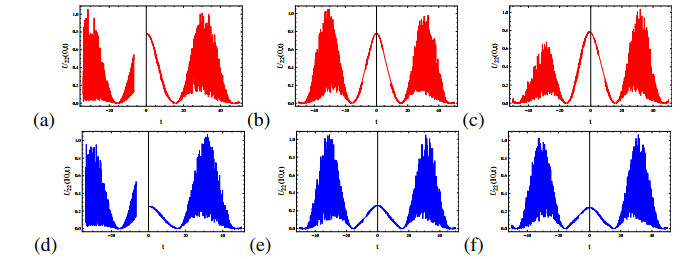
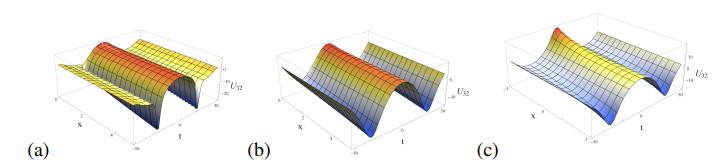
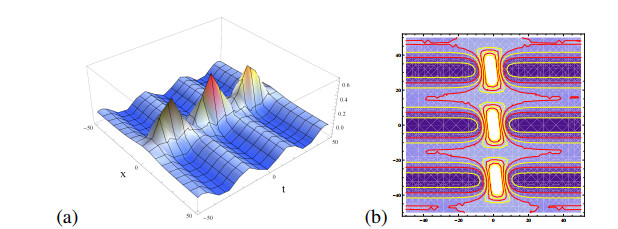
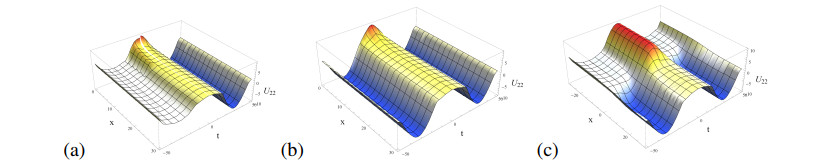
Remark 3.2. Wick-type exact traveling wave solution (3.23) of Eq (1.2) is depending on white noise functionals $A(t), C(t)$ and a parameter function $q(t)$ by a relation of $p(t) = -q(t)$. There are some relations between white noise functionals and parameter functions such as $\{C(t) = 0.053 A^{2}(t), p(t) = -11.4244q(t)\}$, $\{C(t) = -0.175 A^{2}(t), p(t) = 2.7321 q(t)\}$ and $\{C(t) = -0.175 A^{2}(t), p(t) = 0.2679 q(t)\}$. So we know that these solutions (3.24)–(3.26) are only depending on white noise functional $A(t)$ and parameter function $q(t)$. Specially, we perform the dynamics of the non-Wick-type exact traveling wave solution (3.28) without white noise $(W(t) = 0)$ has different soliton-type behaviours in Figure 1 and we perform the dynamics of (3.28) with white noise $W(t) = - \cosh(0.1 {\rm RandomReal}[t])$ in Figure 2, as the fractional orders $\alpha = 0.3, 0.5$ and the integral order $\alpha = 1$, under $k = 0.5, q(t) = 0.1\cos(0.1t), f_1(t) = -0.1 \cos(0.1t)$, respectively. And we represent that the non-Wick-type exact traveling wave solution (3.29) without white noise $(W(t) = 0)$ has different soliton-type behaviours in Figure 3 as the fractional orders $\alpha = 0.1, 0.5$ and the integral order $\alpha = 1$, under $k = 0.5, q(t) = 0.1\cos(0.1t), f_1(t) = -0.1 \cos(0.1t)$.

4.   Exact traveling wave solutions of FNPDEs

4.1.   The fractional SK equation (1.3)

In order to solve the fractional SK equation (1.3), substituting the transformation $U(t, x) = \textsf{u}(\zeta)$ and traveling wave variable

where $T = t^{\alpha}/\alpha$ into Eq (1.3), Eq (1.3) can be converted to the ordinary nonlinear differential equation

where $\textsf{u}^{(n)} = d^n \textsf{u}/d \zeta^n$ is the $n$th order derivative of $\textsf{u}$ with respect to $\zeta$ and $n$ is the positive integer number.

Equation (1.3) has two exact traveling wave solutions with the use of the part of Section 2 as follows; the first exact traveling wave solution of Eq (1.3) is expressed by

where

$\tau = [\alpha s]^{1/\alpha}$, $T = t^{\alpha}/\alpha$ and with a relation of $p(t) = -q(t)$, and the second exact traveling wave solution of Eq (1.3) is given by

where

$\tau = [\alpha s]^{1/\alpha}$, $T = t^{\alpha}/\alpha$ and with a relation of $p(t) = -q(t)$.

Example 4.1. For the integral order $\alpha = 1$, substituting constant coefficients $f_1(t) = 5, f_2(t) = 5$ and $W(t) = 0$ into non-wick-type exact traveling wave solution (3.27), and a new version of exact traveling wave solution of Eq (1.2) is given by in the form of

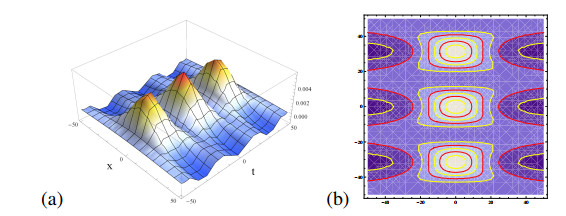
where $\zeta(x, t) = kx + \int_0^t \frac{55}{2} k^5 q^4(s) ds$, and with a relation of $p(t) = -q(t)$. We expect that this solution has periodic solitons in the dynamics to be seen in Figure 6.

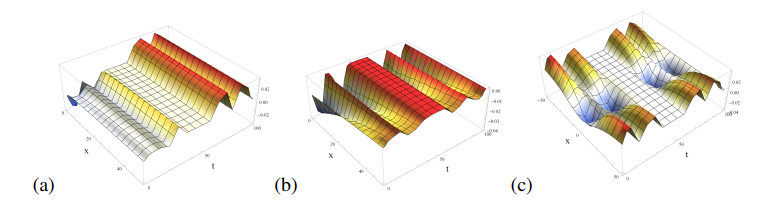
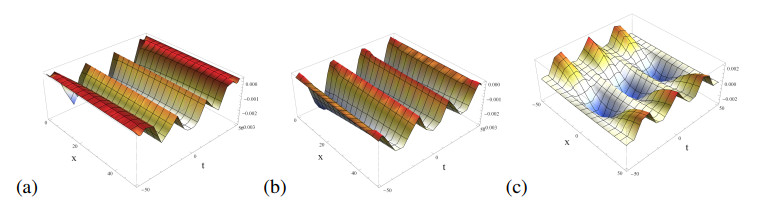
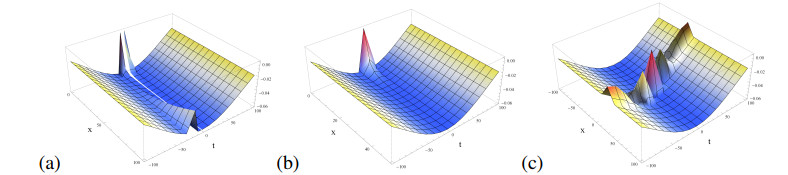
Remark 4.2. We discuss the dynamical behaviours of the obtained exact traveling wave solutions in order to describe physical interpretation of the fractional SK equation. The fractional SK equation has two nontrivial exact traveling wave solutions with a relation of time-dependent parameters as $p(t) = -q(t)$ as follows; exact traveling wave solution (4.3) gives the dynamics as irregular traveling waves for the fractional orders $\alpha = 0.1, 0.5$ and dark-type solitons for the integral order $\alpha = 1$ with suitable parameters $k = 0.002, q(t) = 20\cos(0.1t)+15\sin(0.2t)$ in Figure 4. In Figure 5, exact traveling wave solution (4.4) describes solitary waves for the fractional orders $\alpha = 0.2, 0.5$ and the integral order $\alpha = 1$ with $k = 0.002, q(t) = 20\cos(0.1t)$. The dynamics of exact traveling wave solution (4.5) represent periodic solitons feature and the density plot by $k = 0.002, q(t) = 20 \cos (0.1t)$ in Figure 6.

4.2.   The fractional CDG equation (1.4)

In order to solve Eq (1.4), substituting the transformation $U(t, x) = \textsf{u}(\zeta)$ and traveling wave variable (4.1) into Eq (1.4), Eq (1.4) is expressed by in the form of

Similarly, we use the method in Section 4.1 to find exact traveling wave solutions of Eq. (1.4) and so we obtain the followings; the first exact traveling wave solution of Eq (1.4) is expressed by

where $\zeta_1(x, t) = \frac{k x^{\alpha}}{\alpha} + \int_0^T 85.2814 k^5 q^4(\tau) ds, \tau = [\alpha s]^{1/\alpha}$, $T = t^{\alpha}/\alpha$ and with a relation of $p(t) = -q(t)$, and the second exact traveling wave solution of Eq (1.4) is given by

where $\zeta_2(x, t) = \frac{k x^{\alpha}}{\alpha} + \int_0^T 35.0311 k^5 q^4(\tau) ds, \tau = [\alpha s]^{1/\alpha}$, $T = t^{\alpha}/\alpha$ and with a relation of $p(t) = -q(t)$.

Example 4.3. For the integral order $\alpha = 1$, substituting $f_1(t) = 30, f_2(t) = 180$ and $W(t) = 0$ into non-Wick-type exact traveling wave solution (3.27) and then we have a new version of exact traveling wave solution of Eq (1.2) expressed by in the form of

where $\zeta(x, t) = kx - \int_0^t \frac{55}{2} k^5 q^4(s) ds$, and with a relation of $p(t) = -q(t)$.

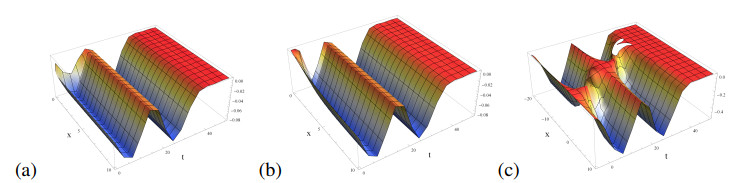
Remark 4.4. There are some performances of the obtained solutions of the fractional CDG equation. Exact traveling wave solution (4.7) gives different waves for the fractional orders $\alpha = 0.1, 0.5$ and the dark-type solitons solution for the integral order $\alpha = 1$, respectively, under $k = 0.002, q(t) = 20\cos(0.1t)$ in Figure 7. In Figure 8, exact traveling wave solution (4.8) performs solitary wave for $\alpha = 0.1$ a soliton-like for $\alpha = 0.5$ and solitons for the integral order $\alpha = 1$, respectively, under $k = 0.017, q(t) = 20\cos(0.1t)$. Figure 9 performs (a) the dynamic of exact traveling wave solution (4.9) with periodic solitons and (b) the density plot, under $k = 0.003, q(t) = 20 \cos (0.1t)$.

5.   Conclusions

In this paper, we obtained new Wick-type and non-Wick-type versions of exact traveling wave solutions of the stochastic Wick-type fractional CDGSK equation and new exact traveling wave solutions of the fractional SK and CDG equations by employing the sub-equations method. The considered equations provided us more new exact solutions than the solutions by other existing methods and these solutions might be of great importance in various fields of applied science for interpreting some physical phenomena by performing the dynamics of the obtained solutions under suitable physical parameters. We believe that the sub-equations method is very straightforward and powerful to find exact solutions of the nonlinear evolution equations.

Acknowledgement

This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (No. NRF-2019R1A6A1A10073079).

Conflict of interest

The authors declare no conflict of interest.