Finite-time contraction stability of a stochastic reaction-diffusion dengue model with impulse and Markov switching

1.   Introduction

Over the past few decades, considerable attention has been paid to the rigorous analysis of mathematical models describing tumor growth and great progress has been achieved. Most work in this direction focuses on the sphere-shaped or nearly sphere-shaped tumor models; see ^{[1,2,3,4,5,6,7,8,9]} and the references therein. Observing that the work concerning models for tumors having different geometric configurations from spheroids is less frequent, in this paper we are interested in the situation of tumor cord–a kind of tumor that grows cylindrically around the central blood vessel and receives nutrient materials (such as glucose and oxygen) from the blood vessel ^[10]. The model only describes the evolution of the tumor cord section perpendicular to the length direction of the blood vessel due to the cord's uniformity in that direction. Assume that the radius of the blood vessel is $r_0$ and denote by $J$ and $\Gamma(t)$ the section of the blood vessel wall and the section of the exterior surface of the tumor cord, respectively, then $J = \left\{x\in\mathbb{R}^{2};|x| = r_{0}\right\}$. We also denote by $\Omega(t)$ the region of the section of the tumor cord, so that $\Omega(t)$ is an annular-like bounded domain in $\mathbb{R}^{2}$ and $\partial\Omega(t) = J\cup\Gamma(t)$. The mathematical formulation of the tumor model under study is as follows:

Here, $\sigma$ and $p$ denote the nutrient concentration and pressure within the tumor, respectively, which are to be determined together with $\Omega(t)$, and $c = T_{\rm diffusion}$ $/T_{\rm growth}$ is the ratio of the nutrient diffusion time scale to the tumor growth (e.g., tumor doubling) time scale; thus, it is very small and can sometimes be set to be 0 (quasi-steady state approximation). Assume that the time delay $\tau$ is reflected between the time at which a cell commences mitosis and the time at which the daughter cells are produced and $\xi(s; x, t)$ represents the cell location at time $s$ as cells are moving with the velocity field $\vec{V}$, then the function $\xi(s; x, t)$ satisfies

In other words, $\xi$ tracks the path of the cell currently located at $x$. (1.3) is further derived from (1.10) under the assumption of a porous medium structure for the tumor, where Darcy's law $\vec{V} = -\nabla p$ holds true. Because of the presence of time delay, the tumor grows at a rate that is related to the nutrient concentration when it starts mitosis and a combination of the conservation of mass and Darcy's law yields (1.2), in which $\mu$ represents the growth intensity of the tumor and $\tilde{\sigma}$ is the nutrient concentration threshold required for tumor cell growth. Additionally, $\bar{\sigma}$ is the nutrient concentration in the blood vessel, $\bar\sigma > \tilde\sigma$, $V$, $\kappa$ and $\vec\nu$ denote the normal velocity, the mean curvature and the unit outward normal field of the outer boundary $\Gamma(t)$, respectively, $\vec n$ denotes the unit outward normal field of the fixed inner boundary $J$, and $\gamma$ is the outer surface tension coefficient. Thus, the boundary condition $\sigma = \bar{\sigma}$ on $J$ indicates that the tumor receives constant nutrient supply from the blood vessel, $\partial_{\vec\nu}\sigma = 0$ on $\Gamma(t)$ implies that the nutrient cannot pass through $\Gamma(t)$, $\partial_{\vec{n}} p = 0$ on $J$ means that tumor cells cannot pass through the blood vessel wall, $p = \gamma \kappa$ on $\Gamma(t)$ is due to the cell-to-cell adhesiveness, and $V = -\partial_{\vec\nu} p$ on $\Gamma(t)$ is the well-known Stefan condition representing that the normal velocity of the tumor cord outer boundary $\Gamma(t)$ is the same with that of tumor cells adjacent to $\Gamma(t)$. Finally, $\sigma_0(x)$, $p_0(x)$, $\Gamma_0$ are given initial data and $\Omega(t) = \Omega_0$ for $-\tau\le t\le0$.

Before going to our interest, we prefer to recall some relevant works. Models for the growth of the strictly cylindrical tumor cord were studied in ^[11,12,13]. For the model (1.1)–(1.9) without the time delay, if $c = 0$, Zhou and Cui ^[14] showed that the unique radially symmetric stationary solution exists and is asymptotically stable for any sufficiently small perturbations. Meanwhile, if $c > 0$, Wu et al. ^[15] proved that the stationary solution is locally asymptotically stable provided that $c$ is small enough. On the other hand, Zhao and Hu ^[16] considered the multicell spheroids with time delays. For the case $c = 0$, they analyzed the linear stability of the radially symmetric stationary solution as well as the impact of the time delay.

Motivated by the works ^[14,15,16], here we aim to discuss the linear stability of stationary solutions to the problem (1.1)–(1.9) with the quasi-steady-state assumption, i.e., $c = 0$, and investigate the effect of time delay on tumor growth. Our first main result is given below.

Theorem 1.1. For small time delay $\tau$, the problem (1.1)–(1.9) admits a unique radially symmetric stationary solution.

Next, in order to deal with the linear stability of the radially symmetric stationary solution, denoted by $(\sigma_\ast, p_\ast, \Omega_\ast)$, where $\Omega_\ast = \big\{x\in \mathbb{R}^2:$ $r_0 < r = |x| < R_\ast\big\}$, we assume that the initial conditions are perturbed as follows:

The linearized problem of (1.1)–(1.9) at $(\sigma_\ast, p_\ast, \Omega_\ast)$ is then obtained by substituting

into (1.1)–(1.9) and collecting the $\varepsilon$-order terms. Now, we can state the second main result of this paper.

Theorem 1.2. For small time delay $\tau$, the radially symmetric stationary solution $(\sigma_\ast, p_\ast, \Omega_\ast)$ of (1.1)–(1.9) with $c = 0$ is linearly stable, i.e.,

for some positive constants $C$ and $\delta$.

Remark 1.1. Compared with results of the problem modeling the growth of tumor cord without time delays in ^[14], the introduction of the time delay does not affect the stability of the radially symmetric stationary solution even under non-radial perturbations. However, as we shall see in Subsection 3.3, the numerical result shows that adding time delay would result in a larger stationary tumor. Moreover, the stronger the growth intensity of the tumor is, the greater the influence of time delay on the size of the stationary tumor is.

Remark 1.2. Compared with results of the nearly sphere-shaped tumor model with time delays in ^[16], which state that the radially symmetric stationary solution is linearly stable for small $\mu$ in the sense that $\lim_{t\to\infty}\max_{0\leq \theta\leq2\pi}|\rho(\theta, t)-(a_1\cos\theta+b_1\sin\theta)| = 0$ for some constants $a_1$ and $b_1$, the radially symmetric stationary solution of tumor cord with the time delay is linearly stable for any $\mu > 0$ in the normal sense.

This paper is organized as follows. In Section 2, we give the proof of Theorem 1.1 by first transforming the free boundary problem into an equivalent problem with fixed boundary and then applying the contraction mapping principle combined with $L^p$ estimates to this fixed boundary problem. In Section 3, we prove Theorem 1.2 and Remark 1.1 by first introducing the linearization of (1.1)–(1.9) at the radially symmetric stationary solution $(\sigma_\ast, p_\ast, \Omega_\ast)$, and then making a delicate analysis of the expansion in the time delay $\tau$ provided that $\tau$ is sufficiently small. A brief conclusion in Section 4 completes the paper.

2.   Radially symmetric stationary solutions

In this section, we study radially symmetric stationary solutions $(\sigma_\ast, p_\ast, \Omega_\ast)$ to the system (1.1)–(1.9), which satisfy

where $\Delta_r$ is the radial part of the Laplacian in $\mathbb{R}^2$.

Before proceeding further, let us recall that the modified Bessel functions $K_n(r)$ and $I_n(r)$, standard solutions of the equation

have the following properties:

and

Proof of Theorem 1.1 In view of (2.5), the solution of (2.1) is clearly given by

Introducing the notations:

(2.1)–(2.4) reduces to the following system after dropping the "$\; \hat{}\;$" in the above variables:

It is clear that (2.12) can be solved explicitly. For convenience, we extend the solution of (2.12) outside [0, 1]:

Assume that $R_{\min}$ and $R_{\max}$ are positive constants to be determined later and $r_0 < R_{\min} < R_{\max}$. For any $R_\ast\in[R_{\min}, R_{\max}]$, we will prove that $p$ is also uniquely determined by applying the contraction mapping principle.

Noticing that 0 is a lower solution of (2.14), but there is no assurance that $\xi(s; r, 0)\le1$ for $-\tau\le s\le0$, we suppose $\xi(s; r, 0)\in[0, 2]$ and take

where $M > 0$ is to be determined. For each $p\in X$, we first solve for $\xi$ from (2.14) and substitute it into (2.13), then the following system

allows a unique solution $\bar{p}\in W^{2, \infty}[0, 1]$. Applying the strong maximum principle combined with the Hopf lemma to (2.1) shows that $\sigma(r; R_\ast)\leq\bar{\sigma}$. Thus, integrating (2.17), we obtain

Define the mapping

then $\|\mathcal{L}p \| \in W^{2, \infty}[0, 2]$ and $\|\mathcal{L}p \|_{W^{2, \infty}[0, 2]} \leq 2\|\bar{p}\|_{W^{2, \infty}[0, 1]}.$ Combining (2.18)–(2.20), we find

If we choose $M \geq M_1$, then $\mathcal{L}p \in X$ by (2.21) and $\mathcal{L}$ maps $X$ to itself.

We now show that $\mathcal{L}$ is a contraction. Given $p^{(1)}, p^{(2)} \in X$, one can first get $\xi^{(1)}, \xi^{(2)}$ from the following two systems:

Integrating (2.22) and (2.23) with regard to $s$ over the interval $[-\tau, 0]$ and making a subtraction yield

for all $-\tau \leq s \leq 0$ and $0 \leq r \leq 1$. Consequently,

Next, we substitute $\xi^{(1)}, \xi^{(2)}$ into (2.17) and solve for $\bar{p}^{(1)}$ and $\bar{p}^{(2)}$, respectively, then it follows from (2.17) that $\left(\bar{p}^{(1)}-\bar{p}^{(2)}\right)(1) = 0$, $\frac{\partial}{\partial r}\left(\bar{p}^{(1)}-\bar{p}^{(2)}\right)(0) = 0$ and

Using (2.24), we derive

and similarly,

where

Here, we employed the fact that

by (2.1) and $\sigma\leq\bar{\sigma}$. Let $M_5 = M_2+M_3+M_4$, then $M_5$ is independent of $\tau$ and

which together with $\mathcal{L}p^{(1)}(1) = \mathcal{L}p^{(2)}(1) = \frac{\gamma(R_\ast-r_0)}{R_\ast}$ and $(\mathcal{L}p^{(1)})^\prime(0) = (\mathcal{L}p^{(2)})^\prime(0) = 0$ implies that

Hence, if $\tau$ is sufficiently small such that $2M_5 \tau < 1$, then we derive a contracting mapping $\mathcal{L}$. The existence and uniqueness of $p$ are therefore obtained.

It suffices to prove that there exists a unique $R_\ast \in[R_{\min}, R_{\max}]$ satisfying (2.15). Substituting (2.16) into (2.15), we find that it is equivalent to solving the following equation for $R$:

Clearly,

Using Lemma 3.1 and Theorem 3.2 in ^[14] and the condition $\bar{\sigma} > \tilde{\sigma}$, we know that

which implies that the equation $G(R, 0) = 0$ has a unique solution, denoted by $R_S$, and

Since

when $\tau$ is sufficiently small, $\frac{\partial G(R, \tau)}{\partial R}$ and $\frac{\partial G(R, 0)}{\partial R}$ have the same sign. Thus, $G(R, \tau)$ is monotone decreasing in $R$. Using the fact that $G(R, \tau)$ is continuous in $\tau$, we further have

Hence, when $\tau$ is sufficiently small, the equation $G(R, \tau) = 0$ has a unique solution $R_\ast$. Taking $R_{\min } = \frac{1}{2} (R_{S}+r_0)$ and $R_{\max } = \frac{3}{2} R_{S}$, we complete the proof of the theorem.

3.   Linear stability

This section is devoted to the linear stability of the radially symmetric stationary solution $(\sigma_\ast, p_\ast, \Omega_\ast)$ of the problem (1.1)–(1.9) and the effect of time delay on the stability and the size of the stationary tumor. Let $(\sigma, p, \Omega(t))$, given by (1.11)–(1.13), be solutions to (1.1)–(1.9), and denote by $\vec{e}_r$, $\vec{e}_\theta$ the unit normal vectors in $r$, $\theta$ directions, respectively. Written in the rectangular coordinates in $\mathbb{R}^2$,

Using the notation $\xi_1(s; r, \theta, t)$, $\xi_2(s; r, \theta, t)$ for the polar radius and angle of $\xi(s; r, \theta, t)$, respectively, we have

Expand $\xi_1$, $\xi_2$ in $\varepsilon$ as

then we derive from (1.3) and (1.13) that

It is evident that $\xi_{20}\equiv\theta$. Noticing that the equation for $\xi_{10}$ is the same as that for $\xi_\ast$ in the radially symmetric case, $\xi_{10}$ is independent of $\theta$.

Substituting (1.11)–(1.13) and (3.1)–(3.5) into (1.1), (1.2), (1.4)–(1.6), using the mean-curvature formula in the 2-dimensional case for the curve $r = \rho(\theta)$:

and collecting the $\varepsilon$-order terms, we obtain the linearized system in $B_{R_\ast}\times\{t > 0\}$:

Due to the presence of the time delay, the linearization problem (3.6)–(3.8) cannot be solved explicitly. Assume that $\omega, q$, $\rho$ and $\xi_{11}$ have the following Fourier expansions:

Substituting (3.9) into (3.6)–(3.8) yields the following system in $B_{R_\ast}\times\{t > 0\}$:

Since it is impossible to solve the systems (2.1)–(2.4) and (3.10)–(3.17) explicitly and the time delay $\tau$ is actually very small, in what follows, we analyze the expansion in $\tau$ for (2.1)–(2.4) and (3.10)–(3.17).

3.1.   Expansion in $\tau$

Let

Substitute these expansions into (2.1)–(2.4) and (3.10)–(3.17). Since $a_n(t)$ and $b_n(t)$ have the same asymptotic behavior at $\infty$, we will only make an analysis of $a_n(t)$. For this, we discuss the expansions of $R_\ast$, $\sigma_\ast$, $p_\ast$, $A_n$, $E_n$ and $a_n$. Since the equations for the expansions of $\sigma_\ast$, $p_\ast$, $A_n$, $E_n$ and $a_n$ are the same as those in ^[16], here we only compute the expansions of the boundary conditions of $\sigma_\ast$, $p_\ast$, $A_n$ and $E_n$.

● Expansions of the boundary conditions of $\sigma_\ast$:

It follows from (2.10) and (2.11) that

which implies

By the boundary conditions in $(2.1)$, we find

● Expansions of the boundary conditions of $p_\ast$:

One obtains from the boundary conditions in (2.2) that

● Expansion of (2.4):

In view of $(4.31)$ in ^[16], there holds

Using (3.18), we compute

A combination of (3.20) and (3.21) gives

● Expansions of the boundary conditions of $A_n$:

We derive from the boundary conditions in (3.10) that

● Expansions of the boundary conditions of $E_n$:

Substituting the expansion of $E_n$ into the boundary conditions in (3.12) yields

3.2.   Zeroth-order terms in $\tau$

Collecting all zeroth-order terms in $\tau$ leads to the following system for $r_0 < r < R^0_\ast$:

A direct calculation gives

where

Let $\eta^0_n = E^0_n+\mu A^0_n$, then we find from (3.26) and (3.28) that $\eta^0_n$ satisfies

whose solution is

and thus,

where $C_1(t)$ and $C_2(t)$ are to be determined by the boundary conditions in (3.28). By (2.10), (3.34), (3.35) and (3.37), we get

Using (3.35) and (3.38)–(3.40), we further derive

Substituting (3.33) and (3.41) into (3.30) yields

whose solution is explicitly given by

Here,

It was proven in Lemma 4.4 of ^[14] that $U_n(r_0, R^0_\ast) < 0$ for any $n\geq 0$. Thus, we have the following:

Lemma 3.1. For any $n\geq 0$, there exists $\delta > 0$ such that $|a_0^n(t)|\leq|a_0^n(0)|e^{-\delta t}$ for all $t > 0$.

Lemma 3.1 shows that $a_n^0(t)$ decays to $0$ exponentially at $+\infty$; hence, when $\tau = 0$, the radially symmetric stationary solution is asymptotically stable for all $\mu > 0$.

3.3.   Sign of $R^1_\ast$

Recalling that $R_\ast = R^0_\ast + \tau R^1_\ast + O(\tau^2)$, in order to see the effect of the time delay $\tau$ on the size of the stationary tumor, in this subsection we discuss the sign of $R^1_\ast$ by a theoretical analysis combined with numerical simulations.

We obtain from (3.22) that

then by using (2.6)–(2.10), (3.18), (3.19), (3.25) and (3.32), one can solve (3.45) to obtain

where

Since

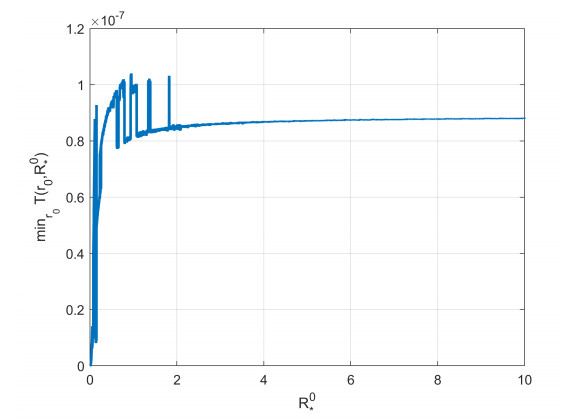
by (3.44), we know $S(r_0, R^0_\ast) < 0$. Additionally, we numerically compute the function $T(r_0, R^0_\ast)$ and find it is positive (see Figure 1). Hence, it follows from (3.46) that $R^1_\ast > 0$ and $R^1_\ast$ is monotone increasing in $\mu$.

Remark 3.1. The discussion above indicates that the presence of the time delay leads to a larger stationary tumor. Furthermore, the bigger the tumor aggressive parameter $\mu$ is, the greater the effect of time delay on the size of the stationary tumor is.

3.4.   First-order terms in $\tau$

Now, we tackle the system consisting of all the first-order terms in $\tau$ for $r_0 < r < R^0_\ast$:

To obtain the asymptotic behavior of $a_n^1(t)$ as $\infty$, by (3.54) and the boundedness of the modified Bessel functions $I_n(r)$ and $K_n(r)$ on $[r_0, R^0_\ast]$, it suffices to analyze $\frac{\partial E^1_n}{\partial r}(R^0_\ast, t)$. For this purpose, in view of (3.52), we first compute $A^1_n(r, t)$. Solving (3.50) yields

with

where we have employed (2.8)–(2.10), (3.19), (3.36) and (3.37). Furthermore,

Next, being similar to the computation of $E^0_n$, we set $\eta^1_n = E^1_n+\mu A^1_n$, then we derive from (3.50), (3.52) and (3.56) that

For brevity, we introduce the differential operator $L_n = -\partial_{rr}-\frac1r\partial_r+\frac{n^2}{r^2}$ and write $\eta^1_n = u^{(1)}_n+u^{(2)}_n+u^{(3)}_n+u^{(4)}_n$, where $u^{(1)}_n$, $u^{(2)}_n$, $u^{(3)}_n$ and $u^{(4)}_n$ solve the following problems, respectively:

Let us first estimate $u^{(1)}_n$. By (3.18), (3.41) and (3.59), we have

Based on the properties of the modified Bessel functions $I_n(r)$ and $K_n(r)$, the righthand side of (3.63) is less than $Q(n)a^0_n(t)$ when $r_0 \leq r < R^0_\ast$. Here, $Q(n)$ denotes a polynomial function of $n$. Similar estimates can be established for $u^{(2)}_n$ and $u^{(3)}_n$ by (3.60) and (3.61).

Lemma 3.2. Consider the elliptic problem

where $\Omega_R = \big\{x\in \mathbb{R}^2: r_0 < |x| < R\big\}$. If $b(x, t) = b(|x|, t)$ and $b(\cdot, t)\in L^2(\Omega_R)$, then the problem (3.64) and (3.65) admits a unique solution $\omega$ in $H^2(\Omega_R)$ with estimates

where the constant $C$ in (3.66) and (3.67) is independent of $n$.

The lemma can be proven by combining the proofs of [16, Lemma 4.6] and [17, Lemma 3.2]. The details are omitted here.

Lemma 3.2 ensures the existence and uniqueness of $u^{(k)}_n$ in $H^2(\Omega{_\ast})$ for $k = 1, 2, 3$. Furthermore, there holds

Obviously, the solution $u^{(4)}_n$ to the problem (3.62) has the form:

where $C_5(t)$ and $C_6(t)$ are determined by the boundary conditions in (3.62). Using (2.10), (3.41), (3.56), (3.57) and the boundary conditions in (3.52), we get

where $H_1$, $H_2$ are functions of $r_0$, $R^0_\ast$ and $R^1_\ast$.

Now, since

we derive

By (3.33), (3.57) and (3.69)–(3.72), we obtain from (3.54) that

where $\tilde{H}$ is a known function of $n$, $r_0$, $R^0_\ast$, $R^1_\ast$ and satisfies

Thus, using Lemma 3.1, (3.68) and (3.73) gives

In addition, for $n\geq0$, Lemma 3.1 implies

Therefore, applying [16, Lemma 4.7] to (3.74) yields

i.e., $a^1_n(t)$ decays exponentially as $t\to\infty$. Noticing that $b_n(t)$ and $a_n(t)$ have the same asymptotic behavior, we also have

Proof of Theorem 1.2 The desired result (1.14) follows from Lemma 3.1, (3.75) and (3.76). The proof is complete.

Remark 3.2. The results on tumor cord without time delays in ^[14] show that the radially symmetric stationary solution is asymptotically stable under nonradially symmetric perturbations. Here, our Theorem 1.2 says that such asymptotic stability does not be affected by small time delay.

4.   Conclusions

In this paper, we have investigated the effects of a time delay in cell proliferation on the growth of tumor cords, where the domain is a bounded subset in $\mathbb{R}^2$ and its boundary consists of two disjoint closed curves, one fixed and the other moving and a priori unknown. The existence, uniqueness and linear stability of the radially symmetric stationary solution were studied.

Here are some interesting findings. 1) Adding the time delay would not change the stability of the radially symmetric stationary solution when compared with the same system without delay ^[14], but adding the time delay would result in a larger stationary tumor. The bigger the tumor growth intensity $\mu$ is, the greater impact that time delay has on the size of the stationary tumor. 2) By the result of ^[16], we know that for tumor spheroids with the same time delay, there exists a threshold $\mu_\ast > 0$ for the tumor aggressiveness constant $\mu$ such that only for $\mu < \mu_\ast$, the radially symmetric stationary solution is linearly stable under non-radial perturbations. For tumor cords, however, from Theorem 1.2 we saw that the radially symmetric stationary solution is always linearly stable, regardless of the value of $\mu$. It showed that there is an essential difference between tumor cords and tumor spheroids with the same time delay.

We think that the linear stability analysis for the full system without quasi-steady state simplification, i.e., $c > 0$, may be very challenging, which we expect to solve in future work.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to thank the reviewers for their valuable suggestions. This work was partly supported by the National Natural Science Foundation of China (No. 12161045 and No. 12261047), Jiangxi Provincial Natural Science Foundation (No. 20224BCD41001 and No. 20232BAB201010), the Science and Technology Planning Project from Educational Commission of Jiangxi Province, China (No. GJJ2200319), the Scientific Research Project of Hunan Provincial Education Department, China (No. 22B0725, No. 23B0670 and No. 23C0234), and the Research Initiation Project of Hengyang Normal University, China (No. 2022QD01).

Conflict of interest

The authors declare there is no conflict of interest.