On a generalized Klausmeier model

1.   Introduction

Desertification is a phenomenon that is increasing over time and causing a negative impact around the world. This phenomenon affects a large part of the global population and has important consequences for the global economy. Different institutions, such as, the United Nations, United Nations Convention to Combat Desertification and National Commission for Arid Zones, have developed strategies to combat desertification. The damage caused can be reversed and raise awareness about this serious situation. One way to study this type of phenomenon is through mathematical models, which have a low cost, and it is not necessary to wait years for vegetation growth.

In his paper from 1999, the American ecologist Christopher A. Klausmeier introduced the first two-component model named after him, to describe vegetation growth in arid and semi-arid zones ^[1]. The Klausmeier model consists of two nonlinear differential equations with the variables "$w$" and "$u$", which denote the density of water and vegetation, respectively.

This model has been studied by several authors, including Jonathan A. Sherratt, who focused on analyzing the parameter region in which vegetation patterns exist ^[2,3,4]. Some other authors have focused on studying generalized Klausmeier models, including modified terms related to water infiltration and functional dependence of the inertial times on vegetation biomass and soil ^[5] and including linear and non linear diffusion of water ^[6].

Many natural phenomena are governed by behaviors that do not obey a model with integer derivatives. An important tool for their study is fractional calculus which has gained importance in the field of applications. Using fractional derivatives, some models have been studied and approximated more accurately than with integer derivatives. In this direction we refer to ^[7], where a fractional logistic model is considered. Other relative works include a fractional Gaussian model for the motion of electrons ^[8], a Drude model ^[9] and a fractional model involving study of the tuberculosis ^[10]. Some of the first and most popular fractional derivatives are the Riemann-Liouville and Caputo derivatives, which are based on the Cauchy formula for the iterated integral.

Some other definitions of fractional derivatives are given by limits. These definitions entail perturbing the increment by means of certain positive functions. These types of derivatives are known as local fractional derivatives. Given its diverse characteristics, the topic of local fractional derivatives has been of increasing interest for mathematicians. Recently, this concept has gained much relevance. Properties such as the Leibniz product rule, the chain rule and the quotient rule prevail, although the memory condition inherent to the usual fractional derivatives is lost. Also, we would like to mention that local fractional integral transforms have been introduced and studied in ^[11,12].

In this paper we will work with the following generalized fractional derivative $G_{T(t, \alpha)}^{ \alpha}$ for $\alpha\in(0, 1]$:

where $T$ is a positive continuous function. This derivative admits some well-known local fractional derivatives as particular cases. Here are a few examples:

i) If $T(t, \alpha) = t^{1- \alpha}$, then we get the Khalil derivative ^[13].

ii) If $T(t, \alpha) = [k(t)]^{1- \alpha}$ and $k:[a, b]\to\mathbb{R}$ is a continuous nonnegative map, then we recover the general conformable fractional derivative defined in ^[14].

iii) We have the beta derivative if $T(t, \alpha) = { \left(t+\frac { 1 }{ \Gamma (\alpha) } \right) }^{ 1-\alpha }$ ^[15].

iv) The nonconformable fractional derivative is obtained if $T(t, \alpha) = \exp({{t^{- \alpha}}})$ ^[16].

One of the advantages of using this derivative $G_T^\alpha$ is that it allows us to vary the order and the function $T(t, \alpha)$ according to the requirements of each problem. We study a generalized Klausmeier model by focusing on the derivative $G_T^\alpha$. First, we will make a qualitative analysis of the solutions and establish stability conditions for the equilibrium points of the proposed model. Consequently, the stability of solutions via second member variation and some classical methods will be discussed. In the last section, an inverse problem using Bayesian inference is considered.

2.   Definitions and basic properties

As mentioned in the introduction a definition of local fractional derivative, called the $"$ generalized derivative" is given as follows ^[17].

Definition 1. Suppose that there is a real interval $I$, a function $f: I \rightarrow {\mathbb{R}}$, $\alpha \in \mathbb{R}^+$ and the function $T(t, \alpha)$ that is continuous and positive on the interval $I$; the generalized derivative, denoted as $G_{T}^{\alpha }f$, of the function $f$ and order $\alpha$ at the point $t$ of the interval $I$, is defined by

If $a = \inf\{t \in I\}$ (respectively, $b = \sup\{t \in I\}$), then $G_{T}^{\alpha }f(a)$ ($G_{T}^{\alpha }f(b)$) is defined by using $\epsilon\to 0^-$ ($\epsilon\to 0^+$) instead of $\epsilon\to 0$ in the limit.

Throughout this paper, $I\subseteq \mathbb{R}$ denotes a real interval and $\alpha \in \mathbb{R}^+$. The following result in ^[17] contains some basic properties of the derivative $G_{T}^{ \alpha}$.

Theorem 1. Let $f: I \rightarrow {\mathbb{R}}$ and $t_0\in I$ such that $T(t_0, \alpha)\not = 0$. The following statements hold:

i) If $(G_1^\alpha f)(t_0)$ exists, then $f$ is $G_{T}^ \alpha$-differentiable at $t_0$ and $(G_{T}^{\alpha }f)(t_0) = (T(t_0, \alpha))^{\lceil \alpha \rceil}(G_1^\alpha f)(t_0)$.

ii) If $\alpha$ is in $(0, 1]$, then the function $f$ is $G_{T}^ \alpha$-differentiable at the point $t_0$ if and only if the function $f$ is differentiable at the point $t_0$; in this case, we have that $(G_{T}^{\alpha }f)(t_0) = T(t_0, \alpha) f'(t_0)$.

In ^[10], an integral operator $J_{T, a}^\alpha$ is defined as follows. Let $a, t \in I$; the integral operator $J_{T, a}^ \alpha$ is given as

for every locally integrable function $f$ on the interval $I$.

Proposition 1. Let $a\in I$ and $\alpha\in(0, 1]$; then,

for every $f$ that is continuous on the interval $I$.

Some nice generalizations have been obtained. For example, in ^[18] a generalized Laplace transform was defined as follows. Consider the function $T$ that is continuous and positive on the interval $(0, \infty)$ such that it satisfies for some $\epsilon > 0$ that

we define a function $E_{\alpha}$ as below:

Definition 2. Given $0 < \alpha \leq 1$ and a function $f : [0, \infty) \rightarrow {\mathbb{R}}$ that is measurable, then the generalized Laplace transform of the function $f$ is defined as follows:

if $\mathcal{L}_{T}^{\alpha}[\mid f \mid](s) < \infty$.

In Subsection 3.3 we also use the Padé approximants.

Definition 3. Let $\sum_{k = 0}^\infty a_kx^k$ be the Maclaurin series of a function $f(x)$ and let $C\geq 0$ and $D\geq 1$ be two integers. The $[C/D]$ Padé approximant is the following rational function:

such that $f^{(j)}(0) = \{[C/D]\}^{(j)}(0)$, $j = 0, ..., C+D$. Thus

3.   Klausmeier model with the generalized derivative

The well-known reaction-diffusion-advection model by Klausmeier describes two-dimensional vegetation pattern formation as a function of the resource water. This model is given as follows:

Here $w$ and $u$ represent water density and plant biomass, respectively. In this model the constant $a$ represents the precipitation rate, $b$ denotes the rate of water evaporation, $c$ is the rate of water absorption by vegetation and $v$ represents the velocity of the water flowing downhill. On the other hand, $d$ is the mortality rate of the vegetation, $e$ is the rate of use of the water consumed by the vegetation ($e = jc$, where $j$ is the yield of plant biomass per unit water consumed) and $k$ represents the dispersion of the vegetation. The simplified model with ordinary derivatives describes the dynamics between vegetation and water, without taking into account the spatial dispersion (in the absence of advection and diffusion):

For standard literature on the subject one may refer to the references ^{[19,20,21,22]}. The Klausmeier model (3.2) with the generalized derivative (2.1) takes the following form:

where $\alpha, \beta\in(0, 1]$. From now on, the system (3.3) will be referred to as the "generalized Klausmeier model". To standardize the notation, we will use the following as the initial condition throughout the paper: $(w, u)|_{t = t_0} = (w_0, u_0)$. The use of this generalized derivative allows us to vary $T$ and the order in such a way that we can obtain some interesting properties, although in some cases the model becomes nonautonomous. We define the region of interest of the model as follows:

and, the parameters are defined below:

3.1.   Nonspatial equilibria and differential flow-induced instability

A model is in a steady state if the state variables which define the behavior of the model are unchanging in time. Patterns can arise when a homogeneous steady state is unstable. Klausmeier showed that regular vegetation patterns in the semi-arid environments can result from traveling-wave instability ^[1]. On slopes, water flow downhill causes striped patterns which move uphill and not all of the possible patterns are stable as solutions of the system.

We will now focus on analyzing Lyapunov stability according to the first approach. A detailed justification of the stated procedure and the claimed stability is in ^[23]. Unlike the Caputo derivative, the Routh-Hurwitz stability criterion remains invariant. It should be pointed out that the following stability analysis is essentially the same as in the classical case, but for the convenience of the reader it was included here due to obtain some untreated conditions. Considering the regions of interest, the equilibrium points of (3.3) are given by the solutions of the system:

The following proposition gives necessary and sufficient conditions for their existence.

Proposition 2. Given the system (3.3), the following statements hold:

i) If $u = 0$ there exists a unique equilibrium point

ii) There exist two different equilibrium points

and

if and only if $u\neq 0$ and $a > \frac{2d\sqrt{bc}}{e}$.

iii) There exists a unique equilibrium point $P_{4} = \left(\frac{a}{2b}, \frac{2db}{ea}\right)$ if $u\neq 0$ and $a = \frac{2d\sqrt{bc}}{e}$.

Briefly, we will show some conditions for the stability of the equilibrium points $P_j$ ($j = 1, ..., 4$). First, the Jacobian matrix of the system (3.3) is given by

then this matrix evaluated at $P_1$ gives us

The eigenvalues of $J(P_{1})$ are negative. Therefore, $P_1$ is asymptotically stable. Now we evaluate the system at points $P_2$ and $P_3$:

where $u_{i}$ stands for the coordinate $u$ associated with each equilibrium point $P_i$ for $i = 2, 3$. Thus the characteristic polynomial is given by

which has the following solutions

Now the stability depends on $\lambda_{\pm}$. First, we see that if $\left(cu_{i}^{2}+b-d\right)^{2}-4\left(-db+cdu_{i}^{2}\right) = 0$ then

which implies that $P_i$ is asymptotically stable if

and it is otherwise unstable. We can see that if $\left(cu_{i}^{2}+b-d\right)^{2}-4\left(-db+cdu_{i}^{2}\right) < 0$ then analogous to the previous case, the stability conditions will be given by the condition (3.6). The last case is when $\left(cu_{i}^{2}+b -d\right)^{2}-4\left(-db+cdu_{i}^{2}\right) > 0$; then, $\lambda_{1, 2}$ denotes different real eigenvalues. Thus if

then

hence,

If it is also satisfied that

then

Hence $P_i$, $i = 2, 3$, will be asymptotically stable, whereas if $cu_i^2+b-d < 0$ then both points are unstable. Now if $-db+cdu_{i}^{2} < 0$ we have

hence,

Thus,

and

arriving at instability of the study points. In conclusion, when the condition

is satisfied, then the points $P_i$, $i = 2, 3$, are asymptotically stable if

is fulfilled for $i = 2, 3$.

Finally, we analyze point $P_4$. We have

which has the following characteristic polynomial:

The solutions of $p(\lambda) = 0$ are

Of course, $P_{4}$ is unstable.

Turing instability is mostly studied in extended Klausmeier models in which there is diffusion throughout the dynamics and the diffusion constants differ ^[24,25,26]. In the generalized Klausmeier model, Turing instability is not possible because diffusion only exists in the biomass equation. However, a differential flow exists in this model with advection and diffusion. In other words, the biomass advection and the water advection differ, which can result in instabilities. We assume small perturbations:

Then, the following equation (3.10) describes the evolution of perturbations:

where $J$ is the Jacobian evaluated at the equilibrium point with $p_{ij}$ denoting the entries of the matrix. Next we apply the following nonuniform exponential perturbation in time:

Thus the eigenvalue equation is as follows:

where $M$ denotes the system matrix. The eigenvalues $\lambda_{\pm}$ are given by

The instability now depends on the parameters $v$ and $r_2$ such that there exists an eigenvalue with a positive real part. Differential flow-induced instability exists for the reference values. For example, at equilibrium point $P_1 = (a/b, 0)$, we have

therefore, if $vr_2 > b$ then $P_1$ becomes unstable in this sense.

3.2.   Stability of solutions via second member variation

We have the generalized Klausmeier model (3.3) and let us now consider the perturbed model given by

where the perturbations $\theta_1(t, w, u)$ and $\theta_2(t, w, u)$ are continuous functions in a closed domain $D$. Suppose that in $D$ we have

for $\epsilon_1, \epsilon_2 > 0$. Therefore, if $(w, u)$ and $(\widetilde{w}, \widetilde{u})$ are solutions of models (3.3) and (3.11), respectively, which satisfy the same initial condition

then

where $M_1 = \max_{(t, w, u)\in D}\left|\frac{b+cu^2}{T(t, \alpha)}\right|$ and $M_2 = \max_{(t, w, u)\in D}\left|\frac{d-2euw}{T(t, \beta)}\right|$. By (3.12), if the perturbations are sufficiently small then the difference between the solutions of models (3.3) and (3.11) will be small over a finite interval of variation of $t$. In this situation, the system can be seen under the action of short duration perturbations. A respective stability analysis under constant action perturbations is also available where the results of Malkin and Duboshin can be generalized to this approach ^[27,28,29]. In general, the latter circumstance allows us to solve approximately complicated fractional differential equations by replacing them with rationally chosen equations. We illustrate this with a particular example.

Consider $T(t, \alpha) = \exp[{(\alpha-1)t}]$. We want to find in the orthohedron $D = \{0\leq t\leq 2, 1\leq w\leq 2, 1\leq u\leq 2\}$ an approximate solution to the generalized Klausmeier model:

Let us analyze the following simple model:

The model (3.14) has the solution

which, for the values of $0\leq t\leq 2$ remains inside $D$. We will consider this solution as the approximate solution of the generalized Klausmeier model (3.13) in $D$. We now proceed as follows:

on the other hand we have the following in $D$:

Therefore

for $0\leq t\leq 2$. Note that the solution of the generalized Klausmeier model (3.13) remains within $D$. The error is acceptable but not desirable. The difficulty of this method lies in finding the perturbed model that sufficiently minimizes the error in the study region.

3.3.   Homotopy perturbation method

In his PhD dissertation from 1992, Liao introduced the homotopy analysis method (HAM), which employs the definition of a homotopy to generate a convergent homotopy-Maclaurin series solution for nonlinear systems ^[30]. Nowadays it is a very effective and well-known method, to such an extent that it has been applied to Navier-Stokes equations. In 1999, He proposed the homotopy perturbation method (HPM), which maintains the essence of the HAM ^[31]. Liu suggested artificial parameter methods and Liao contributed the HAM to eliminate small parameter assumption ^[32,33,34]. He treated two effective techniques, i.e., the variational iteration method and HPM in which no small parameter assumptions are required ^[35]. A brief mathematical description of the HPM is shown below.

Consider the boundary value problem given by

where $D$ denotes a general differential operator, $E$ represents a boundary operator and $f(r)$ is an analytic function. Usually, the operator $D$ can be decomposed into two parts, i.e., a linear part denoted by $\mathcal{L}$ and a nonlinear part denoted by $\mathcal{N}$. Equation (3.15) may then be rewritten as follows:

We can construct a homotopy $\mathcal{H}(\tilde{w}, \rho):\Omega\times[0, 1]\to R$ in the form of (3.17) such that it satisfies

or equivalently

where $\hat{w}$ is an initial approximation of (3.15) in such a way that it satisfies the given boundary conditions. Note that

and

that is, we have a homotopy between the nonlinear system and a linearization. As $\rho$ changes from $0$ to $1$, $\tilde{w}$ changes from $\hat{w}(r)$ to $w(r)$, so one equation deforms into the other. Since $\rho \in[0, 1]$ is a small parameter, we expand $\tilde{w}$ in a Taylor series about $\rho = 0$. We have the homotopy-Maclaurin series as follows:

Thus, the approximate solution of (3.15) may then be obtained as

The convergence of the series solution (3.20) has been given in ^[31]. The convergent rate depends upon the nonlinear operator $N(w)$.

Next, we apply the modified HPM ^[36] to solve the generalized Klausmeier model (3.3), subject to the following initial conditions:

We construct homotopies as below:

We consider solutions of (3.22) in the series form as follows:

Then, we get

Hence

where $W_j$ and $U_j$ are real constants which depend on the initial conditions. Successively, $\tilde{w}_j$ and $\tilde{u}_j$ are found due to the recursive process in order to obtain that

Some suggestions to ensure convergence are as follows. The product of $T(t, \beta)$ and the water density $w(t)$ must be small because the parameter $\rho$ may be large. The norms of $c(G_{T(t, \alpha)}^\alpha w+bw)^{-1}u^2$ and $2e(G_{T(t, \beta)}^\beta u+du)^{-1}uw$ must be smaller than $1$ to ensure that the series converges ^[31]. We truncate the series solution (3.25) and use the k-th order of the perturbation only, such that the approximate solutions are given by

Now we take the generalized Laplace transform (2.3) of $W(t)$ and $U(t)$. The next step is to find the Padé approximants of $\mathcal{L}_T^\alpha[W]$ and $\mathcal{L}_T^\alpha[U]$. Using the $[C/D]$ Padé approximants with $C > 0$ and $C+D < k+2$ we will arrive at a better approximation of the solution than that achieved by truncating its series. Finally, by applying the inverse generalized Laplace transform to the $[C/D]$ Padé approximants, we obtain a better approximation ^[36].

3.4.   Adams-Bashforth formulas

The Adams-Bashforth method is an explicit linear multistep method. The Euler method is a particular case of this method. For our fractional model we have

The generalized Adams-Bashforth method up to four steps, is as follows:

The Adams-Bashforth method needs more than one value when the step is greater than $1$. Missing values can be found by performing any of the above steps. For the stability analysis of these numerical methods we refer the reader to ^[37]. These formulas will be used in the next section in some computational algorithms.

4.   Data analysis and computational statistics

In this section we will present the computational analysis for the generalized Klausmeier model.

4.1.   MATLAB implementation

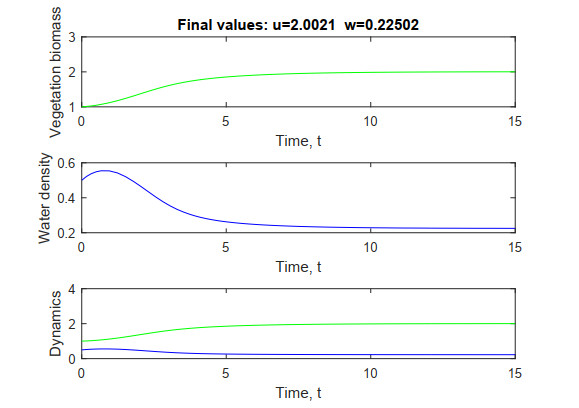
Using MATLAB, we have written a script to enable numerical calculation of the solution of the generalized Klausmeier model (see Annexes). For the implementation we have used the efficient ode45 function based on the Runge-Kutta method. Some graphs of generalized models with different $T$ functions are shown below. An observable feature is that the models in Figures 2 and 3 resemble the ordinary one, whereas the last model of Figure 4 with different $T$ functions is quite pathological. Note that in this last model with $T(t, \alpha) = (t^2+0.01)^{1-\alpha}$ and $\widetilde{T}(t, \beta) = (\sin^2 t+0.01)^{1-\beta}$, the final value of $w$ is greater than the final value of $u$. Whether or not this generalized Klausmeier model in Figure 4 has a physical or ecological interpretation is left as an open question.

4.2.   Bayesian inversion

System (3.3) can be nondimensionalized to

The nondimensionalized model (4.1) has only two parameters: $a$, which controls water input; and $m$, which measures plant losses. The Bayesian approach will be used to estimate the parameters of model (4.1). In this framework, the parameters in the model are described in terms of a probability model. Let $Y = (y_1, \ldots, y_n)'$ be a set of observations where $y_i = (y_{i1}, y_{i2})'$, which represents a solution for the model (4.1) at the time $t_i$ for $t_i \in [0, T]$, $i = 1, \ldots, n$, with an additive error. Therefore, the observation models can be written as

where $x(t_i; \kappa) = (w(t_i), u(t_i))'$ is a solution for (3.3), parameters of interest $\kappa = (\alpha, \beta, a, m)'$, $\eta$ denotes the function of observation and $\varepsilon_i$ represents independent Gaussian errors. These have a mean equal to zero and covariance matrix ($\Sigma$) denoted by $\varepsilon_i\sim N_2(0, \Sigma)$. The parameters associated with the priori distribution are usually known as "hyperparameters'', and the distributions associated with the parameters have to be chosen according to the a priori information about the possible values of the parameters. Given the knowledge it has of the parameters, uniform distributions will be used that are non-informative. Specifically, $\alpha\sim U(0, 1)$, $\beta\sim U(0, 1)$, $a\sim U(0, 2)$, $m\sim U(0, 2)$ and $U$ denotes the uniform distribution; then, the joint a priori distribution can be written as

Hence, the likelihood function is given by

and the posterior distribution using Bayes theorem is calculated as

where $\Theta$ denotes the parameter space of $\kappa$. The denominator in (4.2) just scales the posterior density to make it a suitable density, and the sampling density is proportional to the likelihood function. Bayes theorem is usually stated as follows:

The posterior distribution is usually approximated by sampling posterior draws of $\kappa$ from $\pi(\kappa\mid Y)$ by using a Markov Chain Monte Carlo (MCMC) algorithm ^[38] through the use of the JAGS package ^[39] in R software. The posterior distribution can be used with the objective to obtain some estimates associated with the parameters of the model and credibility intervals.

4.2.1.   Model checking

Evaluating the efficiency of a proposed model is essential, especially for Bayesian data analyses. Any meaningful Bayesian study must include some validation of the fit of the model to the data. Different tools are available for this purpose. In this work we use posterior predictive model checking (PPMC), a popular Bayesian model-checking tool suggested by ^[40] to calculate model data fit. PPMC can provide some graphical or numerical assurance about the model misfit. This method compares the observed data with the replicated data that are generated by the model. If we find systematic differences between the simulations and the data, then this would indicate potential flaws in the model. A discrepancy measure is defined to make the comparison between the model and data, and it is a scalar summary of the parameters and data. An important issue to consider is the choice of discrepancy measure. Here, we apply the observed score distribution (OSD) that was applied in this context in ^[41]. This discrepancy measure is given by

where $y_i$ denotes the value of total biomass production or precipitations and $E$ is the expected value of $y_i$. Also we take into account the DIC, that is, the deviance information criterion in the model selection, which can provide a dependable criterion of out-of-sample efficiency; also, it is simple to compute given samples from the posterior distribution of the model parameters. The DIC combines a measure of the goodness of fit and a measure of model complexity. Models with a smaller DIC are favored over models with a larger DIC ^[42].

4.2.2.   A real data example

For this comparison study, a site was selected in Somalia with coordinates $(8^\circ 08'26''N; 47^\circ 21'47'' E)$, which is located in the Haud pastoral region. This site mainly includes banded vegetation and has a ground slope near 0%. The vegetation is mainly perennial grass, which typically has an average lifetime of 1-7 years ^[43]. The Food and Agriculture Organization (FAO) portal to monitor water productivity through open access of remotely sensed derived data (WaPOR) provides data for precipitation ($w$) and total biomass production ($u$) annually ^[44]. We used a set of data from 2009 to 2022 for these parameters at the selected point (see Figures 5 and 6).

Four models of system (4.1) were analyzed. Model I corresponds to the ordinary model. Model II was studied with $T(t, \alpha) = t^{1-\alpha}$, while Model III was analyzed with $T(t, \alpha) = \exp(t^{-\alpha})$. Finally, Model IV was developed with $T(t, \alpha) = \exp({(\alpha-1)t})$. For each model, using the solutions of the direct problem given by any of the formulas of the Adams-Bashforth method, as described by (3.27)-(3.28)-(3.29)-(3.30), the likelihood functions were obtained. The MCMC method through the JAGS package within R software was used to get the posterior distributions for each parameter of interest. Specifically, two chains were used, each with 10000 iterations, and the first 100 were discarded; then, 19800 posterior samples were generated to get the summary statistics associated with the parameters of interest. Standard convergence diagnostics were performed; for example, the value of Rhat for each parameter of interest was quite close to 1 for all models considered. The parameter estimation for each model is shown in Table 1, where MOD is an abbreviation for the mean orthogonal distance.

In Figures 7 and 8, we show estimations, where the gray band is a 90% probability interval (that is, 90% of the total chains obtained are shown) and the blue line corresponds to the mean (estimated prediction). As we can see, only the graphs of Model II are shown; this is because this is the one with the best results.

A simulation of 1000 replicated data points was conducted based on the marginal distribution for each parameter of interest. To evaluate the fit of each model, PPMC was applied. The values of the discrepancy measure OSD were calculated and, from this, the MODs from the line of $45^\circ$ to the points given by the OSDs were calculated. A quantitative measure of the fit was provided via the MOD (included in Table 1). A large value of the MOD suggests bad fit of the model to the data. The MOD values indicate that all models fit the biomass data better than the precipitation data.

5.   Conclusions

In this work we studied a generalized Klausmeier model by focusing on the local fractional derivative $G_{T(t, \alpha)}^{\alpha}$. First, a stability analysis was performed by considering the Lyapunov approximation and the method of variation of the second members. The instability of the system induced by the differential flow was studied, as well as the HPM. Adams-Bashforth formulas were given for this fractional context. Subsequently, an inverse problem based on real data in a region of Somalia was solved by considering different functions of $T(t, \alpha)$. As a result, it was obtained that for the data set considered, the model with the best fit was Model II associated with the function $T(t, \alpha) = t^{1-a}$, which corresponds to the conformable fractional derivative named after Khalil. In general, the different models considered fitted the data associated with plant biomass well; however, less favorable results were obtained for precipitation. We conclude with a number of open questions that will guide our future research. These include the following:

$1.$ What would happen if other functions were considered and would some indicators improve?

$2.$ How can we find a function that fits much better to the data studied?

$3.$ In our study we considered $T$ to be equal for both environmental condition cases but with different $\alpha$; could it improve some results to vary $T$ in the simulations?

$4.$ What interesting facts would be found if extended Klausmeier models were generalized by global or hybrid derivatives?

All of these questions allow us to go deeper into these more general systems.

Use of AI tools declaration

The authors declare that they have not used artificial intelligence tools in the creation of this article.

Acknowledgments

Martha Paola Cruz de la Cruz, Daniel Alfonso Santiesteban and Luis Miguel Martín Álvarez gratefully acknowledge the financial support of the Postgraduate Study Fellowship of the Consejo Nacional de Humanidades, Ciencias y Tecnologías (CONAHCYT) (grant numbers: 893915, 1043969, 962684).

Conflict of interest

The authors have no conflict of interest.

MATLAB script for the nonspatial generalized Klausmeier model

$\texttt{%% MATLAB SCRIPT FOR SOLVING THE NONSPATIAL GENERALIZED KLAUSMEIER MODEL}$

$\texttt{function gklausmeier}$

$\texttt{ global a b c d e}$

$\texttt{ %% Parameters}$

$\texttt{ a = ; % Enter a value for a }$

$\texttt{ b = ; % Enter a value for b }$

$\texttt{ c = ; % Enter a value for c }$

$\texttt{ d = ; % Enter a value for d }$

$\texttt{ e = ; % Enter a value for e }$

$\texttt{ %% Initial conditions}$

$\texttt{ u_0 = ; % Enter a value for u at t = 0 }$

$\texttt{ w_0 = ; % Enter a value for w at t = 0 }$

$\texttt{ %% Function T(t, alpha) }$

$\texttt{ T_1 = ; % Enter function T(t, alpha) }$

$\texttt{ T_2 = ; % Enter function T(t, beta) }$

$\texttt{ %% Solve system}$

$\texttt{ tmax = 15;}$

$\texttt{ [T, Y] = ode45(@gklausmeier, [0 tmax], [u_0 w_0]); %%ode45 is based on an explicit Runge-Kutta formula, the Dormand-Prince pair. In general, ode45 is the best function to apply as a first try for most problems.}$

$\texttt{ u = Y(:, 1); }$

$\texttt{ w = Y(:, 2); }$

$\texttt{ %% Plot results }$

$\texttt{ figure; }$

$\texttt{ subplot(3, 1, 1); }$

$\texttt{ plot(T, u, 'green'); }$

$\texttt{ xlabel('Time, t'); }$

$\texttt{ ylabel('Vegetation biomass'); }$

$\texttt{ title(strcat('Final values: u = ', num2str(u(end)), ' w = ', num2str(w(end)))); }$

$\texttt{ subplot(3, 1, 2); }$

$\texttt{ plot(T, w, 'blue'); }$

$\texttt{ xlabel('Time, t'); }$

$\texttt{ ylabel('Water density'); }$

$\texttt{ subplot(3, 1, 3); }$

$\texttt{ plot(T, u, 'green', T, w, 'blue'); }$

$\texttt{ xlabel('Time, t'); }$

$\texttt{ ylabel('Dynamics'); }$

$\texttt{ %% Function gklausmeier }$

$\texttt{ function dy = gklausmeier(t, r) }$

$\texttt{ global a b c d e }$

$\texttt{ dy = zeros(2, 1); }$

$\texttt{ dy(1) = (T_2)^(-1)*[-d*r(1)+e*r(1)*r(1)*r(2)]; }$

$\texttt{ dy(2) = (T_1)^(-1)*[a-b*r(2)-c*r(1)*r(1)*r(2)]; }$