Figure 1.
Lumbar spine and visualization system hardware components.
Minimum spanning tree (MST)-based clustering algorithms are widely used to detect clusters with diverse densities and irregular shapes. However, most algorithms require the entire dataset to construct an MST, which leads to significant computational overhead. To alleviate this issue, our proposed algorithm R-MST utilizes representative points instead of all sample points for constructing MST. Additionally, based on the density and nearest neighbor distance, we improved the representative point selection strategy to enhance the uniform distribution of representative points in sparse areas, enabling the algorithm to perform well on datasets with varying densities. Furthermore, traditional methods for eliminating inconsistent edges generally require prior knowledge about the number of clusters, which is not always readily available in practical applications. Therefore, we propose an adaptive method that employs mutual neighbors to identify inconsistent edges and determine the optimal number of clusters automatically. The experimental results indicate that the R-MST algorithm not only improves the efficiency of clustering but also enhances its accuracy.
Citation: Hui Du, Depeng Lu, Zhihe Wang, Cuntao Ma, Xinxin Shi, Xiaoli Wang. Fast clustering algorithm based on MST of representative points[J]. Mathematical Biosciences and Engineering, 2023, 20(9): 15830-15858. doi: 10.3934/mbe.2023705
| [1] | Xiaoming Liu, Zhonghan Liu, Yaqin Pan, Yufeng Huang, Desheng Wu, Zhaoyu Ba . Full-endoscopic transforaminal procedure to treat the single-level adjacent segment disease after posterior lumbar spine fusion: 1–2 years follow-up. Mathematical Biosciences and Engineering, 2019, 16(6): 7829-7838. doi: 10.3934/mbe.2019393 |
| [2] | Wei-wei Jiang, Guang-quan Zhou, Ka-Lee Lai, Song-yu Hu, Qing-yu Gao, Xiao-yan Wang, Yong-ping Zheng . A fast 3-D ultrasound projection imaging method for scoliosis assessment. Mathematical Biosciences and Engineering, 2019, 16(3): 1067-1081. doi: 10.3934/mbe.2019051 |
| [3] | Kai Cheng, Lixia Li, Yanmin Du, Jiangtao Wang, Zhenghua Chen, Jian Liu, Xiangsheng Zhang, Lin Dong, Yuanyuan Shen, Zhenlin Yang . A systematic review of image-guided, surgical robot-assisted percutaneous puncture: Challenges and benefits. Mathematical Biosciences and Engineering, 2023, 20(5): 8375-8399. doi: 10.3934/mbe.2023367 |
| [4] | Wei-wei Jiang, Xin-xin Zhong, Guang-quan Zhou, Qiu Guan, Yong-ping Zheng, Sheng-yong Chen . An automatic measurement method of spinal curvature on ultrasound coronal images in adolescent idiopathic scoliosis. Mathematical Biosciences and Engineering, 2020, 17(1): 776-788. doi: 10.3934/mbe.2020040 |
| [5] | Biao Cai, Qing Xu, Cheng Yang, Yi Lu, Cheng Ge, Zhichao Wang, Kai Liu, Xubin Qiu, Shan Chang . Spine MRI image segmentation method based on ASPP and U-Net network. Mathematical Biosciences and Engineering, 2023, 20(9): 15999-16014. doi: 10.3934/mbe.2023713 |
| [6] | Yongde Zhang, Qihang Yuan, Hafiz Muhammad Muzzammil, Guoqiang Gao, Yong Xu . Image-guided prostate biopsy robots: A review. Mathematical Biosciences and Engineering, 2023, 20(8): 15135-15166. doi: 10.3934/mbe.2023678 |
| [7] | Won Man Park, Young Joon Kim, Shaobai Wang, Yoon Hyuk Kim, Guoan Li . Investigation of lumbar spine biomechanics using global convergence optimization and constant loading path methods. Mathematical Biosciences and Engineering, 2020, 17(4): 2970-2983. doi: 10.3934/mbe.2020168 |
| [8] | Liwei Deng, Zhen Liu, Tao Zhang, Zhe Yan . Study of visual SLAM methods in minimally invasive surgery. Mathematical Biosciences and Engineering, 2023, 20(3): 4388-4402. doi: 10.3934/mbe.2023203 |
| [9] | Tong Sun, Xin Zeng, Penghui Hao, Chien Ting Chin, Mian Chen, Jiejie Yan, Ming Dai, Haoming Lin, Siping Chen, Xin Chen . Optimization of multi-angle Magneto-Acousto-Electrical Tomography (MAET) based on a numerical method. Mathematical Biosciences and Engineering, 2020, 17(4): 2864-2880. doi: 10.3934/mbe.2020161 |
| [10] | Yali Ouyang, Zhuhuang Zhou, Weiwei Wu, Jin Tian, Feng Xu, Shuicai Wu, Po-Hsiang Tsui . A review of ultrasound detection methods for breast microcalcification. Mathematical Biosciences and Engineering, 2019, 16(4): 1761-1785. doi: 10.3934/mbe.2019085 |
Minimum spanning tree (MST)-based clustering algorithms are widely used to detect clusters with diverse densities and irregular shapes. However, most algorithms require the entire dataset to construct an MST, which leads to significant computational overhead. To alleviate this issue, our proposed algorithm R-MST utilizes representative points instead of all sample points for constructing MST. Additionally, based on the density and nearest neighbor distance, we improved the representative point selection strategy to enhance the uniform distribution of representative points in sparse areas, enabling the algorithm to perform well on datasets with varying densities. Furthermore, traditional methods for eliminating inconsistent edges generally require prior knowledge about the number of clusters, which is not always readily available in practical applications. Therefore, we propose an adaptive method that employs mutual neighbors to identify inconsistent edges and determine the optimal number of clusters automatically. The experimental results indicate that the R-MST algorithm not only improves the efficiency of clustering but also enhances its accuracy.
As a minimally invasive interventional surgery, percutaneous puncture has the advantages of minimal trauma, fast recovery and strong targeting [1], and it is widely used in human tissue biopsies and drug-directed treatment. Among the various procedures, lumbar puncture is often used for the diagnosis of various central nervous system inflammatory diseases, vascular diseases, spinal cord diseases, intracranial-space-occupying diseases, unknown nervous system diseases and spinal angiography. In addition, lumbar puncture is also a common clinical diagnosis and treatment method for drug injection treatment and decompression due to the high cerebrospinal fluid pressure caused by central nervous system diseases [2,3].
In traditional lumbar puncture surgery, doctors use medical imaging equipment and their clinical experience to determine the location of the needle puncture point on the skin. Medical imaging mainly includes computed tomography, magnetic resonance imaging and ultrasound imaging [4]. Compared with computed tomography and magnetic resonance imaging, ultrasound imaging has the advantages of being low cost, no radiation and real-time image generation [5]. Therefore, it has become the best choice for doctors in lumbar puncture surgery. However, the time and results required to complete a scan are dependent exclusively on the skills and experience of the doctor. In addition, ultrasound scanning requires a complex posture of the hands of doctors to maintain a certain contact force; hence, long-term work may cause complications such as arthritis [6,7]. The use of electric power to operate a mechanical arm can reduce the burden on doctors.
During an operation, the robotic arm puncture system has the advantages of high precision, good stability and simple and efficient operation [8]. Aiming at the clinical needs of lumbar puncture, the present study involved the design of a robotic-assisted ultrasound scanning system for lumbar puncture. The computer-controlled robotic arm clamps the ultrasound probe and automatically scans the patient's lumbar spine.
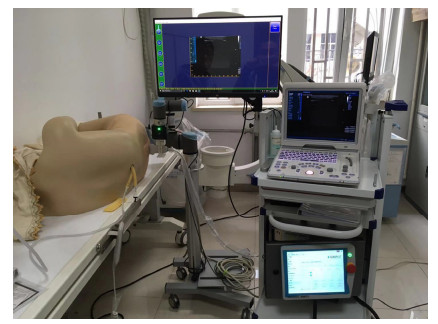
The proposed system is shown in Figure 1, and it mainly included DP-50 portable ultrasound diagnostic equipment (Shenzhen Mindray Biomedical Electronics Company) for acquiring the two-dimensional ultrasound images, a six-degree-of-freedom robotic arm (UR3, Universal Robots A/S, Odense, Denmark) for controlling the movement of the ultrasound probe, a main control computer with an Intel Core i7-7700 processor to control the robot arm and process the image, a video capture card (Epiphan DVI2USB3.0) for acquiring two-dimensional ultrasound images and transmitting them to a computer and a GRIPKIT-E gripper (Weiss Robotic Company) for holding the ultrasonic probes.
The system was divided into three main parts: control, acquisition and visual processing. Among them, the control part mainly involved the main control computer (including software), the robot arm control box and the structure of the robot arm; the acquisition part mainly involved the portable ultrasonic scanning system and the video capture card; the visualization processing was mainly realized through the software on the main control computer in which the code was embedded. In the operation of the system, the operator controlled the control program interface through the peripheral equipment of the main control computer and monitored the running state of the system in real time through the display, and the robot arm and the control box communicated with the computer through the Transmission Control Protocol/Internet Protocol. When the operator determined the starting point and end point of the scan, the control program automatically controlled the robot arm holding the ultrasound probe to scan the lumbar vertebrae and collect two-dimensional ultrasound images. The collected ultrasound images were transmitted to the main control through the data acquisition card. The computer then processed and saved the images. After the scan was completed, the visualization toolkit (VTK) 3D image reconstruction program was employed to perform the 3D reconstruction of the scanned images. The reconstruction result can provide a reference and guidance, thereby enabling the doctor to determine the puncture point.
The control software was developed by using the Microsoft C# programming language, which mainly included five modules. The user interface module (LumbarPunctureSystem) was the main module of the system; it had the main following functions: parameter setting, operation control, process control, image display and system status display. The surgery module (SurgeryModule) was used to create new cases, hardware (robot arm, ultrasound) start and control and system settings. The robot control module (RobotModule) realized the motion control of the robot arm so that the robot arm could independently move along the axes of the base coordinate system and the tool coordinate system. The ultrasound imaging module (ImagingModule) was used to collect the ultrasound images and record information, such as the position of the robot arm and the size of the torque during the acquisition process, and to perform 3D reconstruction after the acquisition. The button control module (EnhancedGlassButton) was used to create button controls for the interface.
Initially, the control software was launched; the program automatically connected the robot arm and the acquisition card. After the connection was successfully established, the new case button in the operation control area was activated. The operator created a case and filled in relevant information by clicking the new case button. Subsequently, after the successful creation, the tool button was activated.
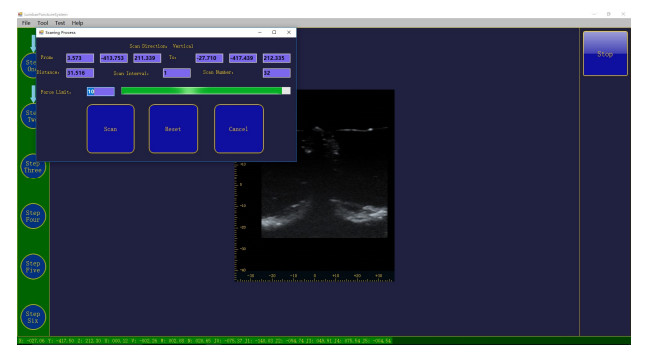
After the operator clicked the tool button, the program controlled the robot arm to grab the ultrasonic probe placed at a fixed position, activated the button to set the scanning start point and prompted the robot arm motion control panel to appear on screen. The operator adjusted the robot arm through the control panel by moving it to the starting point of the model scan and pressed the start button to activate the scanning end button. Similarly, the probe could be moved to the end point, after which the end point button could be pressed. Subsequently, the program launched the scan control interface, which displayed the corresponding information and supported the modification of some settings. Finally, when the operator pressed the scan button, the program automatically controlled the robot arm to move along a specific path from the scan start point to the scan end point and performed real-time image storage. During the scanning process, every time the robot arm moved 0.5 mm, the program acquired an ultrasound image, as shown in Figure 2. During this process, the robotic arm was set to run in force mode to ensure that the probe was in effective contact with the measured object. After artificial planning, the robotic arm moved in the lumbar spine direction and it automatically adjusted the position in the vertical direction, following force-limited parameters in grip, thereby acquiring a good ultrasound image. It is worth noting that, before the scan started, information such as the pressure of the robot arm and the interval of image acquisition was set on the scan control interface. In addition, once the new case was created, the program automatically activated the stop button in the operation control area. At any time during the scan, the program could be terminated by pressing this button to prevent accidents and ensure the safety of the scan.
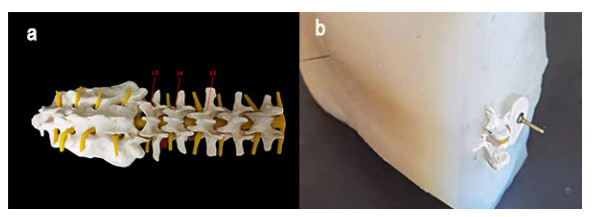
The lumbar spine model used in this study was the Enovo Medical Model (Shanghai, China) shown in Figure 3. Ultrasound has a good propagation speed in hydrogel material [9], and it produces a good coupling between the model and the probe. As a result, the experimental model for scanning was made in an acrylic material container (made in our laboratory), the spine model was put in it and the mixture of hydrogel and pure water was poured for lumbar region modeling. The liquid surface was 1–2 cm above the model. The ultrasonic probe model included a 75L38EA linear array, and the ultrasonic frequency was 8.5 MHz, the scan width was 3.8 cm and the depth was 4.6 cm. According to clinical experience, lumbar puncture is usually performed at the 3rd to 4th lumbar vertebral space, and in children under 4 years old, it needs to be punctured at the 4th to 5th spinous process space of the lumbar vertebrae. Therefore, the scanning range of this experiment was L3–L5. In the experiment, the main control program controlled the robot arm to clamp onto the ultrasonic probe to determine the scanning start and end points. The acquisition interval (0.5 mm) and force mode value (2N) were set to perform the two-dimensional ultrasound image acquisition. Then, the obtained image was processed for the 3D reconstruction and visualization.
After successfully acquiring the two-dimensional ultrasound tomographic image, the 3D reconstruction button in the main control program was activated. The operator pressed this button to perform the VTK-based 3D ultrasound image reconstruction and display, which can provide a reference and serve as guidance for determining the location of the puncture point and surgical path planning.
The VTK is an open-source visualization development tool developed by the Kitware Company, and it is widely used in the fields of visualization and 3D graphics, as well as other fields. The 3D visualization process generally involves medical image data reading, data preprocessing, visual mapping, reconstruction and interactive operation. Image data acquisition is a two-dimensional tomographic medical image sequence obtained by scanning real objects by using an imaging device. The format of the read image included the DICOM format and BMP format. Data preprocessing was carried out because the quality of the image may be reduced to a certain extent during the image output, transmission and conversion, and due to the introduction of noise. Hence, the image needed to be preprocessed by filtering. Visual mapping converted the processed raw data into geometric pixels and attributes for drawing, including the display shape, color and other attribute settings. Common methods for reconstruction include surface and volume rendering. Surface rendering describes the 3D structure of organs or tissues by fitting the surface information of the structure by data splicing, and the key technology sets a threshold to extract the isosurface according to the needs [10]. Volume rendering directly synthesizes the 3D images by resampling the volume data based on the principle of vision. This method treats each voxel as a particle that can receive or emit light, and it configures the light intensity and opacity, integrates along the line of sight and finally forms a projected image. Because surface rendering may lead to the reduction of detailed information, resulting in poor authenticity, this study adopted the use of the volume rendering method for 3D reconstruction. The interactive operation was performed on the basis of the appearance of the 3D reconstruction results. By clicking the mouse, the reconstruction body could be rotated to any angle.
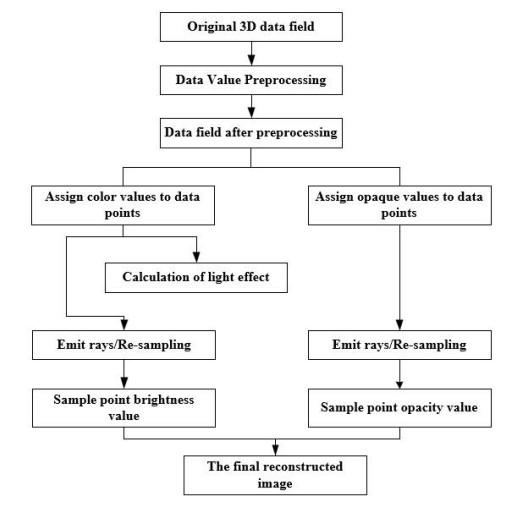
The main methods of volume rendering are ray casting, maximum intensity projection and texture mapping [11]. Since the image quality obtained by the ray-casting algorithm is high, it is most widely used. The flowchart of the ray-casting algorithm is shown in Figure 4. The specific steps of the ray-casting method in the VTK were as follows. First, the bitmap (BMP) picture was read through the vtkBMPReader class. Subsequently, the vtkPiecewiseFunction class was used to determine the opacity of each voxel through the addition of numerical points, and the vtkColorTransferFunction class was employed to implement the color transfer function to add color values or a gray degree value. Then, by selecting different vtkVolumeMapper classes in the drawing pipeline, different volume rendering algorithms were implemented, among which the ray-casting algorithm used the vtkVolumeRayCastMapper class. Finally, the vtkVolumeActor class was used to specify the scene lighting, perspective, focus and other information, and the vtkRender class was used to render the entities in the drawn scene. The VTK also provides the widget base class. In this experiment, the vtkImagePlaneWidget class was used to create cutting plane objects, and the cross section, coronal plane and sagittal plane were successfully displayed.
In this study, the two-dimensional ultrasound images collected by the control program were saved as an 8-bit BMP grayscale image. Subsequently, the reconstruction program was employed to visualize the 3D reconstruction, and the images were processed by using the median filtering method. According to the two-dimensional images collected every 0.5 mm, the ultrasound acquisition depth and probe width were set corresponding to the pixel points of the BMP image in order to calculate the difference between the data points. This was done to ensure that the image scale and size were consistent with the real object. Interactive operation was also set in the program. When the reconstruction result was obtained, the operator could place the mouse cursor in this area and hold down the left mouse button to move it arbitrarily. The operator could then rotate the 3D reconstruction body to any angle for full observation. The zoom function was also realized by rolling the mouse wheel.
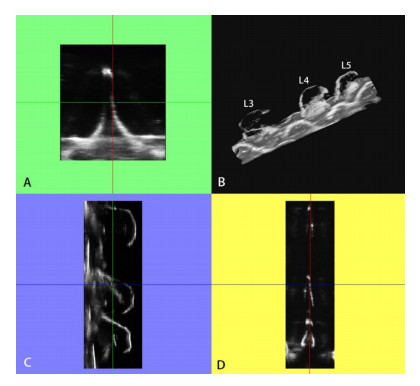
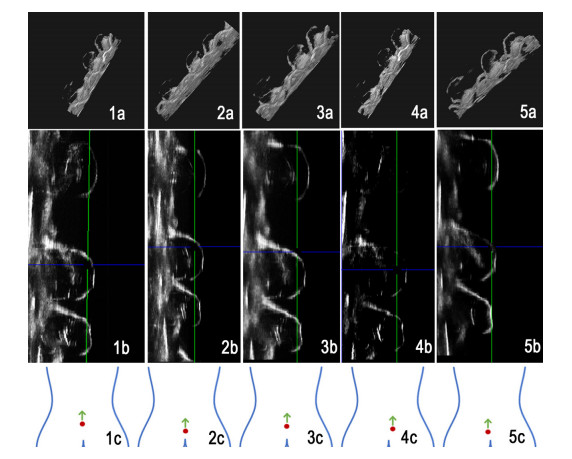
A total of 136 two-dimensional ultrasound images were collected in the lumbar spine model experiment, and the dimensions (in pixels) were 393 × 473. After preprocessing by enhancing the contrast of and denoising the original ultrasound images, the ray-casting algorithm was used to perform the 3D reconstruction of the lumbar spine model. The reconstruction results are shown in Figure 5. Figure 5B is the 3D reconstruction result of the volume rendering ray-casting method, and Figure 5A, C, D are the cross section, sagittal plane and coronal plane after reconstruction, respectively.
Repeated experiments with different entry points were performed and recorded, following the parameters above; the results are shown in Figure 6. The 3D images and corresponding sagittal plane slice images were labeled to show the reproducibility for this model.
Due to the propagation characteristics of the ultrasound along a straight line, the information of the spinous processes perpendicular to the ultrasound linear array was lost. Thus, the reconstructed structure was defective; however, the location of the spinous process gap could be determined by using the sagittal and coronal images, which can be used as a follow-up reference basis for the puncture surgery. The repeated experiment data with different entry points (Figure 6) shows the anatomical structural changes in grey value and sharpness of boundary, which might have been caused by entry point changes, along with shape changing on the back during the scanning of the model.
In recent years, with the gradual maturity of the robotic technology, puncture surgery systems assisted by a robotic arm have developed rapidly. Nelson et al. [12] developed a set of ultrasound image-guided breast biopsy systems for the detection of early breast cancer; it was shown to have good repeatability and less than 0.5% variation. Podder et al. [13] designed a multichannel robot system based on the ultrasound guidance, and it comprised multiple particle implantation needles, especially for the implantation of radioactive particles in the prostate [14]. An experiment revealed a conveyor accuracy within 0.2 mm. Kojcev et al. [15] used both arms to design a set of ultrasound-guided auxiliary puncture systems; it implemented the closed-loop control of the planning-imaging-needle insertion to adjust and plan the puncture path in real time. Xu et al. [16] developed a minimally invasive robotic system for the ultrasound-guided microwave ablation of the liver. This system could perform 3D reconstruction of the liver tumor before surgery and plan the puncture path; it assisted the doctors in sending the puncture needle to the target point during an operation. The above-mentioned previous studies mainly involved ultrasound guidance and included location planning of the body or probe through the use of computed tomography, optical assisted technology and other imaging methods, instead of the robotic arm automatic guidance with force feedback. Our study provides an easier way to employ ultrasound scanning, find the precise location and simplify the complicated operation. In this study, the scanned ultrasound images were processed and reconstructed in all three dimensions. After experimental verification, the system was shown to be able to collect two-dimensional ultrasound images and reconstruct 3D lumbar spine images, thereby providing the doctors with stereoscopic visualization guidance, laying the foundation for subsequent robot-assisted puncture surgeries.
Regarding the usage of this methodology in actual clinical practice, more studies need to be done in the future, such as the use of an automatic drawing point and trajectory as a reference for the doctor, the addition of the modules for different types of conditions, like leukemia cerebrospinal fluid examination, scoliosis and larger body habitus and the redesign of different algorithms for robotic arm motion and puncture planning.
The present study was purposed to design a 3D visualization-enabled robotic-assisted ultrasound automatic scanning system for the lumbar spine. The control program for the robotic arm was developed using the C# language, and a 3D reconstruction program for the ultrasound images was developed based on the VTK. The system controlled the robotic arm to automatically scan and collect the ultrasound images of the lumbar spine model through the program; it subsequently performed the 3D reconstruction. The system could operate normally and achieved the target function. The experimental results for the lumbar spine model showed that the scanning system could effectively collect the images of the model, visualize the 3D reconstruction, realize a full-dimensional stereoscopic display and provide a reference basis for lumbar puncture surgery.
This study was supported by grants from the CAMS Innovation Fund for Medical Science (No. 2021-I2M-1-042, 2021-I2M-1-015, No. 2017-I2M-1-016).
The authors declare that there is no conflict of interest.
| [1] |
X. Xue, J. Chen, Matching biomedical ontologies through compact differential evolution algorithm with compact adaption schemes on control parameters, Neurocomputing, 458 (2021), 526–534. https://doi.org/10.1016/j.neucom.2020.03.122 doi: 10.1016/j.neucom.2020.03.122
|
| [2] |
X. Xue, Y. Wang, Ontology alignment based on instance using NSGA-Ⅱ, J. Inf. Sci., 41 (2015), 58–70. https://doi.org/10.1177/0165551514550142 doi: 10.1177/0165551514550142
|
| [3] |
D. S. Silva, M. Holanda, Applications of geospatial big data in the Internet of Things, Trans. GIS, 26 (2022), 41–71. https://doi.org/10.1111/tgis.12846 doi: 10.1111/tgis.12846
|
| [4] |
T. Xu, J. Jiang, A graph adaptive density peaks clustering algorithm for automatic centroid selection and effective aggregation, Expert Syst. Appl., 195 (2022), 116539. https://doi.org/10.1016/j.eswa.2022.116539 doi: 10.1016/j.eswa.2022.116539
|
| [5] | F. U. Siddiqui, A. Yahya, F. U. Siddiqui, A. Yahya, Partitioning clustering techniques, in Clustering Techniques for Image Segmentation, Springer, (2022), 35–67. https://doi.org/10.1007/978-3-030-81230-0_2 |
| [6] | F. U. Siddiqui, A. Yahya, F. U. Siddiqui, A. Yahya, Novel partitioning clustering, in Clustering Techniques for Image Segmentation, Springer, (2022), 69–91. https://doi.org/10.1007/978-3-030-81230-0_3 |
| [7] | C. K. Reddy, B. Vinzamuri, A survey of partitional and hierarchical clustering algorithms, in Data Clustering, Chapman and Hall/CRC, (2018), 87–110. https://doi.org/10.1201/9781315373515-4 |
| [8] |
S. Zhou, Z. Xu, F. Liu, Method for determining the optimal number of clusters based on agglomerative hierarchical clustering, IEEE Trans. Neural Networks Learn. Syst., 28 (2016), 3007–3017. https://doi.org/10.1109/TNNLS.2016.2608001 doi: 10.1109/TNNLS.2016.2608001
|
| [9] |
E. C. Chi, K. Lange, Splitting methods for convex clustering, J. Comput. Graphical Stat., 24 (2015), 994–1013. https://doi.org/10.1080/10618600.2014.948181 doi: 10.1080/10618600.2014.948181
|
| [10] | M. Ester, H. P. Kriegel, J. Sander, X. Xu, A density-based algorithm for discovering clusters in large spatial databases with noise, in kdd, 96 (1996), 226–231. |
| [11] |
P. Bhattacharjee, P. Mitra, A survey of density based clustering algorithms, Front. Comput. Sci., 15 (2021), 1–27. https://doi.org/10.1007/s11704-019-9059-3 doi: 10.1007/s11704-019-9059-3
|
| [12] |
A. Rodriguez, A. Laio, Clustering by fast search and find of density peaks, Science, 344 (2014), 1492–1496. https://doi.org/10.1126/science.1242072 doi: 10.1126/science.1242072
|
| [13] |
S. Sieranoja, P. Fränti, Fast and general density peaks clustering, Pattern Recognit. Lett., 128 (2019), 551–558. https://doi.org/10.1016/j.patrec.2019.10.019 doi: 10.1016/j.patrec.2019.10.019
|
| [14] |
A. Joshi, E. Fidalgo, E. Alegre, L. Fernández-Robles, SummCoder: An unsupervised framework for extractive text summarization based on deep auto-encoders, Expert Syst. Appl., 129 (2019), 200–215. https://doi.org/10.1016/j.eswa.2019.03.045 doi: 10.1016/j.eswa.2019.03.045
|
| [15] | J. Xie, R. Girshick, A. Farhadi, Unsupervised deep embedding for clustering analysis, in International Conference on Machine Learning, PMLR, (2016), 478–487. https://doi.org/10.48550/arXiv.1511.06335 |
| [16] | M. Gori, G. Monfardini, F. Scarselli, A new model for learning in graph domains, in Proceedings. 2005 IEEE International Joint Conference on Neural Networks, IEEE, (2005), 729–734. https://doi.org/10.1109/IJCNN.2005.1555942 |
| [17] | C. Wang, S. Pan, R. Hu, G. Long, J. Jiang, C. Zhang, Attributed graph clustering: A deep attentional embedding approach, preprint, arXiv: 1906.06532. |
| [18] |
R. Jothi, S. K. Mohanty, A. Ojha, Fast approximate minimum spanning tree based clustering algorithm, Neurocomputing, 272 (2018), 542–557. https://doi.org/10.1016/j.neucom.2017.07.038 doi: 10.1016/j.neucom.2017.07.038
|
| [19] |
J. C. Gower, G. J. Ross, Minimum spanning trees and single linkage cluster analysis, J. R. Stat. Soc. C, 18 (1969), 54–64. https://doi.org/10.2307/2346439 doi: 10.2307/2346439
|
| [20] |
C. T. Zahn, Graph-theoretical methods for detecting and describing gestalt clusters, IEEE Trans. Comput., 100 (1971), 68–86. https://doi.org/10.1109/T-C.1971.223083 doi: 10.1109/T-C.1971.223083
|
| [21] | O. Grygorash, Y. Zhou, Z. Jorgensen, Minimum spanning tree based clustering algorithms, in 2006 18th IEEE International Conference on Tools with Artificial Intelligence (ICTAI'06), IEEE, (2006), 73–81. https://doi.org/10.1109/ICTAI.2006.83 |
| [22] | A. C. Müller, S. Nowozin, C. H. Lampert, Information theoretic clustering using minimum spanning trees, in Joint DAGM (German Association for Pattern Recognition) and OAGM Symposium, Springer, (2012), 205–215. https://doi.org/10.1007/978-3-642-32717-9_21 |
| [23] |
M. Gagolewski, M. Bartoszuk, A. Cena, Genie: A new, fast, and outlier-resistant hierarchical clustering algorithm, Inf. Sci., 363 (2016), 8–23. https://doi.org/10.1016/j.ins.2016.05.003 doi: 10.1016/j.ins.2016.05.003
|
| [24] |
Y. Ma, H. Lin, Y. Wang, H. Huang, X. He, A multi-stage hierarchical clustering algorithm based on centroid of tree and cut edge constraint, Inf. Sci., 557 (2021), 194–219. https://doi.org/10.1016/j.ins.2020.12.016 doi: 10.1016/j.ins.2020.12.016
|
| [25] |
G. Mishra, S. K. Mohanty, A fast hybrid clustering technique based on local nearest neighbor using minimum spanning tree, Expert Syst. Appl., 132 (2019), 28–43. https://doi.org/10.1016/j.eswa.2019.04.048 doi: 10.1016/j.eswa.2019.04.048
|
| [26] |
F. Şaar, A. E. Topcu, Minimum spanning tree‐based cluster analysis: A new algorithm for determining inconsistent edges, Concurrency Comput. Pract. Exper., 34 (2022), e6717. https://doi.org/10.1002/cpe.6717 doi: 10.1002/cpe.6717
|
| [27] |
H. A. Chowdhury, D. K. Bhattacharyya, J. K. Kalita, UIFDBC: Effective density based clustering to find clusters of arbitrary shapes without user input, Expert Syst. Appl., 186 (2021), 115746. https://doi.org/10.1016/j.eswa.2021.115746 doi: 10.1016/j.eswa.2021.115746
|
| [28] |
R. C. Prim, Shortest connection networks and some generalizations, Bell Syst. Tech. J., 36 (1957), 1389–1401. https://doi.org/10.1002/j.1538-7305.1957.tb01515.x doi: 10.1002/j.1538-7305.1957.tb01515.x
|
| [29] |
F. Ros, S. Guillaume, Munec: a mutual neighbor-based clustering algorithm, Inf. Sci., 486 (2019), 148–170. https://doi.org/10.1016/j.ins.2019.02.051 doi: 10.1016/j.ins.2019.02.051
|
| [30] |
D. Steinley, Properties of the hubert-arable adjusted rand index, Psychol. Methods, 9 (2004), 386. https://doi.org/10.1037/1082-989X.9.3.386 doi: 10.1037/1082-989X.9.3.386
|
| [31] |
P. A. Estévez, M. Tesmer, C. A. Perez, J. M. Zurada, Normalized mutual information feature selection, IEEE Trans. Neural Networks, 20 (2009), 189–201. https://doi.org/10.1109/TNN.2008.2005601 doi: 10.1109/TNN.2008.2005601
|
| [32] | M. Sato-Ilic, On evaluation of clustering using homogeneity analysis, in IEEE International Conference on Systems, Man and Cybernetics, IEEE, 5 (2000), 3588–3593. https://doi.org/10.1109/ICSMC.2000.886566 |
| [33] | P. Fränti, Clustering datasets, 2017. Available from: https://cs.uef.fi/sipu/datasets. |
| [34] |
P. Fränti, S. Sieranoja, K-means properties on six clustering benchmark datasets, Appl. Intell., 48 (2018), 4743–4759. https://doi.org/10.1007/s10489-018-1238-7 doi: 10.1007/s10489-018-1238-7
|
| [35] | D. Dua, C. Graff, UCI Machine Learning Repository, 2017. Available from: https://archive.ics.uci.edu/ml. |
| [36] | J. B. Kruskal, On the shortest spanning subtree of a graph and the traveling salesman problem, Proc. Am. Math. Soc., 7 (1956), 48–50. |
| 1. | Xingmao Shao, Lun Xie, Chiqin Li, Zhiliang Wang, A Study on Networked Industrial Robots in Smart Manufacturing: Vulnerabilities, Data Integrity Attacks and Countermeasures, 2023, 109, 0921-0296, 10.1007/s10846-023-01984-2 | |
| 2. | Xiaoyu Wang, Tianbo Liu, Songping Mai, Respiratory motion tracking of the thoracoabdominal surface based on defect-aware point cloud registration, 2024, 14, 2093-9868, 1057, 10.1007/s13534-024-00390-3 | |
| 3. | Shuai Hu, Rongjian Lu, Yinlong Zhu, Wenhan Zhu, Hongzhe Jiang, Suzhao Bi, Application of Medical Image Navigation Technology in Minimally Invasive Puncture Robot, 2023, 23, 1424-8220, 7196, 10.3390/s23167196 | |
| 4. | Silong Zhang, Jicheng Chen, Hengkai Sun, Zhi Qi, Hui Zhang, A scientometric review of medical flexible needle systems in surgery: signal processing, navigation and control, 2024, 18, 1863-1703, 627, 10.1007/s11760-024-03179-0 |
Figures(18) / Tables(6)
Hui Du, Depeng Lu, Zhihe Wang, Cuntao Ma, Xinxin Shi, Xiaoli Wang. Fast clustering algorithm based on MST of representative points[J]. Mathematical Biosciences and Engineering, 2023, 20(9): 15830-15858. doi: 10.3934/mbe.2023705
DownLoad:
