Improved prognostic prediction model for liver cancer based on biomarker data screened by combined methods

1.   Introduction

Liver cancer is a common cause of death from cancer in the population and its mortality rate is the 4th highest among cancer deaths worldwide ^[1]. The high recurrence rate of liver cancer after surgery is an important cause of high mortality among patients, and the recurrence rate after radical resection of liver cancer remains high, with a recurrence rate of 60–70% at 5 years after surgery, and overall survival rates remain unsatisfactory ^[2].

The development of gene chips, gene sequencing, and information technology has made it possible to obtain, store and share gene expression data. In-depth studies on genetic data can provide big data-based findings for medical research from multiple perspectives and provide new molecular biomarkers for early diagnosis and treatment of tumors, etc. ^[3]. Clinically, the problem facing the application of cancer biomarkers is how to organically integrate various cancer biomarkers for cancer diagnosis and treatment, and ensure certain predictive effect. Extensive clinical studies are an essential step in the investigation of tumor biomarkers, and artificial intelligence techniques ^[4] are needed to integrate tumor biomarkers and build tumor prediction models to improve the early detection of malignant tumors and to effectively assess patient prognosis.

From the results of domestic and international studies on biomarkers of liver cancer recurrence, Peng et al. ^[5] found that an increase in AFP-L3 was closely related to the strong invasiveness of liver cancer cells, and that AFP-L3 could be used as an indicator for the early diagnosis of liver cancer. However, the specificity and sensitivity of AFP for the diagnosis of recurrent liver cancer are not very satisfactory. In a study by Yang et al. ^[6], the overall survival of patients in the VEGF positive expression group was significantly lower compared to the negative expression group, and the upregulation of VEGF expression increased the aggressiveness of hepatocellular carcinoma cells. It was demonstrated that TGF-β could inhibit the recurrence of hepatocellular carcinoma by suppressing the expression of Sox2, and the detection of TGF-β expression level could help predict the risk of recurrence of hepatocellular carcinoma ^[7]. Shinichi et al. ^[9] found that G protein-coupled receptor 155 (GPR155) predicted the initial site of recurrence of hepatocellular carcinoma and that patients with downregulated GPR155 had a worse prognosis after therapeutic resection. Roessler et al. analyzed gene expression data from two independent cohorts of patients with hepatocellular carcinoma and identified 161 genetic biomarkers to assess the risk of postoperative recurrence and overall survival in patients with HCC using a Cox proportional risk regression model with principal component analysis ^[10].

In the past, many scholars focused on individual biomarkers and investigated the impact of individual markers on the recurrence mechanism of liver cancer, but it has the disadvantage of requiring a large number of clinical samples for validation and lacking in model accuracy. However, if machine learning methods are used to screen biomarkers, they have some predictive accuracy, but the screening process does not provide a good explanation of the biology of the biomarkers.

Therefore, in view of the large amount of gene sequencing data, a suitable screening process is needed to select biomarkers and establish a predictive model with certain predictive effect for clinical research and targeted therapy for patients with recurrent liver cancer. Therefore, in this study, we proposed a combination method to screen genetic biomarkers related to recurrence of hepatocellular carcinoma after resection by analyzing the genetic sequencing data of hepatocellular carcinoma patients, and constructed a recurrence prediction model based on biomarkers with a random forest-based improved feature screening method. The obtained biomarkers are rich in biological meaning and can significantly narrow the feature set with little reduction in accuracy, providing a reference for diagnosis and treatment of patients after resection.

2.   Combination of biomarker screening for recurrence of hepatocellular carcinoma

2.1.   Data sources

The main data in this paper are the gene sequencing data of liver cancer patients, which are obtained from the open database TCGA by transcriptome sequencing and the clinical data of the corresponding samples. A total of 409 patients with hepatocellular carcinoma were documented, including gene expression in cancerous tissues, gene expression in normal tissues and the corresponding clinical data of the patients.

2.2.   Data processing

The samples selected from TCGA liver cancer patients were screened according to the following criteria:

1) Normal tissue samples were excluded to ensure that all samples analyzed were liver cancer tissue samples.

2) Selecting samples from patients with R0 resection of liver cancer tissue for the surgical procedure will exclude the possibility of recurrence of liver cancer due to invasion of residual tumor cells and enhance the interpretation and rigor of the analysis of the effect of genetic biomarkers on recurrence of liver cancer.

3) Excluding samples with missing information on both recurrence and eventual survival. Based on the clinical information of the patients, the above screening process was completed and 327 usable samples were obtained, including 163 recurrence samples and 164 non-recurrence samples after hepatectomy.

2.3.   Combined methods for screening biomarkers

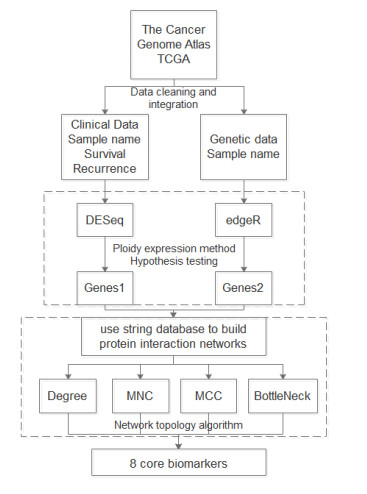
Each sample of liver cancer patients contains up to 30,000 genes. To address the large amount of data, a combinatorial approach is proposed to screen genes as biomarkers of liver cancer recurrence, as shown in Figure 1.

Figure 1.  Combined biomarker screening method for liver cancer recurrence.

DownLoad: Full-Size Img PowerPoint

First, the gene expression data from two groups of samples with and without recurrence of liver cancer were analyzed by the ploidy expression method and hypothesis testing to initially screen for biomarkers of liver cancer recurrence, which was achieved by DESeq and edgeR methods. Next, a protein interaction network of differential genes was constructed. Four network topology algorithms, Degree, MNC, MCC, and BottleNeck, were used to rank the importance of each node in the protein interaction network, and the intersection of the important genes selected by each algorithm was taken to screen the core biomarkers of liver cancer recurrence.

2.3.1.   Preliminary screening

The edgeR package and DESeq package of R language were used to process and calculate the differential genes of relapsed samples and non-recurrence samples, and the genes with log2FC absolute value greater than 1 and P value less than 0.05 were used as the differential genes between the liver cancer recurrence group and the non-recurrence group, and the FDR (False Discovery Rate) and false discovery rate were increased. Since the differential expression analysis of transcriptome sequencing is an independent statistical hypothesis test for a large number of gene expression values, there will be a problem of false positives, so in the process of differential expression analysis, the recognized Benjamini-Hochberg correction method is used to correct the significance p-value obtained by the original hypothesis test, and finally, FDR is used as the key indicator of differential expression gene screening. Generally, FDR < 0.01 or 0.05 is used as the default standard. See Figures 2 and 3, where red indicates up-regulated differential genes expressed in patients with liver cancer recurrence, green indicates down-regulated differential genes expressed in patients with liver cancer recurrence, and gray dots indicate genes that do not differ significantly between the two groups.

Figure 2.  Differential genes in the recurrence group.

DownLoad: Full-Size Img PowerPoint

Figure 3.  Differential genes in the non-recurrence group.

DownLoad: Full-Size Img PowerPoint

The specific number of differential genes screened by DESeq and edgeR is shown in Table 1. The total number of differential genes screened by the two methods differed significantly, with the number of down-regulated differential genes much higher than the number of up-regulated differential genes in the recurrent liver cancer group.

Table 1.  The number of differential genes identified.

Method	Up-regulated genes	Down-regulated genes	Total
DESeq	59	168	227
edgeR	36	92	128

---

 | Show Table

DownLoad: CSV

Table 2.  Ranking table of gene scores for different topological algorithms.

Scoring order	Topology algorithm
	Degree	MCC	MNC	BottleNeck
1	CRH	CRH	CRH	CALCA
2	MUC6	MUC6	MUC6	CEACAM5
3	MUC1	MUC1	MUC1	WNT3A
4	TAC1	TAC1	TAC1	FGF8
5	CALCA	CALCA	CALCA	FGF23
6	MUC5B	MUC5B	MUC5B	CRH
7	MUCL1	MUCL1	MUCL1	MUC1
8	GALNT17	GALNT17	GALNT17	KLK3
9	SST	SST	SST	LEP
10	NTS	NTS	NTS	ACP3
11	WNT3A	WNT3A	WNT3A	CYP24A1
12	WNT2B	WNT2B	WNT2B	MSMB
13	WNT7A	WNT7A	WNT7A	RGS11
14	SFRP1	SFRP1	SFRP1	TWIST1
15	FZD9	FZD9	FZD9	MAGEA4
16	LEP	FGF8	LEP	JPH2
17	ADIPOQ	LEP	ADIPOQ	MLANA
18	KLK3	ADIPOQ	KLK3	NKX2-5
19	ACP3	KLK3	ACP3	ATP1A2
20	MYL9	ACP3	MYL9	MUC6

---

 | Show Table

DownLoad: CSV

Correlation analysis was performed on the common difference genes made by DESeq and edgeR. 22 genes were intersected between the two, and the correlation coefficients between each gene were calculated and correlation plots were drawn, and the correlation plots are shown in Figure 4. The blue color in the correlation plot indicates a positive correlation between genes and the red color indicates a negative correlation between genes. From Figure 4, it can be seen that there is a strong correlation between some of the differential genes and the correlation is very significant.

Figure 4.  Heat map of gene correlation coefficients.

DownLoad: Full-Size Img PowerPoint

The blue cluster contains a number of IGHV, IGKV, and IGLV related genes that show a high positive correlation. These related genes are immunoglobulin-related genes, which are antigen-recognition molecules for B lymphocytes and are closely related to the immune function of the body. This suggests that alterations in immune-related genes among patients with liver cancer may lead to differences in immune function, which may affect the likelihood of recurrence of liver cancer, and that there is an interaction between the differential genes

Therefore, protein interaction networks were performed to further explore the differential genes and demonstrate the interaction between genes. A small number of genes were further screened based on the protein interaction network as core biomarkers of liver cancer recurrence, aiming to predict the risk of liver cancer recurrence with a small number of genetic markers and reduce the cost of testing for patients.

2.3.2.   Construction of protein interactions network

DESeq and edgeR were taken together and then the network relationships were constructed using the background data provided by the string database, as shown in Figure 5, where brown is the up-regulated gene and green is the down-regulated gene, and each network node acts as the protein product of a gene, with the connections of the edges showing the interactions between the nodes.

Figure 5.  Protein interaction network diagram.

DownLoad: Full-Size Img PowerPoint

2.3.3.   Core biomarker screening

The network was then analyzed using the cytohubba plugin, screening Degree, MNC, MCC, and BottleNeck, respectively, to score and rank the protein nodes in the protein interactions network.

The top 20 genes calculated by each algorithm were intersected, i.e., the genes ranked in the top 20 in all four topological algorithms were used as the core biomarkers for the screening, which increased the reliability of the gene ranking (as shown in Figure 6). Eight genes were identified as core biomarkers for postoperative recurrence of hepatocellular carcinoma: CRH, MUC6, MUC1, CALCA, WNT3A, LEP, KLK3, and ACP3.

Figure 6.  Intersection of the top 20 genes ranked by different topology algorithms.

DownLoad: Full-Size Img PowerPoint

3.   Biomarker functional studies

The GO enrichment analysis was performed on the above 8 biomarker genes and 22 intersecting genes, and the GO categories with a test P value less than 0.05 were used as the enriched functional categories, and the enrichment results obtained are shown in Figures 7 and 8. The enrichment results are shown in Figures 7 and 8. It can be seen from Figure 7 that the differential genes were significantly enriched in 36 biological functional categories, of which the most enriched categories were biological process (BP) functional categories with 22 categories, while the significantly enriched cellular component (CC) and molecular function (MF) functional categories were 6 and 8 respectively.

Figure 7.  Map of GO functional categories for differential gene enrichment.

DownLoad: Full-Size Img PowerPoint

Figure 8.  Differential gene GO enrichment scores.

DownLoad: Full-Size Img PowerPoint

Further analysis of the GO functional categories that were significantly enriched for the selected differential genes in Figure 8 showed that the three GO functional categories with the highest enrichment scores were the extracellular region, the plasma membrane, the complement activation, and the classical pathway. classical pathway). It is hypothesized that the abnormal expression of differential genes in patients with hepatocellular carcinoma undergoing R0 resection leads to altered immune function and thus affects the likelihood of recurrence of hepatocellular carcinoma after resection. This finding explains well the mechanism of biomarkers' influence on the development of liver cancer.

Using the NCBI gene font library to query the biological functions of 8 core genes, see Table 3, some biomarkers are associated with the occurrence and development of cancer, making the adhesion ability of cancer cells reduced and thus more likely to metastasize and recur, some markers affect the immune function of the organism, and then may affect the body's anti-cancer function. Some biomarkers play a role in the formation of cells.

Table 3.  Direction of modulation and biological functions of the eight genes.

Gene	Gene modulation direction	Genetic function
CRH	Downregulated	Encoding adrenocorticotropic release factors, protein levels are associated with Alzheimer's disease
MUC6	Upregulated	A member of the family encodes mucins, secretes, and forms an insoluble mucus barrier that protects the intestinal lumen
MUC1	Upregulated	Plays an important role in the formation of a protective mucosal barrier on the surface of the cell epithelium
CALCA	Downregulated	Encodes the peptide hormone calcitonin, which is involved in calcium regulation and plays a role in regulating phosphorus metabolism
WNT3A	Downregulated	It is related to tumorigenesis and developmental processes, including regulating cell fate and patterns during embryogenesis.
LEP	Downregulated	Mutations in the gene and its regulatory region, which play a major role in regulating energy homeostasis, can lead to severe obesity in human patients and pathological obesity with hypogonadism
KLK3	Downregulated	It has the potential to act as a biomarker for novel cancers and other diseases and can be used to diagnose and monitor prostate cancer
ACP3	Downregulated	Encode longer variants of the same type of variable splicing transcription

---

 | Show Table

DownLoad: CSV

4.   Model building and analysis of results

4.1.   Algorithm improvement

For high-dimensional data, dimensionality reduction or feature selection is generally performed in order to reduce the difficulty of model learning ^[11]. The presence of redundant features makes feature selection more necessary, and removing these irrelevant features not only reduces the learning effort, but also facilitates data collection.

In this paper, a faster feature selection algorithm is designed based on the basic method of feature selection using random forests proposed by Genuer R et al. in 2010 and Yao Dengju et al. in 2014 ^[12]. The set of features from the previous round is used as the result.

The essence of this strategy is to prioritize the smallest subset of features within a given error range, rather than the one with the highest test accuracy, thus allowing the screening to be stopped early and saving a lot of time.

Let the original feature set be A and the sample set be D. The algorithm design is described by a pseudo code as follows:

Minimum number of features to be initialized m Total number of initialized cross-validations k Initialize the proportion of features removed each time r Initialize the maximum error increment δ def ChooseFeatures (D, A) Let the candidate feature set A′ = A while |A′| ≥ m bestAcc = 0 for i in range (k) Divide the training set D1, test set D2 from D RF = CreateRandomForest (D1, A′) Calculate the accuracy of RF on D2 acci if acci > bestAcc bestAcc = acci bestRF = RF # Random forest with highest accuracy for labeling test to rank features Accuracy of this round is taken as mean, accuracy = mean (acci) if first time in the loop Benchmarking accuracy baseAcc = accuracy elif baseAcc - accuracy > δ # Stop iteration if error increment is too large break Let current filter Abest = A′ The features in A′ are sorted by importance using bestRF to obtain the sequence L. A portion of the features are removed from the end of L in proportion r, and the remaining features are used as A′ return Abes

---

 | Show Table

DownLoad: CSV

As the cross-validation process generates multiple random forests, the one with the highest test accuracy is selected to calculate the feature importance order for the current round. The flow chart for calculating feature importance is shown in Figure 9.

Figure 9.  Flow chart of feature importance calculation.

DownLoad: Full-Size Img PowerPoint

4.2.   Model evaluation

Since this is a classification problem, the loss function of the model is 0–1 loss, and the test error of the model is its average loss over the test set ^[13]. Let the input to the model f be X, Y be the true value of the corresponding X, and the test sample size be N. The formal definitions of the loss function L, the test error e and the test accuracy r are as follows:

where I is the indicator function.

The complexity of the model can be measured directly by the running time of the code segment on the same computer, or it can be compared by the number of leaf nodes in the decision tree. Recorded runtimes are obtained from a Python timer. The model was evaluated using a leave-out method, whereby 70% of the sample was divided into a training set and 30% into a test set; if an independent pruning set was required, both the training and pruning sets were 40% and the remaining 20% was the test set. In order to obtain stable evaluation results, random partitioning is repeated for training and testing, with the final observations averaged over five tests for simple cross-validation purposes.

4.3.   Analysis of results

The random forest was tested and analyzed in the following areas: comparison with ordinary decision trees, testing the effect of generalization of the number of weak classifiers, and feature selection algorithms.

4.3.1.   Comparison of ordinary decision trees

The sample sets were divided as follows: training set sample size 229; test set sample size 98. The construction parameters of the random forest and decision tree were all default, and the decision trees for comparison were no pruning and pessimistic error pruning, respectively, as shown in Table 4.

Table 4.  Comparative analysis of decision trees and random forests.

Models	Pruning algorithm	Training time	Prediction time (ms)	Test accuracy (%)
No pruning decision tree	/	7.18 s	1.73	86.12
Pessimistic error pruning decision tree	PEP	7.18 s + 3.78 ms	0.76	89.19
Random forest	/	1.56 s	17.73	92.14

---

 | Show Table

DownLoad: CSV

4.3.2.   Feature filtering algorithm

The iteration stopping parameters are the minimum number of features and the permissible error increment, which have default values of 5 and 2.5% respectively. Other parameters that affect the execution time are the number of decision trees included in the random forest (default 10), the number of cross-validations (default 3), and the proportion of features rejected in each round (default 0.15). Because of the limited number of cases obtained, most of the parameters do not have a significant impact on the final results, so only the error increments are adjusted and the results are analyzed. The eight feature genes CRH, MUC6, MUC1, CALCA, WNT3A, LEP, KLK3, and ACP3 were coded in the order of bits 1–8. The column shows the test accuracy of the resulting model trained using the screening results.

In general, the size of the filtered feature sets ranged from 3 to 6 (4.3 on average), which was higher than the original feature size; and their corresponding test accuracy did not decrease much compared to that before the screening (92.14%), but was within 2%, and could be the same as before the screening after adjusting the parameters. This proves that the algorithm used is effective and gives more accurate screening results, which are more accurate and feasible. Looking at the latter two cases in Table 5, it can be seen that they are both comparable to the pre-screening accuracy, but with maxAccurDesc of 2.5, fewer features are screened out overall, making this setting more appropriate for the current dataset.

Table 5.  Results of feature selection.

maxAccurDesc	Filtered features (in order of importance)	Test precision accuracy (%)
2.5 (default)	3, 7, 4, 6	90.38
	4, 8, 6	91.32
	4, 5, 8, 1, 6	91.28
	8, 4, 5, 3, 6	90.78
1.5	4, 5, 8, 6, 7, 3	92.08
	8, 4, 6, 5, 3, 1	92.19
	8, 5, 4, 6	92.58
0.5	8, 4, 6, 3, 1, 6	92.01
	4, 8, 1, 7	92.62

---

 | Show Table

DownLoad: CSV

5.   Prognostic effect of biomarkers of liver cancer recurrence

The influence of the screened biomarkers on the prognosis of patients is explored here, so the eight gene expression levels screened above are included as the independent variables of the Cox regression model, namely CRH, MUC6, MUC1, CALCA, WNT3A, LEP, KLK3, ACP3. In addition, because the prognosis of liver cancer patients may be related to some clinical factors, some clinical indicators of patients are also included, including the patient's age, gender, tumor grade and TMN stage. The distribution of sample data is shown in Table 6.

Table 6.  Categorical variable display table.

Clinical variables	category	quantity
Survival state	Survive	204
	Death	98
Gender	Female	99
	Male	203
Tumor grade	G1	45
	G2	142
	G3	105
	G4	10
TMN staging	Ⅰ	154
	Ⅱ	78
	Ⅲ-Ⅳ	70

---

 | Show Table

DownLoad: CSV

5.1.   Univariate Cox regression analysis

First, univariate Cox regression is performed separately for each variable, and the individual impact of each variable on survival is considered. The univariate Cox regression results for each variable are shown in Table 7. Univariate Cox regression showed that MUC1, CALCA, age, and TMN staging had a significant impact on patient survival. The effect of variables on a patient's risk of death can be seen by the coefficients and HR values. A coefficient greater than 0 indicates that an increase in the value of the variable has a positive effect on the risk of death, and a decrease below 0 indicates that an increase in the value of the variable has a negative effect on the risk of death. An HR value greater than 1 indicates that an increase in the value of the variable increases the risk of death, and an increase in the value of the variable decreases the risk of death.

Table 7.  Results of single-factor Cox proportional hazard regression.

Variable	Coefficient	HR value	Lower HR limit (95%CI)	Higher HR limit (95%CI)	P value
CRH	0.097	1.102	0.973	1.248	0.126
MUC6	-0.030	0.971	0.814	1.158	0.739
MUC1	-0.123	0.882	0.786	0.991	0.035*
CALCA	0.157	1.170	1.019	1.343	0.026*
WNT3A	-0.068	0.934	0.793	1.100	0.416
LEP	-0.023	0.978	0.887	1.078	0.650
KLK3	0.059	1.061	0.955	1.179	0.272
ACP3	-0.051	0.950	0.866	1.043	0.283
Age	0.016	1.017	1.000	1.033	0.044*
Gender (female)
Male	-0.235	0.791	0.529	1.183	0.253
Tumor grade (G1)
G2	0.301	1.351	0.714	2.556	0.355
G3	0.382	1.465	0.761	2.818	0.253
G4	0.750	2.117	0.679	6.604	0.196
TMN staging (Ⅰ)
Ⅱ	0.548	1.730	1.051	2.847	0.031*
Ⅲ-Ⅳ	1.063	2.896	1.819	4.611	< 0.001***
Note: p < 0.05*, p < 0.01**, p < 0.001***.

---

 | Show Table

DownLoad: CSV

From the results of univariate Cox regression analysis, it can be seen that the risk of death is significantly increased by the decrease of MUC1 expression, and the increase of CALCA expression is significantly increased in the risk of death. Age is also an indicator of a significant impact on the risk of death, and older patients have a higher risk of death after resection of liver cancer. Although the tumor grade was not significant, the patients with G2, G3, and G4 had higher HR values and increased risk of death compared with patients with G1. Patients with TMN stage Ⅱ, Ⅲ, and Ⅳ had a significantly higher risk of death than patients with stage Ⅰ. TMN staging had a significant effect on survival, indicating that even after surgical resection, the development and malignancy of the tumor before resection would significantly affect the survival of patients after resection.

5.2.   Multivariate Cox regression analysis

Univariate Cox regression identified variables that had a significant impact on survival, namely MUC1, CALCA, age, and TMN stage. Next, these variables were incorporated into multivariate Cox regression to jointly construct a postoperative prognosis model for patients with liver cancer. The results of the multivariate Cox regression analysis are shown in Table 8.

Table 8.  Multivariate Cox proportional hazard regression results.

Variable	Coefficient	HR value	Lower HR limit (95%CI)	Higher HR limit (95%CI)	P value
MUC1	-0.132	0.877	0.777	0.989	0.032*
CALCA	0.175	1.192	1.036	1.371	0.014*
Age	0.020	1.020	1.004	1.036	0.015*
TMN staging (Ⅰ)
Ⅱ	0.385	1.470	0.881	2.453	0.140
Ⅲ-Ⅳ	1.051	2.862	1.795	4.563	< 0.001***

---

 | Show Table

DownLoad: CSV

As can be seen from Table 8, the HR value of MUC1 is less than 1, while the HR value of GLI2, Age, and TMN Staging Ⅱ, Ⅲ-Ⅳ is greater than 1. Explanations The increased expression of MUC1 reduces the risk of postoperative death in patients with liver cancer. Increased expression of CALCA, as well as an increase in age and TMN stage, significantly increase the risk of postoperative death in patients with liver cancer.

6.   Conclusions

In this paper, a method was developed to screen for genetic biomarkers of hepatocellular carcinoma recurrence by combining differential ploidy, hypothesis testing, and network topology analysis, and to obtain and integrate genetic sequencing data and clinical data from the TCGA database. The differential genes were examined and GO enrichment analysis was performed to investigate the functional mechanisms of these differential genes, which were found to play an important role in the immune function and cellular constitutive function of the body. Further, a protein interaction network of differential genes was constructed using the String database, and eight genetic biomarkers for liver cancer recurrence were identified by ranking the importance of the nodes in the network using four topological algorithms and taking the intersection.

The results showed that the random forest has better generalization ability and training speed than the pruned decision tree, and the improved feature screening algorithm can significantly reduce the feature set while maintaining the prediction accuracy.

This study was conducted only for one cancer type, liver cancer, and the screening method and model construction process of this paper can be applied to other cancer types in order to obtain a universal method that can be applied to many different cancer types.

Acknowledgments

The manuscript is an original work on its own merit, that it has not been previously published in whole or in part, and that it is not being considered for publication elsewhere. All authors have read the final manuscript, have approved the submission to the journal, and have accepted full responsibilities pertaining to the manuscript's delivery and contents.

Conflict of interest

The authors declare there is no conflict of interest.