Effect of travel restrictions, contact tracing and vaccination on control of emerging infectious diseases: transmission of COVID-19 as a case study

1.   Introduction

In December 2019, the novel coronavirus (COVID-19) was first reported in Wuhan, a city of Hubei Province with 11.212 million inhabitants ^[1]. Considering that the coming Chinese Lunar New Year may lead to the further dispersal of COVID-19, the Chinese government banned travel to and from Wuhan at 10:00 a.m. on January 23, 2020. With the further development of the epidemic, the shortage of doctors and medical resources is becoming more and more serious. To alleviate the situation, medical teams and a lot of medical resources were dispatched to Wuhan from other places in China ^[2]. At the same time, Huo Shen Shan Hospital and Lei Shen Shan Hospital were officially admitted to the patient on February 3 and February 8, respectively ^[3]. Since February 4, a number of fangcang shelter hospitals have been put into use one after another. Then, by the middle of February, the daily number of new confirmed cases started to decrease. At 00:00 on April 8, the Chinese government lifted the travel restrictions in Wuhan ^[4]. As for Mainland China (outside Wuhan), the early transmission is mainly caused by the cases exported from Wuhan. Due to the timely and effective prevention and control policy of Chinese government, the epidemic was quickly brought under control. And some cities of Mainland China (outside Wuhan) began to resume work on February 10 after extended Spring Festival holiday ^[5].

However, due to the extreme infectivity of COVID-19, it spread quickly all over the world. The World Health Organization (WHO) made the assessment that "COVID-19 could be characterized as a pandemic" on March 11, 2020 ^[6]. As of 15 November 2021, there have been 252,902,685 confirmed cases and 5,094,826 confirmed deaths all over the world ^[7], of which there have been 98,337 confirmed cases and 4,636 confirmed deaths in Mainland China ^[8]. The epidemic posed a severe threat to public health worldwide and has caused serious damage to global social and economic development. In order to control the epidemic, many countries have adopted various control measures, such as travel restrictions, closing entertainment venues, and banning public gathering, isolation of the confirmed cases, tracing and quarantining the contacts of confirmed cases, and so on.

Meanwhile, many scholars have carried out in-depth scientific research from different perspectives, in order to reveal some of the inherent transmission mechanisms of the COVID-19 epidemic and provide a basis for the prevention and control of disease transmission. Some of them studied the epidemiological characteristics of the COVID-19 epidemic ^[9,10,11]; some predict the further development trend of the COVID-19 epidemic ^[12,13]; some focus on studying the supply and demand of medical resources during the outbreak of the COVID-19 epidemic ^[14,15]; some assessed the effectiveness of prevention and control measures ^{[16,17,18,19,20]}; some of them do research on vaccination ^{[21,22,23,24]}.

However, the interplay between travel restrictions, contact tracing, vaccination and COVID-19 dynamics remains unclear. In order to fill this gap, we establish a SIAHRQ-type patch model. Patch models can well reflect the influence of spatial heterogeneity and population movement between different regions on disease transmission which has been applied to the research of many diseases. Gao et al. ^[25] proposed a SIRUV-type three-patch model with animal movement to study the spatial spread of Rift Valley fever in Egypt. Zhang et al. ^[26] formulated a two-patch model for the spread of West Nile virus with the host birds migrating between regions. Mukhtar et al. ^[27] formulated an SIR-type model that describes the transmission dynamics of malaria disease between multiple patches. Sun et al. ^[28] established a SEIYQR-type two-patch model reflecting the mobility of population between Hubei and regions outside Hubei to study when to lift the lockdown in Hubei during the COVID-19 epidemic.

In the following, Mainland China is divided into two patches: Wuhan as one patch, is recorded as patch 1; Mainland China (outside Wuhan) as the other patch, is marked as patch 2. Through theoretical analysis and numerical simulation, we mainly evaluate the role of travel restrictions, contact tracing and vaccination in transmission and control of COVID-19 epidemic.

The structure of this paper is organized as follows. In the next section, the dynamic model is established. In Section 3, the dynamic analysis is carried out to prove the positivity of the solution and the existence of the final size. In Section 4, the least square method (LSM) is used to fit some model parameters, and then the effect of different prevention and control measures on disease transmission is studied. Section 5 gives a conclusion and discussion of this work.

2.   Model formulation and analysis

In this subsection, we will establish two dynamic models, one is in isolated environment model with contact tracing, the other is in connected environment model with contact tracing. Then carry on the dynamic analysis.

2.1.   The dynamic model in an isolated environment

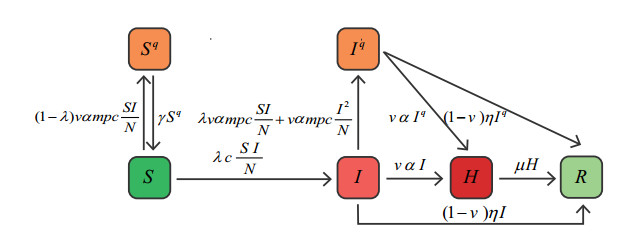
The unit of time is days, and regardless of the birth and death of the population. At time $t$, the internal individuals for each patch are divided into six categories according to the state of the disease: susceptible individuals $(S(t))$, pre-symptomatic infected individuals ($I(t)$), hospitalized individuals ($H(t)$), recovered individuals ($R(t)$), quarantined susceptible individuals ($S^{q}(t)$) and isolated pre-symptomatic infected individuals ($I^{q}(t)$) due to contact with pre-symptomatic infected individuals who will be diagnosed later. The population is recorded as $N(t)$. In unit time, an individual who is susceptible can come into contact with pre-symptomatic infected individuals and become infected with the probability of $\lambda$; the pre-symptomatic infected individuals with the proportion of $v$ will be diagnosed after time $\frac{1}{\alpha}$, the proportion of $1-v$ will not be diagnosed and then recover after time $\frac{1}{\eta}$; hospitalized individuals will recover after time $\frac{1}{\mu}$, and the recovered individuals will no longer be infected within the length of time taken into account. When conducting an epidemiological investigation of hospitalized individuals, the close contacts within $m$ days before diagnosis will be traced and quarantined with probability $p$, and then will not participate in the spread of the disease. After the quarantined period $\frac{1}{\gamma}$, the quarantined susceptible individuals will become susceptible individuals who can participate in normal social activities. The isolated pre-symptomatic infected individuals will be diagnosed, or recover after a period of time. The dynamic process of COVID-19 transmission in an isolated environment is described in the flow chart (Figure 1). According to the flow chart, the following mathematical models can be established:

For the first equation of system (2.1), $\lambda c\frac{S(t)}{N(t)}I(t)$ represents the number of newly infected individuals, which can be interpreted as: the number of effective contacts ($\lambda c$) produced by a pre-symptomatic infected individual, multiplied by the proportion of susceptible individuals in the population, $\lambda c\frac {S(t)}{N(t)}$, indicates the number of susceptible individuals infected by a pre-symptomatic infected individual. Then, multiplied by the number of pre-symptomatic infected individuals, $\lambda c \frac{S(t)}{N(t)}I(t)$, indicates the number of susceptible individuals who are infected by all pre-symptomatic infected individuals. $(1-\lambda)v \alpha pc\frac{S(t)}{N(t)}I(t)$ represents the number of newly quarantined susceptible individuals who are successfully traced as close contacts, which can be interpreted as: $(1-\lambda) c S(t)\frac{I(t)}{N(t)}$ represents the susceptible individuals are not infected after contact with the pre-symptomatic infected individuals. Then, multiplied by $v \alpha$ means the pre-symptomatic infected individuals with the proportion of $v$ will be diagnosed and become hospitalized individuals after time $\frac {1}{\alpha}$. Last, multiplied by $mp$ means to conduct an epidemiological investigation of newly diagnosed pre-symptomatic infected individuals, tracing the susceptible individuals who are in contact with them within m days before diagnosis with the probability of $p$. $\gamma S^q(t)$ indicates that the isolated susceptible individual become susceptible individuals again who can participate in normally social activities after the isolation period. $v\alpha m p c \frac{I^{2}(t)}{N(t)}$ represents the number of newly quarantined pre-symptomatic infected individuals who are successfully traced as close contacts due to contact with the other pre-symptomatic infected individuals. $\lambda v \alpha m p c\frac{S(t)}{N(t)}I(t)$ represents the number of newly quarantined pre-symptomatic infected individuals, that is the susceptible individuals are infected by pre-symptomatic infected individuals who will be diagnosed, when conducting epidemiological investigation the infected susceptible individuals are successfully traced as close contacts. $v \alpha I(t)$ represents the number of newly hospitalized individuals. $(1-v)\eta I(t)$ represents the number of newly recovered individuals. The meaning of other items can be obtained in a similar way.

In the following, we first consider the positivity of the solution, and then study the stability of disease-free equilibrium and give the expression of control reproduction number. Finally, we prove the existence of final size, which represents the total number of population that have been infected at the end of the epidemic, namely $R(\infty)$ ^[29].

Lemma 1. All solutions of system (2.1) are in the set

that is, $\Omega$ is a positive invariant set of system (2.1).

Proof. First of all, there is no birth or death of the population, so

It can be obtained from the second equation of system (2.1)

then, if $I(0)\geqslant 0$, $I(t)\geqslant 0.$ Next, we consider the first and fifth equation of system (2.1):

Based on theorem 3.2.1 of reference ^[30], we have $S(t)\geqslant 0, S^{q}(t)\geqslant0$, if $S(0)\geqslant 0, S^{q}(0)\geqslant0$.

By calculating, we have

And if $H(0)$, $R(0)$, $I^q(0)\geq 0$, then $H(t)$, $R(t)$, $I^q(t)\geq 0$.

Therefore, all solutions of system (2.1) are in the set

that is to say, $\Omega$ is a positive invariant set of system (2.1).

Let the right hand of system (2.1) be zero, we obtain the disease-free equilibrium $E_{00} = (N(0), 0, 0, 0, 0, 0)$. Through the stability analysis at the disease-free equilibrium point $E_{00}$, we have:

Lemma 2. The control reproduction number of system (2.1) is

If $p = 0$, we obtain the basic reproduction number

and

Then, we have the following conclusion:

$\bf{Theorem\ 1.}$ If $R^c_{00} < 1$, the disease-free equilibrium $E_{00}$ is stable, otherwise, $E_{00}$ is unstable.

The proof of Theorem 1 is given in Appendix A.

Next we will study the existence of final size of system (2.1).

$\bf{Theorem\ 2.}$ For the isolated environment system (2.1), $I(\infty) = 0, H(\infty) = 0, S^q(\infty) = 0, I^q(\infty) = 0,$ and $S(\infty), R(\infty)$ exist.

Proof. If we sum all the equation of system (2.1) except the fifth, then the following relationship will hold

we see that $S(t)+I(t)+H(t)+S^q(t)+I^q(t)$ is decreasing. In addition, $0\leq S(t)+I(t)+H(t)+S^q(t)+I^q(t)\leq N(0)$, hence, it has a limit. Moreover, $\frac {d\left(S(t)+I(t)+H(t)+S^q(t)+I^q(t)\right)}{dt}$ is bounded due to $-\mu H-\eta(1-v)(I(t)+I^q(t))$ is bounded. According to the fluctuation Lemma ^[31], we have

On the other hand, $I(t)\geq 0, H(t)\geq 0, I^q(t)\geq 0$, thus we have

Considering $I(\infty) = 0$, $(1-\lambda)v\alpha mpc\frac{S(t)}{N(0)}$ is bounded, then we have

where $M = I(t)(1-\lambda)v\alpha mpc\frac{S(t)}{N(0)}$. Hence, for any $\varepsilon > 0$, there exists a $\delta > 0$, if $|t| > \delta$, then

So, if $t$ is sufficiently large, we have

It can be obtained according to the comparison theorem that

Thus

Sum the first and the fourth equation of system (2.1), we have

that is, $S(t)+S^q(t)$ is decreasing. Since $S(t)+S^q(t))\geq 0$, $\mathop{\lim}\limits_{t\rightarrow \infty}\left(S(t)+S^q(t)\right)$ exists. Considering $\mathop{\lim}\limits_{t\rightarrow \infty} S^q(t) = 0$, so, we have $S(\infty) = \mathop{\lim}\limits_{t\rightarrow \infty}S(t)$ exists.

Further more, $R(\infty) = \mathop{\lim}\limits_{t\rightarrow \infty}\left(N(0)-S(t)\right) = N(0)-S(\infty)$ exists. That is to say the final size exists.

2.2.   The dynamic model in a connected environment

We divide the population into two patches, one is recorded as patch 1, the other is patch 2. The population of two patches is recorded as $N_{1}(t)$, $N_{2}(t)$ respectively. And we assume only susceptible individuals, pre-symptomatic infected individuals and recovered individuals can move between two patches. In addition, the mobility rate of susceptible, pre-symptomatic infected and recovered individuals from patch 1 to patch 2 are recorded as $a_{12}$, $b_{12}$, $e_{12}$ respectively, and from patch 2 to patch 1 are recorded as $a_{21}$, $b_{21}$, $e_{21}$ respectively. The dynamic process of COVID-19 transmission in a connected environment is described in the flow chart (Figure 2).

According to the flow chart, the following mathematical models can be established:

Here, $i, j\in{1, 2}$ and $i\neq j$.

In the following, we will study the population dynamics in connected environment with contact tracing.

$\bf{Lemma\ 3.}$ All the solutions of the system (2.2) are in the set

here, ${D_{1} = \left(S_{1}(t), I_{1}(t), H_{1}(t), R_{1}(t), S_{1}^q(t), I_{1}^q(t), S_{2}(t), I_{2}(t), H_{2}(t), R_{2}(t), S_{2}^q(t), I_{2}^q(t)\right)}$. That is, $D$ is a positive invariant set of system (2.2).

Proof. For system (2.2),

the following relationship holds:

Consider solutions with non-negative initial values. Next, we will prove $S_{1}(t)\geq 0, S^q_{1}(t)\geq0, I_{1}(t)\geq0, S_{2}(t)\geq 0, S^q_{2}(t)\geq 0, I_{2}(t)\geq0$, if $t > 0$ and $S_{1}(0)\geq 0, S^q_{1}(0)\geq0, I_{1}(0)\geq0, S_{2}(0)\geq 0, S^q_{2}(0)\geq 0, I_{2}(0)\geq0$. According to the continuity of solutions with respect to initial conditions, we have if the initial value is non-negative there is a very small $\tau_{1}$ such that $S_{1}(t)\geq 0, S^q_{1}(t)\geq0, I_{1}(t)\geq0, S_{2}(t)\geq 0, S^q_{2}(t)\geq 0, I_{2}(t)\geq0$ for $t \in (0, \tau_{1})$. Let

and assume $S_{1}(t^*) = 0$, then from the first equation of system (2.2), we have at $t = t^*$

Thus, there is a $t_{11}$ such that $S_{1}(t) > 0$ for $t\in(t_{1}, t_{11})$ and $S_{1}(t_{11}) = 0$. So, $S_{1}(t)\geq0, S^q_{1}(t)\geq0$, $I_{1}(t)\geq0, S_{2}(t)\geq 0, S^q_{2}(t)\geq 0, I_{2}(t)\geq0$ for $t\in(0, t_{11}]$. In this way, we finally get $S_{1}(t)\geq0, S^q_{1}(t)\geq0, I_{1}(t)\geq0, S_{2}(t)\geq 0, S^q_{2}(t)\geq 0, I_{2}(t)\geq0,$ if $S_{1}(0)\geq 0, S^q_{1}(0)\geq0, I_{1}(0)\geq0$, $S_{2}(0)\geq 0, S^q_{2}(0)\geq 0, I_{2}(0)\geq0$.

Similar to the proof of $I^q(t)$ in Lemma 1, we can get

Further more, we have $H_{1}(t)\geq0, H_{2}(t)\geq0$, if $H_{1}(0)\geq0, H_{2}(0)\geq0$.

Next, we consider the forth and tenth equation of system (2.2):

Based on theorem 3.2.1 of reference ^[30], we have $R_{1}(t)\geqslant 0, R_{2}(t)\geqslant0$, if $R_{1}(0)\geqslant 0, R_{2}(0)\geqslant0$.

Thus, all solutions of system (2.2) are in the set

$D = \left\{D_{1}\in R^{12}_{+}: 0\leq\mathop{\sum}\limits_{i = 1}^{2}\left(S_{i}(t)+I_{i}(t)+H_{i}(t)+ R_{i}(t)+S^q_{i}(t)+I^q_{i}(t)\right) = N_{1}(0)+N_{2}(0)\right\},$ namely, $D$ is a positive invariant set of system (2.2).

Let the right hand of system (2.2) be zero, then we have $E_{0} = (N_{1}(0), 0, 0, 0, 0, 0, N_{2}(0), 0, 0, 0, 0, 0)$ and

Next, we have the following conclusion:

$\bf{Theorem\ 3.}$ The control reproduction number of system (2.2) is:

Here, $R^c_{0i} = \frac {\lambda_{i} c_{i}}{\lambda_{i} v_{i} \alpha_{i} mp_{i}c_{i}+v_{i} \alpha _{i} +(1-v_{i})\eta}, i = 1, 2$. And if $R^c_{0} < 1$, the disease-free equilibrium $E_{0}$ is stable.

Otherwise, $E_{0}$ is unstable.

Proof. The Jacobin matrix of system (2.2) at disease-free equilibrium $E_{0}$ is given by

here,

Replace 1 of all the subscripts in $D_{11}$ with 2, 2 with 1, we can get $D_{22}$. Do the same to $D_{12}$, we can get $D_{21}$. The corresponding characteristic equation is:

here, $M = (q-M_{1})(q-M_{2})-b_{12}b_{21},$ $M_{1} = \lambda_{1}c_{1}-\lambda_{1} v_{1}\alpha_{1}mp_{1}c_{1}-v_{1}\alpha_{1}-(1-v_{1})\eta-b_{12},$ $M_{2} = \lambda_{2}c_{2}-\lambda_{2} v_{2}\alpha_{2}mp_{2}c_{2}-v_{2}\alpha_{2}-(1-v_{2})\eta-b_{21}.$ The ten characteristic roots of Eq (2.4) are all less than or equal to zero. The remaining two characteristic roots satisfy the following equation:

Hence,

When $R^c_{0} < 1$, characteristic roots of Eq (2.4) are all less than or equal to zero and the disease-free equilibrium $E_{0}$ is stable. When $R^c_{0} > 1$, $E_{0}$ is unstable.

$\bf{Theorem\ 4.}$ For system (2.2), $I_{1}(\infty) = H_{1}(\infty) = S^q_{1}(\infty) = I^q_{1}(\infty) = I_{2}(\infty) = H_{2}(\infty) = S^q_{2}(\infty) =$ $I^q_{2}(\infty) = 0,$ and $\mathop{\lim}\limits_{t\rightarrow \infty}S_{1}(t)$, $\mathop{\lim}\limits_{t\rightarrow \infty}S_{2}(t)$, $\mathop{\lim}\limits_{t\rightarrow \infty}\left(S_{1}(t)+S_{2}(t)\right)$, $\mathop{\lim}\limits_{t\rightarrow \infty}\left(R_{1}(t)+R_{2}(t)\right)$ exist.

The proof of Theorem 4 is similar to the proof of Theorem 2 and is given in Appendix B.

3.   Numerical simulation

Due to the large error of the previous data, the study starts from January 15, 2020. China banned travel to and from Wuhan at 10:00 a.m. on 23 January, 2020. According to Baidu Migration data and Yuan ^[32], we calculate that from 15 January to the implementation of the travel restrictions, there were 4,238,344 people travelling out of Wuhan and 1,903,606 people traveled to Wuhan. And then, we calculate that every day the average movement rate from Wuhan to other places of Mainland China (outside Wuhan) is about 0.0475 and from Mainland China (outside Wuhan) to Wuhan is about 0.000152. In the following, for each patch we assume that the travel rates of the susceptible individuals, the pre-symptomatic infected individuals and the recovered individuals are the same: $a_{12} = b_{12} = e_{12}\approx 0.0475$, $a_{21} = b_{21} = e_{21}\approx 0.000152$. After closure, the study period of Mainland China (outside Wuhan) is divided into two phases according to people's different understanding of COVID-19, one is from January 24 to January 31 and the other is from February 1 to February 28, after which the international importation cases become predominant. As for Wuhan, due to the lack of medical resources, the study period is divided into two phases, one from January 24 to February 4 and the other from February 5 to April 8, the day Wuhan lifts travel restrictions. We apply the daily reported cumulative confirmed cases collected from the website of National Health Commission of the People's Republic of China to implement parameter estimation ^[33]. In phase 1, we think that the number of contacts and infection rate between Wuhan and Mainland China (outside Wuhan) are the same. Let $Y_{11}(t)$, $Y_{12}(t)$ be theoretical cumulative cases for Wuhan and Mainland China (outside Wuhan) respectively. $\widehat{Y_{11}}(t)$, $\widehat{Y_{12}}(t)$ be the reported cumulative confirmed cases for Wuhan and Mainland China (outside Wuhan) respectively. Then we use the least square method (LSM) to find the parameter value to minimize the objective function ^[34]:

where $n_{1}$ is the size of sample data. Before the implementation of travel restrictions, the confirmed cases of Mainland China were mainly in Wuhan, so in the expression of $J_{1}$, the first term was multiplied by the weight coefficient $\frac{2}{3}$, and the second term was multiplied by the weight coefficient $\frac{1}{3}$. This method is implemented by running the command fminsearch from the optimization toolbox in MATLAB. We obtain the estimated parameter values $c = 27.88, \lambda = 0.0156, I_{1} = 239.2681$ (For the selection of other parameters and initial values, please refer to Tables 1 and 2).

In phase 2 and phase 3, due to the lockdown of Wuhan, Wuhan and Mainland China (outside Wuhan) become two isolated patches. Then, for Wuhan in phase 2, the objective function of LSM is :

The initial values are the end values of the Phase 1. Also, by running the command fminsearch in MATLAB, we obtain the estimated parameter values $c_{1} = 4.97, \lambda_{1} = 0.0645, p_{1} = 0.6617.$ Similarly, we can get the parameter values of other phases of the two patches.

Remark. For Wuhan, phase 1 is from January 15 to 23, 2020, phase 2 is from January 24 to February 4, 2020 and phase 3 is from February 5 to April 8, 2020. While, for Mainland China (outside Wuhan) phase 1 is also from January 15 to 23, 2020, phase 2 is from January 24 to January 31 and phase 3 is from February 1 to February 28, 2020.

3.1.   Impact of travel restrictions on the spread of COVID-19 epidemic

In this subsection we will study the impact of travel restrictions on the spread of COVID-19. Model parameters are set as phase 1 in Table 1 and the initial values are set as Table 2. Through numerical simulation and combined with Figure 4(a), we have that the implementation of travel restrictions without changing other prevention and control policies is beneficial to Mainland China (outside Wuhan) for the number of cumulative confirmed cases has been reduced 48,003 until February 7, which is bad for Wuhan because the cumulative confirmed cases has increased 37,719. In addition, the implementation of travel restrictions reduces the total number of confirmed cases. And the later the travel restrictions are imposed, the fewer confirmed cases are in Wuhan, the more confirmed cases are in Mainland China (outside Wuhan) and the more confirmed cases are in the whole Mainland China.

In phase 1, it is calculated that $R^{c}_{0} = 4.0741$, $R^{c}_{01} = 6.1281$, $R^{c}_{02} = 3.2161$. Further more, we have

due to $R^{c}_{01} > R^{c}_{02}$. Combined with Figure 4(b), we have the control reproduction number $R_{0}^c$ decreases with the increase of $b_{12}$ if fix $b_{21}$. While, $R_{0}^c$ increases with the increase of $b_{21}$ if fix $b_{12}$. That is to say, if the travel rate of pre-symptomatic infected individuals from Mainland China (outside Wuhan)to Wuhan is smaller and from Wuhan to Mainland China (outside Wuhan) is bigger, the control reproduction number is smaller. However, in our study the value of the control reproduction number is very big, and the change of travel rates have little effect on it.

From Figure 4(c) we have that for Wuhan, the final size increases with the increase of travel rates, while for Mainland China (outside Wuhan), the final size decreases with the increase of travel rates. As for the whole Mainland China, the final size decreases with the increase of travel rates. However, if Wuhan imposed travel restrictions on January 14, there would be no people infected in Mainland China (outside Wuhan) under the assumption of our model.

The implementation of travel restrictions has little impact on the control reproduction number. But it can greatly reduce the confirmed cases, and the earlier the implementation, the smaller the total number of infections. Generally speaking, the implementation of travel restrictions is beneficial to control the spread of COVID-19.

3.2.   Effects of contact tracing on spread of COVID-19 epidemic

Epidemiological investigation of confirmed cases and then isolation of close contacts are common prevention and control measures to control the spread of infectious diseases. According to Baidu Migration data, we count the migration index of Wuhan to Mainland China (outside Wuhan) from March 9, 2021 to June 20. Then we have 239,557 people who moved from Wuhan to Mainland China (outside Wuhan) every day ^[32]. Before the outbreak of COVID-19, every day the number of people moving in and out of Wuhan are the same for a long time. Therefore, we assume that the number of people moving into and out of Wuhan are both equal to 239,557. Then, we calculate that every day the average travel rate from Wuhan to Mainland China (outside Wuhan) is about 0.0214, and from Mainland China (outside Wuhan) to Wuhan is about 0.00017. And in the following, we assume $b_{12}\approx 0.0214$, $b_{21}\approx0.00017$. Based on the parameters of phase 1 in Table 1 and the initial values in Table 2, we obtain Figure 5(a) from which we find that before the implementation of the travel restrictions in Wuhan, even if the contact tracing rates increased to 1, $R^c_{0}$ will not be less than 1 and the epidemic could not be controlled. In addition, we do a sensitivity analysis about travel rates. From Figure 5, we can see that under different travel rates, no matter how big contact tracing rates are, $R^c_{0}$ will not be less than 1 and the disease cannot be controlled. After the travel restrictions are enforced, from Figure 6(a) we have $R_{01}^c$ can never be less than 1, that means the epidemic of Wuhan will not be contained under current control measures. While from Figure 6(b), we can see that for Mainland China (outside Wuhan), if the contact tracing rate increases to $38.77\%$, $R_{02}^c < 1$ and the epidemic will be brought under control. According to phase 2 of Table 1, the contact tracing rate of Mainland China (outside Wuhan) is about $31.35\%$ and is too small to control the epidemic. In phase 3, the Chinese government further strengthened prevention and control measures. Soon after, the control reproduction number $R_{01}^c = 0.0016$ and $R_{02}^c = 0.6969$ were less than 1, and the disease was brought under control.

We assume phase 2 of Mainland China (outside Wuhan) is also from January 24 to February 4 and the parameters are the same as phase 2 of Table 1. Make the same assumption for phase 3. From Figure 7(a), we have that at the end of phase 2, if lifted travel restrictions, no matter how high the contact tracing rates are, $R^{c}_{0}$ will not be less than 1. So, the travel restrictions of Wuhan cannot be lifted at the end of phase 2. From Figure 7(b), we can see that at the end of phase 3, if lifted travel restrictions, $R^{c}_{0}$ can be less than 1 as long as the contact tracing rates are high enough. Thus, the travel restrictions of Wuhan can be lifted at the end of phase 3.

We plot two phase diagrams (Figure 8) illustrating how the control reproduction number is shaped by the contact tracing rate and the transition rate of pre-symptomatic infected individuals to hospital. The phase transition occurring at $R^c_{01} = 1$ ($R^c_{02} = 1$) which separate two different regimes, $R^c_{01} > 1$ and $R^c_{01} < 1$($R^c_{02} > 1$ and $R^c_{02} < 1$). Furthermore, we observe that as the contact tracing rates increase, the transition points are reached for smaller values of the transition rates of pre-symptomatic infected individuals to hospital. In additon, from Figure 8(b) we can see that the transition being lost for very small values of $p_{2}\leq0.1$. That is to say, if the contact tracing rate is too small, then no matter how large the transition rate of pre-symptomatic infected individuals to hospital is, the value of $R^c_{02}$ cannot be less than 1. As a result, if you want to control the emerging infectious diseases as soon as possible, you must combine a variety of prevention and control strategies.

3.3.   The effect of vaccination on the spread of COVID-19 epidemic

In this subsection, we consider the effect of vaccination on COVID-19 epidemic spread. The dynamic model with vaccination of system (2.1) becomes

Here, $d_{i}$ means the protection rate of herd immunity, defined as the product of the vaccination rate and the effective protection rate. If take $a_{ij} = a_{ji} = b_{ij} = b_{ji} = e_{ij} = e_{ji} = 0$, the one patch model with vaccination is obtained. Through the similar calculation methods of control reproduction number in Theorem 1 and Theorem 3, we obtain the following conclusions:

(1) the control reproduction number with vaccination of one patch model is:

and $\frac{R^{cv}_{0i}}{dd_{i}} < 0$;

(2) the control reproduction number of system (3.1) is:

where, $U = \left(\left(\lambda_{1} c_{1}(1-d_{1})-\frac{\lambda_{1} c_{1}(1-d_{1})}{R^{cv}_{01}}-b_{12}\right)-\left(\lambda_{2} c_{2}(1-d_{2})-\frac{\lambda_{2} c_{2}(1-d_{2})}{R^{cv}_{02}}-b_{21}\right)\right)^2+4b_{12}b_{21}.$ If $d_{1} = d_{2} = d_{v}$ and the parameter value is taken as phase 1 of Table 1, then $\frac{dR^{cv}_{0}}{dd_{v}} < 0$.

We can see from Figure 9 that the bigger the protection rate of herd immunity, the smaller the value of the control reproduction number, the more conducive to the control of the disease. In Figure 9(a), we present the control reproduction number will be less than 1, namely the disease will be brought under control if the protection rate of herd immunity reaches $83.5\%$ in phase 1. Then, after imposing travel restrictions in Wuhan, we obtain that the control reproduction number will be less than 1, if the protection rate of herd immunity reaches $87.15\%$ for Wuhan, $55.93\%$ for Mainland China (outside Wuhan). Regard Mainland China as one patch and consider that people have returned to normal life, then, the number of contact will increase to 27.8763 and the contact tracing rates will be reduced to 0. In this case, from Figure 9(b) we can see that the control reproduction number $R^v_{03}$ will be less than 1 if the protection rate of herd immunity reaches $60.63\%$. As of 14 November 2021, Mainland China reported a total of 2.389568 billion doses of COVID-19 vaccine ^[8]. Suppose everyone gets two doses of vaccine, then the vaccination rate of Mainland China is about $85.34\%$. So, if the effective protection rate of the vaccine can be achieved $71.05\%$, we can return to normal life.

4.   Conclusions and discussion

It is a meaningful work to study the internal transmission mechanism of epidemic, predict the development trend and evaluate the effectiveness of prevention and control measures with mathematical model. And then provide a basis for further research and the formulation of reasonable prevention and control policies. With the global outbreak of COVID-19 epidemic, the work is particularly important. Although many scholars have established lots of mathematical models to reflect the real spread of epidemic as much as possible, the combination of travel restrictions, contact tracing, vaccination in patch model is relatively rare, especially for COVID-19 epidemic. In order to fill this gap, we establish a mathematical model with individual movement between two patches to assess the impact of these measures on epidemic transmission.

In this paper, we show that travel restrictions have increased the number of confirmed cases in Wuhan and reduced the number of confirmed cases in Mainland China (outside Wuhan). Overall, the number of confirmed cases in Mainland China has been reduced. The earlier it is implemented, the better it will be for Mainland China. However, it is impossible to control the epidemic and lift the travel ban on April 8, 2020 by simply imposing travel restrictions or increasing the rate of contact tracing in phase 1. In phase 2, the epidemic of Wuhan will not be contained under current control measures. While for Mainland China (outside Wuhan), the epidemic is under control if the contact tracing rate increased to $38.77\%$. In phase 3, with the further strengthening of prevention and control measures, the disease was quickly brought under control. The cities of Mainland China (outside Wuhan) began to resume work one after another on February 10, 2020, and Wuhan officially lifted travel ban at 00:00 on April 8, 2020. However, no matter in which phase of the disease transmission or after people return to normal life, as long as the protection rate of herd immunity is high enough, the disease will soon be brought under control. The results of our research show that the prevention and control measures taken by the Chinese government are timely and effective.

Sun et al. ^[40] established a SEIRQ-type model to study the effects of travel restrictions and medical resources on the spread of COVID-19. And they claimed the later the travel restrictions are enforced, the fewer confirmed cases will be in Wuhan, but the more cases will be exported at the same time, which will adversely affect other cities and even other countries. In this work, We establish a SIAHRQ-type patch model, and through simulation we find that confirmed cases of Wuhan will increase and confirmed cases of Mainland China (outside Wuhan) will decrease with travel restrictions. On the whole, confirmed cases of Mainland China will decrease. The earlier the travel restrictions are enforced, the more confirmed cases are in Wuhan, and the fewer confirmed cases are confirmed in Mainland China (outside Wuhan). And our findings in this work are consistent with Sun et al.. In addition, we also find that the greater the migration rate from Wuhan to Mainland China (outside Wuhan), the smaller the control reproduction number, and the higher the migration rate from Mainland China (outside Wuhan) to Wuhan, the greater the control reproduction number. In the case we consider, because the control reproduction number of phase 1 is relatively large ($R^c_{0} = 4.0741$), the change of travel rates to the control reproduction number is so small that it will not make the control reproduction number less than 1 (Figure 5). If the control reproduction number in phase 1 is about 1, then the travel rates have significant impact on disease control. In references ^[41], Colomer et al. developed an agent-based stochastic model to study the effects of vaccination and contact tracking on COVID-19 in Spain. They thought that vaccination alone can be crucial in controlling COVID-19, and vaccination and contact tracking work best in combination with social control measures. In this paper, through analysis we obtain that COVID-19 can not be contained by contact tracing alone. However, the disease can always be controlled if the protection rate of herd immunity is high enough. So, travel restrictions, contact tracing should be combined with other social control measures in order to contain COVID-19 as soon as possible. This conclusions are consistent with Colomer et al..

However, there are also some problems with our model. The one is that we don't consider the variation of COVID-19. This will be a very meaningful work, considering that vaccines have different protection rates against different viruses. The other is that we approximate the number of people who are traced in $m$ days, that is, multiplying the number of days by the number of people traced on the $t$ day. In fact, the number of people who are traced may be different from day to day. In addition, people of different ages have different contact patterns, mobility patterns and susceptibility to infectious diseases. How to better reflect these factors in model is what we intend to do next.

Acknowledgments

We kindly thank the reviewers and editors for their comments and suggestions. This work is supported by the National Natural Science Foundation of China (No. 61873154), Key R & D projects of Shanxi Province (No. 202003D31011/GZ), Health Commission of Shanxi Province (No. 2020XM18), Shanxi Key Laboratory (No. 201705D111006), Shanxi Scientific and Technology Innovation Team (No. 201805D131012-1), the 1331 Engineering Project of Shanxi Province, Graduate Innovation Project in Shanxi Province (No. 2020BY103), Selected funding Project for Scientific and technological activities of overseas students in 2021 (No. 20210009), Fundamental Research Program of Shanxi Province (No. 20210302124608).

Conflict of interest

All authors declare no conflicts of interest in this paper.

Appendix A.   Proof of Theorem 1

Proof. The Jacobin matrix of system (2.1) at the disease-free equilibrium $E_{00}$ is given by

The corresponding characteristic equation is:

When $R^c_{00} = \frac {\lambda c}{\lambda v \alpha mpc+v \alpha+(1-v)\eta} < 0$, the characteristic roots are all less than or equal to zero. Hence, the disease-free equilibrium $E_{00}$ is stable, otherwise, $E_{00}$ is unstable.

Appendix B.   Proof of Theorem 4

Proof. If we sum all the equation of system (2.2) except $\frac {dR_{1}}{dt}$ and $\frac {dR_{2}}{dt}$, then we have

So, $\mathop{\sum}\limits_{i = 1}^{2}\left(S_{i}+I_{i}+H_{i}+S^q_{i}+I^q_{i}\right)$ is decreasing. In addition, $0\leq \mathop{\sum}\limits_{i = 1}^{2}\left(S_{i}+I_{i}+H_{i}+S^q_{i}+I^q_{i}\right)\leq (N^*_{1}+N^*_{2})$, hence, it has a limit. Moreover, $\frac {d\mathop{\sum}\limits_{i = 1}^{2}\left(S_{i}+I_{i}+H_{i}+S^q_{i}+I^q_{i}\right)}{dt}$ is bounded because $-\mathop{\sum}\limits_{i = 1}^{2}\left(\mu H_{i}+\eta(1-v)(I_{i}+I^q_{i})\right)$ is bounded. Hence, according to the Fluctuations Lemma ^[31], we obtain

On the other hand, $I_{i}(t)\geq 0, H_{i}(t)\geq 0, I^q_{i}(t)\geq 0(i = 1, 2)$, thus we have

Also, we can obtain that

here, the proof is similar to the proof of ${S^q(\infty)}$ in Theorem 2.

Add up the first, the fourth, the seventh and the tenth equation in system (2.2), we have

that is, $\mathop{\sum}\limits_{i = 1}^{2}\left(S_{i}(t)+S^q_{i}(t)\right)$ is decreasing. Since $\mathop{\sum}\limits_{i = 1}^{2}\left(S_{i}(t)+S^q_{i}(t)\right)\geq 0$, $\mathop{\lim}\limits_{t\rightarrow \infty}\mathop{\sum}\limits_{i = 1}^{2}\left(S_{i}(t)+S^q_{i}(t)\right)$ exists. Considering $\mathop{\lim}\limits_{t\rightarrow \infty} S^q_{i}(t) = 0(i = 1, 2)$, so $\mathop{\lim}\limits_{t\rightarrow \infty}(S_{1}(t)+S_{2}(t))$ exists. Further more,

exists.

In the following, we will prove $\mathop{\lim}\limits_{t\rightarrow \infty}S_{1}(t)$, $\mathop{\lim}\limits_{t\rightarrow \infty}S_{2}(t)$ exist in three cases.

(1) If $a_{12}S_{1}(t) = a_{21}S_{2}(t)$, then the first equation of system (2.2) becomes

which is the same as the first equation of system (2.1). Like the method of proof of $\mathop{\lim}\limits_{t\rightarrow \infty}S(t)$ in system (2.1), the existence of $\mathop{\lim}\limits_{t\rightarrow \infty}S_{1}(t)$ can also be proved here. The existence of $\mathop{\lim}\limits_{t\rightarrow \infty}S_{2}(t)$ can also be proved by the same method.

(2) If $a_{12}S_{1}(t) > a_{21}S_{2}(t)$, then add up the first, the fifth equation of system (2.2):

It is the same as the previous method of proving the existence of $\mathop{\lim}\limits_{t\rightarrow \infty}\mathop{\sum}\limits_{i = 1}^{2}\left(S_{i}(t)+S^q_{i}(t)\right)$, we can prove that $\mathop{\lim}\limits_{t\rightarrow \infty}\left(S_{1}(t)+S^q_{1}(t)\right)$ also exists. Considering $\mathop{\lim}\limits_{t\rightarrow \infty} S^q_{1}(t) = 0$, so $\mathop{\lim}\limits_{t\rightarrow \infty}S_{1}(t)$ exists. Thus, $\mathop{\lim}\limits_{t\rightarrow \infty}S_{2}(t)$ exists due to the existence of $\mathop{\lim}\limits_{t\rightarrow \infty}(S_{1}(t)+S_{2}(t)).$

(3) If $a_{12}S_{1}(t) < a_{21}S_{2}(t)$, then add up the seventh, the eleventh equation of system (2.2):

The method of proof is the same as that of (2), and we can get $\mathop{\lim}\limits_{t\rightarrow \infty}S_{2}(t)$ exists. Also, $\mathop{\lim}\limits_{t\rightarrow \infty}S_{1}(t)$ exists.