Coverage control of mobile sensor networks with directional sensing

1.   Introduction

Coverage control is one of the commonly encountered problems in mobile sensor networks ^[1,2], where the mobile sensors are deployed to cover a given area to provide services such as monitoring and wireless communication ^[3,4,5]. In the literature, there are two types of coverage control problems, namely, dynamic and static coverage control. In dynamic coverage control, the purpose is to sweep an area such that each point concerned is explored by the sensors during the movement ^[6,7]. In this paper, however, the static coverage control problem ^{[8,9,10,11,12]} is addressed, where the control laws are designed to drive the mobile sensors from initial configuration to another configuration to cover a given area meanwhile optimizing coverage performance. In coverage control problem, the sensor types and dynamics are critical for developing control strategies. Considering sensor types, commonly addressed sensors are omni-directional sensors the coverage performance of which is not affected by the pointing directions. Plentiful coverage control work focuses on such sensors. In ^{[10,11,13,14,15]}, homogeneous omni-directional sensing ranges are assumed for sensors, which means the sensors have the same sensing capability. To relax the homogeneity assumption, heterogeneous sensing ranges are also addressed in coverage control, see, for example ^[16,17,18]. Other than the continuous coverage control in the above mentioned results, discretized implementations of coverage control algorithms are also proposed in ^[19,20]. In coverage control with omni-directional sensors, the sensing ranges are typically modelled as disks such that the sensing performance regarding a point is only influenced by the distance to the sensors. However, in many application scenarios, omni-directional sensing model cannot well describe the sensing performance of sensors such as cameras, infrared sensors, ultrasound sensors, and radars ^[21]. These sensor are termed as directional sensors in this paper, which indicates the sensing performance of a sensor is also affected by its orientation angle.

There are limited research on coverage control of mobile directional sensors ^[22,23]. In this type of the problem, the sensing ranges are modelled as circular sectors ^[22] or ellipses ^[23]. With these sensing models, the simple form of typical coverage problem will be destructed, which results in difficulties in computation of gradients and designing coverage controllers. For example, the sensing models such as the circular sector result in non-smooth sensing boundaries^[22]. In the following, the typical gradient-based coverage control design is described and the problem encountered with directional sensors will then be presented.

The widely used coverage control algorithm is designed based on gradients of some sensing performance valuation functions. In the scenarios with omni-directional sensors, the value function is only determined by the positions of sensors. It is shown that the gradient of the value function always exists as long as there does not exist two sensor initially at the same position. In another word, the non-differentiable configurations of the sensors' states can be naturally avoided ^[10,11,16]. However, the non-smooth sensing range such as the circular sector makes the non-differentiable scenarios more complex, which needs careful design to avoid these configurations. In our previous work ^[24], this issue is dealt with by approximating the non-smooth sensing range boundaries. Through this approach, the configurations of sensors where the gradient of the performance valuation function is difficult to be defined are avoided under the designed motion control. Due to the complicated computation of gradients and the approximation nature in the above approach, we use another approach in this paper to deal with the issue just mentioned. In such an approach, the configurations of sensors where the gradients are not well defined will be avoided by incorporating an artificial potential function in the coverage valuation function. Moreover, rigorous analysis of gradient computation and convergence property of the coverage control will be included.

As the coverage performance with directional sensors is determined by both the positions and pointing directions of the sensors, a ubiquitous model to describe such dynamics is unicycle model ^[25]. Compared to the typically used single-integral model as in ^[11,15,16], an appropriate gradient-based coverage control design is much harder as such a model is nonholonomic. Considering the difficulties caused by directional sensing ranges and the dynamics of the mobile sensors, this paper aims to design a coverage control law for mobile sensors with directional sensing characteristics.

The sensing range of the directional sensors is modelled as circular sector which is as also pointed out in ^[22,24,26]. To solve the coverage problem, an artificial potential function component is added to the coverage performance valuation function in order to avoid non-differentiable configurations. Based on the gradient of the value function, an innovative non-smooth controller is developed to steer the positions and orientations of the mobile sensors to improve the corresponding coverage performance. Moreover, in order to solve the coverage problem distributedly ^[9,10,11,12], an improved area partition is also defined.

Considering the points mentioned above, the novelty and contributions of this paper are summarized as follows:

1) An optimization problem is constructed to model a novel coverage problem of mobile sensors subject to directional sensing ranges and unicycle dynamics.

2) An innovative distributed gradient-based coverage control algorithm is proposed for the sensors, and its convergence property is rigorously analysed. Moreover, the corresponding gradients are rigorously defined and analysed.

3) By including an artificial potential function component in the coverage performance function, an innovative strategy is developed to avoid the configurations where gradients of the performance function are not properly defined.

The remaining of the paper is organised as follows. Coverage control problem formulation with directional sensors is presented in Section 2. A partition with considering directional sensing characteristics is defined in Section 3. In Section 4, a potential function is adopted to avoid the non-differentiable cases of the performance value function. Computation of gradients is presented in Section 5. Based on the gradients, controller design for the mobile sensors and the corresponding convergence analysis is shown in Section 6. Simulation results are provided in Section 7 to illustrate the coverage performance of the proposed control algorithm. Section 8 concludes the paper and provides some possible future research directions.

2.   Problem formulation

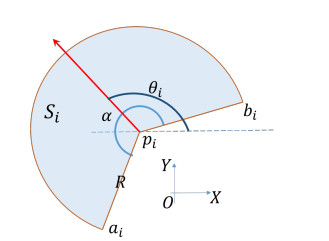
In this paper, a group of mobile sensors are responsible for covering a given compact area $V\in\mathbb{R}^2$. The set of the sensors' indices is denoted as $\mathcal{N} = \{1, \dots, n\}$ with $n$ being the total number of sensors. As illustrated in Figure 1, the position of sensor $i$ is denoted by $p_i = \begin{bmatrix} x_i & y_i\end{bmatrix}^\mathsf{T}$ with $x_i, y_i$ being the coordinates in a given coordinate system $XOY$. The orientation angle of sensor $i$ is represented by $\theta_i$ with positive values indicating counter-clockwise directions. In this paper, unicycle dynamics is assumed for the sensors, which is expressed as

where $v_i$ is the longitudinal speed of sensor $i$, and $\omega_i$ denotes its angular velocity. Here, $v_i$ and $\omega_i$ are the inputs for sensor $i$. In the rest of the paper, states of sensor $i$ are denoted as $z_i = \begin{bmatrix} x_i & y_i & \theta_i \end{bmatrix}^\mathsf{T}$. The sensing range of each sensor is a circular sector denoted as $S_i$ with a centrally spanned angle $\alpha$ and a radius $R$ as in Figure 1.

In this figure, $XOY$ frame denotes the global coordinate system where the positions and the heading angles of sensors are defined. In the considered coverage control problem, the mobile sensors are assumed to have identical sensing ranges. The sensing range is bounded by two line segments $p_i a_i$ and $p_i b_i$ and an arc $\overset\frown{a_ib_i}$. Note that when $R = \infty$, the boundaries are only two lines $p_i a_i$ and $p_i b_i$. The area outside the sensing range (or boundaries) is the dead sensing zone where targets in this area cannot be sensed. For instance, the sensing range of a camera with fish-eye lens can be modelled as such a directional range ^[22].

2.1.   Sensing performance of mobile sensors

The control objective of the coverage problem is to steer a group of mobile sensors to optimize the sensing performance regarding a given region. A value function $f(z_i, q)$ is used to evaluate the coverage performance of sensor $i$ regarding a target point $q = \begin{bmatrix} q_x & q_y \end{bmatrix}^\mathsf{T}$ in the given area $V \in \mathbb{R}^2$. This function not only is related to sensor $i$'s position but also its orientation angle as the directional sensing characteristics.

Inspired by the work in ^[22,26] and coverage problem with omni-directional sensors ^[9,10,11], two principles are generally taken into consideration to select an appropriate $f(z_i, q)$. One is that the function $f(z_i, q)$ is non-negative and its value is $0$ if and only if $q$ is in the dead sensing zone of sensor $i$. The other one is that the sensing performance degrades as the distance between $q$ and $p_i$ increases. Considering these two principles, the following performance value function is adopted:

where $\mathbf{1}_{S_i}(q)$ is the indicator function with its value being $1$ if $q\in S_i$ and $0$, otherwise, and $D$ is a positive design parameter with $\frac{1}{D}$ denoting the decaying rate of sensing performance regarding the distance to the sensors. For convenience of presentation, we also denote $e^{-\frac{\sqrt{ (q_x - x_i) ^2 + (q_y - y_i)^2}}{D}}$ as $g(p_i, q)$.

Remark 1. In the coverage control problem with omni-directional sensors, the value of the sensing performance function is only determined by the distances between a point and the sensors ^[11,16]. When the sensors are with directional sensing ranges as in this paper, the sensing performance is also affected by the orientation angles of sensors. Other than the sensing performance model in this paper, other models to describe the directional sensing characteristics can also be found in ^[22,23]

As the derivatives corresponding to $S_i$'s boundaries will be used later for gradient computation. We now provide the mathematical expressions of them. The boundaries $p_ia_i$ and $p_ib_i$ (see Figure 1 for more details) are specifically expressed as

where $x, y$ denote the coordinates of points on the corresponding boundaries and $\mathfrak{R}(\theta)$ is defined as $\mathfrak{R}(\theta) : = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin{\theta} & \cos{\theta} \end{bmatrix}$. Moreover, the points on boundary $\overset\frown{a_ib_i}$ are defined as

With the sensing performance value for each individual sensor defined, the coverage value function considering all sensors regarding the given area $V$ is constructed as

where $Z$ denotes the stack of states of all sensors, which is $Z = \begin{bmatrix} z_1^\mathsf{T} & \dots & z_n^\mathsf{T} \end{bmatrix}^\mathsf{T}$. As the states of sensors vary with time, to specifically indicate the value function at time $t$, it is written as $H_1(t) = H_1(Z(t)) = \int_{V}\max_{i\in \mathcal{N}} f(z_i, q) dq$.

The objective of the coverage control problem is to design control strategies to maximize the coverage performance value function of the sensors for a give area $V$. More precisely, the following static optimization of the value function is used to describe the objective:

According to typical approaches in ^[10,11], in order to design an appropriate control law that can drive the system to one of the optimal solutions or local optimal solutions of the value function $H_1(Z)$, the gradient of the value function is required to be computed. Moreover, in order to design distributed control laws, computation of gradients is also preferred to be local.

3.   Partition of area $V$

In order to design a distributed gradient based controller, a Voronoi partition of the area $V$ is typically employed in the literature ^[11,27]. In the following, we present the partition which will be used for gradient computation in this paper and rewrite the performance value function according to the partition cells.

To address the sensing performance regarding the points in $V$, naturally a partition regarding $f(z_i, q), \forall i \in \mathcal{N}$ is defined as

where $S_C$ denotes the set of points where the partition is not properly defined, which will be analysed next, and $S(z_i)$ denotes the sensing range $S_i$, as in Figure 1, regarding the sensor $i$'s state $z_i$. When the spanned angle $\alpha$ of each sensing range is $2\pi$, $S_C$ is the set when there exist two sensors at the same position as pointed in ^[13]. For a general value of $\alpha$, a modified definition should be proposed with considering the directional sensing ranges of sensors.

We define a set

which represents the set of points regarding which there are two sensors have the same sensing performance. As the partition cells $V_i, \forall i\in \mathcal{N}$ should satisfy the condition that they have disjoint interiors, the measure of set $\mathcal{A}(Z)$ shall be zero for all $Z\in \mathbb{R}^{3n} \setminus \mathcal{S}_C$. Otherwise, the partition according to the partition rule in Eq (3.1) fails, which renders the distributed calculation of gradients difficult. A case when the partition rule fails is illustrated as in Figure 2.

It shows that when $\alpha < \pi$ and the angle between $\theta_i$ and $\theta_j$ is less than $\alpha$, the sensing performances regarding $i$ and $j$ within the grey area are the same. This renders a non-zero measure of $\mathcal{A}_Z$ and thus fails the partition in Eq (3.1). When $\alpha > \pi$, it is easily to show that the partition fails when $p_i = p_j$ for some $i\neq j$. Thus, we have the following formal definition of $\mathcal{S}_C$:

Note that when $\alpha > \pi$, $S_C$ can also be written as $\mathcal{S}_C = \{Z\in \mathbb{R}^{3n} | \exists i, j \in \mathcal{N}, i \neq j \text{ s.t. } p_i = _j\}$.

Define $S_I$ as

Then the partition in Eq (3.1) is properly defined on $S_I$ and the value function $H_1(Z)$ in Eq (2.5) can be rewritten as

It is noted that a partition cell $V_i$ may consist of several separate planar pieces, which is caused by the directional sensing ranges, and the union of all the partition cells might not cover the whole $V$ due to the limited sensing radius $R$. Thus it is slightly abuse of the term partition.

Remark 2. The idea of the partition is inspired by the Voronoi partition. However, the partition defined in this paper might not cover a given set in some cases, which is partially caused by the directional sensing ranges and slightly different from the definition of commonly used Voronoi partition in coverage problems. Readers may refer to abstract Voronoi partition as in ^[28] for more information.

Here we provide a definition of neighbours for further expression. The neighbourhood of sensor $i$ regarding the proposed partition is defined as $\mathcal{N}_i = : \{j | V_i\cap V_j \neq \emptyset\}$. Moreover, we assume each sensor $i$ can communicate with its neighbours. Based on the form of the value function as in Eq (3.5), the gradient regarding each sensor state $z_i$ can now be computed distributedly on $S_I$ by only using information from neighbours. However, the gradient on $S_C$ is still difficult to define, let alone distributed computation of it. In this paper, we design artificial potential functions to generate potential field to prevent the sensors' states from entering $S_C$.

4.   Performance value function improvement with potential function design

Due to the directional sensing ranges of sensors, the set $S_C$ in which the gradients of the value function are not properly defined cannot be naturally avoided as in the omni-directional sensor coverage problem ^[15]. Thus artificial potential functions are designed to prevent sensors' states from entering $S_C$. Another benefit brought by such an approach is collision avoidance of sensors as in real applications the sensors possibly collide with each other though their sizes are small compared to the size of the area to be covered. In the following, first the potential functions is presented. Then the performance value function is modified by incorporating the potential functions.

Remark 3. Another strategy to avoid the configurations where the gradient of the value function is not properly defined is proposed in our previous work in ^[24]. In this strategy, the straight line boundaries of the sensing ranges $S_i$ are approximated by some properly designed curves and sensing performance function is also slightly modified, which leads to positive invariant property of the set $S_I$ when a gradient based coverage controller is applied on sensors.

To avoid set $S_C$, an artificial potential function is adopted for each pair of sensors to repel them away from each other, which is

where $\eta$ and $\rho_0$ are positive constants to be selected. In implementation, $\rho$ is usually selected to be slightly larger than the size of the sensors in order to avoid collision and reduce the influence of the potential functions on coverage performance at the same time. For instance, if the sensors are in a disc shape, $\rho$ can be a value which is slightly larger than the disc's radius. For the same purpose, $\mu$ is usually selected to be small and can be selected from the interval $[0.1, 1]$. Based on the definition of the potential functions, a graph $G^p(Z) = (\mathcal{N}, \mathcal{E}^p(Z))$ is induced with $\mathcal{E}^p(Z) : = \{\{i, j\} | \|p_i - p_j\| \leq \rho_0 \}$ and the neighbourhood of sensor $i$ regarding $G^p$ is defined as $\mathcal{N}_i^p = \{j | \{i, j\} \in \mathcal{E}^p \}$. By incorporating the artificial potential functions into the performance function, a new performance function is constructed as

where

As the control objective is to maximize the value function, the negative sign in Eq (4.3) implies the gradient direction of $H_2$ is along the direction of increasing the distances between sensors. In Section 6, it will be shown that the designed gradient based controller based on the performance valuation function $H(Z)$ keep the sensors' states from entering $S_C$.

5.   Computation of gradients

Distributed computation of gradients of $H(Z)$ in $S_I$ with respect to sensors' states are presented in the following based on the partition in Eq (3.1).

To help present computation of the gradients of $H(Z)$, several sets are first defined. We use $\partial V_i$ and $\partial S_i$ to denote the boundaries of the areas $V_i$ and $S_i$, respectively, $\partial S_i^B$ is defined as $\partial S_i^B : = p_i a_i\cup p_i b_i$ and $\partial S_i^C$ represents the set of points on the arc part of $S_i$'s boundary, which is $\partial S_i^C = \partial S_i \setminus \partial S_i^B$. The partial derivatives of $H(Z)$ with respect to sensors' states can be locally computed as

where $s$ parameterizes the corresponding boundary and $\mathbf{n}$ denotes the outward unit normal of the corresponding boundary. Note that $s$ and $n$ have different expressions for different boundaries. We show the derivation of these partial derivatives in the proof of Proposition 1.

Proposition 1. Assume the boundary of $V$ is a simple closed curve. Given the performance function $f$, the function $g$ and potential functions $h_{i, j}(Z), \forall \{i, j\} \in \mathcal{E}^p(Z)$, the value function $H(Z)$ is continuous differentiable on $S_I$, where for each $i\in \mathcal{N}$ the partial derivatives are computed as in Eqs (5.1)–(5.3).

Proof. According to the definition, $g(p_i, q)$ is continuously differentiable with respect to $(p_i, q)$ for $p_i\in \mathbb{R}^{3}$ and $q\in V_i(P)$, $\forall i \in \mathcal{N}$. Thus, both $f(z_i, q)$ and $\frac{\partial g(p_i, q)}{\partial Z}$ are integrable on $V_i(Z)$ for each $i\in \mathcal{N}$ and $Z \in S_I$.

If $Z \notin S_C$, the set $\mathcal{A}(Z)$ has measure zero. As the boundaries of $S_i, \forall i\in \mathcal{N}$ are finite number of straight lines and arcs and the common boundaries between any two sensors' ranges are finite number of straight lines, it can be concluded that $V_i(Z)$ has finite number of separate subsets $\forall Z\in S_I, \forall i\in\mathcal{N}$. Based on the above two facts, $\{V_i(Z) | Z\in S_I\}$ is a piecewise smooth family for each $i\in\mathcal{N}$. Now, we can apply the differentiation process as in ^[29].

First the partial derivatives of $H_1(Z)$ are considered. For each $i\in\mathcal{N}$, we have

Now, we consider the partial derivative at a point $Z_0$. The corresponding entries of $Z_0$ are similarly denoted as $x_{i, 0}$, $y_{i, 0}$, $\theta_{i, 0}$ and $p_{i, 0} = \begin{bmatrix}x_{i, 0} & y_{i, 0}\end{bmatrix}^\mathsf{T}$. By chain rule, the first term on the right hand side in Eq (5.4) is expressed as

where $g(x_i, y_{i, 0}, q) = g(\hat{p}_{i, 0}, q)$ with $\hat{p}_{i, 0}: = \begin{bmatrix}x_i & y_{i, 0} \end{bmatrix}^\mathsf{T}$ and $Z_{0, x_i}$ denotes the vector whose entries are the same as $Z_0$ expect for the entry $x_{i, 0}$ which replaces $x_i$. Inspired by the derivation in ^[29], the second term on the right hand side of Eq (5.5) is computed as

where the last equality is established with the fact that $\partial V$ does not vary with $Z$ and $V_i(Z_{0, x_i})$ is simplified as $V_i$ for expression convenience.

With similar derivation, as $\frac{\partial g(p_{j, 0}, q)}{\partial x_i} = 0$, each summand in the second term on the right hand side of Eq (5.4) can be written as

On the boundary segments $(\partial V_i \cap \partial V_j) \cap \partial S_i^B$, for each $j\in \mathcal{N}_i$, it is easily to check that $g(p_{i, 0}, q) = g(p_{j, 0}, q)$ for all $q$ on such segments based on the definition of the partition Eq (3.1), and the two corresponding outward unit normal point opposite directions. Thus the integral terms regarding these segments in Eqs (5.6) and (5.7) will cancel each other when they are substituted into Eq (5.4). Substitute Eq (5.6) into (5.5) and substitute Eqs (5.5) and (5.7) into (5.4), and apply the above deduction processes to every $Z\in S_I$, the partial derivative of $H_1(Z)$ with respect to $x_i$ is computed as

Similar results can be achieved for the partial derivatives with respect to $y_i$ and $\theta_i$ for all $i\in\mathcal{N}$.

With the definition of $H_2$ and $h_{ij}$, it is easy to conclude that $H_2(Z)$ is continuously differentiable on $S_I$. The partial derivative of $H_2(Z)$ with respect to $x_i$ is expressed as

Combining Eqs (5.8) and (5.9), the partial derivative in Eq (5.1) is established. Similarly, the partial derivatives in Eqs (5.2) and (5.3) can also be achieved with just noting that $\frac{\partial H_2(Z)}{\partial \theta_i} = 0$.

Note that in the case when the sensing radius $R$ is infinity, the integral terms regarding $\partial V_i \cap \partial S_i^C$ shall be zero in the partial derivatives. Each point on the boundary $\partial S_i^B$, which is defined in Eq (2.3), can further be expressed as:

where $\rho(s) \in [0, R]$ and $\epsilon(s) \in \{-\frac{1}{2}\alpha, \frac{1}{2}\alpha\}$ are neither depend on states of sensors. Thus, the partial derivatives of $s$ with respect to $z_i$ are expressed as

The outward unit $\mathbf{n}$ on the boundary $p_i a_i$ as expressed in Eq (2.3) is calculated as

where $\mathfrak{R}(\theta)$ is defined in Eq (2.3). Similarly, the outward unit on the boundary $p_i b_i$ is calculated as

According to the expression in Eq (2.4), the partial derivatives of any $s$ on $S_i^C$ are the same as in Eq (5.10), and the outward unit at a point $s$ on the boundary $S_i^C$ is determined as

By substituting Eqs (5.10)–(5.13) into (5.1)–(5.3), the partial derivatives of $H(Z)$ with respect to each $z_i$ can be calculated and directly implemented.

6.   Gradient-based coverage controllers

Based on the gradients calculated in Eq (5.1)–(5.3), an innovative controller is designed for each mobile sensor to optimize the coverage performance of the given area $V$. This section presents the controller design and the convergence analysis.

6.1.   Controller design of mobile sensors

In most of the coverage control literature such as ^[15,22,23], the control of positions and orientation angles of sensors are decoupled due to simple dynamics. However, in the dynamics of sensors in Eq (2.1), position and orientation angle control are coupled. Thus new controllers are needed to be designed using the gradient information of $H(Z)$ to maximize the performance function. It is noted that the dynamics of sensors presented is nonholonomic. Such systems do not satisfy Brocketts necessary smooth feedback stabilization condition ^[30]. In order to achieve the optimal performance with respect to the value function $H(Z)$, the following non-smooth distributed gradient-based control law is proposed for the $i^{th}$ sensor:

where $sign(x) = -1~~\text{ if } ~~x < 0$ and $sign(x) = 1 \text{ if } x\geq 0$, $k > 0$, $k_1 > 0$ and $k_2 > 0$ are tuning parameters and $g_i(Z)$ is defined as

Remark 4. Due to the non-smooth component in the control input $\omega_i$, chattering might happen in implementation. To alleviate such a phenomenon, a low path filter can be introduced to smooth out the control input signal with with sacrificing the performance, i.e., the states of the system might converge to a neighbourhood of the theoretical convergence point.

Next, it shows that if the states of the sensors initially lie in the continuous differentially set $S_I$, it will stay in that set forever.

6.2.   Positive invariance of $S_I$

To stay away from the set $S_C$ where differentiability of $H(Z)$ is hard to analyse, we show that the set $S_I$ is positively invariant. That is, once the initial state of sensors lies within $S_I$, it will stay in this set at any future time under the dynamics in Eq (2.1) and control law designed in Eq (6.1). Letting $S_I$ be defined as in Eq (3.4), the first main result is summarized in Theorem 1.

Theorem 1. For the dynamics Eq (2.1) with the control inputs proposed in Eq (6.1), the set $S_{I}$ is positively invariant.

Proof. For each $i$, denote $z_i(\cdot)$ as a Filippov solution of Eq (2.1) with the controller as in Eq (6.1), which satisfies

where $g(z_i) : = \begin{bmatrix} v_i \cos \theta_i \\ v_i \sin \theta_i \\ \omega_i \end{bmatrix}$ and $K[g](z_i)$ denotes the Filippov of $g$ ^[31,32]. If $Z(0)\in S_N$, according to the definition of $H(Z)$ in Eq (4.2), its derivative along the trajectories of Eq (2.1) exists as

where

where

As each element in $\dot{\tilde{H}}$ is greater than or equal to $0$, the derivative of $H(t)$ is non-negative. It can be concluded that $H(t)$ is non-increasing along the trajectory. Therefore,

Next, we proof the conclusion by contradiction. If there exists a time instant $\tau$ such that: as $t$ tends to $\tau$, $\|p_i(t) - p_j(t)\|$ tends to $0$. That is, $\lim_{t\rightarrow \tau} h_(ij)(Z(t)) = \infty$. This leads to $\lim_{t\rightarrow \tau} H(t) < H(0)$, which contradicts the condition in Eq (6.6). This implies that the state $Z(t)$ cannot leave the set $S_I$ if $Z(0) \in S_I$. Thus $S_I$ is positively invariant.

Define the maximum of $H_1(Z)$ as $H^*_1$, that is, $H^*_1 = \max_{Z \in \mathbb{R}^{3n}} H_1(Z)$. Then the distance between any two sensors can be bounded below as in Proposition 2.

Proposition 2. If $Z(0) \in S_N$, then for any $t\geq 0$, $\max_{ \{i, j\} \in \{\{i, j\} | i, j\in\mathcal{N}, i\neq j\} } h_{ij}(t) \leq \frac{\rho_0\sqrt{\eta}}{\sqrt{\eta}+\rho_0 \sqrt{2(H(0) - H_1^*)}}$.

Proof. From the definition of $H(t)$ in Eq (4.2), we have

At the same time, $H(t) \geq H(0)$ as in Eq (6.6). Thus,

Based on the definition of $h_{ij}$ in Eq (4.1), the conclusion is achieved.

6.3.   Convergence properties of coverage control

Instead of achieving the optimal value of the coverage performance value function as in omni-directional sensor cases, the coverage control with directional sensors can only achieve local optimum of the performance function $H(Z)$ due to its non-convex feature. Denote $S_{critical} = \left\{Z\in \mathbb{R}^{3n}\left|\frac{\partial H}{\partial Z} = 0\right.\right\}$. With the result presented in Theorem 1, Theorem 2 shows the convergence of the closed loop system which consists of the dynamics Eq (2.1) and the control inputs proposed in Eq (6.1). More precisely, the sensors' state will asymptotically converge to $S_{critical}$.

Theorem 2. Suppose that initial states of sensors satisfy $Z(0)\in S_I$. The states of the mobile sensor system with the sensor dynamics Eq (2.1) and the control inputs Eq (6.1) will converge to $S_{critical}$.

Proof. As $H_1$ is bounded above and $H_2$ is negative, it is obvious that $H(Z)$ is bounded above. Denote $\bar{H}$ as an upper bound of $H(Z)$ and define $V_E$ as $V_E(t): = \bar{H} - H(Z(t))$. Thus, $V_E(t)$ is positive definite. In the following, $V_E$ is selected as a Lyapunov candidate. According to the derivative computation in Eq (6.3), the derivatives of $V_E$ along the trajectories of the dynamic system (2.1) satisfies

As $V_E$ is bounded above, the state $Z$ converges to a point $Z^*$ in $\Omega$ with $\Omega$ being denoted as

Note that $\Omega$ is set of all points where $0 \in \dot{\tilde{H}}(Z)$. Next we show the sensors' state will finally converge to the set of $S_{critical}$. We now focus on the states in set $\Omega$. Two subsets of $\Omega$ are defined as

and

Based on these definitions, it can be checked that $\Omega = \mathcal{M} \cup \mathcal{E}$ and $\mathcal{M} \cap \mathcal{E} = 0$. For each element in $\mathcal{E}$, there exists a sensor $i\in \mathcal{N}$ such that $\frac{\partial H}{\partial x_i} \neq 0$ or $\frac{\partial H}{\partial y_i} \neq 0$. Combining this condition with the following fact $\begin{bmatrix} \cos\theta_i & \sin\theta_i \end{bmatrix}^\mathsf{T} \perp \begin{bmatrix} -\sin\theta_i & \cos\theta_i \end{bmatrix}^\mathsf{T},$ it can be concluded that $\begin{bmatrix} -\sin\theta_i & \cos\theta_i \end{bmatrix} \begin{bmatrix} \frac{\partial H}{\partial x_i} & \frac{\partial H}{\partial y_i} \end{bmatrix}^\mathsf{T} \neq 0$. Due to the definition of $\arctan (\cdot)$ and $sign(\cdot)$, the control input $\omega_i$ is not equal to $0$ and $\theta_i$ will change in such cases. As $\theta_i$ changes, the condition $\frac{\partial H}{\partial x_i}\cos \theta_i + \frac{\partial H}{\partial y_i}\sin\theta_i = 0$ is violated, which implies the set $\mathcal{E}$ is not an positive invariant set. Moreover, it is easy to check that $\mathcal{M}$ is invariant, which implies $\mathcal{M}$ is the largest invariant set in $\Omega$. According to LaSalle's theorem^[25,33], we conclude that the state of sensors $Z$ will converge to a point in $\mathcal{M}$ which is the same as $S_{critical}$. The conclusion is drawn.

In implementations, when the parameter $\rho_0$ in Eq (4.1) is chosen small enough, $H_2(Z(t))$ usually tends to zero as $Z(t)$ converges. This implies the state $Z(t)$ usually converges into the set $\left\{Z\in \mathbb{R}^{3n}\left|\frac{\partial H_1}{\partial Z} = 0\right.\right\}$, which means the potential functions only slightly affect the original coverage performance determined by $H_1$.

7.   Simulation results

7.1.   Simulation results of the proposed coverage control

The numerical simulations in this section are conducted in Python software. The closed-loop system with the unicycle dynamics model in Eq (2.1) and the controllers in Eq (6.1) are numerically simulated in discrete form with a sampling period $0.1s$.

To illustrate the performance of the proposed coverage control method, simulation results with $3$ and $5$ mobile sensors are presented. Each sensor has the same directional sensing range with $R = 60 m$ and $\alpha = \frac{4}{3}\pi$. In the performance function in Eq (2.2), $D$ is set as $60$. In the artificial potential function, $\eta$ and $\rho_0$ are set as $0.2$ and $5.0$, respectively. Note that, as only numerical simulations are conducted and the sizes of the sensors are not specified, $\rho$ is selected arbitrarily as long as it is not too large. The principles of selecting $\eta$ and $\rho_0$ in practice are stated in Section 4.

The given area $V$ to be covered is set as a square with coordinate $X$ ranging from $0$ to $80 m$ and $Y$ from $0$ to $80 m$. The coefficients in the controllers are tuned by trials, which are $k = 0.05$, $k_1 = 0.003$ and $k_2 = 0.005$. The initial states of the sensors are depicted as in Figures 3a and 4a regarding $3$ and $5$ sensors cases, respectively. The red disks indicate positions of the sensors, and the arrows indicate their orientations. Patches with different colours represents the covered area by different individual sensors, that is $V_i$s, and dashed lines denote the boundaries of corresponding sensors' sensing ranges, where the same coloured patches and lines correspond to the same sensor. As declared before, a partition $V_i$ might include several separate parts.

By implementing the control inputs as designed in Eq (6.1) and executing the controllers for $200.0 s$, the states of sensors and their coverage performance at some selected time instants are shown in Figures 3 and 4. The results imply that the states of sensors tend to be stable as time proceeding. The final coverage results in Figures 3f and 4f imply that the partition cells tend to be equally distributed over the given area, which is in line with the common sense.

The values of the overall coverage performance function $H(Z)$ evolving with time in $3$ and $5$ sensors' cases are depicted in Figures 5 and 6.

It can be seen that the value function $H(Z)$ increases along the time and gradually converges to its steady-state value. The values of $H_1(t)$ and $H_2(t)$ are also depicted in Figures 5 and 6. The values of $H_2(t)$ are very small compared to $H(Z)$ and tend to zero quickly, which implies the artificial potential function component $H_2(t)$ barely has influence on the final coverage performance of sensors.

Comparing the results with $3$ and $5$ sensors, the execution times do not increase with the number of sensors as the coverage control algorithm proposed is in a distribute style. Note that, it even takes more time for the $3$ sensors case to converge to a critical point. The time cost of the algorithm depends on many factors such as initial states and the given area $\mathcal{V}$. However, the value of the performance function $H(Z)$ with $5$ sensors is larger than with $3$ sensors, which is in line with the common sense that more sensors imply a better coverage performance. As the coverage control algorithm only converge to some critical points as claimed in Theorem 2, its performance depends on initial states of the sensors. We illustrate this phenomenon by adding a simulation case still with $5$ sensors but with different initial states. The initial states, final states and the values of the performance function are shown in Figures 7 and 8. Compared with Figures 4 and 6, the final states of sensors and the values of $H(Z)$ in this case are different.

7.2.   Comparison with other coverage control strategies

As stated in Section 1, there are limited results ^[22,23,24] that can address the directional sensor coverage problem considered in this paper. The strategy in ^[22] does not consider the dead sensing zone beyond the sensing boundaries and the movement of sensors is not affected by their orientation angles, which renders the result not suitable for our problem setting. Similar concerns also exist in the strategy proposed ^[23]. One strategy that could properly address the proposed coverage problem is our previous work presented in ^[24], where performance value function $f(z_i, q)$ and boundaries $p_ia_i, p_ib_i$ are approximated in order to prevent the sensors' states from entering set $S_C$. In this work, $f(z_i, q)$ is approximated by $\hat{f}(z_i, q) = e^{-\frac{\sqrt{\beta (q_x - x_i) ^2 + (q_y - y_i)^2}}{D}} \mathbf{1}_{S_i}(q)$, and $p_i a_i, p_ib_i$ are approximated by $\widehat{p_i a_i} :$ $\begin{bmatrix} x & y \end{bmatrix}^\mathsf{T}$ $: =$ $\mathfrak{R}(\theta_i+\frac{\alpha}{2})$ $\begin{bmatrix} \tau & \frac{ - \gamma}{1 + e^{-\tau}} \end{bmatrix}^\mathsf{T} + p_i,$ $\widehat{p_i b_i} :$ $\begin{bmatrix} x & y \end{bmatrix}^\mathsf{T}$ $: =$ $R(\theta_i - \frac{\alpha}{2})$ $\begin{bmatrix} \tau & \frac{\gamma}{1 + e^{-\tau}} \end{bmatrix}^\mathsf{T} + p_i,$ $\tau \in [0, R).$

By choosing $\beta = 0.9$ and $\gamma = 0.2$ and making other settings the same as in the simulation case in Figure 4f, the simulation results using the control algorithm in ^[24] are depicted in Figures 9 and 10.

Comparing the results in Figures 4, 6, 9 and 10, the coverage performances of the two methods are similar. Note that approximations used in ^[24] have negative influence on coverage performance though slightly. Moreover, due to the approximation of boundaries, computation of the corresponding gradients is more complex than the proposed approach in this paper.

8.   Conclusions

In this paper, coverage control using directional mobile sensors with non-linear dynamics and non-smooth sensing ranges is considered. The dynamics of each sensor is modelled by a unicycle model while the sensing range of each sensor is modelled as a circular sector. Within the sensing ranges, the coverage performance value is determined by the distances and orientation angles of the sensors. Moreover, potential functions penalizing the distances between sensors are incorporated into coverage performance valuation function, which renders the gradient of the coverage performance function well-defined along the trajectory of the closed-loop system. Based on the gradient of the performance value function, a novel non-smooth coverage controller is proposed for sensors and its convergence property is analysed. Simulation results are provided to illustrate the performance of the proposed coverage control strategy. As there are oscillations caused by the non-smooth property of the closed-loop system and the discretization in implementation, a future direction of this work is to analyse the discrete implementation of the coverage controller to mitigate this phenomenon. In the proposed control strategy, the communication between neighbouring sensors is assumed to be perfect. However, imperfect communication is a commonly encountered problem in practical applications and should be addressed in controller development as pointed in ^[34,35]. Thus, coverage control with addressing imperfect communication links is a future direction of this work. Moreover, to alleviate the computation burden in calculating gradients and address a more practical sensing performance, some model-free gradient estimation based control methods, such as extremum seeking strategy, can be exploited in coverage control design.

Acknowledgments

This work was supported in part by Defense Industrial Technology Development Program.

Conflict of interest

The authors declare there is no conflict of interest.