1. Abiotic stress conditions and nitric oxide (NO)
Abiotic stress conditions such as drought, salinity, metal toxicity, extreme temperatures, low nutrient availability, and high ultraviolet radiation exposition impose restrictions to plant development [1,2]. In order to cope with challenging environment, plants have developed adaptive defense responses along their evolution. Recent studies successfully demonstrated that the ability of plants to overcome challenging environment conditions is linked to signaling events in which NO is a key player in the modulation of gene expression and protein activity, interacting with reactive oxygen species (ROS), and controlling hormone actions [2,3]. The protective effects of NO in plants subjected to abiotic stresses are induced by low concentrations of this signaling molecule (nano to micromolar), whereas millimolar concentrations of NO may exert toxicity with induction of nitrosative stress and cell death, which highlights the Janus face of NO [1].
This review summarizes the current state of the art in the beneficial actions upon applications of NO donors in the following abiotic stresses: drought, salinity, metal toxicity, and extreme temperatures. The mechanisms of action of NO donors in plants under these abiotic stress conditions are also discussed. Finally, the perspective of using NO donors, in particular, NO-releasing nanomaterials in agriculture is highlighted. Taken together, the administration of NO donors in plants under abiotic stress conditions is a promising strategy to improve agriculture, however new studies are required in this field.
2. Drought and NO
Drought stress is one of the most common challenging environmental factors that impair crop productivity [4,5,6]. Drought stress increases the generation of superoxide (O2∙−), hydrogen peroxide (H2O2), singlet oxygen (1O2), and other ROS that can damage plant proteins, DNA, lipids, nucleic acids, and carbohydrates [7,8,9]. Severe water deficit may impair plant metabolic processes such as photosynthesis and nutrient uptake and assimilation [6]. Plants havedeveloped strategies to combat the deleterious effects of drought stress by increasing the activity of antioxidant enzymes for scavenging ROS, proline accumulation, modulation of the expression of stress-responsive genes, and stomatal closure [10]. Proline is an osmoprotectant that accumulates in plants under abiotic stresses [1].
Several papers reported an augmentation in NO levels in plants under drought stress, which is likely to help plant mechanisms to mitigate the negative effects of water deficit [6,10,11]. NO increases the activities of antioxidant enzymes such as catalase (CAT), superoxide dismutase (SOD), ascorbate peroxidase (APX), glutathione reductase (GPX), and peroxidase (POD) [6]. CAT is found in plant peroxisomes, an organelle with active ROS metabolism [12,13]. SOD catalyzes the dismutation of O2− to H2O2 and O2, while CAT, APX and GPX scavenge H2O2 and other peroxides [12,13].
NO acts also as a signaling molecule in the modulation of stomatal movement. Many studies have shown that NO is an important player together with H2O2 and Ca2+ in abscisic acid-induced stomatal closure minimizing plant transpiration [1]. However, at high concentrations, NO constitutively S-nitrosylates the open stomata 1 (OST1) protein kinase, which negatively regulates abscisic acid signaling and results in stomatal opening [14]. Thus, the mechanisms by which NO controls the stomatal movement remain to be completely elucidated.
Applications of NO donors in plants under drought conditions
The NO donors sodium nitroprusside (SNP) and potassium nitrite (PN) at 150, 200, and 250 µM concentrations were applied on grass cultivation (Poa pratensis, Lolium pereme, and Cytonodon dactylon) under drought stress (with irrigation intervals of 3, 5, 7, and 9 days) [7]. Both NO donors enhanced the activity of antioxidant enzymes, in a concentration dependent manner. Indeed, application of 200 µM of SNP or PN led to maximal activity of SOD, POD, CAT and APX, in investigated species under 7 or 9 days of water deficit stress [7]. The same NO donor, SNP (50-250 µM) was applied on wheat (Triticum aestivum) leaves under drought stress [4]. The NO treatment elevated APX and CAT activities and efficiently suppressed lipid peroxidation in plants under drought. Malondialdehyde (MDA) is a cytotoxic product of lipid peroxidation, and it is considered as an indicator of oxidative damage induced by ROS generation [15]. Accumulation of MDA and H2O2 was observed in dehydrated wheat leaves, which indicates ROS formation and oxidative damages. After 3 h of dehydration, the MDA level increased by 37%, whereas application of SNP brought an MDA increase by only 11% over the control level. Drought decreased CAT activity, while application of 50, 100, and 250 µM of SNP increased the enzyme activity by 35, 25 and 42%, respectively [4]. Similarly, sunflower (Helianthus annuus) plants under drought stress were treated with SNP (1, 10, and 100 µM) [8]. The water stress enhanced MDA and proline levels, while reduced POD activity. SNP treatment on water-stressed sunflower plants increased POD activity, relative water content (RWC), and proline concentration, and decreased MDAlevel. In contrast, sunflower plants under water deficit and no SNP treatment resulted in about 231% increment of MDA content in comparison with well-watered plants (control group). Moreover a suppression of 35% of MDA content in the plant leaves was reported upon foliar application of 10 µM SNP compared with plants under drought stress in the absence of SNP treatment [8]. These results indicate that low micro-molar concentrations of SNP are able to alleviate negative effects of plants under water deficit.
Fan and Liu [9] reported the effects of application of SNP and the nitric oxide synthase (NOS) inhibitor NG-nitro-L-arginine-methyl ester (L-NAME) on drought tolerance of Poncirus trifoliate. As expected an increase in the endogenous NO levels was observed upon SNP treatment, while L-NAME reduced it in plants with or without drought stress. Upon dehydration and SNP application, leaves showed lower ROS generation, enhanced activities of antioxidant enzymes, decreased electrolyte leakage, lower water loss, and smaller stomatal apertures, in comparison with the control group. Drought decreased the water content in stressed plants, which may lead to cellular dehydration and plant death. The application of SNP reduced stomatal apertures, in comparison with the control group (plant not treated with SNP). In fact, SNP reduced by 45% the stomatal apertures in seedlings compared to the control, while administration of L-NAME increased by 15% stomatal aperture. In addition, SNP treatment increased total chlorophyll content in seedlings [9]. Therefore, SNP treatment alleviated drought stress in seedlings by increasing chlorophyll content and controlling stomatal apertures.
The same research group evaluated the protective effects of SNP (50 µM) on the tube seedlings of Dendrobium huoshanense treated with 10% polyethylene glycol (PEG-6000) to mimic drought stress [11]. SNP treatment increased RWC and decreased MDA level by 25%, and upon 7-days of SNP administration, the activities of CAT, POD, and SOD increased by 29.84, 33.3, and 29.26%, respectively. Interestingly, water deficit might induce genome-wide changes in DNA methylation status. Demethylation ratio of methylated sites increased upon plant treatment with 50 µM SNP, suggesting that exogenous NO may trigger the expression of some genes in response to drought stress [11]. Indeed, large scale transcriptomic analyses have identified a high number of NO-responsive genes, including stress-related transcripts and genes coding for antioxidant enzymes [16,17,18]. However, a genomic scale analysis of NO-mediated gene expression during drought stress is still lacking.
In a similar manner, SNP (150 µM) increased RWC and decreased ion leakage in two turfgrass species (creeping bentgrass and tall fescue) under drought condition [5]. SNP-sprayed on both turfgrass species enhanced proline and chlorophyll levels of water deficit plants, compared to control plants. In addition, NO application rescued the activities of SOD and APX [5]. Arasimowicz-Jelonek et al. [19] reported the use of the NO-selective fluorophore, DAF-2DA, on SNP-treated cucumber (Cucumis sativus cv. Dar) seedling roots. Drought stress increased endogenous NO production in cells of root tips and at the surrounding zone, upon 5 and 10 h of water deficit (mild stress). In contrast, severe water deficit (17 h) yielded intensive NO production, especially above the elongation zone, whereas the NO scavenger cPTIO blocked NO detection by DAF-2DA. In the same study [19], under severe drought stress, administration of exogenous NO donors (SNP or S-nitrosoglutathione, GSNO, both at 100 µM) decreased lipoxygenase (LOX) activity, which in turn led to alleviation of lipid peroxidation and water deficit-induced membrane permeability. Thus, the authors suggested that increase in the endogenous NO production is a defense mechanism for plants to cope with tissue dehydration to mitigate the severe water deficit in roots of cucumber seedlings [19]. Moreover, exogenous NO application significantly reduced the LOX activity, which is assigned to the terminal reaction between NO and the enzyme-bound lipid peroxyl radical [19].
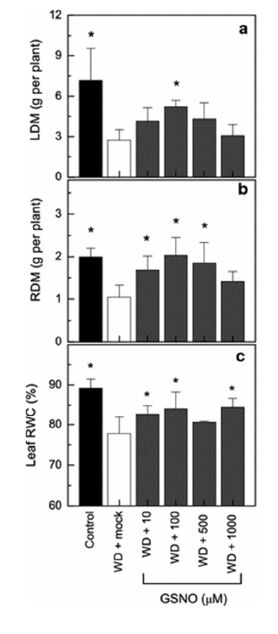
Recently, Silveira et al. [20] reported the beneficial effects due to the application of the NO donor S-nitrosoglutathione (GSNO) (10-1000 µM) in alleviating the deleterious effects of drought in sugarcane (Saccharum spp.) plants by improving photosynthesis and root growth. GSNO belongs to the class of S-nitrosothiols, which are widely employed in several biomedical applications, and less explored in agriculture applications [21,22,23]. Application of sprayed GSNO (at different concentrations) in sugarcane leaves enhanced RWC, leaf and root dry matter under water deficit, in comparison with well-watered plants. In addition, GSNO-treatment increased photochemical activity and leaf gas exchange parameters, in comparison to plants under water deficit in the absence of GSNO treatment (mock-plants) [20]. Figure 1a and b shows that water deficit (WD) decreased root (−47%) and leaf (−62%) dry matter in sugarcane. In addition, Figure 1c demonstrates a reduction in 13% of leaf RWC in plants under drought stress compared to well-watered sugarcane. Overall, sugarcane under water deficit and treated with 100 µM GSNO display similar leaf and root dry matter and leaf RWC to well-watered plants (Figure 1). Interestingly, plants under drought stress and treated with GSNO displayed a protective effect that was maintained even after 11 days of the last NO donor application, indicating a long-last protective effect. Furthermore, GSNO treatment raised total S-nitrosothiol content, suggesting a long-term role of the NO donor in the mediation of plant responses to water deficit stress. As an S-nitrosothiol, GSNO is involved in S-nitrosylation of specific cysteine residues of proteins, a post-translational modification (PTM) that affects the activity of proteins [20].
Another class of NO donor, diethylenetriamine/NO adduct (DETA/NO), was applied to maize (Zea mays) seedlings under water deficit [24]. Application of DETA/NO (200 µM) on roots and leaves of maize seedlings, treated with L-NAME, reversed the negative effects of the NOS inhibitor on APX activity and glycine betaine (GB) content. The accumulation of GB in the cytosol of plants is a consequence of plant combating osmotic stress, since GB is related to the plant tolerance to abiotic stress. Maize seedlings treated with L-NAME resulted in an increase of 68 and 134% of H2O2 levels, in roots and leaves, respectively, compared to untreated control plants. However, combined administration of 2 mM of L-NAME and 200 µM of DETA/NO effective removed the negative effects of NOS inhibition on lipid peroxidation [24].
Zhang et al. [25] demonstrated the potential of SNP in improving drought tolerance of apple rootstocks (Malus spp.). Indeed, application of 300 µM of SNP decreased ion leakage, lipid peroxidation, ROS generation, accumulation of soluble proteins and MDA, while increased SOD activity in M. hupehensis and M. sieversii under drought stress. In contrast, plants treated with the NO scavenger (cPTIO) demonstrated increased deleterious effects caused by drought stress. Similarly, SNP alleviated leaf dehydration of drought-stressed plants, whereas cPTIO inhibited this alleviation [25].
Finally, Ziogas et al. [26] elegantly performed a proteomic approach to investigate the S-nitrosylated proteins in citrus leaves under drought stress and treated with SNP or NaHS (a H2S donor). Along with NO, H2S has been considered an important signaling molecule to enhance plant acclimation to abiotic stress. The authors demonstrated that citrus plants could acclimate to subsequent drought stress, as evaluated by chlorophyll content, ion leakage, photosynthetic performance, lipid peroxidation, along with phenotypic observations after SNP and NaHS pre-treatments. Both SNP and NaHS primed citrus plants against water deficit via PTMs. In fact, the NO and H2S donors significantly decreased the levels of tyrosine nitration similar to the values found to unstressed control roots. The results indicated that SNP modulates the plant response to drought stress by controlling the level of nitrosative stress. S-nitrosylation results in changes in protein activity and interaction, therefore the distribution of S-nitrosoproteome is important to understand the biological processes that lead to plant acclimation to stress situations. In this direction, the authors identified 25 S-nitrosylated proteins in leaves, most of them associated with photosynthesis suggesting that the photosynthetic system is targeted by NO donors in S-nitrosylation pathway upon drought stress. Therefore, SNP and NaHS play a key role in plant acclimation to drought stress, through mechanism that involves a specific proteome reprogramming [26]. NO donors have been also shown to enhance drought tolerance of Antiaris toxicaria seeds by increasing the antioxidant protein S-nitrosylation levels and reducing H2O2 accumulation [27]. More proteomics studies are necessary to further investigate the target proteins directly involved in plant defense to drought stress under NO treatment.
3. Salinity and NO
Salt stress is considered one of the major factors that compromise the agricultural production, in particular the sustainable agriculture [28,29,30,31]. Indeed, salinity reduces growth and biomass yield, decreasing chlorophyll content and RWC [32,33]. Salinity increases carotenoid content and electrolyte leakage, enhancing the levels of osmolytes in plants, H2O2, and MDA [32]. Under salinity stress, there is an increase in the level of ROS, consequently, an important adaptive strategy of plants to cope with salinity is the activation of antioxidant plant defense system to minimize oxidative damage [15,34,32]. Therefore, in plant defense against salinity the activities of antioxidant enzymes, such as GPX, APX, CAT, POD, and SOD, are increased [32].
Plants have developed the following mechanisms to sense and survive in high salinity environment (in special with excess of Na+): (i) control of ion uptake by roots and their transport into leaves; (ii) selective accumulation of ions; (iii) compartmentalization of ions at cellular levels; (iv) changes in photosynthetic pathways; (v) induction of plant hormones; (vi) induction of antioxidant enzymes [34]. For plant survival under salinity, the control of ion uptake and transport is crucial. This can be explained by considering that plant exposed to high content of salts are subjected to accumulation of Na+ and Cl- ions, creating ionic toxicity, disturbing mineral homeostasis, and impairing plant development [35]. Hence, soil salinity is one of the major threats to plant growth due to the induction of the ROS production, which damages membrane lipids, nucleic acid, and proteins [29,35].
Due to its chemical nature, the highly diffusible NO is an important signaling molecule, which plays key roles in several processes in plant, including adaptation and growth of plants under salinity stress conditions [32,34]. Indeed, increased NO production (and its derivatives) is reported for plants that undergo long stress conditions [36]. Salinity is known to affect plant metabolism by enhancing the synthesis of NO, among other signaling molecules such as salicylic acid and Ca2+, and those molecules are important to ensure plant plasticity and acclimation to challenging environmental conditions [36]. NO is able to relax the plant cell wall and enhance membrane fluidity, inducing cell expansion and consequently plant growth [32]. Moreover, NO increases plant cell osmotic pressure optimizing the cytoplasmatic viscosity. In plants under salinity conditions, the RWC is affected mainly by the higher NaCl concentration, decreasing water uptake and causing the damage of root system. Supplementation of NO is capable to maintain normal levels of RWC in plants under salinity, enhancing plant tolerance to salinity [29,32].
ROS are intimately linked to salinity. ROS are not only byproducts of aerobic metabolism, but also key players in plant defense and cellular signaling [37]. The deleterious effects of ROS can be suppressed/decreased by NO, which enhances the antioxidant enzyme activities, regulating the expression of several stress-responsive genes under salinity stress, decreasing the rates of O2− formation in the mitochondria, and hence impairing lipid peroxidation [35].
Applications of NO donors in plants under salinity stress conditions
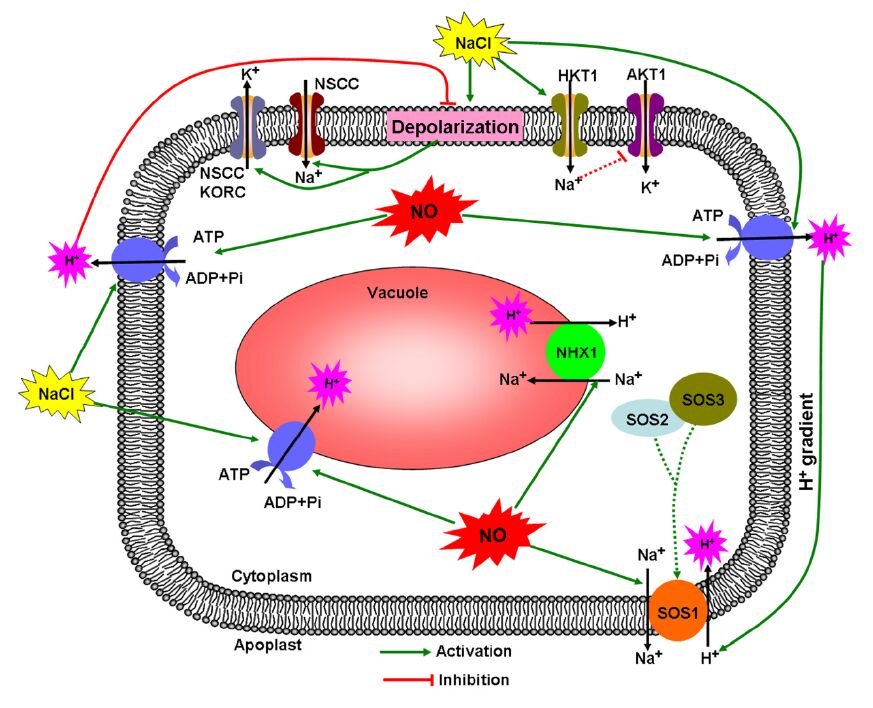
Salinity leads to accumulation of toxic ions (Na+ and Cl−) in various parts of the plant, while reduces the content of essential mineral nutrients (Ca, K, N, and P) [38]. Ion homeostasis is essential for plant surviving under salinity stress [39]. Several papers report that administration of low molecular weight NO donors improves plant ability to equilibrate ion homeostasis, under high salinity conditions (reviewed by Poor et al.) [40]. The NO donor SNP at 100 µM significantly increased K+ and decreased Na+ levels in Kanadelia obovata, a mangrove species [41]. The expression of important proteins related to the ionic balance, plasma membrane (PM) H+-ATPase and vacuolar Na+/H+ antiporter, was increased upon plant treatment with SNP, as evidenced by western-blot analysis. Figure 2 shows the schematic representation of K+/Na+ balance mediated by NO in plants under salinity stress condition. Initially, the enhanced H+ extrusion by H+-ATPase yields the inhibition of NaCl-induced plasma membrane depolarization, impairing K+ efflux by the depolarization-activated channels (NSCCS and KORCs). In the next step, the increased H+ pumping might sustain H+ gradient resulting in the extrusion of Na+ out of the cytosol through Na+/H+ antiporter (SOS1) across the plasma membrane. Exogenous NO is able to directly activate the Na+/H+ antiporter system leading to the efflux of Na+, maintaining cell homeostasis (Figure 2) [41].
Similarly, exogenous administration of SNP contributed to alleviate the adverse effects of salinity in maize cultivars by decreasing Na+ content, while increasing Ca2+, K+, N and P levels, maintaining the ion homeostasis of salt stressed plants [38]. In addition, SNP reduced toxic levels of MDA and H2O2, and increased the content of photosynthetic pigments in salt-stressed plants [38]. Application of 75 µM of SNP on strawberry (Fragaria ananassa) plants, for one week before the start of salinity stress, increased the K+/Na+ ratio of the plants, in comparison with non-SNP treated ones [42]. This result suggests a protective effect of the NO donor in the prevention of salinity stress condition.
Foliar administrations of SNP (0.1 mM) or/and salicylic acid (SA, 0.1 mM), a plant hormone, on cotton (Gossypium hirsutum) seedlings under high salinity were investigated [43]. Combined therapeutic applications of SNP and SA alleviated the inhibition of H+-ATPase in plasma membrane caused by NaCl, enhanced photosynthesis and transpiration rates, decreased H2O2 accumulation, and increased the activities of antioxidant enzymes, which decreased ROS generation in cotton seedlings under high NaCl condition [43].
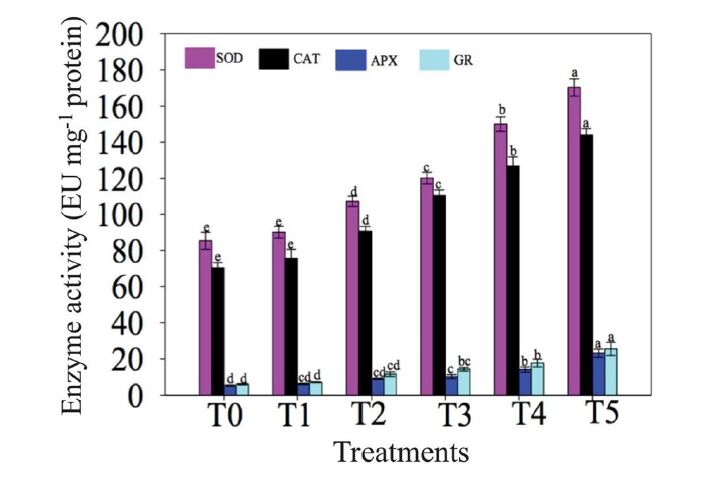
Recently, the NO donor S-nitroso-N-acetylpenicillamine (SNAP), which belongs to the class of S-nitrosothiols, was applied on chickpea (Cicer arietinum) plants under salt stress condition caused by 100 µM of NaCl [32]. Application of 50 µM of SNAP to salinized chickpea increased plant growth parameters, photosynthetic pigment and osmolytes contents, and leaf RWC. SNAP also increased the activities of the antioxidant enzymes SOD, CAT, APX, and glutathione reductase (GR) in leaves of chickpea plants under NaCl stress (Figure 3). Indeed, increased enzymatic activities for SOD, CAT, APX and GR were found in chickpea after 100 mM NaCl and 50 µM SNAP treatments (T5) compared with chickpea treated only with 100 mM NaCl (T4 treatment) (Figure 3) [32].
Therefore, the results revealed that SNAP application protects chickpea plants to salinity-induced oxidative damage by increasing the activities of antioxidant enzymes, which is responsible for plant growth and development under high salt content. In addition, SNAP increased the photosynthetic pigment contents in chickpea plants under NaCl stress, by avoiding the destruction of chlorophyll pigments, and decreased MDA and H2O2 contents, impairing electrolyte leakage [32].
In a similar manner, the NO donor SNP (100 µM) alleviated the oxidative stress in leaves of a salt-stressed mangrove species, Aegiceras corniculatum, by increasing the content of antioxidant molecules such as GSH and polyphenols, and photosynthetic pigments, and by reducing H2O2 and MDA contents and consequently, lipid peroxidation [15]. The administration of 100 µM of SNP increased GSH and polyphenol contents by 15.6 and 52.1%, respectively, compared to plants exposed to 350 mM NaCl treatment. Polyphenols are important molecules to efficiently scavenger ROS under abiotic stress conditions, leading to the inactivation of lipid free radicals and preventing the decomposition of hydroperoxides into free radicals [15].
Du et al. [33] demonstrated that the application of NO gas in NaCl-treated spinach (Spinacia oleracea) plants significantly increased the contents of several antioxidant molecules (GSH, ascorbate, polyphenols, flavonoids, proline), and the activities of antioxidant enzymes (SOD, CAT, and POD). It should be noted that the protective effects of NO in plants under salinity stress conditions can be achieved by either the application of NO donors or by NO gas. Moreover, NO administration enhanced the quality of the vegetables, since elevated levels of GSH, polyphenols, flavonoids and ascorbate is desirable for health requirements [33].
The NO donor diethylenetriamine (DETA/NO) was applied on long-term salt stressed soybean plants [28]. The plants were stressed over 16 days upon 80 mM of NaCl, which drastically decreased the biomass of roots, shoots and nodules of soybean (Glycine max). Long-term salt stress resulted in 49% decrease in the root weight of soybean, in comparison with control plants (non-NaCl treated plants), whereas combined application of NaCl with DETA/NO decreased root weight by only 16%. Overall, DETA/NO alleviated the reduction of shoot, root and nodule weights of NaCl-stressed soybean plants [28]. In a similar manner, the addition of SNP in NaCl (150 mM) solution attenuated the salt stress effect on cucumber seed germination, in a dose-dependent manner [44]. The optimal dose of SNP was 50 µM, which accelerated seed germination and promoted fresh weight increase of germinating seeds. Moreover, SNP increased the activities of antioxidant enzymes and decreased the MDA content. In fact, the activity of SOD increased 1.38-fold due SNP treatment under NaCl stress, in comparison with the NaCl treatment alone [44]. The same research group reported that the application of SNP (100 µM) enhanced salt tolerance in cucumber seedlings by modulating free polyamine levels, which are low molecular weight aliphatic amines that regulate plant growth and development [34]. After 8 days of salt stress, the levels of polyamines were significantly reduced in comparison with the control group. Administration of SNP decreased the polyamine accumulation in the leaves of NaCl-treated plants. The authors stated that NO generated from SNP enhanced NaCl tolerance in cucumber seedlings by modulating the biosynthesis of polyamines [34].
Recently, Mostofa et al. [45] demonstrated that NO also modulates H2O2 and SA-induced salt tolerance in rice (Oryza sativa) seedlings, by reducing ROS generation and by increasing antioxidant defense and methylglyoxal (MG) detoxification. MG is a cytotoxic compound formed during lipid, carbohydrate and amino acid metabolisms [46]. Since MG concentrations can reach a lethal level upon severe abiotic stress [47], plants possess a detoxification process, the glyoxalase system, to protect cells from toxicity. Indeed, glyoxalase II activity increased by 15% in NaCl-treated seedlings, in comparison with the control group. Pre-treatment of plants with SA and H2O2 before exposure to high salinity caused an additional increase in glyoxylase II activity. In addition, the authors elegantly demonstrated that application of a NO scavenger (hemoglobin) in combination with H2O2 and SA pretreatment abolished all the beneficial effects of H2O2 and SA. Seedlings pretreated with H2O2 and SA increased endogenous NO production, which reduced ROS generation. Elimination of NO by the addition of hemoglobin subsequently damaged the seedlings, even in the presence of H2O2 and SA, indicating that the salt stress protective effect is due to the presence of NO [45]. Similarly, Gomes et al. [48] have previously demonstrated that the crosstalk among SA, NO and H2O2 in the acclimation of tomato (Solanum lycopersicum) plants to high salinity.
SNP at a concentration of 150 µM was sprayed on leaves of soybean seedlings for 2 days at 24 h intervals, followed by the addition of 200 mM of NaCl [49]. Sprayed SNP increased RWC, total chlorophyll levels and the plant hormone abscisic acid (ABA) content. Water balance was achieved by lowering stomatal conductance. The increased ABA content by SNP was related to the induction of glutathione-S-transferase (GTSs) activity by exogenous NO administration [49]. Taken together, administration of exogenous NO donors, especially SNP, has an important effect in plant acclimation under salinity stress, mainly by increasing the activities of antioxidant enzymes and reducing ROS generation.
Recently, we demonstrated that NO-releasing nanoparticles alleviate the negative effects of salt stress in maize plants [50]. Although NO-releasing nanoparticles are extensively explored in biomedical applications, and the nanotechnology is a useful tool in agriculture, the combination of NO donors and nanoparticles had not been applied in agriculture. In this direction, to our best knowledge, our paper is the first publication to describe the positive impacts of NO-releasing nanoparticles in plants under salinity stress [50]. The low molecular weight NO donor, S-nitroso-mercaptosuccinic acid (S-nitroso-MSA) was encapsulated (encapsulation efficiency of 91%) in chitosan/tripolyphosphate nanoparticles (CS NPs). Chitosan is a biodegradable and biocompatible polysaccharide used in drug delivery system for biomedical applications. The obtained nanoparticles have spherical shape, low nanoparticle dispersion, and average hydrodynamic size of 39 nm. The encapsulation of the NO donor (S-nitroso-MSA) in CS NPs promoted a sustained NO release profile, by following the Fickian diffusion mechanism. Salt-stressed maize plants were treated with encapsulated or free S-nitroso-MSA (at 50 or 100 µM concentrations). Administration of NO-releasing CS NPs increased the leaf content of S-nitrosothiols, in comparison with free S-nitroso-MSA. Furthermore, encapsulated S-nitroso-MSA significantly alleviated the deleterious effects of salt stress, compared to free S-nitroso-MSA, in photosystem II activity, chlorophyll content and growth of the plants. A lower dose of the NO donor was more effective than a higher dose, upon the encapsulation of the NO donor. Taking together, these results demonstrated the effective positive impacts of NO-releasing nanoparticles in plants under salinity stress, by improving plant growth at lower NO concentrations compared to plant treatment with free NO donor [50]. In this sense, more studies based on the administration of NO-releasing nanomaterials in plants under abiotic stress represent a promising approach to be further investigated.
4. Metal toxicity and NO
The contamination of the environment by metals/metalloids (hereafter called metals) has been increasing in last decades due to anthropogenic activities, such as rapid industrialization, intensive agriculture and mining [51,52]. In addition to the direct input of metallic pollutants to soil and water, practices leading to soil acidity increase the availability of toxic forms of abundant elements in the soil solution, as occur for aluminum [53]. Some metals (like copper, manganese, nickel and zinc) act as essential micronutrients for plant growth, but their excess in the soil and accumulation in the tissues results in toxicity to plants. Other metals (like aluminum, arsenic, cadmium and lead) do not have any known biological function in plants, being toxic at very low levels [51,52].
The negative effects of the accumulation of diverse metals in plants include decrease of photosynthesis and other metabolic processes, altered water and nutrient balances, leaf chlorosis and reduced growth, ultimately leading to plant death [51,54]. Metal toxicity is usually associated with the induction of oxidative stress. Redox active metals participate directly of the formation of ROS through Fenton and Haber-Weiss reactions, whereas other metals induce oxidative stress indirectly by affecting the antioxidant system and ROS-producing enzymes [51]. Other mechanisms of metal toxicity involve the competition with nutrient cations for absorption, displacement of essential metals from biomolecules and interaction with sulfhydryl groups leading to protein inactivation [51,52].
Metal chelation by thiol (GSH, phytochelatins, metallothioneins) and non-thiol (amino acids, organic acids) compounds is an important mechanism of tolerance to metal stress, since it maintains low levels of free metals in the cytosol [55]. The induction of enzymatic and non-enzymatic antioxidant mechanisms also plays an important role in the plant response to metal toxicity [52,56,57].Additional mechanisms for tolerance to metal stress include the modulation of the pH in the rizosphere, immobilization of metals in plant cell wall and sequestration in the vacuole [58,59].
Several studies have demonstrated the alleviation of metal toxicity in plants by the application exogenous NO donors [60]. This beneficial effect of exogenous NO is usually related to a prevention of oxidative stress by the direct scavenging of ROS or activation of antioxidant enzymes [61]. However, the role of endogenously synthesized NO in plant response to metal stress is still under debate [60]. For example, few hours after cadmium (Cd) treatment, NO production was induced in roots of Arabidopsis thaliana and barley (Hordeum vulgare) [62,63], whereas decreased NO levels were observed in rice (Oryza sativa) and Medicago truncatula roots after 24 and 48 h of Cd exposure, respectively [64,65]. A depression of NO synthesis was also detected in pea (Pisum sativum) roots during long term exposure to Cd [66,67]. NO production by plants treated with Cd has been shown to contribute to metal-induced root growth inhibition in A. thaliana and barley plants [62,63]. Increased endogenous NO contents, together with H2O2 accumulation, were also associated with zinc (Zn)-induced inhibition of root growth [68]. Differently, assays with soybean seedlings treated with the NO scavenger cPTIO showed that endogenous NO mediates the induction of genes involved in the response to short-term Cd stress [69].Moreover, NO-deficient plants have been shown to be more severely affected by copper (Cu) toxicity, indicating the importance of endogenous NO in response to metal stress [70,71].
These apparently conflicting results may be explained by the Janus face of NO. Depending on the concentration, cellular localization and temporal distribution of NO, this molecule may stimulate either death pathway or survival signaling of plant cells under metal stress [60,61]. For example, in wheat plants, an early NO burst in root tips 3 h after exposure to aluminum (Al) was associated with higher induction of antioxidant mechanisms and tolerance to this metal, while sensitivity to Al was related to the production of extremely high NO levels after 12 h of exposure [72]. In A. thaliana seedlings, NO intensified Cu sensitivity under mild stress, but it promoted better viability when plants were exposed to severe Cu excess by preventing ROS accumulation [73]. Thus, it was suggested that the beneficial or deleterious effects of endogenous NO on plants exposed to Cu excess depends on the strength of metal stress and the interaction with ROS [73].
Applications of NO donors in plants under metal toxicity conditions
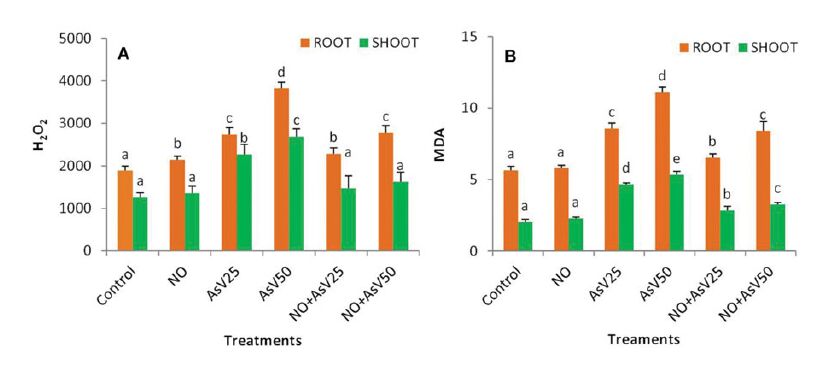
The NO donor SNP has been applied to plants submitted to arsenic (As) stress. In a study with hydroponically-grown rice plants [74], the treatment with 25 or 50 µM arsenate (Na2HAsO4: AsV) led to an augment of root and shoot H2O2 and MDA contents, but the levels of both oxidative stress biomarkers were decreased when AsV-treated plants were supplemented with 100 µM SNP (Figure 4). In addition to reduce oxidative stress, exogenous NO supplementation prevented the deleterious effects of AsV in plant growth through the reduction of AsV accumulation in the tissues, the reversion of the AsV-induced iron deficiency and the modulation of thiol metabolism [74]. The exogenous NO supply by SNP (100 µM) also alleviated the toxic effects of AsV on photosynthetic parameters of Luffa acutangula seedlings, as well as it induced the antioxidant response [75]. The involvement of direct ROS scavenging by NO in the alleviation of AsV toxicity has been also shown in rice plants treated with 50 µM SNP [75].
Many studies have demonstrated the protective effect of exogenous NO in plants treated with cadmium (Cd), a common environmental contaminant that is phytotoxic even at low levels. The incubation of rice seeds with 30 µM SNP alleviated the Cd-induced inhibition of germination and seedling growth by improving the antioxidant capacity (induction of SOD, APX, POD and CAT activities) and reducing H2O2 and MDA contents [61]. The protective effect of the NO donor was also related to a reduced Cd accumulation in the seedlings [61]. In addition to the prevention of oxidative stress, the treatment of Cd-stressed barley seedlings with SNP (250 µM) increased chlorophyll content and net photosynthesis and ameliorated Cd-induced damage to leaf and root ultrastructure [76]. In hydroponics-grown white clover (Trifolium repens) plants, SNP (50 µM) prevented the growth inhibition caused by Cd stress and stimulated enzymatic and non-enzymatic ROS-scavenging mechanisms, as well as it modulated hormonal homeostasis and promoted the H+-ATPase activity and the absorption of essential nutrients [77]. In a study with Cd-stressed Boehmeria nivea plants, the alleviation of oxidative stress by 100 µM SNP was associated with an increased S-nitrosylation level [78]. When a higher dosage of SNP (400 µM) was applied to the hydroponic solution, the protective effect of the NO donor was weakened due to the intensive consumption of GSH [78]. In one of the few studies which used an NO donor other than SNP, the exogenous NO supply by SNAP (30 µM) was also proved to be effective in the protection of rice seedlings to Cd stress [79].
Cooper (Cu) and zinc (Zn) are essential micronutrients that are phytotoxic when applied in high level and SNP treatment has been proven to be efficient for reducing their toxicity. In wheat and bean (Phaseolus vulgaris) seedlings exposed to Zn excess, 100 µM SNP maintained suitable Zn concentrations in the plants and modulated free/total SH levels, GSH content and SOD activity [80]. A lower SNP concentration (10 µM) was enough for ameliorating the phytotoxic effects of Zn nanoparticles in rice seedlings [81]. In the case of Cu excess, the application of 200 µM SNP alleviated Cu-induced growth inhibition and chlorophyll content decrease in barley seedlings [71]. The NO donor protected barley plants from oxidative damage by enhancing the activity of antioxidant enzymes (SOD, GR, CAT and APX) [71]. In A. thaliana seedlings, the treatment with a low concentration of SNP (10 µM) prevented the loss of cell viability in root tips induced by Cu excess [73]. In the case of Cu-treated Catharanthus roseus plants, 50 µM SNP induced secondary metabolism, regulated nutrient absorption and reestablished H+-ATPase activity for protection against Cu toxicity [82].
The effect of exogenous NO application in the protection of plants exposed to toxic levels of other metals has been demonstrated. The treatment with 250 µM SNP alleviated aluminum-induced root growth inhibition, callose production and oxidative stress in wheat plants [72]. In lead (Pb)-treated wheat plants, 100 µM SNP reduced the accumulation of oxidative stress biomarkers and partially ameliorated Pb toxicity [83]. Evidence for the amelioration of metal toxicity by SNP treatment has been also observed in Matricaria chamomilla plants treated with manganese [84] and Brassica napus leaves under nickel stress [85].
5. Extreme temperatures and NO
Climate extremes including very low or high temperatures are known to affect plant growth and physiology, with an important impact on agricultural yield and natural ecosystem functioning [86,87]. Both cold and heat stresses are associated with alterations in protein function and membrane fluidity, ROS overproduction and cell damage, leading to impaired plant growth and ultimately to death [86,88,89,90]. In the case of plants exposed to high temperatures, there is an increase of membrane fluidity accompanied by changes in the structure and function of organelles, as well as protein denaturation and misfolding [86,89]. Photosynthesis is particularly sensitive to high temperatures, resulting in a carbon imbalance of heat-stressed plants [91,92]. Low temperatures also negatively affect membrane processes, but by increasing membrane rigidity [88,90]. The dehydration of cells and tissues and rupture of cell membranes may additionally occur as water freezes [93].
The tolerance to extreme temperatures includes changes in membrane lipid composition and the induction of antioxidant mechanisms [88,89]. Cold-induced tolerance also involves the accumulation of compatible osmolytes with cryoprotective activity, such as proline, glycine betaine and raffinose [88]. The synthesis of heat-shock proteins, which act as chaperones preserving the stability of other intracellular proteins, is crucial for the tolerance to heat stress [89].
Several studies have shown an increase of NO production by plants of different species in response to low temperatures [94]. The involvement of NO in cold tolerance has been further demonstrated by studies with NO-deficient mutants or NO synthesis inhibitors. The nia1 nia2 nitrate reductase-deficient mutant of A. thaliana has been shown to present reduced NO synthesis and impaired cold acclimation response [95,96]. Moreover, the treatment with mammalian NO synthase inhibitors negatively affected the NO production and the protection response of Chorispora bungeana cells against chilling [97]. The NO produced during cold stress is associated with increased accumulation of the osmoprotectant proline, the production of lipid signaling molecules and the induction of antioxidant machinery [95,96,97,98]. These NO actions may involve the regulation of gene expression and the modulation of cold-responsive proteins through PTM [94,99].
NO production has been also shown to be induced in heat-stressed plant cells [100], as well as NO-deficient mutants have been shown to present a higher sensitivity to high temperature conditions [101]. NO is involved in signaling pathways which results in the accumulation of heat shock proteins and antioxidant enzymes during heat stress [101,102]. However, the disruption of NO homeostasis caused by NO overproduction or SNOs accumulation may be associated with increased heat sensitivity, due to the establishment of nitrosative stress and the inhibition of proteins by tyrosine nitration [103,104].
Applications of NO donors in plants under extreme temperature conditions
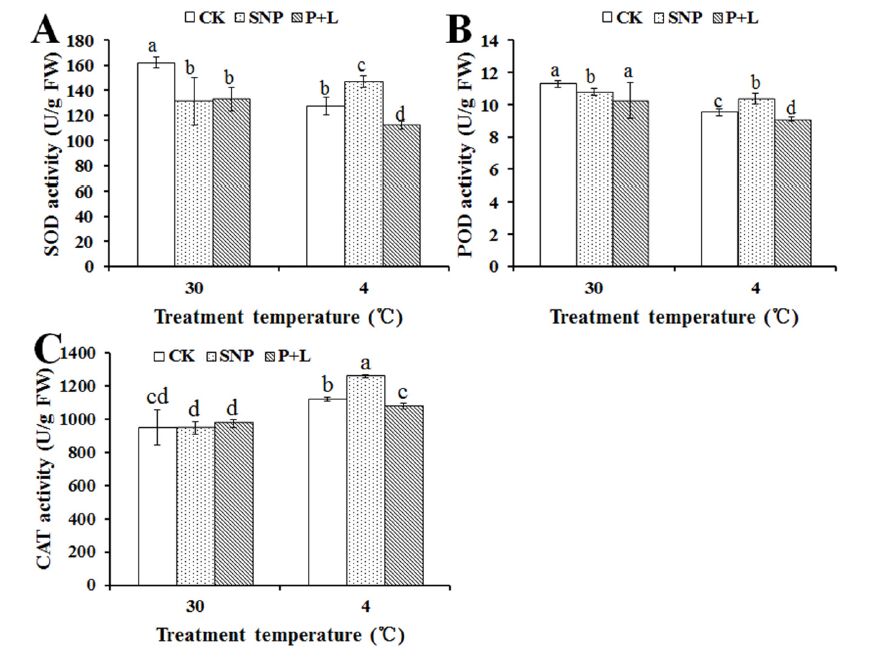
One of the major causes of injuries in plants under extreme temperatures is the increased production of ROS [86,88,89,90]. Many studies have demonstrated the effect of NO donors in preventing the oxidative stress in plants submitted to cold stress. In a study with bermudagrass (Cynodon dactylon) plants growing at 4 °C [105], the treatment with 100 µM SNP induced the activity of SOD, POD and CAT (Figure 5). In contrast, the application of the NO scavenger PTIO and the NOS inhibitor L-NAME resulted in lower activities of the antioxidant enzymes in cold-stressed plants (Figure 5). The protective effect of the NO donor in bermudagrass plants exposed to low temperature was also related to the maintenance of the stability of cell membrane, the expression of cold-responsive genes and the recovery of photosystem II activity [105]. Spraying wheat leaves with 100 µM SNP enhanced SOD, CAT and POX activities and decreased the H2O2, O2− and MDA contents of seedlings exposed to chilling conditions [106]. Similarly, the application of SNP (0.1 and 1 µM) to leaves improved chilling tolerance in maize plants by inducing SOD and POX activities [107]. In this study, SNP was also shown to increase the apoplastic ice nucleation activity in maize leaves, which indicates a decrease in freezing temperature [107]. In addition to leaves, NO has been shown to ameliorate the deleterious effects of cold stress in other plant organs or structures. Pre-soaking of seeds with 100 µM SNP stimulated the germination of wheat seeds and seedling growth under low temperature, which was associated with a promotion of energy metabolism and the induction of antioxidant response [108]. In apricot (Prunus armenica) flower buds, the treatment with SNP at 1 and 2 mM reduced the oxidative stress and alleviated freezing injury [109]. Moreover, the fumigation with NO gas has been shown to reduce the chilling injury symptoms of many fruits stored at low temperatures, by suppressing ethylene formation and inducing the antioxidative defense systems [110,111,112,113].
The ameliorating effect of NO donors in the oxidative stress caused by high temperatures has been also reported in several plant species. Heat stress induced lipid peroxidation and ion leakage in reed (Phragmites communis) calluses, which were alleviated by the application of 200 µM SNP [100]. In two wheat cultivars, the treatments with SNP at 50 µM and especially at 100 µM induced the activity of diverse antioxidant enzymes in seedlings cultivated under continuous high temperature, resulting in a decrease of lipid peroxidation and in an increase of cell membrane stability and cell viability [102]. In a study with maize seedlings, pretreatment with SNP concentrations ranging from 50 to 200 µM alleviated the heat-induced increases of MDA content and electrolyte leakage, thus improving the heat tolerance of maize seedlings [114]. Additionally, SNP induced the synthesis of H2S by heat-stressed maize seedlings, a molecule also involved in the response to abiotic stresses [114]. Plants of Chrysanthemum morifulium sprayed with SNP (200 µM) over three days presented higher SOD, POD, CAT and APX activities and a lower increase in leaf MDA content when exposed to 45 °C [115]. Additionally, SNP partially alleviated the heat-induced decrease of net photosynthesis and photosynthetic pigment content [115]. Similarly, the pre-treatment of tall fescue (Festuca arundinacea) leaves with SNP (100 µM) resulted in lower levels ROS and improved the photosynthetic electron transport under heat stress [116].
NO is also involved in the promotion of the synthesis of compatible solutes in plants exposed to extreme temperatures. The treatment of Medicago falcata leaflets with SNP (100 µM) induced the expression of the gene MIPS1 and the accumulation of myo-inositol, which was associated with tolerance to cold and freezing [117]. In leaves of winter wheat, SNP (75 and 150 µM) enhanced the synthesis of fructans, carbohydrates that protect plants against cold stress through membrane stabilization [118]. In A. thaliana seedlings, treatment with SNP (50 and 200 µM) induced the expression of P5CS1 (a gene coding for a key enzyme in the proline synthesis pathway) with concomitant accumulation of the osmoprotectant proline, as well as the same NO donor at 200 µM increased the survival rate of the seedlings exposed to freezing temperatures [95]. The effect of SNP (1 and 2 mM) in promoting proline accumulation was also observed in apricot flowers exposed to freezing temperatures [109]. The upregulation of P5CS gene by SNP (1 µM) was also detected in rice seedlings, whose survival after exposition to 50 °C was increased by the pre-treatment with the NO donor [119]. In the same study, it was shown that SNP induced the expression of a gene encoding for a heat shock protein (HSP26), as well as it enhanced the activity of antioxidant enzymes [119].
6. How do NO donors protect plants from abiotic stresses?
The literature presented and discussed in this review highlights that application of micromolar concentrations of NO donors have protective effects in alleviating plant abiotic stresses caused by salinity, drought, metal toxicity and extreme temperatures. The main protective action of NO is the induction of plant antioxidative defense system by enhancing the enzymatic activities of antioxidant enzymes (SOD, CAT, APX, POD, and GR) [31,38]. NO prevents oxidative damage in stressed plants by regulating redox homeostasis, increasing the enzymatic activities of H2O2-scavenging enzymes, by decreasing the levels of ROS, by scavenging O2∙−, and free radicals (R∙) [29]. NO is a potent inhibitor of the propagation phase of lipid peroxidation, scavenging peroxyl radical (LOO∙). Lipid peroxidation is recognized as a deleterious component in oxidative stress process during abiotic stresses [2]. In addition, NO protects DNA cleavage upon production of hydroxyl radical (∙OH) in plants under abiotic stresses [31]. At low concentrations, NO reacts with superoxide leading to the formation of peroxynitrite (ONOO-), according to equation 1:
Therefore, toxic O2∙− is scavenged by NO, and the yielding peroxynitrite, which can be further scavenged by other cellular reactions. Peroxynitrite is extremely toxic in animals cells, however, at low levels, peroxynitrite is not harmful to plant cells [1,29].
In addition to the actions of NO in avoiding oxidative damages caused by ROS, NO also has protective effects on plants upon regulation of key proteins by means of their PTM (S-nitrosylation, metal-nitrosylation and tyrosine nitration) [30,36,120]. In particular, S-nitrosylation (the addition of a NO+ group on cysteine, Cys, residues of thiol-containing proteins) is a signaling pathway in which a redox reversible PTM occurs in a spatial and temporal specificity modifying protein activity [31]. PTM is recognized as important mechanism to plant defense allowing plant acclimation during the stress [1,26,31]. For example, the S-nitrosylation of NADPH oxidase and glycolate oxidase has been shown to inhibit the ROS production by these enzymes [121,122]. CAT and APX have been also detected as targets of S-nitrosylation. While CAT is inhibited by this PTM [122], contrasting results regarding the activation or inhibition of APX by S-nitrosylation have been obtained [123]. S-nitrosylation-mediated activation of APX was associated with salt stress tolerance in pea plants [124], while the inactivation of APX by this PTM resulted in the programmed death of tobacco cells under heat stress [125].
The increase of antioxidant protein S-nitrosylation levels has been associated with reduced H2O2 accumulation and therefore decreased protein oxidation in recalcitrant seeds [27]. It is assumed that protein S-nitrosylation (a reversible and transient modification) may protect proteins by preventing the irreversible loss of protein functions due to protein oxidation (irreversible protein modification). Thus, S-nitrosylation would lock protein structure in a state which the S-nitrosylated proteins are insensitive to the attack of ROS [31,123].
NO may also react with transition metal centers in proteins (such as iron in heme groups and Fe/S centers) forming metal-nitrosyl complexes [126]. This PTM regulates the activity of enzymes such as cytochrome P450 and aconitase [127,128]. The formation of heme-nitrosyl complex in cytochrome c oxidase decreases plant mitochondrial respiration and contributes to the acclimation to hypoxic stress [129]. Tyrosine nitration of proteins (the addition of a nitro, NO2, group to one or two carbons of the aromatic ring of tyrosine residues) is a recognized biomarker of systemic nitro-oxidative stress, inducing protein structural and functions changes, which may contribute to changes in cell homeostasis [31,130]. Protein Tyr nitration has been established as a biomarker of "nitro-oxidative stress", leading plant metabolism to a pro-oxidant status that disrupts NO signaling and induces protein structural and functional changes, some of which contribute to altered cell and tissue homeostasis [131].
In addition to PTM, the modulation of gene expression and the interaction with plant hormones underlie the functions of NO in plants under abiotic stresses. NO may regulate the expression of genes involved in a broad range of processes in plants, including those related to the response to abiotic stresses, such as genes coding for antioxidant enzymes [18]. NO may also modulate the homeostasis and signal transduction of different plant hormones, as well these molecules may influence NO levels in plant cells [3].
Figure 6 summarizes a general schematic representation of the main defense mechanisms upon application of NO donors in plants under abiotic stresses.
Plants are able to develop enhanced ability to resist to abiotic stresses, upon treatment with chemical compounds, a phenomenon known as priming. In this sense, abiotic stress conditions may prime plants, via chemical reactions including S-nitrosylation, altering protein activity [31]. Therefore, plants are able to develop some stress "memory" (also known as stress imprinting), upon a first exposition to a stress condition, leading to acclimation to a later abiotic stress condition. Consequently, stressed plants can induce defense responses to several stresses, through priming process, with minimal energy demanding. Several papers suggest that NO and its derivatives play key roles in priming process in stresses plants [132]. The detailed characterization of NO and its role in priming phenomenal in plants need to be further investigated.
7. Concluding remarks and perspectives
This review highlights that exogenous application of low molecular weight NO donors has positive effects on plant acclimation to abiotic stress (salinity, drought, metal toxicity and extreme temperatures). Similar to other biological systems [23], the effects of NO in plants depend on its concentration, flux, duration, and location [29]. High NO concentrations may cause deleterious effects such as inhibition of root and shoot growth, membrane damage, damages in the photosynthetic electron transport, and DNA fragmentation [133]. On the other hand, at lower concentrations, NO contributes to plant development, growth, and protection [21]. Therefore, the control of the amount of NO delivery to plants under abiotic stress needs to be well-established. Usually, exogenous chemical agents, including NO donors, at low concentrations can be effective, suggesting low cost of treatment. In addition, the deleterious effects of uncontrolled/higher concentrations of NO donors (as well as other chemical agents) might be avoided by using smart technological approaches [134]. In this sense, the combination of nanotechnology and NO donors is an effective strategy to carry and delivery therapeutic amounts of NO, with minimum side effects [22,23].Although very often in biomedical application, NO-releasing nanoparticles have not been further explored in agriculture [21]. To our best knowledge, we reported for the first time that administration of NO-releasing nanoparticles alleviates the deleterious effect of salinity on maize plants [50]. This approach might find important applications in the acclimation of plants under abiotic stresses by controlling the rates and the amounts of NO release from the encapsulated NO donors into the nanomaterials to the plants. This promising strategy needs to be further investigated.
As discussed in this review, SNP is the most commonly used low molecular weight NO donor in agriculture. However, caution must be taken by using this NO donor, since, in addition to NO, SNP may release cyanide and iron ions as toxic byproducts [135]. In contrast, S-nitrosothiols (RSNOs), such as S-nitrosoglutathione, are natural reservoir of NO in biological systems, releasing free NO and yielding the oxidized thiol, oxidized glutathione (in the case of GSNO), according to equation 2:
Thus, RSNOs are promising NO donors for agriculture applications since nontoxic sub products are formed [20,50].
In this context, by selecting a NO donor in agriculture applications an important consideration is to clarify the complete mechanism of NO release from the donor, including the potential toxicity and bioactivities of byproducts [1]. In addition, the possible interactions of the NO donor with the surrounding environment needs to be addressed, since the NO release profile from the NO-donor is dependent on the environmental conditions, such as light, temperature, chemical nature of the tissue, etc.
In summary, this review highlights important and recent publications demonstrating that exogenous applications of NO donors in plants under abiotic stress conditions have beneficial effects for plant survival in a challenging environment. In addition to the application of NO donors, the manipulation of endogenous NO levels by the use of genetically modified plants may be an alternative that can be explored in future researches. More studies are still necessary to further understand the molecular mechanisms of NO signaling, in particular, to clarify the role of PTMs of important proteins and NO interactions with other signaling molecules. In this regards, this review aims to open new avenue in this promising and exciting field.
Acknowledgments
This work was supported by FAPESP (Proc. 2016/10347-6), the Brazilian Network on Nanotoxicology (Grant number: 552120/2011-1) (MCTI/CNPq), the Laboratory of Nanostructure Synthesis and Biosystem Interactions-NANOBIOSS (MCTI) (Grant number: 402280-2013).
Conflict of Interest
There is no conflict of interest.









 DownLoad:
DownLoad: