In this paper we describe a coupled model for flow and microbial growth as well as nutrient utilization. These processes occur within and outside the biofilm phase formed by the microbes. The primary challenge is to address the volume constraint of maximum cell density but also to allow some microbial presence outside the contiguous biofilm phase. Our model derives from the continuum analogues of the mechanism of cell shoving introduced in discrete biomass models, and in particular from the models exploiting singular diffusivity as well as from models of variational inequality type which impose explicit constraints. We blend these approaches and propose a new idea to adapt the magnitude of the diffusivity automatically so as to ensure the volume constraint without affecting the reactions; this construction can be implemented in many variants without deteriorating the overall efficiency. The second challenge is to account for the flow and transport in the bulk fluid phase adjacent to the biofilm phase. We use the Brinkman flow model with a spatially variable permeability depending on biomass amount. The fluid flow allows some advection of the nutrient within the biofilm phase as well as for the flow even when the pores are close to being plugged up. Our entire model is monolithic and computationally robust even in complex pore-scale geometries, and extends to multiple species. We provide illustrations of our model and of related approaches. The results of the model can be easily post—processed to provide Darcy scale properties of the porous medium, e.g., one can predict how the permeability changes depending on the biomass growth in many realistic scenarios.
Citation: Choah Shin, Azhar Alhammali, Lisa Bigler, Naren Vohra, Malgorzata Peszynska. Coupled flow and biomass-nutrient growth at pore-scale with permeable biofilm, adaptive singularity and multiple species[J]. Mathematical Biosciences and Engineering, 2021, 18(3): 2097-2149. doi: 10.3934/mbe.2021108
| [1] | Blessing O. Emerenini, Stefanie Sonner, Hermann J. Eberl . Mathematical analysis of a quorum sensing induced biofilm dispersal model and numerical simulation of hollowing effects. Mathematical Biosciences and Engineering, 2017, 14(3): 625-653. doi: 10.3934/mbe.2017036 |
| [2] | Fazal Abbas, Rangarajan Sudarsan, Hermann J. Eberl . Longtime behavior of one-dimensional biofilm models with shear dependent detachment rates. Mathematical Biosciences and Engineering, 2012, 9(2): 215-239. doi: 10.3934/mbe.2012.9.215 |
| [3] | Yousef Rohanizadegan, Stefanie Sonner, Hermann J. Eberl . Discrete attachment to a cellulolytic biofilm modeled by an Itô stochastic differential equation. Mathematical Biosciences and Engineering, 2020, 17(3): 2236-2271. doi: 10.3934/mbe.2020119 |
| [4] | Mudassar Imran, Hal L. Smith . A model of optimal dosing of antibiotic treatment in biofilm. Mathematical Biosciences and Engineering, 2014, 11(3): 547-571. doi: 10.3934/mbe.2014.11.547 |
| [5] | Alma Mašić, Hermann J. Eberl . On optimization of substrate removal in a bioreactor with wall attached and suspended bacteria. Mathematical Biosciences and Engineering, 2014, 11(5): 1139-1166. doi: 10.3934/mbe.2014.11.1139 |
| [6] | Sambasiva Rao Katuri, Rajesh Khanna . Kinetic growth model for hairy root cultures. Mathematical Biosciences and Engineering, 2019, 16(2): 553-571. doi: 10.3934/mbe.2019027 |
| [7] | Nikodem J. Poplawski, Abbas Shirinifard, Maciej Swat, James A. Glazier . Simulation of single-species bacterial-biofilm growth using the Glazier-Graner-Hogeweg model and the CompuCell3D modeling environment. Mathematical Biosciences and Engineering, 2008, 5(2): 355-388. doi: 10.3934/mbe.2008.5.355 |
| [8] | Xiong Li, Hao Wang . A stoichiometrically derived algal growth model and its global analysis. Mathematical Biosciences and Engineering, 2010, 7(4): 825-836. doi: 10.3934/mbe.2010.7.825 |
| [9] | Wenzhang Huang . Weakly coupled traveling waves for a model of growth and competition in a flow reactor. Mathematical Biosciences and Engineering, 2006, 3(1): 79-87. doi: 10.3934/mbe.2006.3.79 |
| [10] | Vincenzo Luongo, Maria Rosaria Mattei, Luigi Frunzo, Berardino D'Acunto, Kunal Gupta, Shankararaman Chellam, Nick Cogan . A transient biological fouling model for constant flux microfiltration. Mathematical Biosciences and Engineering, 2023, 20(1): 1274-1296. doi: 10.3934/mbe.2023058 |
In this paper we describe a coupled model for flow and microbial growth as well as nutrient utilization. These processes occur within and outside the biofilm phase formed by the microbes. The primary challenge is to address the volume constraint of maximum cell density but also to allow some microbial presence outside the contiguous biofilm phase. Our model derives from the continuum analogues of the mechanism of cell shoving introduced in discrete biomass models, and in particular from the models exploiting singular diffusivity as well as from models of variational inequality type which impose explicit constraints. We blend these approaches and propose a new idea to adapt the magnitude of the diffusivity automatically so as to ensure the volume constraint without affecting the reactions; this construction can be implemented in many variants without deteriorating the overall efficiency. The second challenge is to account for the flow and transport in the bulk fluid phase adjacent to the biofilm phase. We use the Brinkman flow model with a spatially variable permeability depending on biomass amount. The fluid flow allows some advection of the nutrient within the biofilm phase as well as for the flow even when the pores are close to being plugged up. Our entire model is monolithic and computationally robust even in complex pore-scale geometries, and extends to multiple species. We provide illustrations of our model and of related approaches. The results of the model can be easily post—processed to provide Darcy scale properties of the porous medium, e.g., one can predict how the permeability changes depending on the biomass growth in many realistic scenarios.
The main purpose of this paper is to present a new model for biofilm-nutrient-flow dynamics in porous media at pore-scale. These complex coupled processes are traditionally described in a staggered way, with biomass-nutrient model and the flow model solved in disparate spatial domains and at distinct time steps. An alternative is to use various model reductions or model approximations based on assumptions on the leading process. In contrast, our model is of continuum type, and is a coupled system of partial differential equations with which we treat the processes monolithically.
The study of microbial communities which are omnipresent in natural and engineered systems is important for a variety of applications including biofouling and bioremediation in engineering applications, and in medicine including tissue engineering field, e.g., in artificial regeneration of articular chondrocytes [1]. In particular, of central interest is the study of biofilms. Biofilms are complex structures made of gel-like polymeric substance called EPS, and of microbial cells which produce this EPS. Given access to sufficient nutrient resources, the microbes multiply until their maximum density is achieved, after which the biofilm domain expands through the interface with the surrounding liquid. The liquid and biofilm are separated by a sharp or diffuse interface, and together they form a fluid with very complex properties, such as those studied by phase field models or the Flory-Huggins theory of mixtures [2,3,4,5] or volume averaging [6]. The hypothesized purpose of biofilms in their various agammaegative, architectural and protective types is to promote the growth and protect the cells, e.g., from the environmental conditions such as desiccation, high temperature and competing microbes [2,7,8]. We refer to review articles [2,7,9] for an overview of modeling challenges, more references, and applications in human engineering systems, e.g., in selective plugging [10,11,12,13].
Next, as stated in [13], "the overwhelming majority of bacteria live in porous environments" such as "soil-like materials, industrial filters" and medical devices [14]. Thus there is significant interest but also new challenges in studying biofilm at pore-scale supported by experiments and imaging [11,12,15,16,17]. First, the length scales typical for the processes at the pore-scale involve micrometers [μm] rather than [mm]; the latter are considered, e.g., in the detailed studies in bulk fluid [2,4,18]. Second, in addition to the interface between the bulk fluid and the biofilm, at the pore-scale one also has to handle the interface between the grains and the fluids. In fact, the character itself of the biofilm-nutrient dynamics coupled to the flow may be distinct from that in an unconfined setting. In particular, [14] points out the importance and influence of "streamers" (long filamentous structures) on the clogging of pore-scale in contrast to the surface attached biofilm.
The challenges of disparate length and time scales as well as of the coupled nature of flow motivate our new model development. We aim for a monolithic adaptive and robust model in its ability to be extended and simulated. We improve the model we proposed in [17] by blending its biofilm-nutrient dynamics part with a modified version of singular diffusivity model in [19,20] extended to a novel model—adaptive treatment of the free boundary arising at the interface between the biofilm and the surrounding bulk fluid. We also improve the flow model in [17] by applying a variant of Brinkman flow model to the entire domain rather than a staggered-in-time treatment. These extensions allow (a) more complex spreading and growth mechanisms than those we proposed in [17], (b) permeable biofilm phase, and an easy generalization to (c) multiple microbial species to study scenarios of competition and cooperation. Our computational model has a fairly simple monolithic structure with which we can run simulations of representative elementary volumes in close to real time. We are able to simulate a variety of practical scenarios in complex geometries by only changing the parameters rather than an entire model construction. In particular, our model does not explicitly track the domains where biomass is present, and does not require that it is contiguous, thus it can account for the presence of streamers which seem to be important [14].
In the end, our model can be used as part of a multiscale study with which we upscale the flow properties affected by biofilm growth to Darcy scale. The modeling precision we adopt seems adequate for the Reynolds and Peclet numbers typically encountered in porous media, but our model has some limitations. While it is more complex than those in [16,21], it studies fewer details of the bio-gel than those considered in bulk-flow with phase-field models in [2,3,4,22]. While our model can simulate many interesting aspects of competition and cooperation between multiple species, it is less flexible than individual based [23] or other discrete models. Finally, we do not explicitly address important modeling components such as quorum sensing, detachment, cell death, abiotic cell decay, metabolic lag and so on, however we see these as possible straightforward additions which leave substantial flexibility to a modeller.
To provide context for our work we overview the results from literature and illustrate the new features with numerical simulations. We do not provide numerical analysis of the approximate model but we refer to the work on its somewhat simplified form in [24,25].
The outline of the paper is as follows. We provide notation and define the basic model elements in Section 2; this material is well known and fairly standard. Our new model discussed in Section 3 is an adaptive nonsingular version of singular diffusivity models [19,20] blended with variational inequality models [17]. The heterogeneous Brinkman flow model is introduced and illustrated in Section 4, with results of coupled flow and nutrient dynamics given in Section 5. Extensions of the model to multiple species are described in Section 6. We summarize in Section 7. Section 8 contains substantial supporting material and in particular additional details on numerical schemes as well as an extensive discussion of literature models including (ⅰ) discrete, (ⅱ) phase-field, and (ⅲ) osmotic-pressure approaches compared to our new model.
In this section we set up notation for the rest of the paper. Most of the material is fairly standard. We consider a region Ω⊂Rd,t>0, and x=(xi)di=1∈Ω with its Euclidean norm |x|. Partial derivatives are denoted by ∂t,∂i,∇=(∂1,…∂d), for time t and x. We also use δJδu for the differential of a functional J:V→R, but denote by dfdu the derivative of a function f:R→R. The symbol χS denotes the characteristic function of set S. For functional spaces, we use the Lebesgue spaces Lp(Ω) with the norm ||⋅||p and the Sobolev spaces Hk(Ω). We denote V=H1(Ω), and use, e.g., L∞(L2) to denote the space L∞(0,T;L2(Ω)), with similar notation for other Lebesgue and Sobolev spaces.
In this paper we follow closely the notation from [20] blended with that from [26] and from the porous media community, i.e., [21,27].
We consider several microbial species each with concentration Bk together denoted by B=(Bk)k, with their sum B=∑kBk. The species include the solid phase called EPS. We will use a given fixed number B∗>0 to denote the maximum concentration of biomass, and some 0<B∗<B∗, where B∈[B∗,B∗] indicates what we call a "mature" biofilm. In this paper we choose B∗=0.9B∗. The precise definition and units of Bk,B∗, B∗ will be given later.
We also consider nutrient and metabolic product species N=(Nl)l. For simplicity in this paper we consider only one N=N, which can be oxygen, carbon, glucose, ammonia, or more generically some substrate. The diffusivity of N depends on the nutrient type.
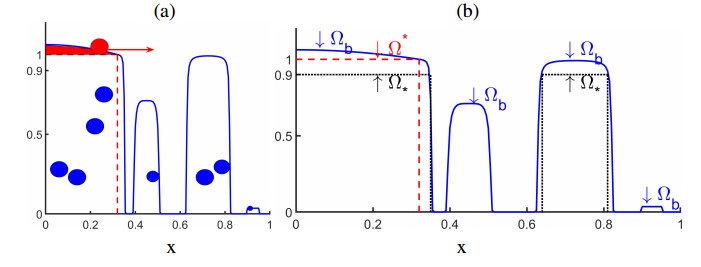
We will consider the domain Ω and identify the different regions in which the flow and the reaction processes have different properties; see Figure 1 for illustration.
| Ω0(t)={x:B(x,t)=0},no microbes present; bulk fluid | (2.1a) |
| Ωb(t)={x:B(x,t)>0},microbes present | (2.1b) |
| Ω∗(t)={x:B∗≤B(x,t)≤B∗},mature biofilm | (2.1c) |
| Ω∗(t)={x:B(x,t)≥B∗},B exceeds the maximum | (2.1d) |
| Ω∗b(t)=Ω∗∪Ω∗,biofilm domain. | (2.1e) |

The definition of regions such as Ωb varies in the literature, where it is used for convenience of notation, or in reference to the properties observed in experiments. In particular, in [17] we used x-ray micro-CT tomography imaging to identify the region Ω∗ as the opaque region from which the contrast agent barium is excluded. With some models, Ωb is assumed contiguous, i.e., simply connected, and only its boundary is tracked, but with other models including our model not so. In some literature the region Ω∗ is called the boundary layer in which much growth occurs and which propagates the fastest.
In addition, some authors [28,18,13,9] distinguish
| Ωa(t)={x∈Ωb:N(x,t)>N∗},enough nutrient for active metabolism | (2.1f) |
as the "metabolically active" region with N∗ denoting the minimum amount of nutrient needed for species maintenance. Typically we set N∗≈O(10−2kN) with respect to the Monod half-life constant kN defined below.
When working with flow coupled to biomass-nutrient dynamics, we need to define the flow domains. At the pore-scale, we consider an open bounded pore-scale domain Ω=Ωr∪Ωn∪Γrn (rock, no-rock, wall interface). We allow Ωr=∅ and assume that the volume |Ωn|>0; see Figure 2. We recognize a fixed rock wall boundary Γrn, and consider the flow of water in Ωn, and Ωr≠∅. Generally we denote by Ωw the bulk fluid domain, which in our model may or may not coincide with the domain Ω0 with no microbes present. For the flow, we denote by u the velocity and by p the fluid pressure. We use Γin and Γout to denote the inlet and outlet boundaries, respectively.

The many different models we cite in this paper come each with a different system of variables and units, and use different data, e.g., for rate constants in their examples. For example, the units for B,N range from [kg/m3], [g/cm3], [ppm], or [g/L], or are non-dimensional, as in [20,29]. In this paper we follow closely the non-dimensional notation from [20] blended whenever possible with that from the porous media community, i.e., [21,26]. The different symbols we define and typical parameter values are listed in Table 1.
| Symbol | Description | Value/Units |
| k | Index of microbial species 1≤k≤K. | |
| ρk | Dry mass density of species k | ∼1.1[g/cm3] |
| ρ∗B | Maximum mass density of biomass | 24×103[g/cm3] |
| θk | Volume fraction of species k | [−] |
| Bk | Concentration of species k, defined by Eq (2.3) | [−] |
| B∗ | Maximum total concentration of biomass | 1[−] |
| B∗ | Threshold for mature biofilm | 0.9B∗[−] |
| N | Concentration of the nutrient relative to ρ∗B | [−]∼O(10−4)[kg/m3]/ρ∗B |
| kN | Monod half-life [can vary by factor 10s, s≈6; see [30]] | same as N |
| κ | Specific substrate uptake rate | ∼O(10s)[1/h], s∈[−2,0] |
| κk, κB | Growth constant incorporating yield coefficient | ∼O(1)[−] |
| dm | Molecular diffusivity | 6.84[mm2] |
| dk,dB | Diffusivity of species k | ∼O(1)[mm2] |
| dN | Diffusivity of N; see (2.13) | ∼O(1)[mm2] |
| T | Time scale | ∼O(101)[h] |
| μ | Viscosity | 8.9×10−4[Pa s] |
| u | Velocity in the Brinkman flow model | ∼O(10−1)[mm/h] |
| p | Pressure in the Brinkman flow model | [Pa] |
| kb | Resistance term in Brinkman flow model | [mm2] |
| kΩ | Darcy permeability | ∼O(10−7)[mm2] |
| γ(t) | Biofilm interface location in 1d models, γ(t)=|Ω∗(t)| | ∼O(10−2)[mm] |
| a(t) | Width of the active layer in 1d models, a(t)=|Ωa(t)| | ∼O(10−2)[mm] |
| v | Local shoving velocity in osmotic pressure models | ∼O(10−5)[mm/h] |
| h,τ | Spatial and time discretization parameters | ∼O(1)[μm],O(1)[h] |
We denote by ρw the water density, and by μ its viscosity. The water occupying Ω or, more precisely Ωn, has several suspended microbial components and several dissolved nutrient components. The mass and volume contribution of the microbial species compared to that of water is significant; their presence also changes the properties of the phase, and we address this later. The nutrients are not accounted for in mass balances.
We consider K microbial species, each with (dry mass) density ρk. If EPS is modeled, we denote it as the species number k=K. Typically ρk≈const=ρ0B for all live species, and ρEPS≈1/2ρ0B, but for simplicity we ignore this distinction here. At the microscopic level at any point x of the small volume ω(x) surrounding x we have either water, or microbial species present, thus it makes sense to define the volume occupied by the water w and by the species k by ωk, with ω=⋃kωk. Now we set the volume fractions
| θk=|ωk||ω|, for k=w,1,…,K, with ∑k=w,1…Kθk=1. |
The volume fractions θk(x,t), the total volume fraction θB(x,t)=∑Kk=1θk=1−θw of biomass, and the microbial mass density ρB(x,t)=ρ0BθB(x,t) vary in time and space. (In some literature θw is fixed; e.g., see θw≈0.9 [21], and thus expresses the "porosity" of biofilm). Since the cells have finite volume, there is a maximum density of cells allowed, e.g., it is given in [20] as ρ∗B=24×103[g/cm3]. 0≤ρB(x,t)≤ρ∗B. Equivalently θB≤ρ∗Bρ0B, which relates to the minimum possible porosity of biofilm. The total mass M(t) of fluids and microbial mass in a region Ω at time t is given by
| M(t)=∫Ω(∑k=w,1,…Kθkρk)dx=ρw∫Ωθw(x,t)dx+∫ΩρB(x,t)dx. | (2.2) |
Finally, as in [20] we set
| Bk=θkρkρ∗B=θkρ0Bρ∗B, | (2.3) |
which are non-dimensional, and we obtain for the sum B of all species
| B=∑kBk≤B∗=1. | (2.4) |
We consider nutrient concentration N. We follow [20] where N is nondimensional, with its unit involving the mass density of nutrient per ρ∗B. We recall the well known Monod functions, with the nutrient consumption m(N) given by the Monod expression
| m(N)=κNN+kN. | (2.5) |
The constant kN is called Monod half-life (in the same units as N), and κ is the specific substrate uptake rate, with a typical value =O([1/h]). The reaction rates to be used in mass balance equations for non-EPS species k=1,…,K−1 involve the growth and utilization rates
| rgrowthk(Bk,N)=κkBkm(N)=κkBkκNN+kN, | (2.6a) |
| ruse,kN(Bk,N)=−Bkm(N)=−BkκNN+kN, | (2.6b) |
with typical values κk≈0.5, typically incorporating some yield coefficient and maximum uptake rate. If K=1, or if all constants κk are identical, we set κk=κB.
We recall the standard underlying models. A differential equation models the growth of species Bk and consumption of nutrient N
| ddtBk=rk(B,N);t>0,Bk(0)=Bk,init, | (2.7a) |
| ddtN=rN(B,N);t>0,N(0)=Ninit. | (2.7b) |
The specific details of rk,rN for the individual species Bk in B are provided in various ways, e.g., by specifying the reaction stoichiometric coefficients as in [31]. These involve the growth rgrowthk and utilization ruseN rates defined above plus additional terms. When transport is involved, these equations are expanded to account for advection with velocity u and diffusion with diffusivities dk>0 in Bk equations and dN>0 in the nutrient equations, to be defined later
| ∂tBk+∇⋅(uBk)−∇⋅(dk∇Bk)=rk(B,N);x∈Ω,t>0, | (2.8a) |
| ∂tN+∇⋅(uN)−∇⋅(dN∇N)=rN(B,N);x∈Ω,t>0. | (2.8b) |
If K=1, we set dk=dB.
We set up initial and boundary conditions as follows. We set Neumann no-flux conditions on ∂Ω for each Bk and N. For nutrient for some cases we also allow a Dirichlet boundary ΓD⊂∂Ω through which nutrient can be supplied.
| dk∇Bk⋅ν|∂Ω=0,Bk(x,0)=Bk,init(x),x∈Ω, | (2.8c) |
| N|ΓD=Nbd,dN∇N⋅ν|∂Ω∖ΓD=0,N(x,0)=Ninit(x),x∈Ω. | (2.8d) |
Here ν is the unit outward normal to ∂Ω. The initial data is denoted by subscript init and the boundary data with subscript bd.
In general, we may allow non-smooth data, thus (2.8) is posed in the sense of distributions rather than in the classical sense. We annotate what is known about well-posedness of the models in appropriate functional spaces in Section 8.1.
We discuss now the approximation of the PDEs of the form (2.8) for simplicity only for single species K=1 and d=2. We generally follow the established notation, e.g., from [32]. The case of 1d and 3d domains can be handled analogously.
Spatial discretization. We cover Ω by a general uniform rectangular grid with size (hx,hy). Such grids are most convenient and efficient when working with voxel data from imaging as indicated in [33,34]. In fact we typically a refinement of a voxel grid, with h=hx=hy. We denote by M the overall number of degrees of freedom which for microbial species B we enumerate Bj, 1≤j≤M and collect in Bh=(Bj)j. For approximation of (2.8) we use mixed finite element method of lowest RT0 type on hexahedral grids implemented as CCFD (cell centered finite differences) which provide a natural connection to the flow solution with the MAC scheme given in Section 8.3.2 and are locally mass conservative [35].
We seek (Bh,Nh)∈RM×RM, and calculate the right hand side rB(Bh,Nh),rN(Bh,Nh) by evaluating them at the degrees of freedom of (Bh,Nh). We denote by ABh(Bh) the discrete counterpart of −∇⋅(dB(B)∇), and ABh(Bh)Bh approximates −∇⋅(dB(B)∇B). Similar notation is applied in the nutrient equation with ANh(Bh)Nh.
As typical for CCFD, we use harmonic averages to get diffusivities at the cell edges internal to Ωb; this supports mass conservation [35]. However, due to high degree of degeneracy of dB in (8.3) as B↓0, we apply arithmetic averaging to encourage diffusion towards the region Ω0.
Time discretization. We use time steps 0=t0,t1,t2,…tN=T, with uniform τ so that tn=nτ. For nonlinear terms we use time- or step- or iteration lagging. In other words, our schemes can be called semi-implicit, with variants as indicated below.
We approximate the solutions to (2.8) by operator splitting [32]; we solve the advection step explicitly with some transport method
| ~Bnh−Bn−1hτ+∇h⋅(uhBn−1h)=0. | (2.9) |
Here ∇h⋅(uhBn−1h) denotes the explicit upwind fluxes. An analogous model finds ~Nnh.
Next we solve the reaction and diffusion steps. We can solve the reaction step separately as if we were solving (2.7) itself with the initial condition ~Bnh known after the advection step
| ^Bnh−~Bnhτ=rB(~Bnh,~Nnh), | (2.10a) |
| ^Nnh−~Nnhτ=rN(~Bnh,~Nnh), | (2.10b) |
followed by the diffusion step with step-lagging of ABh,ANh
| (I+τABh(^Bnh))Bnh=^Bnh, | (2.11a) |
| (I+τANh(^Bnh))Nnh=^Nnh. | (2.11b) |
Another possibility is to solve the reaction and diffusion steps together,
| (I+τABh(~Bnh))Bnh=GB,nh=~Bnh+τrB(~Bnh,~Nnh), | (2.12a) |
| (I+τANh(~Bnh))Nnh=GN,nh=~Nnh+τrN(~Bnh,~Nnh). | (2.12b) |
Other schemes and refinements are possible; see, e.g., [32,36].
A typical domain Ω we consider has diameter L=O(10a[mm]) with a∈[−2,0], while the microbial cells have size ranging in hc∈[0.5,20][μm] [23,31]. However, typical pore sizes in meso-scale or unconsolidated porous media range in O(10s)[μm] with s∈[0,1] [37], while the grain size in glass-bead packs used for observation can range from O(10s)[μm], with s∈[1,2] [17,38,39,40]. The time scale is T=O(10[h]), and thus the time steps for realistic simulation scenarios should be on the order of at least seconds. We also aim to use discretization parameter h=O(hc) so the continuum models apply.
In this paper we do not use explicit non-dimensionalization of PDE models. Even though such a step provides useful insights and reduces dependence from a multitude of parameters to fewer, it is case dependent. Rather, our simulations are carried out with codes which use an internal self-consistent unit system.
The bio-gel is most viscous and the nutrient diffusivity is the smallest in Ω∗b inhibiting nutrient supply outside the so-called "active layer". Following [20,28,30] we define dN,w as the diffusivity of N in Ωn∖Ωb, dN,b to be its decreased value in Ωb, and RN,bw=dN,b/dN,w, with values RN,bw≈0.4 in [20], or even RN,bw=0.01 for some nutrients [28,30], with dN given
| from [28]: dN(x,t)=χΩw(x)dN,w+χΩ∗b(x)dN,b, | (2.13a) |
| from [20]: dN(x,t)=(B∗−B(x,t))dN,w+B(x,t)dN,b. | (2.13b) |
The biofilm model we propose in this paper addresses several challenges and blends ideas from literature. The main characteristic of biofilm is that it is a phase distinct from ambient fluid. In the biofilm phase the cells agammaegate, but are subject to volume constraint (2.4), which means that the region occupied by the phase grows when the cells divide and are "shoved" by their neighbors, and this in turn requires modeling of the free boundary. The spreading mechanism is accounted for in a variety of ways; see Table 2 for a summary, and Figure 1 for the basic idea. The approaches in literature handle these challenges differently, and their particular focus depends on the length scale. For example, one can make an assumption on whether the biofilm growth is nutrient-limited or diffusion-limited, and assume appropriate simplifications of (2.8). Additional challenges arise when coupling to ambient flow in porous domains. We provide extensive literature notes in Section 8.1.
| Model and reference | Scale | L | # active species | # nutrients |
| Experimental data on |Ωa|=O(10s[μm]), 1≤s≤2. | ||||
| [28,30] | interface | L=O(10[mm]) | K=1 | >1 |
| (ⅰ) Discrete (IbM, CA) and hybrid models [23,31,42,43,44,45] | ||||
| interface d=2,3 | L=O(1[mm]) | K=1 | 1 | |
| [23] | interface d=2 | L=O(1[mm]) | K=2 | >2 |
| (ⅱ) Phase field models for bio-gel mechanics, and calcite precipitation [2,3,4,5] | ||||
| d=2 | L=O(1[mm]) | K=1 | 10 | |
| (ⅲ) Osmotic pressure with advective motion of interface [21,26,46] | ||||
| [26] | interface | K>>1 | >1 | |
| [21] | pore-scale | L=O(1[μm]) | K=1+EPS | 1 |
| [46] | core-scale | L=O(0.1[mm]) | 1 | |
| (ⅳ) Singular diffusion models | ||||
| [20] | interface, 1d | K>1 | ||
| (ⅴ) Variational inequality models | ||||
| [17,25] | d=1,2,3 | L∈[10−2,1][mm] | K=1 | 1 |
| Model in this paper | any d | any L | K>1 | 1 |
Our model for biomass growth builds on (2.8). In this section we focus on one species, set K=1, and do not model the flow or advection, which are handled in the rest of the paper. The main feature we discuss now is that we apply the reaction–diffusion (2.8) in the entire domain Ω allowing for microbial mass to grow anywhere, not necessarily only within the biofilm phase. At the same time we account for agammaegation and spreading of biofilm through the interface using the degenerate and singular diffusivity dB(B), a modification of that used in [19,20,41]; these models can also be related to phase-field models; see comparisons in Section 8.1.
We pick two ad-hoc parameters α≥2 and ˉB∗>B∗ and define the diffusivity
| dB(α;B)={dB,0(B¯B∗−B)α,B≤B∗,dB,0(B∗ˉB∗−B∗)αB>B∗. | (3.1) |
Here the motility coefficient dB,0≈7×10−9[m2/ day ], which is very small (about 10−5 smaller than the molecular diffusivity dm≈2×10−4[m2/ day ]). This formula modifies dB(B) proposed in [19,20,41] to be nonsingular on [0,B∗]; see more on dB and the connection to phase-field models in Section 8.1.
We present our model in two variants: unconstrained and constrained in Section 3.1. They are compared in Section 3.2 and blended in an adaptive model presented in Section 3.3 in which the constrained model serves as an auxiliary practical algorithm. In Section 3.4 we present examples in 2d pore-scale geometry with focus on length scales.
Consider a fixed ˉB∗>B∗, and a given α. We state first the unconstrained model which we annotate with subscript ∘. Its main feature is the fact that the diffusivity dB is singular as B↑ˉB∗>B∗ and degenerate dB↓0 as B↓0, but bounded as long as B≤B∗.
| P∘:( unconstrained nonsingular )_: given α,dB(α;B) by (3.1), solve (2.8). Numerical solution: at every tn, solve (2.12) written as F∘(α;Bnh,Nnh)=0. | (3.2) |
The solution B(x,t) spreads fast as B↑ˉB∗ with the strength depending on α, and B cannot increase past ˉB∗. While the model is robust since the diffusivity dB is bounded when B≈B∗, there is no mechanism ensure that the solution B satisfies (2.4).
Introducing a constraint. In [17] we postulated a modification of (2.8) with an explicit constraint enforcing (2.4) using the operator ∂I(−∞,B∗], the subetaadient of the indicator function I(−∞,B∗] which is zero on (−∞,B∗] and equals ∞ outside this set. The operator ∂I(−∞,B∗] acts as a constraint operator which enforces that B(x,t) is in its domain, i.e., that (2.4) holds. Such models are known as parabolic variational inequalities. With additional coarsening terms these give Allen–Cahn (rather than Cahn–Hilliard) phase evolution models.
In practice ∂I(−∞,B∗](B) is replaced by a Lagrange multiplier; in a smooth phase field model it can be replaced by a penalty function. This is a well-known and well-studied construction known as variational inequality [47,48,49], and we refer, e.g., to [50] for its numerical analysis. The model reads
| ∂tB−∇⋅(dB(B)∇B)+∂I(−∞,B∗](B)=rB(B,N),x∈Ω, | (3.3a) |
| ∂tN−∇⋅(dN(B)∇N)=rN(B,N),x∈Ω. | (3.3b) |
This model guarantees that the volume constraint (2.4) holds, but it might exclude some reactions that could take place in the active layer when B≈B∗.
The model (3.3) is approximated by a scheme in which we modify (2.12a) to impose a constraint, and we solve for (Bnh,λnh,Nnh) the stationary problem
| (I+τABh(Bnh))Bnh+τλnh=GB,nh=Bnh+τrB(Bnh,Nnh), | (3.4a) |
| (I+τANh(Bnh))Nnh=GN,nh=Nnh+τrN(Bnh,Nnh). | (3.4b) |
The additional equation binding λnh and Bnh is min(B∗−Bnh,λnh)=0 or pointwise
| min(B∗−Bnj,λnj)=0,∀j. | (3.4c) |
The system (3.4) is written in residual form, and is solved with semi-smooth Newton method [51]. Due to the only piecewise-smooth character of (3.4c), the solver is expected to converge with a less-than quadratic rate. However, with the typical time steps we use in our model, the solver takes usually under 3 iterations. We refer to the finite element analysis in [24,25], with simulations testing different variants of mildly and fast growing dB(B) other than (3.1).
We summarize the constrained model annotated with the subscript ◻.
| P◻:( constrained nonsingular )_:givenα,dB(α;B) by (3.1), solve (3.3). Numerical solution: at every tn, solve (3.4) written as F◻(α;Bnh,λnh,Nnh)=0. | (3.5) |
Numerical approximations for P∘ and P◻ are quite robust; in addition, our tests in Section 8.3 indicate convergence.
Remark 1. The interpretation of the action of ∂I(−∞,B∗](B) in (3.3a) is similar but not identical to the a-priori truncation of the source term such as in the model
| ∂tB−∇⋅(dB(B)∇B)=rB(B,N)χB≤B∗,x∈Ωn. | (3.6) |
In this equation the source rBχB≤B∗ prevents the growth above B∗, and is discontinuous in B. In contrast, in (3.3a) the operator ∂I(−∞,B∗](B) acts to ensure B≤B∗ for all x. This is a subtle but important difference. In particular, an implicit solver for (3.6) generally struggles with the discontinuous character of the forcing, thereby requiring additional care. In contrast, our approach (3.4) is quite robust.
We now illustrate the main features of the nonsingular diffusivity models and sensitivity to parameters. We start with a 1d example which we call "basic".
Example 3.1. Let Ω=(0,L) model a "tube", and imagine am impermeable "wall"at x=0. The tube contains a set of microbes initially with B≈0.5B∗ in [0,0.1] close to x=0. For B, we use Neumann no-flux conditions also at x=L, and set B(x,0)=Binit(x) with Binit depending on a case. For N, we use Dirichlet condition at ΓD:x=L. We set Ninit(x)=const=Nbd=N|ΓD on ΓD relative to kN≈2×10−3. In particular, the case Nbd to be 1, 0.1,…, with the first for nutrient-rich environment, and the smallest values for a nutrient-deficient environment. We also set κB=0.44, but we vary κ=O(1) depending on the case. The data is in Tables 3 and 4.
| Parameters and units |
| L[mm], T[h], |
| dN,w=dm=6, dB,0=10−4, kN=1.18×10−3, κB=0.44, ˉB∗=1.01B∗. |
| L | T | h | τ | Binit[−] | Ninit[−] | RN,bw | κ | α | |
| (A), basic | 1 | 3 | 0.01 | 10−3 | 0.5χ[0,0.1] | 1 | 0.1 | 2 | 2 |
| (A'), more singular | 1 | 3 | 0.01 | 10−3 | 0.5χ[0,0.1] | 1 | 0.1 | 2 | 2.5 |
| (B), short domain | 0.1 | 3 | 0.01 | 10−3 | 0.5χ[0,0.01] | 1 | 0.1 | 2 | 2 |
| (C), nutrient deficient | 1 | 3 | 0.01 | 10−3 | 0.5χ[0,0.1] | 0.1 | 0.1 | 2 | 2 |
| (D), slow reaction | 1 | 3 | 0.01 | 10−3 | 0.5χ[0,0.1] | 1 | 0.1 | 1 | 2 |
| (E), easy penetration | 1 | 3 | 0.01 | 10−3 | 0.5χ[0,0.1] | 1 | 1 | 1 | 2 |
We apply both the unconstrained model (3.2) dubbed as "no λ" (without Lagrange multiplier) and (3.5) dubbed "with λ" (that is, with constraints implemented with Lagrange multiplier λ). In Figure 3 we present the profile of biomass as well as of the decaying nutrient amount at t=T.
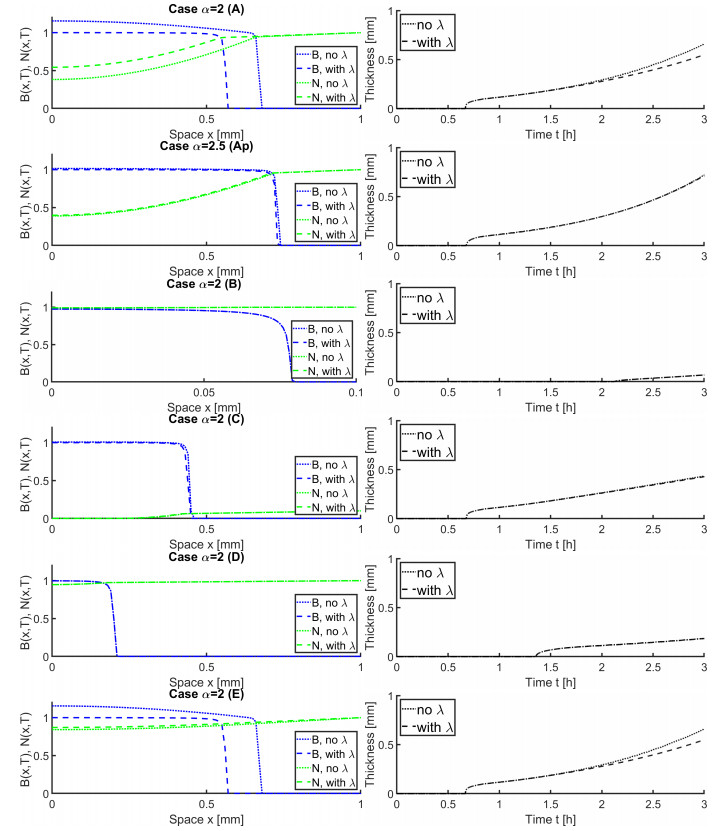
To describe the dynamics of spreading, we also plot γ(t)=|Ω∗(t)|, the thickness of biofilm domain. We see that γ(t)=0 until B(x,t) reaches and exceeds B∗.
In (A), the biomass grows until about t≈0.6 when it forms mature biofilm. After this time the biofilm domain Ω∗ primarily grows through the interface. In the nonsingular unconstrained model (3.2) B(x,t) grows and spreads but reaches above B∗; this happens because α is fixed and somewhat small. The constrained model (3.5) prevents this at the expense of cutting off the reaction in Ω∗, resulting in smaller thickness γ(t) compared to the unconstrained case. The front γ(t) is approximately equal to the thickness of Ωb, and it propagates essentially linearly in time, i.e., dγdt(t)≈const, up until about t≤T=2 when the front reaches about half of the domain and benefits from higher nutrient supply.
Next we study the dependence of the propagation of the biofilm front to parameters and to the difference between the constrained and unconstrained models. The basic case (A) is compared to cases (A', B, … E). In particular, we study the effect of α in A', the length of the domain i.e., more nutrient availability in (B), and nutrient deficiency in C. In D we consider slow reaction rate, and in E we consider effect when diffusivity dN is not altered by the presence of biofilm and thus nutrient can propagate more into Ωb. With some parameters in cases (A–E) we see that the differences between (3.2) and (3.5) are small, e.g., for large α, small κ, or small Nbd, or when L is small. The front speed is not always constant. Overall, the difference between (3.2) and (3.5) can be significant, especially in nutrient–abundant cases. We discuss the dependence of γ(t) on nutrient availability and the related reduced models in Section 8.2.
We summarize now the disadvantages of (3.2) and (3.5), and present an adaptive model which improves on both. Both models use the diffusivity model (8.3) which feature an exponent α of singularity and parameter ˉB∗. To simplify the discussion we assume that the other fixed parameter ˉB∗ in (3.1) is fixed and large enough so that B is never close to ˉB∗.
The disadvantage of unconstrained model (3.2) illustrated in Figure 3(A) is that its solutions do not satisfy a-priori the volume constraint (2.4) because biofilm does not spread fast enough (diffusivity is too small with the chosen α=2). In turn, in the same illustration we see that (2.4) is enforced as a hard constraint in (3.5), but the presence of λ≈∂I(−∞,B∗] in (3.5) limits the growth in Ω∗, thus the front γ(t) is delayed, and (3.5) carries a modeling error whose magnitude depends on the width a(t) of active layer Ωa. (We explored a(t) and this aspect later in Section 8.2).
At the same time we see that the "speed" of front propagation is ∝dB(α;B)(B−0)≤dB(α;B) which increases with α. Our Example 3.1 (A') illustrates well that with larger α=2.5 the solutions spread faster. In addition, the solutions to (3.2) and (3.5) essentially coincide, i.e., the constraint in (3.5) is not active. In other words, the continuum counterpart of the "shoving" of the microorganisms, i.e., of the front spreading, seems to be in place. However, fixing the parameter α a-priori to be large leads to the unphysical effect of the microbial mass spreading faster than it grows before it forms the mature state. The natural question therefore is which α is most appropriate. We explore this first by trial and error in the next example and eventually adaptively later.
Example 3.2. We follow Example 3.1 (A), but vary α to illustrate the dependence of thickness γ(t) of the biofilm domain on the parameter α of spreading in the nonsingular unconstrained model (3.2). We also find α(t) by trial and error at each time step to make sure the solution satisfies the volume constraint (2.4).
The solutions are shown in Figure 4 which illustrates a very strong influence of α on spreading. First, with α=4, the biomass spreads faster than it grows from the initial values Binit=0.5, thus the threshold value B∗ is not reached until t≈1.5[h] and spreading is overpredicted. With smaller α, this value is reached about t=0.6 and there is less spreading. Also, for α≤3 the fronts initially coincide for unconstrained and constrained models with more-or-less constant speed of γ(t) but about t=2 more vigorous spreading is needed to prevent constraint from being active. In this case α(t)>2 for t>2 is needed.
Main idea. These observations motivate the following. We aim to find the speed of propagation from dB(α;⋅) and the corresponding α(t) parameter adaptively "as needed" to keep B≤B∗. With this approach we eliminate the limitations of both models (3.2) and (3.5): the constraint (2.4) holds automatically for (3.2) and Lagrange multiplier in (3.5) equals 0 and does not inhibit reactions.
While seeking α(t) requires extra computational effort, the adaptive model is quite robust. Formally, at given t, we consider the problem dubbed (P∗(t)): Find α∗(t)=min{α(t): the solution (B(x,t),N(x,t)) to (3.2) satisfies (2.4)}.
In the computational model, we search for the optimal αn∗… at every time step tn, and we proceed by iteration. We seek the solution to the stationary problem (2.12a) with the dependence of the discrete diffusion matrix ABh=ABh(α;Bnh). on α made explicit. Assuming that GB,nh is known we solve
| (PB;h,n∗): find αn∗=min(α:Bnj≤B∗,∀j) where Bnh solves(I+τABh(α;Bnh))Bnh=GB,nh. | (3.7) |
Two remarks are in order. First, we do not have a proof that the algorithm we will propose for (3.7) works, but we demonstrate the idea and the algorithm in Section 3.3.1. Second, when GB,nh depends on Bnh and Nnh, we must iterate further. This iteration along with an efficient use of the constrained model are discussed later in Section 3.3.2.
Consider some g∈R and some A(α;p) with values in R and an analogue Ps∗ of (3.7)
| (Ps∗): find α∗=min{α:p≤1} where p solves A(α;p)=g, | (3.8) |
in which p replaces Bnh. Let α0≥0 and let A(α;p), α∈[α0,∞);p∈[0,∞) be a given smooth positive function strictly increasing in both variables, and such that for a fixed p>0, limα→∞A(α;p)=∞. Let also g>A(α0;0). From monotonicity of A which implies injectivity, and since g is in its range, the problem A(α;p)=g is uniquely solvable.
Example 3.3. We pick A(α;p)=pafun(p,α) where afun(p,α)=1+0.05(p1.3−p)α, and g=1.5. We illustrate the problem Ps∗ in Figure 5.
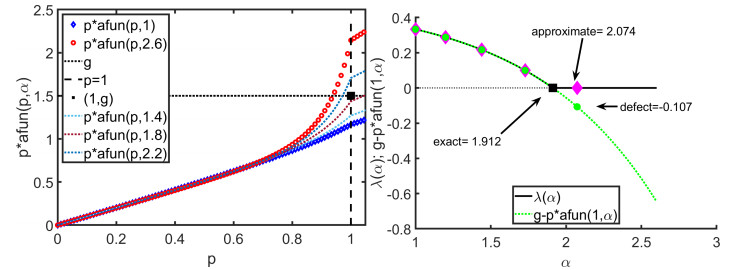
We discuss now the the algorithm to solve Ps∗. Let α,g be given and p=p(g;α) solve A(α;p)=g. From implicit function theorem and monotonicity of A we see that dpdα<0. Thus (3.8) has a solution α∗ characterized by A(α∗;1)=g. However, finding α∗ directly may not be feasible, and we proceed by iteration starting with α0. We set up an auxiliary problem for Ps∗
| Find (p,λ): A(α;p)+λ=g,min(1−p,λ)=0. | (3.9) |
Now, for a given α the nonlinear complementarity constraint in (3.9) [51] can be written out as (p,λ):p≤1,λ≥0,(1−p)λ=0 and its solution is given as λ=max(0,g−A(α;1)). Thus dλdα≤0 as visible in Figure 5, therefore increasing the guesses α(m) may eventually produce λ=0. We start with some initial guess α(1)=α0, and proceed with α(m) for m=1,… until done. In each iteration m we solve (3.9) as an auxiliary step
| Find (p(m),λ(m)): A(α(m),p(m))+λ(m)=g,min(1−p(m),λ(m))=0. | (3.10) |
If |λ(m)|<tol at some iteration m=m∗, then we are done and α∗=α(m∗). If not, we continue with a new α(m+1) = α(m)+Δα(m). We set Δα(m)=ηα(m) with η=0.2 which works well for this example. The iterates are shown in Figure 5, along with an illustration of the residual g−A(α(m∗);1), which matches λ(m) until we reach convergence. The final iterate α(m∗) overpredicts α∗. To refine the search and iterate further between α(m∗−1) and α(m∗) one can proceed by binary search (bisection) on g−A(α,p(α)) which we just bracketed at α=α(m∗−1) and α=α(m∗).
The algorithm for Ps∗ is extended next to solve the biofilm model. For the unconstrained nonsingular model (3.2) we restate the search for α as follows
| (Ph,n∗,∘):Find αn∗,∘=min{α:F∘(α;Bnh,Nnh)=0:so that Λ∘(α;Bnh)=∫Ω(B∗−Bnh(x,t))+dx≤tol}. | (3.11) |
The auxiliary scalar Λ∘(α;Bnh) measure the excess of Bnh above B∗ in the unconstrained model.
Now we find it useful to exploit the constrained nonsingular problem (3.5). Here we want to keep the Lagrange multiplier as small as possible so that the constraints are not actually active, or are active only at a few points up to some tolerance, this reactions are active. The search for the best α is thus stated as
| (Ph,n∗,◻):Find αn∗,◻=min{α:F◻(α;Bnh,λnh,Nnh)=0 so that Λn◻=∫Ωλnh(x,tn)dx≤tol}. | (3.12) |
Here the auxiliary scalar Λ◻(α;Bnh) measures the reactions inhibited due to the constraint. The quantities Λ∘ and Λ◻ for the same data are qualitatively similar but not identical due to the nonlocality mentioned earlier.
Now, each Ph,n∗,∘ and Ph,n∗,◻ can be solved by iteration similarly as proposed for (3.10). Using the common symbol Ph,n∗ for both, the following iteration tries the value α(m) and finds Λn,(m) (unified notation of Λn for Λn∘ and Λn◻ and F=0 in place of F∘=0 or F◻=0), with
| Given a guessα(m), solve for (Bn,(m)h,Nn,(m)h) so that F=0, | (3.13a) |
| Calculate Λn,(m).Check if Λn,(m)≤tol. | (3.13b) |
If Λn,(m)≤tol, we are done. Otherwise, we set the new guess α(m+1)=α(m)+Δα(m) with Δα(m) based on Λn,(m). We iterate until we have found the optimal αn,(m∗)∗ for some m=m∗.
The algorithm works quite well, but requires a few iterations. If this is not practical, one can also use an approximation (ˉPh,n◻) in which we do not iterate for αn∗, but rather use a time–lagged value guided by the previous time step Λn−1◻ obtained with the constrained model. We illustrate and compare the algorithms Ph,n∗,∘ and ˉPh,n◻ in the next example.
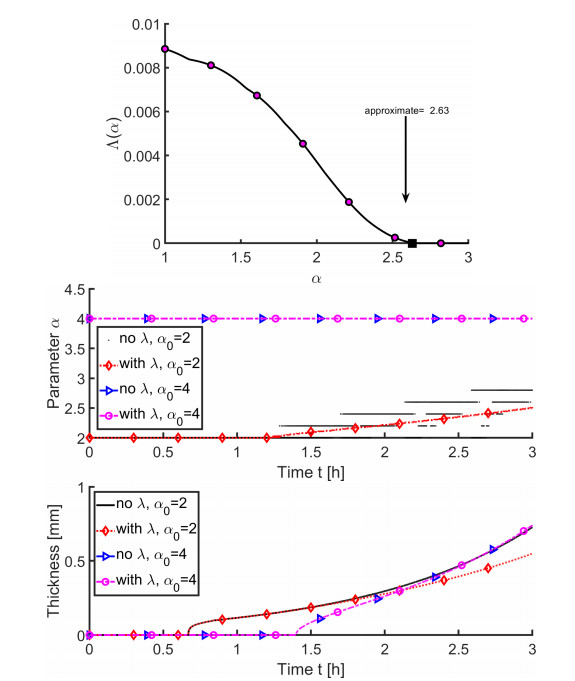
Example 3.4 (Finding αn∗ adaptively and ˉαn by time–lagging). First we construct a somewhat contrived case based on Example 3.2 with Binit=0.99 and κ=200. With these, the growth is vigorous and requires α1∗>α0=2 already in its first time step. We see that the behavior of Λ∘(α) is similar to that in the scalar case in Example 3.3 and Figure 5.
Next we revisit Example 3.2 to present the correlation between the variable α(t) and the changes in the thickness γ(t). We also compare the results from Ph,n∘ dubbed "no λ" and those for ˉPh,n◻ dubbed "with λ".
As shown in Figure 6 the values αn∗,∘ found by Ph,n∘ are not uniformly increasing in time, because with small time steps even a small α0 suffices until reactions build Bnh up locally before (2.4) is violated. This feature explains the success of the very inexpensive algorithm ˉPh,n◻ whose results match closely those of Ph,n∘ until about t=2, when the growth becomes very vigorous due to proximity of the Dirichlet boundary. After t=2 however, the thickness appears under–predicted with ˉPh,n◻. In the future we plan to improve the update αn→αn+1 based on dΛ◻dt rather than on Λ◻, which seems too conservative.
Remark 2. An alternative to Ph,n∗,∘, Ph,n∗,◻, ˉPh,n∗,◻ is to solve each of these not as a coupled diffusion–reaction system, but instead by operator splitting, where each of the biofilm and nutrient parts of (3.4) is replaced by an appropriately modified reaction–diffusion components (2.10)–(2.11) With the latter, after ^Bnh is known from advection and reaction steps, we proceed to identify αn∗ in a loop so as to guarantee (2.4). This robust algorithm is applied in the multi–component case to avoid solving a large diagonal diffusion system for K>1.
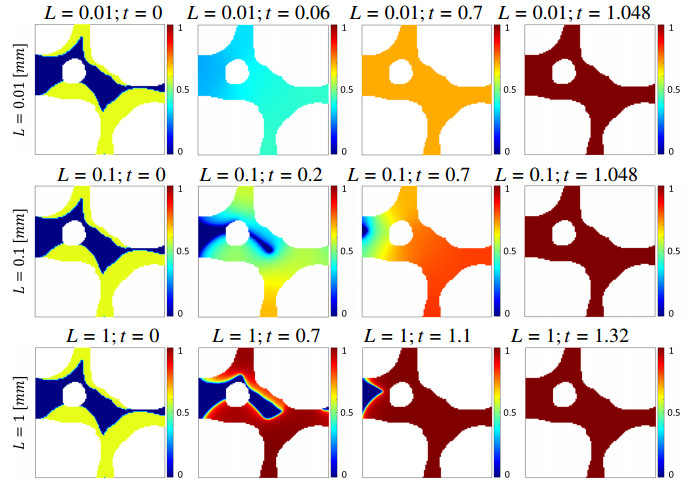
In this section we present our first example in d=2. We demonstrate the growth of biofilm using our constrained model (3.5), and its regularized version. We choose a realistic one-pore example with geometry as in Figure 2(c), and consider several length scales L for this geometry to illustrate the connection between L and the time scales when the pore is filled up.
Example 3.5 (Biofilm growth pattern in a nutrient-rich porous medium). We compare the biofilm growth patterns in Ω=(0,L)2[mm2] for L={0.01,0.1,1}, with other parameters as below, with dm=O(1).
| B∗ | B∗ | Binit | Ninit=Nbd | dB,0 | dN,w | RN,bw | κ | α |
| 1 | 0.9B∗ | 0.6B∗χΩb(0) | 100 | 10−4dm | dm | 0.1 | 2 | 2 |
Figure 7 shows the evolution of biofilm growth. As expected, the micro–pores gets filled up faster than the macro–pores. Qualitatively, the pattern of formation is independent of L and T.
Next we compare the PVI model (3.5) with its smooth variant motivated by (ⅱ) from Section 8.1.2. Smooth phase field approximation may be advantageous since there is a large body of literature on computational schemes and their analyses.
We fix B∗=1, and consider a smooth approximation of (3.5) in which we fix N≈const>>kN, and replace the constraint operator ∂I(−∞,B∗] by a smooth penalty term. More precisely, we recall the Allen-Cahn model ∂tB−∇⋅(d∇B)+s(B3−B)=0 in which d=const, and s=const together controlling the width of the interface region between the stable equilibria B=−1 and B=1. This model is a smooth approximation to ∂tB−∇⋅(d∇B)+∂I[−1,1]−sB=0. With nonnegative initial data and under Neumann boundary conditions, the Allen-Cahn model and the constrained model analogous to (3.5) are expected to produce solutions which eventually converge to B=1. Now in the analogous model (3.5), under the assumption of abundant nutrient we can set the parameter s≈κκB≈1, and consider the nonlinear diffusivity version of Allen–Cahn model given by
| ∂tB−∇⋅(~dB(B)∇B)+B3−B=0,x∈Ωn. | (3.14) |
(See (8.1) with g(ϕ)=ϕ−ϕ3). This class of methods when dB=d=const is well known [52,53,54]. We find that instead of singular and degenerate diffusivity dB given by (8.3), we must use a less degenerate version guarding against the unstable equilibrium B=0 with
| ~dB(α;B)={dB,0(1+(B¯B∗−B)α),B≤B∗,dB,0(1+(B∗ˉB∗−B∗)α),B>B∗. | (3.15) |
Example 3.6 (Biofilm growth pattern in a nutrient-rich porous medium using smooth phase field model). We consider (3.14) discretized as described in section 2.5 using CCFD with harmonic averages for the diffusivities at cell edges, and use parameters as in Example 3.5.
We compare the biofilm growth pattern from this model given in Figure 8 with that in Figure 7. We see good qualitative agreement between the models, but also more diffuse profiles, as expected, and different time scales.
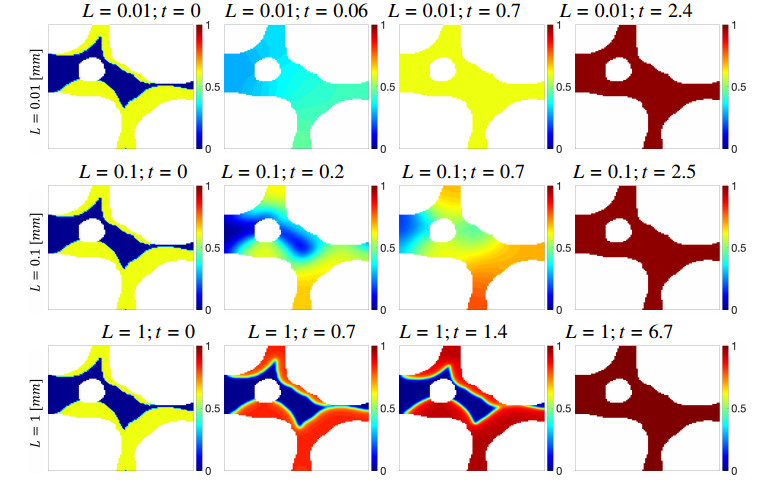
With both models, in the micro–pores L=0.01[mm] the biomass growth is dominated by (fast) diffusion; Ωb spreads until it fills Ωn and then B increases. In the macro-pores L≥1[mm], the sequence is almost opposite: B increases fast locally prior to, and during the expansion of Ωb. These effects are somewhat more pronounced for (3.14) than for the biofilm growth modeled by (3.5).
Now we consider biofilm growth in porous media at the pore–scale, with the pores filled with ambient fluid which flows. The simulations of flow at pore–scale, i.e., at complex pore–scale geometries are important for the qualitative and quantitative prediction of the macro–scale properties when the geometry changes, e.g., due to precipitation or dissolution, phase transitions, or biomass growth. We recall the classical connection between the Stokes flow in a periodic pore–scale geometry and Darcy permeability kΩ, established in [55], as well as the classical formula by Kozeny–Carman equation [56] which approximates porous medium geometry as a bundle of interconnected tubes, and gives kΩ=kΩ(ϕΩ) as a function of the porosity ϕΩ. With the wide availability of pore images, and abundant calculations of kΩ from flow using these images, the assumptions on periodicity or channel–like geometry as in Kozeny–Carman assumptions seem to be less relevant than in the past; see, e.g., recent analysis in [37] for a variety of granular, volcanic and other porous media which show that the algebraic correlations for kΩ=kΩ(ϕΩ) are not universally close approximations.
The relevant body of literature is now substantial. In a typical workflow one proceeds image →DNS→kΩ, where DNS means "Direct Numerical Simulations", with flow simulations over a representative elementary volume (REV) extracted out of a voxelized image, followed by a numerical homogenization or upscaling to the permeability kΩ. A recent systematic study with a review of scales, geometrical assumptions, and approximations for single–phase flow was undertaken in [57,58]. In our work [33,34,59,60] followed by [17,27,61] we established techniques to obtain flow rate dependent anisotropic kΩ for an non–Darcy model for synthetic and for realistic pore geometries; we also considered numerical accuracy and efficiency as well as reduced models for large scale evolving pore–scale geometries; see also recent extensions in [62].
In this paper we require a robust and efficient flow model which works well for an essentially stationary flow at low Reynolds numbers and capable of working in complicated pore–scale geometries such as that in Figure 2 across the different length scales. We focus on the flow in the presence of biofilm; see Tables 5 and 6 for overview of models and upscaling. The flow models range from Navier–Stokes models extended by inclusion of additional stress tensor in [3,2] through Navier–Stokes models for large velocity in [17] and Stokes and Brinkman flow models in [21,46]. For biofilm, validation and experimental insight are difficult due to the numerous challenges of imaging microbial growth in synthetic or real porous media [17,34,39]; sometimes the best one can do is to study the upscaled properties such as kΩ as in [17] with the flow confined to Ωn∖Ω∗b, i.e., an impermeable biofilm. In this case the flow ceases when some pores are plugged with biofilm, while full clogging is not a universally realistic scenario.
| Model and [reference] | Flow in Ωn | Free boundary | Constraint on B | biomass in Ωw |
| (ⅰ) Discrete and hybrid | no | not explicit | inequality | |
| IbM & continuum | cell shoving | yes | ||
| (ⅰ) Phase field models [2] | yes, extended N–S | diffuse | yes | no |
| (ⅲ) Osmotic π, level–set | sharp | |||
| [26] | no | advective, with v=−∇π | ||
| [21,46] | Brinkman in Ωb Stokes in Ωw |
sharp | equality | no |
| (ⅳ) Singular diffusion [20] | no | implicit | property | yes |
| (ⅴ) Variational inequality [17] | N–S in Ωn∖Ω∗b | implicit | inequality | yes |
| Model in this paper | Brinkman in Ωn | implicit | inequality | yes |
| Reference | Geometry and Scale | Permeability |
| [26] | channel | |
| [13] | channels, many--pore | no |
| [16] | thin strip (1d) | yes |
| [21,46] | channel | yes |
| [25] | 1d & many-pore | |
| [17] & our model | channel, one-pore, many-pore | yes |
In this paper we consider partially permeable biofilm phase with a heterogeneous Brinkman flow model which allows (some) flow through the pores filled with biofilm, and is an "interpolation" between Stokes flow and Darcy flow. More generally, Brinkman flow is applicable, e.g., for porous media with large cavities or more generally with large porosity [63,64].
Brinkman model augments the well known Stokes model with the Darcy resistance term [65,66]. We present its heterogeneous version
| −μΔu+μk−1bx(x)u+∇p=f,x∈Ωn, | (4.1a) |
| ∇⋅u=0,x∈Ωn, | (4.1b) |
where u is the velocity, p is the pressure, and the resistance term ∼k−1bx related to the inverse of permeability is locally defined and kbx(x)=kbχΩ∗b(x). Of interest are the extreme cases when kb↓0, i.e., the obstacle region Ωb is impermeable, and when kb↑∞ and the flow in the entire Ωn is essentially of Stokes type. We note that this means that kbx implicitly depends on B(x,t). One could expand this dependence to make it vary with B or with the amount of EPS, which would make kbx vary smoothly with x, but we have not done this. The model (4.1) is stationary but with time–dependent data.
We impose the no–slip condition on Γrn as well as the Dirichlet condition on the inflow Γin, and natural outflow conditions on Γout, both portions of ∂Ωn, respectively
| u|Γrn=0,u|Γin=uD(x), and μ∇u⋅ν−pν=0 on Γout. | (4.1c) |
In the examples we also use ¯uD to denote the average of uD(x) over Γin, and we usually set up a parabolic inflow profile on Γin.
We acknowledge here the important analyses of the influence of shear stress between the Stokes and Darcy domain discussed, e.g., in [67,68,69,70]; these relate to the Beavers-Joseph-Saffman interface condition imposed at fixed interfaces such as soil–surface water interface. Instead, in our heterogeneous Brinkman flow (4.1) we allow the permeability kbx to vary, and in which k−1bx↓0 when B↓0, such as close to the interface ∂Ωb. This is important because the "interface" between Ωb and the "bulk fluid" may not be very well defined, and at the length scales involved we believe it is not critical to resolve the fine details of the fluid flow normal to that interface, see, e.g., the comments in [21]. In the end, the Brinkman model we use in this paper improves on the use of Stokes flow outside Ω∗b with no-slip condition as in [17], and we defer a more detailed study to future work.
We describe now the upscaling technique described in [34,71] in which kΩ is found as a proportionality constant between the averages of velocity and of pressures and allows to measure how the presence of biofilm may change the macro–scale properties of porous media. The flow and kΩ depend on the resistance k−1bx of of the obstacle in (4.1). While kbx could be found experimentally, the values reported in literature vary. In [21,46], kb=10−9 or kb=10−10[m2] were used and [72] consider kb∈[10−15,5×10−9][m2]. We illustrate this dependence next in Ω=(0,L)2[mm2] with the bio–gel of permeability kb.
Example 4.1. Consider Ω=(0,L)2[mm2] with bio–gel in the center as in Figure 2(a) with varying kb. The fluid flows from left to right, with average of the inflow values ¯uD=36[mm/hr]. After (u,p) is found, we compute kΩ of Ω by the volume averaging from [34]. We vary L and kb while fixing other parameters.
The results are shown in Figure 9 and Table 7. The transition of the flow from inside to the outside of Ω∗b over a large range of choices of L,kb is smooth which suggests that the model (4.1) and our implementation are robust, but more analysis is needed (underway).
| Data | Results | |||
| L[mm] | kb[mm2] | kΩ[mm2] | |‖ | |
| (a) | 0.01 | 0 | 1.75\times 10^{-7} | 1.58\times 10^{2} |
| (b) | 0.01 | 10^{-5} | 7.8\times 10^{-6} | 3.42\times 10^{-1} |
| (c) | 0.01 | 10^{-4} | 5\times 10^{-6} | 3.37\times 10^{-1} |
| (e) | 0.1 | 0 | 1.75\times 10^{-5} | 1.58\times 10^{2} |
| (f) | 0.1 | 10^{-5} | 3.17\times 10^{-5} | 5.87\times 10^{-1} |
| (g) | 0.1 | 10^{-4} | 1.28\times 10^{-4} | 3.08\times 10^{-1} |
| (i) | 1 | 0 | 1.75\times 10^{-3} | 1.58\times 10^{2} |
| (j) | 1 | 10^{-5} | 1.69\times 10^{-3} | 9.84\times 10^{-1} |
| (k) | 1 | 10^{-4} | 1.45\times 10^{-3} | 8.94\times 10^{-1} |
Furthermore, the flow depends significantly on L and k_b , as expected; see, e.g., the plots of |u(L/2, y)| in Figure 9. In a small pore with L = 0.01\; \left[ {{\rm{mm}}} \right] , the flow streamlines and velocity magnitude appear as if there was no obstacle, but for larger pores the flow is directed partially outside the obstacle, and with L = 1\; \left[ {{\rm{mm}}} \right] the flow behaves as if the obstacle was impermeable. In Table 7 for intermediate L = 0.1\; \left[ {{\rm{mm}}} \right] we see that as k_b increases, the resulting {{k}_{\Omega }}\to k_b , but the effect for the large pore is less significant for the k_b we used.
Another class of approaches direct their focus on thickness of biofilm as an independent variable rather than on B itself; this is essentially a "model reduction" which we illustrate now.
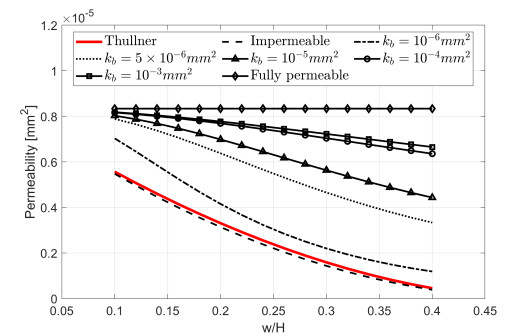
Example 4.2. Consider flow in a channel \Omega = (0, 1.5)\times (0, 0.1)\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] with biofilm growing next to the walls; see Figure 2(b). While this study for k_b = 0 and k_b \uparrow \infty can be reduced to the Poiseuille flow example [33]. When k_b > 0 there is additional flow through the biofilm layer, and we compare the variation of Darcy permeability {{k}_{\Omega }} with different k_b \in \{0, 10^{-6}, 5\times 10^{-6}, 10^{-5}, 10^{-4}, 10^{-3}, \infty\}\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] , where w represents the assumed width of one side of biofilm in this channel of height H = 0.1\; \left[ {{\rm{mm}}} \right] .
Figure 10 shows that, as expected, {{k}_{\Omega }} decreases with w/H \uparrow for all k_b < \infty . As k_b \uparrow , the biofilm presence affects the flow less, as expected. Our result for the impermeable case aligns well with the Thullner's permeability–porosity correlation model [73].
Furthermore, motivated by recent work in [13] we illustrate flow pattern through converging channels filled with biofilm of different widths; here the flow could be coupled with a reduced model for \gamma(t) \approx w(t) similar to that we explain in Section 8.2. Overall, the reduced models are successful only within a certain range of parameters.
Example 4.3. We consider flow from left to right through three channels that converge together as illustrated in Figure 2(e), with \Omega embedded in (-L, 2L)\times (0, L)\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] . The width of two diagonal channels are 0.18L , the middle channel is 0.09L , and the merged channel is 0.404L thick. Two diagonal channels are filled with biofilm next to the walls of different widths, 0.045L and 0.043L for top and bottom channels, respectively; see Figure 2(e). We use L = 1 , \overline{u}_D = 3.6\; \left[ \text{mm/hr} \right] , and solve for flow without obstacles, i.e., k_b = \infty . Then we compare calculated {{k}_{\Omega }} to the cases with biofilm of k_b = 0 or k_b = 10^{-3}\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] .
Results for Example 4.3 are shown in Figure 11 and Table 8. Figure 11(a) with k_b = \infty illustrates symmetric flow behavior with highest flow rate through the wider channels. When partially permeable biofilm of different widths is present, we lose the symmetric behavior. Since 83\% of lower diagonal channel is filled with biofilm while only 50\% of upper diagonal channel is filled, we see more flow goes through upper channel than the lower one. Also, the upper diagonal channel permits more flow than the middle channel due to the difference in channel widths. With k_b = 0 , the width of upper diagonal and middle channels are the same 0.045L , but we see higher flow traffic in the middle than upper diagonal channel because we set the parabolic inflow condition \overline{u}_D(-L, y) . We also confirm that {{k}_{\Omega }} \downarrow as k_b\downarrow .
| Parameter/Result | Value | ||
| k_b \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | \infty | 10^{-3} | 0 |
| {{k}_{\Omega }} \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | 2.6386\times 10^{-3} | 1.4765\times 10^{-3} | 8.6665\times 10^{-4} |
| {{\left| \left\| u \right\| \right|}_{\infty }} \left[ \text{mm/hr} \right] | 13.82 | 17.26 | 32.98 |
After substantial further testing (not shown) we believe our flow model is robust and ready to be coupled with the full biomass–nutrient dynamics. This will be done in Section 5.
Now we discuss the coupling of the flow model (4.1) and biomass–nutrient model (3.5), both written in domain \Omega_n as is done usually in porous media, in every time step
| \text{flow} \to \text{advection} \to \text{reaction–diffusion}. |
See, e.g., [36,74] for the workflow.
We choose h to adhere to the voxel resolution of the image, and to ensure reasonable accuracy of the biofilm layer. In particular, we typically choose h = O(10^{-2}L) . We also choose \tau to satisfy at least the CFL condition, as well as to obtain reasonable accuracy and resolution of the nonlinear reaction–diffusion dynamics. A fully coupled model requires that we solve for the flow at many time steps. Since calculating u at every time step is computationally expensive, we update the flow u only every so many time steps. For example, in a complex porous medium \Omega = (0, 1)^2\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] illustrated in Figure 2(d) with h = h_x = h_y = 0.005\; \left[ {{\rm{mm}}} \right] , and \tau = 10^{-3}\; \left[ {\rm{h}} \right] with flow Pe\approx 30 , we observe that there is little change in the flow pattern for 0.2\; \left[ {\rm{h}} \right] . Thus, for our examples we choose \tau = 10^{-2}\; \left[ {\rm{h}} \right] and compute u at every 10\tau = 0.1\; \left[ {\rm{h}} \right] , so that u(x, t) = u(x, t^n) for t\in[t^n, t^{n+10}) .
Now we move to the coupled flow and transport examples; we aim to improve on those from [17] by including permeable biofilm and adaptive singularity without inhibiting reactions. We focus now on whether an enhanced presence of nutrient due to the flow in \Omega_b enhances the ability to model the growth and spreading of the biofilm. The answer very much depends on the length and time scales at which this is evaluated. Since d_{N, w} > > d_{N, b} , the penetration of nutrient depends on the length scale; see more details in Section 8.2. At large L , the partially permeable biofilm phase allows more nutrient to penetrate through \Omega_b through advection. At small L , i.e., in micro-pores, the nutrient penetration in \Omega_b is more abundant. The biofilm growth pattern and reaction time depend significantly on the availability of N .
We start with an example in a small channel (micro–pore) in Example 5.1 and study the coupled effects of flow and biomass-nutrient. Next we consider a many-pore example.
In a micro–pore with L = O(60\; \left[ {\mu {\rm{m}}} \right]) , in order to see the evolution of nutrient penetration in \Omega_b^* , we must consider very small time scale and small \tau . At high flow rates some microbes within x: B(x, t) < B_* can be carried away by advection before nutrient arrives which may result in limited biomass growth in that particular pore.
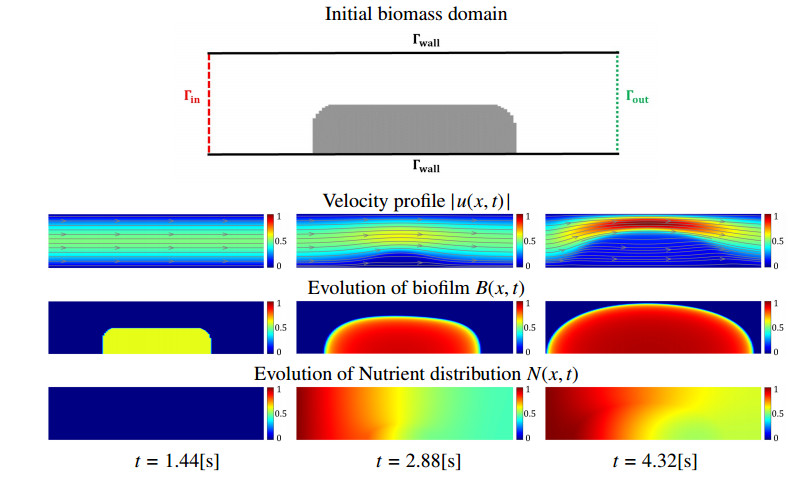
Example 5.1 (Coupled flow and biomass–nutrient dynamics, micro–pore geometry). We consider the biofilm growth and nutrient consumption coupled to the flow in a micro–channel \Omega = 65 \times 130\; \left[ \mu {{\text{m}}^{2}} \right] . We use the following parameters:
| \rho_B B^*\; \left[\mathrm{kg} / \mathrm{m}^{3}\right] | B_* | B_{init} | B_{inlet} | N_{init} | \rho_N N_{inlet}\; \left[\mathrm{kg} / \mathrm{m}^{3}\right] |
| 10^{-4} | 0.9B^* | 0.6B^*\chi_{\Omega_b(0)} | 0 | 0 | 10^{-2} |
| d_{B, 0}\; \left[\mathrm{mm}^{2}\right] | d_{N, w} | R_{N, bw} | {k_{_N}}, \kappa, \alpha | \overline{u}_D\; \left[ {\rm{mm/h}} \right] | k_b\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] |
| 0.1 | d_m | 0.1 | 2 | 0.5148 | 10^{-5} |
The velocity, biofilm, and nutrient profiles at selected time t \in \{1.44, 2.88, 4.32\}\; \left[ \text{s} \right] are shown in Figure 12. We see that since the nutrient enters from the left, there is less microbial growth near the right boundary, and biomass and biofilm grow initially faster on the left side than on the right side. This lack of symmetry disappears later.
In our next example we compare biofilm–nutrient dynamics under the conditions when \Omega_b is permeable and impermeable. We consider a complex "many–pore" geometry shown in Figure 2(d).
Example 5.2 (Coupled flow and biomass–nutrient dynamics, many–pore geometry). Assume parameters as follows
| B^* | B_* | B_{init}, B_{inlet} | N_{init}, N_{inlet} | d_{B, 0} | d_{N, w}, R_{N, bw} | {k_{_N}}, \kappa | \alpha | \overline{u}_D |
| 1 | 0.9 B^* | 0.6B^*\chi_{\Omega_b(0)}, 0 | 0, 1 | 3.6\times 10^{-4} | d_m, 0.1 | 2 | 2 | 0.1 |
with \Omega as in Figure 2(d). Consider dynamics of biofilm growth and nutrient consumption when the nutrient is injected from the left boundary of \Omega . Assume the natural outflow boundary conditions for B and N on the right boundary, and no–flow conditions on top and bottom. Consider two cases when k_b = 0 or when k_b = 10^{-4}\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] .
From the initial state shown in Figure 13 (left) at t = 0 , some of the microbes at low concentrations are first transported by advection before nutrient arrives, and are transported away before reaching more mature phase with B \approx B_* as you can see in Figure 13 (second column) at t = 0.1 , with the results almost identical to the case k_b = 0 and k_b = 10^{-4} . However, once they reach some of the pore throats with low flow rates |u| , and the nutrient becomes available, they grow and reach mature state.
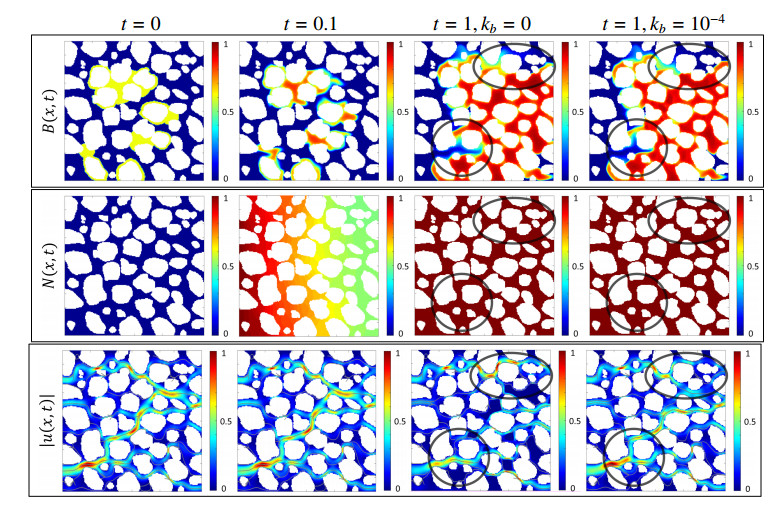
The results at t = 1 look similar at glance, but they show different biofilm formation patterns. For example, we focus on two regions as indicated by ellipses and located in the bottom left and top right in Figure 13 for k_b = 0 to k_b = 10^{-4} . At t = 1\; \left[ {\rm{h}} \right] , the nutrient has reached steady state and fully penetrates the entire domain \Omega .
We also show the permeability of this entire volume in Table 9. The flow rates are lower when k_b > 0 , but overall the permeability {{k}_{\Omega }} is higher for the case of partially permeable biofilm.
| k_b\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | {{k}_{\Omega }}\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | {{\left| \left\| u \right\| \right|}_{\infty }}\; \left[ \text{mm/hr} \right] |
| 0 | 3.0059\times 10^{-5} | 1.6391 |
| 10^{-4} | 5.6532\times 10^{-5} | 1.2816 |
Now we generalize the preceeding biomass–nutrient dynamics models to describe multiple interacting microbial species. We consider several microbial species present in \Omega_n . Each may have different roles and rules. We enumerate the species as B_1, B_2, \ldots B_K , recall \mathcal{B} = (B_k)_k and B = \sum_k B_k . Our model for the growth and spreading is the reaction–diffusion system (2.8) with the nonsingular diffusivity (3.1) and an adaptive \alpha(t) as in Section 3.3. We recall that the robust model either finds \alpha(t^n) by iteration as in (3.13) with nonsingular unconstrained or constrained model, or uses \alpha^n found by time-lagging.
There is no inherent difficulty in numerical solution with multiple species which follows the algorithm outlined in Section 2.5. However, the key challenge is to show how to model and implement volume constraints when K > 1 . For large time steps, we find that imposing nonnegativity constraints is useful.
First we make precise the reaction and growth terms in Section 6.1. Since K > 1 , we must specify how to handle the constraint on the sum of the species \sum_k B_k \leq B^* rather than on the individual species; this is done in Section 6.2. We want to allow for individual variance of "shoving mechanisms" which are discussed in the literature; this is done by varying the diffusivities and the constraints.
The numerical solutions are denoted by B_{k, h}^n and \mathcal{B}_h^n = (B_{k, h}^n)_k , with B_h^n = \sum_k B_{k, h}^n . For large K , the step-lagged or time-lagged operator split version (2.10) followed by (2.11), with inner iteration for accuracy, is easier to control than a monolithic nonlinear solver for (2.12).
Several modeling questions arise for multiple species in the literature. Some authors [21,46] distinguish between cells that are metabolically active and dead. Additionally, some authors recognize the "detached cells" which presumably travel as colloids in the water phase. In this paper and in our model we do not need to distinguish between these categories since \Omega_b can be equal to \Omega_n . We follow the focus of [20,23,31,45] on metabolically active cells, and focus on models for EPS formation as well as on the mechanism for "shoving". We also relate the modeling to the efforts in [23] using IbM and hybrid models.
EPS formation. EPS is an abbreviation for "extracellular matrix component"; which is built with extracellular polysaccharides; see, e.g., [7] for a thorough review of different type and role of EPS produces by different microbial species. The production of EPS is important for survival of biofilms [23,31,45]. However, when K > 1 species are present, they may contribute to EPS production in different proportion which leads to a competition for resources, and in turn leads to different survival rates of the individual strains of microbes. This aspect is explored in [13,23,31], with the strands distinguished as cooperative (or altruistic) (EPS+) or noncooperative (or selfish) (EPS–), and one can pursue the study of social evolution based on some assumed models and parameters defining the competition.
As an aside, we mention that the biochemical processes which govern the classification as EPS+ or EPS– include quorum sensing and genetic selection. Further questions include those on whether EPS continues to form, and whether the cells continue to reproduce when nutrient is depleted, and whether it is formed by mature cells or by "younger ones", and whether there is a threshold of "density" of B_k or B required for EPS production.
We aim now to demonstrate that our model from Section 3 can be extended to multiple species. As a motivation towards this study we choose the modeling concept of cooperation and competition. Following [23] the cooperative species is the species who contribute to the production to EPS, since the EPS benefits all microbes equally. However, production of EPS slows down the ability of species to reproduce, thus is considered as an "unselfish" action.
We follow the prevailing model for EPS production from species k < K as follows. Assume that B_K denotes the EPS component produced with rate r_K , and that B_1, B_2, \ldots B_{K-1} are the active species contributing to the EPS formation with rates r_k^K
| r_k = r_k^{growth} - r_k^K; \;\; 1\leq k \leq K-1; \;\; r_K = \sum\limits_{k = 1}^{K-1} r_k^K. | (6.1) |
In this paper r_k^{growth} are the Monod rates given by (2.6), and we follow [20,23] who assume EPS production as proportional to cell growth
| r_k^K = r_k^K(B_k) = {{\varepsilon }_{k}} r_k^{growth} | (6.2) |
and 0 \leq {{\varepsilon }_{k}} < 1 is the EPS production factor. Note that if K = 2 , one can easily lump (2.8) into one equation for B = B_1+B_2 since the EPS rate r_1^2 cancels with -r_1^2 .
With K = 3 species, [23] set up {{\varepsilon }_{1}}+{{\varepsilon }_{2}} = 1 and vary {{\varepsilon }_{1}} , with choices {{\varepsilon }_{1}} \in \{1/6, 1/3, 1\} , which helps to study cooperation and competition. Other models are possible, e.g., where r_k^K(B_k) = {{\varepsilon }_{k}} B_k .
Rearrangement of biofilm or "shoving" to enforce volume constraint. Concerning the rearrangement of species, the discrete models recognize different mechanisms of "shoving" including proportional, or with preferential treatment for some species [23,31]. In the continuum models (3.2) and (3.5) the analogy of "shoving" is carried out with the use of singular diffusivity d_B(B) (8.3). With K > 1 in [20] the model d_B(B) is extended verbatim to
| d_k(\mathcal{B}) = d_B(\mathcal{B}), \; \forall k | (6.3) |
which applies to each species including the EPS. Note that this means that the sum B = \sum_k B_k diffuses with d_B(\mathcal{B}) , and that the discrete diffusion operator A_h^B applies equally to each of the k component equations.
In our models (3.12) and (3.11) we use nonsingular d_B(\alpha; \mathcal{B}) with \alpha found adaptively. Furthermore, inspired by [23] we extend (6.3) and allow species to have different diffusivities
| d_k = \delta_k d_B(\mathcal{B}),\;\; \delta_k\geq 0,\;\; \forall k; \;\; \sum\limits_k \delta_k = K. | (6.4) |
Here \delta_k are adjustable nonnegative parameters, and we set \sum_k \delta_k = K in (6.4) for consistency with (6.3), but this is not needed in the \alpha –adaptive models, since the overall diffusivity is adapted automatically. In the numerical model, (6.4) gives rise to A_h^k = \delta_k A_h^B . The choice of \delta_k aims to model the propensity of some species to be able to "shove" their off-spring more vigorously than others "shove"; this may be accompanied by larger use of N , and reflected in the parameter {\kappa _k} as in [20].
We recall now the robust mechanism to impose volume constraint via the constraint operator \partial I_{(-\infty, B^*]}(B) in Section 8.1.5 which we use in (3.12), and which is replaced in the numerical model by the Lagrange multiplier \lambda_h^n . The extension for multiple species means we require that \mathcal{B}_j^n \in \Delta_* , where
| \Delta_* = \{\mathcal{B} \in \mathbb{R}^K: B = \sum\limits_k B_k \leq B^*\} | (6.5) |
is below the hyperplane B = B^* in \mathbb{R}^K . Furthermore, for robustness when using large time steps we find it necessary to impose nonnegativity on the variables, with
| \Delta_{*+} = \Delta_* \cap \Delta_+ \subset \mathbb{R}^K,\;\; \Delta_+ = (\mathbb{R}_+)^K = [0,\infty)^K. | (6.6) |
The convex set \Delta_* is a generalized tetrahedron in \mathbb{R}^K illustrated in Figure 14 when K = 2 . The nonnegativity constraints in (6.6) are needed to ensure a physically meaningful solution, and imposing nonnegativity constraints is common when solving for equilibria in chemical reactions [75]. In principle, nonnegativity should be an intrinsic property of solutions to a well–posed ODE or PDE model, but a numerical solution found with an iterative solver and a fixed time step may need to be nudged towards this property, or require very small time steps.
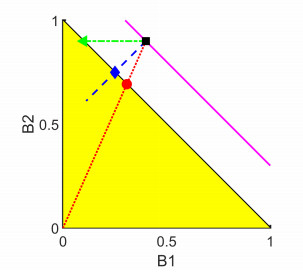
To enforce \mathcal{B} \in \Delta_{*+} in each of the k 'th equations we set \partial I_{\Delta_{*+}}(\mathcal{B}) = \partial I_{\Delta_*}(\mathcal{B}) + \partial I_{\mathbb{R}_+}(B_k) . In the corresponding discrete system each of these is replaced by a separate Lagrange multiplier, respectively, \lambda_h^n and \lambda_{k, h}^n . The system extending (3.4a) is
| (I+A^k_h(\mathcal{B}^n_h))B^n_{k,h}+ \lambda_h^n - \lambda_{k,h}^n = G^{\mathcal{B},n}_{k,h},\;\; \forall k | (6.7a) |
with the additional equations binding \lambda_h^n , and the sum B_h^n of species, and \lambda_{k, h}^n and each B_{k, h}^n , all pointwise as in (3.4c)
| \mathrm{min}(B^*-B^n_h,\lambda^n_h) = 0; \;\; \mathrm{min}(B^n_{k,h},\lambda^n_{k,h}) = 0; \; \forall k, | (6.7b) |
Remark 3. It is easy to see that, with time–lagged or iteration–lagged diffusivities A^k_h = A^k_h(\mathcal{B}^{n-1}_h) and reaction rates in (6.7), the stationary solution can be found as the unique solution for the associated constrained quadratic minimization problem calculated with the Lagrange multiplier.
However, it is not clear that the Lagrange multiplier solution found by optimization is necessarily the same as the solution justified from modeling point of view. In particular, multiple species may have "preference" in deciding which microbial species are subject to more stifled growth and/or more vigorous shoving than others. In particular, one can always find a "proportional" solution in \Delta_{*+} as shown in the next example. We leave the choice as an option in our model, but do not see a significant difference in results.
Example 6.1. We illustrate now \Delta_{*+} and solving under constraints when K = 2 . Consider the minimization problem with J(\mathcal{B}) = \frac{1}{2}(A_1 B_1^2 + A_2 B_2^2)-G_1 B_1 -G_2 B_2 , with some given G_1\geq 0, G_2 \geq 0, A_1 > 0, A_2 > 0 . The unconstrained solution is clearly B_k = G_k/A_k . The solution under constraints \mathrm{min}_{\mathcal{B} \in \Delta_{*+}} J(\mathcal{B}) always exists and is unique, and may fall in the interior of \Delta_{*+} if \sum_k G_k/A_k \leq B^* = 1 . Otherwise, it is found at the intersection of the normal to B_1+B_2 = \sum_k G_k/A_k with the line \sum_k B_k = 1 . In turn the proportional solution is that found at the intersection of the line from the point (G_1/A_1, G_2/A_2) to the origin with the boundary of \Delta_{*+} .
These are implemented in the reaction step of the operator split, but could also be incorporated in the reaction-diffusion step, a modification of P_* from Section 3.3
| \partial_t B_k - \nabla \cdot (d_k(\alpha_*(t);\mathcal{B}) \nabla B_k) + \partial I_{\Delta_{*+}}(\mathcal{B}) = r_k(\mathcal{B},\mathcal{N}), \; 1 \leq k \leq K | (6.8) |
with numerical approximation (3.7). We will not dwell on the different variants, but rather present a few examples.
Example 6.2. We set up an example with K = 3 components as a modification of Example 3.1 with data modified from Tables 3 and 4(A).
| L | T | h | \tau | B_{k, init} | \Gamma_D and N_{bd} = N_{init} | R_{N, b w}, d_{N, b} | \kappa | \alpha |
| 3 | 20 | 0.01 | 10^{-3} | in text | x = 0, 0.1 | 0.1; (2.13b) | 2 | \alpha_*(t) |
| Mildly competitive case: {{\varepsilon }_{1}} = 0.5, {{\varepsilon }_{2}} = 0.2, \delta_1 = \delta_2 = \delta_3 = 1. | ||||||||
There are two active microbial species k = 1, 2 and the EPS component k = 3 . We set {{\varepsilon }_{1}} > {{\varepsilon }_{2}} which makes species 1 the more cooperative or "altruistic" since species 1 contributes more strongly to the production of EPS from which all species benefit. The initial condition is B_{1, init} = 0.2\chi_{[0.45, 0.55]\cup [1.45, 1.55]} , B_{2, init} = 0.2\chi_{[0.85, 0.95]} , and B_{3, init}\equiv 0 . The case is somewhat nutrient deficient. We also test the case when EPS is immobile, and we set \delta_1 = 1.5;\delta_2 = 1.49;\delta_3 = 0.01 .
The time evolution for this example shown in Figure 15 illustrates that the less cooperative species k = 2 features more vigorous growth. The constraint on B_1+B_3 and B_2+B_3 becomes active around t = 4 . Around t = 5 the two clusters of B_1, B_2 coalesce and continue expanding to the left towards the nutrient supply. The dependence on the nutrient is also evident from the slightly skewed profiles of B_2 , as well as the behavior of the right–most cluster of B_1 which is growing the slowest.
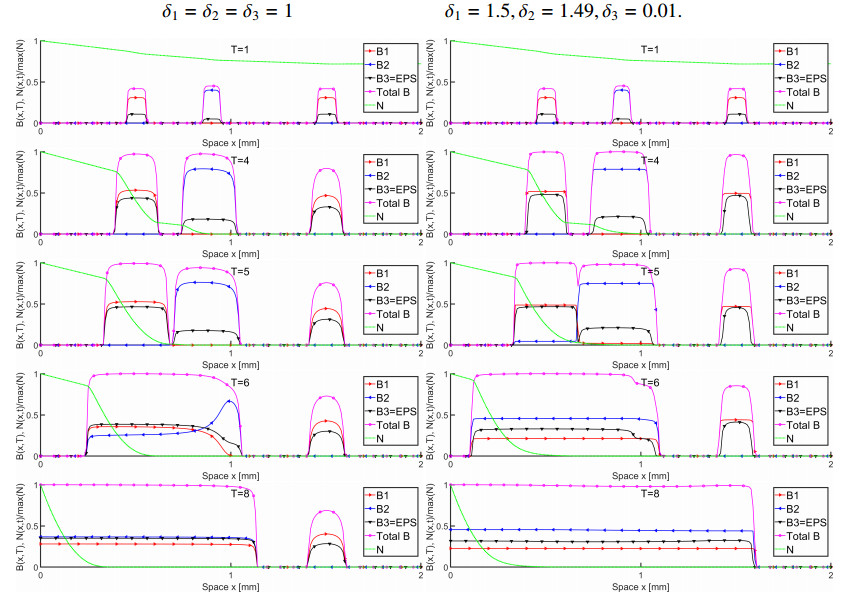
The evolution when EPS is immobile reveals a slightly different overall dynamics of B(x, t) for t > 4 , and overall much stronger spreading of the active species, eventually leading to the right–most cluster being overtaken at t = 8 , not seen at this time for equal diffusivities.
Example 6.3. In this example we explore the issues of cooperation and competition. We set
| L | T | h | \tau | B_{k, init} | \Gamma_D and N_{bd} = N_{init} | R_{N, b w}, d_{N, b} | \kappa | \alpha |
| 2 | 20 | 0.01 | 10^{-3} | in text | x = 0, x = L, 0.01 | vary; (2.13b) | 2 | \alpha_*(t) |
| Highly competitive case: {{\varepsilon }_{1}} = variable, {{\varepsilon }_{2}} = 0, \delta_1 = 2.98; \delta_2 = \delta_3 = 0.01. | ||||||||
We set up the case with identical initial conditions for both microbial species B_{1, init} = B_{2, init} = 0.45\chi_{[0.95, 1.05]} , and with B_{3, init} = 0.05 \chi_{[0.95, 1.05]} . We assume species 2 does not contribute to EPS production thus {{\varepsilon }_{2}} = 0 . We vary the rate of EPS production for the cooperative species {{\varepsilon }_{1}} \in [0.05, 0.2] as well as the nutrient penetration parameter R_{N, b w} to assess whether the cooperative species have the advantage. See Figure 16.
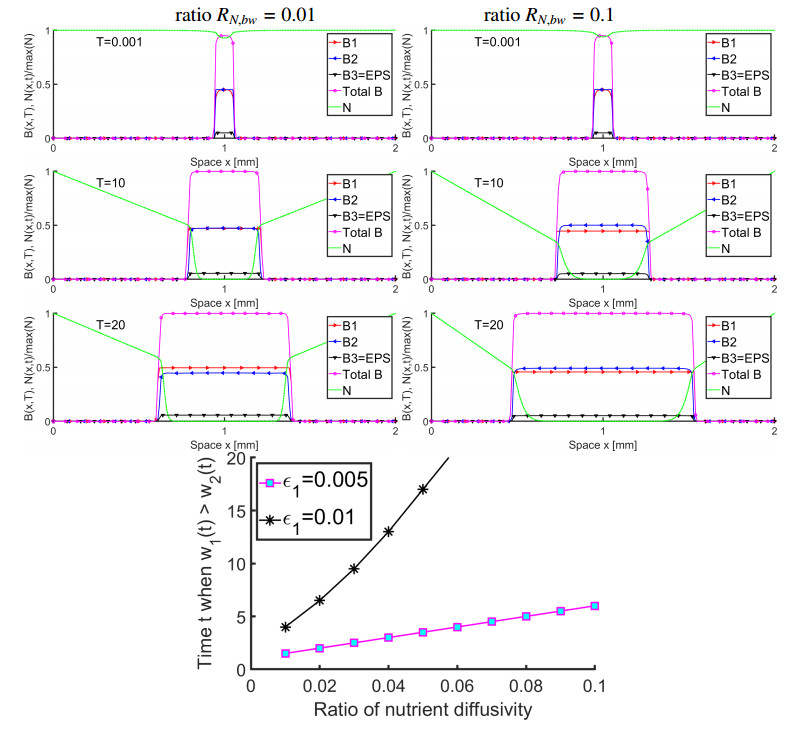
As expected, the species B_2 seems to have a clear advantage over B_1 , since the former does not spend energy producing EPS and can reproduce faster. However, if species B_1 has the ability to shove its members more vigorously than those of B_2 , then over long time, the species B_1 may regain some advantage as long as the nutrient has sufficiently poor abilities to penetrate into the mature biofilm where B_2 dominates. This is illustrated in the top rows of Figure 16.
To provide a more concise analysis of this competition, we follow [23] and calculate the dependence of the total amount \mathcal{T} _k(t) = \int_{\Omega}B_k(x, t)dt of species k , as well as its fitness w_k(t) = log\left(\frac{\mathcal{T} _k(t)}{\mathcal{T} _k(0)}\right) . With this quantity we check if there is t \in [0, 20]: w_1(t)\geq w_2(t) , and consider the time t_{1, win} = \mathrm{min}\{t \in [0, 20]: w_1(t)\geq w_2(t)\} when species 1 begin to show some advantage. We set t_{1, win} = 21 if this never happens and if w_1(t) < w_2(t)), \forall t \in [0, 20] . The results are plotted at the bottom of Figure 16.
In this paper we formulated a model for biofilm-nutrient dynamics which can be coupled to the flow at pore-scale. The model is continuum and monolithic, i.e., it is written as a system of partial differential equations for the microbial species and nutrient (\mathcal{B}(x, t), N(x, t)) , and for fluid flow variables (u, p) over the entire domain \Omega where fluid and microbes and nutrient exist.
Our model improves those known from the literature. For the biomass-nutrient model, it finds automatically and adaptively the appropriate degree of singularity of diffusivity which guarantees that the maximum volume constraint on B(x, t) is satisfied. In this sense, it realizes very closely the same principles as the discrete models of "cell shoving". In addition, our model does not explicitly track any interfaces or free boundaries; tracking free boundaries puts an additional burden on the solver and may require regridding. Instead, the interfaces can be found implicitly in our model by postprocessing the values of B(x, t) . Finally, our model is very easily applied to multiple species and allows a multitude of extensions towards the study of their cooperation and competition.
For the flow we use a new approach by blending the Brinkman flow in (somewhat) permeable biofilm domain with that in the bulk fluid: this is done with a Brinkman flow model in which we adapt the biofilm permeability coefficient k_B(x) depending on the microbial concentration B(x, t) .
With these two new model developments we can solve the coupled flow and biomass–nutrient model in complex geometries. We demonstrate robustness of the model and compare it with other closely related continuum models. The search for adaptively chosen singularity parameter \alpha requires additional computational effort, but we indicated how one can use its time-lagged form dubbed \bar{P}_{*, \square}^{h, n} in which we exploit the non-singular constrained model. Furthermore, the adaptation might not be practical for large scale simulations in d = 3 . For these one can guide the choice of an appropriate \alpha(t) by studying a sub-problem in d = 1 or d = 2 off-line first.
More work is needed to study, analyze, and extend the model, and some is underway. In particular, more analysis of the adaptive model for biofilm propagation is desired, including how to improve the search for optimal \alpha . Further, more numerical analysis is needed to study the fine properties of the CCFD schemes in the context of degenerate and singular diffusivities. In addition, while we demonstrated that the heterogeneous Brinkman flow model works well for our purposes, more analysis is needed to study our model in relation to other coupled models for the bulk fluid-Darcy flows including the considerations of Beavers-Joseph-Saffman condition.
The challenges remain as length scales are concerned, since we wish to apply the model from the single micro-pore size of 10 micron size through columns of mm size. The inclusion of modeling components which describe biofilm adhesiveness to the grains as well as setting thresholds for EPS production are underway. Finally, the computational complexity of our models is considerable for 3d; we refer to, e.g., [62] for non-DNS alternatives.
Finally, we wish to make concrete connections to some experimental data across the different length scales L and for different microbial species. Such studies would guide future work towards improving and refining the model, as well as towards other applications.
In this section we provide additional details. In particular, we provide an extensive discussion of literature models which motivate our model in Section 3. We also present further details on numerical schemes and their convergence; see Table 10 for summary.
| Ref. | space | time | \Gamma_{bw} | flow solver |
| (ⅱ) [4,5] | FD | C-N | projection | |
| (ⅲ) [26] | O(\tau^3) -TVD | level set, WENO | none | |
| [21,46] | Galerkin linear FE | BE & semi-implicit | ALE | COMSOL |
| (ⅳ) [20] | FD-based FV | semi-implicit | implicit | none |
| (ⅴ) [17] | CCFD | BE, semi-smooth Newton | staggered in time | Fluent |
| [25] | Galerkin FE | BE | implicit | none |
| Our model | CCFD | BE & semi-implicit | operator split | MAC scheme |
The discussion here supports the development of our new model in Section 3 which blends (ⅳ) and (ⅴ) models; these in turn draw from (ⅰ)–(ⅲ). When comparing models from Table 2, we face a challenge that each works with a different system of variables and units, and uses different data in their examples, e.g., a range of rate constants. Thus our comparisons are qualitative only. We divide our discussion into (ⅰ) discrete models, and four different types (ⅱ)–(ⅴ) of continuum models for biomass evolution extending (2.8a). In turn, the evolution of nutrient species \mathcal{N} is governed by advection-reaction-diffusion (2.8b); the species are assumed soluble in water and with density small enough so that their presence does not affect the flow. The different modeling variants include steady-state approximation, and the use of analytical solution, which we connect to the class (ⅲ) of reduced models.
We start with Eqs (2.2) and (2.4), which express the mass conservation and volume constraint, respectively. The quantity M(t) increases due to microbial growth: both \theta_k and the volume |\Omega| of \Omega may contribute to this increase. Literature provides several ways in which these changes are modeled.
In discrete models (ⅰ) one solves a system of ODEs such as (2.7a) governing the growth and transport of individual cells or their agammaegates. The total mass B(t) is a sum of masses of the individuals. Discrete models allow \theta_k to increase until a threshold is reached and |\Omega| must increase. In (ⅰ) discrete models, the cells are subject to "shoving", a mechanism through which they reallocate to nearby location as close as possible to the existing phase, thus maintaining a contiguous phase. In hybrid models EPS can be modeled as a continuum, but the live cells are modeled as individuals. Nutrient and metabolic products are typically modeled by a coupled transient PDE or by some simplified variant.
In continuum models (ⅱ)–(ⅴ) the biomass amount is represented by a variable such as concentration B(x, t) with the growth and transport governed by PDE (2.8a). The definitions of the variables, of the "biofilm domain", and the assumptions made on the evolution differ substantially between the modeling variants. The main difference between these models is whether microbial species are modeled in the entire region \Omega or rather only in its subset \Omega_b , and the definitions of \Omega_b and the model of its evolution vary substantially between models. Continuum models achieve the spreading of biomass via nonlinear diffusion or another mechanism. Several ingenious mechanisms are proposed to track the boundary of \Omega_b which can be divided roughly to (ⅱ) Cahn–Hilliard-like phase field models with focus on detailed local description of the biofilm-water interface, (ⅲ) level-set type interface tracking models which track the boundary \Gamma_{b0} of \Omega_b based on a predefined model for its velocity, (ⅳ) singular nonlinear diffusion PDEs, and (ⅴ) nonlinear diffusion PDEs under constraints, with the growth only allowed when B < B^* .
The discrete models such as IbM (Individual based Models) or CA (cellular automata) follow simple rules on growth and cell division which are appealing and can be motivated entirely by biological principles. They set up ODE growth models based on (2.7a) for each individual or agammaegate of the microbial species, and account for spatial distribution of N with a PDE such as (2.8b). The biomass is redistributed, if needed after cell division, based on the volume and whether the cells overlap. For example, they manage redistribution of cells so that B \leq B^* is satisfied by devising simple rules such as "shoving", i.e., reallocating cells to the nearest available location selected randomly (CA), or by disallowing cell overlaps (IbM). Some models such as [44] are "hybrid" and model the EPS phase with a PDE.
As stated in [44], there are advantages and disadvantages to the discrete treatment of biomass models, as opposed to continuum models. First, their results are not easy to reproduce or analyse and are discretization dependent. In addition, while they work well at the interface scale, their computational complexity seems prohibitive for studies at the scale of the pores or at the core scale.
The physio-chemical and mechanical processes involved in biofilm growth and deformation at the interface scale and at the cellular and molecular scales are very complex. Some literature appeals to the rigorous theory, e.g., Ginzburg–Landau theory of phase transitions, or to the Flory–Huggins theory of mixtures [2,3,4,5] or other theories [6]; these apply to the evolution of the polymer network and the bio-gel formed by the microbes within the surrounding solvent. We recall the main ideas.
The phase field models constrain the phase variable \phi , the volume fraction of the polymer network, and promote the phase agammaegation in a mixture of fluids, i.e., they develop a model which drives \phi to one of the model's equilibria \phi = 1 or \phi = 0 . Common themes (A) are the constitutive equations which describe the driving force(s) for motion such as the differential of the osmotic pressure \pi(\phi) , or the differential of chemical potential, itself defined as the differential \frac{\delta f}{\delta \phi} of the free energy density of mixing f(\phi) . These definitions are complemented by (B) a momentum equation for the fluid phase velocity v , similar to Navier–Stokes model or written as a simple potential equation [26]. Finally, (C), the motion of \phi is linked to (A–B) and to the biomass growth Bm(N) in some fashion.
Towards (A), we briefly recall the Flory–Huggins free energy density from [2,3,4,5]
| {{f}_{FH}}(\phi) = \chi \phi(1-\phi)+\frac{1}{N_0}\phi \ln(\phi) + (1- \phi) \ln(1-\phi) +\frac{\gamma_0}{2} ||\nabla \phi||{}^2. |
Typical values are \chi \approx 0.5, N_0 = 10^3 while the distortional energy parameter \gamma_0 might be even 10^{-10} smaller than \chi . Different approximations for \frac{d f_{FH}}{ d \phi} and the connections to \pi(\phi) are carried out in the literature. In [2] the authors aim to describe the bio-gel from first principles using a "two-fluid" approach, with the notion of osmotic or swelling pressure \pi(\phi) . In turn, [3,4] use the "one–fluid" multicomponent approach and define the chemical potential \frac{d f_{FH}}{d \phi} which includes terms similar to \pi augmented by -\gamma_0 \nabla^2 \phi ; the latter leads to Cahn-Hilliard equation; see also [3]. Assuming small \gamma_0 , and dropping the term with \gamma_0 , one obtains [2] that \frac{df_{FH}}{d\phi}\approx \pi \approx \phi^2(\phi-\phi_{ref}) , with \phi_{ref}\approx 0.6 , or \frac{df_{FH}}{d\phi} \approx - (log(1-\phi)+\phi+\chi \phi^2) \approx -(log(1-\phi)+\phi) . Setting the formulaic differences aside, \pi(\phi) for 1 > \phi > > 0 is an increasing convex function with an asymptote as \phi \uparrow 1 , with \frac{d\pi}{d\phi} of related properties.
For (B), in [2] the momentum equation of Navier–Stokes type balances the fluid deformation by -\nabla \pi(\phi) , and in [3] this term is replaced by \frac{d f_{FH}}{d \phi} . In turn, the momentum equation in [26] is simplified to that of potential flow type so that v = -\nabla \pi .
(C) The evolution of \phi is governed by
| \partial_t \phi + \nabla \cdot(\lambda(\phi) v \phi) = g(\phi), | (8.1) |
and another version can be obtained by setting \gamma_0 = 0 , i.e., ignoring the Cahn–Hilliard terms
| \partial_t \phi -\nabla \cdot \left(\lambda(\phi) \frac{d^2f_{FH}}{d\phi^2} (\phi) \nabla \phi\right) = \phi m(N). | (8.2) |
In the literature the parameter \lambda = const , or \lambda(\phi) \sim \phi . The source g(\phi) \sim Bm(N) in [4], but in other papers this connection is indirect. Furthermore, an equation similar to (8.1) with constant \lambda can be written for the solvent phase variable 1-\phi . From this, by summing the evolution equations for \phi and 1-\phi one gets a "pressure equation" similar to \nabla \cdot v = g(\phi) .
Remark 4. The model (8.2) is a quasilinear diffusion equation with a singular diffusion coefficient d(\phi) = \lambda(\phi) \frac{d^2f_{FH}}{d\phi^2} ; this motivates singular diffusion models (iv) discussed in Section 8.1.4, as well as nonsmooth phase field models modeled with a variational inequality (v) in Section 8.1.5. In turn, (8.1) predicts advective motion of phase boundaries, models discussed in Section 8.1.3.
Overall, phase field models are quite challenging in analysis and approximation and difficult to validate experimentally. The models we discuss next in Section 8.1.3 are their approximations and lead to even more simplified reduced models. We come back to (8.2) in Section 8.1.4.
Following Remark 4 we consider now a class of models [18,26] and [21,46] which solve for advective motion of the biofilm phase boundary as in (8.1). The models are not monolithic, and write different equations in \Omega_b(t)\subset \Omega and in \Omega_0 ; here we recall that (2.1b) defines \Omega_b(t) as the region with nonzero presence B of microbes, and \Omega_0 is the "bulk fluid" without microbes. Some authors assume existence of a sharp boundary between \Omega_b and \Omega \setminus \Omega_b , and some allow a boundary layer region between \Omega_0 and a region similar to what we denoted \Omega_b^* . This class of models does not allow redistribution of cells due to motility, and share the following strategy associated with the simplified momentum equation v = -\nabla \pi of potential type for the local "shoving velocity" v as a gradient of osmotic pressure \pi with \pi\vert_{\Omega_0} = 0 from Section 8.1.2 and [26], sometimes referred to as being of "Darcy" type which seems confusing given the length scale especially in this paper.
Most recently, [21,46] overlay this continuum "local shoving" model over the Brinkman flow model for some flow velocity in \Omega_b , and implicitly assume that the microbial growth in the region \Omega_b is mature, i.e., that \theta_w = const = 0.9 thus fixing \theta_B = \sum_{k = 1}^K\theta_k = \theta^0 = 0.1 in \Omega_b(t) = \{x: \sum_{k = 1}^K\theta_k = \theta^0\} . In these models no microbes exist outside the contiguous phase \Omega_b , the detached cells cannot reproduce, and the model prescribes only the expansion of |\Omega_b(t)| on some finite time scale, rather than instantaneously as in (ⅰ).
We are not aware of well-posedness analysis for the models in the class (ⅲ) and recognize the challenges which require, e.g., front tracking such as ALE (Arbitrary Lagrangian Eulerian), or level set approaches for the advective term [26]. Even though these were implemented in [21] for pore-scale simulations, we find that the approaches that require tracking of \partial \Omega_b explicitly are less robust computationally than other continuum models plus require special handling of the front when it reaches pore walls. The assumption of contiguous \Omega_b limits the applicability of this reduced model only to some channel geometries. Nevertheless the osmotic pressure models can be useful for the study of nutrient dependence in reduced models; see Section 8.2.
Now we consider a particular class of models which are directly motivated by the phase field models such as (8.2) in which we replace \phi by B . The model proposed in [19,20,41] is (2.8) with degenerate and singular diffusivity
| d_{\alpha,\beta;B}(B) = d_{B,0} \frac{B^\beta}{({B^*}-B)^{\alpha}}. | (8.3) |
We see that \lim_{B\to B^*}d_B(B) = \infty and \lim_{B\to 0}d_B(B) = 0 which features both the agammaegation (thanks to degeneracy of d_B as B \downarrow 0 ), and the volume constraint, i.e., (2.4) (thanks to the singularity as B \uparrow B^* ). Here d_{B, 0} is as in (3.1). The location and evolution of \Omega_b follows implicitly from the model, with the strength of the singularity controlled by some ad-hoc parameters \alpha, \beta ; in [19,20,41] these are \alpha = \beta = 4 .
Remark 5. The analysis of well-posedness of the model (2.8) with (8.3) involves the primitive D(B): = \int_0^B d_B(\psi)\; d\psi, \; 0\le B\le 1 of d_B(B) , with which some of the assumptions on data and some results on the solutions, are made. With \Gamma_D \neq \emptyset , and with smooth and bounded initial data (B_{init}, N_{init}) , Theorem 5.1 in ([29], page 96), states existence of solutions (B, N) which satisfies (2.4) but also is sought in a rather weak sense (B, N) \in L^\infty(R_+\times \Omega)\cap C([0, \infty), L^2(\Omega)) with (D(B), N) \in L^\infty(R_+, H^1(\Omega))\cap C([0, \infty), L^2(\Omega)) .
The lack of smoothness indicated by the theory means that the model (8.3) is also very hard to work with numerically. The main disadvantage is that it requires very small time steps, since the discrete diffusion matrix A^B_h(B^n_h) for (8.3) is singular as B_j^n \uparrow B^* . More broadly, for problems of fast diffusion type with singularity d(B) = \sim |{B}|^{a-1} with 0 < a < 1 , the convergence of finite element scheme is of first order O(\tau + h) in a norm close to L^{2}(L^{2}) [76]. In turn, [41] use only time-lagged d_B(B) for (8.3) which does not exactly enforce the volume constraint (2.4), unless very small time steps are used. In our experiments we found that (8.3) requires time steps of order of milliseconds or less, which increases the computational complexity by orders of magnitude as well as the accumulated approximation error. These facts as well as the need for robustness motivate our constrained model discussed next and the use of nonsingular adaptive diffusivity in Section 3.
The concerns about the model in Section 8.1.4 motivated our work in [17] for pore-scale modeling, where we considered
| \partial_t B -\nabla \cdot (d_B(B) \nabla B) +\partial I_{(-\infty,B^*]}(B) = r_B, \; x \in \Omega, t > 0, | (8.4) |
and its extension with advection, complemented by a Navier-Stokes fluid flow model for (u, p) in \Omega \setminus \Omega_* . In other words, we assumed that \Omega_* was impermeable to flow.
Remark 6. For a bounded and uniformly positive d_B = d_B(x) under mixed boundary conditions (8.4) has a unique solution B \in W^{1, 2}(V) \cap W^{1, \infty}(L^2) according to ([48], Theorem 5.2, page 214). The major difficulty is the lack of smoothness of \partial^2_{tt} B which leads to sub–optimal convergence rates of finite element approximations [50]. Furthermore, recent work in [77,78] analyzes a model inspired by (8.4) and similar to a Stefan free boundary problem. With u \neq 0 given by a coupled Navier-Stokes model and under Dirichlet boundary conditions for B the solution B exists in a subset of W^{1, 2}(V')\cap L^\infty (\Omega \times [0, T]) .
The model (8.4) is quite robust and can be extended from d_B(x) to (3.1). However, there is a concern that it truncates reactions when B = B^* . To understand the significance of the associated modeling error, we study the size of the active layer \Omega_a(t) relative to |\Omega| ; this discussion is blended with that for reduced models (ⅲ) next.
In Example 3.1 we saw that the thickness \gamma(t) of biofilm domain increases in time in nutrient-abundant cases. We refine now the study of the width a(t) = |\Omega_a(t)| of the active layer which is dependent on the nutrient supply N_{bd} , the uptake rate \kappa , factor R_{N, b w} in (2.13a), and domain size L . This analysis aims to explain the modeling error in the constrained model due to the truncation of reaction in \Omega_a in (3.5), and the validity of reduced models in the literature which commonly assume a(t) = const .
The issue of nutrient "penetration" through \Omega_b is exploited in the experimental literature [28,30] for prediction of the growth of \Omega_b . The authors approximate a(t)\approx const and assume \Omega_b^* = \Omega_b and stationary character of (2.8b). Their analytical and numerical calculations for some microbial species and nutrient pairs predict a(t) \in [25,200]\; \left[ {\mu {\rm{m}}} \right] [28,30] but can vary widely. Similar formulas are derived in [18] for large L\to \infty and small N_{bd} so that a linear limiting approximation to m(N) is valid. These give a(t) = const = a(\{N_{bd}; \kappa; R_{N, b w}\}) and are followed by various stability analyses. Consequently one can set up a practical reduced model which ties a(t) to the speed of \gamma(t) ; see e.g., [13] without the need for finding B(x, t) pointwise in \Omega_b . We explain this derivation based on model (iii) from Section 8.1.3, provide additional estimates of a = a(\{N_{bd}; \kappa; R_{N, b w}; L\}) for realistic L < < \infty and arbitrary N_{bd} in Section 8.2.3, and compare these formulas to numerical estimates.
Example 8.1. We start with our model (3.5) from Example 3.1 (A) with a fixed \alpha = 2 and N_{init} = N_{bd} = 1 which we compare with the cases with smaller nutrient supply N_{init} = N_{bd} = 10^s , with s\in [-2, -1.5, -1, 0] . We also consider longer domain L = 3 . We study the sensitivity of the nutrient penetration shown by a(t) and correlation with the speed of the front \gamma(t) depending on N_{bd} and L .
The results in Figure 17 confirm the intuition that \frac{d \gamma(t)}{dt} and a(t) are smaller when N_{bd} is small, or L is large. However the approximation \frac{d \gamma(t)}{dt} \approx const and a(t) = const is not accurate for all parameters. We compare these results next with those of the osmotic pressure model (ⅲ) and analytical formulas.
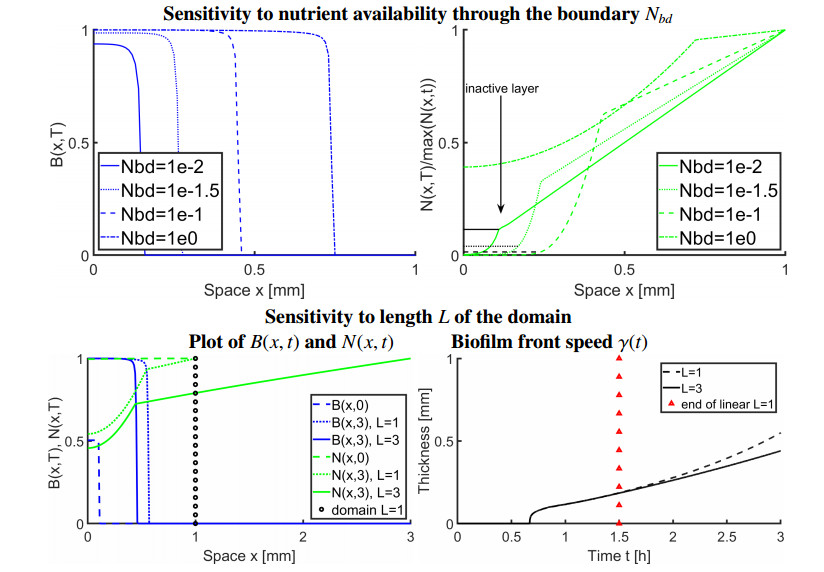
The model (ⅲ) [18,21,26,46] assumes that the microbes live only within contiguous domain \Omega_b\approx \Omega_* , with \theta_1 = \theta^0 , thus B\vert_{\Omega_b} \approx 1 , while \Omega_b expands due to the local shoving velocity v . Assuming \gamma(t) > 0 and N\vert_{\Omega_b} are known, at every t we solve for \pi and v
| \nabla \cdot v \; = \; \kappa_B m(N);\; v = -\nabla \pi, \;\; x \in (0,\gamma); | (8.5a) |
| \tfrac{d \pi}{dx}(0) \; = \; 0, \ \pi(\gamma(t)) = 0. | (8.5b) |
Further we have nutrient model (2.8b) in \Omega , which requires \gamma(t) and uses (2.13a) for d_N
| \partial_t N - \nabla \cdot (d_N \nabla N) \; = \; -\chi_{(0,\gamma)}m(N), \;\; x\in (0,L); | (8.5c) |
| d_{N,b} \tfrac{d N}{dx}(0,t)\; = \;0, \, N(L,t) = N_{bd}. | (8.5d) |
The velocity of the free boundary x = \gamma(t) is given by \frac{d\gamma}{dt} = v \bigr \rvert_{\gamma(t)} .
Example 8.2. We set up an example similar to Example 8.1 adapted to the use of (iii) model. We work in a small channel L = 0.1\; \left[ {{\rm{mm}}} \right] , B_{init}(x) = 1\chi_{[0, 0.05]}(x) thus \gamma(0) = L/2 ; this allows a detailed study of the thickness of active layer. We use M = 100 with a grid that varies when \gamma(t) moves, \tau = 0.0015 , and other parameters as follows
| B_{init} | \Gamma_D | N_{bd} = N_{init}\; \left[\mathrm{g} / \mathrm{cm}^{3}\right] | R_{N, b w} | {k_{_N}}\; \left[\mathrm{g} / \mathrm{cm}^{3}\right] | \kappa \; \left[ {{\text{h}}^{-1}} \right]{h^{-1}} | \kappa_B |
| 1\chi_{[0, 0.05]} | x = L | 10^{-9} | 0.01 | 2\times 10^{-8} | 0.072 | 0.5 |
In Figure 18 we plot both the solutions B(x, t), N(x, t) as well as the analytically calculated active layer depth with formulas given in Section 8.2.3. The plots are qualitatively similar to those in Example 8.1, with the exception of B(x, t) which is piecewise constant in Figure 18, but varies smoothly when using our new model in Figure 17. This lack of smoothness is a feature of simplified model which is compensated by its simplicity. Still, the reduced model (ⅲ) can only be applied in the limited set of circumstances as described in Section 8.1.3.
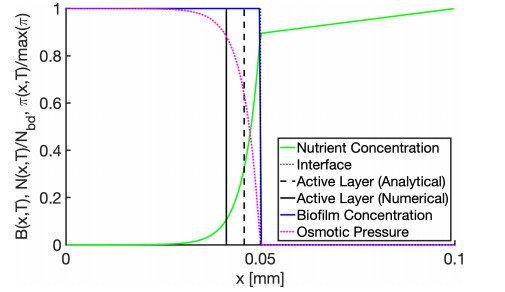
Continuing with the osmotic pressure model (8.5), we revisit the calculations of M(t) given by (2.2) to understand the validity of reduced models as in [13]. With B\vert_{\Omega_b} = 1 , we have M(t) = \int_{\Omega_b(t)} B(x, t)dx = \gamma(t) . Also, we have r_B = {\kappa _B} m(N(x, t)) B(x, t) = {\kappa _B} m(N(x, t))\chi_{[0, \gamma(t)]} is nonzero only for x \in \Omega_b(t) . Now we write the balance \frac{d}{dt}M(t) = \int_{\Omega} r_Bdx = \int_{\Omega_b(t)} r_B dx , which is a limit, as \Delta t \to 0 , of M(t+\Delta t) = M(t)+\Delta t \int_0^{\gamma(t)} {\kappa _B}m(N(x, t))dx .
We consider two extreme cases of the magnitude of N . If N\vert_{\Omega_b} is large, then m\vert_{\Omega_b} \approx const = \kappa , and we infer exponential motion of the interface
| \frac{d \gamma(t)}{dt} = {\kappa _B} \kappa \gamma(t). | (8.6) |
However, if N_{bd} is not large, or if L is large, the assumption m \approx const is not accurate. In fact, as shown by Examples 8.1 and 8.2, N(x, t) is depleted in \Omega_b during vigorous growth of B(x, t) , and does not penetrate well into \Omega_b with small R_{N, b w} < 1 , and may decay in \Omega_b .
Assuming now that N is small, with support in \Omega_a , if a(t) \approx const , we obtain \int_0^{\gamma(t)} m(N(x, t))dx \approx\int_{\gamma(t)-a(t)}^{\gamma(t)} m(N(x, t))dx\approx \bar{m} a , with some average value \bar{m} , and the linear model for \gamma(t) follows
| \frac{d\gamma(t)}{dt} = a(t) \bar{m}\approx const. | (8.7) |
The two cases (8.6) and (8.7) are similar to those postulated in [13] and used in [16,21].
We see now that this reduced model for \gamma(t) agrees with the analytical formulas but only for some values of \{L, R_{N, b w}, \kappa, N_{bd}\} . For small L or intermediate N , the evolution of \gamma(t) is likely somewhere between (8.6) and (8.7), and the reduced model and the osmotic pressure models are not accurate.
Now we provide additional analytical calculations for (8.5), assuming as in [18] that it is stationary as confirmed by our numerical simulations (not shown) for L \sim O(10^s) \left[ {{\rm{mm}}} \right] with s \in [-3, 0] . At every t , assuming known \gamma(t) , we obtain N(\gamma(t), t) as a solution of the stationary 2–point boundary value problem. Analytical formulas are available only for simplified m(N) when it can be approximated by a constant or a term linear in N . We recall that at x = \gamma(t) we have the transmission conditions of continuity of N and of its fluxes, and we can calculate the solution as below.
| \begin{eqnarray} N > > {k_{_N}} \implies m(N) \approx \kappa,\; \; N(x) & = &\begin{cases} \frac{R_{N, b w} \kappa}{2d_{N,b}}(x^2 - \gamma^2) + N_{\gamma}^c \ , \ x \in (0,\gamma), \\ \frac{N_{bd} - N_{\gamma}^c}{L-\gamma} \left(x - \gamma \right) + N_{\gamma}^c \ , \ x \in (\gamma, L), \end{cases} \end{eqnarray} | (8.8a) |
| \begin{eqnarray} N_{\gamma}^c & = & \left(\tfrac{N_{bd}}{L - \gamma} - \tfrac{R_{N, b w}^2 \kappa \gamma}{d_{N,b}} \right)(L - \gamma). \\ N < < k_N \implies m(N) = \frac{\kappa}{k_{_N}}N,\;\; N(x) & = & \begin{cases} \frac{N_{\gamma}^l}{e^{\rho \gamma} + e^{-\rho \gamma}}(e^{\rho x} + e^{-\rho x}) \ ,\ x \in (0,\gamma), \\ (\frac{N_{bd} - N_{\gamma}^l}{L - \gamma})(x - \gamma) + N_{\gamma}^l \ , \ x \in (\gamma, L), \end{cases} \end{eqnarray} | (8.8b) |
| \begin{eqnarray} \nonumber N_{\gamma}^l = \left(\tfrac{N_{bd}}{L - \gamma}\right)\left( R_{N, b w} \rho \tanh{(\rho \gamma)} + \tfrac{1}{L - \gamma}\right)^{-1}, \; \rho & = & \sqrt{\tfrac{R_{N, b w} \kappa}{d_{N,b} k_N}} = \sqrt{\tfrac{\kappa}{d_{N,w} k_N}}. \end{eqnarray} |
A semi–analytical model could find a(t) using (8.1) or (8.2) by solving for x_* \in (0, \gamma(t)): N(x_*, t) = N_* , and setting a(t) = \gamma(t)-x_* . A particularly simple form reported in [18] follows as L \to \infty
| \begin{eqnarray} a(t) = const = \sqrt{\tfrac{d_{N,b} N_{bd}}{m(N_{bd})}} = \sqrt{\tfrac{R_{N, b w} d_{N,w} N_{bd}}{m(N_{bd})}}. \end{eqnarray} | (8.9) |
A separate study of the dependence of a(t) and v = \tfrac{d\gamma(t)}{dt} (not shown here) reveals, e.g., quadratic dependence of v on N_{bd} , and linear on {\kappa _B} . It also shows discrepancy with factor \approx 2 – 3 between the predictions of a(t) using (8.4) and our numerical simulations.
To make the presentation self-contained, we describe now studies on convergence of (3.5) and (3.2). We also provide details on the MAC and CCFD schemes.
Earlier we explained that numerical approximation of nonlinear diffusion models is challenging. However, for validation of numerical models it is important but not straightforward to study their convergence. Analytical solutions are not available, thus we must use fine grid solutions as a "proxy". For the cases here, we use L = 1 , h_{fine} = 2 \times 10^{-4} and \tau_{fine} = 2 \times 10^{-5} . We recall that the case is hard since it is closely related to the problems studied in [25,76]. The theory predicts less than first order convergence in L^2(L^2) , which is actually hard to verify. Instead we define, for the error in B ,
| \lVert B_{err} \rVert_p = \max\limits_n ||B_h^n-B(\cdot;t^n)||{p} \approx \max\limits_n ||B_h^n-B_{fine}(t^n)||{p} | (8.10) |
where B_{fine} is the numerical solution computed with h_{fine}, \tau_{fine} .
We start with convergence of the numerical scheme for (3.5) with (3.1). We use parameters as in Example 3.1(A). The error is shown in Table 11. We test for the corresponding order of convergence \sigma denoted by \lVert B_{err}\rVert_p = O(h^{\sigma}) called \lVert B_{err}\rVert_p –order while varying \tau = O(h) . We note the convergence is approximately order 1 in the \lVert B_{err}\rVert_1 norm and approximately order of 0.6 for the \lVert B_{err}\rVert_2 norm. The nonsmooth nutrient convergence rates are shown in Table 11 with the order for the \lVert N_{err}\rVert_1 norm and the \lVert N_{err}\rVert_2 norm being approximately 1.
| Convergence for model (3.2) | |||||
| h | \tau | ||B_{err}||_1 | ||B_{err}||_2 | ||B_{err}||_1 –order | ||B_{err}||_2 –order |
| 0.0200 | 0.0200 | 2.2841e-02 | 1.2888e-01 | ||
| 0.0100 | 0.0100 | 1.0625e-02 | 8.4240e-02 | 1.1041 | 0.6134 |
| 0.0050 | 0.0050 | 4.7579e-03 | 5.2546e-02 | 1.1591 | 0.6809 |
| 0.0020 | 0.0020 | 1.4853e-03 | 2.3676e-02 | 1.2706 | 0.8701 |
| h | \tau | ||N_{err}||_1 | ||N_{err}||_2 | ||N_{err}||_1 –order | ||N_{err}||_2 –order |
| 0.0200 | 0.0200 | 1.0799e-03 | 1.2420e-03 | ||
| 0.0100 | 0.0100 | 5.2719e-04 | 6.0268e-04 | 1.0345 | 1.0432 |
| 0.0050 | 0.0050 | 2.6730e-04 | 3.0657e-04 | 0.9799 | 0.9752 |
| 0.0020 | 0.0020 | 1.0957e-04 | 1.2733e-04 | 0.9733 | 0.9589 |
| Convergence for model (3.5) | |||||
| h | \tau | ||B_{err}||_1 | ||B_{err}||_2 | ||B_{err}||_1-order | ||B_{err}||_2-order |
| 0.0200 | 0.0020 | 2.2599e-02 | 1.2806e-01 | ||
| 0.0100 | 0.0010 | 1.0496e-02 | 8.3966e-02 | 1.1064 | 0.6089 |
| 0.0050 | 0.0005 | 4.7056e-03 | 5.2642e-02 | 1.1574 | 0.6736 |
| 0.0020 | 0.0002 | 1.4779e-03 | 2.4410e-02 | 1.2639 | 0.8387 |
| h | \tau | ||N_{err}||_1 | ||N_{err}||_2 | ||N_{err}||_1--order | ||N_{err}||_2--order |
| 0.0200 | 0.0020 | 1.0701e-03 | 1.2318e-03 | ||
| 0.0100 | 0.0010 | 5.1824e-04 | 6.0381e-04 | 1.0460 | 1.0286 |
| 0.0050 | 0.0005 | 2.5751e-04 | 2.9023e-04 | 1.0090 | 1.0569 |
| 0.0020 | 0.0002 | 1.0449e-04 | 1.1946e-04 | 0.9844 | 0.9688 |
To solve the coupled flow and transport model with reaction, we use the operator splitting method to handle advection term explicitly first by the first-order Godunov method, then the diffusion-reaction implicitly by CCFD (cell-centered finite difference) method. When we solve for advection, we also need to resolve the flow. Here we expand the so-called MAC scheme (Marker and Cell) [79] to solve (4.1) on the staggered grid. A sketch of staggered grid is in Figure 19 with the variables associated with mass or with pressure defined at the cell centers and velocities and fluxes at the cell edges.
We describe the MAC scheme for the Brinkman equations (4.1). We discretize \Omega into M = N_x\times N_y rectangles of size h_x\times h_y . The degrees of freedom are as follows. Let i \in \{1, 2, \dots, N_x\} and j\in \{1, 2, \dots, N_y\} . Pressure P_{i, j} are defined at the cell centers, x- and y- directional velocities (U_{i\pm 1/2, j}, V_{i, j\pm 1/2}) are defined at the cell edges; see Figure 19. We use the 5–point stencil for \Delta U and \Delta V and the centered difference for \nabla P . We evaluate k_b^{-1} at the cell edges using the harmonic average and denote cell edge values by k_{b, i\pm 1/2, j}^{-1}\in \{k_{b, u}\} and k_{b, i, j\pm 1/2}\in \{k_{b, v}\} .
Under the boundary conditions (4.1c) for the horizontal flow, we have
| U_{1/2,j} = u_D(y_j), \quad V_{0,j\pm 1/2} = 0, | (8.11a) |
| \mu \frac{U_{N_x+3/2,j}-U_{N_x+1/2,j}}{h_x}-P_{N_x+1,j} = 0, \quad V_{N_x+1,j\pm 1/2} = V_{N_x,j\pm 1/2}. | (8.11b) |
The discrete system for (U_h, V_h; P_h) in the matrix form reads:
| \begin{eqnarray*} \left[\begin{array}{ccc} A_{uu}+ \mu k_{b,u}^{-1} I_u& & A_{up} \\ & A_{vv} + \mu k_{b,v}^{-1} I_v & A_{vp} \\ A_{up}^T & A_{vp}^T & \\ \end{array}\right] \left[\begin{array}{c} U_h \\ V_h \\ P_h\end{array}\right] = F \end{eqnarray*} | (8.12) |
where A_{uu}U_h, A_{vv}V_h, A_{up}P_h, A_{vp}P_h are approximations of -\mu \Delta u_1, -\mu \Delta u_2, p_x, p_y , resp., and I_u, I_v are identity matrices of sizes (N_x+1)N_y and N_x(N_y+1) , respectively.
The authors would like to thank the editors and anonymous referees whose comments helped to improve the exposition. We also want to thank our collaborator, late Dr. A. Trykozko from University of Warsaw, for providing the original inspiration for the work in [17], and motivation for the continuation towards this paper. We also thank other collaborators on [17] for providing data at the pore-scale.
This work was partially supported by the National Science Foundation DMS-1912938 and DMS-1522734, and by the NSF IRD plan 2019-21 for M. Peszynska. This material is based upon work supported by and while serving at the National Science Foundation. Any opinion, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. Choah Shin would like to thank Larry Martin and Joyce O'Neill for the generous support with the endowed College of Science at Oregon State fellowship 2019-20.
The authors declare no conflict of interest.
| [1] |
R. Sacco, P. Causin, C. Lelli, M. T. Raimondi, A poroelastic mixture model of mechanobiological processes in biomass growth: theory and application to tissue engineering, Meccanica (Milan), 52 (2017), 3273–3297. doi: 10.1007/s11012-017-0638-9

|
| [2] |
N. G. Cogan, J. P. Keener, The role of the biofilm matrix in structural development, Math. Med. Biol.: J. IMA, 21 (2004), 147–166. doi: 10.1093/imammb/21.2.147

|
| [3] |
T. Zhang, N. G. Cogan, Q. Wang, Phase-field models for biofilms. ⅰ. theory and one-dimensional simulations, SIAM J. Appl. Math., 69 (2008), 641–669. doi: 10.1137/070691966

|
| [4] |
T. Zhang, I. Klapper, Mathematical model of biofilm induced calcite precipitation, Water Sci. Technol., 61 (2010), 2957–2964. doi: 10.2166/wst.2010.064

|
| [5] |
T. Zhang, I. Klapper, Mathematical model of the effect of electrodiffusion on biomineralization, Int. J. Non-linear Mechanics, 46 (2011), 657–666. doi: 10.1016/j.ijnonlinmec.2010.12.008

|
| [6] |
B. D. Wood, S. Whitaker, Diffusion and reaction in biofilms, Chem. Eng. Sc., 53 (1998), 397–425. doi: 10.1016/S0009-2509(97)00319-9

|
| [7] | D. H. Limoli, C. J. Jones, D. J. Wozniak, Bacterial extracellular polysaccharides in biofilm formation and function, Microb. Biofilms, (2015), 223–247. |
| [8] | F. S. Colwell, R. W. Smith, F. G. Ferris, A. L. Reysenbach, Y. Fujita, T. L. Tyler, et al., Microbially mediated subsurface calcite precipitation for removal of hazardous divalent cations: microbial activity, molecular biology, and modeling, in ACS Symposium Series, American Chemical Society, (2005), 117–137. |
| [9] |
I. Klappe, J. Dockery, Mathematical description of microbial biofilms, SIAM Rev., 52 (2010), 221–265. doi: 10.1137/080739720

|
| [10] |
F. A. MacLeod, H. M. Lappin-Scott, J. W. Costerton, Plugging of a model rock system by using starved bacteria, Appl. Environ. Microbiol., 54 (1988), 1365–1372. doi: 10.1128/AEM.54.6.1365-1372.1988

|
| [11] |
M. Thullner, Comparison of bioclogging effects in saturated porous media within one-and two-dimensional flow systems, Ecol. Eng., 36 (2010), 176–196. doi: 10.1016/j.ecoleng.2008.12.037

|
| [12] |
A. Ebigbo, R. Helmig, A. B. Cunningham, H. Class, R. Gerlach, Modelling biofilm growth in the presence of carbon dioxide and water flow in the subsurface, Adv. Water Resources, 33 (2010), 762–781. doi: 10.1016/j.advwatres.2010.04.004

|
| [13] |
K. Z. Coyte, H. Tabuteau, E. A. Gaffney, K. R. Foster, W. M. Durham, Microbial competition in porous environments can select against rapid biofilm growth, Proc. Natl. Aca. Sci., 114 (2017), E161–E170. doi: 10.1073/pnas.1525228113

|
| [14] |
K. Drescher, Y. Shen, B. L. Bassler, H. A. Stone, Biofilm streamers cause catastrophic disruption of flow with consequences for environmental and medical systems, Proc. Natl. Aca. Sci., 110 (2013), 4345–4350. doi: 10.1073/pnas.1300321110

|
| [15] |
Y. Tang, A. J. Valocchi, C. J. Werth, H. Liu, An improved pore-scale biofilm model and comparison with a microfluidic flow cell experiment, Water Resources Res., 49 (2013), 8370–8382. doi: 10.1002/2013WR013843

|
| [16] | T. L. van Noorden, I. S. Pop, A. Ebigbo, R. Helmig, An upscaled model for biofilm growth in a thin strip, Water Resources Res., 46 (2010), W06505–1/14. |
| [17] |
M. Peszynska, A. Trykozko, G. Iltis, S. Schlueter, D. Wildenschild, Biofilm growth in porous media: Experiments, computational modeling at the porescale, and upscaling, Adv. Water Resources, 95 (2016), 288–301. doi: 10.1016/j.advwatres.2015.07.008

|
| [18] |
I. Klapper, J. Dockery, Finger formation in biofilm layers, SIAM J. Appl. Math., 62 (2002), 853–869. doi: 10.1137/S0036139900371709

|
| [19] |
H. J. Eberl, C. Picioreanu, J. J. Heijnen, M. C. M. van Loosdrecht, A three-dimensional numerical study on the correlation of spatial structure, hydrodynamic conditions, and mass transfer and conversion in biofilms, Chem. Eng. Sci., 55 (2000), 6209–6222. doi: 10.1016/S0009-2509(00)00169-X

|
| [20] |
M. R. Frederick, C. Kuttler, B. A. Hense, H. J. Eberl, A mathematical model of quorum sensing regulated eps production in biofilm communities, Theor. Biol. Med. Model., 8 (2011), 8. doi: 10.1186/1742-4682-8-8

|
| [21] |
D. Landa-Marbán, N. Liu, I. S. Pop, K. Kumar, P. Pettersson, G. Bødtker, et al., A pore-scale model for permeable biofilm: numerical simulations and laboratory experiments, Transp. Porous Media, 127 (2019), 643–660. doi: 10.1007/s11242-018-1218-8

|
| [22] | T. Zhang, N. Cogan, Qi Wang, Phase-field models for biofilms ⅱ. 2-d numerical simulations of biofilm-flow interaction, Commun. Comput. Phys, 4 (2008), 72–101. |
| [23] |
J. B. Xavier, K. R. Foster, Cooperation and conflict in microbial biofilms, Proceedings of the National Academy of Sciences, 104 (2007), 876–881. doi: 10.1073/pnas.0607651104

|
| [24] | A. Alhammali, Numerical Analysis of a System of Parabolic Variational Inequalities with Application to Biofilm Growth, Ph.D thesis, Oregon State University, 2019. |
| [25] |
A. Alhammali, M. Peszynska, Numerical analysis of a parabolic variational inequality system modeling biofilm growth at the porescale, Numer. Methods Partial Differ. Equations, 36 (2020), 941–971. doi: 10.1002/num.22458

|
| [26] |
E. Alpkvist, I. Klapper, A multidimensional multispecies continuum model for heterogeneous biofilm development, Bull. Math. Bbiol., 69 (2007), 765–789. doi: 10.1007/s11538-006-9168-7

|
| [27] |
T. B. Costa, K. Kennedy, M. Peszynska, Hybrid three-scale model for evolving pore-scale geometries, Comput. Geosci., 22 (2018), 925–950. doi: 10.1007/s10596-018-9733-9

|
| [28] | S. J Pirt, A kinetic study of the mode of growth of surface colonies of bacteria and fungi, Microbiology, 47 (1967), 181–197. |
| [29] | M. Efendiev, Evolution Equations Arising in the Modelling of Life Sciences, Springer Basel AG, Basel, 2013. |
| [30] | K. Williamson, P. Mccarty, A model of substrate utilization by bacterial films, Water Pollut. Control Fed., 48 (1976), 9–24. |
| [31] | J. U. Kreft, C. Picioreanu, M. C. M van Loosdrecht, J. W. T. Wimpenny, Individual-based modelling of biofilms, Microbiol. (Soc. General Microbiol.), 147 (2001), 2897–2912. |
| [32] | R. J. LeVeque, Finite Difference Methods for Ordinary and Partial Differential Equations: Steady-state and Time-Dependent Problems, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 2007. |
| [33] | M. Peszynska, T. Anna, Convergence and stability in upscaling of flow with inertia from porescale to mesoscale, Int. J. Multiscale Comput. Eng., 9 (2011), 215–229. |
| [34] |
M. Peszynska, A. Trykozko, Pore-to-core simulations of flow with large velocities using continuum models and imaging data, Comput. Geosci., 17 (2013), 623–645. doi: 10.1007/s10596-013-9344-4

|
| [35] | T. F. Russell, M. F. Wheeler, Finite element and finite difference methods for continuous flows in porous media, in The Mathematics of Reservoir Simulation (ed. R. E. Ewing), SIAM, Philadelphia, (1983), 35–106. |
| [36] | M. Peszynska, S. Sun, Reactive transport model coupled to multiphase flow models, in Computational Methods in Water Resources (eds. S. M. Hassanizadeh, R. J. Schotting, W. G. Gray and G. F. Pinder), Elsevier, (2002), 923–930. |
| [37] |
N. Nishiyama, T. Yokoyama, Permeability of porous media: role of the critical pore size: critical pore zize-permeability relation, J. Geophysical Res. Solid Earth, 122 (2017), 6955–6971. doi: 10.1002/2016JB013793

|
| [38] |
A. B. Cunningham, W. G. Characklis, F. Abedeen, D. Crawford, Influence of biofilm accumulation on porous media hydrodynamics, Environ. Sci. Technol., 25 (1991), 1305–1311. doi: 10.1021/es00019a013

|
| [39] | S. Bryant, L. Britton, Mechanistic Understanding of Microbial Plugging for Improved Sweep Efficiency, Technical report, The University Of Texas At Austin, 2008. |
| [40] |
S. Schlüter, A. Sheppard, K. Brown, D. Wildenschild, Image processing of multiphase images obtained via x-ray microtomography: a review, Water Resources Res., 50 (2014), 3615–3639. doi: 10.1002/2014WR015256

|
| [41] | H. J. Eberl, L. Demaret, A finite difference scheme for a degenerated diffusion equation arising in microbial ecology, Electron. J. Differ. Equations, 15 (2007), 77–95. |
| [42] |
C. Picioreanu, M. C. M van Loosdrecht, J. J. Heijnen, Mathematical modeling of biofilm structure with a hybrid differential-discrete cellular automaton approach, Biotechnol. Bioeng., 58 (1998), 101–116. doi: 10.1002/(SICI)1097-0290(19980405)58:1<101::AID-BIT11>3.0.CO;2-M

|
| [43] |
C. Picioreanu, M. C. M van Loosdrecht, J. J. Heijnen, A new combined differential‐discrete cellular automaton approach for biofilm modeling: application for growth in gel beads, Biotechnol. Bioeng., 57 (1998), 718–731. doi: 10.1002/(SICI)1097-0290(19980320)57:6<718::AID-BIT9>3.0.CO;2-O

|
| [44] |
E. Alpkvist, C. Picioreanu, M. C. M. van Loosdrecht, A. Heyden, Three-dimensional biofilm model with individual cells and continuum eps matrix, Biotechnol. Bioeng., 94 (2006), 961–979. doi: 10.1002/bit.20917

|
| [45] |
P. G. Jayathilake, S. Jana, S. Rushton, D. Swailes, B. Bridgens, T. Curtis, et al., Extracellular polymeric substance production and aggregated bacteria colonization influence the competition of microbes in biofilms, Front. Microbio., 8 (2017), 1865–1865. doi: 10.3389/fmicb.2017.01865

|
| [46] |
D. Landa-Marbán, G. Bødtker, K. Kumar, I. S. Pop, F. A. Radu, An upscaled model for permeable biofilm in a thin channel and tube, Transp. Porous Media, 132 (2020), 83–112. doi: 10.1007/s11242-020-01381-5

|
| [47] | R. Glowinski, Numerical Methods for Nonlinear Variational Problems, Springer Series in Computational Physics, Springer-Verlag, New York, 1984. |
| [48] | V. Barbu, Nonlinear Differential Equations of Monotone Types in Banach Spaces, Springer Monographs in Mathematics, Springer, New York, 2010. |
| [49] | R. E. Showalter, Monotone Operators in Banach Space and Nonlinear Partial Differential Equations, American Mathematical Society, Providence, RI, 1997. |
| [50] |
C. Johnson, A convergence estimate for an approximation of a parabolic variational inequality, SIAM J. Numer. Anal., 13 (1976), 599–606. doi: 10.1137/0713050

|
| [51] | M. Ulbrich, Semismooth Newton Methods for Variational Inequalities and Constrained Optimization Problems in Function Spaces, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 2011. |
| [52] | X. Chen, Convergence of numerical solutions to the Allen–Cahn equation, Appl. Anal., 69 (1998), 47–56. |
| [53] |
J. Shen, X. Yang, Numerical approximations of Allen–Cahn and Cahn–Hilliard equations, Discrete. Contin. Dyn. Syst., 28 (2010), 1669–1691. doi: 10.3934/dcds.2010.28.1669

|
| [54] | A. Visintin, Models of Phase Transitions, Birkhäuser, Birkhäuser Boston, 1996. |
| [55] | L. Tartar, Incompressible fluid flow in a porous medium–convergence of the homogenization process, in Nonhomogeneous Media and Vibration Theory, Springer-Verlag, Berlin, (1980), 368–377. |
| [56] | J. Bear, A. H. D. Cheng, Modeling Groundwater Flow and Contaminant Transport, Theory and Applications of Transport in Porous Media, Springer Netherlands, 2010. |
| [57] |
R. Schulz, N. Ray, S. Zech, A. Rupp, Peter Knabner, Beyond Kozeny–Carman: predicting the permeability in porous media, Transp. Porous Media, 130 (2019), 487–512. doi: 10.1007/s11242-019-01321-y

|
| [58] |
N. Ray, A. Rupp, R. Schulz, P. Knabner, Old and new approaches predicting the diffusion in porous media, Transp. Porous Media, 124 (2018), 803–824. doi: 10.1007/s11242-018-1099-x

|
| [59] | M. Peszynska, A. Trykozko, K. Augustson, Computational upscaling of inertia effects from porescale to mesoscale, in ICCS 2009 Proceedings, LNCS 5544, Part I (eds. G. Allen, J. Nabrzyski, E. Seidel, D. van Albada, J. Dongarra and P. Sloot), Springer-Verlag, Berlin-Heidelberg, (2009), 695–704. |
| [60] | M. Peszynska, A. Trykozko, W. Sobieski, Forchheimer law in computational and experimental studies of flow through porous media at porescale and mesoscale, GAKUTO Internat. Ser. Math. Sci. Appl., 32 (2010), 463–482. |
| [61] |
A. Trykozko, M. Peszynska, M. Dohnalik, Modeling non-Darcy flows in realistic porescale proppant geometries, Comput. Geotechnics, 71 (2016), 352–360. doi: 10.1016/j.compgeo.2015.08.011

|
| [62] | M. Peszynska, J. Umhoefer, C. Shin, Reduced model for properties of multiscale porous media with changing geometry, Computation, 9 (2021), 28. |
| [63] |
T. Arbogast, H. L. Lehr, Homogenization of a Darcy–Stokes system modeling vuggy porous media, Computat. Geosci., 10 (2006), 291–302. doi: 10.1007/s10596-006-9024-8

|
| [64] |
M. Krotkiewski, I. S. Ligaarden, K. A. Lie, D. W. Schmid, On the importance of the Stokes-Brinkman equations for computing effective permeability in karst reservoirs, Commun. Comput. Phys., 10 (2011), 1315–1332. doi: 10.4208/cicp.290610.020211a

|
| [65] | H. C. Brinkman, A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles, Appl. Sci. Res. Sec. A—Mechanics Heat Chem. Eng. Math. Methods, 1 (1947), 27-34. |
| [66] |
R. Guibert, P. Horgue, D. Gerald, M. Quintard, A comparison of various methods for the numerical evaluation of porous media permeability tensors from pore-scale geometry, Math. Geosci., 48 (2016), 329–347. doi: 10.1007/s11004-015-9587-9

|
| [67] |
J. Alberto Ochoa-Tapia, S. Whitaker, Momentum transfer at the boundary between a porous medium and a homogeneous fluid—i. theoretical development, Int. J. Heat Mass Transfer, 38 (1995), 2635–2646. doi: 10.1016/0017-9310(94)00346-W

|
| [68] |
J. Alberto Ochoa-Tapia, S. Whitaker, Momentum transfer at the boundary between a porous medium and a homogeneous fluid—ii. comparison with experiment, Int. J. Heat Mass Transfer, 38 (1995), 2647–2655. doi: 10.1016/0017-9310(94)00347-X

|
| [69] |
F. A. Morales, R. E. Showalter, A Darcy–Brinkman model of fractures in porous media, J. Math. Anal. Appl., 452 (2017), 1332–1358. doi: 10.1016/j.jmaa.2017.03.063

|
| [70] |
M. Discacciati, E. Miglio, A. Quarteroni, Mathematical and numerical models for coupling surface and groundwater flows, Appl. Numer. Math., 43 (2002), 57–74. doi: 10.1016/S0168-9274(02)00125-3

|
| [71] | A. Trykozko, M. Peszynska, Pore-scale simulations of pore clogging and upscaling with large velocities, GAKUTO Int. Ser., Math. Sci. Appl., 36 (2013), 277–300. |
| [72] |
W. Deng, M. Bayani Cardenas, M. F. Kirk, S. J. Altman, P. C. Bennett, Effect of permeable biofilm on micro- and macro-scale flow and transport in bioclogged pores, Environ. Sci. Technol., 47 (2013), 11092–11098. doi: 10.1021/es402596v

|
| [73] |
M. Thullner, J. Zeyer, W. Kinzelbach, Influence of microbial growth on hydraulic properties of pore networks, Transp. Porous Media, 49 (2002), 99–122. doi: 10.1023/A:1016030112089

|
| [74] | M. Peszynska, S. Sun, Reactive Transport Module TRCHEM in IPARS, Technical report, TICAM Report 01-32, 2001. |
| [75] | F. Saaf, A Study of Reactive Transport Phenomena in Porous Media, Ph.D thesis, Rice University, 1996. |
| [76] |
C. Ebmeyer, W. B. Liu, Finite element approximation of the fast diffusion and the porous medium equations, SIAM J. Numer. Anal., 46 (2008), 2393–2410. doi: 10.1137/060657728

|
| [77] |
M. Gokieli, N. Kenmochi, M. Niezgódka, Variational inequalities of Navier-Stokes type with time dependent constraints, J. Math. Anal. Appl., 449 (2017), 1229–1247. doi: 10.1016/j.jmaa.2016.12.048

|
| [78] |
M. Gokieli, N. Kenmochi, M. Niezgódka, Mathematical modeling of biofilm development, Nonlinear Anal. Real World Appl., 42 (2018), 422–447. doi: 10.1016/j.nonrwa.2018.01.005

|
| [79] | S. V. Patankar, Numerical Heat Transfer and Fluid Flow, Series in Computational Methods in Mechanics and Thermal Sciences, Routledge, 1980. |
| 1. | Malgorzata Peszynska, Joseph Umhoefer, Choah Shin, Reduced Model for Properties of Multiscale Porous Media with Changing Geometry, 2021, 9, 2079-3197, 28, 10.3390/computation9030028 | |
| 2. | Lisa Bigler, Malgorzata Peszynska, Naren Vohra, Heterogeneous Stefan problem and permafrost models with P0-P0 finite elements and fully implicit monolithic solver, 2022, 30, 2688-1594, 1477, 10.3934/era.2022078 | |
| 3. | Malgorzata Peszynska, Naren Vohra, Lisa Bigler, Upscaling an Extended Heterogeneous Stefan Problem from the Pore-Scale to the Darcy Scale in Permafrost, 2024, 22, 1540-3459, 436, 10.1137/23M1552000 | |
| 4. | Wenqiao Jiao, David Scheidweiler, Nolwenn Delouche, Pietro de Anna, Alberto Guadagnini, Intrinsic permeability of heterogeneous porous media, 2024, 9, 2469-990X, 10.1103/PhysRevFluids.9.094102 | |
| 5. | Rachel Shen, Benedict Borer, Davide Ciccarese, M. Mehdi Salek, Andrew R. Babbin, Katherine McMahon, Microscale advection governs microbial growth and oxygen consumption in macroporous aggregates, 2024, 9, 2379-5042, 10.1128/msphere.00185-24 | |
| 6. | M. Peszynska, Z. Hilliard, N. Vohra, Coupled flow and energy models with phase change in permafrost from pore- to Darcy scale: Modeling and approximation, 2024, 450, 03770427, 115964, 10.1016/j.cam.2024.115964 | |
| 7. | Zachary Hilliard, T. Matthew Evans, Malgorzata Peszynska, Modeling flow and deformation in porous media from pore-scale to the Darcy-scale, 2024, 22, 25900374, 100448, 10.1016/j.rinam.2024.100448 | |
| 8. | Petro Martyniuk, Natalia Ivanchuk, Effect of the Microorganisms Dynamics on the Base Subsidence of the Solid Household Waste Storage During Consolidation, 2024, 11, 2414-9381, H21, 10.21272/jes.2024.11(1).h3 | |
| 9. | Yu Fu, Ganlin Yuan, Linlin Feng, Hao Gu, Mingwei Wang, Numerical simulation of two-phase oil–water flow in fractured-vuggy reservoirs based on the coefficient of porous medium proportion and coupled regions, 2024, 36, 1070-6631, 10.1063/5.0225461 | |
| 10. | Adedola Adeboye, Helen Onyeaka, Zainab Al-Sharify, Nnabueze Nnaji, Rajat Suhag, Understanding the Influence of Rheology on Biofilm Adhesion and Implication for Food Safety, 2024, 2024, 2356-7015, 10.1155/ijfo/2208472 |
| Symbol | Description | Value/Units |
| k | Index of microbial species 1\leq k \leq K . | |
| \rho_k | Dry mass density of species k | \sim 1.1\; \left[\mathrm{g} / \mathrm{cm}^{3}\right] |
| \rho_B^* | Maximum mass density of biomass | 24\times 10^3\; \left[\mathrm{g} / \mathrm{cm}^{3}\right] |
| \theta_k | Volume fraction of species k | \left[ - \right] |
| B_k | Concentration of species k , defined by Eq (2.3) | \left[ - \right] |
| B^* | Maximum total concentration of biomass | 1 \left[ - \right] |
| B_* | Threshold for mature biofilm | 0.9 B^* \left[ - \right] |
| N | Concentration of the nutrient relative to \rho_B^* | [-] \sim O(10^{-4})\; \left[\mathrm{kg} / \mathrm{m}^{3}\right]/\rho_B^* |
| {k_{_N}} | Monod half-life [can vary by factor 10^s , s\approx 6 ; see [30]] | same as N |
| \kappa | Specific substrate uptake rate | \sim O(10^{s}) \left[ {1/{\rm{h}}} \right] , s\in[-2, 0] |
| {\kappa _k} , {\kappa _B} | Growth constant incorporating yield coefficient | \sim O(1)\left[ - \right] |
| d_m | Molecular diffusivity | 6.84\; \left[\mathrm{mm}^{2}\right] |
| d_k, d_B | Diffusivity of species k | \sim O(1)\; \left[\mathrm{mm}^{2}\right] |
| d_N | Diffusivity of N ; see (2.13) | \sim O(1)\; \left[\mathrm{mm}^{2}\right] |
| T | Time scale | \sim O(10^1)\; \left[ {\rm{h}} \right] |
| \mu | Viscosity | 8.9 \times 10^{-4}\; \left[ \text{Pa}\ \text{s} \right] |
| u | Velocity in the Brinkman flow model | \sim O(10^{-1})\; \left[ {\rm{mm/h}} \right] |
| p | Pressure in the Brinkman flow model | \left[ {\rm{Pa}} \right] |
| k_b | Resistance term in Brinkman flow model | \left[ {{\rm{m}}{{\rm{m}}^2}} \right] |
| {{k}_{\Omega }} | Darcy permeability | \sim O(10^{-7})\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] |
| \gamma(t) | Biofilm interface location in 1d models, \gamma(t)=|\Omega_*(t)| | \sim O(10^{-2})\; \left[ {{\rm{mm}}} \right] |
| a(t) | Width of the active layer in 1d models, a(t)=|\Omega_a(t)| | \sim O(10^{-2})\; \left[ {{\rm{mm}}} \right] |
| v | Local shoving velocity in osmotic pressure models | \sim O(10^{-5})\; \left[ {\rm{mm/h}} \right] |
| h, \tau | Spatial and time discretization parameters | \sim O(1)\; \left[ {\mu {\rm{m}}} \right], O(1)\; \left[ {\rm{h}} \right] |
| Model and reference | Scale | L | # active species | # nutrients |
| Experimental data on |\Omega_a|=O(10^s \left[ {\mu {\rm{m}}} \right]) , 1\leq s\leq 2 . | ||||
| [28,30] | interface | L=O(10\left[ {{\rm{mm}}} \right]) | K=1 | >1 |
| (ⅰ) Discrete (IbM, CA) and hybrid models [23,31,42,43,44,45] | ||||
| interface d=2, 3 | L=O(1\left[ {{\rm{mm}}} \right]) | K=1 | 1 | |
| [23] | interface d=2 | L=O(1\left[ {{\rm{mm}}} \right]) | K=2 | > 2 |
| (ⅱ) Phase field models for bio-gel mechanics, and calcite precipitation [2,3,4,5] | ||||
| d=2 | L=O(1\left[ {{\rm{mm}}} \right]) | K=1 | 10 | |
| (ⅲ) Osmotic pressure with advective motion of interface [21,26,46] | ||||
| [26] | interface | K > > 1 | > 1 | |
| [21] | pore-scale | L=O(1 \left[ {\mu {\rm{m}}} \right]) | K=1 +EPS | 1 |
| [46] | core-scale | L=O(0.1\left[ {{\rm{mm}}} \right]) | 1 | |
| (ⅳ) Singular diffusion models | ||||
| [20] | interface, 1d | K > 1 | ||
| (ⅴ) Variational inequality models | ||||
| [17,25] | d=1, 2, 3 | L\in [10^{-2}, 1]\left[ {{\rm{mm}}} \right] | K=1 | 1 |
| Model in this paper | any d | any L | K > 1 | 1 |
| Parameters and units |
| L\; \left[ {{\rm{mm}}} \right] , T\; \left[ {\rm{h}} \right] , |
| d_{N, w}=d_m=6 , d_{B, 0}=10^{-4} , {k_{_N}}=1.18 \times10^{-3} , {\kappa _B}=0.44 , \bar{B}^*=1.01B^* . |
| L | T | h | \tau | B_{init}\left[ - \right] | N_{init}\left[ - \right] | R_{N, b w} | \kappa | \alpha | |
| (A), basic | 1 | 3 | 0.01 | 10^{-3} | 0.5\chi_{[0, 0.1]} | 1 | 0.1 | 2 | 2 |
| (A'), more singular | 1 | 3 | 0.01 | 10^{-3} | 0.5\chi_{[0, 0.1]} | 1 | 0.1 | 2 | 2.5 |
| (B), short domain | 0.1 | 3 | 0.01 | 10^{-3} | 0.5\chi_{[0, 0.01]} | 1 | 0.1 | 2 | 2 |
| (C), nutrient deficient | 1 | 3 | 0.01 | 10^{-3} | 0.5\chi_{[0, 0.1]} | 0.1 | 0.1 | 2 | 2 |
| (D), slow reaction | 1 | 3 | 0.01 | 10^{-3} | 0.5\chi_{[0, 0.1]} | 1 | 0.1 | 1 | 2 |
| (E), easy penetration | 1 | 3 | 0.01 | 10^{-3} | 0.5\chi_{[0, 0.1]} | 1 | 1 | 1 | 2 |
| B^* | B_* | B_{init} | N_{init} = N_{bd} | d_{B, 0} | d_{N, w} | R_{N, bw} | \kappa | \alpha |
| 1 | 0.9 B^* | 0.6B^*\chi_{\Omega_b(0)} | 100 | 10^{-4}d_m | d_m | 0.1 | 2 | 2 |
| Model and [reference] | Flow in \Omega_n | Free boundary | Constraint on B | biomass in \Omega_w |
| (ⅰ) Discrete and hybrid | no | not explicit | inequality | |
| IbM & continuum | cell shoving | yes | ||
| (ⅰ) Phase field models [2] | yes, extended N–S | diffuse | yes | no |
| (ⅲ) Osmotic \pi , level–set | sharp | |||
| [26] | no | advective, with v=-\nabla \pi | ||
| [21,46] | Brinkman in \Omega_b Stokes in \Omega_w |
sharp | equality | no |
| (ⅳ) Singular diffusion [20] | no | implicit | property | yes |
| (ⅴ) Variational inequality [17] | N–S in \Omega_n \setminus \Omega_b^* | implicit | inequality | yes |
| Model in this paper | Brinkman in \Omega_n | implicit | inequality | yes |
| Data | Results | |||
| L\left[ {{\rm{mm}}} \right] | k_b \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | {{k}_{\Omega }} \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | {{\left| \left\| u \right\| \right|}_{\infty }} \left[ \text{mm/hr} \right] | |
| (a) | 0.01 | 0 | 1.75\times 10^{-7} | 1.58\times 10^{2} |
| (b) | 0.01 | 10^{-5} | 7.8\times 10^{-6} | 3.42\times 10^{-1} |
| (c) | 0.01 | 10^{-4} | 5\times 10^{-6} | 3.37\times 10^{-1} |
| (e) | 0.1 | 0 | 1.75\times 10^{-5} | 1.58\times 10^{2} |
| (f) | 0.1 | 10^{-5} | 3.17\times 10^{-5} | 5.87\times 10^{-1} |
| (g) | 0.1 | 10^{-4} | 1.28\times 10^{-4} | 3.08\times 10^{-1} |
| (i) | 1 | 0 | 1.75\times 10^{-3} | 1.58\times 10^{2} |
| (j) | 1 | 10^{-5} | 1.69\times 10^{-3} | 9.84\times 10^{-1} |
| (k) | 1 | 10^{-4} | 1.45\times 10^{-3} | 8.94\times 10^{-1} |
| Parameter/Result | Value | ||
| k_b \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | \infty | 10^{-3} | 0 |
| {{k}_{\Omega }} \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | 2.6386\times 10^{-3} | 1.4765\times 10^{-3} | 8.6665\times 10^{-4} |
| {{\left| \left\| u \right\| \right|}_{\infty }} \left[ \text{mm/hr} \right] | 13.82 | 17.26 | 32.98 |
| \rho_B B^*\; \left[\mathrm{kg} / \mathrm{m}^{3}\right] | B_* | B_{init} | B_{inlet} | N_{init} | \rho_N N_{inlet}\; \left[\mathrm{kg} / \mathrm{m}^{3}\right] |
| 10^{-4} | 0.9B^* | 0.6B^*\chi_{\Omega_b(0)} | 0 | 0 | 10^{-2} |
| d_{B, 0}\; \left[\mathrm{mm}^{2}\right] | d_{N, w} | R_{N, bw} | {k_{_N}}, \kappa, \alpha | \overline{u}_D\; \left[ {\rm{mm/h}} \right] | k_b\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] |
| 0.1 | d_m | 0.1 | 2 | 0.5148 | 10^{-5} |
| B^* | B_* | B_{init}, B_{inlet} | N_{init}, N_{inlet} | d_{B, 0} | d_{N, w}, R_{N, bw} | {k_{_N}}, \kappa | \alpha | \overline{u}_D |
| 1 | 0.9 B^* | 0.6B^*\chi_{\Omega_b(0)}, 0 | 0, 1 | 3.6\times 10^{-4} | d_m, 0.1 | 2 | 2 | 0.1 |
| k_b\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | {{k}_{\Omega }}\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | {{\left| \left\| u \right\| \right|}_{\infty }}\; \left[ \text{mm/hr} \right] |
| 0 | 3.0059\times 10^{-5} | 1.6391 |
| 10^{-4} | 5.6532\times 10^{-5} | 1.2816 |
| L | T | h | \tau | B_{k, init} | \Gamma_D and N_{bd} = N_{init} | R_{N, b w}, d_{N, b} | \kappa | \alpha |
| 3 | 20 | 0.01 | 10^{-3} | in text | x = 0, 0.1 | 0.1; (2.13b) | 2 | \alpha_*(t) |
| Mildly competitive case: {{\varepsilon }_{1}} = 0.5, {{\varepsilon }_{2}} = 0.2, \delta_1 = \delta_2 = \delta_3 = 1. | ||||||||
| L | T | h | \tau | B_{k, init} | \Gamma_D and N_{bd} = N_{init} | R_{N, b w}, d_{N, b} | \kappa | \alpha |
| 2 | 20 | 0.01 | 10^{-3} | in text | x = 0, x = L, 0.01 | vary; (2.13b) | 2 | \alpha_*(t) |
| Highly competitive case: {{\varepsilon }_{1}} = variable, {{\varepsilon }_{2}} = 0, \delta_1 = 2.98; \delta_2 = \delta_3 = 0.01. | ||||||||
| Ref. | space | time | \Gamma_{bw} | flow solver |
| (ⅱ) [4,5] | FD | C-N | projection | |
| (ⅲ) [26] | O(\tau^3) -TVD | level set, WENO | none | |
| [21,46] | Galerkin linear FE | BE & semi-implicit | ALE | COMSOL |
| (ⅳ) [20] | FD-based FV | semi-implicit | implicit | none |
| (ⅴ) [17] | CCFD | BE, semi-smooth Newton | staggered in time | Fluent |
| [25] | Galerkin FE | BE | implicit | none |
| Our model | CCFD | BE & semi-implicit | operator split | MAC scheme |
| B_{init} | \Gamma_D | N_{bd} = N_{init}\; \left[\mathrm{g} / \mathrm{cm}^{3}\right] | R_{N, b w} | {k_{_N}}\; \left[\mathrm{g} / \mathrm{cm}^{3}\right] | \kappa \; \left[ {{\text{h}}^{-1}} \right]{h^{-1}} | \kappa_B |
| 1\chi_{[0, 0.05]} | x = L | 10^{-9} | 0.01 | 2\times 10^{-8} | 0.072 | 0.5 |
| Convergence for model (3.2) | |||||
| h | \tau | ||B_{err}||_1 | ||B_{err}||_2 | ||B_{err}||_1 –order | ||B_{err}||_2 –order |
| 0.0200 | 0.0200 | 2.2841e-02 | 1.2888e-01 | ||
| 0.0100 | 0.0100 | 1.0625e-02 | 8.4240e-02 | 1.1041 | 0.6134 |
| 0.0050 | 0.0050 | 4.7579e-03 | 5.2546e-02 | 1.1591 | 0.6809 |
| 0.0020 | 0.0020 | 1.4853e-03 | 2.3676e-02 | 1.2706 | 0.8701 |
| h | \tau | ||N_{err}||_1 | ||N_{err}||_2 | ||N_{err}||_1 –order | ||N_{err}||_2 –order |
| 0.0200 | 0.0200 | 1.0799e-03 | 1.2420e-03 | ||
| 0.0100 | 0.0100 | 5.2719e-04 | 6.0268e-04 | 1.0345 | 1.0432 |
| 0.0050 | 0.0050 | 2.6730e-04 | 3.0657e-04 | 0.9799 | 0.9752 |
| 0.0020 | 0.0020 | 1.0957e-04 | 1.2733e-04 | 0.9733 | 0.9589 |
| Convergence for model (3.5) | |||||
| h | \tau | ||B_{err}||_1 | ||B_{err}||_2 | ||B_{err}||_1-order | ||B_{err}||_2-order |
| 0.0200 | 0.0020 | 2.2599e-02 | 1.2806e-01 | ||
| 0.0100 | 0.0010 | 1.0496e-02 | 8.3966e-02 | 1.1064 | 0.6089 |
| 0.0050 | 0.0005 | 4.7056e-03 | 5.2642e-02 | 1.1574 | 0.6736 |
| 0.0020 | 0.0002 | 1.4779e-03 | 2.4410e-02 | 1.2639 | 0.8387 |
| h | \tau | ||N_{err}||_1 | ||N_{err}||_2 | ||N_{err}||_1--order | ||N_{err}||_2--order |
| 0.0200 | 0.0020 | 1.0701e-03 | 1.2318e-03 | ||
| 0.0100 | 0.0010 | 5.1824e-04 | 6.0381e-04 | 1.0460 | 1.0286 |
| 0.0050 | 0.0005 | 2.5751e-04 | 2.9023e-04 | 1.0090 | 1.0569 |
| 0.0020 | 0.0002 | 1.0449e-04 | 1.1946e-04 | 0.9844 | 0.9688 |
| Symbol | Description | Value/Units |
| k | Index of microbial species 1\leq k \leq K . | |
| \rho_k | Dry mass density of species k | \sim 1.1\; \left[\mathrm{g} / \mathrm{cm}^{3}\right] |
| \rho_B^* | Maximum mass density of biomass | 24\times 10^3\; \left[\mathrm{g} / \mathrm{cm}^{3}\right] |
| \theta_k | Volume fraction of species k | \left[ - \right] |
| B_k | Concentration of species k , defined by Eq (2.3) | \left[ - \right] |
| B^* | Maximum total concentration of biomass | 1 \left[ - \right] |
| B_* | Threshold for mature biofilm | 0.9 B^* \left[ - \right] |
| N | Concentration of the nutrient relative to \rho_B^* | [-] \sim O(10^{-4})\; \left[\mathrm{kg} / \mathrm{m}^{3}\right]/\rho_B^* |
| {k_{_N}} | Monod half-life [can vary by factor 10^s , s\approx 6 ; see [30]] | same as N |
| \kappa | Specific substrate uptake rate | \sim O(10^{s}) \left[ {1/{\rm{h}}} \right] , s\in[-2, 0] |
| {\kappa _k} , {\kappa _B} | Growth constant incorporating yield coefficient | \sim O(1)\left[ - \right] |
| d_m | Molecular diffusivity | 6.84\; \left[\mathrm{mm}^{2}\right] |
| d_k, d_B | Diffusivity of species k | \sim O(1)\; \left[\mathrm{mm}^{2}\right] |
| d_N | Diffusivity of N ; see (2.13) | \sim O(1)\; \left[\mathrm{mm}^{2}\right] |
| T | Time scale | \sim O(10^1)\; \left[ {\rm{h}} \right] |
| \mu | Viscosity | 8.9 \times 10^{-4}\; \left[ \text{Pa}\ \text{s} \right] |
| u | Velocity in the Brinkman flow model | \sim O(10^{-1})\; \left[ {\rm{mm/h}} \right] |
| p | Pressure in the Brinkman flow model | \left[ {\rm{Pa}} \right] |
| k_b | Resistance term in Brinkman flow model | \left[ {{\rm{m}}{{\rm{m}}^2}} \right] |
| {{k}_{\Omega }} | Darcy permeability | \sim O(10^{-7})\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] |
| \gamma(t) | Biofilm interface location in 1d models, \gamma(t)=|\Omega_*(t)| | \sim O(10^{-2})\; \left[ {{\rm{mm}}} \right] |
| a(t) | Width of the active layer in 1d models, a(t)=|\Omega_a(t)| | \sim O(10^{-2})\; \left[ {{\rm{mm}}} \right] |
| v | Local shoving velocity in osmotic pressure models | \sim O(10^{-5})\; \left[ {\rm{mm/h}} \right] |
| h, \tau | Spatial and time discretization parameters | \sim O(1)\; \left[ {\mu {\rm{m}}} \right], O(1)\; \left[ {\rm{h}} \right] |
| Model and reference | Scale | L | # active species | # nutrients |
| Experimental data on |\Omega_a|=O(10^s \left[ {\mu {\rm{m}}} \right]) , 1\leq s\leq 2 . | ||||
| [28,30] | interface | L=O(10\left[ {{\rm{mm}}} \right]) | K=1 | >1 |
| (ⅰ) Discrete (IbM, CA) and hybrid models [23,31,42,43,44,45] | ||||
| interface d=2, 3 | L=O(1\left[ {{\rm{mm}}} \right]) | K=1 | 1 | |
| [23] | interface d=2 | L=O(1\left[ {{\rm{mm}}} \right]) | K=2 | > 2 |
| (ⅱ) Phase field models for bio-gel mechanics, and calcite precipitation [2,3,4,5] | ||||
| d=2 | L=O(1\left[ {{\rm{mm}}} \right]) | K=1 | 10 | |
| (ⅲ) Osmotic pressure with advective motion of interface [21,26,46] | ||||
| [26] | interface | K > > 1 | > 1 | |
| [21] | pore-scale | L=O(1 \left[ {\mu {\rm{m}}} \right]) | K=1 +EPS | 1 |
| [46] | core-scale | L=O(0.1\left[ {{\rm{mm}}} \right]) | 1 | |
| (ⅳ) Singular diffusion models | ||||
| [20] | interface, 1d | K > 1 | ||
| (ⅴ) Variational inequality models | ||||
| [17,25] | d=1, 2, 3 | L\in [10^{-2}, 1]\left[ {{\rm{mm}}} \right] | K=1 | 1 |
| Model in this paper | any d | any L | K > 1 | 1 |
| Parameters and units |
| L\; \left[ {{\rm{mm}}} \right] , T\; \left[ {\rm{h}} \right] , |
| d_{N, w}=d_m=6 , d_{B, 0}=10^{-4} , {k_{_N}}=1.18 \times10^{-3} , {\kappa _B}=0.44 , \bar{B}^*=1.01B^* . |
| L | T | h | \tau | B_{init}\left[ - \right] | N_{init}\left[ - \right] | R_{N, b w} | \kappa | \alpha | |
| (A), basic | 1 | 3 | 0.01 | 10^{-3} | 0.5\chi_{[0, 0.1]} | 1 | 0.1 | 2 | 2 |
| (A'), more singular | 1 | 3 | 0.01 | 10^{-3} | 0.5\chi_{[0, 0.1]} | 1 | 0.1 | 2 | 2.5 |
| (B), short domain | 0.1 | 3 | 0.01 | 10^{-3} | 0.5\chi_{[0, 0.01]} | 1 | 0.1 | 2 | 2 |
| (C), nutrient deficient | 1 | 3 | 0.01 | 10^{-3} | 0.5\chi_{[0, 0.1]} | 0.1 | 0.1 | 2 | 2 |
| (D), slow reaction | 1 | 3 | 0.01 | 10^{-3} | 0.5\chi_{[0, 0.1]} | 1 | 0.1 | 1 | 2 |
| (E), easy penetration | 1 | 3 | 0.01 | 10^{-3} | 0.5\chi_{[0, 0.1]} | 1 | 1 | 1 | 2 |
| B^* | B_* | B_{init} | N_{init} = N_{bd} | d_{B, 0} | d_{N, w} | R_{N, bw} | \kappa | \alpha |
| 1 | 0.9 B^* | 0.6B^*\chi_{\Omega_b(0)} | 100 | 10^{-4}d_m | d_m | 0.1 | 2 | 2 |
| Model and [reference] | Flow in \Omega_n | Free boundary | Constraint on B | biomass in \Omega_w |
| (ⅰ) Discrete and hybrid | no | not explicit | inequality | |
| IbM & continuum | cell shoving | yes | ||
| (ⅰ) Phase field models [2] | yes, extended N–S | diffuse | yes | no |
| (ⅲ) Osmotic \pi , level–set | sharp | |||
| [26] | no | advective, with v=-\nabla \pi | ||
| [21,46] | Brinkman in \Omega_b Stokes in \Omega_w |
sharp | equality | no |
| (ⅳ) Singular diffusion [20] | no | implicit | property | yes |
| (ⅴ) Variational inequality [17] | N–S in \Omega_n \setminus \Omega_b^* | implicit | inequality | yes |
| Model in this paper | Brinkman in \Omega_n | implicit | inequality | yes |
| Reference | Geometry and Scale | Permeability |
| [26] | channel | |
| [13] | channels, many--pore | no |
| [16] | thin strip (1d) | yes |
| [21,46] | channel | yes |
| [25] | 1d & many-pore | |
| [17] & our model | channel, one-pore, many-pore | yes |
| Data | Results | |||
| L\left[ {{\rm{mm}}} \right] | k_b \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | {{k}_{\Omega }} \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | {{\left| \left\| u \right\| \right|}_{\infty }} \left[ \text{mm/hr} \right] | |
| (a) | 0.01 | 0 | 1.75\times 10^{-7} | 1.58\times 10^{2} |
| (b) | 0.01 | 10^{-5} | 7.8\times 10^{-6} | 3.42\times 10^{-1} |
| (c) | 0.01 | 10^{-4} | 5\times 10^{-6} | 3.37\times 10^{-1} |
| (e) | 0.1 | 0 | 1.75\times 10^{-5} | 1.58\times 10^{2} |
| (f) | 0.1 | 10^{-5} | 3.17\times 10^{-5} | 5.87\times 10^{-1} |
| (g) | 0.1 | 10^{-4} | 1.28\times 10^{-4} | 3.08\times 10^{-1} |
| (i) | 1 | 0 | 1.75\times 10^{-3} | 1.58\times 10^{2} |
| (j) | 1 | 10^{-5} | 1.69\times 10^{-3} | 9.84\times 10^{-1} |
| (k) | 1 | 10^{-4} | 1.45\times 10^{-3} | 8.94\times 10^{-1} |
| Parameter/Result | Value | ||
| k_b \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | \infty | 10^{-3} | 0 |
| {{k}_{\Omega }} \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | 2.6386\times 10^{-3} | 1.4765\times 10^{-3} | 8.6665\times 10^{-4} |
| {{\left| \left\| u \right\| \right|}_{\infty }} \left[ \text{mm/hr} \right] | 13.82 | 17.26 | 32.98 |
| \rho_B B^*\; \left[\mathrm{kg} / \mathrm{m}^{3}\right] | B_* | B_{init} | B_{inlet} | N_{init} | \rho_N N_{inlet}\; \left[\mathrm{kg} / \mathrm{m}^{3}\right] |
| 10^{-4} | 0.9B^* | 0.6B^*\chi_{\Omega_b(0)} | 0 | 0 | 10^{-2} |
| d_{B, 0}\; \left[\mathrm{mm}^{2}\right] | d_{N, w} | R_{N, bw} | {k_{_N}}, \kappa, \alpha | \overline{u}_D\; \left[ {\rm{mm/h}} \right] | k_b\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] |
| 0.1 | d_m | 0.1 | 2 | 0.5148 | 10^{-5} |
| B^* | B_* | B_{init}, B_{inlet} | N_{init}, N_{inlet} | d_{B, 0} | d_{N, w}, R_{N, bw} | {k_{_N}}, \kappa | \alpha | \overline{u}_D |
| 1 | 0.9 B^* | 0.6B^*\chi_{\Omega_b(0)}, 0 | 0, 1 | 3.6\times 10^{-4} | d_m, 0.1 | 2 | 2 | 0.1 |
| k_b\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | {{k}_{\Omega }}\; \left[ {{\rm{m}}{{\rm{m}}^2}} \right] | {{\left| \left\| u \right\| \right|}_{\infty }}\; \left[ \text{mm/hr} \right] |
| 0 | 3.0059\times 10^{-5} | 1.6391 |
| 10^{-4} | 5.6532\times 10^{-5} | 1.2816 |
| L | T | h | \tau | B_{k, init} | \Gamma_D and N_{bd} = N_{init} | R_{N, b w}, d_{N, b} | \kappa | \alpha |
| 3 | 20 | 0.01 | 10^{-3} | in text | x = 0, 0.1 | 0.1; (2.13b) | 2 | \alpha_*(t) |
| Mildly competitive case: {{\varepsilon }_{1}} = 0.5, {{\varepsilon }_{2}} = 0.2, \delta_1 = \delta_2 = \delta_3 = 1. | ||||||||
| L | T | h | \tau | B_{k, init} | \Gamma_D and N_{bd} = N_{init} | R_{N, b w}, d_{N, b} | \kappa | \alpha |
| 2 | 20 | 0.01 | 10^{-3} | in text | x = 0, x = L, 0.01 | vary; (2.13b) | 2 | \alpha_*(t) |
| Highly competitive case: {{\varepsilon }_{1}} = variable, {{\varepsilon }_{2}} = 0, \delta_1 = 2.98; \delta_2 = \delta_3 = 0.01. | ||||||||
| Ref. | space | time | \Gamma_{bw} | flow solver |
| (ⅱ) [4,5] | FD | C-N | projection | |
| (ⅲ) [26] | O(\tau^3) -TVD | level set, WENO | none | |
| [21,46] | Galerkin linear FE | BE & semi-implicit | ALE | COMSOL |
| (ⅳ) [20] | FD-based FV | semi-implicit | implicit | none |
| (ⅴ) [17] | CCFD | BE, semi-smooth Newton | staggered in time | Fluent |
| [25] | Galerkin FE | BE | implicit | none |
| Our model | CCFD | BE & semi-implicit | operator split | MAC scheme |
| B_{init} | \Gamma_D | N_{bd} = N_{init}\; \left[\mathrm{g} / \mathrm{cm}^{3}\right] | R_{N, b w} | {k_{_N}}\; \left[\mathrm{g} / \mathrm{cm}^{3}\right] | \kappa \; \left[ {{\text{h}}^{-1}} \right]{h^{-1}} | \kappa_B |
| 1\chi_{[0, 0.05]} | x = L | 10^{-9} | 0.01 | 2\times 10^{-8} | 0.072 | 0.5 |
| Convergence for model (3.2) | |||||
| h | \tau | ||B_{err}||_1 | ||B_{err}||_2 | ||B_{err}||_1 –order | ||B_{err}||_2 –order |
| 0.0200 | 0.0200 | 2.2841e-02 | 1.2888e-01 | ||
| 0.0100 | 0.0100 | 1.0625e-02 | 8.4240e-02 | 1.1041 | 0.6134 |
| 0.0050 | 0.0050 | 4.7579e-03 | 5.2546e-02 | 1.1591 | 0.6809 |
| 0.0020 | 0.0020 | 1.4853e-03 | 2.3676e-02 | 1.2706 | 0.8701 |
| h | \tau | ||N_{err}||_1 | ||N_{err}||_2 | ||N_{err}||_1 –order | ||N_{err}||_2 –order |
| 0.0200 | 0.0200 | 1.0799e-03 | 1.2420e-03 | ||
| 0.0100 | 0.0100 | 5.2719e-04 | 6.0268e-04 | 1.0345 | 1.0432 |
| 0.0050 | 0.0050 | 2.6730e-04 | 3.0657e-04 | 0.9799 | 0.9752 |
| 0.0020 | 0.0020 | 1.0957e-04 | 1.2733e-04 | 0.9733 | 0.9589 |
| Convergence for model (3.5) | |||||
| h | \tau | ||B_{err}||_1 | ||B_{err}||_2 | ||B_{err}||_1-order | ||B_{err}||_2-order |
| 0.0200 | 0.0020 | 2.2599e-02 | 1.2806e-01 | ||
| 0.0100 | 0.0010 | 1.0496e-02 | 8.3966e-02 | 1.1064 | 0.6089 |
| 0.0050 | 0.0005 | 4.7056e-03 | 5.2642e-02 | 1.1574 | 0.6736 |
| 0.0020 | 0.0002 | 1.4779e-03 | 2.4410e-02 | 1.2639 | 0.8387 |
| h | \tau | ||N_{err}||_1 | ||N_{err}||_2 | ||N_{err}||_1--order | ||N_{err}||_2--order |
| 0.0200 | 0.0020 | 1.0701e-03 | 1.2318e-03 | ||
| 0.0100 | 0.0010 | 5.1824e-04 | 6.0381e-04 | 1.0460 | 1.0286 |
| 0.0050 | 0.0005 | 2.5751e-04 | 2.9023e-04 | 1.0090 | 1.0569 |
| 0.0020 | 0.0002 | 1.0449e-04 | 1.1946e-04 | 0.9844 | 0.9688 |