Multi-source remote sensing image classification based on two-channel densely connected convolutional networks

1.   Introduction

It is one of the most important application fields of remote sensing technology to study the classification of ground surface covering using remote sensing data. At present, with the development of multi-source remote sensing technology and the further improvement of remote sensing image resolution, the techniques and methods for processing and analyzing multi-source remote sensing data are gradually increasing. The multi-source data system composed of HSI and LiDAR provides a way to obtain ground-truth information. The HSI contain abundant spectral information and can be used for the classification of ground objects. The LiDAR are used to provide structural information of surface features. In fact, the value of big data is concentrated in the multi-agent decision-making, multi-perspective integration, cross-border correlation and the interaction between internal and external data. Therefore, the analysis of remote sensing data from a single source is difficult to meet the needs of management decisions, and how to mine value from the multi-source fusion of remote sensing big data and provide support for management decisions is an urgent problem to be solved.

The classification of ground objects in remote sensing images is a long-standing topic, among which the classification of HSI is the most attractive. In the development of HSI, there are many classification methods, and different methods have different performance under different conditions. According to the algorithm used in the classification, it can be divided into two categories: classification method based on spectral matching and classification method based on statistical features ^[1]. The spectral angle matching, Euclidean distance and spectral information divergence methods are the main classification method based on spectral matching. The maximum likelihood classification, support vector machine, sparse representation and neural network methods are the main classification method based on statistical features. According to whether to use the training sample, it can be divided into supervised classification method and unsupervised classification method. The K-means clustering and ISODATA methods are the main unsupervised classification method. With the development of artificial intelligence, supervised classification methods have developed from the classical Bayesian theory and linear discriminant analysis to the most popular deep learning method in recent years. Among them, the idea of machine learning runs through the whole research system of HSI classification.

Most of the research on collaborative classification of multi-source images is based on HSI. More research focuses on information extraction and collaborative processing of multi-source images. Benediktsson ^[2] researched the decision fusion classification of multi-source images such as HSI. FChen et al. ^[3] researched the influence of different RS feature on classification performance. The data of Landsat-8 land imager, moderate resolution imaging spectrometer, China environment 1 series and space borne thermal emission and reflection digital elevation model are integrated. In particular, the time feature with abundant vegetation information significantly improves the overall accuracy of classification. Mahmood et al. ^[4] proposed a method for collaborative classification of HSI and high-resolution color images based on background context information to perform sub pixel classification mapping. Goodenough et al. ^[5] researched the fusion classification mapping of Hyperion hyperspectral, ALI (Advanced Land Imager) multispectral and Landsat multispectral images based on the forest coverage in parts of North America. Dimitris et al. ^[6] researched the method of classification mapping by using decision level method to merge hyperspectral and multispectral images for forest plant species. The problem of forest biomass mapping by using Hyperion images, tandem-x and worldview-2 images. Four machine learning algorithms were used to estimate the biomass and find the optimal combination ^[7]. Delalieux et al. ^[8] researched Unmixing-based fusion of hyperspatial and hyperspectral airborne imagery for early detection of vegetation stress. Packard et al. ^[9] introduces a method of detection and classification of small targets combining hyperspectral and high-resolution images, The suspected targets is detected by using HSI anomaly detection algorithm, and then the suspected targets is classified by using spatial features of high-resolution images. Kaufman et al. ^[10] aimed at the problem of target recognition and classification of airborne hyperspectral and high-resolution images, the advantages of spatial-spectral joint feature versus spectral feature, spatial feature and pixel fusion method are compared and analyzed in detail. Chang et al. ^[11] aimed at the eutrophication of water, researched the use of hyperspectral and multispectral images for the monitoring of microcystin in water. On the other hand, some achievements have been made in the cooperative application of HSI and LiDAR. Dalponte et al. ^[12] studied the fine classification of vegetation using HSI and LiDAR in complex and dense forest areas. Merentitis et al. ^[13] used the random forest method to classify different features extracted from hyperspectral and LiDAR images. The data fusion competition has been held by IEEE earth science and remote sensing association, the subject is the fusion and classification of hyperspectral and LiDAR images, which has been supported by scholars at home and abroad and has made some breakthroughs ^[14]. In addition, some scholars have researched the fusion classification and recognition of optical images (hyperspectral/multispectral/panchromatic images) and Synthetic Aperture Radar (SAR) images.

However, most of above classification methods based on multi-source data are performed by the shallow machine learning algorithms, and they generally suffer from the low utilization rate of low-level features, over reliance on artificial experiences in the selection and combination optimization of feature vectors, the poor automation level in extraction process and the unsatisfactory extraction accuracy.

In recent years, deep learning has been widely used in the HSI classification, due to the deep learning can extract distinguishing features. Among the numerous algorithms based on deep learning, Stack Denoising auto-coder (SDAE) ^[15] and Convolutional Neural Network (CNN) ^[16] are the most representative classification methods. Chen et al. ^[17] applied SAE to extract features of HSI. Firstly, PCA was used to reduce the dimension of the original HSI, and then the neighborhood information of each pixel was extracted and converted into a one-dimensional vector, which was then connected with the spectral vector. Finally, SAE was used for feature extraction and LR was used as a classifier for classification. Ma et al. ^[18] proposed an improved SAE algorithm for HSI classification, In order to improve the classification accuracy of HSI a regular term is added to describe the spectral similarity. Mughees ^[19] proposed another HSI classification algorithm. Firstly the spectral information of HSI is extracted by SAE, and then the spatial information of image is extracted by the segmentation algorithm based on edge adjustment, and finally the classification result is obtained by the voting method. CNN is also widely used in HSI classification because it can extract spatial features of two-dimensional images very well ^[20,21]. Yue et al. ^[22] first transform the one dimensional spectral vector into two-dimensional spectral features, then the PCA algorithm is used to reduce the dimension of the original HSI. The rectangular window is used to extract the neighborhood information of each pixel as the training sample. Finally separately with two characteristic figure to CNN for training, get the depth characteristics, The CNN was trained with two kinds of feature maps, and the CNN was classified with LR. W.Z.Zhao and S.H.Du proposed a HSI classification algorithm based on dimension reduction and deep learning ^[23]. Firstly, the spectral dimension of HSI was reduced by balanced local discriminant embedding (BLDE). Then, the spatial feature of HSI was extracted by CNN. Finally, the fused features were classified by SVM. Santara et al. ^[24] proposed a new CNN framework for HSI classification (Band-Adaptive Spectral Spatial feature learning neural network, BASS). The algorithm is divided into three steps. Firstly, spectral feature selection and band segmentation are carried out for the original HSI, and a few bands are selected. Secondly, each band is trained by CNN. Finally, the output results of each CNN are connected and classified by softmax classifier. Compared with other HSI classification algorithms based on CNN, this algorithm can alleviate the problem of lacking training samples due to the feature selection.

Although the models have been used for HSI classification and achieved state-of-the-art results, it is counterintuitive that the classification accuracy decreases with the increase of convolutional layers after four or five stacked layers ^[25]. Inspired by the latest deep residual learning framework proposed in ^[26], this deteriorating issue can be solved by adding shortcut connections between every other layer and propagating the value of features. Residual Networks can be regarded as an extension of Convolutional Neural Networks with skip connections that facilitate the propagation of gradients and performed robustly with very deep architecture.

In order to solve these problems, a novel multi-source remote sensing image classification model based on two-channel densely connected convolutional networks (TDCC) was proposed. The main contributions of this paper includes the following aspects: (1) a spatial-spectral feature extraction model of HSI based on dual-channel DenseNet was proposed. The spatial-spectral feature was extracted by densely connected convolutional networks with different dimensions, the spatial feature was extracted by 2D-DenseNet and the spectral was extracted by 1D- DenseNet. (2) A cascade DenseNet model is designed for extracting LiDAR features, the multilevel feature was reused and the discriminate spatial feature was extracted by the model. (3) A feature fusion network is designed to fuse the HSI features extracted from part (1) and LiDAR features extracted from part (2). The fused features were classified and the output result is the category of the corresponding pixel. The experiment results show that compared with the current mainstream classification methods of remote sensing images, the proposed network has a well classification performance and achieves the optimal classification effect in OA, AA and Kappa.

The remainder of this paper is organized as follows: In Section 2, we provide a description of related work. In Section 3, we provide an overview of the proposed model first, and then elaborated the detail of the framework of the proposed model. In Section 4 presents the experimental results and discussions. Finally, we draw conclusions in Section 5.

2.   Related works

2.1.   Neural network

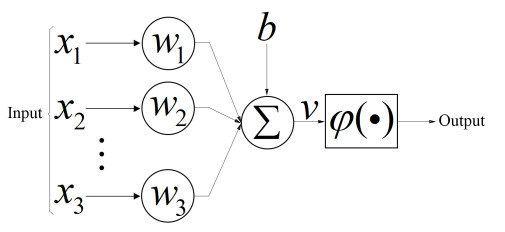
Neural network is a network that composed of individual neurons hierarchy connected. Figure 1 is a single neuron network model. The calculation method of output y is shown as Eq (2.1):

Figure 1.  The single neuron network model.

DownLoad: Full-Size Img PowerPoint

$v$ is the output, $x$ is the input, $w$ is the weight, $b$ is the bias, $\varphi()$ is the activation function, $y$ is the output after being activated.

The topology consists of the neurons connected by a hierarchy. It is divided into input layer, hidden layer and output layer. As shown in Figure 2:

Figure 2.  The architecture of neuron network.

DownLoad: Full-Size Img PowerPoint

A neural network with more than 3 layers is capable of feature learning. The more layers the model has, the more complex and abstract features it can express. Typically, deep neural networks contain many hidden layers. Suppose there are $m$ neurons in the $l-1$ layer, Then the output $a_{j}^{l}$ of the $jth$ neuron in the $l$ layer. The calculation method is as Eq (2.2)

The process described above is called forward propagation algorithm. During the training, the values of parameters $w$ and $b$ are constantly updated. Before the first forward propagation of the network, $w$ is initialized by Xavier method ^[27], and $b$ was initialized to $0$. Then the values of $w$ and $b$ are updated by Back propagation algorithm. It is difficult to be satified at one time, and it needs to be updated through multiple iterations, until the error between the output value of the model and the true value is less than a certain threshold. The difference between the predicted value and the true value is the loss function. Cross entropy is the most commonly used loss function, it is shown as Eq (2.3)

$y_{i}$ is the true value of the input data $x_{i}$, $P_{i}$ is the predict value of the input data $x_{i}$. And then $w$ and $b$ are updated by the Eq (2.4)

2.2.   CNN and DenstNet

2.2.1.   CNN

In recent years, deep learning has been widely used in the classification of images because it can extract discriminative features. CNN is the most representative remote sensing image classification method based on deep learning. CNN originated from Lenet-5 proposed by Lecun et al. ^[28]. It is an end-end mapping method, the procedure can be formulate as Eq (2.5):

$f(\bullet)$ is the activation function, $x$ is the input data, $W$ is the convolution kernel function, $h$ is the feature map. The eigenvector $h$ calculated by convolution kernel $W$ at each layer is a feature map. Each convolution layer contains several convolution kernels, which are used to extract features of different positions in the image. The feature map is extracted by each convolution layer, the data is in three-dimensional form. It can be viewed as a stack of many two-dimensional images, each of which is called a feature map. In the input layer, if it is a grayscale image, there is only one feature map. If it is a color image, there are 3 feature maps (red, green and blue). There are several convolution kernels between layers, Convolution operation is performed between each feature map of the upper layer and each convolution kernel, and the feature map is input to the next convolution layer. In this paper, feature map represents the features obtained through convolution calculation, while 2D spatial map represents the final classification results. The single-layer network can be continuously stacked as a deep network, and the underlying features can be gradually abstracted into higher-order features. Finally, the classification can be completed by a classifier. VGG ^[29] proposed by Simonyan indicated that the deeper the network, the better the recognition effect. Because the deeper network can combine the continuous feature to form the high-dimensional feature and the correlation between the sample data can be represented. However, when the network deepens to a certain number, the classification and recognition effect will become worse. The main reason is that the deeper the network is, the more likely it is to produce gradient disappearance phenomenon, fall into local minimum value, and train concussion phenomenon in the learning process. Therefore, it is difficult to make use of the powerful feature extraction ability of deep layer network by stacking shallow layer network into deep network.

2.2.2.   DenseNet

To solve this problem, Huang et al. ^[30] proposed a dense connected convolutional networks (DenseNet) in 2017. The advantages of deep residual network (ResNet) and Inception network have been utilized by DenseNet. However, the methods of deepening network layers (ResNet) and widening network architecture (Inception) are not adopted to improve network performance. The detection accuracy and network parameters can be improved by setting feature multiplexing and bypass connection from the point of view of optimal feature.

The gradient of the front layer can be calculated by the product of the back layer's gradient in the multilayer depth network. With the increase of network depth, the learning rate of the hidden layer in front may be lower than that of the hidden layer behind, gradient disappearance or gradient explosion occurs. The output of DenseNet unit is shown as Eq (2.6):

$x_{l}$ is the output of the $lth$ layer. $H_{l}$ represents the nonlinear transformation. It can be seen that the output of the $lth$ layer is the sum of the nonlinear transformation of the $x_{l-1}$ layer's output and $x_{l-1}$ layer's output. The features extracted from each layer of the traditional deep network are equivalent to a nonlinear transformation of the input data, so the complexity of increases with the increase of the depth. DenseNet's input for each layer comes from the output of all previous layers, which is equivalent to each layer directly connecting the input layer and the loss layer, the network structure became more compact and the gradient disappearance was alleviated. The output is shown as Eq (2.7):

$[x_{0}, x_{1}, \dots, x_{l-1}]$ represents the cascading of the $0th$ layer to $(l-1)th$ layer's feature map.

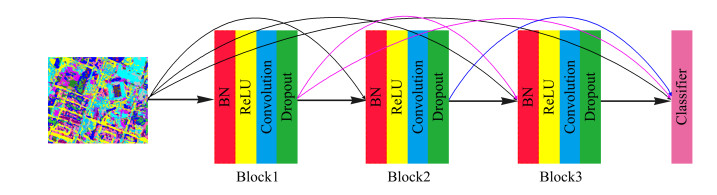
In order to make the DenseNet more suitable for the classification of hyperspectral remote sensing images. In this paper, the architecture of DenseNet is redesigned according to the characteristics of HSI. DenseNet consists of several units, and each unit contains BN, ReLU, convolution and dropout operations. As shown in Figure 3.

Figure 3.  The architecture of DenseNet.

DownLoad: Full-Size Img PowerPoint

2.3.   BN, Relu and Dropout

2.3.1.   BN

Batch Normalization ^[31] was invented by Google inc. in 2015. This is a technique for training deep neural networks. It can not only accelerate the convergence speed of the model, but also alleviate the problem of "gradient dispersion". It makes the training process much easier. In the previous neural network training, we only normalized the input data, but did not normalize the middle layer data. However, the data distribution of the input data is likely to be changed after matrix multiplication and nonlinear operation such as $σ(wx+b)$. With the multi-layer computation in the deep network, the data distribution will be changed more and more. The emergence of BN breaks this rule, and we can normalize the data at any layer in the network. In this paper, BN optimization method is adopted for each layer in the network. The algorithm of BN is as Table 1:

Table 1.  The algorithm of BN.

Input: mini-batch $X:\{\ x_{1}, x_{2}, \cdots, x_{m} \}$ Output: Normalized $y_{i} = BN_{\gamma, \beta}(x_{i})$
(1) $\mu_{\beta}\longleftarrow \frac{1}{m}\sum_{i = 1}^{m}x_{i}$ (2) $\sigma_{\beta}^{2}\longleftarrow \frac{1}{m}\sum_{i = 1}^{m}(x_{i}-\mu_{\beta})$ (3) $\hat{x} \longleftarrow \frac{x_{i}-\mu_{\beta}}{\sqrt{\sigma_{\beta}^{2}+\epsilon}}$ (4) $y_{i} \longleftarrow \gamma\hat{x}_{i}+\beta = BN_{\gamma, \beta}(x_{i})$ (5) return $y$

---

 | Show Table

DownLoad: CSV

(1) Calculate the mean value of each small batch training data;

(2) Calculate the variance of each small batch of training data;

(3) the training data of this batch is normalized by using the mean and variance;

(4) the network can recover the characteristic distribution by training the parameters A and B for translation and scaling calculation;

(5) Return y.

2.3.2.   Relu

In the multi-layer neural network, there is a relationship between the output of the upper layer and the input of the lower layer, which is called activation function. Relu function is a common activation function, and its formula is as Eq (2.8):

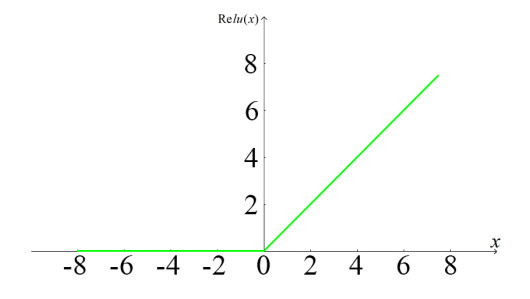
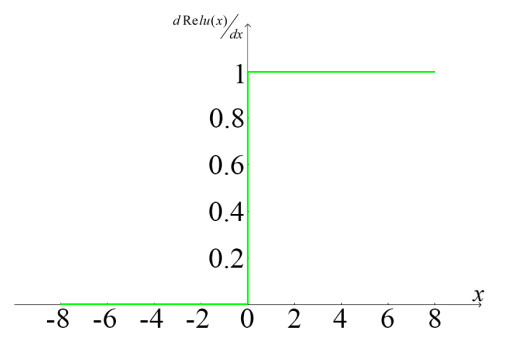
We can draw the curve of Relu and the curve of its derivative as Figures 4 and 5.

Figure 4.  The curve of Relu.

DownLoad: Full-Size Img PowerPoint

Figure 5.  The curve of Relu's derivative.

DownLoad: Full-Size Img PowerPoint

It is obvious from the expression and the graph that the ReLU function is a piecewise linear function, turning all negative values into 0, while the positive values remain the same. This means that only a few neurons are activated at the same time, which makes the network sparse and thus very efficient for computing. Specifically, in the deep neural network model, when the layers of the model is N, the activation rate of ReLU will decrease by $2^n$ power.

Relu has the following advantages: (1) No saturation region, no gradient disappearance problem; (2) No complex exponential operation, high computational efficiency; (3) Fast convergence; (4) More in line with biological mechanisms. Therefore, Relu is selected as the activation function in this paper.

2.3.3.   Dropout

The classification model of remote sensing image based on machine learning often has too many parameters and too few training samples. Therefore, the trained model is prone to overfitting. The model has smaller loss function and higher prediction accuracy on training data. However, the loss function is relatively large and the prediction accuracy is low on testing data.

Dropout ^[32] have been proposed in 2012. In each training batch, overfitting can be significantly reduced by ignoring half of the feature detectors (leaving half of the hidden node values at 0). In a nutshell, Dropout means that when we propagate forward, the activation value of a certain neuron stops working with a certain probability p, which makes the model more generalized because it does not rely too much on some local features. Assuming that the input data is X and the output data is Y, the process of Dropout is as follows:

(1) The probability vector R is generated by Bernoulli function, and the hidden neurons in the network are deleted with probability vector R. The input and output neurons remain unchanged. (The dotted line in Figure 6 is part of the neurons that have been temporarily deleted.)

Figure 6.  The neuron network with Dropout.

DownLoad: Full-Size Img PowerPoint

(2) The loss value is calculated by the forward propagated algorithm though the modified network. After executing this process in a small batch of training samples, the corresponding parameters $(w, b)$ were updated in accordance with the stochastic gradient descent method on the network of undeleted neurons.

(3) Repeat the process: resume the deleted neurons, select another batch of neurons in the hidden layer and delete them, select a small batch of training samples, forward propagated and then back propagate, and update parameters $(w, b)$ according to stochastic gradient descent method.

(4) Keep repeating (1)$-$(3) until the iterations is reached.

Currently, Dropout is widely used in deep neural networks. As a super parameter, Dropout needs to be tried according to the network and application field.

3.   Proposed methods

Due to the strong feature extraction capability of DenseNet network. In this paper, a two-channel densely connected convolutional network is proposed to extract the features of remote sensing data. The network can organically combine the features of HSI with other data sources, such as LiDAR data. This section mainly introduces the basic network architecture and flow of multi-source remote sensing image classification method based on two-channel densely connected convolutional network.

3.1.   Overview of the architecture

The basic spatial unit is that the HSI data comes in pixels and the LiDAR derived Digital Surface Model (DSM) both at the same spatial resolution (2.5 m). The hyperspectral imagery consists of 144 spectral bands in the 380 nm to 1050 nm region and has been calibrated to at-sensor spectral radiance units, SRU = μW/(cm2sr nm). The corresponding co-registered DSM consists of elevation in meters above sea level (per the Geoid 2012A model). The data was acquired by the NSF-funded Center for Airborne Laser Mapping (NCALM) over the University of Houston campus and the neighboring urban area. The LiDAR data was acquired on June 22, 2012, between the time 14:37:55 to 15:38:10 UTC. The average height of the sensor above ground was 2000ft; The hyperspectral data was acquired on June 23, 2012 between the times 17:37:10 to 17:39:50 UTC. The average height of the sensor above ground was 5500ft.

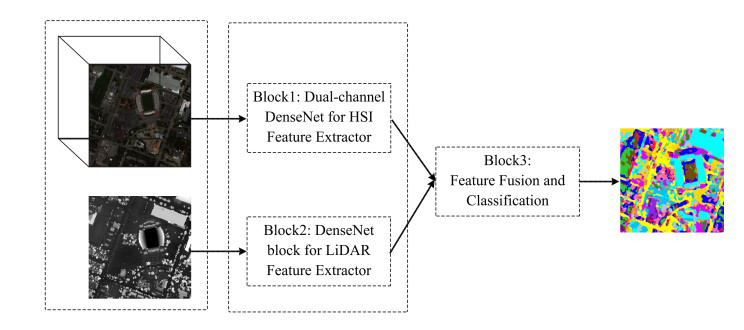
Overview of the architecture is shown as Figure 7. The multi-source remote sensing image classification method based on two-channel densely connected convolutional network consists of three parts:

Figure 7.  Overview of the proposed architecture.

DownLoad: Full-Size Img PowerPoint

(1) Block1: Dual-channel DenseNet for HSI feature extractor. A dual-channel DenseNet network is proposed to extract both spatial feature and spectral feature. Different dimensional were used to extract the features of HSI, in which 2D-DenseNet is used to extract the spatial feautre, and 1D-DenseNet is used to extract the spectral feature. Subsequently, spatial features and spectral features are fused in the subsequent network layers.

(2) Block2: Cascade DenseNet for LiDAR feature extractor. The cascade DenseNet is designed to reuse multilevel features. The cascade DenseNet consists of three units, and each unit contains BN, ReLU, Convolution and Dropout operation. The network can reuse multilevel features of the LiDAR to improve the classification accuracy.

(3) Block3: Feature fusion and classification module. The DenseNet network was designed to fuse the HSI features extracted from Block1 and LiDAR remote sensing image features extracted from Block2, and classify the fused features. The output result is the category of the corresponding pixel.

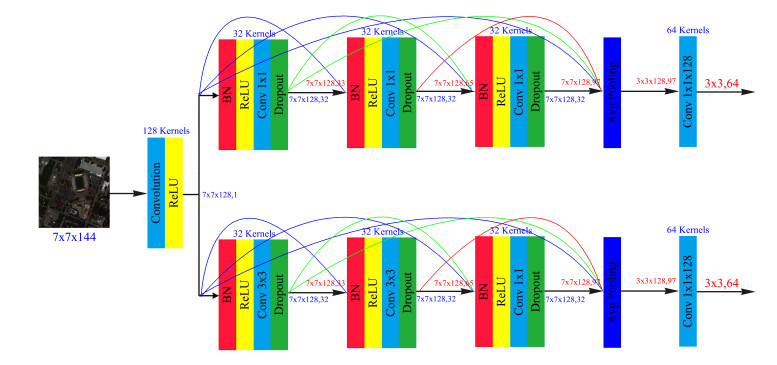
3.2.   Dual-channel DenseNet for HSI feature extractor

The spatial and spectral feature extraction channel of HSI was designed. The network consists of dual-channel: spectral channel and spatial channel. The architecture of this model is shown in Figure 8.

Figure 8.  The architecture of dual-channel DenseNet for HSI feature extractor.

DownLoad: Full-Size Img PowerPoint

First, a convolution layer followed by a rectified liner unit is used to limit the number of feature maps sent to dual-channel DenseNet for HSI feature extractor. The number of feature maps can be limited in a reasonable range through the setting of kernel number.

Let $N^{k}$ be the number of filters and $X$ denote the input data, $\bullet$ is the convolution operator, and $W$ and $b$ are the filter and bias, respectively. Output $Y$ is shown as Eq (3.1):

The ReLU function is defined as Eq (3.2):

Where $Z$ is the input of the ReLU function.

Then the network is fed with discriminative spectral features and well-preserved spatial features, which makes the subsequent spectral-spatial feature learning process easier.

Since the spectral dimension of HSI is one-dimensional, the convolution operation is one-dimensional convolution. The spectral feature extraction channel is composed of three DenseNet units, each of which contains the Batch Normalization, ReLU, convolution layer and Dropout operation. Since the spectral dimension of HSI is one-dimensional vectors, we defined it as a scalar, the convolution operation is one-dimensional convolution. The traditional ReLU function is used to modify the distribution of data. The process of spectral feature extraction is as follows: the spectral vector for the pixel at the location $p_{ij}$ is denoted as $H_{ij}^{spectral}$. $H_{ij}^{spectral}$ is a one dimension vector. It is input into the spectral feature extraction channel. The output is the spectral feature $F_{ij}^{spectral}$ after the batch normalization, ReLU, convolution, dropout operation. The procedure can be formulated as Eq (3.3):

The spatial feature is a two-dimenional matrix centered at $p_{ij}$ and r is its radius. It is input into the spatial. The architecture of the spatial feature extraction channel is the same as the spectral feature extraction channel. The process of spatial feature extraction is as follows: the spatial vector for the pixel at the location $p_{ij}$ is denoted as $H_{ij}^{spatial}$. $H_{ij}^{spatial}$ is a two dimension vector centered with $p_{ij}$ and $r$ is its radius. We defined it as a matrix. It is input into the spatial feature extraction channel. The output is the spatial feature $F_{ij}^{spatial}$ after the batch normalization, ReLU, convolution, dropout operation. In order to ensure the integrity of the features extracted from spectral and spatial dimension, the network depth and architecture of the two channels are consistent. The procedure can be formulated as Eq (3.4):

BN is illustrated as Eq (3.5)

Where $X^{k}$ denotes the $kth$ layers batch feature maps and $E(X^{k})$ denotes the expectation of $X^{k}$. Similarly, $VAR(X^{k}$ is the variance of $X^{k}$ and $\hat{X}^{k}$ is the normalization result of the input data. This strategy enables deep neural networks to converge more smoothly. Subsequently, the BN results are convolved with $1 \times 1$ and $3 \times 3$ matrices after applying ReLU as the activation function.

To further address the over fitting problem, we add a dropout operation after ReLU. This operation sets the output maps generated by some neurons to zero with a specific probability. In this paper, the dropout rate is set to 0.5, which is commonly used in DL models. Subsequently, an average pooling layer is used with the kernel size 3 and the stride 2.

In the end, the generated feature maps are concatenated and fed to Block 3, which finally fuses the extracted spectral spatial features.

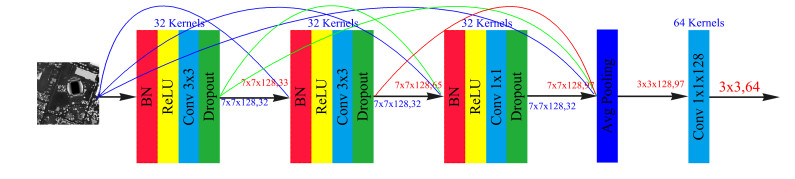
3.3.   Block2: cascade DenseNet for LiDAR feature extractor

Inspired by ResNet and DenseNet's work on image classification, we designed the cascade DenseNet for LiDAR feature extractor which is composed of three DenseNet unit. Each DenseNet unit contains the Batch Normalization layer, activation function layer, convolution layer and Dropout layer. The activation function here is ReLU. The architecture of cascade DenseNet for LiDAR Feature Extractor is shown in Figure 9.

Figure 9.  The architecture of cascade DenseNet for LiDAR Feature Extractor.

DownLoad: Full-Size Img PowerPoint

In this branch, an image block with radius r of the central pixel is first extracted and then fed into the network. The feature map of the preceding network is directly transferred backward by adding the feature map in pixel level. In network forward calculation, the feature graphs of different layers can be transferred backward through different paths, and the chain rule should be followed when the parameters of convolution kernel are updated and propagated back.

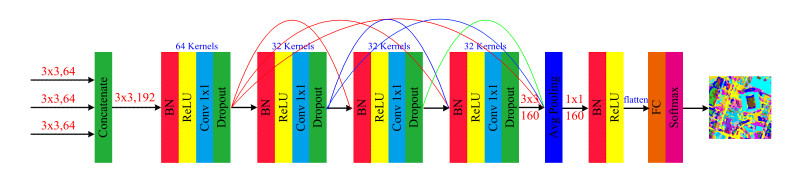
3.4.   Block3: feature fusion and classification

In this block, the features extracted from Block1 and Block2 will be fused and classified. Firstly, the features extracted by Block1 and Block2 are connected and calculated to obtain 192 features with the size of $3\times 3$. Then the features were input the DenseNet unit, and after three Dense units, we get 160 features with the size of $3\times 3$. After the last Dense unit, we insert a global average pooling, the purpose of using the global average pooling is to replace the FC layer with it, The global average pooling layer contains a much smaller number of parameters than FC layers and can retain remarkable localization ability for a network. It is efficient to consider two main problems in HSI classification: the overfitting phenomenon caused by the large model scale with limited training data, and the effective extraction for both spectral and spatial features After the FC layer, a softmax layer is used to obtain the final classification result. The architecture of feature fusion and classification is shown in Figure 10.

Figure 10.  The architecture of feature fusion and classification.

DownLoad: Full-Size Img PowerPoint

3.5.   The training and optimizing process

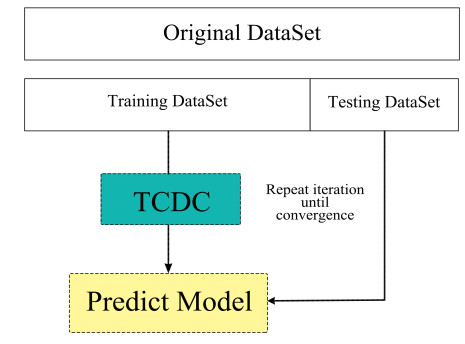
In order to obtain the model with the best classification accuracy, we divided the experimental dataset into three groups: training set, verification set and test set. The training set $Z_{1}$ and its corresponding label $Y_{1}$ are used to update the network parameters. The validation set $Z_{2}$ and its corresponding label $Y_{2}$ are used to monitor intermediate models generated during the training process. The testing set $Z_{3}$ used to evaluate the optimal training network. As shown in Figure 11.

Figure 11.  The training and optimizing process.

DownLoad: Full-Size Img PowerPoint

In Figure 11 the $80\%$ samples were input into the network as training sets to obtain the initial model, and the $20\%$ samples were used as verification sets to update the intermediate model. After multiple updates and iterations, the optimal model was retained. Finally, the remaining $20\%$ samples were used as test sets to predict the category labels of samples through the optimal model. In the iterative update process, the difference between the real class label $Y_{3} = \left\lbrace y_{1}, y_{2}, \cdots, y_{L}\right\rbrace$ and the predicted class label $\hat{Y}_{3} = \left\lbrace \hat{y}_{1}, \hat{y}_{2}, \cdots, \hat{y}_{L}\right\rbrace$ is estimated using the cross entropy loss function, as shown in Eq (3.6)

$L$ is the total number of categories for each dataset, $y_{i}$ is the real category of the sample, $\hat{y_{i}}$ is the prediction category of the sample.

4.   Experimental results and discussions

We evaluated the performance of the proposed network on the publicly available HSI datasets: University of Houston campus and the neighboring urban area. First, the main components of the HSI model based on DenseNet are tested, including the input image size, the number of kernels, learning rate and the training sample size on classification accuracy. Then, the competitive performance of the TDCC with respect to classification performance compared with other state-of-the-art classification methods in terms of the overall accuracy, average accuracy and kappa coefficient. The hardware and software environment used in the experimentation is shown in Table 2.

Table 2.  The hardware and software environment.

Category	Items	Parameters
Hardware Environment	CPU	Intel E5-1620 v4
	GPU	GTX 1080 Ti
	Memory	32 GB
	Hard Disk	1 TB
Software Environment	OS	Ubuntu16.04
	IDE Environment	TensorFlow-GPU 1.8.0
	Development Language	Python 3.5

---

 | Show Table

DownLoad: CSV

The overall accuracy (OA), average accuracy (AA), and the kappa coefficient (K) are adopted to qualitatively evaluate the classification results.

Overall accuracy: refers to the probability that the classified result is consistent with the test data category for each random sample. The overall accuracy is equal to the sum of the pixels that correctly classified divided by the total pixels. The calculation method is shown as Eq (4.1):

Average accuracy: refers to the average of classification accuracy of each category. The calculation method is shown as Eq (4.2):

Kappa coefficient is another method to calculate classification accuracy. The Kappa coefficient is between -1 and 1. But usually Kappa coefficient falls between 0 and 1, $Kappa = 1$ indicates complete agreement between the two judgments, $Kappa \geq 0.75$ indicates a satisfactory agreement, $Kappa < 0.4$ indicates less than ideal. It is an ideal index to describe the consistency of diagnosis, so it has been widely used in practical engineering. The calculation method is shown as Eq (4.3):

4.1.   Description of experimental data sets

The Houston data consists of hyperspectral data and LiDAR data, the data was first published in the 2013 GRSS data fusion contest. The data were collected at the University of Houston and its surrounding area. The image resolution is $349\times1905$, the pixel resolution is 2.5 meters. The HSI consists of 144 bands, ranging in wavelength from 380 to 1050 nm, and it includes 15 kinds of ground truth objects. The number of samples for Houston Data is shown in Table 3.

Table 3.  Number of samples for Houston Data.

No.	Class	Num. of Samples
1	Health grass	198
2	Stressed grass	190
3	Synthetic grass	192
4	Tress	188
5	Soil	186
6	Water	182
7	Residential	196
8	Commercial	191
9	Road	193
10	Highway	191
11	Railway	181
12	Parking lot 1	192
13	Parking lot 2	184
14	Tennis court	181
15	Running track	187
Total		2832

---

 | Show Table

DownLoad: CSV

4.2.   Experimental setup for classification of labeled pixels

To set the parameters of the proposed model, we determined the optimal parameters of the TDCC through a series of experiments, which included the input image size, the number of kernels, learning rate and the training sample size in each batch.

4.2.1.   Effect of the input image size

Table 4 shows the classification accuracy comparison results of different input image size. As we can see from the table, OA, AA and Kappa coefficients increased with the increase of input image size. As the size increased to $7\times7$, the accuracy increases slowly or stops increasing. Therefore, the input image size of the model was selected with $7\times7$ based on the main evaluation indexes.

Table 4.  OA comparison under different spatial size.

Kernels Depth	Houston
	OA	AA	Kappa
$3\times3$	82.56	84.73	0.8131
$5\times5$	87.66	89.13	0.8678
$7\times7$	91.69	92.75	0.9109
$9\times9$	82.09	85.26	0.8081

---

 | Show Table

DownLoad: CSV

4.2.2.   Effect of the number of kernels

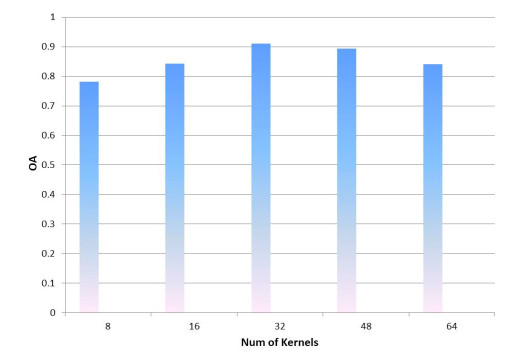
This experiment analyzes the effect of convolution kernel number on classification results. During the experiment, the convolution kernel number of each DenseNet unit was set as 8, 16, 32 and 64, respectively, and the classification accuracy under different convolution kernel numbers was recorded to evaluate the effect of convolution kernel number on classification results.

Figure 12 shows the experimental results. It can be seen from the experimental results that under certain conditions, increasing the number of convolution kernel can improve the classification accuracy; But the classification accuracy does not increase linearly with the increase of convolution kernel number; With the increase of the convolution kernel number, the classification accuracy rises first and then fall; The experiment results show that the classification accuracy is the highest when the number of convolution kernel is 32. It also can be seen from experiment results that as the number of convolution kernels increases, the computational complexity of the model increases and the time used for classification increases. Therefore, considering the classification accuracy and time complexity, the number of convolution kernel in the convolutional layer is set to 32.

Figure 12.  Classification results by different kernels.

DownLoad: Full-Size Img PowerPoint

4.2.3.   Effect of learning rate

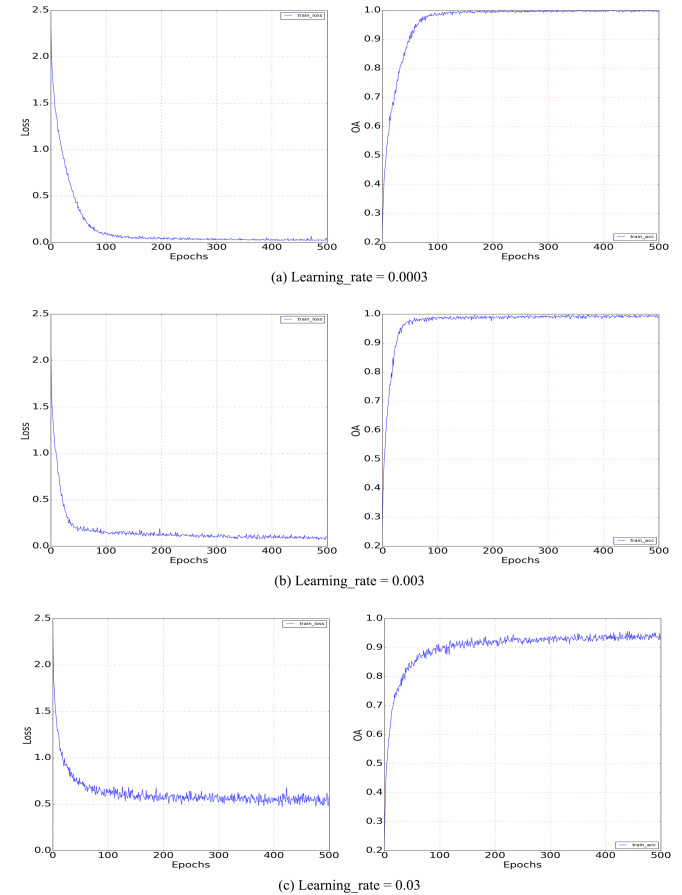
The learning rate is an important factor that affects the convergence of network, and will affect the performance of network indirectly. The learning results were set as 0.0003, 0.003, and 0.03, respectively. It was found that the convergence effect was best when the learning rate was 0.0003 and the learning strategy was RMS. Although the convergence rate was slightly improved when a larger learning rate was selected, the classification accuracy fluctuated. When the learning rate was 0.03, the classification accuracy decreased significantly. The experimental results are shown in Figure 13.

Figure 13.  Classification result of different learning rate.

DownLoad: Full-Size Img PowerPoint

4.2.4.   Effect of the training sample size

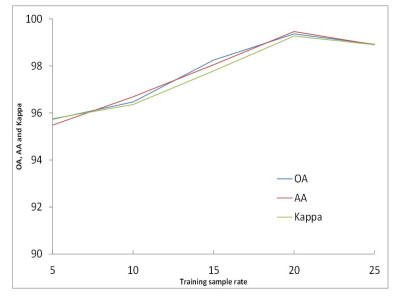
Figure 14 shows the accuracy of the three evaluate parameters under different percentage training sets. It can be clearly seen from figure that when the training set is between 5 and $15\%$, the classification accuracy increases significantly, and when the percentage reaches $20\%$, the classification accuracy increases slowly. Therefore, $20\%$ of the training samples are selected for the dataset.

Figure 14.  The accuracy of the three evaluate parameters under different percentage training sets.

DownLoad: Full-Size Img PowerPoint

4.3.   Classification results of each dataset by different training sample size

In order to verify the classification effect of the TDCC in this paper, we compared the method with three other classical HSI classification methods from the OA, AA and Kappa coefficients. These four methods include: Support Vector Machine method, extreme learning machine, and CNN-PPF ^[33]. SVM and ELM use the official open source code. Table 5 shows the experiment results of each method on Houston dataset. In the table, SVM(H) represents the experiments and results of SVM on HSI, and SVM(H+L) represents the experimental results of HSI and LiDAR joint classification. Figure 15 is the visualization of experimental results.

Table 5.  The experiment results of each method on Houston dataset.

No.	SVM (H)	SVM (HL)	ELM (H)	ELM (HL)	CNN-PPF (H)	CNN-PPF (HL)	Proposed (H)	Proposed (HL)
1	81.86	82.43	82.91	83.10	82.24	83.57	93.66	89.25
2	82.61	82.05	83.93	83.70	98.31	98.21	86.22	95.66
3	99.80	99.80	100.00	100.00	70.69	98.42	95.17	88.19
4	92.50	92.80	91.76	91.86	94.68	97.73	81.03	96.36
5	98.39	98.48	98.77	98.86	97.25	96.50	87.91	93.59
6	94.41	95.10	95.10	95.10	79.02	97.20	86.94	95.50
7	76.87	75.47	89.65	80.04	86.19	85.82	90.83	94.72
8	43.02	46.91	49.76	68.47	65.81	56.51	90.69	96.36
9	79.04	77.53	81.11	84.80	72.11	71.20	94.96	91.39
10	58.01	60.04	54.34	49.13	55.21	57.12	86.81	85.60
11	81.59	81.02	74.67	80.27	85.01	80.55	94.28	91.89
12	72.91	85.49	69.07	79.06	60.23	62.82	80.64	85.10
13	71.23	75.09	69.81	71.58	75.09	63.86	98.31	94.71
14	99.60	100.00	99.19	99.60	83.00	100.00	96.41	95.27
15	97.57	98.31	98.52	98.52	52.64	98.10	88.16	93.58
OA	79.00	80.49	79.87	81.92	78.35	83.33	86.59	91.69
AA	81.94	83.37	82.57	84.27	77.10	83.21	90.14	92.75
Kappa	0.7741	0.7898	0.7821	0.8045	0.7646	0.8188	0.8562	0.9109

---

 | Show Table

DownLoad: CSV

Figure 15.  Dataset visualization and classification maps for the Houston data obtained with different methods.

DownLoad: Full-Size Img PowerPoint

As can be seen from the table: the multi-source remote sensing classification model based on two-channel DensetNet proposed in this paper is superior to other classification methods in OA, AA and Kappa. On the OA index, the method proposed in this paper is $8.36\%$ higher than cnn-ppf, and about $9.77$ and $11.20\%$ higher than SVM and ELM, respectively. Therefore, it can be concluded that the combined classification of HSI and LiDAR can yield higher classification accuracy, especially for some similar categories, such as Parking lots and roads. In order to avoid the one-sided description of the experimental results by a single index, a variety of indicators were selected to evaluate the results. A similar conclusion can be drawn from the consistency test of Kappa coefficient.

Figure 15 shows the visualization effect of classification results of different methods. At the same time, the truth value map is also displayed for the convenience of comparison. These figures correspond to the results in table 5. Obviously, the method presented in this paper has fewer error-marked areas than SVM, ELM and CNN-PPF on the classification diagram.

5.   Conclusions

In order to improve the classification performance of HSI, a multi-source remote sensing image classification model based on two-channel Densely connected convolutional networks was proposed in this paper. Considering the problems of HSI with multi-source, multi-bands, data redundancy and limited training samples. The discriminative spectral-spatial features were extracted by using two-channel Densely connected convolutional networks, the features of different block can be shared and the information flow can be enhanced, which solves the problem of multi-source remote sensing image classification. At the same time, in order to improve the classification performance, DenseNet unit is introduced into the TDCC that overcomes the gradient disappearance problem. Comparing classification accuracy with available HSI classification methods on public HSI dataset, the proposed method shows very promising results, and is much effective for dataset. There is still plenty of room to grow in our proposed method, such as more successful strategies in multi-scale feature fusion and robust classification accuracy to the boundary region. Besides, parallel and distributed fusion strategy, such as ^[34], will be great in accelerating computation efficiency in practice.

Acknowledgments

This research was funded by the National Natural Science Foundation of China (11901173), the Heilongjiang Province Natural Science Found (LH2019A030), the Agricultural Science and Technology Project of Taizhou (20ny13), the Innovation Team Project of Heilongjiang Institute of Technology (2018CX17) and the Cultivating Science Foundation of Taizhou University(2019PY014, 2019PY015).

Conflict of interests

The authors declare no conflict of interest.