Asymptotic profile of endemic equilibrium to a diffusive epidemic model with saturated incidence rate

1.   Introduction

To understand the dynamics of disease transmission in a spatially heterogeneous environment, an SIS epidemic reaction-diffusion model was proposed in ^[1], satisfying the parabolic system

where $\bar{S}(x, t)$ and $\bar{I}(x, t)$ denote the densities of susceptible and infected individuals at position $x$ and time $t$, respectively; the positive constants $d_S$ and $d_I$ are the diffusion rates of the susceptible and infected individuals; the habitat $\Omega$ is assumed to be a bounded domain in $\mathbb{R}^n (n\geq1)$ with smooth boundary $\partial\Omega$; the positive Hölder-continuous functions $\beta(x)$ and $\gamma(x)$ on $\bar{\Omega}$ represent the rates of disease transmission and disease recovery at $x$, respectively; the homogeneous Neumann boundary condition means that there is no flux across the boundary $\partial\Omega$, and $\partial/\partial \nu$ is the outward normal derivative to $\partial\Omega$.

In ^[1], under the assumption that the total population keep constant, the existence and uniqueness of the endemic equilibrium (EE) were achieved in terms of the basic reproduction number $\mathcal {R}_0$. Furthermore, the asymptotic profile of EE was obtained for small diffusion rate of susceptible individuals. To further understand the impact of large and small diffusion rates on the persistence and extinction of the disease, the global stability and asymptotic behavior of EE for system (1.1) were investigated in ^[20,21,22]. In ^[23], Peng and Zhao considered the diffusive SIS model with spatially heterogeneous and temporally periodic disease transmission and recovery rates. The authors in ^[4,5,11] studied the effects of diffusion and advection for a spatial SIS model in heterogeneous environments. Their results suggest that advection can help speed up the elimination of disease. Other related works on (1.1) can be found in ^{[8,9,13,14,15]}.

The aforementioned studies adopt the standard incidence rate $\beta \bar{S}\bar{I}/(\bar{S}+\bar{I})$. Another most frequently used incidence rate is the bilinear incidence rate $\beta \bar{S}\bar{I}$ (see ^[2,10]), which gives rise to the dependence of the basic reproduction number on the total population. For the diffusive SIS epidemic model with the bilinear incidence rate, Deng and Wu discussed the existence and the global attractivity of the EE in ^[7]. In the continued work ^[25], Wu and Zou explored the asymptotic profile of EE for large and small diffusion rates of the susceptible and infected individuals. They observed some new interesting profiles for such model. In contrast, Capasso and Serio in ^[6] pointed out that the number of effective contacts between infective individuals and susceptible individuals cannot always increase linearly with $I$; the bilinear incidence rate might be true for a small number of infectives, but unrealistic for large $I$. They introduced a saturated incidence rate $g(\bar{I})\bar{S}$ into epidemic models based on the study of the cholera epidemic spread in Bari of Italy, where

Such an incident rate seems more realistic in certain situations because the number of effective contacts between infective individuals and susceptible individuals may saturate at high infective levels due to crowding of the infective individuals or due to the protection measures by the susceptible individuals. Here $\beta\bar{I}$ measures the infection force of the disease, $1/(1+m\bar{I})$ measures the inhibition effect from the behavioral change of the susceptible individuals when their number increases or from the crowding effect of the infective individuals, $m > 0$ is the saturation coefficient. This type of incidence rate has been adopted by many authors ^{[12,19,26,27]}.

However, to our best knowledge, little work has been devoted to the study of the diffusive epidemic model with saturated incidence rate. Inspired by the above research, we here consider an SIS epidemic reaction-diffusion model with saturated incidence rate. We are interested in the existence of the EE and particularly the effects of the diffusion rates and the saturated coefficient on asymptotic profile of EE. In contrast to ^[1] and ^[25], for some special case, such as the rate of disease transmission $\beta$ being a constant and $\Omega$ being a high-risk domain, our results indicate that it is not enough to just restrict the movement of the susceptible individuals to completely eradicate the disease in the whole habitat; however, if the inhibition effect is large, the infectious disease will extinct eventually (see Theorem 1.3 and Corollary 1.5). In general, we conclude that the infective individuals cannot persist if the saturated coefficient is large with fixed diffusion rates of the susceptible and infected individuals (see Theorem 1.9).

1.1.   The model

In this paper, we are concerned with the following SIS epidemic reaction-diffusion model with saturated incidence rate:

where the parameters are described as before. We assume that the initial data satisfies the following hypothesis.

(H) $\bar{S}(x, 0), \ \bar{I}(x, 0)\geq 0$ are nonnegative continuous functions in $\bar{\Omega}$, and the number of initial infectious individuals in the region is positive, i.e, $\int_\Omega \bar{I}(x, 0)dx > 0$.

By a similar argument as in ^[1], it is easy to show that system (1.2) admits a unique global classical solution $(\bar{S}(x, t), \bar{I}(x, t))$. Let

be the total number of individuals in $\Omega$ at $t = 0$. Adding the two equations in (1.2) and integrating over the domain $\Omega$, we get

Hence, the total population size is a constant, i.e.,

In the current paper, we mainly focus on the nonnegative equilibrium of problem (1.2), which is the nonnegative solution of the following semilinear elliptic system:

Here $S(x)$ and $I(x)$ denote the densities of susceptible and infected individuals at $x\in \bar{\Omega}$, respectively. In view of (1.3), we have to impose the additional hypothesis:

Obviously, system (1.4)–(1.5) always has a solution $E_0 = (N/|\Omega|, 0)$, which is the uniquedisease-free equilibrium (DFE). On the other hand, a nonnegative solution $E_1 = (S, I)$ of (1.4)–(1.5) with $I(x)\geq 0, \not\equiv0$ is called an endemic equilibrium (EE) of (1.4)–(1.5).

1.2.   Statements of the main results

Similar to ^[1,7], let us define the basic reproduction number $\mathcal {R}_0$ for (1.2) as follows:

where $H^1(\Omega) = \{u: u \in L^2(\Omega), Du \in L^2(\Omega)\}$. Denote the high-risk set and low-risk set respectively by

and

We say the domain $\Omega$ is a high-risk domain if $\frac{N}{|\Omega|}\int_\Omega\beta(x)dx\geq\int_\Omega\gamma(x) dx$ and it is a low-risk domain if $\frac{N}{|\Omega|}\int_\Omega\beta(x)dx < \int_\Omega\gamma(x) dx$.

We begin with some properties of $\mathcal {R}_0$ which is similar to Lemmas 2.2 and 2.3 in ^[1].

Proposition 1.1. The basic reproduction number $\mathcal {R}_0$ has the following properties.

(ⅰ) $\mathcal {R}_0$ is positive decreasing function of $d_I > 0$;

(ⅱ) $\mathcal {R}_0\rightarrow \frac{ N}{|\Omega|}\max\limits_{x\in\bar{\Omega}}\frac{\beta(x)}{\gamma(x)}$ as $d_I\rightarrow 0^+$, and $\mathcal {R}_0\rightarrow \frac{ N}{|\Omega|}\frac{\int_\Omega \beta(x) dx}{\int_\Omega \gamma(x) dx}$ as $d_I\rightarrow \infty$;

(ⅲ) if $\Omega$ is a high-risk domain, then $\mathcal {R}_0 > 1$ for $d_I > 0$;

(ⅳ) if $\Omega$ is a low-risk domain with nonempty $\Omega^+$, then there exists $d_I^* > 0$ such that $\mathcal {R}_0 = 1$ when $d_I = d_I^*$, $\mathcal {R}_0 > 1$ when $d_I < d_I^*$, and $\mathcal {R}_0 < 1$ when $d_I > d_I^*$;

(ⅴ) $\mathcal {R}_0 > 1$ implies $\frac{ N}{|\Omega|} > \min\limits_{x\in\bar{\Omega}}\frac{\gamma(x)}{\beta(x)}$.

The first goal of this paper is to establish the existence of EE.

Theorem 1.2. The following statements hold.

(ⅰ) If $d_S\geq d_I$, there exists a unique EE when $\mathcal {R}_0 > 1$ and EE does not exist when $\mathcal {R}_0\leq1$;

(ⅱ) if $d_S < d_I$, there exists an EE when $\mathcal {R}_0 > 1$ and EE does not exist when $\mathcal {R}_0\leq d_S/d_I$.

Theorem 1.2(ⅰ) indicates that $\mathcal {R}_0 = 1$ is the critical value for the existence of EE when $d_S\geq d_I$. However, if $d_S < d_I$, we do not know whether an EE exists or not in the case of $\mathcal {R}_0\in (d_S/d_I, 1)$.

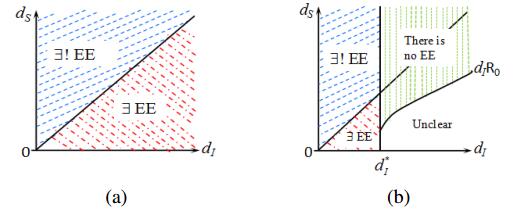
A combination of Proposition 1.1 and Theorem 1.2 implies that the EE always exists when $\Omega$ is a high-risk domain (see Figure 1(a)) or $\Omega$ is a low-risk domain with nonempty $\Omega^+$ and $0 < d_I < d_I^*$ (see Figure 1(b)), where $d_I^* > 0$ is uniquely determined in Proposition 1.1(ⅳ).

The second goal of this paper is to investigate the effects of diffusion rates and saturation coefficient on asymptotic profiles of the EE when it exists. Here we consider the following three cases: (ⅰ) small diffusion, (ⅱ) large diffusion, (ⅲ) large saturation.

The following theorem presents the asymptotic profile of EE when $d_S$ is sufficiently small or large.

Theorem 1.3. Let $d_I$ and $m$ be fixed. Assume $\mathcal {R}_0 > 1$ and $(S(x), I(x))$ is an EE of (1.2). Then the following statements hold.

(ⅰ) $(S, I)\rightarrow (S^*, I^*)$ in $C^2(\bar{\Omega})$ when $d_S\rightarrow\infty$, where $I^*$ is the unique positive solution of the following problem

and

(ⅱ) $(S, I)\rightarrow (S^*, I^*)$ in $C(\bar{\Omega})$ when $d_S\rightarrow0^+$, where $S^*$ and $I^*$ satisfy

or $I^* = 0$ and

where $\check{I} > 0$ satisfies the following problem

Corollary 1.4. Suppose that $\mathcal {R}_0 > 1$ and $N < \int_\Omega \gamma/\beta dx$. Then, for any fixed $d_I > 0$ and $m > 0$, the EE $(S, I)\rightarrow (S^*, 0)$ in $C(\bar{\Omega})$ as $d_S\rightarrow0^+$, where $S^*$ satisfies (1.8).

Corollary 1.5. Fixed $d_I > 0$ and $m > 0$. Suppose $\mathcal {R}_0 > 1$ and $N > \int_\Omega \gamma/\beta dx$. Then the EE $(S, I)\rightarrow (S^*, I^*)$ in $C(\bar{\Omega})$ as $d_S\rightarrow 0^+$, where $(S^*, I^*)$ satisfies (1.7) if one of the following conditions holds:

(ⅰ) $\beta$ is a positive constant;

(ⅱ) $\frac{N}{|\Omega|} > \max\limits_{x\in\bar\Omega}\frac{\gamma(x)}{\beta(x)}$;

(ⅲ) $\frac{\gamma(x)}{\beta(x)} = r$ for any $x\in \bar{\Omega}$, where $r$ is some positive constant.

Corollary 1.5 implies that the infectious disease may persist even if the movement of the susceptible population is controlled to be very small, which is in sharp contrast to the epidemic model in ^[1].

Next, we are going to explore the asymptotic profile of EE as $d_I\rightarrow0^+$ and $d_I/d_S\rightarrow d > 0$.

Theorem 1.6. Let $m$ be fixed. Assume that $\Omega^+$ is nonempty. Then the following statements hold:

(ⅰ) If $d_I\rightarrow0^+$ and $d_I/d_S\rightarrow d\in (0, \infty)$, then $(S, I)\rightarrow(S^*, I^*)$ in $C(\bar{\Omega})$, where $I^*$ is the unique positive solution of

and $S^*$ is given by

(ⅱ) If $d\in(0, 1)$, then $\{x\in \Omega: I^* > 0\}\subsetneqq\Omega^+$; if $d\in(1, \infty)$, then $\{x\in \Omega: I^* > 0\}\supseteqq\Omega^+$ and this inclusion is strict if $\Omega^-$ is nonempty.

Remark 1.7. If $d = 1$ in Theorem 1.6, then

which implies that $\{x\in \Omega: I^* > 0\} = \Omega^+$. It follows from Theorem 1.6(ii) that, in this situation, the ratio $d_I/d_S$ plays a critical role in determining the existing region of the infected population. If $d = 1$, the infected individuals survive exactly in the high-risk set; if $d\in(0, 1)$, the habitat of infected individual is confined within some subset of the high-risk set; if $d > 1$, the infected individuals only die out at part of the low-risk sites.

We now establish the asymptotic profile when the diffusion rate $d_I$ is large.

Theorem 1.8. Let $m$ be fixed. Suppose that $\Omega$ is a high-risk domain. Then the following statements hold.

(ⅰ) If $d_I\rightarrow\infty$ and $d_S\rightarrow\infty$, then $(S, I)\rightarrow(S^*, I^*)$ in $C^2(\bar{\Omega})$, where $S^*$ and $I^*$ are positive constants satisfying

(ⅱ) If $d_S$ is fixed, then there exists a sequence $\{d_{I_n}\}$ with ${d_{I_n}}\rightarrow\infty$ as $n\rightarrow\infty$ such that the corresponding EE $(S_n, I_n)\rightarrow(S^*, I^*)$ in $C^2(\bar{\Omega})$, where $I^*$ is a positive constant and $S^*$ is the positive solution of the following problem

Furthermore, if $d_{S}\rightarrow 0^+$ in (1.11), then $(S^*, I^*)\rightarrow(\hat{S}^*, \hat{I}^*)$ in $C^1(\bar{\Omega})$, where $\hat{S}^*$ and $\hat{I}^*$ satisfy (1.7) or $\hat{I}^* = 0$ and $\hat{S}^*$ satisfies

with $K_1$ being a positive constant.

Finally, we describe the asymptotic profile when the saturated coefficient $m$ is large.

Theorem 1.9. Suppose that $\mathcal {R}_0 > 1$. Then for any fixed $d_I > 0$ and $d_S > 0$, the corresponding EE $(S, I)$ of (1.2) satisfies $(S, I)\rightarrow (N/|\Omega|, 0)$ in $C(\bar{\Omega})$ as $m\rightarrow \infty$. Furthermore, either $\|mI\|_\infty\rightarrow\infty$ or $mI\rightarrow w_*$ as $m\rightarrow\infty$, where $w_*$ is the unique positive solution of the following problem

Theorem 1.9 implies that large saturated coefficient can help to eliminate the disease. That is, if the susceptible individuals change the behavior when their number increases or the infective individuals produce crowding effect, the infectious disease may extinct eventually.

The rest of this paper is arranged as follows. In Section 2, we focus on the existence, uniqueness and nonexistence of the EE, and give the proof of Theorem 1.2. In Section 3, the impacts of diffusion rates and saturated coefficient on the persistence and extinction of the infectious disease are studied. Then, we illustrate the influences of the population diffusion and the saturation coefficient on system (1.2) numerically in Section 4. In Section 5, we conclude the paper with some discussion of the epidemiological implication of our theoretical results. Finally, some well-known facts, which are frequently used in the proofs of our main results, are collected in the appendix.

2.   The existence and nonexistence of the EE

Since the existence of the EE is related to the stability of the DFE, we first investigate the stability of the DFE. To this end, we linearize (1.2) around the DFE to obtain

Here $\eta(x, t) = \overline{S}(x, t)-N/|\Omega|$ and $\xi(x, t) = \overline{I}(x, t)$. Let $(\eta(x, t), \xi(x, t)) = (e^{-\lambda t}\phi(x), e^{-\lambda t}\psi(x))$ be the solution of the linear system. Then, we derive an eigenvalue problem

with boundary conditions

In view of (1.3), we impose an additional condition

Indeed, it suffices to consider the eigenvalue problem

It is well known that all eigenvalues of (2.4) are real, and the principal eigenvalue, denoted by $\lambda^*$, is simple, and its corresponding eigenfunction $\psi^*$ can be chosen positive on $\Omega$. Furthermore, the eigenvalue $\lambda^*$ is given by the variational characterization

It has been shown in ^[7] that the basic reproduction number $\mathcal {R}_0$ and the principal eigenvalue $\lambda^*$ has the following relationship.

Lemma 2.1. $1-\mathcal {R}_0$ and $\lambda^*$ have the same sign.

As discussed in Lemma 2.4 of ^[1], the stability of the DFE depends on the value of $\mathcal {R}_0$.

Lemma 2.2. The DFE is linearly stable if $\mathcal {R}_0 < 1$ and unstable if $\mathcal {R}_0 > 1$.

To study the existence of the EE, we first convert problem (1.4)-(1.5) to an equivalent but more accessible problem.

Lemma 2.3. The pair $(S, I)$ is a nonnegative solution of problem (1.4)-(1.5) if and only if $I$ is a nonnegative solution of the following problem

and

Proof. By standard calculations, one can easily check that $(S, I)$ is a nonnegative solution of problem (1.4)-(1.5) if and only if it solves the following problem:

where $\kappa$ is some positive constant independent of $x \in \Omega$.

Now we show the equivalence between problems (2.7)-(2.10) and (2.5)-(2.6).

Suppose that $(S, I)$ is a nonnegative solution of (2.7)-(2.10). By (2.7), we have $d_S(S+I) = \kappa+(d_S-d_I)I$. Integrating it over $\Omega$ and using (2.10), we get $d_SN = \kappa |\Omega|+(d_S-d_I)\int_\Omega Idx$. Substituting (2.7) into the equation gives

That is, (2.6) holds. Substituting such $S$ into (2.8), we get (2.5).

Suppose that $(S, I)$ is a nonnegative solution of problem (2.5)-(2.6). Substituting (2.6) into (2.5) yields (2.8). Clearly, $\partial S/\partial \nu = 0$, i.e., (2.9) holds. Integrating both sides of (2.6) over $\Omega$, we get (2.10). Applying the Laplace operator to both sides of (2.6), we find that $d_S\Delta S = -d_I\Delta I$ which means $\Delta(d_S S+d_I I) = 0$. Since $\frac{\partial}{\partial\nu} (d_S S+d_I I) = 0$, the maximum principle implies that $d_S S+d_I I$ is a constant. In view of (2.10), this constant must be positive, which yields (2.7).

The nonlocal elliptic problem (2.5) has the following estimate.

Lemma 2.4. If $I \in C^2(\Omega)\cap C^1(\bar{\Omega})$ is a nonnegative solution of the nonlocal elliptic problem (2.5), then we have

Proof. It is easy to see that (2.11) holds if $I\equiv0$ on $\bar{\Omega}$. Suppose $I\geq0, \not\equiv0$. Then there exists some $x_0\in\bar{\Omega}$ such that $I(x_0) = \max\limits_{x\in\bar{\Omega}} I(x) > 0$. By Lemma A.3, we have

which implies that

The conclusion holds.

Set

If follows from Lemma 2.4 that $S$ is nonnegative. Hence the pair $(S, I)$ solves problem (2.5)–(2.6) as well as (1.4)–(1.5). Next, we focus on the existence of positive solution to the nonlocal elliptic problem (2.5) that only involves $I$.

Let $\Gamma = \{\tau\in [0, \infty): N-(1-d_I/d_S)\tau\geq0\}$ and $Y = \{z\in C^{2+\alpha}(\bar{\Omega}): \partial z/\partial \nu = 0 \ \text{ on}\ \partial\Omega\}$. Define a mapping $F : \Gamma\times Y \rightarrow C^\alpha(\bar{\Omega})$ by

with

Then $I$ is a nonnegative solution of (2.5) if and only if $F(\tau, I) = 0$ and $\tau = \int_\Omega Idx$.

Now we consider the following problem:

It is easy to check that (2.13) meets all the requirements of Lemma A.2. Thus the existence of positive solution of (2.13) is tightly related to an eigenvalue $\lambda_1(d_I, f(\tau, 0))$, which is defined by (8.1). For simplicity, we denote $\lambda_\tau = \lambda_1(d_I, f(\tau, 0))$, and hence $\lambda_0 = \lambda^*$, where $\lambda^*$ is the principal eigenvalue of (2.4).

Lemma 2.5. Suppose that $\tau \geq0$.

(ⅰ) If $\lambda_\tau\geq 0$, the only nonnegative solution of (2.13) is $I = 0$;

(ⅱ) if $\lambda_\tau < 0$, there is a unique positive solution $I\in Y$ of (2.13).

We are now ready to prove Theorem 1.2. To this end, we need to prove several lemmas as follows.

Lemma 2.6. Suppose $\lambda^* < 0$.

(ⅰ) If $d_S > d_I$, then there exists a smooth curve $(\tau, I_\tau(x))$ in $\Gamma \times Y$ such that $F(\tau, I_\tau) = 0$. Moreover, there is a $\Lambda > 0$ such that $I_\Lambda = 0$ and $I_\tau(x) > 0$ for all $x\in \bar{\Omega}$, $\tau\in [0, \Lambda)$. Furthermore, $I_\tau$ is decreasing and continuously differentiable with respect to $\tau$ in $(0, \Lambda)$;

(ⅱ) if $d_S < d_I$, then there exists a smooth curve $(\tau, I_\tau(x))$ in $[0, \infty)\times Y$ such that $F(\tau, I_\tau) = 0$ with $I_\tau > 0$ for $x\in \bar{\Omega}$ and $\tau\in [0, \infty)$. Moreover, $I_\tau(x)$ is increasing and continuously differentiable in $\tau$ on $(0, \infty)$, and it satisfies the following estimate:

Proof. (ⅰ) Suppose that $(\tau_0, I_{\tau_0}(x))\in\Gamma \times Y$ satisfies $F(\tau_0, I_{\tau_0}) = 0$ and $I_{\tau_0} (x) > 0$ on $\bar{\Omega}$. The Fr$\acute{e}$chet derivative of $F$ is given by

for all $w\in Y$, where

We claim that $F_I(\tau_0, I_{\tau_0})$ is invertible. To this end, we need to show the unique solvability of the following problem for any $h\in C^\alpha(\bar{\Omega})$,

Since $F(\tau_0, I_{\tau_0}) = 0$, i.e. $d_I\Delta I_{\tau_0} + I_{\tau_0}f(\tau_0, I_{\tau_0}) = 0$, we see that $\lambda_1(d_I, f(\tau_0, I_{\tau_0})) = 0$ and $I_{\tau_0}$ is a corresponding eigenvector by (8.1). It follows from Lemma A.1 and $f_I(\tau_0, I_{\tau_0}) < 0$ that $\lambda_1\left(d_I, f(\tau_0, I_{\tau_0})+f_I(\tau_0, I_{\tau_0})I_{\tau_0} \right)$$> \lambda_1(d_I, f(\tau_0, I_{\tau_0})) = 0$. So all eigenvalues of the problem

are positive. By the Fredholm alternative, (2.15) has a unique solution for every $h\in C^\alpha(\bar{\Omega})$. The continuity of the unique solution follows from the classical Schauder estimate. Since $\lambda_0 = \lambda^* < 0$, there exists a unique positive $I_0\in Y$ such that $F(0, I_0) = 0$ by Lemma 2.5. Hence, by the implicit function theorem, there is a unique $I_\tau \in Y$ such that $F(\tau, I_\tau) = 0$ for $\tau \in [0, \hat{\tau})$ with $\hat{\tau} > 0$, and $I_\tau$ is continuously differentiable with respect to $\tau$.

Now we show that $I_\tau$ is decreasing with respect to $\tau$. Suppose that $0 < \tau_1 < \tau_2 < \hat{\tau}$. Since $d_S > d_I$, we have that $F(\tau_1, I_{\tau_2}) > F(\tau_2, I_{\tau_2}) = 0$. Hence, $I_{\tau_2}$ is a lower solution of the equation $F(\tau_1, I) = 0$. On the other hand, we choose a sufficiently large number as an upper solution of the equation $F(\tau_1, I) = 0$. Then, by the method of upper/lower solutions and the uniqueness of the positive solution of $F(\tau_1, I) = 0$, we obtain that $I_{\tau_1} > I_{\tau_2}$.

The curve $(\tau, I_\tau)$ satisfying $F(\tau, I_\tau) = 0$ will continue as long as $I_\tau > 0$, i.e., $\lambda_\tau < 0$, due to Lemma 2.5. By the variational formula, $\lambda_\tau$ is increasing with respect to $\tau$ and $\lambda_\tau > 0$ for large $\tau$. It follows from Lemma 2.5 again that, there is no positive solution of $F(\tau, I) = 0$ if $\tau$ is large, i.e., $I_\tau = 0$ for large $\tau$. Let $[0, \Lambda)$ be the maximal interval of existence of $\tau$ such that $I_\tau > 0$. Then $I_\Lambda = 0$.

(ⅱ) The existence and continuous differentiability of the curve $(\tau, I_\tau)$ can be obtained by a similar argument as in the proof of (ⅰ). And one can check that $I_\tau$ is increasing with respect to $\tau$ since $d_S < d_I$. Thus the curve is continuous with respect to $\tau$ on $[0, \infty)$.

To show (2.14), let $I_\tau(y_0) = \max\limits_{\bar{\Omega}}I_\tau(x)$. Applying Lemma A.3 to the first equation of (2.13), we obtain that

which implies

and hence

for any $x\in \bar{\Omega}$. It follows that (2.14) holds by integrating the above inequality over $\Omega$.

Lemma 2.7. Suppose $\mathcal {R}_0 > 1$. Then there exists a unique EE if $d_S\geq d_I$, and there exists at least one EE if $d_S < d_I$.

Proof. If $d_S = d_I$, then $\lambda_\tau = \lambda^* < 0$ based on $\mathcal {R}_0 > 1$. The result follows directly from Lemma 2.5.

For $d_S > d_I$, by Lemma 2.6 (ⅰ), there is a smooth curve $(\tau, I_\tau)$ satisfying $F(\tau, I_\tau) = 0$. By the definition of $F$, $I_\tau$ is a solution of problem (2.5) if $\tau = \int_\Omega I_\tau dx$. Let $H(\tau) = \int_\Omega I_\tau dx-\tau$. Then $H(\tau)$ is continuous and strictly decreasing with respect to $\tau$ in $[0, \Lambda)$ because of the continuity and monotonicity of $I_\tau$. Since $\int_\Omega I_0dx > 0\ \text{and} \ 0 = \int_\Omega I_\Lambda dx < \Lambda$, we have $H(0) > 0, \ H(\Lambda) < 0$. Then, there exists a unique $\tau_0 \in (0, \Lambda)$ such that $H(\tau_0) = 0$, i.e. $\tau_0 = \int_\Omega I_{\tau_0}dx$. Hence problem (2.5) has a unique positive solution.

For $d_S < d_I$, by Lemma 2.6 (ⅱ), there exists a smooth curve $(\tau, I_\tau)$ satisfying $F(\tau, I_\tau) = 0$. We also take $H(\tau) = \int_\Omega I_\tau dx-\tau$. Then it is continuous with respect to $\tau$. The estimate (2.14) implies that $H(\tau)\leq \frac{d_S}{d_I}(N-\tau)$. Since $H(0) > 0$ and $H(\tau) < 0$ with $\tau > N$, there exists a $\tau_0 > 0$ such that $H(\tau_0) = 0$, i.e. $\tau_0 = \int_\Omega I_{\tau_0}dx$. Hence, problem (2.5) has at least one positive solution.

Lemma 2.8. The EE does not exist if one of the following conditions holds:

(i) $d_S\geq d_I$ and $\mathcal {R}_0\leq1$;

(ii) $d_S < d_I$ and $\mathcal {R}_0\leq d_S/d_I$.

Proof. (ⅰ) The case $d_S = d_I$ follows directly from Lemma 2.5. We analyze the case $d_S > d_I$ indirectly. Assume that an EE $(S^*, I^*)$ exists if $\mathcal {R}_0 \leq1$. Then there is a $\tau^* > 0$ such that $\tau^* = \int_\Omega I^* dx$ and $F(\tau^*, I^*) = 0$. By Lemma 2.5, we know $\lambda_{\tau^*} < 0$, which leads to $\lambda^* = \lambda_0\leq\lambda_{\tau^*} < 0$ since $f(\tau, 0)$ is decreasing in $\tau$ when $d_S > d_I$. Then $\mathcal {R}_0 > 1$ by Lemma 2.1, which is a contradiction.

(ⅱ) The case $d_S < d_I$. Assume to the contrary that an EE $(S^*, I^*)$ exists when $\mathcal {R}_0 \leq d_s/d_I$. Let $\tau^* = \int_\Omega I^* dx$. Then $I^*$ is also the positive solution of $F(\tau^*, I^*) = 0$, and it satisfies (2.11) for all $x\in\bar{\Omega}$, i.e.

Integrating this inequality over $\Omega$, we get $\tau^* = \int_\Omega I^* dx\leq N$. Noting that $\lambda_{\tau^*} < 0$ by Lemma 2.5 and $f(\tau, 0)$ is increasing in $\tau$ provided $d_S < d_I$, Lemma A.1 implies that $\lambda_N\leq\lambda_{\tau^*} < 0$, where $\lambda_N$ is the principal eigenvalue of the following problem

Define

Then $\mathcal {R}'_0 > 1$ if and only if $\lambda_N < 0$, which can be obtained as the properties of $\mathcal {R}_0$. Since $\mathcal {R}'_0 = d_I\mathcal {R}_0/d_S$ and $\lambda_N < 0$, we have $\mathcal {R}_0 > d_S/d_I$, which is a contradiction.

Proof of Theorem 1.2. Theorem 1.2 follows from Lemmas 2.6, 2.7 and 2.8.

3.   Asymptotic profiles of the EE

The goal of this section is to investigate the asymptotic profile of EE. To this end, we always assume $\mathcal {R}_0 > 1$, so that (1.2) has an EE. As a first step, we establish the priori estimates of any EE.

Lemma 3.1. Assume that $(S, I)$ is a nonnegative solution of (1.4)-(1.5). Then

Proof. By (1.5), we have $\int_\Omega Idx\leq N$. Applying the inequality (2.11), we get

Let $S(x_0) = \max\limits_{x\in\bar{\Omega}}S(x)$, $S (y_0) = \min\limits_{x\in\bar{\Omega}}S (x)$. We apply Lemma A.3 to the first equation of (1.4) to obtain that

which imply $S (x_0)\leq\frac{ \gamma(x_0) }{\beta(x_0)}(1+mI (x_0))$ and $S (y_0)\geq\frac{ \gamma(y_0) }{\beta(y_0)}(1+mI (y_0))$. Hence (3.2) holds.

Lemma 3.2. Assume that $(S, I)$ is an EE of (1.4)-(1.5). Then $I$ and $S$ are uniformly bounded in $L^\infty(\bar{\Omega})$ if $d_S/d_I\rightarrow\infty$.

Proof. Note that $(S, I)$ satisfies (1.4)-(1.5) (or (2.5)-(2.6)). By (2.6), we have $S\leq N/|\Omega|$ provided $d_S/d_I\rightarrow\infty$. Then, we are going to derive a priori estimate of $I$ when $d_S/d_I\rightarrow\infty$ by the Harnack inequality. Applying Lemma A.4 to the second equation of (1.4), we obtain that there is a positive constant $C_0$ such that $\max\limits_{\overline{\Omega}} I\leq C_0\min\limits_{\overline{\Omega}} I$. In view of $N\geq \int_\Omega Idx\geq |\Omega|\min\limits_{\overline{\Omega}} I\geq|\Omega|\max\limits_{\overline{\Omega}} I/C_0$, we conclude that $\|I\|_\infty\leq C_0N/|\Omega|$.

Now, we are ready to investigate the asymptotic profiles of the EE when $d_S$ is sufficiently small or large. To this end, we show the existence and uniqueness of the solution (1.6).

Lemma 3.3. Suppose $\mathcal {R}_0 > 1$. Then (1.6) has a unique positive solution.

Proof. Since $\mathcal {R}_0 > 1$ is equivalent to $\lambda_1(d_I, N\beta/|\Omega|-\gamma) = \lambda^* < 0$ by Lemma 2.1. Taking

and by similar arguments as in Lemma 2.7, we get that (1.6) has a unique positive solution.

Proof of Theorem 1.3.. It follows from Theorem 1.2 that an EE $(S, I)$ exists provided $\mathcal {R}_0 > 1$ for any $d_S > 0$.

(ⅰ) We consider the asymptotic profile when $d_S\rightarrow\infty$. By Lemma 3.2, $I$ and $S$ are uniformly bounded in $C(\bar{\Omega})$ for fixed $d_I > 0$ and $d_S\rightarrow\infty$. Then using the elliptic estimate and the Sobolev embedding theorem for (1.4), there exists a sequence $\{d_{S_n}\}$ with ${d_{S_n}}\rightarrow\infty$ as $n\rightarrow\infty$ such that the corresponding EE $(S_n, I_n)\rightarrow(S^*, I^*)$ in $C^2(\bar{\Omega})$. Letting $n\rightarrow\infty$ in (2.5), we get that $I^*$ satisfies (1.6) which has a unique positive solution by Lemma 3.3. Thus, the strong maximum principle implies that there are two possibilities: $I^* > 0$ or $I^*{\equiv}0$. By (2.5) and the positivity of $I_n$, we have

If $I^*{\equiv}0$, letting $n\rightarrow\infty$ in (3.3), we have $\lambda_1(d_I, N\beta/|\Omega|-\gamma) = 0$, i.e. $\lambda^* = 0$, which contradicts $\mathcal {R}_0 > 1$ by Lemma 1. Hence $I^*$ is the positive solution of (1.6). By (1.4), $S^*$ satisfies

The strong maximum principle implies that $S^*$ is a constant. Furthermore, it follows from (1.5) that

(ⅱ) We analyze the asymptotic profile when $d_S\rightarrow0^+$. It follows from (3.1) that $I$ is uniformly bounded for fixed $d_I$ and small $d_S$. Hence there exists a sequence $\{d_{S_n}\}$ with $d_{S_n}\rightarrow0^+$ as $n \rightarrow\infty$ such that the corresponding EE $(S_n, I_n)$ satisfies

It then follows that

Hence, for any $\epsilon > 0$, there exists $n_1 > 0$ such that for $n\geq n_1$,

We claim that

Noting that $I_n$ satisfies (2.5), we rewrite it as

It follows from (3.5) that $I_n$ is a lower solution of the problem

On the other hand, (3.1) and (3.5) imply that

for $n\geq n_1$. Meanwhile, $I_n$ is an upper solution of the problem

Observing that $I = \frac{K+\epsilon}{|\Omega|}$ is the unique positive solution of (3.8) and $I = \frac{K-\epsilon}{|\Omega|}-\frac{\epsilon}{d_I}\left(1+\frac{2mN}{|\Omega|}\right)$ is the unique positive solution of (3.10), we have

Since $\epsilon > 0$ is arbitrary, (3.11) indeed implies that $I_n\rightarrow \frac{K}{|\Omega|}$ uniformly on $\bar{\Omega}$ as $n \rightarrow\infty$.

Now, we have two possibilities $K > 0$ or $K = 0$. First, we consider the case $K > 0$. Obviously, $S_n$ satisfies

By the fact that $I_n\rightarrow \frac{K}{|\Omega|}$ and Lemma A.2, we can prove that

uniformly on $\bar{\Omega}$ as $n \rightarrow\infty$. Since $(S_n, I_n)$ satisfies (1.5), letting $n\rightarrow \infty,$ we have

which implies that $K = \frac{|\Omega|(N-\int_\Omega \gamma/\beta dx)}{|\Omega|+m\int_\Omega \gamma/\beta dx}$ when $N > \int_\Omega \gamma/\beta dx$. By (3.6) and (3.13), we know that (1.7) holds provided $N > \int_\Omega \gamma/\beta dx$.

For the case $K = 0$, we have $I_n\rightarrow 0$ uniformly on $\bar{\Omega}$ as $n \rightarrow\infty$. Passing to a subsequence if necessary, we then have either case (1) $\|I_n\|_\infty/d_{S_n}\leq C$ with $C\geq0$, or case (2) $\|I_n\|_\infty/d_{S_n}\rightarrow\infty$ as $n \rightarrow\infty$.

If the case (1) occurs, then $\int_\Omega I_n dx/d_{S_n}\leq \|I_n\|_\infty/d_{S_n}\leq C$. Let $\check{I}_n: = I_n/d_{S_n}.$ Then $\|\check{I}_n\|_\infty\leq C$ and $\check{I}_n$ satisfies

Since the right hand of this equation is uniformly bounded in $L^\infty(\Omega)$, by standard elliptic regularity we know that $\{\check{I}_n\}$ is precompact in $C^1(\bar\Omega)$. Hence by passing to a subsequence we may assume that $\check{I}_n\rightarrow\check{I}\geq0$ in $C(\bar \Omega)$. Moreover, $\check{I}$ satisfies (1.9), i.e.

We claim that $\check{I} > 0$. To this end, we assume $\check{I}\equiv0$ on $\bar{\Omega}$, i.e, $\check{I}_n\rightarrow 0$ in $C(\bar\Omega)$. Let $\tilde{I}_n = \check{I}_n/\|\check{I}_n\|_\infty.$ Then $\|\tilde{I}_n\|_\infty = 1$ and $\tilde{I}_n$ satisfies

Similarly, by passing to a subsequence we may assume that $\tilde{I}_n\rightarrow\tilde{I}$ in $C(\bar\Omega)$. Furthermore, $\|\tilde{I}_n\|_\infty = 1$ and $\tilde{I}$ satisfies

It follows from the strong maximum principle that $\tilde{I} > 0$ on $\bar{\Omega}$. Hence, the definition of $\mathcal {R}_0$ and (3.15) implies that $\mathcal {R}_0 = 1,$ which is a contradiction. Therefore, $\check{I}\geq0, \not\equiv0$. By the strong maximum principle again, we get $\check{I} > 0$ on $\bar{\Omega}$. Hence, $\int_\Omega I_n/d_{S_n}dx\rightarrow \int_\Omega\check{I}dx > 0$ in $C(\bar\Omega)$ as $n\rightarrow\infty$. However, if $\|I_n\|_\infty/d_{S_n}\rightarrow0$, then $\int_\Omega I_n/d_{S_n}dx\rightarrow 0$. It's a contradiction. Therefore, it remains $\|I_n\|_\infty/d_{S_n}\rightarrow C_1$ with some $C_1 > 0$. In this case, $I_n\rightarrow 0$ in $C(\bar\Omega)$ and by passing to a subsequence

as $n\rightarrow\infty$, i.e. (1.8) holds.

If case (2) occurs, i.e., $\|I_n\|_\infty/d_{S_n}\rightarrow\infty$. Recalling $I_n\rightarrow0$ uniformly on $\bar{\Omega}$ as $n\rightarrow\infty$, we have $\|I_n\|_\infty\rightarrow 0$. By Lemma 3.1, we know that $S_n$ is uniformly bounded. Let $\tilde{I}_n = I_n/\|I_n\|_\infty.$ Then $\|\tilde{I}_n\|_\infty = 1$ and $\tilde{I}_n$ satisfies

By the standard elliptic estimates, $\tilde{I}_n$ is uniformly bounded in $C^1(\bar{\Omega})$ for fixed $d_I > 0$. So passing to a subsequence if necessary, we have $\tilde{I}_n\rightarrow\tilde{I}$ in $C(\bar\Omega)$ with $\|\tilde{I}\|_\infty = 1$. By the Harnack inequality, there is a positive constant $K_*$ independent of $n$ such that

Hence ${\min _{x\in\bar{\Omega}}\tilde{I}}\geq 1/K_* > 0$, i.e. $\tilde{I}$ is strictly positive. We now turn to consider the equation (3.12) for $S_n$. Dividing (3.12) by $\|I_n\|_\infty$, we have

Since $d_{S_n}/\|I_n\|_\infty \rightarrow 0^+$, $I_n/\|I_n\|_\infty \rightarrow \tilde{I}$ and $I_n\rightarrow0$, it follows from Lemma A.2 that

Moreover by (1.5) and $I_n\rightarrow0$, we get

which is a contradiction if $\int_\Omega\gamma/\beta dx\not = N.$ But if $\int_\Omega\gamma/\beta dx = N$, (1.7) holds.

Proof of Corollary 1.4. From the proof of Theorem 1.3, we know that if $\mathcal {R}_0 > 1$ and $N < \int_\Omega \gamma/\beta dx$, then $I_n\rightarrow 0$ uniformly on $\bar{\Omega}$ as $n \rightarrow\infty$ and $\|I_n\|_\infty/d_{S_n}\leq C$ with $C\geq0$. In this case, $S^*$ satisfies (1.8).

Proof of Corollary 1.5. From the proof of Theorem 1.3, we only need to rule out $I^* = 0$.

(ⅰ) Suppose that $\beta$ is a positive constant. Then $N > \int_\Omega \gamma/\beta dx$ implies that $\frac{N}{|\Omega|}\int_\Omega \beta dx > \int_\Omega \gamma dx$, i.e., $\Omega$ is a high-risk domain. By Proposition 1.1(ⅲ) and Theorem 1.2, we know that the EE $(S, I)$ exists for all $d_I > 0$ and $m > 0$. Multiplying both sides of the first equation of (2.5) by $(1+mI)/I$ and integrating it over $\Omega$, we get

which implies that

Since $\beta$ is a constant, it follows from the above inequality that

On the other hand, by Theorem 1.3, we know that $(S, I)\rightarrow (S^*, I^*)$ in $C(\bar{\Omega})$ as $d_{S}\rightarrow0$, where $I^*$ is a nonnegative constant. Letting $d_S\rightarrow 0^+$, the inequality (3.17) implies that

Hence $I^* > 0$, which indicates that $(S^*, I^*)$ satisfies (1.7).

(ⅱ)-(ⅲ). From (3.6), we know $I^* = K/|\Omega|$. We need to prove $K > 0$.

If $K = 0$, there are three cases to consider: (1) $\|I_n\|_\infty/d_{S_n}\rightarrow C_1 > 0$, (2) $\|I_n\|_\infty/d_{S_n}\rightarrow 0$, and (3) $\|I_n\|_\infty/d_{S_n}\rightarrow\infty$. If $N > \int_\Omega \gamma/\beta dx$, from the proof of Theorem 1.3, the case (2) and (3) are excluded directly. It remains to consider case (1). In this case, $I_n/d_{S_n}\rightarrow \check{I} > 0$, where $\check{I}$ satisfies (1.9). Next, we show that (1.9) has no positive solution under the conditions (ⅱ) or (ⅲ), which will deduce a contradiction. Take

and consider the problem

Repeating the arguments as in the proof of Theorem 1.2, we can prove that there exists a smooth curve $(\tau, \tilde{I}_\tau(x))$ in $[0, \infty)\times Y$ such that $F_1(\tau, \tilde{I}_\tau) = 0$ with $\tilde{I}_\tau > 0$ for all $x\in \bar{\Omega}$ and $\tau\in [0, \infty)$ if $\mathcal {R}_0 > 1$. Moreover, $\tilde{I}_\tau(x)$ is strictly increasing and continuously differentiable with respect to $\tau$ in $(0, \infty)$. It is easy to see that $\tilde{I}_\tau$ is a positive solution of (1.9) if and only if $\tau = \int_\Omega \tilde{I}_\tau dx$.

Let $x_\tau, y_\tau \in \bar\Omega$ satisfy $\tilde{I}_\tau(x_\tau) = \min\limits_{x\in\bar\Omega}\tilde{I}_\tau(x)$ and $\tilde{I}_\tau(y_\tau) = \max\limits_{x\in\bar\Omega}\tilde{I}_\tau(x)$. Using Lemma A.3 to (3.18), it is easy to check that, for every $\tau\in [0, \infty)$

Then for every $\tau\in [0, \infty)$, we have

which implies that

Note that $\mathcal {R}_0 > 1$ implies $N/|\Omega| > \min\limits_{\bar\Omega}\gamma(x)/\beta(x)$ by Proposition 1.1(v). It follows from (3.20) that $\tau\not = \int_\Omega I_\tau dx$ for every $\tau\in [0, \infty)$ provided $N/|\Omega| > \max\limits_{\bar\Omega}\gamma(x)/\beta(x)$ or $\gamma(x)/\beta(x) = r$. Hence (1.9) has no positive solution under the conditions (ⅱ) or (ⅲ). $K = 0$ is impossible and we complete the proof of Corollary 1.5.

Next, we will prove Theorem 1.6. To this end, we first give the following result.

Lemma 3.4. Assume that $\Omega^+$ is nonempty and $d$ is a positive constant. Then the following equation

has a unique nonnegative solution.

Proof. It is easy to see that (3.21) has a unique nonnegative solution $I = \frac{[\beta(x)N/|\Omega| -\gamma(x)]^+}{\beta+m\gamma}$ if $d = 1$. Hence, we only consider $d\in (0, 1)\cup(1, +\infty)$ below. Let

If $d\in(0, 1)$, then $\int_\Omega G_\tau dx$ is non-increasing in $\tau$ for $\tau\geq 0$ and $\int_\Omega G_\tau dx = 0$ for sufficiently large $\tau$. Define

Since $\Omega^+$ is nonempty, we conclude that $\int_\Omega G_0 dx = \int_\Omega \frac{[\beta(x)N/|\Omega|-\gamma(x)]^+}{d\beta(x)+m\gamma(x)}dx > 0$ and $\int_\Omega G_\tau dx$ is decreasing with respect to $\tau\in [0, \tau_0]$. Hence, there exists a unique $\tau^*\in (0, \tau_0)$, such that $\int_\Omega G_{\tau^*} dx = \tau^*$, i.e., $G_{\tau^*}$ is the unique nonnegative solution of (3.21).

If $d > 1$, then $\int_\Omega G_\tau dx$ is non-decreasing in $\tau$ for $\tau\geq 0$ and $\int_\Omega G_\tau dx\rightarrow\infty$ as $\tau\rightarrow\infty$. We notice that

Since the right hand side of the above inequality is linear in $\tau$ with slope less than 1, there exists $\tau^* > 0$ such that $\int_\Omega G_{\tau^*} dx = \tau^*$, which implies that $G_{\tau^*}$ is a solution of (3.21). On the other hand, since $\int_\Omega G_\tau dx$ is concave up in $\tau$, $\tau^*$ is the unique solution of $\int_\Omega G_\tau dx = \tau$. Hence, (3.21) has a unique nonnegative solution. The proof is complete.

Proof of Theorem 1.6. Since $\Omega^+$ is nonempty, the EE $(S, I)$ exists if $d_I$ is small by Proposition 1.1 and Theorem 1.2.

First, we prove the conclusion for the case $d < 1$. We claim that $\int_\Omega Idx\rightarrow \int_\Omega I^*dx$ as $d_I\rightarrow0^+$ and $d_I/d_S\rightarrow d$, where $I^*$ is the unique solution of (3.21). Since $\int_\Omega Idx \leq N$, there exist two sequences $\{d_{I_n}\}$ and $\{d_{I_n}/d_{S_n}\}$ with $d_{I_n}\rightarrow0^+$ and $d_{I_n}/d_{S_n} \rightarrow d$ as $n\rightarrow\infty$ such that the corresponding EE $(S_n, I_n)$ satisfies $\int_\Omega I_ndx\rightarrow K_0\in[0, N]$. Then, for any $\epsilon > 0$, there exists $n^* > 0$ such that $K_0-\epsilon < \int_\Omega I_ndx < K_0+\epsilon$ and $d-\epsilon < d_{I_n}/d_{S_n} < d+\epsilon$ when $n > n^*$. Therefore, $I_n$ is a lower solution of the problem

and is an upper solution of the problem

for $n > n^*$. Denote the unique positive solutions of (3.22) and (3.23) by $I_{n, -\epsilon}$ and $I_{n, +\epsilon}$ respectively if they exist; otherwise, let $I_{n, -\epsilon} = 0$ ($I_{n, +\epsilon} = 0$). Then, it follows from an upper-lower solution argument that $I_{n, +\epsilon}\leq I_n\leq I_{n, -\epsilon}$ for $n > n^*$. Furthermore, by Lemma A.2, we have

in $C(\bar{\Omega}),$ where

Since $\epsilon > 0$ is arbitrary, by Lemma 3.4 we obtain

Now, we show $I\rightarrow I^*$ as $d_I\rightarrow0^+$ and $d_I/d_S\rightarrow d$. Substituting $K_0 = \int_\Omega I^*dx$ into (3.24), we get that

and hence

as $d_I\rightarrow0^+$ and $d_I/d_S\rightarrow d$.

The proof of the case $d\geq1$ is similar, so we omit it here. The conclusion in (ⅱ) is easily obtained from equation (3.21).

Proof of Theorem 1.8. Since $\Omega$ is a high-risk domain, the EE $(S, I)$ always exists for any $d_S > 0$ and $d_I > 0$. By Lemmas 3.1 and 3.2, we know that $I$ and $S$ are uniformly bounded in $L^\infty (\Omega)$ for any positive $d_I$ and $d_S$.

(ⅰ) We consider the asymptotic profile of the EE when $d_I\rightarrow \infty$ and $d_S\rightarrow \infty$. Note that $\beta SI/(1+mI)-\gamma I$ is uniformly bounded in $L^\infty (\Omega)$. Applying the standard elliptic estimate arguments, we obtain that $S$ and $I$ are uniformly bounded in $C^{2+\alpha}(\bar{\Omega})$ for all $\alpha\in (0, 1)$, $d_S, d_I\geq 1$. It then follows from the compactness of the embedding $C^{2+\alpha}(\bar{\Omega})\hookrightarrow C^{2}(\bar{\Omega})$ that there exist sequences $\{d_{S_n}\}, \{d_{I_n}\}$ with ${d_{S_n}}\rightarrow\infty, {d_{I_n}}\rightarrow\infty$ as $n\rightarrow\infty$ such that the corresponding EE $(S_n, I_n)\rightarrow(S^*, I^*)$ in $C^{2}(\bar{\Omega})$, where $(S^*, I^*)$ satisfies

By the strong maximum principle, $S^*$ and $I^*$ are constants. Let $\tilde{I}_n = I_n/\|I_n\|_\infty$. By (1.4), we have

Since $\|\tilde{I}_n\|_\infty = 1$ and $I_n, S_n$ are uniformly bounded, it follows from the elliptic estimate and the Sobolev embedding theorem that $\tilde{I}_n$ is uniformly bounded in $C^{2+\alpha}(\bar{\Omega})$. Passing to a subsequence if necessary, we have $\tilde{I}_n\rightarrow \tilde{I}$ in $C^{2}(\bar{\Omega})$, where $\tilde{I}$ satisfies

Using the strong maximum principle again, $\tilde{I}$ is a constant. And then $\tilde{I}\equiv1$ since $\|\tilde{I}_n\|_\infty = 1$. Integrating both sides of the first equation in (3.25) over $\Omega$, we find

Letting $n \rightarrow\infty$, we have

Noticing that $\int_\Omega(S^*+I^*)dx = N$ and $S^*, I^*, m$ are constants, we have

(ⅱ) Now we consider the asymptotic profile of the EE when $d_I\rightarrow\infty$. The proof is similar to (ⅰ) and Theorem 1.3, so we sketch it in the following.

Suppose $d_S$ is fixed. By the elliptic estimate, the Sobolev embedding theorem and the maximum principle, there exists a sequence $\{d_{I_n}\}$ with ${d_{I_n}}\rightarrow\infty$ as $n\rightarrow\infty$ such that the corresponding EE $(S_n, I_n)\rightarrow(S^*, I^*)$ in $C^2(\bar{\Omega})$, where $I^*\geq0$ is a constant. If $I^* = 0$, then $S^*$ satisfies (3.4), which indicates that $S^*$ is also a constant. As in the proof of (ⅰ), we also introduce $\tilde{I}_n = I_n/\|I_n\|_\infty.$ Then we can prove $\tilde{I}_n\rightarrow1$ in $C^2(\bar{\Omega})$ as $n\rightarrow\infty$, which leads to

and so $S^* = \int_\Omega\gamma dx /\int_\Omega\beta dx$. On the other hand, one can see from (1.5) that $S^* = N/|\Omega|$ when $I^* = 0$. Hence, $\frac{N}{|\Omega|}\int_\Omega\beta dx = \int_\Omega\gamma dx$, which contradicts the assumption that $\Omega$ is a high-risk domain. Therefore $I^*$ is a positive constant, and $S^* > 0$ satisfies (1.11).

Furthermore, let $d_{S}\rightarrow0^+$. There exists a sequence $\{d_{S_n}\}$ with ${d_{S_n}}\rightarrow0^+$ as $n\rightarrow\infty$ such that the corresponding solution $(S_n^*, I_n^*)$ of (1.11) satisfies $d_{S_n}/I^*_n\rightarrow0$, or $d_{S_n}/I^*_n\rightarrow \infty$, or $d_{S_n}/I^*_n\rightarrow K_1$ for some positive constant $K_1$. If $d_{S_n}/I^*_n\rightarrow0$, we have $(S_n^*, I_n^*)\rightarrow(\tilde{S}^*, \tilde{I}^*)$ in $C(\bar{\Omega})$. Rewrite the equation of {$S_n^*$} as

Letting $n\rightarrow\infty$, we obtain

which implies that $(\tilde{S}^*, \tilde{I}^*)$ satisfies (1.7).

If $d_{S_n}/I^*_n\rightarrow K_1$, by passing to a subsequence, we have $(S_n^*, I_n^*)\rightarrow(\tilde{S}^*, 0)$ in $C(\bar{\Omega})$ as $d_{S_n}\rightarrow 0^+$. Rewrite the equation of $S_n^*$ as follow

Letting $n\rightarrow\infty$, we obtain $\tilde{S}^*$ satisfies (1.12).

If $d_{S_n}/I^*_n\rightarrow\infty$ as $d_{S_n}\rightarrow0^+$, by passing to a subsequence, we have $(S_n^*, I_n^*)\rightarrow(\tilde{S}^*, 0)$ in $C(\bar{\Omega})$ and $S_n^*$ satisfies (3.26). Letting $n\rightarrow\infty$, we know that $\tilde{S}^*$ is a constant. By the last equation of (1.11), we actually have $\tilde{S}^* = \frac{ N}{|\Omega|}$. Integrating both sides of the first equation in (1.11), we get $\int_\Omega\left[-\beta S_n^*/(1+mI_n^*)+\gamma\right]dx = 0$. Letting $n\rightarrow\infty$, we find $\frac{N}{|\Omega|}\int_\Omega\beta dx = \int_\Omega\gamma dx$, which contradicts the assumption that $\Omega$ is a high-risk domain. Hence $d_{S_n}/I^*_n\rightarrow\infty$ is impossible. The proof is complete.

Proof of Theorem 1.9. Since $\mathcal {R}_0$ is independent of $m$, the EE $(S, I)$ exists for any $m > 0$ provided $\mathcal {R}_0 > 1$ by Theorem 1.2. It follows from (3.1) that $I$ is uniformly bounded for fixed $d_I > 0, d_S > 0$. Hence there exists a sequence $\{m_n\}$ with $m_n\rightarrow\infty$ as $n \rightarrow\infty$ such that the corresponding EE $(S_n, I_n)$ satisfies

Since the right hand of the above equation is uniformly bounded in $L^\infty(\Omega)$, by standard elliptic regularity we know that $\{I_n\}$ is precompact in $C^1(\Omega)$. Hence by passing to a subsequence we may assume that $I_n \rightarrow I_*\geq 0$ in $C(\bar\Omega)$. There are two possibilities (a) $\|m_nI_n\|_\infty\rightarrow\infty$ as $n\rightarrow\infty$ or (b) $\|m_nI_n\|_\infty\leq C$, where $C$ is a positive constant.

If (a) occurs, then $I_*$ satisfies

The Fredholm alternative implies that $I_* = 0$.

If (b) occurs, then $I_n\rightarrow 0$ uniformly on $\bar{\Omega}$ as $n\rightarrow\infty$. Denote $m_nI_n = w_n$. Then $w_n$ is uniformly bounded in $L^\infty(\Omega)$ and $w_n\rightarrow w_*\geq 0$ in $C(\bar\Omega)$, where $w_*$ satisfies

If $w_*\equiv 0$, set $\hat{w}_n = \frac{w_n}{\|w_n\|_\infty}$. Then $\hat{w}_n$ satisfies

By standard elliptic regularity we may assume that $\hat{w}_n\rightarrow \hat{w}$ in $C(\bar\Omega)$. Then $\hat{w}\geq0, \not\equiv 0$ satisfies

It follows from the strong maximum principle that $\hat{w} > 0$ on $\bar{\Omega}$. So $\lambda_1(d_I, \beta N/|\Omega|-\gamma) = \lambda^* = 0$, which implies $\mathcal {R}_0 = 1$. This is a contradiction to the assumption $\mathcal {R}_0 > 1$. Hence $w_*\geq0, \not\equiv 0$ in $\bar{\Omega}$. Using the strong maximum principle again, we know that $w_* > 0$ on $\bar{\Omega}$. It follows from Lemma A.2 that (3.29) has a unique positive solution $w_*$ as $\lambda_1(d_I, \beta N/|\Omega|-\gamma) = \lambda^* < 0$.

4.   Numerical simulation

To illustrate the influences of the population diffusion and the saturation coefficient on system (1.2), we suppose the spatial domain $\Omega = [0, 1]$. Let $\beta(x) = \sin(2\pi x)+a,$ $\gamma(x) = \cos(2\pi x)+b$, where $a > 1, b > 1.$ Take $S(x, 0) = \sin(\pi x)+1,$ $I(x, 0) = \sin(\pi x)+1$, $a = 1.5$, $b = 4.5$. Then $N = \int_\Omega(S(x, 0)+I(x, 0))dx = 3.2731$ satisfies

where $\frac{1}{|\Omega|}\int_\Omega \frac{\gamma(x)}{\beta(x)}dx = 4.0249$. Hence $\Omega^+$, $\Omega^-$ are nonempty, and $\Omega$ is a high-risk domain which implies that $\mathcal {R}_0 > 1$ by Proposition 1.1 (ⅲ).

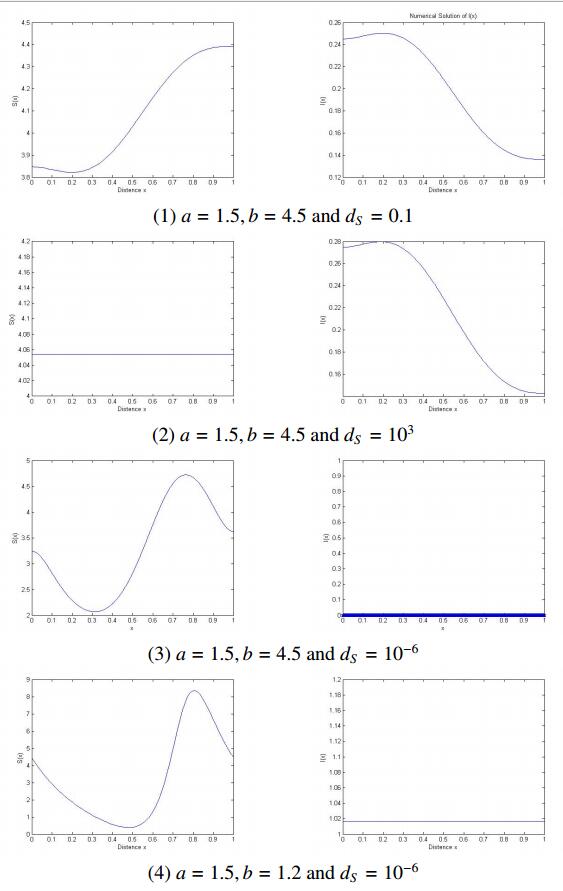
(ⅰ) Firstly, we explore the influence of $d_S$ on system (1.2). Fix $d_I = 0.5$ and $m = 2$. A numerical positive equilibrium solution $(S(x), I(x))$ to (1.2) was computed in Figure 2(1) with $d_S = 0.1$. When $d_S$ is large, we find that $S(x)$ tends to a constant and $I(x)$ closely approximates the unique positive solution of (1.6) (see Figure 2(2) with $d_S = 10^3$), which is consistent with Theorem 1.3 (ⅰ). As $d_S$ decreases, the value of $I(x)$ decreases too. In Figure 2(3), $I(x)$ closely approximates zero with $d_S = 10^{-6}$, which coincides with the results of Theorem 1.3(ⅱ) and Corollary 1.4.

If we take $a = 1.5$ and $b = 1.2$, then $3.2731 = \frac{N}{|\Omega|} > \max\limits_{x\in\bar\Omega}\frac{\gamma(x)}{\beta(x)} = 2.7514$, which implies that $\mathcal {R}_0 > 1$ by Proposition 1.1(ⅰ) and (ⅱ). By taking $d_I = 0.5$ and $d_S = 10^{-6}$, we find that $I(x)$ closely approximates a positive constant (see Figure 2(4)), which coincides with the results of Theorem 1.3 (ⅱ) and Corollary 1.5.

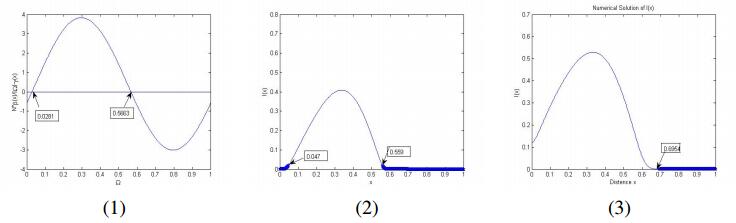
(ⅱ) Secondly, we analyze the asymptotic profile of the equilibrium solution $(S(x), I(x))$ to system (1.2) when $d_S$ and $d_I$ are small. Fix $a = 1.5$, $b = 4.5$ and $m = 2$. Then $\Omega^+$ and $\Omega^-$ are nonempty from (4.1). By taking $d_S = 10^{-4}$ and $d_I = 0.2\times 10^{-4}$, we find that $(0.0470, 0.5590)\approx\{x\in \Omega: I^* > 0\}\subsetneqq\Omega^+ = (0.0281, 0.5663),$ which coincides with the result of Theorem 1.6 with $d < 1$ (see Figure 3(1)–(2)). By taking ${d_S} = 10^{-4}$ and $d_I = 2\times 10^{-4}$, we find that $[0, 0.6954) = \{x\in \Omega: I^* > 0\}\supseteqq\Omega^+ = (0.0281, 0.5663),$ which coincides with the result of Theorem 1.6 with $d > 1$ (see Figure 3(1), (3)).

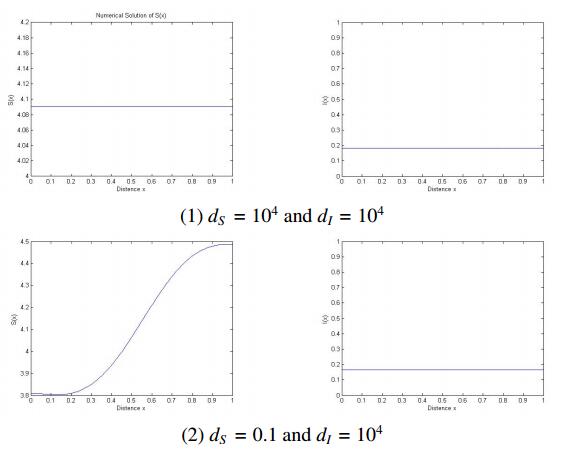
(ⅲ) Thirdly, we explore the asymptotic profile of the equilibrium solution $(S(x), I(x))$ to system (1.2) when $d_I$ is large. Fix $a = 1.5$, $b = 4.5$ and $m = 2$. Then $\Omega$ is a high-risk domain from (4.1). A numerical positive equilibrium solution $(S(x), I(x))$ to (1.2) was computed (see Figure 4). In Figure 4(1), by taking $d_S = d_I = 10^4$, we find that $(S(x), I(x))$ closely approximates a constant equilibrium solution, which coincides with the result of Theorem 1.8(ⅰ). In Figure 4(2), by taking $d_S = 0.1$ and $d_I = 10^{4}$, we find that $I(x)$ closely approximates a positive constant, which coincides with the result of Theorem 1.8(ⅱ).

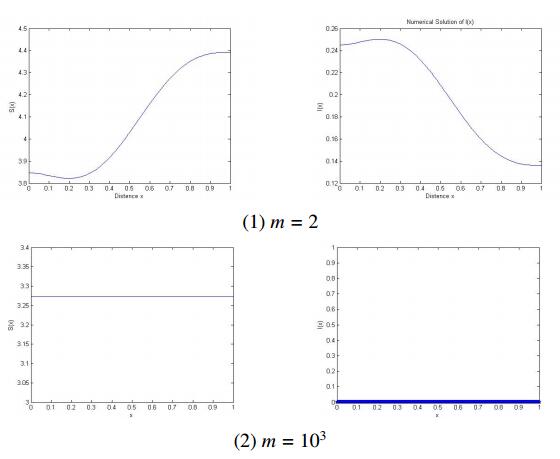
(ⅳ) Finally, we show the influence of saturation coefficient $m$ on system (1.2). Fix $a = 1.5$, $b = 4.5$, $d_S = 0.1$ and $d_I = 0.5$. Then $\mathcal {R}_0 > 1$ from (4.1). A numerical positive equilibrium solution $(S(x), I(x))$ to (1.2) was computed (see Figure 5). In Figure 5(1), by taking $m = 2$, there is a positive equilibrium solution $(S(x), I(x))$ to (1.2). In Figure 5(2), by taking $m = 10^3$, we find that $(S(x), I(x))$ closely approximates the DFE $(N/|\Omega|, 0)$, which coincides with the result of Theorem 1.9.

5.   Discussion

In this paper, we investigate an SIS reaction-diffusion population model (1.2) with saturated incidence rate $\beta\bar{I}\bar{S}/(1+m\bar{I})$. We focus on the existence of EE and particularly the effects of the diffusion rates and the saturated coefficient on asymptotic profiles of EE. Similar questions are addressed for the model with the standard incidence rate $\beta \bar{S}\bar{I}/(\bar{S}+\bar{I})$ in ^[1,20] or the bilinear rate $\beta\bar{S}\bar{I}$ in ^[7,16,25].

Firstly, by introducing the basic reproduction number $\mathcal {R}_0$ as in ^[1,7], we obtain for (1.2) that there is at least one EE if $\mathcal {R}_0 > 1$, especially, EE exists uniquely when $d_S\geq d_I$. In contrast to ^[1], the definition of $\mathcal {R}_0$, $\Omega^+$ and $\Omega^-$ for our model (1.2) depends on the average population density, i.e. $N/|\Omega|$. From the epidemiology point of view, the more crowded the population is, the easier endemic a disease becomes.

Secondly, we analyse the asymptotic profile of EE when it exists. Regarding this, it is worthwhile to mention the following three results.

(ⅰ) The diffusion rate of the susceptible individuals $d_S$ is small. Theorem 4 in ^[1] indicates that the asymptotic profile is some spatially inhomogeneous DFE. However, our results for (1.2) show that EE (if it exists) may approach a coexistence limiting equilibrium where the susceptible individuals spatially heterogeneously exist and the infected population is a spatially homogeneous state (see Theorem 1.3(ⅱ) and Corollary 1.5). Furthermore, we observe that the coexistence limiting equilibrium tends to a spatially inhomogeneous DFE when the saturated coefficient $m$ is large. From a disease control point of view, if a disease is governed by system (1.2), it is not enough to just restrict the movement of the susceptible individuals to completely eradicate the disease in the whole habitat in certain situations, especially if the rate of disease transmission $\beta$ is a constant and $\Omega$ is a high-risk domain; see Corollary 1.5 (ⅰ).

(ⅱ) $d_I\rightarrow0$ and $d_I/d_S\rightarrow d\in(0, \infty).$ Theorem 1.1(2) and Corollary 1.1(ⅰ) of ^[20] show that the existence habitat of the infective individuals is exactly the high-risk set. However, in our results, the ratio $d$ plays a key role (see Theorem 1.6 and Remark 1.7). If $d = 1$, the infected individuals survive exactly in the high-risk set; if $d\in(0, 1)$, the habitat of infected individual is confined within some subset of the high-risk set; if $d > 1$, the infected individuals only die out at part of the low-risk sites. This information suggests that reducing the radio $d$ to less than 1 will help to control disease; in other words, the more isolated the patients become, the better disease control is.

(ⅲ) The saturated coefficient $m$ is large. For model (1.2), Theorem 1.9 indicates that the EE tends to the DFE, i.e., the infective individuals cannot persist. This result seems to coincide with the realistic intuition: the more inhibition effect from the behavioral change of the susceptible individuals when their number increases or from the crowding effect of the infective individuals, the better for disease control.

Finally, we would like to mention some open problems left for future study: (1) the existence of $EE$ when $d_S < d_I$ and $\mathcal {R}_0\in (d_S/d_I, 1)$; (2) the asymptotic profile of EE when $\mathcal {R}_0 > 1$ and $\frac{1}{|\Omega|}\int_\Omega \frac{\gamma(x)}{\beta(x)} dx < \frac{N}{|\Omega|}\leq\max\limits_{x\in\bar\Omega}\frac{\gamma(x)}{\beta(x)}$ as $d_S\rightarrow0^+$; (3) the uniqueness of EE if it exists when $d_S < d_I.$

Acknowledgments

The work of Y. Wang and Z. Wang was supported by the Natural Science Foundation of China (11671243, 61672021, 11771262, 11571274, 11501496), the Fundamental Research Funds for the Central Universities (GK201903088), the Natural Science Basic Research Plan in Shaanxi Province of China (2018JM1020, 2018JQ1021). The work of C. Lei was supported by the Natural Science Foundation of China (11801232), the Priority Academic Program Development of Jiangsu Higher Education Institution, the Natural Science Foundation of the Jiangsu Province(BK20180999), the Foundation of Jiangsu Normal University (17XLR008).

Conflict of interest

The authors declare there is no conflict of interest.

Appendix

We recall the following well-known facts without proof.

Let $\lambda_1(d, g)$ be the principal eigenvalue of

where $g(x)\in L^\infty (\Omega)$ and $d > 0$. It is folklore that $\lambda_1(d, g)$ is given by

The properties of $\lambda_1(d, g)$ are stated as follows; they can be found in ^[1,3].

Lemma A.1.

(ⅰ) If $g_1(x)\leq g_2(x)$ in $\Omega$ with $g_i\in L^\infty (\Omega)$ for $i = 1, 2,$ then $\lambda_1(d, g_1)\geq\lambda_1(d, g_2)$ with equality holds if and only if $g_1 = g_2$ a.e. in $\Omega$;

(ⅱ) if $g\in L^\infty (\Omega)$ is non-constant, then $\lambda_1(d_1, g) < \lambda_1(d_2, g)$ when $d_1 < d_2$;

(ⅲ) $\lambda_1(d, g)$ depends continuously on $g$ and $d$, and it satisfies

The following lemma is about the existence of an elliptic problem and its asymptotic profile (as $d\rightarrow0^+$), which can be found in ^[3] or can be directly proved by an upper/lower solution argument. Let us denote $h^+(x): = \max\{h(x), 0\}$ for any function $h$ defined on $\bar{\Omega}$.

Lemma A.2. Suppose that positive functions $a(x), b(x), d(x)\in C^\alpha(\bar{\Omega})$. Then the following statements hold for the problem

(ⅰ) If $\lambda_1(d, a-c)\geq 0$, then $u = 0$ is the only non-negative solution of (A.4);

(ⅱ) if $\lambda_1(d, a-c) < 0$, then (A.4) has a unique positive solution $u\in C^{2+\alpha}(\bar{\Omega})$. Furthermore, $u\rightarrow \left(\frac{a-c}{bc}\right)^+$ as $d\rightarrow0^+$ provided $a(x_0)-c(x_0) > 0$ for some $x_0\in \bar{\Omega}$.

To obtain the priori estimates for solutions, the following maximum principle (due to Lou and Ni ^[18]) and the Harnack's inequality (see, e.g., ^[17]) are useful.

Lemma A.3. Suppose that $g\in C(\bar \Omega\times\mathbb{R})$.

(ⅰ) Assume that $\omega\in C^2(\Omega)\cap C^1(\bar\Omega)$ and satisfies

If $\omega(x_0) = \max\limits_{x\in\bar\Omega}\omega(x)$, then $g(x_0, \omega(x_0))\geq0.$

(ⅱ) Assume that $\omega\in C^2(\Omega)\cap C^1(\bar\Omega)$ and satisfies

If $\omega(x_0) = \min\limits_{x\in\bar\Omega}\omega(x)$, then $g(x_0, \omega(x_0))\leq0.$

Lemma A.4. Let $w\in C^2(\Omega)\cap C^1(\bar{\Omega})$ be a positive solution of

where $c(x)\in C(\bar{\Omega})$. Then there exists a positive constant $C = C(n, \Omega, \|c\|_\infty)$ such that