Analysis and numerical simulation of an inverse problem for a structured cell population dynamics model

Cell dynamics are classically investigated in the framework of structured populations, and especially of the McKendrick–VonFoerster model. The direct problem associated with the initial and extended formulations of this model has caught most of the attention, both on the theoretical ground (well-posedness, e.g. ^[1,2]) and numerical ground (numerical approximation of the solutions, e.g. ^[3,4,5]). The inverse problems, intending to recover model functions, such as the death or division rate, from observable model outputs, have been much less studied ^[6,7,8,9,10], although they have a particular interest in a cell dynamics context, where a priori information on these rates are often quite poor.

In this work, we study and illustrate the well-posedness of a multiscale inverse problem (IP), defined from a multi-type version of the linear, age-structured formulation of the McKendrick–VonFoerster model, in the specific situation where cell death can only occur at the time of mitosis.

This problem has been initially motivated by a developmental biology issue, namely folliculogenesis, the process of growth and maturation of ovarian follicles. During the first development stages, the growth of ovarian follicles is mainly driven by the proliferation of the somatic cells surrounding the oocyte (egg cell), which progressively builds up several concentric cell layers. In this specific application ^[11], the cell type corresponds to the layer index, and the cell division rate is type-dependent. At the time of mitosis, cells are likely to move to the next layer (unidirectional motion), and the (layer-dependent) migration rate can be seen as the equivalent of a mitosis-induced death rate in the lower layer. As a consequence, the birth rate (boundary condition at birth with age $a = 0$) combines an intrinsic contribution from division and an extrinsic contribution from migration.

Beyond folliculogenesis, such a multi-type formulation can be applied to other cell processes with either spatially oriented development (e.g. cortical neurogenesis) or commitment to a cell lineage or fate (e.g., hematopoiesis).

The multiscale character of the IP ensues from the fact that the observable data (total cell number on each layer) are available on the macroscopic scale and used to recover the microscopic functions entering the system of interconnected McKendrick–VonFoerster PDEs. More specifically, we consider here the problem of recovering the age-dependent division rates, and constant migration rates ruling the cell density in age on each layer, from the knowledge of the total cell number (zero-order moment of the density) on every layers.

In ^[11], we have tackled the simplified case of constant (yet layer-dependent) division rates. In this work, we extend the study to the case of compactly supported (lattice) division rates, in order to stick to a realistic interpretation of the division rate as a distribution of intermitotic times; age is reset to zero at birth, there can be a minimal age compatible with division, and cells can become quiescent beyond a maximal age. We consider initial conditions corresponding either to a synchronized (Dirac mass) or non-synchronized cell population (Dirac comb or continuous function) on the first layer (all other layers are empty). If the well-posedness of the PDEs (1.1) for a $\mathbf{L}_1$ initial condition has been widely studied in the last decades (see for instance, ^[1,2]), the case of Dirac measure initial conditions has been investigated only recently. For instance, in ^[12,13], the authors have introduced the notion of measure solutions for the conservative renewal equation.

In the single layer (not multi-type) case, similar multiscale IP problems, dealing with an age-dependent reproduction rate have been studied ^[6,8]. In ^[6], in the case of a strictly positive, reproduction-independent death rate resulting in an almost sure death before a maximal age $L$, the authors have shown, from the characteristic curves, that the birth rate (boundary condition) verifies a Volterra integral equation of the second kind, and then used the Fredholm alternative to further recover the reproduction rate.In ^[8], starting from the cumulative formulation (renewal equation), and assuming a non-lattice reproduction rate, the authors have studied both the case of reproduction-dependent and reproduction-independent death rate to recover the reproduction and death rates. In the reproduction-dependent (mitosis-dependent) case (see Theorem 4.3), using the Laplace transform, the authors have shown the IP well-posedness for an initial population synchronized at age $0$ (Dirac mass). If, in addition, the total cell number can be expressed as a series of exponential functions, the IP well-posedness is also obtained for a non-synchronized initial population represented by a measure with support on $[0, 1]$ and no atom at $1$.

Also, single-scale IP problems, where observation are available at the microscopic level, have been investigated in a similar age-structured framework ^[7,14,15] or in the size-structured framework ^[16,17,18]. In the semigroup framework, the problem of recovering the death rate from the knowledge of both the age distribution at two different time points and the reproduction rate is studied in ^[7]. A similar problem is considered in ^[15] from the observation of a truncated age distribution at any time. Finally, in a steady state configuration, given a rather mesoscopic observation, the distribution of intermitotic times, one can recover the mitosis-dependent death rate ^[14] from the eigenvalue problem, following the methodological principle introduced in ^[16,17,18].

This paper is organized as follows. In section 1, we present the direct problem (multi-type McKendrick–VonFoerster). Inspired from the single layer case ^[2], we propose a formal solution based on the characteristic curves, and use them to design a numerical scheme, as performed in ^[4]. We check our numerical scheme using the mass conservation property. In Section 2, using a Fredholm integral equation, we show the well-posedness of the IP in the single layer case, when considering a continuous non-synchronized initial condition. Because of the mitosis-dependent death rate, the Fredholm alternative cannot be applied, and we use a constructive approach to obtain the lattice division rate from the knowledge of both the total cell number and a continuous (non-synchronized) initial condition. Then, we take advantage of the unidirectional motion and decompose the $J$th layer model into $J$ submodels, each corresponding to the single layer model with an additional extrinsic term in the boundary condition. We again derive a Fredholm integral equation for each submodel and deduce the well-posedness of the multi-type inverse problem. In section 3, we show the well-posedness of the IP in the single layer case, when considering Dirac masses as initial conditions. After constructing a solution from the characteristic lines, we still obtain a Fredholm integral equation. In each situation, we illustrate numerically our theoretical results. We conclude the paper by a Conclusion/Discussion section. Complements on the numerical scheme construction and the proofs can be found in the Appendix.

1.   Model and discretized solutions

We recall the age and layer structured cell population model considered in ^[11]. Let $J \in \mathbb{N}^*$. The cell population is represented by a population density function $\rho : = (\rho^{(j)}(t, a))_{j \in \left[\kern-0.15em\left[ { 1, J } \right]\kern-0.15em\right]} \in \mathbf{L}_1(\mathbb{R}_+)^J$, where $\rho^{(j)}$ is the cell age density in layer $j$ at time $t$ such that $\rho$ verifies, for all $j \in \left[\kern-0.15em\left[ { 1, J } \right]\kern-0.15em\right]$, for all $t \in (0, +\infty)$,

where $b_j$ are the division rate functions, and $\psi = (\psi_j)_{j \in \left[\kern-0.15em\left[ { 1, J } \right]\kern-0.15em\right]}$ is the initial density such that for all $j \in \left[\kern-0.15em\left[ { 1, J } \right]\kern-0.15em\right]$, $\psi_j \in \mathcal{C}_c(\mathbb{R}_+)$. For all $j \in \left[\kern-0.15em\left[ { 1, J } \right]\kern-0.15em\right]$, the parameter $p_S^{(j)}$ is the probability that a cell taken randomly among both daughter cells, remains on its mother layer $j$. For all $j \in \left[\kern-0.15em\left[ { 1, J-1 } \right]\kern-0.15em\right]$, we take $p_S^{(j)} \in (0, 1)$. On the last layer, $p_S^{(J)}\in (0, 1]$. A natural choice in the multi-layer case is to consider $p_S^{(J)} = 1$ as in ^[11]. The division rate on each layer has a classical probabilistic interpretation ^[1,6,8,14]: the probability that a cell born on the $j$-th layer has not yet divided at age $\alpha$ is

It follows that if $\int_0^{+ \infty} b_j(s)ds = + \infty$, the cell divides almost surely, and conversely, if $\int_0^{+ \infty} b_j(s)ds < + \infty$, a cell may never divide and become quiescent. This will happen in particular if $b_j$ is a bounded, compactly supported function. We investigate the inverse problem associated with the model (1.1):

Definition 1.1.

(IP) Given the initial condition $\psi$, the probability $p_S^{(J)}$ and the functions

defined for all $t \in [0, T)$, with $T > 0$, determine the functions $b_j$ and the probabilities $p_S^{(j)}$, for all $j \in \left[\kern-0.15em\left[ { 1, J - 1 } \right]\kern-0.15em\right]$, such that the direct problem (1.1) is satisfied on $[0, T)$.

The model is completed with a set of hypotheses on the division rate and initial conditions, formulated below.

Hypothesis 1.1. For all $j \in \left[\kern-0.15em\left[ { 1, J } \right]\kern-0.15em\right]$, the division rates $b_j$ are non-negative compactly supported functions: $b_j \in \mathcal{C}_c\left((A_j^{\min}, A_j^{\max})\right)$, where $A_j^{\min}, A_j^{\max} \in \mathbb{R}_+ \cup \{0\} \cup \{+ \infty\}$, such that $A_j^{\min} < A_j^{\max}$.

For the single layer case, note that this hypothesis is more general than the one used either in ^[8] where the division rate function is supposed to be non-lattice or, in the steady state approach ^[14] where $A_1^{\max} = + \infty$.

Motivated by the biological process studied in ^[11], we consider that the system starts with all the layers empty, except the first one. We consider different types of initial conditions: either Dirac measures corresponding to a fully or partially synchronized population, or a continuous function corresponding to a non-synchronized population. In case of a continuous initial condition, we assume that the following hypotheses are verified.

Hypothesis 1.2. For all $j \in \left[\kern-0.15em\left[ { 2, J } \right]\kern-0.15em\right]$ and for all $a \in (0, + \infty)$, we have $\psi_j(a) = 0$ and $\psi_1 \in \mathcal{C}_c\left((a^{\psi}_{\min}, a^{\psi}_{\max})\right)$, with $a^{\psi}_{\min}, a^{\psi}_{\max} \in \mathbb{R}_+$ such that $a^{\psi}_{\min} < a^{\psi}_{\max}$.

If the initial condition is a Dirac measure or Dirac Comb, we assume that:

Hypothesis 1.3. For all $j \in \left[\kern-0.15em\left[ { 2, J } \right]\kern-0.15em\right]$ and for all $a \in (0, + \infty)$, we have $\psi_j(a) = 0$. In addition, we suppose that there exist two sequences of $N+ 1$ positive numbers, with $N \in \mathbb{N}$, $a = (a_i)_{i \in \left[\kern-0.15em\left[ { 0, N } \right]\kern-0.15em\right]} \in \mathbb{R}^N_+ \cup \{0\}$ and $\Psi = (\Psi_i)_{i \in \left[\kern-0.15em\left[ { 0, N } \right]\kern-0.15em\right]} \in \mathbb{R}^N_+$ such that

Then, we define the initial condition on the first layer, for all $a \geq 0$, by

Finally, to show the well-posedness of the inverse problem (IP), we will need two additional hypotheses on the $b_j$ functions.

Hypothesis 1.4. For all $j \in \left[\kern-0.15em\left[ { 1, J } \right]\kern-0.15em\right]$, the division rates $b_j$ are analytic on their support sets.

Hypothesis 1.5. The first division time on Layer 1 is larger than the age of the eldest cells at initial time: $A^{\min}_1 \geq a^{\psi}_{\max}$

Hypothesis 1.1 is quite natural from the biological viewpoint, whereas Hypotheses 4 and 5 are purely technical, yet easily fulfilled.

We follow the same approach as in ^[6,7] and first solve the direct problem (1.1).

1.1.   Formal solutions of the direct problem (1.1)

Even if an explicit solution of the PDEs (1.1) cannot be obtained, one classical way to solve the direct problem when dealing with continuous initial conditions, is to use the method of characteristics ^[2,1]. We integrate the PDEs (1.1) along the characteristics lines $a = a_0 + t$ and $t = t_0 + t$, where $a_0$ and $t_0$ are nonnegative constants. We get for all $j \in \left[\kern-0.15em\left[ { 1, J } \right]\kern-0.15em\right]$ and for all $a \in (0, + \infty)$,

Hence, we obtain an expression for each $\rho^{(j)}$, for $j \in \left[\kern-0.15em\left[ { 1, J } \right]\kern-0.15em\right]$, that depends on the initial density $\psi_j$, the division rate $b_j$, and the boundary condition $\rho^{(j)}$.

To close system (1.5), we need to get an explicit expression for the boundary condition. When $J = 1$, the boundary condition, classically called the birth rate, is solution of a renewal equation ^[8]. In our context, we can retrieve a similar renewal equation verified by the boundary condition:

with $h_j(t) : = 2(1 - p_S^{(j -1)}) \int_{ 0}^{+ \infty} b_{j-1}(a)\rho^{(j-1)}(t, a)da$.

This equation is the deterministic counterpart of the renewal equation obtained from a stochastic equivalent model introduced in ^[11].

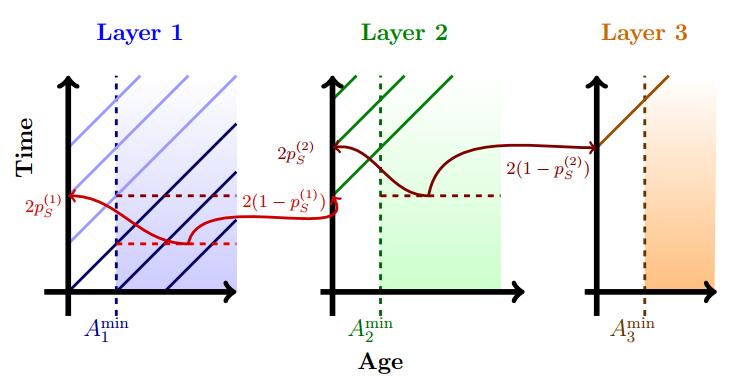
Figure 1 illustrates the characteristic lines obtained from expression (1.5) with $J = 3$. Note that since all layers except the first are empty at initial time, a delay is needed for cells to enter the second and third layers.

1.2.   Numerical scheme to simulate the direct problem (1.1)

In this subsection, we propose a numerical scheme for the direct problem (1.1). The main numerical difficulty associated with the hyperbolic PDEs (1.1) is the assessment of the boundary condition, which has been dealt with by several numerical methods, based either on the method of characteristics ^[3,19,4], escalator boxcar train ^[5] or finite volume method ^[11]. Given that our problem possibly involves a non-continuous initial condition ($\psi_1$), and lattice division rates, the method of characteristics is the most suitable one. In particular, the characteristics-based scheme ensures mass conservation during the transport phase by preventing numerical diffusion when $a < A^{j}_{\min}$. In addition, we will see later that this approach helps designing a numerical scheme for solving the inverse problem (IP).

To obtain a discretized solution of the PDEs (1.1), we write the conservative law for a vector function $\tilde{\rho} = (\tilde{\rho}^{(j)})_{j \in \left[\kern-0.15em\left[ { 1, J } \right]\kern-0.15em\right]}$, defined as: for all $j \in \left[\kern-0.15em\left[ { 1, J } \right]\kern-0.15em\right]$, $t \in (0, + \infty)$ and $a \in (0, + \infty)$,

From the PDEs (1.1), we obtain directly that, for all $t \in (0, + \infty)$ and $a \in (0, + \infty)$,

We now have all the elements to design a numerical scheme.

First, we introduce the notations for the discretized solutions associated with the PDEs (1.1) over the time interval $[0, T]$. We discretize both the age and time intervals with the same size step: $\Delta = \Delta t = \Delta a$, in order to be able to follow the characteristics. Let $M$ be an integer such that $M \geq \lfloor \frac{a^\psi_{\max} + T}{\Delta} \rfloor$. We introduce the age grid points $a_n = n \Delta$, $n = 0, ..., M$ and the time grid points $t_k = k \Delta$, $k = 0, ..., \lfloor \frac{T}{\Delta} \rfloor$. We refer to the grid point $a_n$ by the subscript $n$ and to the time grid point $t_k$ by the subscript $k$. Let $U^j_{k, n}$ be a numerical approximation to $\rho^{(j)}(t_k, a_n)$. We have the following numerical algorithm whose local truncation error is $\mathcal{O}\left(\Delta\right)$, (see details in the Appendix):

The reader can refer to ^[4] for a detailed proof of convergence in the single layer case. In the several layer case, the term corresponding to the intrinsic contribution could be dealt with in a similar way as in the single layer case, yet one should also control the order of the extrinsic term, which is beyond of the scope of this paper.

Remark 1.1 (Mass conservation property). When $J = 1$ and $p_S^{(1)} = \frac{1}{2}$, we can observe that the mass conservation property is verified in the sense that

2.   Analysis of the inverse problem (IP) for continuous initial conditions

In this section, we analyse the inverse problem (IP) enunciated in Definition 1.1 starting with the simplest case of a single layer and considering a compactly supported function as initial condition. We then extend our results to the general case of several layers.

2.1.   Single layer case

In all this subsection, we fix $J = 1$ and consequently, to simplify notations, we drop the index layer so that for instance $\rho^{(1)}$ becomes $\rho$. We thus consider the following PDE, identical to the PDEs (1.1) with $J = 1$:

Note that when $p_S = 1$, PDE (2.1) is the renewal equation. When $p_S < 1$, PDE (2.1) is similar to a McKendrick–VonFoerster equation in which the birth rate would be $2p_s$ times the death rate. We recall that according to the definition of (IP), $p_S = p_S^{(1)} ( = p_S^{(J)})$ is assumed to be known while the division rate $b$ is unknown.

2.1.1.   Well-posedness of the inverse problem (IP)

We first show that the identification problem (IP) is equivalent to an inhomogeneous Fredholm integral equation.

Theorem 2.1. Under Hypotheses 1.1 and 1.2, and supposing that $p_S \neq \frac{1}{2}$, we define $f(t) : = -\frac{1}{2p_S - 1} m_1(t) + \frac{2p_S}{2p_S - 1} m_1 (0)$. Then, we have for all $t \in [0, A^{\min}]$

Before starting the proof of Theorem 2.1, we will need the following lemma:

Lemma 2.1. Under the same hypotheses as Theorem 2.1, we have for all $t \in [0, A^{\min}]$,

Proof. Since both $\psi$ and $b$ are compactly supported, the total number of cells $m_1(t) = \int_{0}^{+ \infty} \rho(t, a)da$ can be decomposed as the sum of the initial cells that have not yet divided and the cells born since time $t = A^{\min} - a^{\psi}_{\max}$:

Using two changes of variables, the translation $s = a -a^\psi_{\min} - t$ and the homothetic transformation $s = \frac{a}{A^{\min} - a^\psi_{\min} + t}$, we can prove formula (2.3). Note that in the general case, corresponding here to $A^{\min} = a^{\psi}_{\min} = 0$ and $A^{\max} = a^{\psi}_{\max} = + \infty$, such changes of variables are not needed to obtain formula (2.3). The detailed proof is exposed in the Appendix.

We can now proceed to the proof of Theorem 2.1.

Proof of Theorem 2.1. To simplify the proof, we do not use expression (2.4) and instead, we write the total number of cells $m_1$ (eq. (1.2)) as the sum of the number of the remaining cells that have not divided yet and the cells born since time $t > 0$, according to the formal solution of $\rho$ (1.5):

We apply Lemma 2.1, for all $t \geq 0$ and we obtain

We suppose that $t \leq A^{\min}$. Hence, the only cells that can divide are the cells present at initial time (mother cells). The newborn daughter cells have not yet had the time to divide (there are no grand-daughter cells). For all $t \in [0, A^{\min}]$,

Since

the definition of $f$ leads to the inhomogeneous Freholm integral equation (2.2).

Remark 2.1. Note that Theorem 2.1 is defined on the time interval $[0, A^{\min}]$. During this interval, only the mother cells coming from the initial condition are dividing. Hence, we can extend this result to the time interval $[0, 2A^{\min} - a^{\psi}_{\max}]$ if $A^{\min} \geq a^{\psi}_{\max}$.

Remark 2.2 (Self-renewal case). Note that, if $p_S = \frac{1}{2}$, the identification problem is not well-posed so that alternative observation data should be used. Indeed, the total number of cells is constant along time whereas the solution of the inverse problem is based on changes in this number.

Usually, the inhomogeneous Fredholm integral equation, which is a particular case of the Volterra integral equation, is studied in the case where the kernel is known. Here, we rather consider the inverse problem of reconstructing the kernel from function $f$ and initial condition $\psi$.

Theorem 2.2. Under Hypotheses 1, 2, 4 and 5, the problem (IP) is well-posed.

Proof. Applying Hypothesis 1.5 to the Fredholm integral equation (2.2), we first deduce that, for all $t \in [0, A^{\min}]$,

Then, using the change of variables $u = a + t$, we obtain that

We can recognize a convolution product. However, since relation (2.5) is verified only for $t \in [0, A^{\min}]$, we cannot use the Laplace transform directly to separate function $\psi$ from the age-dependent function $a \rightarrow \exp(- \int_{A^{\min}}^{a}b(s)ds)$. We rather introduce the truncated functions $\widetilde{f}$ and $\widetilde{b}$ such that:

In other words, function $\widetilde{f}$ coincides with function $f$ on the interval $[0, A^{\min}]$, and function $\widetilde{b}$ coincides with function $b$ on the interval $[0, A^{\min}+ a^{\psi}_{\max}]$. Hence, we deduce from relations (2.5) and (2.6) that for all $t \geq 0$,

Since $f$, $\psi$ and $g(a) : = \exp(- \int_{A^{\min}}^{a}\widetilde{b}(s)ds)$ are constant beyond a given time/age, their associated Laplace transforms exist for all $p > 0$, so that we can apply a Laplace transform to relation (2.7), and deduce that, for all $p > 0$,

where $\mathcal{F}[\widetilde{f}]$ is the Laplace transform associated with function $f$. From relation (2.8), we deduce the uniqueness of the Laplace transform of function $g$. From the injectivity property of the Laplace transform, we deduce the uniqueness of function $g$. From the bijectivity property of function $g$, we then deduce the uniqueness of function $\widetilde{b}$. Finally, from the uniqueness of function $b$ on the interval $[0, A^{\min} + a^{\psi}_{\max}]$, we deduce from Hypothesis 1.4 the uniqueness of function $b$ on the whole interval $\mathbb{R}_+$.

Remark 2.3. The results of Theorem 2.2 can be extended to non-analytic $b$ functions by piecewise reconstruction of $b$ on its whole support $(A^{\min}, A^{\max})$. From the proof of Theorem 2.2, we have the uniqueness of $b$ on the interval $[0, A^{\min} + a^{\psi}_{\max}]$. Then, from the knowledge of $b$ on the interval $[0, A^{\min} + a^{\psi}_{\max}]$ and remembering that the first newborn cells, born at time $2A^{\min} - a^{\psi}_{\max}$ (see Remark 2.1) start to divide at time $t = 3A^{\min} - a^{\psi}_{\max}$, one can derive a Fredholm integral equation for $t \in [0, 3A^{\min} - a^{\psi}_{\max}]$, following the proof of Theorem 2.1, hence deduce the uniqueness of $b$ on the interval $[0, 2A^{\min} + a^{\psi}_{\max}]$. Repeating this operation as many times as needed, we finally obtain the uniqueness of function $b$ on its whole support.

While Theorem 2.2 ensures the uniqueness of function $b$, it does not provide us with a tractable analytic formula to reconstruct it. This issue is addressed in the next paragraph.

2.1.2.   Numerical procedure for non-synchronized populations

We finish the study of the inverse problem (IP) for the single layer case by proposing a numerical procedure to retrieve the division rate $b$ from the total number of cells.

We assume that the initial condition $\psi$ can be discretized using a time sequence $t_k = k \Delta$ and we aim to compute the $b(k \Delta)$ values.

The procedure is based on the fact that we use the same size step $\Delta$ for both the age and time grids. Let the initial sequence $\Psi = (\Psi_i)_{i \in \left[\kern-0.15em\left[ { i_{\min}, i_{\max} } \right]\kern-0.15em\right]}$ where $i_{\min} = \lfloor \frac{a^{\psi}_{\min}}{\Delta}\rfloor$ and $i_{\max} = \lfloor \frac{a^{\psi}_{\max}}{\Delta}\rfloor$.

Between $t = 0$ and $t = A^{\min} - a^{\psi}_{\max}$, cells are aging, hence PDE (2.1) is a pure transport equation. Then, at time $t = A^{\min} - a^{\psi}_{\max}$, the first division happens for cells that have reached age $A^{\min}$.

We fix the initial values of vector $b: = (b_k)_{k \in \left[\kern-0.15em\left[ { 0, N} \right]\kern-0.15em\right] }$ to zero. Each observation of the total number of cells at time $t_k$ will be used to refresh one by one the value of vector $b$ from left to right.

Using the numerical scheme (expressions (1.8) and (1.9)), we define the mass difference at time $t_k$ by:

At time $t_k$, all the $b_n$ for $n \in \left[\kern-0.15em\left[ { 0, i_{\max} + k - 1 } \right]\kern-0.15em\right]$ have been refreshed at time $t_{k-1}$, while the remaining values for indexes $n \in \left[\kern-0.15em\left[ { i_{\max} + k, N } \right]\kern-0.15em\right]$ are still zero. At this time $t_k$, the change in the mass difference can only come from the eldest cells indexed by $i_{\max} + k$. Hence, if $\mu_k = 0$, the eldest cells have not divided yet between $t_{k-1}$ and $t_k$. Otherwise, if $\mu_k \neq 0$, a division has occurred. We recall the reader that $p_S$ is the probability that at least one daughter cell remains on Layer $1$. If $p_S < \frac{1}{2}$, this division results in a negative mass difference, otherwise, if $p_S > \frac{1}{2}$, it results in a positive mass difference.

To compute the $b_{i_{\max} + k}$, we use the mass difference definition (2.9) and the numerical scheme to write the mass balance conservation law:

Since at time $t_k$, $b_{i_{\max} + k}$ is zero before refreshing, we have from the numerical scheme (1.8) that $U_{k - 1, i_{\max} + k - 1 } = U_{k, i_{\max} + k }$. Let $\tilde{u} : = U_{k - 1, i_{\max} + k - 1 }$. From the conservation law (2.10) and the $\mu_k$ definition (2.9), we deduce

with

These steps can be summarized by the following pseudo-code:

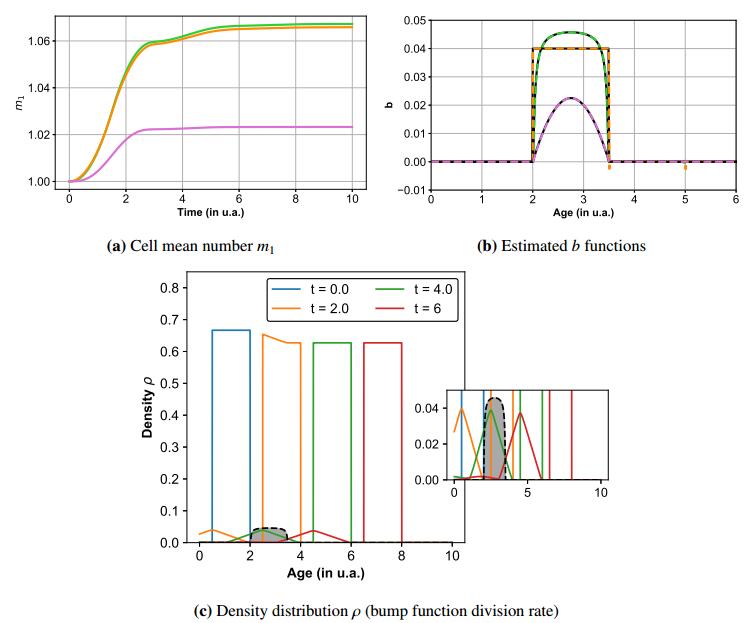
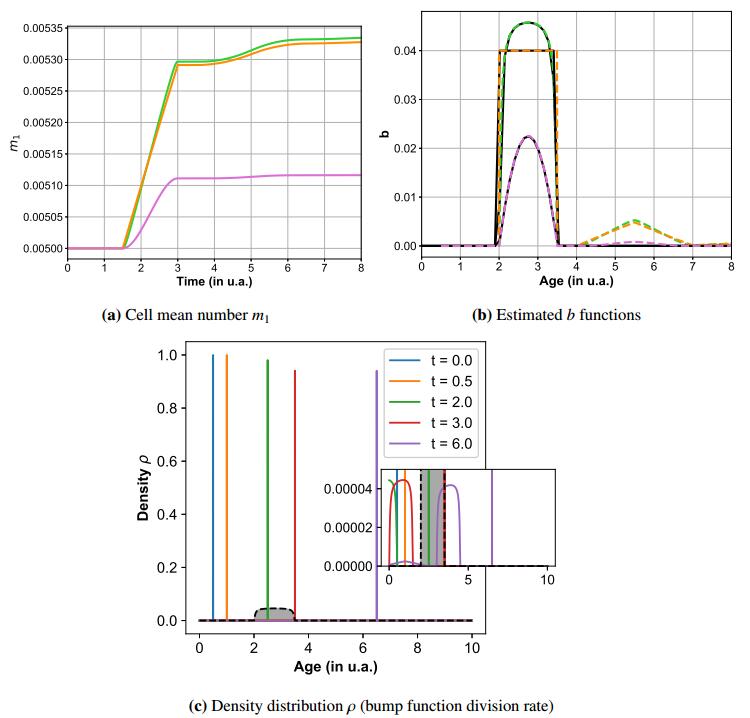
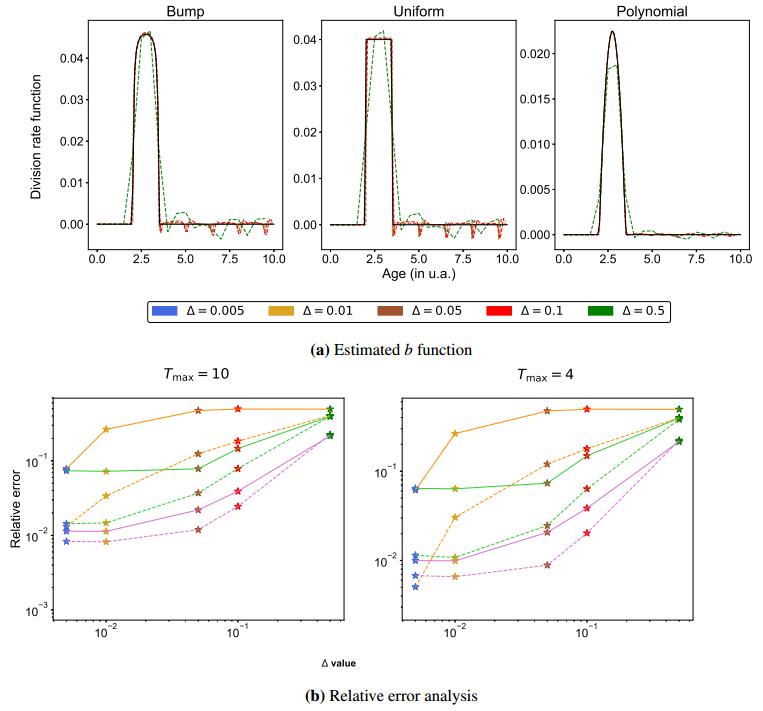
We illustrate this method in Figure 3 and in additional figures in the Appendix. Note that some instabilities appear in the case of the piecewise constant function (orange line) which may be due to its non-smooth character. We also performed a study on the sampling rate $\Delta$ (which appears to be in our case also the age size step) to get practical insight into the numerical convergence (stability) of the reconstruction of the estimated function with respect to $\Delta$ (see Figure 7b in the Appendix).

2.2.   Multi-layer case

We now consider the inverse problem (IP) with two layers (J = 2). We recall the reader that, in this case, we aim to determine all the division rates $b_j$, $j \in \left[\kern-0.15em\left[ { 1, J} \right]\kern-0.15em\right]$ and the probability $p_S^{(j)}$, $j \in \left[\kern-0.15em\left[ { 1, J-1} \right]\kern-0.15em\right]$ knowing the probability $p_S^{(J)}$ on Layer $J$, the initial condition $\psi$ and the mean cell number of each layer $m_j$, $j \in \left[\kern-0.15em\left[ { 1, J } \right]\kern-0.15em\right]$.

Theorem 2.3. Under the same hypotheses as Theorem 2.2, the inverse problem (IP) is well-posed for $J = 2$.

To prove Theorem 2.3, we take advantages of the unidirectional motion of the model (1.1) and split the proof in two parts: the uniqueness of parameter $p_S^{(1)}$ and function $b_1$ (contribution of Layer 1), and the uniqueness of function $b_2$ (contribution of Layer 2).

We start by the analysis of the first layer and get the following lemma:

Lemma 2.2 Under the same hypotheses as Theorem 2.3, function $b_1$ and parameter $p_S^{(1)}$ verifying the inverse problem (IP) depend only on the total number of cells on Layer $1$, $m_1$, and Layer $2$, $m_2$, where $m_1$ and $m_2$ are defined by equation (1.2).

Proof. The first cells coming from the initial condition $\psi_1$ enter Layer 2 at time $S_1 : = A_1^{\min} - a^{\psi}_{\max}$ and start to divide at time $S_2: = A_2^{\min} + S_1$. Layer 2 is empty between $t = 0$ and $t = S_1$. From $t = S_1$ to $t = S_2$, the cells start to enter Layer 2 and are only aging. Hence, the cell density function on Layer 2, $\rho^{(2)}$, solution of the PDEs (1.1), verifies a transport equation with a source term at the boundary condition: for all $t\in [0, S_2]$,

We first show that $b_1$ depends only on $m_1$ and $m_2$. We consider the sum of the cells on the two layers: $\rho = \rho^{(1)} + \rho^{(2)}$ and deduce from the PDEs (1.1) that

Since the $b_1$ function is non-zero on the interval $(A_1^{\min}, A_1^{\max})$, and the density function $\rho^{(2)}(t, \cdot)$ is non-zero on the interval $[0, t-S_1]$ for all $t \in (S_1, S_2)$, we deduce that $(A_1^{\min}, A_2^{\max}) \cap [0, t-S_1] = \emptyset$ when $t < S_1 + A_1^{\min}$. Hence, we can write using expression (2.12) that, for all $t \in (S_1, \min(S_1 + A_1^{\min}, S_2))$, $\partial_t \rho(t, a)+\partial_a \rho(t, a) = -b_1 \rho(t, a)$ and deduce that $\rho$ is solution of the PDE:

Since this PDE is the same as PDE (2.1), we apply Theorem 2.2 and deduce the uniqueness of $b_1$.

We turn now to the uniqueness of parameter $p_S^{(1)}$. Taking the derivative of both $m_1$ and $m_2$, for all $t \in [0, S_2]$, we obtain that:

As there exists at least one $t \in [0, S_2]$ such that $\int_0^{+\infty}b_1(a)\rho^{(1)}(t, a) \, da \neq 0$, we deduce, first,

and then the uniqueness of $p_S^{(1)}$. This ends the proof.

Inverse problem of an age structured population system with source term in the boundary condition   To show the uniqueness of function $b_2$, we first study the following inverse problem.

Let $\eta \in \mathbf{L}_1(\mathbb{R}_+)$, solution of the PDE

with $g$ a differentiable function on $\mathbb{R}_+$ supposed to be known and $\psi \in \mathcal{C}_c((a^{\psi}_{\min}, a^{\psi}_{\max}))$. We also suppose that $b \in \mathcal{C}_c((A^{\min}, A^{\max}))$ (Hypothesis 1.1).

We investigate the inverse problem associated with the model (2.13):

$\widetilde{IP}$ Given the initial condition $\psi$, the function $\widetilde{m}(t) : = \int_0^{+ \infty} \eta(t, a)da$ and the function $g$, both defined for all $t \in [0, T)$, with $T > 0$, determine function $b$ such that the direct problem (2.13) is satisfied on $[0, T)$.

In the same way as in sub-section 2.1, we can show that the inverse problem $\widetilde{IP}$ can be reformulated as a Fredholm integral equation

Lemma 2.3. Under Hypothesis 1.1 and supposing that $\psi \in \mathcal{C}_c((a^{\psi}_{\min}, a^{\psi}_{\max}))$, we define $f_2(t) : = - \widetilde{m}(t) + 2\widetilde{m}(0) + \int_{ 0}^t g(a)da$. Then, we have for all $t \in [0, A^{\min}]$

Proof. In the same way as for the proof of Theorem 2.3, we can write that

To obtain a relation between the boundary condition $\eta(t, 0)$ on the one hand and, $\widetilde{m}(t)$ and $g(t)$ on the other hand, for all $t \geq 0$, we follow the same approach as in Lemma 2.3 and get

Note that here the cells born are both coming from the source term $g$ and the division rate $b$. Using the changes of variables $s = a - a^\psi_{\min} + t$ and $s = \frac{a}{t}$, we obtain that :

If $g$ is lattice, before using the changes of variables, the interval $(0, t)$ needs to be split in as many sub-intervals as necessary, so that the function is non-lattice.

Combining the expression of $\widetilde{m}'$ with expression (2.15) and using that $b \in \mathcal{C}_c((A^{\min}, A^{\max}))$, we deduce that, for all $t \in [0, A^{\min}]$,

We finally deduce expression (2.14) from expression (2.17).

Hence, since $\psi$ is a compactly supported function, we deduce the well-posedness of the inverse problem $\widetilde{IP}$ from the application of Theorem 2.2 with the suitable hypotheses.

We can now proceed to the proof of Theorem 2.3.

Proof of Theorem 2.3. The uniqueness of function $b_1$ and parameter $p_S^{(1)}$ is a consequence of Lemma 2.2. We now prove the uniqueness of function $b_2$. Between $t = S_2$ and $t = S_3: = A^{\min}_2 + S_2$, in the same way as in the single layer case, only cells born from Layer 1 mother cells can divide.

Let $g(t) : = 2(1-p_S^{(1)}) \int_0^{+\infty}b_1(a)\rho_1(t, a) = \frac{2p_S^{(1)} - 1}{2p_S^{(1)}}m_1'(t),$ according to Lemma 2.1. Since $p_S^{(1)}$ is known by definition of our inverse problem (IP), we deduce that $g$ is entirely known. Then, for all $t \in (S_2, S_3)$, $\rho^{(2)}$ verifies

Since this model is equivalent to PDE (2.13) (by performing a time translation $t - S_2$), we can apply Lemma 2.3 and deduce that, for all $t \in (S_2, S_3)$,

where $f_2(t) = - m_2(t) + 2m_2(0) + \int_{ 0}^t g(a)da = - m_2(t) + 2m_2(0) + \frac{2p_S^{(1)} - 1}{2p_S^{(1)}}(m_1(t) - m_1(0)$. Here, the support of the initial condition $\rho^{(2)}(S_2, a)$ is $(0, A_2^{\min})$, so that Hypothesis 1.5 is verified. Applying Theorem 2.2, we deduce that $b_2$ is unique. This ends the proof.

Using the unidirectional motion again, we can extend Theorem 2.3 to the case of more than two layers, $N \geq 2$.

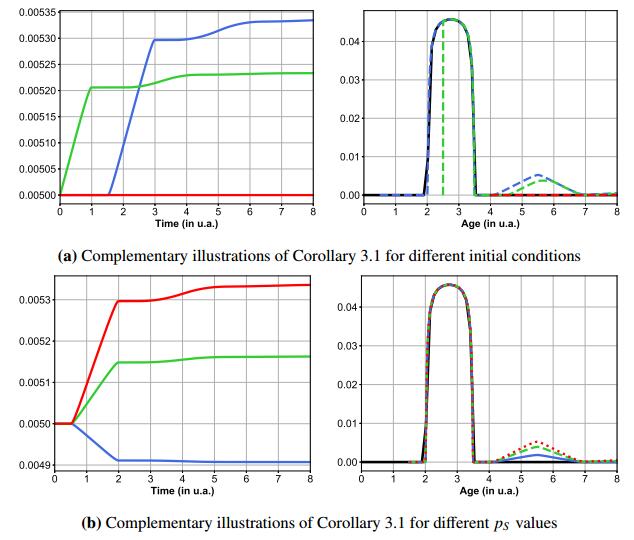
Remark 2.4 (Self-renewal case). If we consider the case when the first layer is self-renewing ($m_1$ is constant), then since $m_1(t) = \bar{m}_1$ implies that $p_S^{(1)} = \frac{1}{2}$, we can nevertheless recover function $b_2$ (and $p_S^{(1)}$) using Theorem 2.3.

3.   Analysis of the inverse problem (IP) for Dirac measure initial conditions

We turn now to the case of Dirac mass as initial condition. We suppose that the results proposed in ^[13,12] for the renewal equation ($p_S = \frac{1}{2}$ and $b$ non-lattice and bounded after a given age $a^{*}$) can be extended to our case ($p_S \in (0, 1]$ and lattice function $b$). We also admit that the characteristic formula (1.5) is verified for the measure solutions $\mu_t \in \mathcal{M}(\mathbb{R}_+)$, the set of signed Borel measures on $\mathbb{R}_+$: for all $t \geq 0$, for all $a \geq 0$,

in the sense that, for all $h \in \mathcal{C}_c(\mathbb{R}_+)$,

In the same way as for the continuous initial condition case, we derive the following equation, which is the formal analog of the Fredholm integral equation in Theorem 2.1.

Theorem 3.1. Under Hypothesis 1.1, and supposing that $\psi \in \mathcal{M}([a^{\psi}_{\min}, a^{\psi}_{\max}])$ and $p_S \neq \frac{1}{2}$, we define $f(t) : = -\frac{1}{2p_S - 1} m_1(t) + \frac{2p_S}{2p_S - 1} m_1(0)$. Then, we have for all $t \in [0, A^{\min}]$

Proof. Taking $h(a) = b(a)$ in relation (3.2), we deduce from formula (3.1) that for all $t \geq 0$,

Then, since $t \in [0, A^{\min}]$, we deduce from Hypothesis 1.1 that

with the change of variables $s = a-t$. Then, using relation (3.4) in (3.2), we obtain that for all $h \in \mathcal{C}_c(\mathbb{R}_+)$,

Taking $h(a) = \mathbf{1}_{[0, a^{\psi}_{\max} + A^{\min}]}(a)$, we deduce from relation (3.5) that:

Since $t \in [0, A^{\min}]$, we have

Then, applying first Fubini theorem then an integration by part, we deduce:

Using relation (3.7) in (3.6), we deduce that

and conclude.

Synchronized population   We consider a synchronized population $\psi(a) = \psi_0\delta_{a_0}(a)$ ($N = 1$ in the definition of $\psi$ (1.4)).

Corollary 3.1 (Synchronized population). Under Hypotheses 1.1 and 1.3, we have, for all $t \in [0, A^{\min}]$,

Proof. Applying Theorem 3.1 with $\psi(a) = \psi_0 \delta_{a_0}(a)$, we obtain for all $t \in [0, A^{\min}]$,

Then, taking the logarithm function and taking the derivative with respect to time, we obtain formula (3.8).

Corollary (3.1) is illustrated in Figure 4 for different $b$ functions. Between $t = 0$ and $t = 4$, the reconstructed $b$ values in the three presented cases are identical to the expected ones. However, we can note that after $t = 4$, the reconstructed $b$ values are no more consistent with the expected ones, which can be explained by the fact that formula (3.8) is verified only for $t \in [0, A^{\min}]$.

If $A^{\min} + a_0 \geq A^{\max}$ and $p_S$ is known, we deduce the uniqueness of the $b$ function from Corollary (3.1). In addition, we have an explicit formula to retrieve $b$ from the observation $m_1$ and the parameter $p_S$, as illustrated in Figure 5. On the contrary, if $A^{\min} + a_0 < A^{\max}$, the $b$ function can only be partially reconstructed on $[0, A^{\min} + a_0)$. In that case, the uniqueness is a consequence of the additional Hypothesis 1.4.

Note that if Hypothesis 1.5 is not verified, i.e. $a_0 > A^{\min}$, the $b$ function can only be partially reconstructed as illustrated in Figure 5.

Discrete non-synchronized population   We now consider a Dirac comb as initial condition: $\psi(a) = \sum\limits_{i = 0}^N \Psi_i \delta_{a_i}(a)$ with $N \geq 2$.

Corollary 3.2 (Discrete non-synchronized population). Under Hypotheses 1.1, 1.3, 1.4 and 1.5, the problem (IP) is well-posed.

Proof. To prove the uniqueness of the $b$ function considering that the $f$ function is known for all $t$, we proceed by induction and first prove that, for all $k \geq 0$,

with the series of functions $\phi_k$ defined as

where $Q(t) : = \Psi_0 \exp (- \int_{A^{\min}}^{a_0 + t}b(s)ds)$ and $R(t) : = \sum_{i = 1}^{N}\Psi_i \exp(- \int_{A^{\min}}^{a_i + t}b(s)ds)$.

For $k = 0$, we apply Theorem 3.1 and obtain that, for all $t \in [0, A^{\min}]$,

Then, assuming that (3.9) is true up to rank $k$, we compute the time derivative of (3.9), so that for all $t \in [0, A^{\min}]$

since $Q'(t) = - b(a_0 + t) Q(t)$ and $\phi_k$ satisfies (3.10). This ends the induction.

We can now turn to the well-posedness of the inverse problem (IP).

From Hypothesis 1.5, we deduce that $A^{\min} > a_i$ for all $i \in \left[\kern-0.15em\left[ { 1, N } \right]\kern-0.15em\right]$. Let us consider the positive time $\tau : = A^{\min} - a_1$. Then, as $b \in \mathcal{C}_c\left((A^{\min}, A^{\max}) \right)$ (Hypothesis 1.1), we obtain that, for all $k > 0$,

Then, from expression (3.11), we get

hence $Q(\tau) = f(\tau) - \sum_{i = 1}^{N} \Psi_i.$ Combining this with (3.12) and (3.11), we deduce that, for all $k \geq 0$,

We thus deduce that, for all $k \geq 0$, $\phi_k(\tau)$ depends only on the $f$ function and the initial condition $\psi$. From the recurrence relation (3.10), we have that $\phi_k$ depends on the $k-1$ first derivatives of $b$. Hence, we deal with an invertible triangular system since the diagonal coefficients are equal to one, and we deduce the uniqueness of $b^{(k)}(a_0 + \tau)$ for each $k \geq 0$. We then deduce the uniqueness of $b$ on its whole support, from Hypothesis 1.4.

Using Corollary 3.2, we can extend the results of Theorem 2.3 to the case of Dirac measures initial conditions.

4.   Conclusion

In this paper, we have analyzed an inverse problem associated with a multi-type version of the McKendrick–VonFoerster model, and consisting of retrieving the division rate functions $b_j$, and the probability of motion $p_S^{(j)}$, for $j \in \left[\kern-0.15em\left[ { 1, J-1 } \right]\kern-0.15em\right]$, from the knowledge on the total cell numbers on each layer. We chose to deal with compactly supported division rates, which account for both a recovery time after birth ($A^{\min}$) and a quiescent state beyond a given age ($A^{\max}$), and we have considered both synchronized or non-synchronized initial populations on the first layer, and supposed that all other layers are empty at initial time. If no division has occurred at the initial time ($A^{\min} - a^{\psi}_{\max} \geq 0$), the entire division rate can be reconstructed. This condition is encountered in the literature, see e.g. ^[15]. For continuous initial conditions, we have shown the well-posedness of the inverse problem, first in the single layer case (see Theorem 2.2), and then in the several layer case (see Theorem 2.3), after introducing a sequence of nested submodels with an additional source term due to migration in the boundary condition. Then, we show the same result in the single layer case for a discrete initial condition (Corollary 3.1); we assume that the PDE (2.1) admits a measure solution, and construct this solution from the characteristic lines. Proving these latter assumptions is beyond the scope of this article and remains as an interesting open problem.

In the self-renewal case ($p_S^{(j)} = \frac{1}{2}$) for a layer $j$, the $b_j$ function cannot be retrieved from the current observation (Remark 2.2), even if the migration proportion parameters can be (Remark 2.4). We speculate that supplying additional observation such as the age-weighted distribution ($\int_0^{\infty}a \rho^{(j)}(t, a)da$) could help to recover the identification property. In the cumulative formulation framework and suitable hypotheses, there is no particular difficulty with this case (see Theorem 4.3, ^[8]).

Instead of the total cell number, we could consider microscopic observation. In ^[7], the authors have shown, using a semi-group approach for the non-renewal version of the McKendrick–VonFoerster equation, that the death rate can be determined from observation of the age distribution at two time points including the initial time. Since, according to Lemma 2.1, there is a link between the net birth function $\rho(t, 0)$ and the total number of cells $m_1$, we expect to be able to obtain similar results.

Acknowledgments

We would like to thank Marie Postel and Peipei Shang for useful discussions. All authors declare no conflicts of interest in this paper.

Appendix

Numerical scheme

Proof. Let $j \in \left[\kern-0.15em\left[ { 1, J } \right]\kern-0.15em\right]$. From the transport equation (1.7) and applying an Euler explicit scheme for the differential operators $\partial_a$ and $\partial_t$, we have, for all $k > 0$,

We deduce first that

Then, applying the $\tilde{\rho}^{(j)}$ definition, we deduce the relation for $U^j_{k, n}$ (1.8). We now tackle the boundary condition. Taking advantage of the unidirectional motion, we proceed by recurrence starting with layer $1$:

Since $b_{1}(a)\rho^{(1)}(t, a) = - \partial_t \rho^{(1)}(t, a) - \partial_a \rho^{(1)}(t, a)$, we deduce that

Applying an Euler implicit scheme to the differential operator $\partial_t$, we obtain

We discretize the integral using a classical left rectangle rule where the integral $\int_{a_k}^{a_{k+1}}g(a)da$ is approximated by $(a_{k+1} -a_k) g(a_k)$, and obtain the following formula:

Combining expressions (4.2) and (4.3), we deduce that

We define $U^1_{n, 0}$ as follow

Using $U^1_{k+1, n}$ definition (1.8), we deduce that

We now consider the case $j > 1$:

We use the same approach to discretize the two integrals in the right-hand side of the equation above and obtain expression (1.9).

Complement of proofs

Proof of Lemma 2.1. Taking the derivative of expression (2.4), we obtain

Since the boundaries of the two right hand-side terms of expression (4.4) depend on time, changes of variables are required to proceed to the derivation.

We first start by the term corresponding to the remaining cells. Applying the change of variables $s = a - a^{\psi}_{\min} -t$, we deduce that, for all $t\geq 0$,

applying first the chain rule then the reverse change of variables $a = s + a^{\psi}_{\min} +t$.

We turn now to the term representing the cells born since time $t = A^{\min} - a^{\psi}_{\max}$. For all $t > A^{\min} - a^{\psi}_{\max}$, we apply the change of variables $a = s (A^{\min} - a^{\psi}_{\max} + t)$ and obtain,

Taking the derivative of this expression and using the chain rule, we obtain:

Using an integration by part, we first deduce that

Combining expressions (4.6) and (4.7), we deduce that

using the reverse change of variables $s = \frac{a}{a^{\psi}_{\max} + t}$.

Finally, combining expressions (4.5) and (4.8), we deduce, for all $t > A^{\min} - a^{\psi}_{\max}$,

From PDEs (1.1), we can write that

and

Using expressions (4.10) and (4.11), we deduce from expression (4.9), that for all $t > A^{\min} - a^{\psi}_{\max}$,

We complete the proof by considering the case when $t \in [0, A^{\min} - a^{\psi}_{\max}]$. In that case, no division has occurred, hence for all $t\in [0, A^{\min} - a^{\psi}_{\max}]$, $\rho(t, 0) = \int_{0}^{\min(0, A^{\min} - a^{\psi}_{\max} + t) } \rho(t, a)da = 0$. In the same way as previously, we obtain that for all $t \in [0, A^{\min} - a^{\psi}_{\max}]$,

since the intersection of the support of $b$, $(A^{\min}, A^{\max})$, and the interval $[a^{\psi}_{\min} + t, a^{\psi}_{\max} + t]$ is empty when $t \in [0, A^{\min} - a^{\psi}_{\max}]$. This ends the proof.

Complementary illustrations of Algorithm 1

We observe that the numerical convergence rate is faster, in both the $L^\infty$ and $L^2$ relative error norms, in the case of a polynomial $b$ function, as well as in the $L^2$ norm in the case of a bump function, compared to the other cases. The convergence pattern differs according to the norm both in the bump and piecewise constant cases. A plateau is reached for relatively high values of $\Delta$ in the case of a bump function and $L^\infty$ norm.