1. Introduction
The biological complexity of tumor growth is astounding [56], as it involves a hierarchy of temporal and spatial scales. Temporal scales range from seconds for individual cell reactions, to years for the emergence of mutation and tumor growth. Spatial scales range from the molecular level of gene regulation, to the cellular level of cell movement, and ultimately to the tissue level of tumor description and nutrient evolution. In addition to the biochemical signal in the tumor microenvironment (TM), tumor cells are also subject to mechanical forces that arise from cell-cell adhesion, cell growth, cell-substrate interaction during movement. Experimental studies have shown that the mechanical property of the TM can have a great impact on tumor growth [72,34]. Moreover, tumor growth is a complex evolutionary process driven by the dynamic feedback between diverse cell populations and the TM [21,41,43]. For instance, the growth of tumor cells often results in a TM of limited oxygen and nutrient, which in its turn requires cells to adapt by altering their metabolism.
It is now commonly accepted that tumors are heterogeneous entities [20,7,29,53,67]. Individual tumors contain diverse cell populations that may differ in important cancer-specific traits and in molecular properties such as adhesion, mobility, growth rate, response to a certain drug, etc. Tumor heterogeneity may result from the accumulation of genetical mutations and epigenetic variation as cells divide. For instance, drug resistance is often developed in the presence of anti-cancer drugs [60]. Moreover, the TM plays a major role in tumor progression and the determination of the heterogeneity within and across tumors [10]. As tumors grow, various environmental pressures select clones which respond to these changes and survive. Eventually, subclones with relative fitness advantage rapidly grow and dominate the tumor. Tumor heterogeneity poses one of the biggest challenges for drug development [30]. For instance, a single agent that is targeted at known tumor types may simply fail due to the presence of distinct non-targeted clones.
Three-dimensional (3D) tumor spheroids in vitro are increasingly recognized as a promising tool to investigate tumor complexity and expand our understanding of the molecular mechanism by which individual cancers are driven [35,46,3,33]. They are also considered as state-of-the-art anti-cancer therapy test platforms. Tumor spheroids are commonly used as 3D multicellular cultures to obtain and maintain the functional phenotype of human tumor in vivo [91,35]. A 3D cell culture is established to restore histomorphological, functional and microenvironmental features of human tumor tissue in vivo, such as cell-cell interaction, cell migration, cellular signaling, and drug penetration, response and resistance [78]. It fills the gap between a conventional 2D culture in vitro and an animal model [93]. Consequently, tumor spheroids have proven to be a prevailing tool for the positive selection in innovative drug development initiatives as well as the study of the microenvironmental regulation of tumor cell physiology and therapeutic problems both in vitro and in silico [35,48,52,68,77,1,28,39,49]. In vitro spheroids are either self-assembling or growing as a cell aggregate from a single cell suspension. The size of a spheroid affects tumor cell growth with respect to microenvironment, metabolic state, response to treatment, etc. Small spheroids, less than 150 μm in diameter, may display 3D cell-cell and cell-matrix interactions but may not have radial proliferative gradient. Chemical gradients begin to develop in medium tumor spheroids. Large tumor spheroids at diameter greater than 500 μm normally consist of three layers which include proliferating and quiescent regions and a necrotic core. Proliferating cells provide the driving force for tumor growth. It is a target of interest for tumor study since a lot of activities occur in this region. Quiescent cells have no growth or active motion but still consume nutrients. The necrotic core is comprised of dead cells which are regarded only as viscoelastic material without living activities. When the nutrient environment changes, proliferating cells may become quiescent cells and eventually die due to the limited distribution of oxygen and nutrients. In addition, quiescent cells may convert to the proliferating type if sufficient nutrients return.
The biological complexity of tumor growth calls for sophisticated mathematical tools to model and analyze its intrinsic mechanism [50,43,12,15]. In particular, to understand how phenotypically distinct tumor cells interact with each other and with the TM, one needs a mathematical model that incorporates appropriate scales for the addressed question [52,68,77,1,28,39,49,2]. Most models treat a tumor either as a spatially-averaged continuum or as a collection of discrete individual cells. In general, a continuum model is computationally inexpensive and may shed light on the generic properties of the system under consideration. But it suffers from the disadvantage that the incorporation of many intro-, extra-, and inter-cellular processes is difficult. Therefore, a continuum model is not suitable for the description of the dynamics of heterogeneous tumor cells in many situations [45,59].
A cell-based model allows one to account for a great variety of processes at the subcellular and cellular levels for individual tumor cells. There are many methods to model individual cells in the literature, such as quasi-sphere method [15,50], subcellular element method in which cell movement is described by the re-assignment of lattices sites at the edge of a cell [61], Voronoi-Delaunay method that models cells as deformable spheres with dynamic radii [73], immersed boundary method in which each cell is treated as an individual body of arbitrary shapes consisting of its own plasma membrane [71], and finite element method that is able to consider arbitrary deformations of cells [89,26]. Concerning the incorporation of intra and intercellular mechanical effects and the resulting shape variation, the shape of a modeled cell matters. Initially proposed by Palsson and Othmer (PO model) [65], the 3D deformable viscoelastic ellipsoid model that uses ellipsoids as building blocks is a good compromise between the use of simple spheres and that of other more complicated geometries. PO model aimed at understanding how cell-cell interaction, adhesion and signaling work together in a coordinated fashion to drive observed complex cell movements in the model system of Dictyostelium discoideum (Dd). It turned out that stiffness and deformability play a very important role in cell sorting and collective motion. The elliptical shape is consistent with what has been observed in 3D matrices of in vitro context [78]. Moreover, an ellipsoid has less degrees of freedom in comparison to other more complex cellular geometries, so it makes feasible the realistic simulation of thousands of cells. Although the shape constraint imposes limitations on admissible deformations, ellipsoids can be used to describe a good range of cell shapes, from a sphere to a very long ellipsoid, subject only to volume conservation. It seems that the constraint is not so important to many studies of cell behaviors. For instance, PO model can accurately reproduce the dynamics of 2D slugs as well as the tissue surface tension [65,64,63]. The model was adopted and improved by Dallon and Othmer in 2004 (DO model) to plausibly predict that the motive force of slug is proportional to the surface area of the slug instead of its volume [11]. Recently, Kim et al applied ellipsoid (2D ellipse in actual computation) to the cell-based component of their hybrid models in which proliferating cells are considered at the cellular level while the quiescent area, necrotic core and external environment are treated as continua [45,42,43]. Cell-based models using either 2D ellipse [37,12] or 3D ellipsoid [44,74] are becoming attractive in the in silico cancer research when morphology plays a vital role in capturing the behavior of developmental tissues.
Recently, attentions have been drawn toward multiscale descriptions of tumor [12,17,76,70]. Some of them are discussed in [50,12]. For a large system, one may describe a tumor at the individual cell level in regions of interest, and describe the remainder of a tumor and the TM as continua to retain the computational advantage [12,45]. That combination becomes promising for a large system containing hundreds of thousands of cells. Nonetheless, complex mathematical and computational problems arise from force transform and mass conservation during conversion between cell-based and continuum descriptions of living tumor cells [12]. In addition, for a medium or large tumor spheroid in vitro, there is no significant computational benefit to treat quiescent cells and the necrotic core as a continuum if proliferating region is described at the cellular level. Consider a medium or large spheroid system in the lab whose diameter normally ranges from 200 μm to 800 μm [91,35], the percentage of proliferating cells is big. Take an example of a large tumor spheroid of 500 μm in diameter and its width of proliferating band in the periphery region is approximately 100 μm, the portion of proliferating cells is about 80 percent in the 3D architecture.
In the present work, a 3D hybrid model is proposed to develop a novel computational tool for the growth of a heterogeneous tumor spheroid in vitro. In this model, the entire tumor spheroid is described as an aggregate of heterogeneous ellipsoids at the cellular level while nutrient and other environmental media are treated as continua. That combination has not yet been proposed in the literature, and its benefit is three-fold. Firstly, a 3D incompressible viscoelastic ellipsoid is considered as a building block to construct the tumor part. As a result, we are able to take into consideration intercellular mechanical effects in order to study the resulting deformation of cells and its impact on cell behaviors. Meanwhile, the model maintains a minimum set of variables of freedom to describe individual cells of complex shape variations. Secondly, a complete cell-based description of the entire tumor spheroid avoids complex mathematical and computational problems involved in the conversion between cell-based and continuum descriptions within a tumor. As far as the computational cost is concerned, this model is greatly suitable for a 3D tumor spheroid in vitro whose size is normally less than 800 μm in diameter [91]. Thirdly, our numerical scheme provides two computational options depending on the tumor size. For a small or medium tumor spheroid, the 3D numerical model can be directly applied. For a large spheroid, we suggest the use of the 3D-adapted 2D cross section configuration, which has not yet been explored in the literature, as an alternative for the theoretical investigation to bridge the gap between the 2D and 3D models. Our 2D numerical model is parametrically adapted by the insights gained from a full 3D simulation. These two options together make it possible to efficiently explore spheroids of various sizes for applications such as cell sorting and migration.
The rest of this paper is organized in three parts. In the model section, a brief description of the mathematical model is given. More details can be found in the Appendix. In the next computational section of numerical implementation and validation, our 3D numerical model and 3D-adapted 2D cross section model are implemented and applied in three steps. In the first place, cell sorting is used as a benchmark to validate the full 3D numerical model [65,89]. Our model supports that differential adhesion alone can lead to various sorting patterns in section 3.1. In the next stage, constant viable rim of a three-layer tumor spheroid and cell internalization are used to test the 3D-adapted 2D numerical model and to show its capability in generating some behaviors of 3D tumor spheroids in section 3.2. Then we take the final step in the computational section to look into the potential of the 3D-adapted 2D cross section configuration in section 3.2.4. This paper ends with a brief summary of current model.
2. Theory of the hybrid model
2.1. The cell-based model
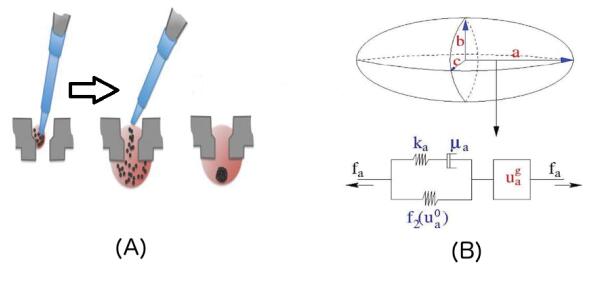
In this work, the cell-based model is modified from previous works [65,11,45]. Its components are briefly described in this subsection, and more details are given in the Appendix. Cells in a cell-based region are represented as oriented ellipsoids in 3D, whose cytoplasm is dominated by actin filaments and microtubules. They are modeled as incompressible viscoelastic solids. Cells are allowed to deform in a volume-preserving fashion according to external forces. To model the viscoelasticity in nature (see Biomechanics Mechanical Properties of Living Tissue by Y.C.Fung), each modeled cell is associated with three major axes to represent an incompressible viscoelastic solid as the so-called Kelvin element which is a nonlinear spring in parallel with a linear spring in series with a dashpot in Figure 1(B). In addition to deformation, cells grow with sufficient nutrient supply, within a certain threshold of mechanical stress. An individual growth rate depends on the experienced stress as well as the surrounding nutrient level. Note that stress is only used to mean mechanical stress in our paper without specified. So, the internal rheology of each cell is characterized by a Kelvin element and growth elements (see Figure 1 (B)). The shape change of cells is governed by cells' internal rheology and external forces upon them.
We will describe the following modeling components in details: (ⅰ) an individual cell's reaction to forces in section 2.1.1, (ⅱ) cells' growth and division, and how nutrient and mechanical stress affect growth in section 2.1.2, (ⅲ) the resulting cell motion in section 2.1.3.
2.1.1. Force analysis on individual cells
In our model, the forces on a cell are [65,11,45] (i) the active force exerted on neighboring cells or the substrate, (ii) the reactive force due to the forces exerted by other cells, (iii) the dynamic drag force that is generated when the adhesive bonds of a moving cell with neighboring cells form or break, and (iv) the static frictional force that exists when cells are attached or close to each other or the substrate. The active force on the ith cell is denoted as Tij, and the reaction force is denoted as Mji. The static force, denoted by Sji, is the attraction or compression force on the ith cell when it is attached or close to the jth cell. Here we have Sji=−Sij.
The total external force on the ith cell is then given by
|
Fi=Mki+∑j∈NaiTji+DRif+∑j∈NdiDRij+DRis+∑j∈NsiSji.
|
(1)
|
where Nai denotes the neighbor of the ith cell, including the substrate, upon which it can exert traction. Ndi is the set of cells that interact with the ith cell via drag forces. Nsi denotes the set of cells that are attractive or repelling to cell i. In addition, DRif,DRij,DRis are the drag forces between cell i and fluid, cell i and cell j, and cell i and substrate surface if present, respectively. Please note that the detailed formulation of each force is given in the Appendix.
2.1.2. Deformation and cell growth
We define V0 as cells' volume attained right after division. It is assumed that stress and nutrient levels affect the growth rate. With sufficient nutrient and without stress limitation, cells grow to the volume 2V0 and then instantly divide into two equal daughter cells. In the presence of extracellular forces, the orientation of cell division is determined by the direction of the net force exerted on the cell. In the context of a tumor spheroid or other tissues, cells interact with neighboring cells and deplete nutrients. That leads to nonuniform growth in the population. Moreover, we assume that growth stops if stress is too big.
The governing equations of a cell's length in the i-axis, i = a, b, c, are based on the model developed by Kim, Stolarska and Othmer (KSO model) [45]
|
(u0i)′=(kiμi[fi(t)+ˉp−f2(u0i)]+f′i(t))(df2(u0i)du0i+ki)−1
|
(3)
|
|
(ugi)′=f1(fi(t)+ˉp)G(cO2,cgl)
|
(4)
|
where ui denotes the change of the length in the ith axis, u0i (ugi) represents the change of the length in the ith axis due to the passive (growth) element, f2 is the nonlinear spring force whose specific forms are given in the Appendix, fi is used for the magnitude of the force applied to each end, μi is the viscous coefficient of the dash-pot, ki is the spring constant for the spring of the Maxwell element, ˉp is the pressure force, f1 is the growth function (Equation (17)), and G(cO2,cgl) is used for nutrient effects.
2.1.3. The equations of motion
Since the Reynolds number of a moving cell is very low, the effect of inertia can be ignored in the present model. As such, the total external force on an individual cell is regarded as zero. Thus the following equation of motion can be derived from Newton's law:
|
Aifμfvi+μcell∑j∈NdiAij(vi−vj)+Aisμsvi=Mki+∑j∈NaiTji+∑j∈NsiSji.
|
(5)
|
HereAif=Aif(t), Aij=Aij(t), Ais=Ais(t) are the lengths of contact regions at time t between cell i and fluid, cell i and cell j, and cell i and substrate if present, respectively. μcell is the degree of adhesiveness between two cells (μs between substrate and cell, μf between fluid and cell). vi is the velocity of cell i. The parameters that characterize cells are given in Table 2. This equation system is solved by Adams fourth-order predictor-corrector solver.
Table 2. Parameters for the cell-based component of the model.
| Parameter |
Description |
Value |
Dimensionless in coding |
Refs. |
| Adhesion parameters |
| μcell |
cell-cell adhesiveness |
27.0 dyn s/cm |
450 |
[11,45] |
| μs |
cell-substrate |
27.0 dyn s/cm |
450 |
[11,45] |
| |
adhesiveness |
|
|
|
| μf |
fluid viscosity |
2.7 dyn s/cm |
450 |
[11,45] |
| Rheological parameters |
| c+ |
growth function |
5.16089×10−9 mm/(min. nN) |
5.16089×10−9 |
[45] |
| σ+ |
growth function |
800 nN |
800 |
[45] |
| σ− |
growth function |
-4 nN |
-4 |
[45] |
| α |
growth function |
0.0 nN |
0.0 |
[45] |
| ka |
standard solid |
163.8 dyn/cm |
163800 |
[11,45,84] |
| k2 |
standard solid |
147.5 dyn/cm, |
147500 |
[11,45,84] |
| μa |
standard solid |
123 dyn min/cm |
123000 |
[11,45,84] |
| fa |
active force |
10 nN |
10 |
in this work |
2.2. Continuum description of nutrient and coupled equation systems
Here oxygen and glucose are considered as nutrients. Their profiles are calculated by classical reaction-diffusion equation, in which diffusion and consumption properties are position-dependent in our model. The reaction term accounts for nutrient uptake. Its consumption rate is decided by local cell density as well as the concentration of other chemical species. The latter effect is described by Michaelis-Menten like kinetics. To incorporate the former, we define a weight function ϕ to represent the local cell density. Its value on each grid is computed by the interpolation of the location information of nearby cells and their volumes, here we assume a linear correlation between cell volume and nutrient uptake [57].
Based on the above considerations, the governing equations for the evolution of nutrients are similar to those in the KSO model [45]
|
∂cO2∂t=∇⋅(Do∇cO2)−ϕO2(AO2+BO2cgl+nO2)(cO2cO2+kO2)inΩ∂cgl∂t=∇⋅(Dg∇cgl)−ϕgl(Agl+BglcO2+ngl)(cglcgl+kgl)inΩcO2=¯cO2,cgl=¯cgl,on∂Ω
|
(6)
|
where cO2 (cgl) is used for the molar concentration of oxygen (glucose). The second term of each equation is a description function of the consumption of oxygen (glucose) by the tumor. Do (Dg) is the position-dependent diffusion coefficient of oxygen (glucose). AO2, Agl, BO2, Bgl, kO2, kgl, nO2, and ngl are parameters which are empirically determined and given in Table (3). And the density function ϕO2=ϕgl relies on cell distribution and volume as described above. In addition, we assume Dirichlet boundary conditions for the RD equation (i.e., the boundary values of the solution are specified as a constant), and the initial value of nutrients in the spheroid simulations is set as the boundary constant value. Numerically, the RD equations (6) are solved on a regular grid domain by an alternating-direction implicit (ADI) scheme together with a nonlinear solver named nksol. The typical spatial grid size in our simulations is hx=hy=hz = 0.01 in the non-dimension domain [0,1]×[0,1]×[0,1].
Finally, data interpolation needs to be done forward and backward between individual cell mass centers and the corresponding neighbor grid points in solving coupled cell-based model and reaction-diffusion equations of fixed boundary values. This is due to the fact that nutrient concentrations by the solution of Reaction-Diffusion (RD) equations are computed and stored in grid points via the finite difference approach, while individual cells are off-lattice in current model. Moreover, the concentration level or gradient, which cells sense for chemotaxis or growth, is assumed to be at their mass center. Therefore, on the one hand, nutrients must be interpolated from the grid to each cell for nutrient involved processes. On the other hand, the consumption/uptake rate at each grid in the RD equation depends on the cell density, which is calculated via the cell distribution information represented by mass center coordinates, axis vectors and radii. The data interpolation is carried out by the trilinear interpolation method. A brief description of our algorithm for solving coupled cell-based and continuum modules is given as follows:
Step 0 Initialization
a) Initialize the cell-based components with spheres of diameter 10 μm and let them approach a mechanical equilibrium to form a spheroid.
b) Set grids for the finite different method and initialize nutrient values to be equal to boundary values
c) Allow nutrient profiles to reach an equilibrium, based on initial cell distributions using the equation (6).
Step 1 Determine if the concentration in each cell's proximity is above a threshold. If so, calculate the direction of nutrient gradient, decide a new cell direction according to the equation (7), and rotate the cell in that direction. Otherwise, direction will be chosen randomly.
Step 2 Locate all cells that are within a given distance from an individual cell and count them as neighbor cells.
Step 3 Find all forces that act on the cell from neighbor cells using the equation (1), (9)-(11) and (12), deform three axes of the ellipsoid according to the calculated forces from the equation (4). If growth is incorporated, allow cells grow according to the nutrient level and stress. Finally move the cell by the motion equation (5)
Step 4 Update the nutrient concentration by the equation (6). One may update the nutrient concentration less as frequent as cell motion.
Step 5 Go back to Step 1 then repeat the iteration.
3. Computational results
Based on our 3D mathematical model, two numerical simulation packages were implemented: (1) 3D spheroid with 3D ellipsoids as building units; (2) 3D-adapted 2D cross section configuration. We point out that here a 2D structure is always considered as a cross section of a spheroid, so heterogeneous nutrient concentration is present. With these two numerical tools, we attempt to develop a platform to theoretically investigate the growth of heterogeneous tumor spheroids of various sizes. The 3D package serves as the primary choice for small and medium spheroids. It is also used to provide insights to adjust the 2D numerical package so that the gap between 2D and 3D cultures can be partly filled according to the targeted phenomena and mechanisms. Consequently, 2D numerical models may become efficient and useful tools for extremely large tumor spheroids. We will discuss some early results from the model and simulation validations in the following numerical implementations. Afterwards, the potential of the 3D-adapted 2D numerical tool will be demonstrated.
3.1. Cell sorting in a 3D heterogeneous spheroid
In this subsection, the 3D numerical package is implemented and validated. A group of small spheroids were constructed to study our 3D model in this preliminary work. As such, there is no three-layer configuration (proliferating, quiescent and necrotic) formation due to the presence of sufficient nutrients. To validate our 3D model, we take the cell sorting as a benchmark [65,89]. In fact, sorting of two types of cells in an aggregate was observed in vitro if these two types possess different cohesion properties [24]. Furthermore, cell sorting and cell movement were observed during tumor spheroid growth [13] and in prostate cancer [22].
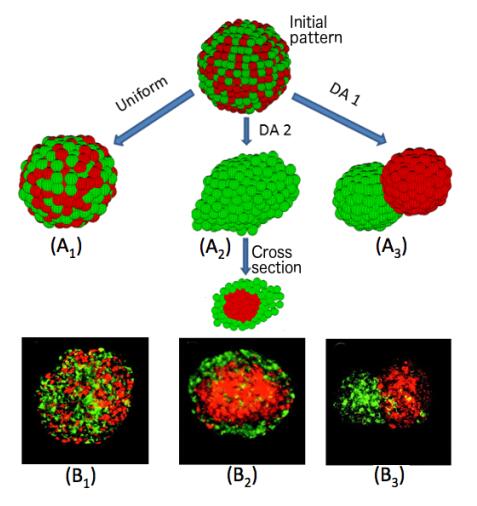
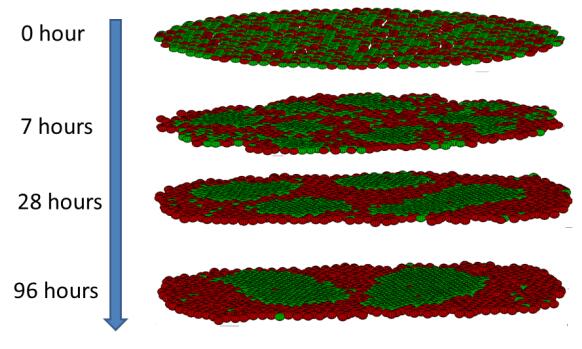
First of all, it is interesting to know whether differential adhesion alone is able to reproduce a variety of sorting phenomena observed in the laboratory: cell sorting, tissue spreading, sorting pathways and so on. To this end, two types of cells G(green) and R (red), expressing different adhesive properties, are mixed in an aggregate. In particular, αg,g, αr,r, αg,r are used to represent relative adhesive strengths between like and unlike cell types. Note that green and red cells are set to differ only in intercellular adhesive strength. It turns out that cells with greater adhesive force move to the center of the aggregate and are enveloped by cells of the other type. That is shown in Figure 2 (A2) where αg,g:αr,r:αg,r=0.4:1:0.7. Sorting does not take place when adhesive strengths are equal. That can be seen in Figure 2 (A1) where αg,g:αr,r:αg,r=1:1:1. Lastly, when the adhesive force of unlike cells is much less than that of like cells, the aggregate evolves into separate islands of cells of the same type. That is evident in Figure 2 (A3) where αg,g:αr,r:αg,r=1:1:0.2. Here parameters are set as follows: random force fr=40nN, and Eb=50nN,Frep=80nN,λ=25. Computational aggregates in this section consist of 1021 cells. The population ratio between red and green cells are 1:1. Once they are completely formed, sorting patterns are stabilized and persist under slight fluctuations inside the system due to cellular random motion. As for the above aggregate of 1021 cells with αg,g:αr,r:αg,r=0.4:1:0.7, we set time T= 7 hours to achieve the engulfment sorting. Afterward, the same configuration is observed. It takes more time to form the same pattern for larger spheroid systems.
Therefore, our cellular dynamic model indicates that the differential adhesion alone can lead to various sorting patterns, which are consistent with those experimental observations given in the literature [80,16,24]. It turns out that the differential adhesion based sorting phenomena are quite robust in our model with a wide range of parameters. For example, various ratios of cohesion can lead to sorting as long as differential adhesion is present among heterogeneous cells. This can be found in Table 1, where the ratio varies among αg,g:αr,r:αg,r and the corresponding sorting results are listed. Actually, we also explored a greater range of parameters for the separation result. It turned out that there is a transition value of αg,r. When αg,r is smaller than the transition value, a complete separation of two types of cells can be achieved very quickly. The greater value of αg,r, the longer time for a system to achieve a complete separation.
Table 1. Sorting in the presence of differential adhesion. Various ratios of cohesion can lead to cell sorting in two types of cells, distinguished by green and red in this work. Here αg,g, αr,r, αg,r represent relative adhesive strengths between like and unlike cells (green and green, red and red, or green and red respectively).
| Index |
αg,g |
αr,r |
αg,r |
Sorting results |
| 1 |
0.4 |
1 |
0.7 |
green envelops red |
| 2 |
0.6 |
1 |
0.8 |
green envelops red |
| 3 |
0.8 |
1 |
0.9 |
green envelops red |
| 4 |
1 |
1 |
1 |
Not sorting |
| 5 |
1 |
1 |
0.2 |
green and red separate |
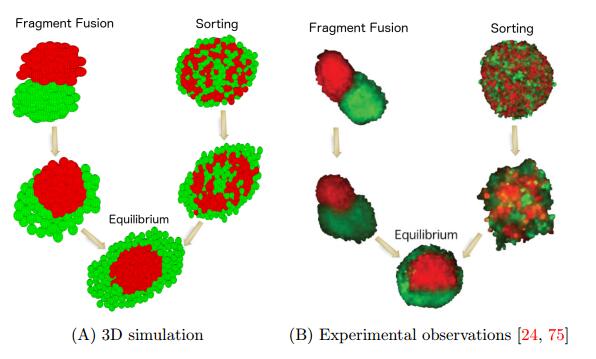
Besides the sorting pathway, our 3D model can further generate an alternative pathway for the engulfment pattern called tissue spreading. In the sorting pathway, intermixed aggregate of two heterotypic cells segregate and rearrange to form an envelopment configuration. In addition to that, tissue spreading was experimentally observed [88]. Namely, the spreading of one tissue mass over another to form an engulfment pattern. To study the spreading process using our model, two cell aggregates are initially placed side by side to share a common contact area (see Figure 3 (A) fragment fusion pathway) where green cells have relatively small intercellular adhesive strength with αg,g:αr,r:αg,r=0.4:1:0.7. As the system evolves, green cells gradually spread over the aggregate of red cells and eventually envelop the latter. We have numerically demonstrated that two pathways, cell sorting and tissue spreading, lead to the same final spacial configuration (See Figure 3 (A)). Our model has also captured the phenomenon that in vitro cells sort by coalescence of smaller islands to form larger ones in an intermixed heterotypic aggregate.
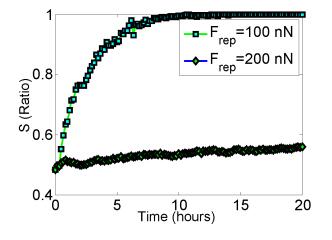
Furthermore, various factors on sorting can be examined in our numerical ellipsoid model. In fact, experimental observations had revealed a variety of factors. For instance, cadherin expression, which changes adhesive strength, is one factor [62]. Initially lacking in cadherins, mouse fibroblasts can not sort in a stirred suspension [23]. Cell mobility is another factor. It is required for the rearrangement inside a population [81]. Besides, sorting is affected by cell deformation, caused by the interplay between adhesion and cortical tension [47,31]. The deformability depends on the influences of the internal fluid and the state of the internal cytoskeleton. It can be regulated via adhesion molecules and ligand-receptor systems [90]. Repelling force arises from a cell's resistance to deformation and counteracts the adhesive force when cells get too close. In this work, we use the effects of repelling strength as an example to demonstrate the capacity of our model. Repelling force constant Frep and viscoelastic parameters k1,k2,μ are together to determine cellular deformability. In particular, the smaller Frep is, the easier cells deform. Previously, it has been demonstrated that deformability is important to cell sorting by manipulating k1,k2 [65]. Now we will look into the role of repelling parameter Frep in cell sorting. With Eb=25nN and fr=40nN fixed, as shown in Figure 4, Frep=100nN leads to cell sorting, while no sorting takes place if Frep=200nN. It suggests that stiffer cells are harder to sort, and no sorting occurs when stiffness reaches a certain level. We conclude that it is necessary to incorporate mechanical effect and deformability into a cell-based model for tumor growth, such as tumor cell migration and aggregation.
3.2. Validation on the 3D-adapted 2D cross section configuration
In this section, let us validate our 2D cross section configuration. As a spheroid grows almost symmetrically, patterns and microenvironment mainly differ in the radial direction inside the spheroid. On that basis, it is feasible to look at a 2D cross section of a 3D spheroid to investigate a tumor's growth pattern at the tissue level, such as the chemotaxis behavior of tumor cells [63]. Our 2D cross section model is to study a dissection of a 3D spheroid instead of an aggregate inside a 2D monolayer, so that it may be considered as an alternative for the full 3D model. As such, nutrient gradients are present in our 2D model, while it is not the case for a 2D monolayer in lab. Nutrients are treated as a continuum and their gradients are obtained by solving 2D Reaction-Diffusion equations with fixed concentration value on the boundary under the assumption that the concentrations are uniform in the z direction. For the 2D cross section configurations, we assume that cell motion vector is limited in the x-y plane and the division direction is parallel to the x-y plane. In addition, we assume that the local consumption rate of nutrients depends on local cell density. As validation results, several in vitro phenomena in a 3D spheroid have been numerically generated by the 2D cross section model. The implementations include the coordination of nutrient and growth to form a three-layer architecture in section 3.2.1, tumor cell internalization in section 2.2.2 and chemotaxis-based cell rearrangement in section 3.2.3. However, some in vitro 3D phenomena under experimentally-measured conditions can not be automatically reproduced in the 2D framework due to the discrepancy between 2D and 3D structures. We will use cell sorting as a case study to demonstrate the necessity of parametric adaption from its corresponding 3D systems [62,82]. We will also discuss its further applications. Note that the 2D cross section configuration can be constructed by either 2D ellipse cells (3.2.1, 3.2.3, 3.2.2) or 3D ellipsoid cells (3.2.4).
3.2.1. Stabilized viable rim of tumor spheroid: A benchmark
It was found in vitro that the width of viable rim, calculated by the difference between the radius of a tumor and its necrotic core, remains roughly constant in many tumor spheroids [58]. Stabilized viable rim has been used as a benchmark to test proposed models [45]. Here we also use it as one of our testing cases to validate the proposed model and to implement the model in cell growth, nutrient uptake and dynamics, and the conversion among different types of cells.
Due to the diffusion limitation and nutrient uptake, nutrient concentration decreases from the outer layer to the inner core inside a spheroid. In this current model, we assume that when one or more nutrient concentrations drop below a certain threshold, proliferating cancer cells enter into a quiescent state in which cells stop growing and moving but still consume nutrient to be alive. Cells experience death when nutrient drops further. Moreover, there is a mutual conversion between proliferating and quiescent cells according to the environmental change. Other than that, tumor cells are described at the cellular level directly with distinct properties. Eventually three layers form inside a growing spheroid; they are called proliferating layer, quiescent layer and necrotic core.
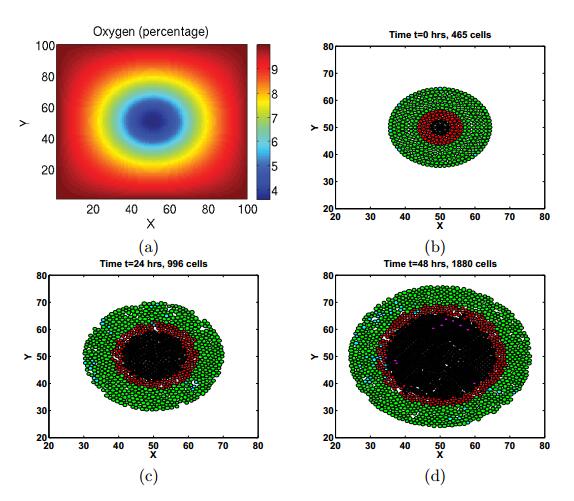
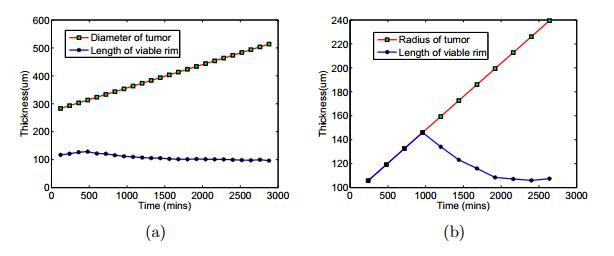
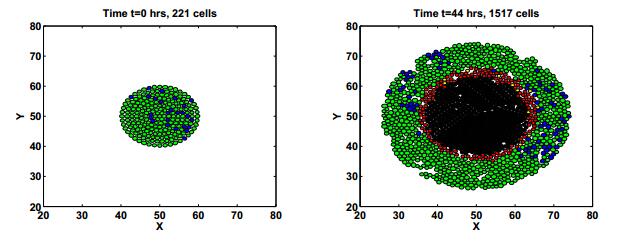
Numerically, we couple together a cell-based model and a continuum based reaction-diffusion model to describe the dynamics of a growing spheroid and its nutrient profile. Due to the growth of a spheroid, interior nutrients decrease and will be depleted. Then proliferating cells may convert into quiescent cells which may die and become part of the necrotic core due to insufficient nutrients. In this simulation, oxygen is chosen as the nutrient to check cell state conversion. Firstly, we used a spheroid with a pre-existing necrotic core. The dynamic process of tumor growth can be seen in Figure 5 for a growing three-layer spheroid, where green (or blue), red, black cells represent proliferating, quiescent and dead cells, respectively. It turns out that the width of the viable rim remains approximately constant about 100 μm. Meanwhile, the increase of spheroid size is only reflected in the region of necrotic core. A constant band size of the viable rim is illustrated quantitatively by a curve drawn in Figure 6 (a). That is quite consistent with the experimental observation and therefore validates our model. It is worthwhile to point out that applying a continuum description to study the emergence of tumor formation is impossible. In the spirit of a continuum description, there must be pre-existing layers for continuum regions to evolve. In contrast, a cell-based model can build up these regions from the smallest unit in a bottom-up fashion. This method is especially suitable for the study of emergent behaviors like drug resistance in which certain types of resistance only emerge at some time point and then gradually dominate.
Moreover, the emergence of quiescent layer and necrotic core are simulated here. To this end, we began with a configuration that only consists of proliferating cells to see how three layers gradually emerge. Again, the width of the variable rim approaches a constant from a certain time point after an initial small increase. The evolution process can be seen in Figure 7 and the length of the viable rim is shown as a blue curve in Figure 6 (b). Here the doubling time for individual cells with sufficient nutrient is T=5 hours in the absence of stress limit. Active force fa for a random motion is 8 nN. In addition, to demonstrate the capability of the cell-based description of tumor in tracking the lineage of a specific cell type and its development, we placed another type of proliferating cell (marked in blue) in the proliferating region from the beginning to perform the simulations shown in Figure 5 and Figure 7. The evolution of its growth and division can be tracked in a straightforward way. More tracking simulations will be provided in the following internalization tests.
3.2.2. Internalization test of homotypic cells
Three-layer multicellular spheroids have been used to study the inward migration of externally introduced tumor cells, such as the cell internalization behavior. In fact, cell internalization behavior is an interesting phenomenon that triggers the study of the underlying mechanism and coordination of tumor cell migration and the resulting tumor growth. For this purpose, many experiments were conducted. Applying three-layer configurations, Dorie et al [14,13] in 1980s investigated the movement and internalization of H-labelled cells and microspheres within EMT6 and RIF-1 spheroids. At the beginning, labelled cells or microspheres were adhered to the surface of a spheroid. After a few days, labelled cells were found to have migrated toward the center of the spheroid, regardless whether the spheroid is growing or not.
Theoretically, mathematical models were proposed to investigate the underlying mechanism of internalization patterns. Supported by their simulation results from a PDE system, McElwain and Pettet (1993) [54] argued that the pressure gradient caused by differential cell proliferation and cell death is the major mechanism of internalization. By another PDE model, Thompson and Byrne (1999)[87] suggested that the internal velocity field generated by differential proliferation and the death of labelled cells leads to internalization. Moreover, Pettet et al (2001)[66] postulated that the chemotactic response of cells in different states (i.e., proliferating and quiescent states) results in internalization. They assumed that quiescent cells possess chemotactic behavior and move toward higher nutrient concentration, and further assumed that cells in the quiescent state are more motile than those in the proliferating state. It is known that PDE-based models are hard to catch individual properties at cellular level, such as cell-cell mechanic interactions and differential adhesion. With the use of a cell-based model, recently Stolarska et al [83] were able to demonstrate that the difference in cell proliferation rates and adhesion among living tumor cells and microspheres can lead to different observable internalization patterns. Their results suggest that active movement is not essential for significant internalization. However, some questions remain open, such as, why do 25 to 50 percent of labelled cells reach depth much greater than that can be accounted for solely by cell growth? How can labelled cells and microspheres still penetrate 180-200 μm after 5 days even in irradiated spheroids where spheroid proliferation has stopped? Note that the necrotic core, developed in the in vitro experiments by Dorie et al [14], was neglected in all of the above computational models.
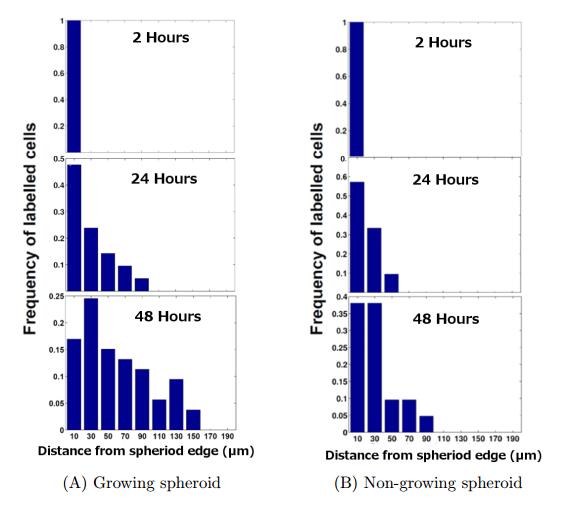
Based on our ellipsoid-based description of the tumor, which is capable of generating a three-layer configuration containing a necrotic core, we found that cell random motion plays an important role in cell internalization in addition to cell growth. To see it, we designed two numerical spheroid experiments. One is for a growing spheroid in which cells proliferate, and the other is for a non-growing spheroid in which cells do not grow. In addition, homotypic labeled cells are initially adhered to the surface of the spheroids. We tracked the labeled cells and recorded the number of those cells in different depths of the spheroids. The evolution process of the growing spheroid can be seen in Figure 5 (b)(c)(d) in which labeled cells are visibly blue. It turns out that the final distribution patterns of labeled cells differ in these two cases (See Figure 8). Specifically, random motion alone causes cells to migrate inwardly to the depth about 80 μm to 90 μm after two days in the non-growing spheroid. In contrast, in the growing spheroid, after 2 days labeled cells can be found at the depth of 160 μm which is greater than the increase in spheroid's radius by about 100 μm.
Our internalization results are consistent with the in vitro internalization patterns in both cases of growing and non-growing spheroids, as well as the percentage of cells at specific depths (See Fig.6 and Fig.11 in the paper [14] by Dorie's et al). It is also shown that both proliferation and random motion are responsible for the cell migration inside a tumor spheroid. This supports that a random walk can play an important role in cell migration and pattern formation as observed both in vitro [81] and in silico [63,64].
3.2.3. Chemotaxis based rearrangement within a heterogeneous spheroid
As described before, cell subpopulations may differ in adhesion, motility, growth rate, and the response to a certain drug, etc. Experimental evidences showed that some cell line moves towards a certain chemical [86]. In a coculture of cancer cells with differential properties, cells tend to relocate themselves to form a certain pattern. For example, in order to study how drug-resistant and sensitive tumor cells settle down in a 3D space, Starzec et al [79] cocultured adriamycin-sensitive (MCF-7S) and -resistant (MCF-7R) human breast cancer cells in long-term nodules. They showed that in mixed nodules, MCF-7R cells accumulated at the periphery, whereas the MCF-7S cells grew toward the central part of the nodules bordering necrosis. The investigation of tumor growth and spatial rearrangement can shed light on the dynamics of cell subpopulations and their differential behaviors, so that an accurate spatial prediction and consequently efficient treatment are made possible.
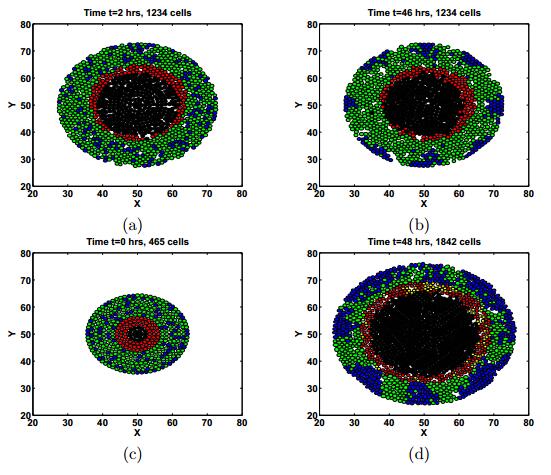
In this subsection, we investigate the role of differential motility in cell population dynamics and self-reposition. To this end, we mixed two types of proliferating cells (green and blue) in the proliferating region. Then different properties, including differential motility, are assigned to these two subpopulations. We allow blue cells' migration to be directed by the gradient of oxygen concentration for a better living environment, and let green cells undergo random motion. It turns out that differential motility alone can lead to cell re-organization with one type of cells accumulating on the periphery of the spheroid. Our results are illustrated in Figure 9(a)(b) for a non-proliferating spheroid cross section. Moreover, if a spheroid is growing, cells with chemotactic behavior eventually dominate the proliferating region even though they are sparsely distributed at the beginning. Figure 9 (c)(d) display the evolution of a growing spheroid with mixed cancer cells, in which the initial percentage of blue cells is 20 percent. Note that yellow cells correspond to quiescent blue cells in Figure 9 (c)(d).
3.2.4. Cell sorting
We have shown that some phenomena in 3D can be reproduced solely by our 2D cross section configuration. In fact, there are spatial limitations for cell motion and contact in a 2D model, either a 2D monolayer model or a 2D cross section configuration. Explained by Brodland, et al [5], the possibility of cells in a 3D system to be connected to each other of same type is much higher than that of cells in a 2D system. Cells are often multi-connected to cells of same type in 3D, but that phenomenon rarely occurs in 2D. Due to structural differences, 2D models may encounter difficulties in some cases to reproduce the corresponding 3D results. Even if our 2D cross section is not a 2D monolayer model, our model restricts cell motion to the cross section. In order to retain as much as possible the predictive power of the full 3D model, we look into the adaptation of parameters for some special cases.
Cell sorting is one such special instance for which the adaptation of the 2D cross section model by its 3D counterpart is required. So it becomes a benchmark to test the implementation of the adapted 2D model. We first investigate whether a complete or partial sorting can be reproduced by our model in 2D under the previous 3D sorting condition. It turned out that the previous 3D sorting condition does not lead to any sorting in a 2D cross section. For example, when αr,r:αg,g:αg,r=0.4:1:0.7 and fr=40nN, Eb=25nN,Frep=100nN,λ=7, a complete sorting is obtained in 3D. But it fails to approach either a complete or partial sorting in 2D (results are not shown). This is consistent with the finding in the literature that conditions suitable for sorting in 3D may not apply to sorting in 2D [82]. The discrepancy can be reasoned as follows. Calculated from adhesive forces, the net force should be strong enough to drive a sorting process. It should be strong enough to allow cells of greater adhesion to attract each other, and to squeeze out other cells of lighter adhesion. Due to dimensionality differences [36], cells in 3D systems have many more neighboring cells and therefore are more likely to be connected to other cells of the same type than their 2D counterparts [4]. Therefore, differential adhesion in 3D is able to exert a much stronger impact on sorting than that in 2D.
Therefore, it is desirable to adapt the 2D cross section model by the insight gained from 3D simulations, in order to study cell sorting, fragment fusion process in a cross section of a 3D tumor, etc. We predicted that in a 2D cross section much stronger individual net adhesive force is required to compensate for much less exposure of a cell to its neighboring cells, so as to attain sufficient driving force to sort. To confirm that, we took the ratio of relative adhesion among cells αr,r:αg,g:αg,r=0.4:1:0.7 from a 3D system of a small spheroid. We adapted them to αr,r:αg,g:αg,r=0.4:1.5:0.7, while fixing all other parameters, and then passed them to the 2D system. By doing so, sorting is achieved. In particular, green cells form islands and are enveloped by red cells. In the first place, multiple internal islands are formed. Then these small islands of green cells fuse into large ones. These are displayed in Figure 10 where we can see that cells do sort numerically in our adjusted 2D setting. Therefore, our 2D cross section configuration can reproduce the experimental observations [27,82,55] that cells sort by coalescence of smaller islands to form larger ones in an intermixed heterotypic aggregate which was also displayed in Figure 3 for the full 3D simulations. It is worthwhile to point out that the parametric adaption from its corresponding 3D systems can be biologically realized via re-distribution of bonding molecules [62]. With further adjustments, our 2D tool has the potential to become an efficient tool to study other properties of a 3D tumor spheroid of large size, such as drug resistance.
4. Conclusion
In this work, we have introduced a hybrid modeling method, which has not yet been proposed in the literature, for the study of heterogeneous tumor spheroid growth. This model enables us to simulate physical movement of living tumor cells in the multicellular context directly and efficiently based on fundamental physical and mechanical force analysis, without the assumption of free energy minimization. The entire tumor spheroid is described by an ellipsoid-based model while nutrient and other environmental factors are treated as continua. Using this specific combination, we have shown three main advantages of our method. The ellipsoid based discrete component is capable of incorporating mechanical effects and deformability, while keeping a minimum set of free variables to describe complex shape variations. Moreover, our purely cell-based description of tumor avoids the complex mutual conversion between a cell-based model and continuum model within a tumor, such as force and mass transformation, required in many hybrid descriptions. This advantage makes it highly suitable for the study of a tumor spheroid in vitro whose size is normally less than 800 μm in diameter [91]. In addition, depending on the available computational resource and tumor size of interest, our numerical scheme makes it flexible to choose the 3D ellipsoid model or the 3D-adapted 2D cross section configuration. Especially, as a new tool developed in this work, the 3D-adapted 2D cross section configuration has exhibited a great advantage in cell sorting, which is generally difficult to achieve in many 2D settings without the assumption of free energy minimization [4,38,85]. To gain those benefits, our model and its implementations have been validated and applied to the studies of cell sorting in heterogeneous aggregates, stabilized viable rim of a three-layer avascular tumor spheroid, internalization test of homotypic cells, and the chemotaxis-based cell reorganization within a heterogeneous spheroid. We have arrived at some main results: differential adhesion alone can lead to a variety of sorting patterns; the increase in deformability raises the possibility of cell sorting; both cell growth and random motion play important roles in cell internalization. Moreover, it has been shown that an interplay between adhesion and other factors (like motility) co-operate to generate the forces required for cell sorting, and that the balance of various factors instead of one single effect may lead to the evolution of tumor growth and its spatial pattern. Our current preliminary work can be extended to investigate specific issues in tumor growth such as drug resistance and dose schedule. Furthermore, as a future improvement of our current work, the mechanical effect from tumor environment besides cell-cell interactions can be incorporated with a continuum description.
Appendix
Force analysis and motion equation (Active force and reactive forces) Concerning active motion, normally cells send out a dominant pseudopod in their desired direction, attache and apply a force to either a neighboring cell or a surface. Then they pull the rest of the body towards the pseudopod. This process involves complicated intracellular molecular reactions and motions as well as conversions of chemical energy into mechanical energy. For the sake of simplicity, we model it only with cell orientation and active forces.
For cell orientation, we set phenomenological rules based on biological observations. If a chemical signal strength is above a threshold, it may provide an orientation stimulus. Otherwise, orientation direction is randomly chosen. Experimentally this process is stochastic and strongly biased toward the chemical gradient in chemotaxis or the previous orientation in random motion [63]. Mathematically, the orientation direction is described by equation (7) with a random Gaussian distribution where the a-axis of the ellipsoid is defined as the anterior-posterior axis of the cell for convenience.
|
→anew={(∇C)+σ1ZifCmax>Cthresh→a0+σ2Zotherwise
|
(7)
|
Here ∇C,→a0,→anew are all normalized vectors and represent the chemical gradient, current a-axis and chosen new a-axis, respectively. σ1,σ2 give the weight of the stochastic part (about 95% of Z value locates in the interval of (−2,2)) Moreover, Z=(Z0,Z1,Z2) is a vector whose components are created by Box-Muller transformation for Gaussian distribution number as follows: Suppose U1 and U2 are independent random variables which are uniformly distributed in the interval of (0, 1]. Then
Z0=√−2lnU1cos(2πU2)
and
Z1=√−2lnU1sin(2πU2)
Here Z0 and Z1 are independent random variables with a standard normal distribution and Z2 is obtained in the same way as Z0 or Z1.
After orientation direction is determined, individual cells rotate. The equation of rotation is given by:
Here α is used for orientation rate. Note that though in reality the realignment is achieved by disassembling and reassembling of several proteins and by internally rearranging structure instead of rotation, we assume that cells reorient their major axis to coincide with the new direction due to ellipsoid shape constraint [11]. The orientation process (called orientation cycle) is carried out for every predetermined tnew. Once its orientation direction is established, a cell begins to apply active forces to the psuedopods attachment for the retraction of the rest of the cell body. Then cells persist in exerting forces in the direction for a time period tmov. Cell rotation is numerically implemented via multiplying the a-axis of the ellipsoid by a rotation matrix. Then b and c axes are determined by the Gram-Schmidt process.
Active force generation is required for the extension of pseudopod and the retraction of the rest of the body. However, forces required for the former is negligible compared to that required for the latter regarding the fact that the pseudopod volume is normally less than 10% of the total volume. Active forces are applied at the site of pseudopod attachment so that they are always directed along the cell's anterior-posterior axis. Computationally, after cell i has been rotated to the new direction, a-axis of the ellipsoid in our model, the pseudopod is attached to a neighboring cell j if they are close enough, namely cell j has the smallest angle between the anterior-posterior axis of cell i and the vector rij connecting the center of cell i and j. Meanwhile an active force Tij is applied to the attachment along with the a-axis of cell i. Thus cell j receives Tij which is added into its total force. At the same time, a reactive force Mji is applied to the cell i, by Newton's law Tij=−Mji. Then cell i keeps its anterior-posterior axis for a certain time length (for instance 70 seconds) and exerts active forces along that direction. The magnitude of active force depends on some factors such as local chemical concentration level and its gradient, cell type, and whether the cell is attached to another cell or the surface. Here we set active force magnitude to be a constant. Constant active forces are set in the range between 0 and 100 nN. That is consistent with experimental measurement [84] as well as other successful theoretical models [65]. In addition, it was observed that cells moving randomly do not migrate as much as those doing chemotactic motion. To account for it, we set one constant fc for chemotactic force and the other constant fr for random motion. From now on, to distinguish random motion from directed motion, active forces in random motion are called random forces, while active forces in directed motion are called chemotactic forces as cells are in respond to chemical signals.
(Drag forces) As done in the DO (Dallon and Othmer) model [11], drag forces are positively proportional to their relative velocity and common contact surface area between two objects. Mathematically, the drag force due to the fluid is given by
Similarly, the drag force caused by cell and surface is
Finally, the drag force that comes from viscosity between moving cells is proportional to relative velocity
|
DRij=−Aijμcell(vi−vj)
|
(11)
|
Where Aif,Ais,Aij are the estimated surface area of cell i in contact with fluid, substrate surface, and another neighboring cell j respectively.
(Adhesive and compression forces) Adhesive forces in our model contain various attractions including mechanical adhesion, chemical adhesion and electrostatic adhesion, etc [40]. They are used to model membrane tension of two cells attracted to each other directly or through ECM. As such, adhesive forces are positively related to the density or adhesion strength of cell-line dependent binding molecules [92]. Moreover, the interaction between cadherin and actin cytoskeleton has been shown to play an important role in adhesiveness. Furthermore, it was found that cells remain attractive to one another through long plasma membrane or tether [51]. Cellular tether or protrusion, which can play an important role in cell sorting, can not be directly described using our current ellipsoid geometry. Therefore, a proximity distance is utilized to compensate the shape constraint. Within a surface distance dad, cells can attract one another. A cell is assumed to feel no further adhesive forces from its neighbors when it is apart further than dad. Once cells get too close they begin to compress one another and their adhesion vanishes.
Here there are some assumptions involved in the modeling according to the biological observation. Firstly, the adhesion force model is based on some qualitative assumption similar to those in Evans' paper [19,18]. It states that the magnitude of the adhesion force between two cells is determined by their proximity, because their proximity gives out the information of how many adhesive molecules in the common membrane area. Secondly, the distance between two cells' surfaces d represents an estimate of how much contact surface area the adjacent cells have instead of providing the actual distance. Cells can reach out to nearby cells and have tendency to contact. Thirdly, when cells get too close, repelling force arises. It implies that the volume exclusion is considered implicitly via repelling force and consequent cell deformation in the model. As such, there is a balance point where the passive force changes from adhesion force to repelling (or compression) force. Fourthly, the passive force is continuous which can appear as either adhesive or compression force. Based on these considerations, we model adhesive and compression forces in the way similar to Palsson's [65] as described in Eqn.(12). It is worthy to point out that with their adhesive and compression formula, calculated magnitude of tissue surface tension was comparable with experimental measurement [65]. In particular, let dj,i be the vector from center of cell i to its edge in the direction of the vector from the center of cell i to the center of cell j, hj,i. The vector sji is from the edge of cell i to the edge of cell j in the direction of hj,i. ˆsji=sji/‖sji‖ and ˆhj,i=hj,i/‖hj,i‖. Then adhesive and compression forces between cells i and j is given by [65]
|
Sji={−Frepχ(−x)3/2ˆsjiifx<0Ebαi,jχ{(x+x0)e−λ(x+x0)2−v0e−λx2}ˆsjiotherwise
|
(12)
|
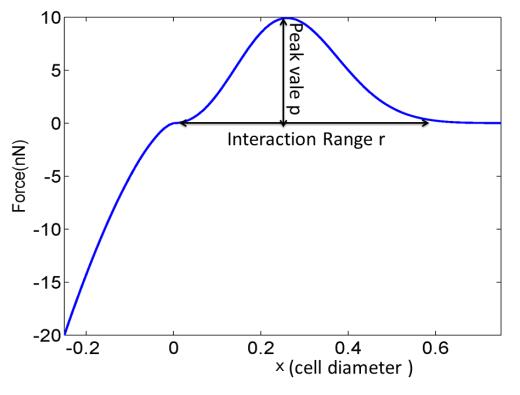
where χ=rcell2(1‖dj,i‖+1‖di,j‖), x=‖sji‖rcell and x0=−√12λ,v0=x0e−λx20. Here Frep is a constant parameter to describe the strength of the compression. rcell is 10 μm for standard cell diameter used in this work. Eb is used to represent the magnitude order of adhesion strength and αi,j is for the relative adhesion level among cell types. x0 and v0 are set to make the magnitude of Sji continuous and equal to zero at x=0. The behavior of the above-described function can be seen in Figure 11 where the picture is plotted for two standard spherical cells of 10 μm in diameter with λ=7.
Cell deformation and growth In equations (2) to (4), f1 is the growth function (Equation (17)). The nonlinear spring f2(x) is given by
|
f2(x)={k2xif(x>−0.6)−0.3k2(x0.3)2if(x<=−0.6)
|
(13)
|
Therefore,
|
df2(ui)dui={k2if(x>−0.6)2k2uiif(x<=−0.6)
|
(14)
|
Notice that k2 can be adapted to the imposed forces as follows:
|
k2=k20(f2i/astiff+1)
|
(15)
|
Where fi is the magnitude of the force applied to each end, i=a, b, c. And astiff is considered as a constant parameter. Moreover, it is assumed that the passive response is incompressible. Therefore three equations for u0a,u0b, and u0c are solved with the volume constraint [45]
|
(u0a)′(u0b+b∗0)(u0c+c∗0)+(u0a+a∗0)(u0b)′(u0c+c∗0)+(u0a+a∗0)(u0b+b∗0)(u0c)′=0
|
(16)
|
where a∗0,b∗0 and c∗0 are the lengths of the three axes a,b,c after growth (a∗0=a0+uga, b∗0=b0+ugb, c∗0=c0+ugc where a0,b0 and c0 are the initial lengths of three axes). This means that the viscoelastic components on the three axes must satisfy the volume constraint.
In addition, the effect of stress and nutrient on growth is described by the equation ˙ugi=f1(σi)∗G(cO2,cgl), for i=a,b,c, where σi is the axial component of the force applied along the ith axis. The form of f1 is based on previous experimental observations [72]. In particular, we use a piecewise linear function to include the effect of tensile as well as compressive stresses. This is the same as that in the KSO model [45]
|
f1(σ)={c−(σ−σ−) if(σ−≤σ≤−α)−c+(α−σ+) if(−α≤σ≤α)−c+(σ−σ+) if(α≤σ≤σ+)0 if (σ>σ+,σ<σ−)
|
(17)
|
where c+,c− are positive constants, σ+>0,σ−<0, [σ−,σ+] is the interval of positive growth, c+(α−σ+)=−c−(−α−σ−).
Finally, G function values under different microenvironments can be computed based on the experimental data which depends on the nutrient concentration. As such, before the calculation of grow rate of each local cell, grid based concentration solution needs to be interpolated into the cell mass center to calculate the nutrient concentration. In this study for cell sorting, G=1 if sufficient nutrients exist for cells to live and grow.
Solving the equations of growth and deformation For each cell, we want to solve the following system
|
u′a=(kaμa[fa(t)+¯pa−f2(u0a)]+f′a(t))(df2(u0a)du0a+ka)−1+f1(fa(t)+¯pa)
|
(18)
|
|
u′b=(kbμb[fb(t)+¯pb−f2(u0b)]+f′b(t))(df2(u0b)du0b+kb)−1+f1(fb(t)+¯pb)u′c=(kcμc[fc(t)+¯pc−f2(u0c)]+f′c(t))(df2(u0c)du0c+kc)−1+f1(fc(t)+¯pc)
|
where ui=u0i+ugi,i=a,b,c, where u0i,ugi are the displacement of i-axis due to the pure viscoelastic deformation and growth, respectively. (ugi)′=f1(fi(t)+¯pi). Total volume due to pure deformation is preserved as follows
|
V(t)=(u0a)′(u0b+b0)(u0c+c0)+(u0a+a0)(u0b)′(u0c+c0)+(u0a+a0)(u0b+b0)(u0c)′=0
|
(19)
|
And the pressure at each direction can be described as
|
¯pa=(Area)(p)=(u0b+b0)(u0c+c0)(p),¯pb=(Area)(p)=(u0a+a0)(u0c+c0)(p),¯pc=(Area)(p)=(u0b+b0)(u0a+a0)(p)
|
(20)
|
where p is the pressure inside a cell. First of all, to get (u0)′=((u0a)′,(u0b)′,(u0c)′), we have to solve 4×4 nonlinear system Ax=b as follows
|
[H100A140H20A2400H3A34−A14−A24−A340][(u0a)′(u0b)′(u0c)′p]=[RHS0(1)RHS0(2)RHS0(3)0]
|
where
|
RHS0(i)=[fi(t)−f2(u0i)]+μikif′i(t),i=a,b,c
|
|
Hi=μiki(df2(u0i)du0i+ki),i=a,b,cA14=−(u0b+b0)(u0c+c0),A24=−(u0a+a0)(u0c+c0),A34=−(u0a+a0)(u0b+b0)
|
Later this type of calculation is performed again to make sure we get the right pressure for each final configuration of cell. Once we find (u0a)′,(u0b)′,(u0c)′, we can simply compute (ugi)′ for the given piecewise linear function f1.
To solve the above system, a system in the form y′=F(t,y) is obtained by using the linear system solver dgesv_ in the LAPACK library, Then dlsode.f solver is used to get the solution value for the next time. It is known that based on the above viscoelastic assumption of cell, if there is no external force enforced on a cell, a cell would relax to a sphere and preserve the volume. We have verified our solving process of deformation by reproducing this relaxation fact.
Solving the equation of motion Adams fourth-order predictor-corrector nonlinear solver is used in our model to solve the equation of motion. The equation (5) reads in Matrix form as
Solving the above linear system leads to
By applying Adams-Bashforth predictor scheme [32,6] we have
|
xn+1∗−xn=h24[55M−1(xn)b(xn,tn)−59M−1(xn−1)b(xn−1,tn−1)+37M−1(xn−2)b(xn−2,tn−2)−9M−1(xn−3)b(xn−3,tn−3)]
|
(22)
|
Here h is used for the computational step size. Finally we use fourth-order Adams-Moulton corrector [32,69] to update the location at tn+1.
|
xn+1−xn=h24[9M−1(xn+1∗)b(xn+1∗,tn+1)+19M−1(xn)b(xn,tn)−5M−1(xn−1)b(xn−1,tn−1)+M−1(xn−2)b(xn−2,tn−2)]
|
(23)
|
Note that without the corrector step, we may get wrong solutions in some extreme situations which break down the system. Because the Adams-Bashforth predictor scheme is an explicit scheme which requires a sufficiently small step size to guarantee its convergence, while the corrector is an implicit scheme [6].
Some detailed description of numerical simulation The cell-based model was written in C and the Reaction-Diffusion (RD) solver was written in Fortran. Then two of them were coupled for running simulations via a main.f90 code that was written in Fortran. In our simulation, normally the time step for cell motion is 0.01 minute and the time step for the RD solver is 0.6 minute. Simulations can be run in either personal desktop computers or clusters. Since our current code is not for parallel computing, computer clusters only have advantage over personal desktop computer in memory or multiple runs. So far we are able to run simulations with ten thousands of cells with a reasonable time period. For instance, for a growth simulation of the general 2D cross section model involving 5000 initial seeding cells, it takes about 15 hours to simulate 40 hours of aggregate growth in a computer of 2.66 GHZ CPU speed and 16331460 KB memory. All of quantities and parameters in the model become dimensionless in the simulation code. For the RD equation, the reference parameters length L, time T, concentration c0 are chosen as 1 mm, 1 hour and 25.0 mM, respectively. Then variables in the RD equation can be nondimensionalized (with ⋆) as follows
|
D⋆(O2,gl)=D(O2,gl)TL2,t⋆=tT,∇⋆=L∇,c⋆(O2,gl)=c(O2,gl)c0,A⋆(O2,gl)=A(O2,gl)Tc0,B⋆(O2,gl)=B(O2,gl)T(c0)2,k⋆(O2,gl)=k(O2,gl)Tc0,n⋆(O2,gl)=n(O2,gl)Tc0
|
Similar nondimensionalizion process is applied to the cell-based model, where the reference parameters length L, time T, force σ0 are given as 1 mm, 1 minute and 1 nN, respectively. All of parameter values and their corresponding dimensionless values are listed in Table 2 and Table 3. Note that some unit conversions are required between the cell-based code and the RD solver. For example, the time scale in the RD solver is 1 hour, while it is 1 minute in the cell-based model.
Table 3. Parameters used in the reaction-diffusion component of the model. We use the cell average packing density carried out 2.01×108cells/cm3 in Casciari etal . [8] to convert uptake parameters AO2,Agl,BO2,Bgl in this table to rates per unit volume.
| P |
Description |
Value |
Dimensionless in coding |
Refs. |
| Diffusion Coefficients of oxygen in each region |
| Dco |
cell based region |
1.82×10−5cm2/s |
6.552 |
[45] |
| Dqo |
continuum region |
2.15×10−6cm2/s |
7.74 |
|
| Diffusion Coefficients of glucose in each region |
| Dpg |
cell based region |
3.0×10−6cm2/s |
1.08 |
this work |
| Dqg |
continuum region |
6.46×10−6cm2/s |
2.3256 |
[45] |
| Coefficients in Uptake Functions |
| AO2 |
oxygen uptake |
1.0642×10−16molcell⋅s |
2.01014 |
[9,45] |
| BO2 |
oxygen uptake |
6.0202×10−17mol⋅mMcell⋅s |
0.0497 |
[8,9,45] |
| Agl |
glucose uptake |
1.0642×10−16molcell⋅s |
2.01014 |
[8,9,45] |
| Bgl |
glucose uptake |
1.7879×10−17mol⋅mMcell⋅s |
0.0107 |
[8,25,45] |
| kO2 |
critical oxygen concentration |
4.640×10−3mM |
1.856×10−4 |
[8,45] |
| kgl |
critical glucose concentration |
4.0×10−2mM |
1.6×10−3 |
[8,45] |
| nO2 |
oxygen uptake |
0.55mM |
2.2×10−2 |
[25,45] |
| ngl |
glucose uptake |
0.04mM |
1.6×10−3 |
[25,45] |
Acknowledgments
Authors give special thanks to Dr. Hans G Othmer of University of Minnesota for invaluable supports and fruitful discussions in the relevant studies. This work was supported in part by Georgia Southern University Research Seed Funding Award. The authors would also like to thank the anonymous reviewers for their valuable comments and suggestions to improve the quality of the paper.









 DownLoad:
DownLoad: