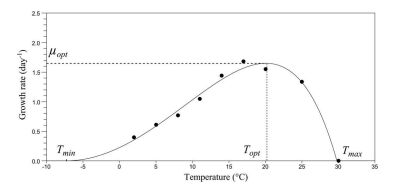
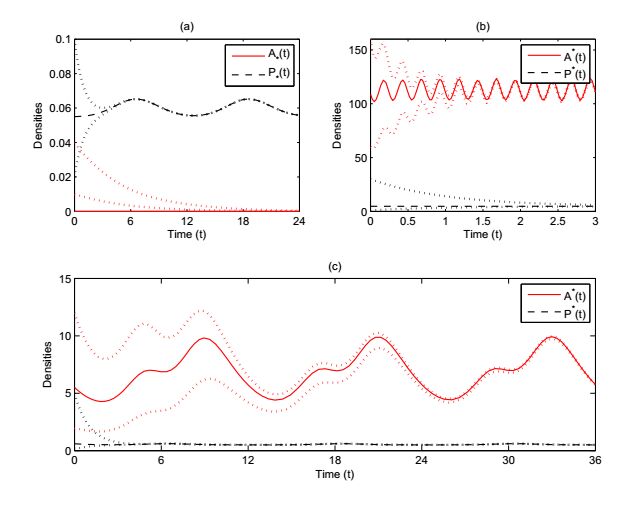
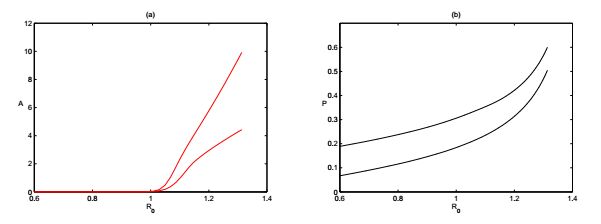
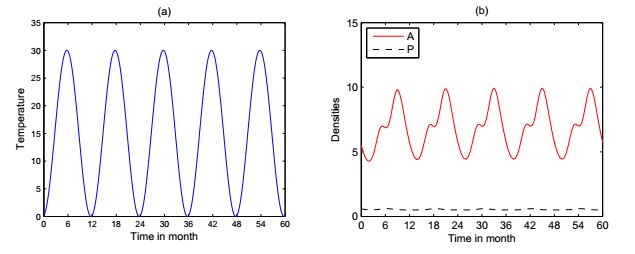
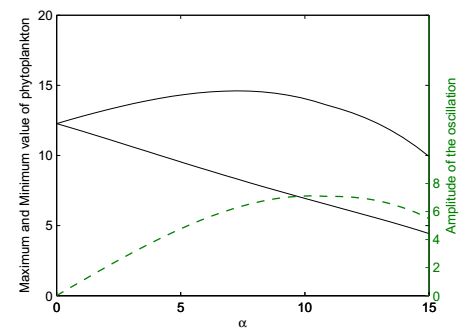
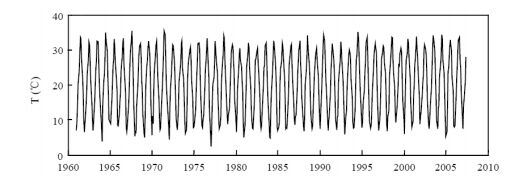
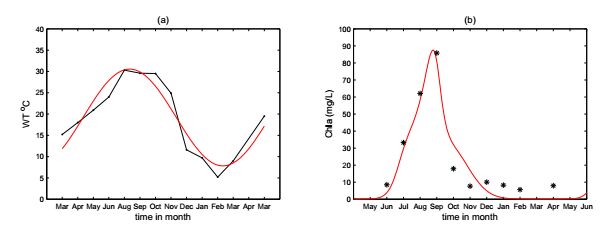
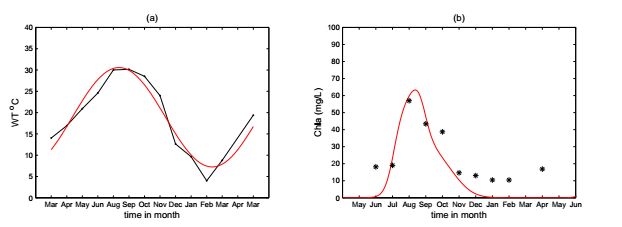
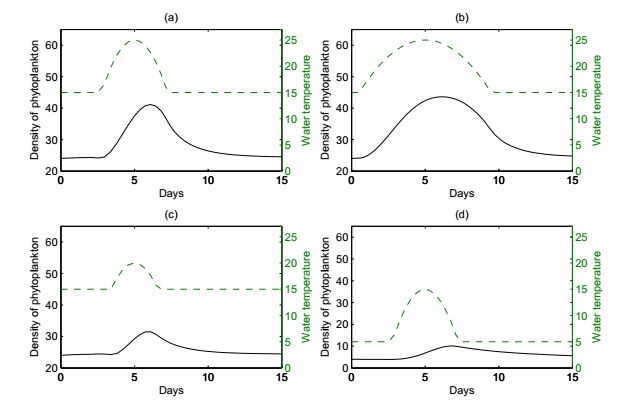
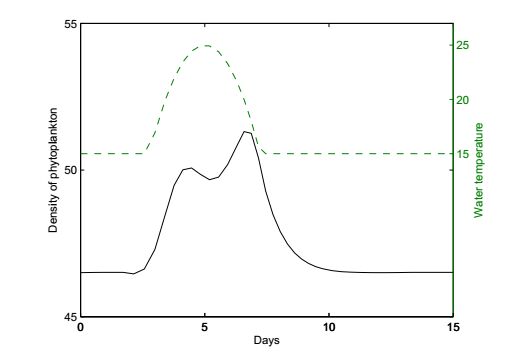
An non-autonomous nutrient-phytoplankton interacting model incorporating the effect of time-varying temperature is established. The impacts of temperature on metabolism of phytoplankton such as nutrient uptake, death rate, and nutrient releasing from particulate nutrient are investigated. The ecological reproductive index is formulated to present a threshold criteria and to characterize the dynamics of phytoplankton. The positive invariance, dissipativity, and the existence and stability of boundary and positive periodic solution are established. The analyses rely on the comparison principle, the coincidence degree theory and Lyapunov direct method. The effect of seasonal temperature and daily temperature on phytoplankton biomass are simulated numerically. Numerical simulation shows that the phytoplankton biomass is very robust to the variation of water temperature. The dynamics of the model and model predictions agree with the experimental data. Our model and analysis provide a possible explanation of triggering mechanism of phytoplankton blooms.
1.
Introduction
A successful business's secret is obtaining better outcomes and performance from similar activities, capital [1], and people [2]. Everything revolves around perceiving, improving, and augmenting the industry's underutilized, hidden, and low-performing opportunities. It is known that every sector is dominated by money [3], management, marketing and sales, product and services, people, processes, and systems. A minor improvement in any of these factors can heavily improve a company's performance. So, most companies search for the newest strategies that can improve time, cost, quality, and productivity dimensions [4].
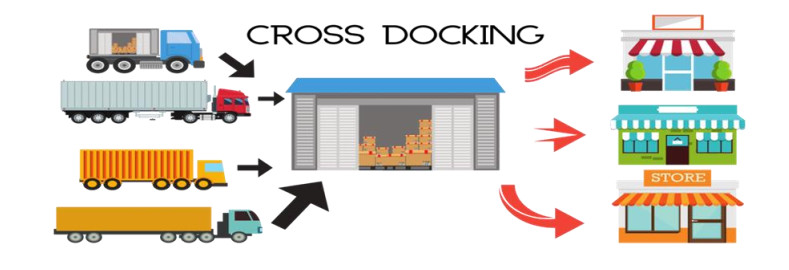
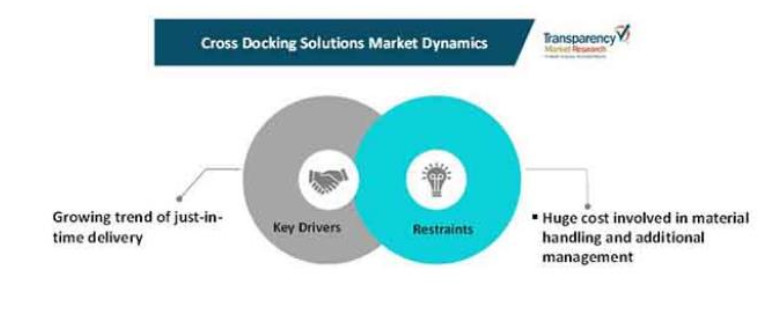
Recent years have seen drastic changes in supply chain management policies [5,6], logistic strategies, inventory management approaches [7,8], and production systems [9,10]. Conventional approaches have been upgraded with smart technologies [11,12] not only to maximize economic benefits [13] but also to minimize the detrimental effect on the environment [14]. The intervention of the newest strategies [15] in transportation models [16] including the introduction of multi-modal transport [17,18], have prioritized customer satisfaction, faster delivery, product quality, environmental benefits [19] as well as have optimized cost and time. Cross-docking is a contemporary logistic strategy that has revolutionized supply chain and warehouse management in achieving these landmarks [20]. According to the cross-docking trend report 2011 [21], the implementation of cross-docking has registered a 7.8% increase in overall cost-effectiveness. The report explained that cross-docking helped improve the service level by 37.9% and reduce the cost of transportation by 32.4%. In the context of the growing demand for minimizing operational costs, cross-docking solutions with just-in-time have made the availability of raw materials or goods easier for manufacturers and end customers (Refer Figure 1). Cross-docking has become a growing trend in countries like North America, Europe, Asia Pacific, the Middle East, and Africa.
Up to this point, an appreciable amount of exploration has taken place in different sectors of cross-docking, with the majority of them focusing on improving two major operational levels of decisions associated with scheduling vehicles in the cross-dock and assignment of doors to docks. A competent TDA system has a significant impact on the overall cross-docking performance. It significantly increases the delivery quality, decreases processing costs, and improves cross-dock service efficiency [22]. A cross-docking center has the provision of operating either on exclusive mode, where dock– doors are assigned to either inbound trucks or outbound trucks, or on mixed mode [23] assigning dock doors to both types of trucks. Though the mixed mode of service expands the adaptability of the cross-docking centers by minimizing the objective function, exclusive modes of service are mostly favored due to the high level of intricacies involved in handling operations in hybrid mode. Based on the criteria of product allocation, cross-docking has been grouped into two categories: pre-distribution and post-distribution [24]. Notwithstanding the objective of items, when information on the exact outbound truck in which the product must be stacked in is known, it is termed pre-distribution. On the off chance that the product's landing place and content are characterized by the quantity of items per each type, the assignment mode is known as post-distribution, and the allocation of goods is mainly done at the cross docks.
Good coordination between the manufacturer and the retailer in a joint economic lot sizing through the delivery pattern is important for balancing the inventory level and optimizing the inventory space limitation [25]. Even though the destination, the specific outbound truck for the desired destination, is known beforehand, the uncertainties in the arrival and departure of the trucks cannot be fully ignored. The tardiness of the inbound trailers and fixed departure time followed by the outbound vehicles results in the landing up of the delayed loads in the temporary storage facilities. The loads are stored until the arrival of the next outbound truck for the same destination.
1 Cross Docking Solutions Market Future Growth Opportunities 2027 (transparencymarketresearch.com), Kingdom Of Bahrain, Accessed 9 Nov, 2022, 12.12 pm
1.1. Research gaps
In the cross-dock door assignment problem, the area of concern has been designing an ideal task plan for doors to docks to diminish the makespan, waiting time, total transportation cost, internal resource cost, operational cost, and penalty cost due to unfulfilled shipments. The goods unloaded at the receiving area are straightforwardly moved to the shipping area and stacked onto outbound trucks. Depending on their demand frequency or loading sequence, they are stored in temporary storage areas. Most research aimed to minimize storage space, travel distance, time of the resources, response time, total transportation cost, and material handling cost while transferring goods from receiving docks to shipping docks. Previous research has prioritized storage location and travel distance to optimize cost or time. A research gap has been noticed. No work has been done on material handling cost, considering the quantity of the delayed loads transferred from the dock door to the storage area and its effect on the total material handling cost. Segregated cost related to this internal operation has not been considered before.
1.2. Contribution
This study has understood the holes and makes the following novel commitment to progressing the information in the field.
● The proposed research has consolidated the material handling cost in terms of the number of pallets of products unloaded from the incoming truck and shifted to the storage zone.
● The model investigated the effect of available material handling resources for product transfer on the material handling cost. Each entry has a fixed number of posted material handling trolleys.
● The model further searched whether the change in the product quantity transferred to the storage area affects the material handling cost.
The rest of this paper has been organized in the given way. The literature review is presented in Section 2. The problem description, notations, and assumptions are addressed in Section 3. Section 4 talks about the mathematical model. Section 5 discusses the solution approach, Section 6 presents the results and discussion, and Section 7 presents the conclusion with recommendations for future research.
2.
Literature review
The Literature review has been designed following the keywords of the research.
2.1. Cross-docking
Cross-docking is one strategy that has highly influenced supply chain management through faster movement of goods, eliminating redundant storage, reducing distribution costs, and improving customer satisfaction [26]. In cross docks, the goods unloaded from an inbound truck are straightforwardly transferred to the shipping dock and are loaded into outbound trucks for dispatching. Thus, enabling the need for proper loading and discharging operations [27] (Figure 2). Cross-docking consolidates smaller shipments between shippers and recipients, using the full truckload and reducing transportation costs [28]. Thus, in a nutshell, the main purpose is to integrate intermediate nodes into the transportation network.
2 Cross-docking, Kingdom of Bahrain, Accessed 30 June, 2022, 23.00, pictures of cross-docking-Bing images
Based on the decision-making level, the familiar decision problems in cross-docking are classified into strategic, tactical, and operational [29]. Strategic decisions about the location or the cross-dock layout, tactical level of decision regarding network design, and the operational decisions of scheduling of trucks, resources, and assignment of doors ponderously influence the performance of a cross-dock. Also, from the swift movement of items inside the cross-dock facilities, it is apparent that the items within the cross-dock invest less or no time in the storage region. Hence, well-thought operational plans for internal transportation, truck-door assignment, consolidation, sorting, product placement, and scheduling expand the effectiveness of the cross-docking framework at the short-term decision level [20].
2.2. Scheduling at cross-docks
As cross-dock focuses on maximizing throughput and minimizing operational time and operational cost, the sequencing and scheduling of vehicles for single cross-docks, multiple cross-docks [30,31] as well as multi-door cross-docks forms an integral part of warehouse management. Scheduling of trucks, the hardest and most significant scheduling problem, has many practical applications in cross-docking and logistics. It has inspired many researchers to invest their time and effort in exploring this area [32]. Finding the ideal situation for the receiving and shipping truck sequences is the goal of this task [33]. Golshahi-Roudbaneh et al. [34] developed a heuristic approach to determine the optimal sequence of shipping trucks. They worked on five metaheuristics and the hybrid one to constitute their proposed model. Dulebenets initiated an extensive study on the evolutionary algorithms designed for scheduling trucks in a CDC [35]. He continued his research and compared the weak and strong mutation mechanisms [36]. He proposed an adaptive polyploid memetic algorithm to relate the scheduling of trucks in the cross-docking facility with the operations planning inside the dock [37]. Dulebenets [38] designed a mixed-integer linear programming model to address the truck scheduling issue at the cross-docks. The products were directly shipped to the shipping dock to be stacked into the suitable outbound truck or briefly put away in the storage region until the suitable outbound trucks were apportioned to the dock door. A delayed start parallel evolutionary algorithm was formulated to support the end goal of minimizing total truck service cost.
Theophilus et al. [39] analyzed the major attributes influencing truck scheduling at the cross-dock centers. These ascribe incorporated terminal shape, entryways, door-service administration mode, preemption, interior transportation mode utilized, the capacity of the temporary storage facility, power of the resources, and the objective and solution methodology considered. They analogized the result obtained based on computational run time and the quality of the acquired solution. Mousavi and Vahdani [40] designed a robust optimization model to overcome the inborn unpredictability of input data in the site and vehicle routing scheduling issues at cross-docking centers. The proposed mixed-integer programming model aimed to locate cross docks and schedule vehicle routing considering multiple cross docks. Zhang et al. [41] in their study presented the collaborative optimization of loading operation planning and vessel traffic scheduling (COLOPVTS) in dry bulk ports. The paper aimed to create the best traffic scheduling and loading operation plans for each vessel simultaneously by investigating how ships approach and exit dry bulk export ports.
Even in cold cross-dock terminals, scheduling trucks is essential since a sizable amount of perishable goods are wasted due to poor supply chain management. Considering the deterioration of perishable goods as they are handled by arriving trucks and the presence of temperature-controlled storage spaces reserved exclusively for perishable goods, Theophilus et al. [42] developed a mixed-integer mathematical formulation for truck scheduling optimization to reduce the overall cost of the truck service. Golshahi-Roudbaneh et al. [43] urged a new model for cross-dock scheduling problems where time windows and delivery deadlines for trucks shipping perishable products were considered. They blended two notable metaheuristics called the Keshtel algorithm (KA) and simulated annealing to formulate a new hybrid algorithm to limit the total cost coming about from the earliness or lateness of shipping trucks. Pan et al. [44] in their study addressed the truck scheduling problem for perishable products in a cross-dock. He presented a mixed integer programming model to evaluate the deterioration risk variation coefficient for perishable products in an unstable logistic environment. Zheng et al. [45] discussed cross-dock truck scheduling problems for refrigerated and frozen items. They formulated a mixed-integer linear programming model to minimize the operational cost. They considered penalties on the inbound truck arrival time in case of contravention of the contracted time windows, tardiness penalties on product delivery, inventory cost, and transportation cost of the outbound truck.
2.3. Advanced logistics
A well-planned logistics is the backbone of any business enterprise. Today's corporate environment is more competitive than ever, and customers' expectations for quicker delivery of goods have increased significantly. These factors have compelled researchers to explore strategies to increase profitability and satisfy customers. Soares et al. [46] developed a conceptual model for a transportation and logistics observatory focusing on six major areas: data, methodology, intelligence, community, governance, and infrastructure. By exploring the relationship between these parameters within the model, the paper suggested the possibility of standardizing goods, services, and procedures for creating a TLO. Forkan et al. [47] discussed a new non-linear optimization model for inventory management, considering a reverse logistic system. The model aimed to optimize holding cost by assuming that the demand for freshly produced and remanufactured items are never the same. Mahjoub et al. [48] studied the optimization and modelling approach of logistic networks with supply chain management. The contribution of the paper was not limited to the modelling of vehicle dynamics and timetables at various locations of suppliers, warehouses, and consumers but also extended to the loading, unloading, and delivery times of goods from suppliers to customers while accounting for their pertinent characteristics (e.g., number, nature, destination).
Attempts to reduce logistic costs gave birth to a successful management strategy of cross-docking [49]. Further exploring new ideas of logistic approaches, Pan et al. [50] addressed the operational solutions for sustainable development, the new difficulties and research opportunities for digital interoperability under the PI paradigm, and how digital interoperability might assist in connecting logistics and supply networks. Chargui et al. [51]introduced physical internet or PI cross-docks. They discussed how this idea modified the traditional cross-docking platform design, management, and optimization practices. To highlight the distinctive features of the PI cross-docks from the "conventional" cross-docking platforms, the various cross-docking optimization issues originating from the PI paradigm were then detailed at the strategic, tactical, and operational decision levels.
2.4. Material handling
It is currently a perceived reality that material dealing is a concentrated work area that influences the complete expense and affects the framework's effectiveness, subsequently convincing the scientists to look for options that could limit the material handling cost. Hence, modernistic optimal plans of assignment of inbound and outbound trucks to corresponding strip and stack doors and product placement operations were laid by many scholars [20]. It is not only the assignment of the door to docking, trucks to exit, or synchronization of the local and network-based cross-docking activities [29] that have captivated the interest of think tanks, but resource management, assignment of handling resources to doors have also niched a mark in the researcher's mind. Mukherjee et al. [52] in their recent work presented a mathematical estimation of the maximum material flow within a cross-dock. Their idea of the paper thrived on the fact that the storage space for a rented cross-dock is limited; hence, the movement of goods should be faster to avoid long waiting queues.
Vieira et al. [53] suggested improvements in internal material handling management. The goal was to assess, deliberately, the effect of executing changes in materials bearing on the client's view of cost, the safety of the resources in service, quality and authenticity of the service offered, agility, and overall contentedness. Das et al. [54] introduced a multi-objective streamlining model incorporating the facility location problem, the solid transportation challenge, and inventory management. The formulation's multiple objectives included finding the most advantageous Euclidean plane locations for potential facilities apart from determining the quantity of distributed commodities, lowering the cost of overall transportation, inventory, and carbon emissions, and reducing transportation time. During the transportation process of goods from the pickup point to the delivery point, the last in–fast out policy is applied during loading, which necessitates rear-loading the vehicle and only allows goods closest to the back door to be unloaded. Cherkesly and Gschwind [55] dealt with the pickup and delivery problem considering time windows, multiple stacks, and handling operations. They attempted to determine the number of vehicles and the vehicle routes required to efficiently fulfill the set of requests while taking into account potential handling procedures. Bertolini et al.[56] suggested a dynamic operative framework in order to adapt to the changes in operational environment during material handling activities. Their aim was not only to ensure good results in terms of productivity, but also to bring reduction in the travel distance of the handling machines, reduction in maintenance and energy consumption costs.
Kucukoglu [57] investigated the effect of cross-dock shapes on the material handling cost. They concluded that I-shaped cross docks were the best, providing the lowest average price among the popular four layout shapes of I, L, T, and U. Nassief et al. [58] studied the dock door assignment problems to cut down the material handling cost. He formulated a new mixed-integer programming model embedded in the lagrangian relaxation. Zhang [59] proposed a mixed-integer programming model considering truck time windows for a particular cross-dock. He aimed to minimize the travel distance and the total cost, including labor and penalty costs due to transportation delays. The proposed results from a diversified resource number helped to obtain the appropriate time. It improved the initial time window, the make span at each work station, the free time interim within the cross-dock, and the free resource number at each period gave pertinent data on the resource administration.
Serrano et al. [60] discussed distribution and operational planning in a cross-dock from the perspective of the automobile industry. They presented an integer linear programming model that minimizes the total cost, including transportation costs from the inbound and outbound trucks, internal resources, and storage costs. Their paper revealed how interrelated tactical and operational decisions are, and treating them jointly could drop the soaring high transportation cost. Shahram fard and Vahdani [61] proposed a bi-objective optimization model to assign cross-dock transportation resources to trucks and doors to minimize their energy utilization. In the second objective function of the model, they prioritized cutting down the waiting time of trucks, inventory holding cost, and trucks' delay in delivering products through a mixed mode of service and scheduling. Fabry et al. [62] investigated the synchronization between related trucks. Their model focused on the assignment and sequencing of trucks to warehouse doors with an end goal to minimize the time spent by the pallets within the system.
2.5. Storage space allocation
Moving items from an inbound truck to an outbound truck is a typical understanding inside a warehouse or cross-dock. This standard conduct now and again gets upset because of the postponement in showing up outward-bound trucks at the loading bay. In the event of non-accessibility of the corresponding truck in cross-dock, the items are moved to the storage region for a more limited period [63]. This assignment of storage area to the stock is one more basic aspect that looks for investigation in distribution center administration. Hence, storage location-allocation problems were examined to demonstrate multiple storage policies for goods to utilize minimum warehouse storage space [64], lessen internal material handling costs, and limit order route length [65] or travel distance.
A cautious investigation of the SLAP approach uncovered that a storage area's performance relies on the amount of space allocated for material allocation and the time for material handling. Reyes et al. [66] reviewed the literature on SLAP and provided a comprehensive analysis of the solution methodologies adopted and the objectives. In many of the cross docks, storage areas were segregated into storage zones depending on the product's storage policy [67] and their demand frequency. Silva et al. [68] studied the impact of the layout of warehouses, the nature of the demand, and staging and routing plans on the solution of zone sizing problems in ABC storage zones in manual warehouses. Zaerpour et al. [69] presented the optimal shape of a storage system to reduce the response time. They successfully established that response time is not dependent on the storage policy adapted or the location of the input or output point.
Sun et al. [70] dealt with the challenges of allocating storage space at an inland bulk stockyard, where the goal was to discover a practical solution to keep the shapeless commodities. They formulated a mixed integer programming model to prevent generating scattered small fields. They viewed the area of each stock pad in the yard as a collection of unit slots.
3.
Problem description
In this research study, we focus on minimizing the material handling cost experienced while unloading the products from the inbound trailers at the assigned doors and then shifting the products from the receiving docks to the designated storage zones by AGVs. The unloaded products, after consolidation operation, are moved to the shipping dock, where they are stacked on the outbound trucks and dispatched to their destinations. The non-availability of assigned outbound trucks at the shipping dock results in storing the products in temporary storage zones depending on their demand and loading sequence. The automated guided vehicles assigned to particular strip doors carry the products to their destinations. In one of the previous studies, the effect of the cross-dock shape on material handling cost was studied, focusing on the assignment of trucks to doors. This paper formulated the model by selecting inbound trucks to doors and from the entries to the respective storage zones by assigned automated guided vehicles. The number of assigned automated guided vehicles per door is fixed.
3.1. Notation
The notation used in the model formulation is presented in this subsection. It comprises indices, decision variables, and parameters.
3.1.1. Indices
The notation used in the model formulation is presented in this subsection. It comprises indices, decision variables, and parameters.
S number of storage zones
M number of incoming trucks
N number of automated guided vehicles (AGVs) assigned
D number of functional doors in a warehouse
P number of products transferred from supplier to the customer per truck
3.1.2. Parameters
rpm number of pallets of the product p in truck m
qps number of pallets of the product p transferred to storage area s
cis transportation cost per pallet of the product from the door i to the storage area s ($/pallet)
cim unloading cost per pallet of the product at door i from the truck m ($/pallet)
3.1.3. Decision variables
xim is a binary variable and equal to 1 if the truck m is assigned to door i and 0; otherwise; i = 1, 2, …, D; m = 1, 2, …, M
xin is a binary variable and equal to 1 if the AGV n is assigned to door i and 0 otherwise; i = 1, 2…D; n = 1, 2..., N
zpis binary variable and equal to 1 if the product p is transported from the door i to storage zone s; i = 1, 2, …, D; s = 1, 2, ..., S; p = 1, 2, …, P
3.2. Assumptions
To structure the proposed model, the accompanying arrangement of assumptions is made to define the limits in the formulation of the model.
1. After passing through the in-gate, inbound trucks are assigned to strip doors where goods are unloaded and shifted to receiving docks. The unloading and loading process is done sequentially, where one inbound truck is given to only one particular door chosen randomly in the planning horizon. Only one inbound trailer and an outbound trailer are set for each location [57].
2. A cross-dock have numerous entryway depending upon its size. A fixed mode of service is considered where all the strip and stack doors are in working mode, and the possibility of using each entry by incoming and outgoing trucks is equal.
3. A pre-distribution product allocation is considered such that the interchangeability of products is ignored. After the trailer is maneuvered into a strip door, all products are unloaded, excluding the possibility of preemption. The product quantity remains the same, ignoring defects, damage, or loss during the handling operation.
4. Material flow from the incoming truck to the storage area has been examined. A storage space with sufficient capacity is available in front of the dock door. The movement of products from temporary storage areas to outgoing trucks is shrugged off [57].
4.
Mathematical model
The mathematical model aims to minimize material handling costs in transferring freight from the dock to the storage area and unloading products from inbound trailers. The first term of the function is the transportation cost, and the second term represents the unloading cost of products.
Assignment constraint
Equation (2) [57] presents that every incoming truck is relegated to a specific door. Once allotted won't be moved to any other door. Equation (3) [57] relates to handling resources with every door.
Resource availability constraint
Equation (4) presents that the allocated resources for each door to transfer freight cannot exceed the total available resources.
Product constraint
The convey time and destinations being known beforehand, products with delayed departure are fetched to storage areas. Equation (5) identifies the product movement from a door to the storage area. Equation (6) elaborates that the amount of product shifted to the storage area is less than the total carrying quantity of the products in all the trucks suggesting that some products are directly shipped to the outbound trailers.
Binary constraints
5.
Solution methodology
The solution methodology for this discussed model demands an approach that can handle various variables. It is a cumbersome effort to deal with an enormous number of variables using the classical optimization technique. Several methodologies can be exerted to obtain an optimal outcome. In this research, we aim to minimize the material handling cost in transporting products to storage areas and unloading the freight. The optimization software LINGO 19.0 was preferred to solve the problem, which offered an optimal result. In this section, we put forward a numerical example to describe the mathematical model. The details and the explanations are as follows.
For the numerical analysis, the data set have been considered from [63,71] with some modification. Table 1. summarizes the result with all possible permutations and combinations of inbound trucks, number of doors, number of products in the inbound trucks, and storage areas abbreviated as m, i, p, s, respectively. a) In the first 14 experimental runs, the number of inbound trucks was kept constant at 4, and possible rearrangements were made for doors, products, and storage areas to obtain the transportation cost of the goods from the door to the storage area. b) In the next 16 scenarios, three inbound trucks were used with variations in the other indices to check the change in transportation cost. c) In the next 20 experimental cases, two inbound trucks were considered to examine their effect on the transportation cost when all other parameters changed. d) Only one inbound truck was considered in the next 11 cases.
6.
Results and discussion
The proposed work emphasized the operational level of decision-making. Within a traditional warehouse or a cross-dock platform, it is essential to have proper synchronization between the inbound trucks at the strip doors and the handling resources entitled to unload and transfer goods to the storage area and the shipping dock. And the cost drivers for the internal activities of relaying goods and the external activities of unloading goods at the receiving docks are considered. In the inbound segment, a variable cost is considered depending on the volume of the product. We felt a fixed cost of transferring whenever a product is shifted from the inbound truck to the storage area in the outbound segment. Indeed even though the modelling approach is based on a case of consideration, it remains moderately non-exclusive and can be adjusted to other cross-dock stages and setups, including more doors, trucks, and AGVs.
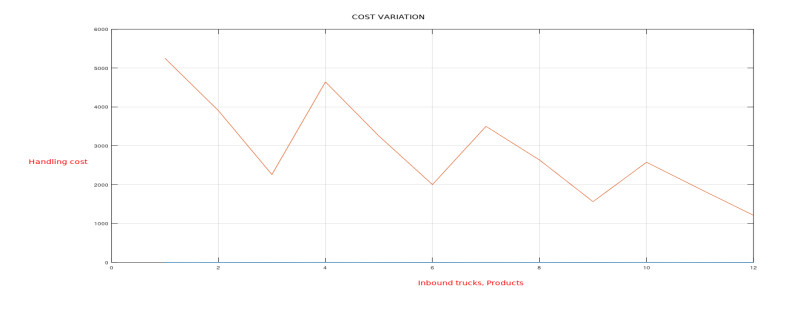
It can be explained from the result in Table 1 that when four inbound trucks are deployed at a receiving door transferring three different types of products of varying quantities, a variation in the handling cost is observed. When three products are unloaded from the four trucks and shifted to a particular storage zone, a handling cost of 5,255 dollars ($) is noted. Considerable drops in an amount in the next 2 cases are recorded at 3,905 dollars ($) and 2,260 dollars ($), respectively, when only two products or 1 product is considered. Thus, the amount of product transferred can influence the material handling cost.
It is observed that using only two inbound trucks recorded a cost of 3,501 dollars ($), a steady drop of 1,144 dollars ($), and assigning only one inbound truck for unloading the product at a specific door brought a sharp decline of around 924 dollars ($). It is also important to mention that reducing the number of trucks from 4 to 3 also induced a noticeable reduction of approximately 610 dollars ($) in the handling cost. Consequently, it can be stated that the changing number of incoming trucks equally influences the cost.
Product quantity is an important parameter for optimizing the cost. It has been observed from the results in Table 2 that increasing or decreasing the product quantity of each variety by 20% has introduced a noticeable amount of change in the net handling cost. An increase of 20% in the unloading price of each pallet of products from inbound vehicles has increased the total material handling cost by 15.90%. However, it is quite interesting to notice that decreasing the number of pallets transferred to the storage area has reduced the total cost by more than 1%. Even though all parameters have been tested against appreciation and depreciation of 20% from their original value, the effect of the change of per pallet unloading cost and transportation cost on the total handling cost is noteworthy. An increase in the transportation cost per pallet of product to the storage area has increased the material handling cost by 4.09%, which is quite mere compared to the huge 15.9% increase in total cost against the 20% increase of per pallet unloading price (Shown in Figure 3). It is certain from the results in Figure 4 that the increase in net material handling cost is maximum against the rise of unloading price compared to other parameters.
In this study, managerial insights are embraced based on the numerical results. Budget being a constraint for the medium or small scale business, plans for optimizing operational cost is a continuous endeavor. Within a warehouse or cross-dock facility, the internal material transfer to different sorting, consolidation, and storage areas contributes to the overall material handling cost. Managers can significantly reduce the overall material handling cost by emphasizing the elements behind material handling, like the number of pallets transferred and the number of trips executed. As labor cost against material handling contributes majorly to the total cost, efforts to implement more automation should be considered. Appropriate use of IoT (Internet of Things) in estimating the arrival time and following a fixed departure time will reduce the delayed loads ending up in storage areas. The result of this study expressly exhibited a guideline for managers to map various aspects of storage and material handling. In brief, the study inspires warehouse managers to facilitate the direct shipment of goods to outbound trucks.
7.
Conclusions and future research
From the results of the discussed model, it can be comprehended that during the peak season of the product demand, when more incoming vehicles are in the planning horizon for unloading, the material handling cost is high due to the higher quantity of the product transference. Thus, it is evident that increasing or decreasing the product quantity affects the net worth. Increasing per pallet unloading price increases the material handling cost tremendously, suggesting lookouts for alternative options to control labor and handling operations. Our proposed case study assigns a fixed number of automated guided vehicles for material transfer. But, it has been noticed in Table 3 that changing the allotted number of AGVs does not affect the material handling cost as the cost is dependent on the number of pallets of product transferred or unloaded. Apparently, from the declined feature of material handling cost in Figure 3. for the reduced number of trucks, the case involving 1inbound truck carrying three different types of product with a handling cost of 2,577 dollars may be the optimal result. But deploying fewer inbound trucks would mean less material flow. Thus, it may increase the shortage of items within the system, delay product delivery, cause long waiting times, lost sales, reduce customer satisfaction, or affect the system's efficiency. Thus, it can be summed up that case eleven would be the best result if the research problem is considered for a very small area. Case 5 would prove to be a good result for a medium-sized research problem. The possible consequence of the large-sized research problem is Case 2, where four inbound trucks and 6 AGVs are assigned to a door for unloading and shifting three types of products to a particular storage area. In other words, the cost can be minimized, or savings can be intensified based on the feasibility of the research problem.
It is evident from the results in Table 2 that transferring fewer products to the storage area would mean a reduction in material handling costs. Reduction in the quantity transferred to storage area means reduced demand for slots results in smaller warehouse space to purchase or rent for product storage as well as fewer shelves, which significantly lessens the impact of these cost entries on business profitability. Thus, it is recommended that systematic planning of truck arrival and departure should be enabled such that the cross-docking approach can be utilized more for product transfer, lessening the possibility of product storage.
Our proposed study has some limitations that can be explored in future research.
● In this model, we have considered the operations within a single cross-dock. However, the model can be extended considering multiple cross-docks with many receiving and shipping docks, and the material handling cost can be determined.
● In light of the rising intricacy of the logistic network, it may be of incredible premium to explore material handling on physical internet (PI) containers when switched from one particular logistics service provider to another.
● It would additionally be fascinating to investigate new and productive heuristics and metaheuristics to take care of the proposed issue and its augmentations with different assumptions or multi-objective models.
● In the proposed model, the transportation cost and unloading costs have been included. Parameters like storage cost, expenses against preserving the quality of the goods within the storage, and carbon emission during the operations are some dimensions that can be investigated while extending the model further.
● The products are stored in a temporary storage facility, and on availability of the outbound truck, the products will be shifted from the storage area to the outbound truck. So, the proposed model can be extended by evaluating the effect of transportation cost and loading cost of the pallets onto the outbound trucks from the storage area and receiving dock.
● In a pre-distribution approach, when the items are not interchangeable, the dispatching information is known from the inbound side, and each product is assigned to a specific outbound vehicle. The model can be further explored by adding the new component of interchangeability of products within the cross-dock.
● The model has been formulated considering a fixed number of available resources. It has been found that the number of resources does not affect the total cost as it is dependent on product quantity. The model can be extended by adding new constraints on the nature, capacity, and energy consumption of the automated handling resources used for pallet handling. Its effect on the obtained cost can be investigated.
Acknowledgments
The authors would like to express their gratitude to the Gulf University in Bahrain for continuing to encourage academic excellence and scientific research.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: