Morrey spaces on weighted homogeneous trees

1.   Introduction

In 1741, Euler ^[1] laid the foundations of graph theory in solving the famous Königsberg Seven Bridges problem. A series of studies on graphs laid the foundation for the development of tree theory, in which trees are acyclic connected graphs. In 1857, Cayley ^[2] introduced the concept of trees while studying saturated hydrocarbon isomers and the counting problems of acyclic graphs. In the 20th century, trees were gradually applied to fields such as signal processing and image analysis, as referenced in ^[3,4].

In recent decades, the theory of function spaces and operators in harmonic analysis based on trees has attracted considerable attention. In 1986, Korányi and Picardello ^[5] investigated the Laplace operator on homogeneous trees and the boundary behavior of its eigenfunctions. The spectral properties of Schrödinger operators on homogeneous root metric trees were studied in 2002 by Sobolev and Solomyak ^[6].

The metric measure spaces $(\mathcal{V}, d, \mu)$ grow exponentially and do not satisfy the doubling condition. Therefore, the classical Calderón-Zygmund decomposition theory is not applicable in this setting. In 2003, Hebisch and Steger ^[7] presented an abstract Calderón-Zygmund decomposition theory, which applied to spaces $(\mathcal{V}, d, \mu)$. They applied this theory to obtain the weak $(1, 1)$ boundedness of the maximal operator related to admissible trapezoids, as well as the properties of multipliers and singular integrals. In 2020, Arditti, Tabacco, and Vallarino ^[8] introduced the atomic Hardy space $H^1$ based on space $(\mathcal{V}, d, \mu)$. In 2021, Arditti, Tabacco, and Vallarino ^[9] studied the BMO space defined on space $(\mathcal{V}, d, \mu)$ and proved that BMO is the dual space of $H^1$.

In 1938, the classical Morrey spaces were introduced by Morrey ^[10] during his study of the regularity of solutions to second order elliptic partial differential equations. They can be regarded as a significant and natural extension of Lebesgue spaces. For more work related to the classical Morrey spaces in this paper, see references ^[11,12,13]. In 1997, Arai and Mizuhara ^[14] defined Morrey spaces on spaces of homogeneous type, which are metric measure spaces $(X, d, \mu)$ that satisfy the doubling condition. That is, there exists a constant $C$ such that

Moreover, Morrey spaces have also been investigated in the setting of metric measure spaces ^{[15,16,17,18]} that do not satisfy the doubling condition.

Due to the important significance of Morrey spaces, many scholars have begun to extend them to discrete metric spaces in recent years. In 2019, Gunawan and Schwanke ^[19] proved the boundedness of the Hardy-Littlewood maximal operator on discrete Morrey spaces by using a discrete Fefferman-Stein inequality. In 2021, Zhang, Liu, and Zhang ^[20] presented the Morrey spaces on infinite connected graphs and established the boundedness of the Hardy-Littlewood maximal operators and their fractional variations on these spaces.

Let us discuss several open problems related to the theory of maximal operators on weighted homogeneous trees, which can guide further research. One significant direction involves investigating the Fefferman-Stein inequality on such trees, as well as norm estimates related to sharp maximal functions and maximal functions. Another research direction is to investigate the boundedness of Riesz transforms and spectral multipliers of the flow Laplacian in Morrey spaces on weighted homogeneous trees, where the $L^p$ estimates for these operators on weighted homogeneous trees are already known.

The aim of this work is to study the Morrey spaces on $(\mathcal{V}, d, \mu)$. The structure of this paper is as follows: In Section 2, we review the definitions of weighted homogeneous trees and admissible trapezoids, examine their corresponding geometric properties, and introduce Morrey spaces and fractional maximal operators associated with admissible trapezoids. In Section 3, we define the preduals of Morrey spaces in terms of block spaces and investigate the boundedness of the maximal operators on these block spaces. Finally, we investigate the boundedness of both the maximal operator and the fractional maximal operator on Morrey spaces.

The symbol $\mathbb{N}$ denotes the set of all positive integers. The statement $A\lesssim B$ indicates that $A\leq CB$, where $C$ is any independent positive constant, and $A\approx B$ indicates that $A\lesssim B \lesssim A$. The characteristic function of a measurable set $E$ is denoted by $\chi_E$. For $1 \leq p \leq \infty$, $p'$ is the conjugate index of $p$, which satisfies the relation $\frac{1}{p} + \frac{1}{p'} = 1$.

2.   Definitions and preliminaries

2.1.   Weighted homogeneous trees

In this subsection, we first review the definition of the infinite homogeneous tree, as well as the distance $d$ and measure $\mu$ defined in this space.

Definition 2.1. ^[7] An infinite homogeneous tree of order $q+1$ is a graph $T = (\mathcal{V}, \mathcal{E})$ that satisfies the following properties:

(ⅰ) $T$ is connected and acyclic;

(ⅱ) Each vertex has exactly $q+1$ neighbors, $q \in \mathbb{N}$,

where $\mathcal{V}$ denotes the set of vertices and $\mathcal{E}$ denotes the set of edges. The distance $d(x, y)$ of $x, \; y\in\mathcal{V}$ is the length of the shortest path connecting $x$ and $y$.

Definition 2.2. ^[7] Let $T = (\mathcal{V}, \mathcal{E})$ be an infinite homogeneous tree, a doubly infinite geodesic $g$ in $T$ is a connected subset $g \subset \mathcal{V}$ such that

(ⅰ) For any element $v \in g$, there are precisely two neighbors of $v$ in $g$;

(ⅱ) For any two vertices $u$, $v \in g$, the shortest path joining $u$ and $v$ is contained within $g$.

Definition 2.3. ^[7] Define a mapping $F$: $g \rightarrow \mathbb{Z}$ such that

The level function $\ell$$: \mathcal{V} \rightarrow \mathbb{Z}$ is defined as

where $x'$ is the only vertex in $g$ for which

This implies choosing an orientation for $g$ and a unique origin $o\in g$, where $F(o) = 0$. In this way, a numbering system for vertices in $g$ is established.

Definition 2.4. ^[7] For any $x, y \in \mathcal{V}$, it is said that $y$ lies above $x$ or $x$ lies below $y$, if

Definition 2.5. ^[7] $T = (\mathcal{V}, \mathcal{E})$ is an infinite homogeneous tree of order $q+1$; Each $f$: $\mathcal{V} \to \mathbb{R}$ is a non-negative measurable function; Let $\mu$ be the measure on $\mathcal{V}$ such that

Remark 2.1. Based on the above, $\mu$ is a weighted counting measure in which a vertex's weight is only reliant on its level, and the weight associated with a certain level is given by $q$ times the weight of the level immediately below it.

Lemma 2.1. ^[8] Let $T = (\mathcal{V}, \mathcal{E})$ be an infinite homogeneous tree of order $q+1$, $x_0 \in \mathcal{V}$, and $r\in\mathbb{N}$. Consider the closed ball $B_r(x_0) = \{ x \in \mathcal{V} : d(x, x_0) \leq r \}$. Its measure is derived as

It is observed that the measures depend on the level of the center $x_0$ and increase exponentially with the radius $r$.

2.2.   Admissible trapezoids and Calderón-Zygmund sets

A weighted homogeneous tree $(\mathcal{V}, d, \mu)$ does not satisfy the doubling condition, so it is useful to introduce a suitable class of subsets of $\mathcal{V}$ called admissible trapezoids. Admissible trapezoids and Calderón-Zygmund sets are introduced in ^[7]. In this subsection, we review their definitions and related properties.

Definition 2.6. ^[7] A subset $R\subset\mathcal{V}$ is called an admissible trapezoid if it satisfies one of the following conditions:

(ⅰ) $R$ consists of just one vertex, i.e., $R = \{x_R\}$, where $x_R \in \mathcal{V};$

(ⅱ) There exists $x_R \in \mathcal{V}$ and $h(R) \in \mathbb{N}$ such that

We specify that in the first case $h(R) = 1$ and in the second case $h(R) = h$. Here $x_R$ is referred to as the root of the trapezoid. In both cases mentioned above, $h(R)$ is referred to as the height of the admissible trapezoid $R$ and coincides with the number of levels spanned by the admissible trapezoid $R$. The quantity $w(R) = q^{\ell(x_R)}$ is referred to as the width of the admissible trapezoid $R$. It follows that

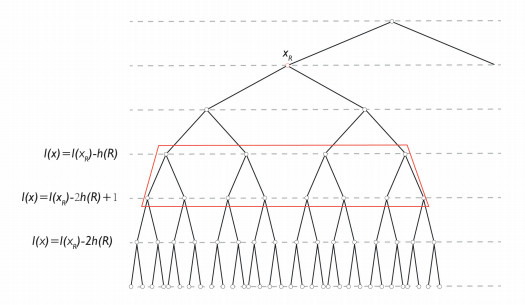
$\mathcal{R}$ is denoted as the set of all admissible trapezoids. The admissible trapezoid $R$ of height $h(R) = 2$ with $x_R$ as the root on a degree $q = 2$ weighted homogeneous tree, as shown in Figure 1.

Definition 2.7. ^[7] Let $R$ be an admissible trapezoid. Define its envelope $\widetilde{R}$ as follows:

(ⅰ) If $R$ consists of just one vertex, then $\widetilde{R} = R$;

(ⅱ) Otherwise,

The envelope of an admissible trapezoid is known as a Calderón-Zygmund set. We specify that $h(\widetilde{R}) = h(R).$ $\widetilde{\mathcal{R}}$ is the set of all Calderón-Zygmund sets. The geometric relationship between the admissible trapezoid $R$ and its envelope $\widetilde{R}$, as shown in Figure 2.

The measure of the set consisting of all points $x \in R$ such that $\ell(x) = \ell(x_R) - h_i$ is given by

Therefore, the measure of each level within the trapezoid $R$ is the same, and it is $q^{\ell (x_R)}$. By definition, it can also be obtained that the measure of each level of $\widetilde{R}$ is $q^{\ell (x_R)}$.

Lemma 2.2. ^[8] Take an admissible trapezoid $R$. Then it holds

Lemma 2.3. ^[8] Take two admissible trapezoids $R_1$ and $R_2$, if $R_1 \cap R_2 \neq \emptyset \mathit{\text{and}} w(R_1) \geq w(R_2),$ then

Lemma 2.4. ^[21] For any $R\in \mathcal{R}$ and its envelope $\widetilde{R}$, there exist three admissible trapezoids $S_1, S_2,$ and $S_3$ such that $\widetilde R \subset S_1 \cup S_2 \cup S_3$ and the following properties hold:

(ⅰ) $w(S_k) > w(R)$ for $k = 1, 2, 3;$

(ⅱ) $\mu(S_k) \leq 2q\mu(\widetilde{R})$ for $k = 1, 2, 3$.

In the following proposition, we will construct a covering of $\mathcal{V}$ using an increasing family of admissible trapezoids.

Proposition 2.1. There exists a family of admissible trapezoids ${\{R_n\}}_{n = 0}^{\infty}$ such that $R_n \subset R_{n+1}$ and $\bigcup_n R_n = \mathcal{V}$.

Proof. Consider the family ${\{R_n\}}_{n = 0}^{\infty}$ where

● $R_0$ is an admissible trapezoid with the root at $x_0$ and height $h = 1$. Here, $x_0$ represents the unique vertex in the double undirected geodesic $g$ such that $\ell(o) = 0.$

● For any $n \geq 1$, $R_n$ represents the admissible trapezoid with a root node $x_n$. Here, $x_n$ serves as the grandfather node of $x_{n-1}$, positioned such that $x_n$ lies above $x_{n-1}$. Additionally, it satisfies the conditions $\ell(x_n) - \ell(x_{n-1}) = 3$ and height $h(R_n) - h(R_{n-1}) = 2$. Then there is $h(R_n) = 2n+1.$

Firstly, we demonstrate that $R_n \subset R_{n+1}$. Take $x\in R_n$. According to the definition, if $x$ is below $x_n$, then it also lies below $x_{n+1}$ by construction. Furthermore, we have $\ell(x_{n+1}) - \ell(x) = \ell(x_n) + 3 - \ell(x)$, and it follows that

Therefore, we can conclude that $x \in R_{n+1}$.

To demonstrate that $\bigcup_n R_n = \mathcal{V}$, let us consider an element $x \in \mathcal{V}$. We denote by $k$ the smallest index such that $x$ lies below $x_k$ (and so $x$ lies below $x_j$ for all $j \geq k$) and set $\ell(x_k) - \ell(x) = d$. We are looking for an index $j \geq k$ such that $x \in R_j$, which can be expressed as

Note that $\ell(x_j) - \ell(x) = \ell(x_j) - \ell(x_k) + \ell(x_k) - \ell(x) = 3(j - k) + d$, which implies

Therefore, it is sufficient to choose $j \geq \max \left\{ k, d-3k-1, 1-d+3k \right\}$.

□

2.3.   Maximal operator and fractional maximal operator

In this subsection, we review the definition of the maximal operator and define the fractional maximal operator associated with the family of admissible trapezoids.

Definition 2.8. ^[8] Given $f$: $\mathcal{V} \to \mathbb{R}$, the maximal operator $M$ is defined as follows:

where the supremum is taken over all admissible trapezoids $R$ containing $x$.

Definition 2.9. Let $0 < \alpha < 1$. Given $f$: $\mathcal{V} \to \mathbb{R}$, we define the fractional maximal operator $M_\alpha$ as follows:

where the supremum is taken over all admissible trapezoids $R$ containing $x$.

Lemma 2.5. ^[8] The maximal operator $M$ is of weak type $(1, 1)$. That is, for any $f \in L^1(\mathcal{V})$ and $\beta>0$,

Utilizing Marcinkiewicz interpolation theorem on measure spaces ^[22], it can be demonstrated that $M$ is $(p, p)$ bounded, where $1 < p < \infty$.

2.4.   Morrey spaces

In this subsection, we introduced two types of Morrey spaces. One is related to admissible trapezoids, and the other is associated with Calderón-Zygmund sets. Subsequently, we proved the equivalence of the norms of these two Morrey spaces. We also explored some properties of Morrey spaces. Let $L^p_{\text{loc}}(\mathcal{V})$ denote the set of all functions $f$ that satisfy $\int_R |f(x)|^p \, d\mu(x) < \infty$ for any $R\in \mathcal{R}$.

Definition 2.10. Let $1 \leq p, \lambda\leq \infty$. The Morrey spaces are

where

Remark 2.2. If $p = \lambda < \infty$, then $\mathcal M^\lambda_p(\mathcal{V}) = L^p(\mathcal{V}).$ When $p\leq\lambda = \infty$, $\mathcal M^\lambda_p(\mathcal{V}) = L^{\infty}(\mathcal{V})$. Additionally, if $\lambda<p$, then $\mathcal{M}_p^\lambda(\mathcal{V}) = \{0\}.$ Therefore, we will only consider the case where $1\leq p \leq \lambda < \infty$.

Definition 2.11. Let $1 \leq p \leq \lambda< \infty$. The Morrey spaces are

where

Proposition 2.2. Let $1 \leq p \leq \lambda< \infty$ and $f \in L^p_{\text{loc}}(\mathcal{V})$. Then,

Proof. According to Lemma 2.2, it is clear that

For the opposite estimate, by Lemma 2.4, we obtain

where $S_k$ is the admissible trapezoid, $k = 1, 2, 3.$ □

Lemma 2.6. For any $1\leq p_1\leq p_2 < \infty$, $q \in \mathbb{N}$,

where $f : \mathcal{V} \to \mathbb{R}$ and $R\in\mathcal{R}$.

Proof. Let $1 \leq p_1 \leq p_2 < \infty$ and $q \in \mathbb{N}$. According to Hölder's inequality, we have

Further simplification gives

This concludes the proof. □

Proposition 2.3. If $1 \leq p_1 \leq p_2\leq \lambda < \infty$. Then $\mathcal M^\lambda_{p_2}(\mathcal{V})\subset\mathcal M^\lambda_{p_1}(\mathcal{V})$ with

for any $f\in{\mathcal M}^\lambda_{p_2}(\mathcal{V}).$

Lemma 2.7. Let $1 \leq p \leq \lambda < \infty$. Then, for any $R_0\in\mathcal{R}$, we have $\chi_{R_0}\in{\mathcal M}^\lambda_{p}(\mathcal{V})$.

Proof. For any $R \in \mathcal{R}$, we will consider the following two distinct cases.

If $\mu(R) > 1$, we can derive

If $\mu(R)\leq1$, it can be inferred that

Our proof is complete. □

3.   Main results

3.1.   The predual spaces of Morrey spaces

The predual spaces of classical Morrey spaces, weighted product Morrey spaces ^[13], and non-double Morrey spaces ^[15] are all block Spaces. In this subsection, we naturally define block spaces that are actually the predual spaces of ${{\mathcal M}^\lambda_{p}(\mathcal{V})}$. Furthermore, it is shown that the maximal operator $M$ is bounded on the block spaces.

Definition 3.1. Suppose $1 \leq \lambda'\leq p' < \infty$; A measurable function $b$ is classified as a $(\lambda', p')$-block if it holds that $\mathrm{supp} b \subset R$, $R\in\mathcal{R}$, and

Define the block space $\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$ as

The block space $\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$ is equipped with the following norm:

We call $\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$ the block space associated with $L^{p'}(\mathcal V)$.

Theorem 3.1. Suppose $1< p\leq\lambda<\infty$, $\frac{1}{p}+\frac{1}{p^{\prime}} = 1$, then we have

This indicates that $\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$ represents the predual space of $\mathcal{M}^{\lambda}_p(\mathcal{V})$.

Proof. Let $b$ be a $(\lambda^\prime, p^\prime)$-block, supported on an admissible trapezoid $R$. For any $f\in{{\mathcal M}^\lambda_{p}(\mathcal{V})}$, the Hölder's inequality of weighted homogeneous tree yields

Therefore, for any $g = \sum_{k = 1}^{\infty} \lambda_k b_k \in \mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$, we derive the following inequality:

Consequently, it follows that ${{\mathcal M}^\lambda_{p}}(\mathcal{V})\hookrightarrow({\mathfrak{B}^{\lambda'}_{p'}}(\mathcal{V}))^*$.

To prove the embedding in the reverse case, we only need to show that any element in $({\mathfrak{B}^{\lambda'}_{p'}}(\mathcal{V}))^*$ can be regarded as a function of ${{\mathcal M}^\lambda_{p}}(\mathcal{V})$.

First, we prove that any bounded linear functional on ${\mathfrak{B}^{\lambda'}_{p'}}(\mathcal{V})$ can be represented by a function from $L_\text{loc}^p(\mathcal{V})$. For $g\in L_\text{loc}^{p^{\prime}}(\mathcal{V})$,

Then G is a $(\lambda', p')$-block. According to the definition of block space, for any $(\lambda', p')$-block $b$, we have $\|b\|_{\mathfrak{B}^{\lambda'}_{p'}}\leq1$, as a result

That means,

In accordance with formula (3.3), $L\in(\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V}))^*$,

For $R\in \mathcal{R}$, consider the set $X = \{ g_{\chi_{R}} : g \in L^{p^\prime}(\mathcal{V}) \},$ which defines $X$ as a subspace of $L^{p^\prime}(\mathcal{V})$. For $R\in \mathcal{R}$ and $L \in (\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V}))^*$, we can define a linear functional $l: X\to\mathbb{C}$ by

where $h = g_{\chi_{R}}$ is an element of $X$ and g belongs to $L^{p^\prime}(\mathcal{V})$.

In accordance with (3.4), it is established that $l$ is bounded on $X$. The Hahn-Banach theorem guarantees the extension of $l$ as a member of ${(L^{p^\prime}(\mathcal{V}))}^*$. The duality $(L^{p^\prime}(\mathcal{V}))^* = L^{p}(\mathcal{V})$ yields a function $f_R \in L^{p}(\mathcal{V})$ such that

Without loss of generality, we assume that $\text {supp}\, f_ R\subset R$. Based on Proposition 2.1, let $\bigcup_n R_n = \mathcal{V}$, such that $R\subset R_i \subset R_{i+1}$, define $f(x) = f_{R_i}(x)$ if $x\in R_i$, which makes sense since

Consequently, for $x \in R \subset R_i \subset R_{i+1}$, it follows that $f_{R_i} = f_{R_{i+1}}$. Furthermore, there exists a unique measurable function $f = f_R$ defined on any set $R$.

Next, we continue to prove that $f\in{{\mathcal M}^\lambda_{p}}(\mathcal{V})$. Let's consider a set $R$ and an index $j$, such that $R \subset R_j$. For $h\in L^{p^{\prime}}(\mathcal{V})$,

is a $(\lambda', p')$-block. In the light of (3.2), we have $\|H\|_{\mathfrak{B}^{\lambda\prime}_{p\prime}}\leq1$, which implies:

We obtain

We can conclude that $L_f = L$ and $(\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V}))^* \hookrightarrow {{\mathcal M}^\lambda_{p}}(\mathcal{V})$. That completes the proof. □

Corollary 3.1. Let $1< p\leq\lambda<\infty$. Then $f\in{{\mathcal M}^\lambda_{p}}(\mathcal{V})$ if and only if for all $g\in\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$, it holds that

Moreover, for all $f\in{{\mathcal M}^\lambda_{p}}(\mathcal{V})$,

Proposition 3.1. Let $1 \leq \lambda'\leq p' < \infty$. If $f \in$ $\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$ and $|h| \leq |f|$, then $h\in$ $\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$.

Proof. Given $f \in \mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$, for any $\epsilon > 0$, there exists a family of $(\lambda', p')$-blocks $\{b_i\}_{i = 1}^{\infty}$ and a family of scalars $\{\lambda_i\}_{i = 1}^{\infty}$ such that $f = \sum_{i = 1}^{\infty} \lambda_i b_i$ and

We express $g = \sum_{i = 1}^{\infty} \lambda_i c_i$, where

Under the condition that $|h| \leq |f|$, the sequence $\{c_i\}_{i = 1}^{\infty}$ is a set of $(\lambda', p')$-blocks. Consequently, it can be inferred that $h \in$ $\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$. Since $\epsilon$ is arbitrary, we can conclude that $\|h\|_{\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})}\leq\|f\|_{\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})}$. □

Theorem 3.2. Let $1 < \lambda'\leq p' < \infty$. Then, $\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})\subset L_{\text{loc}}(\mathcal{V})$ and $\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$is a Banach space.

Proof. By utilizing Lemma 2.7, it follows that $\chi_R \in {\mathcal M}^\lambda_{p}(\mathcal{V})$ for all $R \in \mathcal{R}$. Furthermore, Theorem 3.1 ensures that $\chi_R \in (\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V}))^*$. According to the norm conjugate formula (3.1), it yields

for any $h \in \mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$. This means that $\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V}) \hookrightarrow L_{\text{loc}}(\mathcal{V})$.

To prove $\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$ is a banach space, take $h_i\in\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$, $i\in\mathbb{N}$ satisfying

For any $\epsilon > 0$, there exists a positive integer $N$ such that for all integers $n > N$, it holds that

In light of (3.5), for any $R \in \mathcal{R}$, it follows that

Consequently, the function $h = \sum_{i = 1}^{\infty}h_i$ is well-defined as a Lebesgue measurable function and belongs to $L_{\text {loc}}(\mathcal V)$.

Our next demonstration illustrates that $h = \sum_{i = 1}^{\infty} h_i$ belongs to $\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$. Based on the definition of $\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$, for any $\epsilon > 0$, we have that

where $h_{k, i}$ with $i, k \in \mathbb{N}$ are $(\lambda', p')$-blocks, along with

In addition, for any $1 \leq i \leq N$, there exists a $N_i \in \mathbb{N}$ such that

As a result, for any $R\in\mathcal{R}$, we can deduce that

Combining (3.5) and (3.6) with (3.7) yields that

Thus, $\sum_{i = 1}^{\infty} \sum_{k = 1}^{\infty} \lambda_{k, i} h_{k, i}$ converges to $h$ in $L_{\text{loc}}(\mathcal V)$. As a result, $\sum_{i = 1}^{\infty} \sum_{k = 1}^{\infty}\lambda_{k, i} h_{k, i}$ converges to $h$ in the sense of local measures. Therefore, there exists a subsequence $\left\{ \sum_{i = 1}^{N}\sum_{k = 1}^{M}\lambda_{k, i}{h}_{k, i}\right\}_{N, M}$ which converges to $h$ a.e. Furthermore, $\lambda_{k, i}\text{ with }i, k \in \mathbb{N} \text{ satisfies }$

$\sum_{i = 1}^{\infty} h_i$ converges to $h$ in $\mathfrak{B}^{\lambda'}_{p'}(\mathcal{V})$. As a result, ${\mathfrak{B}_{p'}^{\lambda'}}(\mathcal{V})$ is a Banach space. □

Theorem 3.3. Let $1 < \lambda^\prime \leq {p^\prime} < \infty$ and $R\in \mathcal{R}$. Then, the maximal operator $M$ is bounded on the space ${\mathfrak{B}_{p'}^{\lambda'}}(\mathcal{V})$.

In order to prove Theorem 3.3, it is only necessary to prove the following.

Lemma 3.1. Suppose $b$ is a $(\lambda^{\prime}, p^{\prime})$-block and $R$, $S\in\mathcal{R}$. Then, there exists a sequence ${S_{l, m}} \in \mathcal{R}$, where $l \in \mathbb{N}$ and $m = 1, 2, \cdots, N$, along with a sequence of measurable functions ${h_{l, m}}$ that possess the following properties.

(ⅰ) The pointwise estimate $Mb(x) \leq \sum_{l \in \mathbb{N}} \sum_{m = 1}^{N} h_{l, m}(x), \; x \in \mathcal{V}\setminus \widetilde {R}$ holds.

(ⅱ) $\mu \left(\widetilde{S}_{l, m} \right) \sim 2^l \, \mu \left(R \right),$ where the implicit constants do not depend on $R$ and $l$.

(ⅲ) $0 \leq h_{l, m}(x) \leq \frac{\|b\|_1}{2^{l-1} \mu(R) } \chi_{\widetilde{S}_{l, m}} (x) \; \text{for } x \in \mathcal{V}.$

In particular, there exists $C = C_{\lambda, p}$ so that, for every $(\lambda^{\prime}, p^{\prime})$-block b,

Indeed, upon accepting Lemma 3.1, we can establish Theorem 3.3 through the following approach. First, assume that $f\in{\mathfrak{B}_{p'}^{\lambda'}}(\mathcal{V})$. Consequently, we can identify a sequence of $(\lambda^{\prime}, p^{\prime})$-block denoted as $\{b_j\}_{j \in \mathbb{N}}$ and a corresponding sequence of coefficients $\{\lambda_j\}_{j \in \mathbb{N}}$, such that

By Lemma 3.1, the function $g = \sum_{j = 1}^{\infty} |\lambda_j| Mb_j$ satisfies

According to Proposition 3.1, we conclude that

Proof of Lemma 3.1.

Proof. First construct the desired admissible trapezoid and functions. Let $x \in \mathcal{V} \setminus \widetilde{R}$ and $S, R \in \mathcal{R}$ such that $w(S) > w(R)$, with the condition that $\mathrm{supp} b \subset R$. If $S \cap R \neq \emptyset$, then $R \subset \widetilde{S}$. Therefore, the following can be obtained:

where $x \in \mathcal{V}\setminus \widetilde{R}$. Set

for $l \in \mathbb{N}$. Since $\sup_{S \in S_l}\mu(s)<\infty$, we can apply [23, Lemma 4] to get the existence of sets $S_{l, 1}, \ldots, S_{l, N} \in S_{l}$, such that

holds, where $N$ is independent of $l$. We define

Then we obtain

for $x \in \mathcal{V}$. Consequently, the decomposition stated in Lemma 3.1 is obtained.

We decomposed $Mb$ into two parts by $\widetilde R$, that is, $Mb = B_{1} + B_{2}$, where $B_ {1} = \chi_{\widetilde R} Mb$ and $B_{2} = \chi_{\mathcal{V} \setminus {\widetilde R}} Mb$. This means that the estimate is divided into $\| B_ {1}\|_{\mathfrak{B}_{p'}^{\lambda'}}$ and $\| B_ {2}\|_{\mathfrak{B}_{p'}^{\lambda'}}$ estimates. Based on Lemma 2.5, we know that the operator $M$ is bounded on $L^{p'}(\mathcal{V})$. This implies that

Here, the operator norm is defined as $C_0 : = \|M\|_{L^{p^\prime} \longrightarrow L^{p^\prime}}.$ Then we see that $\frac{B_1}{C_0}$ is a $(\lambda^{\prime}, p^{\prime})$-block. Therefore, the estimate of $\| B_ {1}\|_{\mathfrak{B}_{p'}^{\lambda'}}$ is deemed valid. By utilizing Hölder's inequality, we can discern that

Thus, we deduce that $\frac{2^{{\frac{l-1}{\lambda}}}h_{l, m}}{C}$ constitutes a $(\lambda^\prime, p^\prime)$-block. Given the pointwise estimate $\left| B_2(x) \right| \leq \sum_{l \in \mathbb{N}} \sum_{m = 1}^{N} h_{l, m}(x)$, it follows that $B_2$ belongs to the space ${\mathfrak{B}_{p'}^{\lambda'}}(\mathcal{V})$, with its norm defined by an absolute constant. □

3.2.   Boundedness of maximal operator and fractional maximal operator on Morrey spaces

In this subsection, we focus primarily on the maximal operator $M$ and the fractional maximal operator $M_\alpha$. We present proof of the boundedness of these operators in Morrey spaces. We select an addmissible trapezoid $R$ and decompose the function space based on its envelope $\widetilde{R}$.

Theorem 3.4. Let $1 < p \leq \lambda < \infty$, for all $f\in{{\mathcal M}^\lambda_{p}(\mathcal{V})}$, it holds that $Mf\in{{\mathcal M}^\lambda_{p}(\mathcal{V})}$, and there exists a constant $C > 0$ independent of $f$ such that

Proof. We just need to demonstrate that

according to the definition. Write $f(x) = f_1(x)+f_2(x)$, where $f_1 = f\chi_{\widetilde{R}}$ and $f_2 = f\chi _{\mathcal{V}\backslash {\widetilde{R}}}$, we deduce that

For the first part $I$, by expanding the integral domain and taking advantage of the boundedness of $M$ on $L^p(\mathcal{V})$, we can infer that

Based on Lemmas 2.2 and 2.4, we obtain

and the proof of the first part is now complete.

For the second part $II$, we estimate

When $(\mathcal{V}\backslash\widetilde{R}) \cap S = \emptyset$ or $R\cap S = \emptyset$, the norm result naturally holds. Let's discuss the alternative case in which $(\mathcal{V}\backslash\widetilde{R}) \cap S\neq \emptyset$ and $R\cap S\neq \emptyset$. Since the measure of every level on $R$ and $\widetilde{R}$ is the same as that of $q^{\ell(x_R)}$, we have $q^{\ell(x_S)} > q^{\ell(x_R)},$ that is, $w(S) > w(R).$ With the help of Lemma 2.3, it can be deduced that $R\subset\widetilde{S}$. Therefore,

it follows that

By utilizing Hölder's inequality and Lemma 2.2, we obtain

and all the proofs have been completed. □

Remark 3.1. In ^[19], H. Gunawan and C. Schwanke investigated the boundedness of maximal operators on Morrey spaces over the set of $\mathbb{Z}^d$ ($d = 1, 2, \ldots$). However, it is noteworthy that in the context of our discrete tree, when the degree of the tree is 2, it corresponds to their case of $\mathbb{Z}$, i.e., the results for $d = 1$. Therefore, our results are more general in the one-dimensional setting.

Lemma 3.2. If $1 < p\leq\lambda < \infty$, $0 < \alpha < 1$ and $\lambda < \frac{1}{\alpha}$, then

for every $f\in{\mathcal M}^\lambda_{p}(\mathcal{V}).$

Proof. For each $x\in \mathcal{V}$, we denote $t_x = \| f \|^\lambda _{{\mathcal M}^\lambda_{p}}/Mf(x)^\lambda$. We divide the estimate into two parts, namely

For $L$, we have that

For $LL$, if $\mu(R) > t x$, there exists $i \in \mathbb{N}$ such that $2^{i-1} t_x \leq \mu(R) \leq 2^i t_x.$ Applying Hölder's inequality, we obtain

According to $1 < \lambda$ and $\lambda < \frac{1}{\alpha}$, it can be inferred that

The proof of the lemma is completed. □

Theorem 3.5. If $1 < s\leq r < \infty$, $1 < p \leq \lambda < \infty$, $\alpha = \frac{1}{\lambda}-\frac{1}{r}$ and $\frac{p}{\lambda} = \frac{s}{r}$, then the operator $M_{\alpha}$ is bounded from ${\mathcal M}^\lambda_{p}(\mathcal{V})$ to ${\mathcal M}^r_{s}(\mathcal{V})$.

Proof. We write

by Lemma 3.2, we obtain

since $\alpha = \frac{1}{\lambda}-\frac{1}{r}$ and $\frac{p}{\lambda} = \frac{s}{r}.$ □

4.   Conclusions

This paper defines the Morrey space $\mathcal{M}^\lambda_p(\mathcal{V})$ associated with admissible trapezoids on weighted homogeneous trees and investigates the properties of these spaces. We also study the boundedness of the maximal operator and fractional maximal operator on the Morrey space $\mathcal{M}^\lambda_p(\mathcal{V})$. By constructing the predual space of Morrey space $\mathcal{M}^\lambda_p(\mathcal{V})$, we reveal their structure and analyze their applications in function spaces and operator theory. Our study extends the theory of classical Morrey spaces and applies it to metric measure spaces that do not satisfy the doubling condition.

Author contributions

Xiaoyu Qian: Writing-original draft, investigation, formal analysis; Jiang Zhou: Writing-review and editing, investigation. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors want to express their sincere thanks to the editors and referees for the valuable remarks and suggestions. This work was supported by the National Natural Science Foundation of China (No.12461021).

Conflict of interest

The authors declare that there is no conflicts of interest.