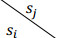Statistical inference of an $\mathit{\alpha }$-quantile past lifetime function with applications

1.   Introduction

High-quality decisions rely on obtained information. When a decision-maker makes a so-called here-and-now (HN) decision, it is necessary to consider the uncertain parameter that reveals in the future, such as market demand in the business setting, or the scale of the disaster in humanitarian relief. Stochastic programming (SP) is an often-used framework for addressing such problems. The distribution of the uncertainty considered by the decision-maker is an approximate representation of the true status. In this setting, to improve decision quality, a possible way is to acquire extra information. However, the information obtained is usually imperfect ^[1,2]. To evaluate the value of the information, a Bayesian calculation is usually required to assess posteriori probabilities of uncertainties ^[3,4,5].

In many applications, however, the probabilistic structure used in the Bayesian update might be unavailable due to the following two reasons.

First, assessing likelihood functions is difficult and uncommon ^[6], as it requires abundant historical data ^[7]. However, data scarcity exists in a wide range of industries ^[8,9,10,11]. For example, during the design and production stage of a new product, information on future demand is usually unavailable. As a consequence, the planning decisions will be made based on limited data. Moreover, in the disaster setting, a serious natural disaster in a given area seldom actually happens in practice. For instance, only seven major earthquakes occurred in the Longmengshan Fault in China since 1933 ^[11]. As a result, the data that disaster preparedness depends on is also scarce. Consequently, many applications are facing the challenge of data scarcity, which makes the classical Bayesian approach inapplicable.

Second, in the setting of exogenous information acquisition, information providers, e.g., consulting firms, may have rich information; while decision-makers, who are in an information disadvantage position, usually fail to get exact probabilistic interdependent relationships. Accordingly, it is a problematic and cumbersome task for decision-makers to evaluate the value of the additional information with the help of Bayes' theorem in such a setting.

Thus, it is necessary to consider the challenge of data scarcity in the interactions between stochastic optimization and information management. The question is how to evaluate and acquire imperfect information for decision-makers using SP in the scarce-data setting.

In the stochastic environment, to evaluate the value of information, a classical way is to focus on the expected value of information (EVOI), which integrates all economic results under the possible final realizations of the uncertainties. As is described before, the posteriori probabilities of the realizations can be calculated by the Bayesian approach under the given likelihood functions. Then, the EVOI can be measured by the expected added value from the additional information, which is the difference between the benefits under the priori and posteriori probabilities. Given the fact that the information acquired may be either accurate or inaccurate, the EVOI is further referred to as the so-called Expected Value of Perfect Information (EVPI) or Expected Value of Imperfect Information (EVII), respectively. The former also provides an upper bound on how much a company could pay for any information acquisition activity ^[3,12,13]. The latter can be used to measure the value of imperfect information ^[1,14] and has drawn lots of research attention ^[15,16,17] in the Bayesian context.

Unlike the aforementioned methods, the model established in this paper focuses on the scarce-data environment where the required probabilistic structure for the Bayesian model is unavailable. Moreover, the following approaches are taken to mitigate the negative influence of data scarcity on decision-making quality.

First, add flexibility to decision-making procedures to improve decision-making outcomes. To be specific, the two-stage optimization approach is incorporated into our study, in which decisions are composed of HN and recourse actions. The former should be determined now, while the latter can be given when uncertain parameters reveal their values. By doing so, much better results can be generated compared to the static decision-making way ^[18]. The two-stage SP model is thus adopted here.

Moreover, acquiring exogenous information is another efficient way to meet the scarce-data challenge. In such a setting, an information acquisition game involving an information provider is designed. The problem is whether it is beneficial to motivate the provider to enhance information accuracy, especially when the enhancement is costly. Does an optimal coordination mechanism exist?

Hence, this paper concentrates on the information evaluation and acquisition for decision-makers who adopt two-stage SP. The EVII evaluation and costly information acquisition game have been extensively studied in previous works, and most assume the probabilistic interdependent relationship is available. However, those studies have actually left the questions mentioned above unexplored. To fill this gap, we perform the following research.

First, a robust way is proposed to identify the worst probabilistic structure. Specifically, to characterize the information imperfectness, a budget value is introduced, i.e., the information inaccuracy ratio (IIR), which can be easily obtained from limited historical observations. Then, under the ambiguity set constrained by the budget value, a robust way is adopted to replace the Bayesian calculation, and thus, the classic wait-and-see (WS) solution in two-stage SP is extended to the robust setting. The problem is formulated as a max-min-min model with a bi-level structure and three ways are developed to address the model optimally. Thus, the EVII can be measured by the difference between the value of the robust WS and the expected value with the priori distribution of underlying uncertainties only. Now that the EVII is calculated, when the imperfect additional information is worthless can also be identified.

Second, a costly information acquisition game is studied, in which the decision-maker, who chooses the two-stage SP, can acquire an imperfect forecast from an exogenous information provider. To model this issue, a Stackelberg game is proposed and a linear compensation contract is designed to realize the global optimum. Finally, we show the application of our study in a two-stage shipment problem.

As such, our study differs from the previous studies in both the problems addressed and the approach used. More specifically, this paper focuses on the two-stage SP with imperfect information update and the costly information acquisition cooperation in the scarce-data setting, which are involved in a broad family of uncertain optimization and decision-making problems. In terms of approach, the classical Bayesian structure is inapplicable due to the unavailability of likelihood functions. Thus, a novel and robust model is created in this paper and under the model, several approaches are proposed to evaluate the EVII by identifying the worst Bayesian structure.

The remainder of the paper is organized as follows. Section 2 reviews the relevant literature and summarizes the contributions. Section 3 focuses on the EVII in the two-stage SP, including its assumption, definition, and computation. Then, the costly information acquisition game is studied in Section 4. Section 5 applies the proposed approach to a two-stage production and shipment problem. Finally, Section 6 contains some concluding remarks. All the proofs are provided in the appendix.

2.   Literature review

This paper connects the studies on the EVOI and costly information acquisition game. In this section, we briefly discuss the literature related to these two streams.

2.1.   Evaluation of EVOI

Here, we focus on the EVOI in terms of the economic consequences of decision-making. To evaluate the EVOI, one of the most well-known metrics is EVPI, which measures the expected gain based on perfect information ^[13]. It has found widespread applications, e.g., in manufacturing ^[19], in supply chain risk mitigation ^[20], and in power planning ^[21].

Nevertheless, in practice, it is impossible to get perfect information ^[1,2]. Thus, an alternative metric, i.e., the EVII, is developed. Howard ^[3] is one of the pioneers who apply the Bayes-based approach in estimating the EVOI. The imperfectness of the information system can be captured by the likelihood functions between the state of nature and additional information. After that, existing works study the combination of decision analysis and EVII in various settings. A few papers focus on specific application areas, such as medical health ^[2], oil and gas ^[6], portfolio ^[22], and newsvendor problems ^[23]. In addition, some studies consider different problem settings, such as multiple information sources ^[14,24], and multicriteria analysis ^[15,16,25]. Furthermore, in a Bayesian update, the additional information can take the forms of point or probabilistic estimates ^[26], which also draws corresponding research ^[27,28]. These works incorporate the EVII into the decision analysis context and evaluate it by economic impacts. However, in the OR context, the literature is limited and some works incorporate Bayesian update into two-stage or multi-stage SP. For instance, Morton et al. ^[29] combine Bayesian prediction and two-stage SP to address uncertain up-times of manufacturing equipment and uncertain production rates in an employee scheduling problem. Dowson et al. ^[30] design a multi-stage SP formulation to incorporate belief states, which can be captured by a Bayesian update.

Unlike the previous works, this paper focuses on the scarce-data challenge, in which the probabilistic structure used in information update might be unavailable. To address this issue, the point estimation way is applicable here and a robust approach is developed to handle the uncertain information update in the two-stage SP setting. Up to now, far too little attention has been paid to this issue.

2.2.   Costly information acquisition game

Our work is also related to the costly information acquisition game, in which most studies focus on the applications for auction or supply chain problems.

Regarding the auction, previous works consider that bidders have no or limited information about their valuations for items sold before the auction begins, and they can determine whether to implement costly information acquisition or not before or during the auction. For example, Compte and Jehiel ^[31] consider the costly information acquisition in an ascending price auction. The bidder acquires his valuation information during the auction at a known cost. Miettinen ^[32] studies a similar problem in a Dutch auction. Azevedo et al. ^[33] design a channel auction that combines English and Dutch auctions. It allows bidders to access the information by incurring a cost. Golrezaei and Nazerzadeh ^[34] design a two-stage mechanism in which the auctioneer can strategically control the information access based on a second-price auction. In these studies, the bidders can refine their valuations through information acquisition.

Moreover, since information is a crucial driver of supply chain performance improvement, there has been a growing body of literature that quantifies the EVOI. Some of them take the costly information acquisition activity into account. For instance, Fu and Zhu ^[35] focus on a two-tier supply chain consisting of a supplier and a buyer with the consideration of quantity discount, buy-back, and revenue-sharing contracts. During the implementation of the contracts, the buyer can acquire endogenous demand information with a cost. Li et al. ^[36] concentrate on upstream firms' information acquisition activities. Differing from these works, Fu et al. ^[37] focus on another market structure composed of two competing firms. Both firms can determine their production quantities with a costly forecast. These papers have all taken uncertain demand into account. Quality information, which can influence market demand, has also drawn some research in recent years ^[38,39].

In summary, the aforementioned works have studied the trade-off between the acquisition cost and the EVOI obtained within auction or supply chain operations, in which Bayesian calculations are performed based on the probabilistic structure of information. In other words, the challenge of data scarcity is ignored. In such a context, a two-stage decision-making way can bring better performance ^[18]. However, how to incorporate the two-stage way into the costly information acquisition game remains unexplored.

2.3.   Our contributions

Based on the aforementioned literature review, the contribution of this paper is twofold.

(ⅰ) Focus on a two-stage SP with imperfect information update and study the EVII in the scarce-data setting, which is ignored in previous works. We develop a novel and robust model to evaluate the WS value, utilizing only an IIR parameter instead of a complicated probabilistic structure. Three ways are taken to address the intractability of the proposed model, including numerical, analytical, and equivalent reformulation, which are suitable for different settings.

(ⅱ) Furthermore, optimization and information management are two significant challenges to many real-world problems. Our study takes the two-stage SP and information quality improvement into account and sheds light on their interactions by developing a costly information acquisition game. Moreover, a win-win coordination mechanism is designed for the game. To the best of our knowledge, no similar work has been done before.

3.   The EVII in two-stage SP

This section first reviews the general formulation of the two-stage SP and the well-known EVPI concept. Second, the robust WS in the imperfect information setting is proposed and a bi-level model is developed to evaluate the robust WS value. Finally, three approaches are designed to calculate the model and then the EVII is obtained in a robust setting.

Before that, the abbreviations, sets, parameters, and variables used in the model formulation, including the evaluation of the EVII and the costly information acquisition game, are given below (see Table 1).

3.1.   Basic concepts in the perfect information setting

Consider a two-stage linear SP, in which HN decisions $x$($\in {\mathbb{R}}^{{n}_{1}}$ or ${\mathbb{Z}}^{{n}_{1}}$) should be determined before uncertain parameters reveal their values, while recourse decisions $y$($\in {\mathbb{R}}^{{n}_{2}}$ or ${\mathbb{Z}}^{{n}_{2}}$) are dependent on $x$ and the realization of the parameters. Let S be the set of scenarios describing the underlying uncertainties and $s(\in S)$ be one realization among the scenarios.

Thus, the objective of the two-stage SP, a.k.a., recourse problem (RP), is to minimize the total cost of two stages, in which the second-stage recourse cost is an expected value under a set of discrete scenarios:

where $X$ is the feasible space of $x$, and $Y(x, s)$ is the feasible space of $y$ defined by the given $x$ and realization $s$. For $y$ and coefficient $q$ are scenario-dependent, denote them as $y\left(s\right)$ and $q\left(s\right)$, respectively. $c\in {\mathbb{R}}^{{n}_{1}}$, $q\in {\mathbb{R}}^{{n}_{2}}$. The RP value gives the expected performance without additional information.

Moreover, Madansky ^[40] introduces WS value. It is an expected value that can be calculated by first acquiring the perfect information and then making the best decision:

where both the HN decisions and recourse decisions are given based on the perfect information $s$. Thus, the WS is an expected value of all possible $s$.

Therefore, the EVPI is, by definition, the difference between the WS and RP, namely,

This metric also measures the upper bound of the cost of acquiring complete (and accurate) information ^[41].

3.2.   The WS value in the imperfect information setting

In this section, the WS value is extended to the imperfect information setting and a robust formulation is developed to address data scarcity.

3.2.1.   The basic explanations

Begin with the description of information inaccuracy. Specifically, consider that the decision-maker has knowledge about the distribution of scenarios, but is usually unsure which one will happen. The decision-maker can learn the future status by a forecast; however, the information obtained is usually inaccurate.

To formulate the case, let ${s}^{*}(\in S)$ be the scenario that will happen in the future, but the point forecast is ${s}_{i}(\in S)$. The probability of the corresponding misinformation is denoted as ${\lambda }_{i}$($\in \left[\mathrm{0, 1}\right]$), and thus, the total inaccurate probability is ${\sum }_{{s}_{i}\in S, {s}_{i}\ne {s}^{*}}{\lambda }_{i}$. Define the IIR, denoted as $\mathrm{\Gamma }$, which is the upper bound of the total inaccurate probability. The exact value of ${\lambda }_{i}$ is hard to obtain. In this case, assume $\mathrm{\Gamma }$ is available to the decision-maker since historical inaccurate forecasts can be observed even the data is scarce. Estimate it by the proportion of the number of inaccurate forecasts to the total number of forecasts. Hence, we have:

Then, evaluate the EVII by estimating the expected gain of imperfect additional information. As is discussed before, the expected benefit without additional information is the RP shown in (1). Thus, the key is to give the WS value in the imperfect information setting.

Obviously, in the perfect information setting, the benefit of the information can be evaluated by making the HN and recourse decisions based on the perfect information. The WS value in such a setting can be obtained by (2). However, when information is imperfect, the forecast and the final scenarios are usually different. In such a setting, decision-makers will of course adjust recourse decisions according to the realization. Thus, the WS value can be obtained by first making the optimal HN decisions with the forecasting scenario and then by making the best recourse decisions with the realization. In this context, the calculation of the two-stage decisions relies on two sequential optimization problems. Next, formulate the WS value and incorporate the information inaccuracy into the evaluation.

3.2.2.   Formulation

Based on the above analysis, at first, focus on how to make the best decisions for the forecast. Specifically, with the forecast ${s}_{i}$, the optimal HN decisions, denoted as ${x}^{*}\left({s}_{i}\right)$, will be given by minimizing the two-stage cost as the following linear program:

It is worth noting that both the HN and recourse decisions are given based on the forecast scenario ${s}_{i}$. Thus, the inner minimization problem in (5) is an estimation of the recourse cost under the forecast scenario ${s}_{i}$. In this way, the value of this additional information can be captured.

Next, the real scenario, denoted as ${s}^{*}$, is revealed. The decision-maker will certainly adjust the recourse decisions, denoted as ${y}^{*}({s}_{i}, {s}^{*})$, to optimize the recourse cost under the given ${x}^{*}\left({s}_{i}\right)$ and ${s}^{*}$. As such, we have the following linear program:

where the feasible space of $y({s}_{i}, {s}^{*})$ is dominated by the HN decisions ${x}^{*}\left({s}_{i}\right)$ and the realization ${s}^{*}$.

Thus, in terms of the forecast scenario ${s}_{i}$ and the final realization ${s}^{*}$, the above two sequential optimization models make the two-stage decisions respectively. The WS value, denoted as $\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}^{*}\right)$, is the sum of the first-stage cost determined by ${x}^{*}\left({s}_{i}\right)$ and the recourse cost based on ${y}^{*}({s}_{i}, {s}^{*})$.

Moreover, since the final realization ${s}^{*}$ is unknown in the first stage, use ${s}_{j}$ to represent the realization and the following formula can be obtained:

Besides, the conditional probability ${\lambda }_{\left(i\right|j)}$ is introduced to indicate the probability of the forecast scenario ${s}_{i}$ occurring given the realization ${s}_{j}$. Thus, for the given realization ${s}_{j}$, the expected value of (7) can be expressed as ${\sum }_{{s}_{i}\in S}{\lambda }_{\left(i\right|j)}\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)$ by considering all possible forecast scenario ${s}_{i}$. Furthermore, after taking all possible realization ${s}_{j}$ into account, the final expected WS value can be written as:

where ${p}_{j}$ is the probability associated with the scenario ${s}_{j}$.

As is mentioned before, this paper focuses on the scarce-data setting, in which the probabilistic interdependent relationship ${\lambda }_{\left(i\right|j)}$ is hard to give. To address this issue, a robust way is adopted to identify the worst probabilistic relationship. Then, the robust WS value under a given IIR $\mathrm{\Gamma }$, denoted as $\overline{{\mathrm{W}\mathrm{S}}_{R}}\left(\mathrm{\Gamma }\right)$, can be given as:

(9b) ensures that the sum of the conditional probabilities for each given realization is 1. (9c) specifies the limit of the IIR $\mathrm{\Gamma }$. Thus, the ambiguity set defined by (9b) and (9c) characterizes all possible probabilistic structures, and the model identifies the worst case.

Finally, two characteristics of model (9) are discussed below:

At first, construct the ambiguity set (9b) and (9c) under the information imperfectness limit $\mathrm{\Gamma }$ to capture possible probabilistic relationships. Such ambiguity set constrained by a budget value is often used in robust optimization ^[42]. Thus, two benefits exist. One is that the exact probabilistic structure is not required here. The other one is that the price of information imperfectness can be explored by varying the budget value, or by comparing various information sources with different information imperfectness limits.

Furthermore, the model is essentially a max-min-min problem with a bi-level structure. The objective (9a) defines the upper-level problem to identify the worst information update structure. The lower-level is composed of two sequential optimization problems, i.e., (5) and (6), due to the two-stage decision-making structure. However, bi-level programs are intractable ^[43]. To further solve the problem, we explore three ways to find its optimal solution.

3.3.   The solving approaches and EVII

In this section, three approaches are developed to address model (9) at first, and then, the EVII concept is discussed.

3.3.1.   The numerical approach

First, consider a scenario pair $\left({s}_{i}, {s}_{j}\right)$ which is composed of the forecast scenario ${s}_{i}$ and the realization ${s}_{j}$. The value of $\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)$, see (7), is irrelevant to ${\lambda }_{\left(i\right|j)}$. Thus, it can be given by solving (5) and (6) sequentially when $i\ne j$, or only by (5) when $i = j$.

All $\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)$ can be obtained by enumerating each scenario pair $\left({s}_{i}, {s}_{j}\right)$, which includes

linear programs. When all $\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)$ is given, the solving of $\overline{{\mathrm{W}\mathrm{S}}_{R}}\left(\mathrm{\Gamma }\right)$, see (9), is a linear program. In summary, solving problem (9) can be decomposed into a $2{\left|S\right|}^{2}-\left|S\right|+1$ small-sized linear programs.

3.3.2.   The analytical approach

Furthermore, when all $\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)$ is given, (9) can also be solved by the following analytical way. To be specific, for each j, denote $\left\langle{i}\right\rangle = \underset{1\le i\le \left|S\right|, i\ne j}{\mathrm{argmax}}\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)$. In other words, ${s}_{\left\langle{i}\right\rangle}$ is the worst forecast scenario for the realization ${s}_{j}$.

Thus, to maximize (9), set ${\lambda }_{\left(\left\langle{i}\right\rangle\right|j)}$ to be $\mathrm{\Gamma }$, and ${\lambda }_{\left(j\right|j)}$ to be $1-\mathrm{\Gamma }$ in line with constraint (9b). As a result, the optimal solution and objective are as below:

Proposition 1. Under (9) and the IIR $\mathrm{\Gamma }$, the optimal $\lambda \left(\mathrm{\Gamma }\right)$ and the corresponding $\overline{{\mathrm{W}\mathrm{S}}_{R}}\left(\mathrm{\Gamma }\right)$ can be given below:

and

where ${G}_{j} = \overline{\mathrm{W}\mathrm{S}}\left({s}_{\left\langle{i}\right\rangle}, {s}_{j}\right)-\overline{\mathrm{W}\mathrm{S}}\left({s}_{j}, {s}_{j}\right)$.

The above proposition provides an analytical way to address problem (9) optimally. Thus, this way can be used in the costly information acquisition game study. Nevertheless, the pre-calculation of all $\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)$ is still required. Next, a one-off way is presented.

3.3.3.   The equivalent reformulation

Finally, if the decisions of two-stage are linear, a robust counterpart of model (9) can be developed. To be specific, re-write problems (5) and (6) as their Karush-Kuhn-Tucker (KKT) conditions. For conciseness, introduce operator ${Cov}_{\mathrm{K}\mathrm{K}\mathrm{T}}(\mathrm{m}\mathrm{i}\mathrm{n}(.\left)\right)$, which is a set of equalities and inequalities, to represent the KKT conditions of the linear program $\mathrm{m}\mathrm{i}\mathrm{n}(.)$. Thus, problems (5) and (6) can be equivalent reformulated as:

and

respectively. In (13), ${x}^{*}\left({s}_{i}\right)$ is the optimal HN decision of (5), which can also be determined by (12). Then, the equivalence can be yielded:

In the objective of this model, ${\lambda }_{\left(i\right|j)}\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)$ is a bi-linear term, which makes the model intractable. Nevertheless, the following tractable equivalence can be given by introducing auxiliary variables and the detailed proof is presented in the appendix.

Proposition 2. Model (9) can be equivalently reformulated as below:

where ${\gamma }_{ij}$ is the binary auxiliary variable, ${\rho }_{ij}$ is the linear auxiliary variable, and M is a number big enough.

Notice that it is unnecessary to calculate $\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)$ in (14c) in advance, for the optimal decisions involved in $\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)$ are directly given by (12) and (13).

In summary, problem (9) can be optimally solved through the three approaches. Both the first and the second approach can address the problems with linear or integer decision variables, while the second one gives the closed-form solution. However, these two approaches can only be adopted to solve a series of small-sized problems. The third approach provides a one-off way but can only address linear decision variables.

3.3.4.   The EVII

The robust WS value can be given by the aforementioned approaches, while the RP can be given by (1). Thus:

which specifies the worst-expected gain that a decision-maker can obtain in the two-stage SP-based manner from an imperfect information source under the IIR $\mathrm{\Gamma }$.

Next, the following are discussed.

At first, the perfect information setting is a special case in our study. To be specific, when $\mathrm{\Gamma } = 0$, it is the perfect information setting. The robust WS value is given from (11), i.e., $\overline{{\mathrm{W}\mathrm{S}}_{R}}(\mathrm{\Gamma } = 0)$, is equivalent to the WS value under the perfect information setting, i.e., (2). Then, $\mathrm{E}\mathrm{V}\mathrm{I}\mathrm{I} = \mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{E}\mathrm{V}\mathrm{P}\mathrm{I}$. In the perfect information setting, it is proved that $\mathrm{E}\mathrm{V}\mathrm{P}\mathrm{I} = \mathrm{R}\mathrm{P}-\mathrm{W}\mathrm{S}$ since $\mathrm{R}\mathrm{P}\ge \mathrm{W}\mathrm{S}$ ^[40]. When imperfect information exists, however, it is evident that $\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)\ge \overline{\mathrm{W}\mathrm{S}}\left({s}_{j}, {s}_{j}\right)$. Thus,

Furthermore, from (9), with the increase of $\mathrm{\Gamma }$, the feasible space enlarges. Thus, the $\overline{{\mathrm{W}\mathrm{S}}_{R}}$ value is non-decreasing, and then, the EVII value is non-increasing with $\mathrm{\Gamma }$. It means that the information imperfectness can deteriorate the EVOI. Hence, a natural question is when the imperfect information is worthless. To answer this question, the following model is developed:

This linear programming model can help to identify the minimal $\mathrm{\Gamma }$, denoted as ${\mathrm{\Gamma }}^{*}$, which makes the imperfect information useless. In other words, when the information imperfectness extent is bigger than ${\mathrm{\Gamma }}^{*}$, the additional information is unnecessary, and thus, RP solution will be better.

4.   How to cooperate with an imperfect information provider

In this section, a costly information acquisition game is designed between a decision-maker (hereafter "he") and an imperfect information provider (hereafter "she"), and a dedicated cooperation mechanism is developed.

Assume that the information provider, with the historical IIR $\mathrm{\Gamma }$, provides information to the decision-maker, who adopts the two-stage SP. The latter applies a win-win mechanism to motivate the provider to improve her information quality to $\mathrm{\Gamma }-\Delta \mathrm{\Gamma }$. We have ${\mathrm{\Gamma }}^{\mathrm{*}} > \mathrm{\Gamma }\ge \Delta \mathrm{\Gamma }\ge 0$. The first inequality holds because, by (16), one can assume that only when the provider's IIR is better than ${\mathrm{\Gamma }}^{*}$, the cooperation will be considered.

The cost of the provider has two parts: $\tau \left(1-\mathrm{\Gamma }\right)$ ($\tau > 0$) and ${\tau }_{1}\Delta \mathrm{\Gamma }+{\tau }_{2}{\Delta \mathrm{\Gamma }}^{2}$ (${\tau }_{1} > 0$, ${\tau }_{2} > 0$). The first is the sunk cost associated with the existing IIR $\mathrm{\Gamma }$. Because perfect information is hard to achieve, the closer to the perfectness of the information improvement is, the more cost is required. Thus, use the quadratic form to capture the increasing incremental cost property for every amount of information quality enhancement. In practical environments, e.g., demand forecast of new products, $\Delta \mathrm{\Gamma }$ can be estimated by the enlargement extent of the market survey scale.

Thus, before the improvement practice, the EVII of the decision-maker dependent on SP is:

The first equality is given by (15), while the second one holds due to ${\mathrm{\Gamma }}^{*} > \mathrm{\Gamma }$. Similarly, when the provider updates her IIR to $\mathrm{\Gamma }-\Delta \mathrm{\Gamma }$, the corresponding EVII equals:

Let ${\pi }_{p}^{0}$ and ${\pi }_{d}^{0}$ be the costs of the information provider and the decision-maker respectively, without the information quality improvement practice, ${\pi }_{p}$ and ${\pi }_{d}$ be the costs of two players respectively, with the implementation of the practice. Thus:

where $\theta (\le \mathrm{E}\mathrm{V}\mathrm{I}\mathrm{I})$ is the payoff from the decision-maker to the provider for her information with the IIR $\mathrm{\Gamma }$.

where $\nu$ is the payment that the decision-maker offers to the provider for her IIR $\mathrm{\Gamma }-\Delta \mathrm{\Gamma }$.

Here, we focus on information quality improvement in the costly information acquisition game. The global optimum is derived first, and then, a mechanism is designed by specifying $\nu$ to realize the optimum.

4.1.   The global optimum

In this section, the global optimum is figured out in the first place and it is then set as the benchmark. To get it, discard the payment $\nu$ and consider the centralized way. Thus, from (18), the global optimization problem can be written as:

where ${\bf{\Lambda }}(\mathrm{\Gamma }-\Delta \mathrm{\Gamma }) = \left\{\lambda :{\sum }_{i}{\lambda }_{\left(i\right|j)} = 1, {\sum }_{i\ne j}{\lambda }_{\left(i\right|j)}\le \mathrm{\Gamma }-\Delta \mathrm{\Gamma }, \ \ \ \forall j; \lambda \succcurlyeq 0;\lambda \in {\mathbb{R}}^{\left|S\right|\times \left|S\right|}\right\}$.

In the robust setting, (19) is a min-max-min-min problem. To be specific, the objective function is in the form of min-max, while the constraints involve two sequential minimization problems, i.e., (5) and (6). To address its intractability, use (11) in Proposition 1 to replace the inner maximization problem in (19). Thus, re-write (19) in the following equivalent way:

Thus, the optimal results of model (20) are given in the following proposition, and its proof is presented in the appendix.

Proposition 3. The optimal solution to model (20), denoted as $\Delta {\mathrm{\Gamma }}_{c}^{*}$, should be:

where ${a}^{+} = \mathrm{m}\mathrm{a}\mathrm{x}\{a, 0\}$.

Next, focus on the problem of when an information quality improvement practice is beneficial. To answer this question, we have:

Corollary 1. Only when ${\sum }_{{s}_{j}\in S}{p}_{j}{G}_{j} > {\tau }_{1}$, the information quality improvement practice is beneficial.

Its proof is given in the appendix. The result coincides with that in Proposition 3. Specifically, when ${\sum }_{{s}_{j}\in S}{p}_{j}{G}_{j} > {\tau }_{1}$, have $\Delta {\mathrm{\Gamma }}_{c}^{\mathrm{*}} > 0$, which means the provider will improve the information accuracy. Therefore, in the next section, only this case will be considered and the design of the coordination mechanism will be discussed. Furthermore, it is easy to give Corollary 2 to show how $\Delta {\mathrm{\Gamma }}_{c}^{\mathrm{*}}$ varies with ${\tau }_{1}$ and ${\tau }_{2}$.

4.2.   Information quality improvement compensation mechanism

In this section, an information quality improvement compensation mechanism is developed for the costly information acquisition game. The Stackelberg game is adopted. To be specific, the decision-maker depending on SP is the leader who specifies the payment $\nu$ as a linear contract, i.e., $\alpha +\beta \Delta \mathrm{\Gamma }$, $\beta > 0$. Thus, the leader's strategy is to determine $\left\langle{\alpha, \beta }\right\rangle$. The information provider is the follower who decides her information quality improvement, i.e., $\Delta \mathrm{\Gamma }$.

The aim is to focus on the optimal design of the contract. Notice that (19) is a min-max-min-min problem, which is intractable. The mechanism design here is more complicated because the optimal decisions of the follower should be taken into account. However, by Proposition 1, the decision-maker's problem can be formulated in the following relatively concise form:

(22b) and (22c) are the individual rationality constraints of the decision-maker and the information provider, respectively.

Solve problem (22) by using backward induction. Start with the best response of the provider, denoted as ${\Delta \mathrm{\Gamma }}_{d}$. According to (18) and $\nu = \alpha +\beta \Delta \mathrm{\Gamma }$, one can obtain the objective of the information provider:

It is a quadratic function of ${\Delta \mathrm{\Gamma }}_{d}$. Similar to the proof of Proposition 3, her best response satisfies:

Then, the optimal solution $\left\langle{{\alpha }^{*}, {\beta }^{*}}\right\rangle$ of the Stackelberg game can be given in the following proposition. The proof is presented in the appendix.

Proposition 4. The optimal strategy and cost of decision-maker can be given as follows:

and

From Propositions 3 and 4, re-write ${\beta }^{*}$ as:

Thus, (23) yields

Hence, $\left\langle{{\alpha }^{*}, {\beta }^{*}}\right\rangle$ in (24) can induce the response of the information provider, i.e., $\Delta {\mathrm{\Gamma }}_{d}^{*}$, which is the same as $\Delta {\mathrm{\Gamma }}_{c}^{*}$ in the global optimum. In other words, the proposed linear contract can help to realize the global optimum.

5.   Application example

In this section, a two-stage production and shipment planning problem is introduced to show the applicability of our study.

5.1.   The two-stage production and shipment planning problem

Suppose a decision-maker, who uses two-stage SP, has $\left|M\right|$ warehouses and $\left|D\right|$ demand points. The decisions occur in two stages. In the first stage, he decides ${x}_{m}$ ($\ge 0$) of units of product to produce and store at warehouse m ($\in M$) at a unit cost of ${c}_{1}$. Next, the sales season begins and a demand scenario $s$ is realized in which the demand of location d ($\in D$) is denoted as ${n}_{d}^{s}$. To satisfy ${n}_{d}^{s}$, he can ship ${y}_{md}^{s}$ ($\ge 0$) of units of product from warehouse m at a unit cost of ${c}_{md}$. If a shortage occurs, he needs to place an additional order ${y}_{m}^{s}$ ($\ge 0$) of units of product to replenish the stock of warehouse m at a cost of ${c}_{2}$ ($> {c}_{1}$) per unit. Thus, the two-stage SP model considered by the decision-maker is given as:

Consider a case with $\left|M\right| = 3$ and $\left|D\right| = 10$. The discrete priori demand scenarios and the shipment costs are given in Tables 2 and 3. Let ${c}_{1}$ = 500 and ${c}_{2}$ = 800.

5.2.   Computational results

The models are optimally calculated on a notebook PC with a 2.3 GHz CPU and 8 GB memory, by using Python and Doc plex.

5.2.1.   The EVPI and EVII results

(1)–(3) can deliver the results in the perfect information setting: WS = 2349542.87, RP = 2475020.77, and EVPI = 125477.9.

Next, consider the information imperfectness in the scarce-data setting. Assume that the decision-maker only has the priori distribution, not the probabilistic structure. By (5)–(7), all $\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)$ is presented in Table 4, in which ${s}_{i} = {s}_{j}$ represents the corresponding perfect information results.

Use the approaches proposed in Section 3.3, the $\overline{{\mathrm{W}\mathrm{S}}_{R}}\left(\mathrm{\Gamma }\right)$ and the EVII under different $\mathrm{\Gamma }$ in Figure 1 can be obtained. Moreover, by model (16), ${\mathrm{\Gamma }}^{*}$ ( = 0.242) can be identified, which makes the information worthless.

5.2.2.   The coordination mechanism results

This section focuses on the game setting based on the above example.

a. The decentralized setting

A dedicated coordination mechanism is required here. In the decentralized setting, the costs of the information provider and the decision-maker are given by (17), in which the transfer from the decision-maker to the provider is specified by $\theta$. It can be a fixed value that is irrelevant to the original information quality $\mathrm{\Gamma }$. Nevertheless, a more reasonable way is to define $\theta$ based on the fixed ratio of the benefit-sharing. For example, define $\theta = 0.6\times \mathrm{E}\mathrm{V}\mathrm{I}\mathrm{I}$, which means that the decision-maker should pay the provider 60% of the benefits for her information.

Obviously, if there is no extra compensation, the provider will not improve her information accuracy. Thus, in the information quality improvement setting, we still consider the fixed benefit-sharing way and study whether it works or not. Accordingly, the objectives of the two participants can be modified, i.e., (18), as below.

where $\theta = 0.6\times \mathrm{E}\mathrm{V}\mathrm{I}\mathrm{I} = 0.6\times (\mathrm{R}\mathrm{P}-\overline{{\mathrm{W}\mathrm{S}}_{R}}\left(\mathrm{\Gamma }-\Delta \mathrm{\Gamma }\right))$ is the fixed share of the gain of the improved information. Moreover, set $\tau = 2\times {10}^{5}$, ${\tau }_{1} = 3\times {10}^{5}$, ${\tau }_{2} = {10}^{6}$ and $\mathrm{\Gamma } = 0.16$. The other parameters are set to be the values given in the last section. Then, give ${\pi }_{p}^{1}$, ${\pi }_{d}^{1}$, and the total cost under different $\Delta \mathrm{\Gamma }$ is shown as below.

Figure 2 indicates that the fixed benefit-sharing way cannot help to achieve the global optimum. To be specific, the optimal choice of the information provider is $\Delta \mathrm{\Gamma } = 0.005$, while the globally optimal $\Delta \mathrm{\Gamma }$ should be 0.109. Thus, a dedicated coordination mechanism is required.

b. The linear compensation mechanism

Still consider the example given in Section 5.2.1.

First, by Corollary 1, ${\tau }_{1} < {\sum }_{{s}_{j}\in S}{p}_{j}{G}_{j} = 517929.2$. Then, Proposition 3 yields Figure 3, which indicates the value of $\Delta {\mathrm{\Gamma }}_{c}^{*}$ w.r.t. ${\tau }_{1}$ and ${\tau }_{2}$ under different $\mathrm{\Gamma }$. To be specific, the straight line specified by each $\mathrm{\Gamma }$ divides the figure into two parts. When (${\tau }_{1},$ ${\tau }_{2}$) lies in the lower-left or upper-right area, $\Delta {\mathrm{\Gamma }}_{c}^{*} = \mathrm{\Gamma }$ or $\frac{{\sum }_{{s}_{j}\in S}{p}_{j}{G}_{j}-{\tau }_{1}}{2{\tau }_{2}}$, respectively. In addition, it is found that the lower-left corner shrinks as $\mathrm{\Gamma }$ increases. It means that $\Delta {\mathrm{\Gamma }}_{c}^{*}$ can be $\mathrm{\Gamma }$ only when (${\tau }_{1},$ ${\tau }_{2}$) is very small. This is because higher $\mathrm{\Gamma }$ means lower information quality, which brings more difficulties to realize the perfect information situation.

In Figure 4, the black columns show the case $\Delta {\mathrm{\Gamma }}_{c}^{*} = \mathrm{\Gamma }$, which is the lower-left corner in Figure 3. When ${\tau }_{1}$ and ${\tau }_{2}$ become big, it is costly to improve the information quality. Thus, the upper extent of information quality improvement is becoming smaller. The changing trend can also be explained by Corollary 2. Moreover, the column under ${\tau }_{1} = 3\times {10}^{5}$ and ${\tau }_{2} = {10}^{6}$ has the corresponding $\Delta {\mathrm{\Gamma }}_{c}^{*} = 0.109$. It is the improvement extent that makes the global optimum happen, as is shown in Figure 2. Thus, the proposed compensation mechanism can help to realize the global optimum.

Next, the focus is on the optimal compensation contract, i.e., $\left\langle{{\alpha }^{*}, {\beta }^{*}}\right\rangle$. First, from Propositions 3 and 4, re-write $\left\langle{{\alpha }^{*}, {\beta }^{*}}\right\rangle$ as below:

The formulas show there are two cases for ${\alpha }^{*}$ and ${\beta }^{*}$. The condition differentiating two cases coincides with that in Figure 3. In each case, ${\alpha }^{*}$ and ${\beta }^{*}$ exhibit distinct changing trends as is shown in Figure 5, in which the first case is specified by the grey columns and the second one by the black area.

It is found that, when both ${\tau }_{1}$ and ${\tau }_{2}$ are small, the compensation is mainly dominated by the fixed term of the contract, i.e., ${\alpha }^{*}$. Then, with the increase of ${\tau }_{1}$ and ${\tau }_{2}$, ${\alpha }^{*}$ decreases linearly with ${\tau }_{2}$ but is irrelevant to ${\tau }_{1}$, while ${\beta }^{*}$ increases linearly with ${\tau }_{1}$ and ${\tau }_{2}$. Thus, ${\beta }^{*}$, the parameter associated with $\Delta \mathrm{\Gamma }$, gradually dominates the contract. Furthermore, when both ${\tau }_{1}$ and ${\tau }_{2}$ are big enough and lie in the grey area, the improvement activity requires more investments. Thus, ${\beta }^{*}$ remains high, and ${\alpha }^{*}$ gradually increases with ${\tau }_{1}$ and ${\tau }_{2}$ to strengthen the compensation.

Finally, observe the objective values of the players. Since the information improvement cost of the provider can be compensated by the contract, we only focus on the benefit of the decision-maker, i.e., $-{\pi }_{d}\left({\alpha }^{*}, {\beta }^{*}\right)$, in Figure 6. It is found that, with the increase of ${\tau }_{1}$ and ${\tau }_{2}$, his benefit will significantly decrease. It is because the improvement activity costs much more, and then, incurs higher compensation.

So far, we have shown how our study can be applied to a practical OR/MS problem. The whole process demonstrates how information quality influences the two-stage SP decision-making performance, and gives the boundary IIR value. Efforts have also been made to address the two-stage SP problem with exogenous costly information acquisition. Our study can be applied to general interactions between information management and stochastic decision-making.

6.   Conclusions and future directions

In this study, a fundamental question is explored: that is to evaluate and acquire imperfect information in the two-stage SP setting with the challenge of data scarcity. To evaluate the EVII, we propose the robust WS concept, which is modeled by a max-min-min problem with the bi-level structure. To find the optimal solution, three ways are developed, including numerical, analytical, and equivalent reformulation, ensuring that the solution is suitable for different settings. Thus, the EVII can be obtained and when imperfect information is worthless can be identified. Furthermore, a Stackelberg game is modeled to study the coordination of the costly information acquisition process between decision-maker, who utilizes the two-stage SP, and the information provider. To realize the global optimum, a linear contract is designed for the decision-maker relying on SP to compensate for the information provider's efforts in information quality improvement. Finally, a two-stage production and shipment model is introduced and our study's effectiveness is validated. Therefore, we provide a novel and unified model to study the interactions between information management and SP in the scarce-data setting.

The following is suggested for future studies. First, in this paper, the budget value is used to capture the information imperfectness in the scarce-data setting. Although such a way is popular in robust optimization, e.g., Bertsimas and Sim ^[42], sometimes, it may lead to over-conservative results. Exploring new approaches is necessary for future studies. For example, the chance-constrained method can be used, and thus, the IIR constraint can be satisfied with a certain probabilistic level. However, the computationally tractable safe approximation of such a chance constraint is often expressed as the conic quadratic constraint ^[44]. Therefore, further study is needed to discuss how to combine it with both the max-min-min problem and the costly information acquisition game. Second, this paper focuses on imperfect information by considering the misinformation probabilities among scenarios. However, in the scenarios, the values associated with the uncertain parameters are ignored in this paper. Thus, a natural extension is to take both the misinformation probabilities and the values associated with the scenarios into account together in the future. Third, it is interesting to extend our study into the predictive context and discuss the value of forecasting methods. For example, the K-Nearest-Neighbor (KNN) technique can predict a set of scenarios. What is the value of this technique from the perspective of the decision-maker adopting SP? To answer this question, probabilistic estimation should be taken into account. This extension is worth conducting because it integrates the predictive decisions into the prescriptive ones in the imperfect information setting. Finally, given that many decision-makers are not risk-neutral, a possible future direction is to encompass non-linear risk preferences. Our study provides the complete analysis framework and solid research foundation for these directions.

Acknowledgments

The authors are grateful for the valuable comments from the academic editor and the two anonymous reviewers. This study is supported by the National Natural Science Foundation of China (No. 71832001), the Natural Science Foundation of Shanghai (No. 20ZR1401900), and the Fundamental Research Funds for the Central Universities (No. 2232018H-07).

Conflict of interest

All authors declare no conflicts of interest in this paper.

Supplementary

Proof of Proposition 2:

At first, linearize the bi-linear terms, i.e., ${\lambda }_{\left(i\right|j)}\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)$, in the objective (9a). Re-call Proposition 1, the optimal value of ${\lambda }_{\left(i\right|j)}$ should be 0 or $\mathrm{\Gamma }$ and there is only one ${\lambda }_{\left(i\right|j)} = \mathrm{\Gamma }$ for each ${s}_{j}$. Thus, introduce a binary variable ${\gamma }_{ij}$ and use $\mathrm{\Gamma }{\gamma }_{ij}$ to replace ${\lambda }_{\left(i\right|j)}$. Then:

Then, a linear auxiliary variable ${\rho }_{ij}$ is introduced to replace ${\gamma }_{ij}\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)$. Therefore, the above model can be linearized as below:

where $M$ is a number big enough. Notice that $\overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)\ge 0$. Constraints (A4) and (A5) enforce ${\rho }_{ij} = 0$ if ${\gamma }_{ij} = 0$ and ${\rho }_{ij} = \overline{\mathrm{W}\mathrm{S}}\left({s}_{i}, {s}_{j}\right)$ if ${\gamma }_{ij} = 1$. Thus, Proposition 2 is obtained.

Proof of Proposition 3:

For the quadratic function (20), it is easy to get that the optimal $\Delta \mathrm{\Gamma }$, i.e., $\Delta {\mathrm{\Gamma }}_{c}^{*}$, should satisfy:

For succinctness, it could be re-written as

where ${a}^{+} = \mathrm{m}\mathrm{a}\mathrm{x}\{a, 0\}$. This proves Proposition 3.

Proof of Corollary 1:

If the information quality improvement is beneficial, by (17) and (18), we have:

Focus on $\Delta \mathrm{\Gamma } > 0$, ${\tau }_{1} > 0$ and ${\tau }_{2} > 0$, thus:

As a result, it is obtained that ${\sum }_{{s}_{j}\in S}{p}_{j}{G}_{j} > {\tau }_{1}$. Then, Corollary 1 is proved.

Proof of Proposition 4:

First, re-write the best response of the information provider, i.e., (23) as below:

Introduce the three ${\Delta \mathrm{\Gamma }}_{d}$ into the provider's individual rationality constraint (22c), and have:

To ensure the satisfaction of the provider's individual rationality constraint (22c), (A10) should hold. Notice that the focus is on the setting of the information quality improvement, in which ${\Delta \mathrm{\Gamma }}_{d} > 0$. Thus, only the last two cases in (A10) will be taken into account. Accordingly, problem (22) can be reformulated into the following two sub-models.

Case 1:

In this case, $0\le \frac{\beta -{\tau }_{1}}{2{\tau }_{2}} < \mathrm{\Gamma }$ and $\alpha +\frac{{\left(\beta -{\tau }_{1}\right)}^{2}}{4{\tau }_{2}}\ge \theta$ with the best response ${\Delta \mathrm{\Gamma }}_{d} = \frac{\beta -{\tau }_{1}}{2{\tau }_{2}}$. Thus, problem (22) can be reformulated as:

Obviously, because the objective is linear w.r.t. $\alpha$, from the last constraint, we have the optimal solution for above satisfies ${\alpha }_{1}^{*} = \theta -\frac{{(\beta -{\tau }_{1})}^{2}}{4{\tau }_{2}}$. Use it to replace $\alpha$ in model (A11), then:

s.t.

Obviously, to ensure the existence of feasible solutions, it is required that $2{\sum }_{{s}_{j}\in S}{p}_{j}{G}_{j}-{\tau }_{1}\ge {\tau }_{1}$. Recall the setting of ${\sum }_{{s}_{j}\in S}{p}_{j}{G}_{j} > {\tau }_{1}$ as given in COROLLARY 1, the optimal solution of (A11) exists. Moreover, since the objective is a quadratic function of $\beta$, it is easy to find the optimal ${\beta }_{1}^{*}$ satisfies:

Thus, we have:

with the objective:

Case 2:

Here, $\mathrm{\Gamma }\le \frac{\beta -{\tau }_{1}}{2{\tau }_{2}}$ and $\alpha -{\tau }_{2}{\mathrm{\Gamma }}^{2}+\left(\beta -{\tau }_{1}\right)\mathrm{\Gamma }\ge \theta$ with the response ${\Delta \mathrm{\Gamma }}_{d} = \mathrm{\Gamma }$. Thus, the variant of (22) can be given as below:

Obviously, form the last two constraints, the optimal solution of (A14) should satisfies ${\beta }_{2}^{*}=2{\tau }_{2}\mathrm{\Gamma }+{\tau }_{1}$ and ${\alpha }_{2}^{*}+{\beta }_{2}^{*}\mathrm{\Gamma }=\theta +{\tau }_{1}\mathrm{\Gamma }+{\tau }_{2}{\mathrm{\Gamma }}^{2}$. Then, ${\alpha }_{2}^{*}=\theta -{\tau }_{2}{\mathrm{\Gamma }}^{2}$. Accordingly, the first constraint can be re-written as:

Recall that when $\mathrm{\Gamma } > 0$, ${\tau }_{1}+{\tau }_{2}\mathrm{\Gamma }\le {\sum }_{{s}_{j}\in S}{p}_{j}{G}_{j}$. When this inequality holds, the optimal solution of (A14) is

with the objective

In summary, with the above two cases combined, the optimal solution of problem (22) satisfies:

with the optimal value of the objective

Furthermore, recall (21), reformulate the optimal solution $\left\langle{{\alpha }^{*}, {\beta }^{*}}\right\rangle$ and the objective ${\pi }_{d}\left({\alpha }^{*}, {\beta }^{*}\right)$ into the following succinct forms:

And

Thus, the proof of Proposition 4 is completed.