1.
Introduction
The time-fractional singular and non-singular operator are widely used in modern sciences and technology to study the behavior and applications of nonlinear ordinary and partial differential equations [1,2,3,4]. Fractional-order models are useful to study numerous real-world problems for longtime memory, and chaotic behaviour [5]. Due to these characteristics, the nonlinear models having fractional-order derivatives have been widely attracted in many areas of fractional calculus including image processing and signal, mechanics, biophysics and bioengineering, electrical engineering, biology, viscoelasticity, rheology, and control theory [6,7,8].
The Korteweg-de Vries (KdV) equation has extensively studied for nonlinear models describing the evaluation in time of long, unidirectional shallow water waves [9]. It was mainly presented by Boussinesq in 1877 and then retrieved by Diederik Korteweg and Gustav-de Vries in 1895 [10]. The existence solution to the a KdV equation can be seen in [11,12]. The KdV system having time-fractional derivatives attained remarkable attention in plasma physics especially in electrons acoustic waves (EAWs) propagation, due to its important role in studying diverse forms of mutual developments experimentally [13,14]. It has observed that the time-fractional operators in the system dramatically change the soliton amplitudes of the electron-acoustic solitary waves. This effects have been particularly equated with the structures of the broadband electrostatic noise experienced in the dayside auroral zone [15]. The system of coupled KdV system plays a leading part in various areas of sciences and engineering, particularly in water waves, quantum field theory, hydrodynamics and plasma physics [16,17]. It also represents the relations in extended waves with altered dispersion relations and describes iterations of water waves [18,19].
Here, we consider the mCKdV in the form [20]
with subsidiary conditions
where λ is a real number to be chosen accordingly.
The proposed mCKdV Eq (1.1) has more interesting features than classical, because the operators will be defined by an integral which play a vital role in modern technology, engineering, plasma physics, hydrodynamics and quantum theory [21]. The nonlinear differential equations contain numerous fractional differential singular and non-singular operators such as Hilfer, Caputo, Caputo-Fabrizio, Riemann-Liouville, Antagana-Balenau in Caputo's sense [22,23,24]. These operators can be reduced in Caputo's form after some parametric addition. One can assume that the fractional operator could provide a power-law estimate of the local conduct of non-differentiable functions [25]. The Caputo operator possesses a power-law kernel and has restrictions to apply in modeling physical phenomena.
A modified laplace decomposition method (MLDM) is applied to Schrodinger-KdV equation in the sense of Atangana-Baleanu derivative in[26]. To deal successfully in such a situation, an alternative fractional operator possess a kernel with exponential decay has been introduced [27]. This novel operator is called the Caputo-Fabrizio (CF) operator which has a non-singular kernel. This operator is broadly applicable for modeling particular type of physical problems which follows the exponential decay law. Currently, mathematical and physical models having the CF operator have a remarkable development. The characteristics and applications of the above derivatives has been extensively studied (see [28,29,30,31,32,33,34,35] and the reference therein).
There are many analytical methods that offer approximate solutions to nonlinear models, for example, perturbation methods [36,37,38], homotopy perturbation [39,40,41,42], the Adomian decomposition methods (ADM) [43,44] and Laplace Adomian decomposition methods (LADM) [45,46,47]. The modified coupled KdV model has been analyzed numerically by applying the q-homotopy approach with Caputo operator by using Petrov-Galerkin method and product approximation technique [20,48]. We will study the mCKdV equations with Caputo and CF derivatives by applying the modified double Laplace transform decomposing method (MDLDM) [49]. The decomposition method has extensively applied for many fractional models in physics and applied mathematics [50,51,52].
Some resent contribution of the time fractional order KdV equations have been studied by using different techniques [53,54,55,56,57]. The proposed method is an essential and effective approach to finding approximate solutions of the nonlinear models having time-fractional derivatives. In the non-linear model (1.1), the time fractional derivative has been taken in the form of Caputo's and Caputo-Fabrizio operator form which have a remarkable advantages in such physical models. The model is solved by using an affective method called modified double Laplace decomposition method (MDLDM) to obtain an approximate solution. The numerical solution of the model has been discuss in the form tables follow by its plots.
The rest of the paper is organized as follows: In Section 2, some main definitions, remarks, important results and a brief discussion of the proposed method is included. The convergence and uniqueness of the proposed method with the help of Banach contraction principle theorems are also studied in Section 3. In Section 4, the problem is discussed in Caputo's and Fabrizio forms and its solutions are obtained in a series form. We consider two numerical examples in Caputo's and Fabrizio form with the application of the proposed method, approximate solutions are obtained in the same section. This section also includes numerical discussion and figures for both the examples. Section 5 concludes the article followed by the Section 6 contain the future work in the manuscript, and Appendix contains the numerical values of the examples in the form of tables and also includes some parameters values.
2.
Materials and methods
2.1. Some basic definitions
In this section, we provide some basic definitions, lemmas and remarks regarding to the proposed method. Here also given some basics rules and definition related to double Laplace transform and decomposition method.
Definition 1. [5,35,58] Caputo's fractional derivative of positive real order α>0 of a function ϕ(x,t) is given by function ϕ:(0,∞)→IR is defined by
where n=[α]+1, [α] denotes the integer part of a real number α, provided the right-hand side is point-wise defined on (0,∞).
Definition 2. [35,59] Let ϕ(x,t)∈H1(a,b), with b>a and α∈(0,1], then the fractional order in sense of Caputo-Fabrizio is define as
where CFDαϕ(x,t) is a fractional operator with Mittage-Leffler kernel in Caputo sense. M(α) is called normalization function with properties M(0)=M(1)=1.
Definition 3. [60] For a ϕ(x,t), where x,t>0 lies in xt-plane, the double Laplace transform of the function ϕ(x,t) is defined by
where p and s are complex numbers.
Definition 4. [61,62] Applying the definition of double Laplace transform on fractional order derivative with respect t and x in Caputo sense is given by
where n=[α]+1, m=[β]+1.
Definition 5. [61,62] Applying the definition of double Laplace transform on fractional order derivative with respect t and x in Caputo-Fabrizio sense is given by
where n=[α]+1, m=[β]+1 for r=0,1. For Eq (2.17), with normalization property hold, we can write
From the above definitions, we can conclude that
The inverse double Laplace transform L−1xL−1t{ˉϕ(x,t)}=ϕ(x,t), is represented by a complex double integral formula
where ˉϕ(p,s) is an analytic function ∀p and s defined in the region by the inequalities Re (p)≥c and Re (s)≥d, where c,d∈R to be considered accordingly.
2.2. Series solutions of mCKdV using the proposed method
The proposed method MDLDM is hybrid method used widely for non-linear ordinary or partial differential equations. It is the combination of double Laplace and Adomian decomposition method to obtain an approximate solution for problems in hand. To discuss the analysis of the proposed method, we consider the following coupled non-linear problems:
where L=cDαt(.) is the fractional-time derivative in Caputo's form, R1, R2 are the operators contains the linear terms of Eq (1.1), N1, N2 are the non-linear operators and f1(x,t), f2(x,t) are some external functions. Applying double Laplace on both sides to Eq (2.21), we obtain
Using the scheme defined above of double Laplace on the nth-derivative in Caputo's form, we obtain
where
Consider the series solution of the form
let N1 and N2 be the non-linear operators in the model are defined by
where An and Bn are well known Adomian polynomials [50] of the functions ϕ0,ϕ1,ϕ2,… and ψ0,ψ1,ψ2,… respectively. For convince consider An can be described by the following formula:
Applying an inverse double Laplace on both sides to Eq (2.3):
equating terms on both sides, we obtain
In general, the following recursive formulas can be obtained, the final solutions can be obtained as
for numerical purposes we take α=1, the exact solution can be obtained as
Similar procedures can be used to a problem having Caputo-Fabrizio fractional-time derivative to obtain a recursive relation.
3.
Convergence analysis of the proposed method
In this section, we are discussing the existence and uniqueness of the solutions (2.29) and (2.30) of the general coupled time fractional non-linear partial differential equation (2.21). The following theorems are taken from [63].
Theorem 1. (Uniqueness theorem) For 0<σ<1, the solution (2.29) of Eq (2.21) is a unique solution, where σ=(κ1+κ2+κ3)tα+1Γ(α).
Proof. We create a mapping T : B→ B where B=(C[J],‖.‖) is the Banach space of all continuous functions on J=[0,T] with the norm ‖.‖. We can write Eq (2.29) in the following form:
where L=−32∂2ψ∂x2+3λ∂2ϕ∂x2, M=−∂3ϕ∂x3 and N=3ϕ2∂2ψ∂x2−3ψ∂ϕ∂x−3ϕ∂ψ∂x. Let Lϕ, Mϕ and Nϕ are also Lipschitzian with |Lϕ−Lˉϕ|<κ1|ϕ−ˉϕ|, |Mϕ−Mˉϕ|<κ2|ϕ−ˉϕ| and |Nϕ−Nˉϕ|<κ3|ϕ−ˉϕ| where κ1, κ2 and κ3 are Lipschitz constants, ϕ and ˉϕ are the function's distinct values. Now we proceed as follow:
The mapping is contraction under the condition 0<σ<1. As a result of the Banach fixed point theorem for contraction, Eq (2.21) has a unique solution. This marks the end of the proof.
Next we discuss convergence analysis of the problem.
Theorem 2. (Convergence theorem) The solution of Eq (2.21) in general forum will be convergence.
Proof. The Banach space of all continuous functions on the interval J with the norm ‖ϕ‖ = maxt∈J‖ϕ‖ is denoted as (C[J],‖.‖). Define the {Sn} sequence of partial sums i.e Sn=∑nj=0. With n≥m, let Sn and Sm be arbitrary partial sums. In this Banach space, we will show that Sn is a Cauchy sequence. We obtain by employing a new formulation of Adomian polynomials.
now
Choosing n=m+1, then
with σ=(κ1+κ2+κ3)tα−1Γ(α), by using the following triangular inequality
Now by definition 0<σ<1, we have 1−σn−m<1, thus we have
and also as |ϕ|<∞ (ϕis bounded), therefore, ‖Sn−Sm‖→0, hence Sn is a Cauchy sequence in the Banach space B, so the series ∑nj=0ϕj is convergent.
Remark 1. Theorems 1 and 2 can also be applicable to the solution (2.30) for its uniqueness and convergent.
4.
Applications of the proposed method
In this section, we illustrate some examples on Eq (1.1) with time-fractional derivatives in the form of Caputo and Caputo-Fabrizio operators in each case, and apply the proposed method discussed in this section with (f1,f2)=0.
Example 1. Consider the following (mCKdV)[20] in Caputo's form
with initial conditions
The exact solution of Eq (4.1) for α=1 is [20]
where
Apply the modified double Laplace transform decomposition (MDLDM) scheme discussed in this section to Eq (4.1) and single Laplace transform to Eq (4.2), we obtain the following recurrence relations:
for n≥0. The Adomian polynomials An,⋯Fn,n=1,2,3, for nonlinearity appears in Eq (4.4) are calculated by using the general rules shown in Eq (2.27)
For more details, one can see [51,52,64]. Plugging Eq (4.5) in Eq (4.4), we obtain
where the coefficients given above can be seen in Appendix. It should be noted that, other terms can be calculated in the similar way. The final solutions can be obtained
For numerical purposes we take α=1, the exact solution can be obtained as
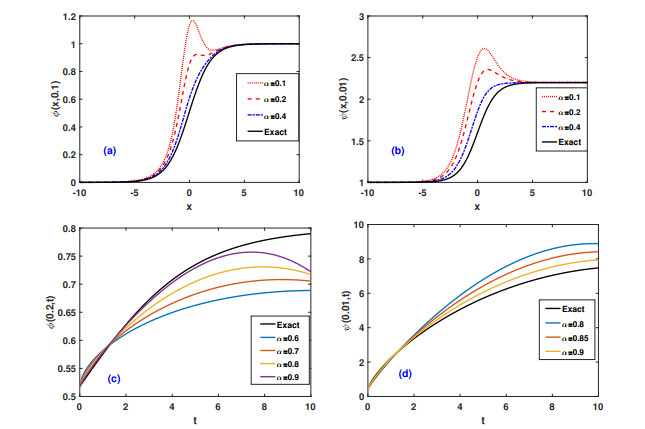
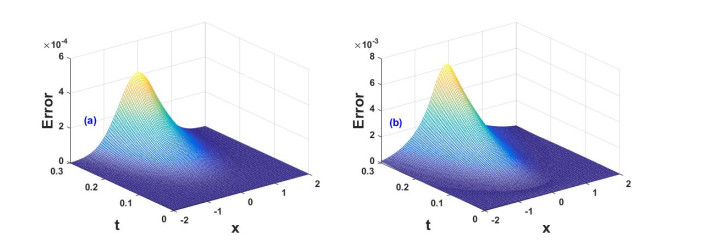
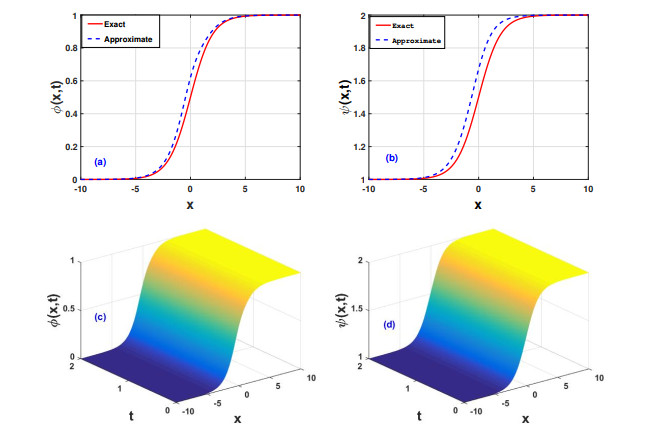
For the numerical illustrations, Figure 1 depicts obtained solutions ϕ and ψ in Eq (4.6) associated with the modified coupled Korteweg-de Vries (mCKdV) Eq (4.1). Thus the waves solutions ϕ(x,t) and ψ(x,t) in Figure 1(a), (b) reveals the evolution of the shock excitations. The three-dimensional profiles of ϕ(x,t) and ψ(x,t) in Figure 1(c), (d) manifest sudden changes in the potential fields for the spatial variables −10≤x≤10. We observe that the mCKdV equations describe nonlinear evolution of the waves, suffered by weak dispersion effect in an inviscid fluid. Thus the nonlinear steeping attributed to temporal evolution excites the shocks. For the impact of the time fraction coefficient α on the waves characteristics, we have displayed solutions (4.6) versus x at α=0.1,0.2,0.4,1, see Figure 2(a), (b). Notice that a degree enhancement in α modifies the steeping effect and therefore rise the waves amplitudes. Similarly Figure 2(c), (d) show the nature of the MDLDM method in Caputo's sense for different values of α and time when spatial variable x is kept constant of the Eq (4.6) in Example 1. The wave solutions are revealing the propagation of monotonic shocks. Figure 3(a), (b) show the error plots of the Table 1 (see Appendix).
Example 2. Consider the following example having time fractional derivative in Caputo-Fabrizio (CF) form
With the help of Eq (2.17) and the procedure used in Example 1, we can obtain the following series solutions in Caputo-Fabrizio form
where
Other terms can be calculated in the similar way. The general solutions can be obtained in the form
For numerical purposes we take α=1, the exact solution can be obtained as
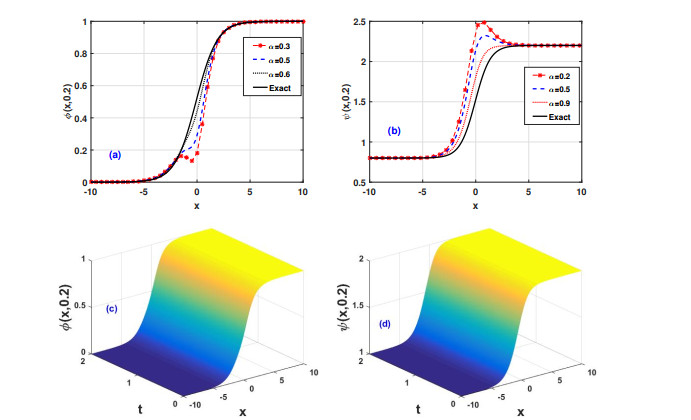
The shock wave solutions ϕ(x,t) and ψ(x,t) in Eq (4.8) for the modified coupled Korteweg-de Vries (mCKdV) Eq 4.1 with Caputo's Fabrizio operators (CF) are depicted in Figure 4(a), (b) against x. Obviously, the approximate Fabrizio solution (red stared dotted and blue dashed, black dotted curves) in both the plots (a) and (b) by MDLDM method is approaching to the exact solution (black solid curve) of the Eq (4.8) in Example 2, the corresponding plots in three dimension are shown in Figure 4(c), (d).
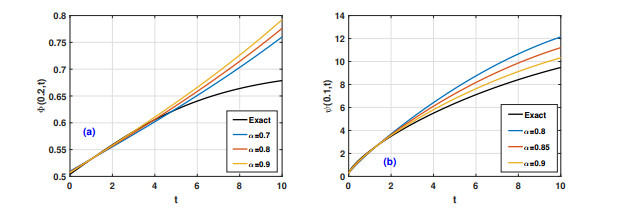
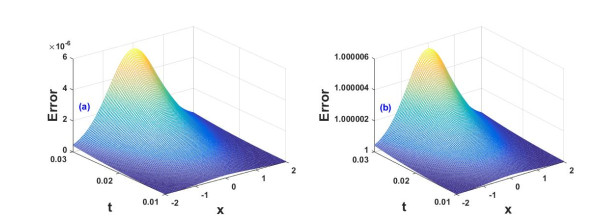
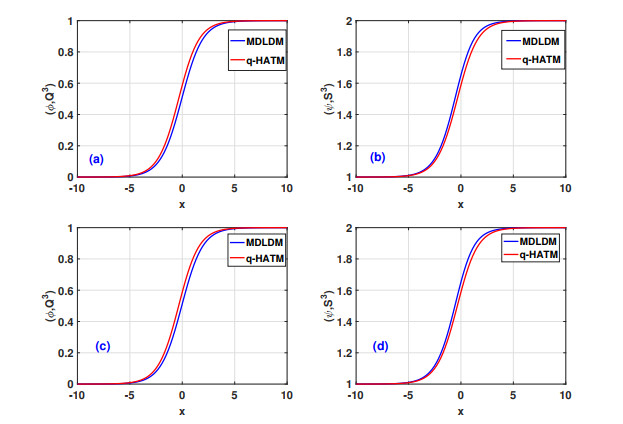
Figure 5(a), (b) show the nature of the MDLDM method in Fabrizio's sense for different values of α and time when spatial variable x is kept constant of the Eq (4.6) in Example 2. For the purpose of error analysis, we have depicted the absolute of the difference of exact and approximate solutions |Exact−(ϕ(x,t)ψ(x,t))| and for mCKdV equation, see Figure 6(a), (b). Notice that the difference of the wave solutions from the exact solutions is much small. It signifies the importance of the MDLDM for the approximate solutions. The observed errors are inserted in Table 2 (see Appendix) and their related plots are shown in Figure 6(a), (b) which shows the effectiveness of our proposed method to such non-linear modified coupled Korteweg-de Vries (mCKdV) equations. A comparative analysing of the problem in Tables 3–6 (see Appendix) between the two methods (MDLDM and q-HATM[20]) are shown. By analysing these tables, one can conclude easily the validation and accuracy of the proposed method over the q-HATM. Figure 7(a)–(d) are also show a remarkable results for the presented method.
5.
Conclusions
We have studied analytically the mCKdV with Caputo's and Caputo-Fabrizio (CF) derivatives using MDLDM. The proposed method is applied to the mCKdV system and approximate results are obtained in the form of series solutions by considering examples. The error analysis of the proposed method is also discussed. It is observed that the suggested scheme is one of the vigorous tools to investigate nonlinear problems. The main advantage of the suggested method is to analyze analytical solutions of the considered problem without using linearization and discretization. For validation, two examples in Caputo's and CF form are studied numerically and the results are compared with the numerical results with a physical interpretation. When non-integer order was employed in models including non-integer order derivatives, many scientists were less interested. For non-integer order fractional time derivative with singular and non-singular kernels of the mKdV equations, the MDLDM can be used. The MDLDM approach for handling nonlinear evolutionary equations was shown to have a broader applicability in this work. Physical meaning was given to the parameters in the resulting travelling wave solution. For varied values of the parameters, a three-dimensional simulation of wave behaviour is built, which alters the wave profile of the equation.The wave dynamics are discussed with the help of simulation. The results show that this strategy worked. The new wave solution presented in this work can open up new avenues for future research.
6.
Future work
A modified coupled time fractional KdV equation with Caputo's and Caputo-Fabrizio operators is considered in this manuscript. The characteristics wave profiles of the solution to the equation show some interesting behaviour especially when altering in the parameters. These interesting behaviours may be more interesting to transform the modified coupled time fractional KdV to modified coupled Schrodinger and sine-Gordon equations with Caputo's and Caputo-Fabrizio operators.
Acknowledgments
The authors are grateful to the Spanish Government for its support through grant RTI2018-094336-B-100 (MCIU/AEI/FEDER, UE) and to the Basque Government for its support through Grant IT1207-19.
Conflict of interest
It is declared that all the authors have no conflict of interest regarding this manuscript.
Appendix
Error analysis tables:
Please notes that, for error analysis, we consider α=1, b=k=0.5, λ=1.5, n = 3 and h = -1.









 DownLoad:
DownLoad: