A new solitary wave solution of the fractional phenomena Bogoyavlenskii equation via Bäcklund transformation

1.   Introduction

The topic of non-linear partial differential equations (NPDEs) is fundamental in progressing every scientific and engineering fields, such as physics, engineering, and chemistry. These equations are developed directly from the first principles to reflect the basic nature of the systems concerned irrespective of the field, such as fluid mechanics, orbital mechanics, structural mechanics, aerodynamics, etc. The solution of nPDEs, either through analytical solutions or numerical approximations, is a great deal in the sense that it gives insights that enhance the understanding of various phenomena. It is evident that several applications of analytical solutions of NPDEs are in the field of fluids engineering, mechanics, economy, solid-state physics, astrophysics, ionized gases, computational mechanics, and hydrodynamics ^[1,2,3,4,5]. In the last few decades, great advancement has been seen in a number of innovative methods and approaches that have been employed and evolved to look for these solutions and improve the modeling features and the predictive behavior of these systems, i.e., (G/G')-expansion technique ^[6], auxiliary equation method ^[7], homotophy analysis technique ^[8], Sine-Gordon expansion technique ^[9], trigonometric function series method ^[10], modified mapping method ^[11], bifurcation method ^[12], and meshfree techniques ^[13,14,15].

Furthermore, fractional calculus (FC) has become increasingly popular in various fields that are related to science and engineering. It has been used to simulate and explain a number of active techniques and complicated non-linear physical phenomena in such areas as physics, electromagnetism, and engineering, as well as anomalous diffusion, chemical kinetics, viscoelasticity, and electrochemistry ^[16,17,18]. Over the last few decades there has been a remarkable increase in the use of fractional calculus in these fields ^[19]. Many algorithms have been designed for solving nonlinear FDEs, which again emphasizes the significance as well as the broad applicability of (FC) in extending the existing knowledge and capability of analyzing and modeling complex processes ^[20,21,22]. Fractional calculus is further enhanced by looking into the impact of fractional-order derivatives on the multi-coupled discrete nonlinear transmission electrical network and the q-deformed Sinh–Gordon equation. Thus, for the first time, the performance and differences between beta, Conformable, M-truncated, and modified Riemann–Liouville derivatives are established. Fractional orders are proved to affect soliton propagation, signal behavior, and wave dynamics, their sensitivity to physical parameters, such as obliqueness angles and initial conditions proving the applicability of the fractional modeling ^[23,24]. From the above discussion, it was clear that these technique enhancements for solving FDEs have spear head the researchers to solve problems that could not be solved before, this has also borne many understandings and ideas in many scientific and engineering disciplines. Several differential operators, such as the fractal Hausdorff derivative and J. H. He fractal derivative, are applied in mathematical modeling of phenomena on fractal geometries especially for solving fractal PDEs ^{[25,26,27,28]}. Nevertheless, in the present work, we investigate another direction, considering the conformable fractional derivative, which enriches standard calculus by taking into account non-local interactions and memory inherent to these systems. In turn, this derivative is most suitable when modeling the time-space fractal nonlinear Bogoyavlenskii equation to determine interactions of waves and dispersion effects more conveniently.

The fractional Bogoyavlenskii equation is one of the important nonlinear dynamical equations that is used to study many important physical applications like the propagation of the wave in shallow water and plasma physics. The classical models often incorporate fractional integro-differential equations rather than such derivatives since it provides the opportunity to describe memory and hereditary effects while modeling realistic systems. Still, the fractional order parameter ($\alpha$) was central to the determination of such wave characteristics as amplitude, velocity, and dispersion. For example, values of ($\alpha$) that are possible indicate a strong memory effect, which in turn leads to slow dispersive waves, while large values of ($\alpha$) signify sharp and localized waves. It is the reason the discovered instances of analytical solutions in the shape of the solitary wave and shock waves give a stable and dynamic view of such physical systems, thus making the fractional Bogoyavlenskii equation relevant in nonlinear wave dynamics. To the equation, the theory of the conformable fractional derivative is used so that the description of systems with memory and non-local effects is possible. Provided assumptions are that nonlinearity or rather its approximation, is quite weak, and the medium is homogeneous, and the time and space effects, are represented by the fractional order ($\alpha$). That is why Eq (1.1) is most suitable for exploring physical processes such as dispersion of perturbations in a fluid and wave processes in plasma, as well as in the case of deviation from standard conditions, it explains the behavior of waves. In this regard, let ($t$) and ($x, y$) be the time and spatial dimensions, respectively. Further, the operator integrating $\alpha$-derivatives of powers agrees exactly to the idea of conformable fractional derivatives ^[29].

In addition, when ($\alpha = 1$), the equation under study can be transformed into the conventional form of the Bogoyavlenskii equation ^[30]. Various solutions to the Bogoyavlenskii equation have been applied for describing the wave propagation process of it. More especially, the shock wave solution and the complex solitary wave solution to the equation were obtained by employing the travelling wave method and the singular manifold method, respectively ^[31]. Malik et al. also discussed the same equation and employed the $G'/G$-expansion method and one of its modifications, finding exact travelling wave solutions of the Bogoyavlenskii equation ^[32]. Zahran and Khater used the method known as the modified extended tanh-function method to investigate travelling wave solutions ^[33]. Furthermore there are obtained several travelling wave solutions by the help of $exp-(-\phi(\xi))$-expansion method ^[34] and other fractional nonlinear partial differential equations ^{[35,36,37,38,39]}.

This work revolves around finding wave solutions of the time–space fractional Bogoyavlenskii equation, more so given the difficulties in simulating wave dispersion and nonlinearity in various systems. It can be very challenging to obtain sharp traveling wave solutions employing such equations within the classical frameworks. To address these challenges, we use the conformable fractional derivative that can effectively incorporate non-local interactions and memory effects existing in the system and follow the structured methodology. Therefore, the purpose of this paper is to obtain more precise and algebraically sound soliton solutions using the Riccati–Bernoulli sub-ODE method and ^[40,41,42] Bäcklund transformation, herein offering a methodological solution to the effect of nonlinear waves in the fractional Bogoyavlenskii system.

2.   Algorithm

Consider a non-linear partial differential equation of the form:

where $h = h(t, x_1, x_2, x_3, \ldots, x_r)$ is an unknown function and $R_1$ is represented as a polynomial in $h$ and its partial derivatives and non-linear terms.

Perform a wave transformation to decompose the given differential equation into a nonlinear ordinary differential equation. $g(\zeta) = h(t, x_1, x_2, x_3, \ldots, x_r)$. This transformation reduces the differential equation to a nonlinear ODE with respect to the variable ($\zeta$) of the form:

Assume that; Eq (2.2) has a formal solution of the form:

where $c_i$ are constants to be determined. It is assumed that, either $c_l \neq 0$ or $c_{-l} \neq 0$ and $G(\zeta)$ are obtained from the following Bäcklund transformation.

The constants ($R$), ($A$), and ($B$) are fixed parameters with $B\neq0$, also $\Theta(\zeta)$ satisfies a generalized Riccati equation:

Hence, the structure of the Riccati equation simplifies the nature of perfectly acceptable multiple solution types ^[43].

It is required to identify the positive integer ($m$) in the assumed solution by comparing the orders of derivative terms and nonlinear terms in the given ordinary differential equation. Substitute the assumed solution, the generalized Riccati equation, into the ODE. Set the coefficients of the obtained expression $\Theta(\zeta)$ equal to zero, and you will receive a set of algebraic equations. Substitute the values of the constants ($c_i$), ($\omega$), ($l$), and ($R$) obtained in the previous step into the algebraic equations, which are derived from the expansion of the functions, and solve them, generally through Maple. Replace the solutions of the algebraic equations into the assumed formal solution to give exact solutions of Eq (2.1). It is helpful for the readers to have the next step clearly outlined as follows to enable them to solve the problem:

1) Output: Introducing a new type of partial differential equations (PDE) widely known as fractional (FPDE).

2) For a direct evolution of FPDE into ODE, it is required to apply the transformation.

3) If one can posit an overall form of a solution.

4) Perform the Bäcklund transformation on the supposed solution.

5) Transform the topological system into an algebraic one.

6) We are to solve the algebraic system of unknown parameters.

7) Replace the parameters into the assumed solution so as to get the exact solutions.

8) Visualize solutions: Plot ($2D$ and intensity).

3.   Problem execution

This section describes a new algorithm to analytically solve the space–time fractional Bogoyavlenskii equation, pertinent especially to the main fluid flow in shallow water waves and plasma physics. The fundamental purpose of the study is to obtain the analytical solitary wave solution for the respective model fractional PDE. Here, $f(x, y, t)$, is considered with respect to the retarded time ($t$) along the direction of propagation ($x$). Thereby, we apply the following wave transformation in order to bring Eq (1.1) into a form of an ordinary differential equation that can be more easily solved analytically.

where ($l$), ($m$), and ($\omega$) are constants to be determined and $0 < \alpha\leq1$. In this respect, the wave transformation $F(\zeta)$ is found to be critical in reducing the generalized nonlinear time-space fractional Bogoyavlenskii equation to the form of an ODE that can easily be solved analytically. The constants ($l$), ($m$), and ($\omega$) contained in this transformation are dimensionally convenient factors that control the nature of and characteristics belonging to the solitary wave solutions. The coefficient ($\omega$) denotes the scaling of the temporal part ($t$), and its relation is closely associated with the temporal behavior of a wave. In a physical sense, it may be taken as a frequency-dependent parameter that defines the rate at which the wave travels. Thus, higher values of ($\omega$) are being associated with the higher rates of oscillations or wavefront advance. This coefficient is basic in explaining the change with time of the wave as it propagates through the medium.

Coefficient ($l$) controls the extent of spatial variable ($x$), the portion of propagation direction riding the wave profile. It is related to the wave amplitude and the wave length in the $x$-direction. Fluctuations in l determine the spatial dimensions of the wave and energy density that can be related to either the wave propagation or dispersion in the direction of the dominant motion axis. Likewise, the coefficient ($m$) controls the transverse spatial variable ($y$) and represents the lateral changes in the profile of the wave. This parameter is important in simulating again transverse distribution or interaction with boundaries in such fields as shallow water waves or plasmas. The fractional order parameter ($\alpha$) makes the system non-local and memory-based, thereby changing the physical context of the parameter space ($l$), ($m$), and ($\omega$) drastically. As ($\alpha$) approaches 1, this yields the more traditional case for the coefficients, and when ($\alpha = 1$), the system is identical to the traditional system. For ($\alpha < 1$), they represent the intricate nature of the fractional-order processes that arise from fractional-order derivatives, including anomalous diffusion and wave transport phenomena, adding depth to the model's utility.

By substituting Eq (3.1) into Eq (1.1), it simplifies the current equation into the form of an ordinary differential equation in the spatial variable ($\zeta$), making the analysis and identification of the solitary wave solution easier.

Integrating the second part of Eq (3.2) and keeping constant of integration zero for simplicity, we have

By substituting Eq (3.3) into the first Eq (3.2), we obtain a nonlinear equation in terms of ($F$). Integrating this equation, with the constant of integration set to zero, we have:

Solving for ($k$) by equating the highest order of derivatives ($F''$) and the nonlinear term ($F^3$), we get $k = 1$ ^[44]. Subsequently, by substituting Eqs (2.4), (2.5), and (2.3) into Eq (3.4), we get the following algebraic equation where the coefficients of $G(\zeta)$ are equal to zero.

Solving this system of algebraic equations using Maple yields the following results:

Case 1:

Case 2:

Case 3:

Solution family 1. In case 1 of Eq (1.1), the solitary wave solutions, under the condition $R < 0$, are presented as follows:

or

Solution family 2. In case 1 of Eq (1.1), the solitary wave solutions, under the condition $R > 0$, are presented as follows:

or

Solution family 3. In case 2 of Eq (1.1), the solitary wave solutions, under the condition $R < 0$, are presented as follows:

or

Solution family 4. In case 2 of Eq (1.1), the solitary wave solutions, under the condition $R > 0$, are presented as follows:

or

Solution family 5. In case 2 of Eq (1.1), the solitary wave solutions, under the condition $R = 0$, are presented as follows:

Solution family 6. In case 3 of Eq (1.1), the solitary wave solutions, under the condition $R < 0$ and $\psi = {\frac {c_{{1}}{x}^{\alpha}}{\alpha}}+{\frac {m{y}^{\alpha}}{\alpha}}- 1/2\, {\frac {{c_{{1}}}^{2}m{t}^{\alpha}}{\alpha}}$, are presented as follows:

or

Solution family 7. In case 3 of Eq (1.1), the solitary wave solutions, under the condition $R < 0$, are presented as follows:

or

Solution family 8. In case 3 of Eq (1.1), the solitary wave solutions, under the condition $R = 0$, are presented as follows:

4.   Results and discussion

In investigating the solutions of our model related to leading fluid flow in shallow water waves and plasma physics, we generated $2D$ and intensity plots and discussed a fractional perspective of solutions. Changing the form from integral to fractional enabled us to put more focus on the localization of the plots, which offered a better understanding of the system tendencies. For solving the given multiple wave patterns, we presented the Riccati-Bernoulli sub-ODE method for lump and kink wave structures through the $2D$ and intensity plots. From different applications of the value of $\alpha$ in the $2D$ representation, we got an updated view regarding these wave structures. The obtained kink and lump soliton solutions have enormous importance in the analysis of leading fluid flow in shallow water waves and plasma science. Following this, we illustrated different types of kink and lump solitons derived from the fractional Bogoyavlenskii equation by graphing them and noting that these are functions of hyperbolic, trigonometric, and rational kinds. In this case, with the help of MATLAB, we adjusted the figures for various parameters to the specific solutions in order to illustrate the kink, as well as the lump solitary wave solution. The following graphical presentations give sufficient information regarding the general nature and characteristics of such solutions so that we are ready to investigate their behavior further.

Figure 1 shows a lump soliton solution changing from an integer type to a fractional type and the intensity plot showing the change. The waveforms obtained with the fractional method are much more localized than in the integer case and are a key component of the model we have developed. This localization means that the fractional method is capable of offering more precision in the description of the wave interactions and energy in the shallow water area and of representing plasma particle confinement and stability in plasma physics and therefore, improving the predictability and the controllability in these applied fields.

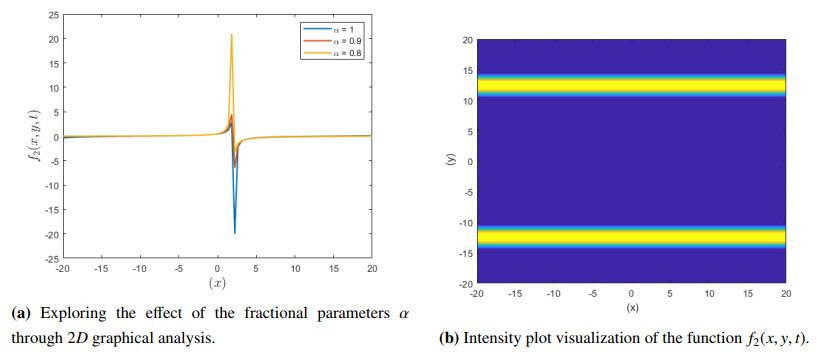
Figure 2 describes the behavior of a lump soliton solution, how it has a transition from integer to fractional, highlighting the localization effect through, intensity plot. Similar to Figure 1, the use of the fractional approach in Figure 2 yields a much more localized wave form than the integer form of the same model, hence displaying the significant effects of fractional models. That this kind of increased localization is possible in the fractional form indicates that the fractional approach can give a closer-to-reality description of the interactions of waves and the distribution of energies in the shallow waters as well as plasma confinements and stabilities. This in turn results in improved accuracy to forecast and control the fluid stream and plasma that is crucial for real-life use in these fields.

In Figure 3, the response of a dark-bright kink soliton solution is shown with reference to the change from integer to fractional. It can be seen that as a consequence of the fractional approach, the waveform of kink is more localized than for the integer case, which reinforces the necessity to apply the fractional modeling in the context of the present work. In the case of shallow water waves, use of this improvement reduces the diffusion in the fractional form, hence it will provide better detail of wave interactions and energy distribution, especially in limited zones. As for the plasma confinement and stability, the so-called localized kink soliton is more appropriate in plasma particle confinement and stability approximation in plasma physics for better understanding and optimization of plasma in applications such as fusion reactors. Obviously, this enhances ability to forecast and dictate fluid and plasma movements much more efficiently as it increases the level of precision.

Figure 4 shows the kink soliton solution of the given model characterized by transformation from integer to fractional forms as indicated by the intensity plot for the soliton envelope, which reveals the localization effect. Hence, the fractional approach leads to a smaller region of the waveform being associated with the kink, as shown in Figure 3, emphasizing the importance of including fractional modeling. This increased localization is important for the realistic modeling of wave interactions and energy distribution characteristics of shallow water waves and for the contouring of the plasma particle confinement and plasma stability in plasma physics. This has improved our capacity to predict control and overall behavior of fluids and plasma in a more realistic manner, which is very vital in these areas especially when working with real-life problems.

In Figure 5, one can see the behavior of a lump soliton solution and the change in forms to integer and fractional, where the intensity plot best demonstrates the soliton localization tendency. As it can be observed, the fractional modeling produces a more localized waveform of the lump than the integer form, providing an evidence for the need to model in fractions. This degree of localization is crucial for the proper depiction of the wave interference pattern and the energy spread of shallow water waves in the fluids, as well as for the portrayal of plasma particle containment and equilibrium in plasma physics uses. It improves the predictive power and manipulation in fluid dynamics and plasma work, which is important for the general advancement in the field of study and work in these areas.

In the present research work, mainly the conformable fractional derivative was used to analyze the nonlinear time-space fractional-order Bogoyavlenskii equation. This approach preserved many solution structures, among them multiple kinks and solitary wave solutions, and demonstrated the utility of the conformable fractional derivative in probing intricate wave behaviors. To enhance the analysis we wanted to introduce the beta fractional derivative. While the conformable fractional derivative mainly established kink solitary wave solutions, the beta fractional derivative established essentially different solitary wave solutions as well as shock wave patterns (see Figure 6). This comparison confirms the stability of the conformable fractional derivative for describing complex wave phenomena and shows that other fractional derivatives can produce complementary physical effects.

Table 1 shows the comparison of the fractional Bogoyavlenskii equation with the variational approach ^[45]. Our intensity plots in the manuscript emphasize the localization features of the fractional solutions within the nonlinear time–space fractional Bogoyavlenskii equation. The intensity plots reveal that the fractional models, especially considering the conformable fractional differential equations, enhance the precision of the wave dynamics, low diffusion, and better predictability of fluids and plasmas.

5.   Conclusions

Therefore, this research examine, the fractional-order derivative parameter ($\alpha$) that controls lump and kink soliton solutions important in the flow of fluids through shallow water and plasma systems. To explain the behavior of the system with respect to this parameter, we show a number of figures with amplitude fluctuations and changes of plot type. To improve our technique further, we included integer as well as fractional orders and compared the solutions of a given nonlinear fractional differential equation by employing the Riccati-Bernoulli sub-ODE method as well as the Bäcklund transformation. This methodology offered a better characterization of dynamic response and particular features of fluid and plasma flow. The conclusion recognizes the importance of the results showing an essential function of the fractional derivatives in understanding the more general perspectives; the results provide valuable insights for the further development of this field of study. For further development of the study, a deeper investigation of the nonlinear time-space fractional Bogoyavlenskii equations could be the focus of future research carried out on the basis of the modern theories of chaos and nonlinear dynamics. The inclusion of fractional order differentials makes it possible to study such phenomena as bifurcations, strange attractors, and sensitivity to initial conditions in models of systems with memory. Also, it seemed possible that by using machine learning algorithms and numeric analysis as tools to predict Parry curves in chaotic regions, some useful information may be provided. More work could also be directed towards the impact of changes of fractional orders on the stability as well as the complexity of chaotic solutions.

Author contributions

Y. J.: Conceptualization, Visualization, Funding, Data curation, Resources, Project administration, Writing-review & editing; H. Y.: Formal analysis, Data curation, validation; A. M. M.: Investigation, Validation, Resources, Software. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (KFU242684).

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (KFU242684).

Conflict of interest

The authors declare that they have no conflict of interest.