Stability of scientific big data sharing mechanism based on two-way principal-agent

1.   Introduction

In recent years, with the continuous improvement of China's scientific and technological innovation capacity and innovation investment, the scientific big data collection and management capacity y has also been improved step by step, but the scientific big data game strategy selection and open sharing incentive mechanism are relatively weak. In the era of big data, scientific and technological innovation is increasingly dependent on the analysis, mining and comprehensive utilization of scientific big data. At the same time, scientific big data is considered as a new engine of scientific discovery and a new scientific research methodology. The sharing of scientific big data is beneficial to promoting scientific progress, reducing repetitive work, improving scientific research ability and improving scientific research efficiency. It is of great significance. Scientific big data ^[1] is a compound term that refers to big data related to scientific research, including big data of scientific knowledge and big data of scientific activities (hereinafter referred to as "scientific data"). Scientific data is mainly derived from the physical world and has many characteristics, such as complexity, multi-source, heterogeneity, etc. It is urging the transformation of scientific research paradigm to data-intensive scientific paradigm ^[2]. Scientific research groups are not only the producers of scientific data, but also the beneficiaries of scientific data. Multi-source heterogeneous data fusion of heterogeneous scientific research groups can effectively release the economic value and scientific research value of scientific data, break down information barriers and information islands among scientific research groups, and achieve the amplification effect of 1+1 > 2. Although there are many benefits in the open sharing of scientific data, the scientific data sharing mechanism is still a complex and difficult issue, involving a series of issues such as sharing strategy, incentive mechanism, intellectual property rights, regulations and policies ^[3].

Since the launch of the scientific data sharing project in 2001, China has implemented strategies, such as the Action Plan for Promoting the Development of Big Data, the 13th Five-Year National Science and Technology Innovation Plan and issued the Scientific Data Management Measures, aiming to improve the scientific data sharing mechanism and improve the scientific data sharing and sharing, so that the open sharing of scientific data is the normal, and the open sharing of scientific data is the exception. The existing research shows that ^[4]: The deep fusion of multi-source and heterogeneous scientific data is not only to improve the academic and economic value of scientific data, but also to improve the innovation ability and efficiency of scientific research groups. Scientific data sharing includes four parts: basic elements ^[5], sharing mode ^[6], sharing mechanism ^[7] and security mechanism ^[8]. Under a suitable sharing mechanism, the basic elements realize the circulation of data resources according to the existing sharing mode, fully release the value co-creation function of data, and the security mechanism focuses on policy, technology and financial support. The influencing factors of scientific data sharing strategy mainly include personal factors ^[9], industry norms ^[10], platforms and governance ^[11] and many factors lead to difficulties in obtaining scientific data and low willingness of scientific research groups to share.

With the expansion and in-depth development of science and technology, it has provided support for alliance and cooperation between scientific research groups. Throughout history, few scientific research groups have completed major breakthroughs in the frontier of science, and most of them have been completed under the alliance and cooperation between heterogeneous scientific research groups. In addition, the quality of talents, research costs, scientific research facilities and the marketization of scientific data require exchanges and multilateral cooperation in different regions and fields to form a dynamic cooperation mechanism for sharing data resources. Data sharing by researchers with different disciplines, academic backgrounds and academic ideas can produce data resource fusion and amplification effect. Therefore, the issue of scientific data sharing mechanism for heterogeneous scientific research groups is crucial. For example, the research and development of the large aircraft C919 has been completed by up to 14 universities in collaboration. A suitable sharing mechanism is the prerequisite for the smooth development of the research and development work.

The core problem of scientific data sharing is the separation of data ownership and use right ^[12]. Due to the existence of information asymmetry and incomplete rationality, it is difficult to choose the sharing strategy between data owners and data users. Scientific research groups have dual identities as owners and users of data. Heterogeneous scientific research groups have both competition and cooperation game relationship and principal-agent relationship. The game relationship of competition and cooperation is that scientific research groups work together to form strategic alliances for data sharing, and at the same time form competitive concerns when facing the distribution of benefits and risks. The principal-agent relationship refers to that scientific research groups entrust each other with the right to use their own data temporarily. At this time, the heterogeneous groups are in the principal-agent relationship with each other. By building a scientific big data sharing ecosystem, this paper proposes two major constraint mechanisms for the evolution of the sharing ecosystem to a higher level, psychological indenture and contract indenture, which analyzes the path of iterative updating of the sharing ecosystem, clarifies the evolution mechanism of the sharing strategy and the incentive mechanism of the sharing strategy, discusses the influencing factors in an uncertain environment and designs the optimal incentive contract. It is expected to enrich the scientific big data sharing theory and provide policy inspiration for China's data sharing cause.

The second part is the basic theory of the scientific big data sharing ecosystem, the third part is the evolution mechanism of sharing strategies from the perspective of psychological contracts, the fourth part is the incentive mechanism of sharing strategies from the perspective of contract contracts, and the fifth part is the research conclusion and inspiration.

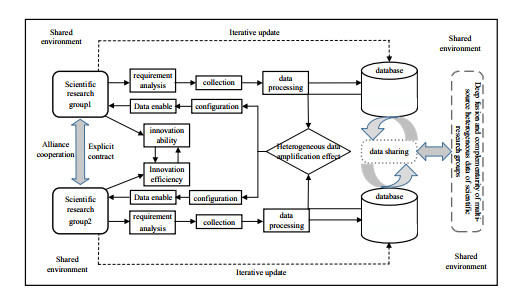
2.   Theoretical basis of scientific big data sharing ecosystem

Scientific research group ^[13] is a relatively loose organization, which generally refers to a group that has common scientific research objectives and is combined in a unique way. There are great differences in the external environment and internal structure of scientific research groups, which leads to heterogeneity among scientific research groups (hereinafter referred to as "heterogeneous scientific research groups"). With the increasing number of scientific research data, open data sharing has become the trend of scientific innovation and even national innovation. In the face of massive multi-source heterogeneous data, scientific research groups voluntarily form strategic alliances for collaborative innovation in order to improve scientific research capacity, improve innovation efficiency, meet diverse innovation and other needs, so as to realize high-speed circulation and sharing of scientific data among different levels, different fields and different standards, effectively reduce data collection costs and improve data utilization efficiency. Scientific research groups and the sharing environment constitute the scientific big data sharing ecosystem (Figure 1). Data is the flowing energy source in the ecosystem. Heterogeneous scientific research group alliance contracts are mainly subject to psychological contracts and contract contracts. Psychological contract is an implicit contract between heterogeneous scientific research groups, which is uncertain and dynamic; The contract is a linear contract between heterogeneous scientific research groups, with legitimacy and equality. Both are referred to as "explicit contract". According to the characteristics of psychological indenture and indenture contract, the stochastic evolutionary game model is used to explore the dynamic equilibrium and influencing factors of sharing strategy, and the two-way principal-agent model is used to explore the incentive mechanism and optimal contract design of sharing strategy. Stochastic evolutionary game theory originates from the fusion of evolutionary game and stochastic differential equation ^[14]. It explains how the sharing strategy of scientific research groups achieves equilibrium by simulating the interference caused by uncertain sharing environment. Uncertain environment mainly refers to the social system where scientific research groups are located is full of uncertainty and is affected by external environment (social culture, social interests, macro policies) and internal environment (group emotion, group organization, individual differences) and other factors; Two-way principal-agent ^[15] is based on asymmetric information game theory, which is used to explain the principal-agent relationship between the participants in the alliance cooperation. The participants share the output value of the alliance and the random risk of the alliance with the goal of maximizing the individual effect function.

The scientific big data sharing ecosystem includes ^[16]: six links: demand analysis, data collection, data processing, heterogeneous data amplification effect, data configuration and data empowerment. Through data sharing flow, the deep integration and complementarity of multi-source heterogeneous data can be realized, and the scientific research ability and innovation efficiency of scientific research groups can be improved. Demand analysis is the analysis and positioning of innovation demand of scientific research groups. With the implementation of national strategies such as Internet plus and big data, the trend of cross collaboration of heterogeneous scientific research groups and deep integration of multi-source heterogeneous data is becoming increasingly obvious, and the data demand is increasingly diversified; data collection means to collect matching data after accurately grasping the needs of scientific research groups. Data can also be obtained through market-oriented transactions as innovative information; data processing is used to extract high-value digital information from a large number of original data, mainly for data collection, storage, retrieval, processing, transformation and transmission; the amplification effect of heterogeneous data refers to the total effect of data fusion greater than the sum of the two, which mainly reflects the complementarity of multi-source heterogeneous data; data configuration is to reconfigure innovation elements after heterogeneous data fusion to realize new innovation value and optimization of innovation elements; data empowerment refers to the integration of different links in the innovation activities of scientific research groups, mainly including research, development and application.

3.   Evolutionary mechanism of sharing strategy from the perspective of psychological contract

3.1.   Subheading stochastic evolutionary game analysis of sharing strategy

Heterogeneous scientific research groups can choose to share or not share two strategies under the constraint of psychological contract mechanism in order to achieve deep integration of multi-source heterogeneous data and form alliance cooperation. The choice of strategy is related to the existence of alliance relationship and the distribution of benefits. The internal influencing factors of strategy choice mainly include: Degree of complementarity, willingness to share, random interference and moral hazard. The degree of complementarity is a quantitative indicator of complementarity, and complementarity is a prerequisite for the sharing of scientific data. In an era of rich and diverse data types, the sharing of complementary data or the cross-fusion of multi-source heterogeneous data is the basis for innovation. Therefore, the identification of the degree of complementarity is an important part of the needs analysis of scientific research groups; the willingness to share is an externalized manifestation of the psychological contract and a subjective indicator to measure the degree of sharing of scientific research groups. The low willingness to share is the key problem leading to the difficulty of scientific data sharing in China. The willingness to share is often inseparable from the trust mechanism and incentive contract. The greater the trust between scientific research groups, the higher the willingness to share, the stronger the incentive degree of incentive contract and the higher the willingness to share; Random interference is a local interference caused by the uncertain environment on the sharing strategy of scientific research groups. It is a non-dominant system that dynamically adjusts the energy, only changes the local state and has no obvious propagation law to follow; Moral hazard is caused by information asymmetry, network externalities, "free ride" and other factors of both sides of the game. One side of the game adopts the sharing strategy to make the other party generate moral hazard and increase its own losses. On the basis of previous studies, this section discusses the dynamic equilibrium and influencing factors of sharing strategy evolution in uncertain environment from the perspective of psychological contract. See Table 1 for model symbols and meanings.

Suppose that the participants are heterogeneous scientific research groups: scientific research group 1 and scientific research group 2. The strategic space of both sides of the game is the same (shared, not shared). Build the benefit matrix of scientific research group game, see Table 2.

The benefit matrix is analyzed as follows:

When both sides of the game choose the sharing strategy, the heterogeneous scientific research groups realize complete docking of multi-source and heterogeneous data, and the benefits are ${x_1} + {\lambda _1}{x_2}$ and ${x_2} + {\lambda _2}{x_1}$; When scientific research group 1 chooses the non-sharing strategy and scientific research group 2 chooses the sharing strategy, the benefit of scientific research group 1 is ${x_1} + {\lambda _1}{x_2}$, the benefits of scientific research group 2 are ${x_2} + {\lambda _2}{\delta _1}{x_1} - \Delta {x_1}$. When scientific research group 1 chooses to share and scientific research group 2 chooses not to share, the benefit of scientific research group 1 is ${x_1} + {\lambda _1}{\delta _2}{x_2} - \Delta {x_1}$, the benefits of scientific research group 2 are ${x_2} + {\lambda _2}{x_1}$; When both sides of the game choose not to share, the bilateral contractual relationship of the strategic alliance cannot exist, the integration of multi-source heterogeneous data cannot be realized, and the benefit of scientific research group 1 is ${x_1}$, the benefits of scientific research group 2 are ${x_2}$.

The author still follows the traditional approach and uses the replication dynamic equation to describe the dynamic evolution mechanism of the sharing strategy. In comprehensive consideration of the existing literature and space limitations, the details of copying dynamic equations are referred to Hingu ^[17], Erwin ^[18] and other achievements. Evolutionary game replication dynamic equation of sharing strategy of heterogeneous scientific research groups:

Scientific research group 1 adopts sharing and non-sharing expected benefits:

When scientific research groups choose to share expected benefits more than not share expected benefits, the proportion of sharing will increase. On the contrary, it also decreases. Scientific research group 1 evolutionary game replicates dynamic equation:

Scientific research group 2 shares and does not share expected benefits:

Scientific research group 2 evolutionary game replicates dynamic equation:

In order to highlight all kinds of random interference in uncertain environment, Gaussian white noise is introduced to describe it. Refer to Xu ^[19] for details.

Equilibrium solution and proof of stochastic dynamic systems need to rely on stochastic theory, mainly referring to Huang ^[20], Hu ^[21] and other works, without focusing on it. Based on this, the stability conditions of heterogeneous scientific research groups under random interference are obtained:

Lemma 1.1. Gives a stochastic differential equation:

Assume existence function $V(t, x)$ and normal numbers ${{c}_{1}}, {{c}_{2}}$ make

1) If there is a normal number $\gamma$, such that

Then the zero solution of Eq (1.6) is exponentially stable and holds the $p$-th moment

2) If there is a normal number $\gamma$, such that

3) The zero solution of Eq (1.6) is exponentially unstable and holds

Among them, $LV(t, x) = {{V}_{x}}(t, x)+{{V}_{x}}(t, x)f(t, x)+1/2{{g}^{2}}(t, x){{V}_{xx}}(t, x)$.

Based on Lemma 1.1, obtain the stability judgment criteria for Eq (1.5).

● For scientific research group 1. When $q(t) \geqslant \frac{{{\lambda _1}{\delta _2}{x_2} - \Delta {x_1} + 1}}{{{\lambda _1}{\delta _2}{x_2} - \Delta {x_1}}}$ and ${\lambda _1}{\delta _2}{x_2} - \Delta {x_1} \lt 0$, then the moment of zero solution of shared evolution of scientific research group 1 is exponentially stable; When $q(t) \lt \frac{{{\lambda _1}{\delta _2}{x_2} - \Delta {x_1} + 1}}{{{\lambda _1}{\delta _2}{x_2} - \Delta {x_1}}}$ and ${\lambda _1}{\delta _2}{x_2} - \Delta {x_1} \gt 1$, then the moment index of the shared zero solution of scientific research group 1 is unstable. Scientific research group 1 will eventually give up the sharing strategy and take the non-sharing strategy as a whole after playing with scientific research group 2 for many times under the condition of meeting the index stability; Under the condition of unstable index, scientific research group 1 is more inclined to adopt sharing strategy.

● For scientific research group 2. When $p(t) \geqslant \frac{{{\lambda _2}{\delta _1}{x_1} - \Delta {x_2} + 1}}{{{\lambda _2}{\delta _1}{x_1} - \Delta {x_2}}}$ and ${\lambda _2}{\delta _1}{x_1} - \Delta {x_2} \lt 0$, then the moment of zero solution shared by scientific research group 2 is exponentially stable; When $q(t) \lt \frac{{{\lambda _2}{\delta _1}{x_1} - \Delta {x_2} + 1}}{{{\lambda _2}{\delta _1}{x_1} - \Delta {x_2}}}$ and ${\lambda _2}{\delta _1}{x_1} - \Delta {x_2} \gt 1$, then the moment index of shared zero solution of scientific research group 2 is unstable. Scientific research group 2 will eventually give up the sharing strategy and take the non-sharing strategy as a whole after playing with scientific research group 2 for many times under the condition of meeting the index stability; Under the condition of unstable index, scientific research group 2 is more inclined to adopt sharing strategy.

To sum up, we should meet $q(t) \geqslant \frac{{{\lambda _1}{\delta _2}{x_2} - \Delta {x_1} + 1}}{{{\lambda _1}{\delta _2}{x_2} - \Delta {x_1}}}$ and ${\lambda _1}{\delta _2}{x_2} - \Delta {x_1} \lt 0$, $p(t) \geqslant \frac{{{\lambda _2}{\delta _1}{x_1} - \Delta {x_2} + 1}}{{{\lambda _2}{\delta _1}{x_1} - \Delta {x_2}}}$ and ${\lambda _2}{\delta _1}{x_1} - \Delta {x_2} \lt 0$, there is a unique stable strategy for shared dynamic evolution $ESS(0, 0)$, that is, scientific research groups will eventually adopt (no sharing, no sharing) strategies. Due to the existence of factors such as opportunism and self-protection awareness of scientific research groups, this non $Nash$ equilibrium strategy appears at the end of the game, which is the fundamental reason for the collapse of the scientific data sharing alliance; When $q(t) \lt \frac{{{\lambda _1}{\delta _2}{x_2} - \Delta {x_1} + 1}}{{{\lambda _1}{\delta _2}{x_2} - \Delta {x_1}}}$ and ${\lambda _1}{\delta _2}{x_2} - \Delta {x_1} \gt 1$, when $q(t) \lt \frac{{{\lambda _2}{\delta _1}{x_1} - \Delta {x_2} + 1}}{{{\lambda _2}{\delta _1}{x_1} - \Delta {x_2}}}$ and ${\lambda _2}{\delta _1}{x_1} - \Delta {x_2} \gt 1$, At this time, there is a unique stable strategy in the evolution process of the shared strategy $ESS(1, 1)$, that is, scientific research groups will eventually adopt (sharing, sharing) strategies.

3.2.   Sensitivity analysis of sharing strategy

Based on the above stochastic evolutionary game model, the sharing strategy of scientific research groups ultimately has two stable strategies: (unshared, unshared) and (shared, shared). This is mainly related to the change of some parameters in the benefit matrix. Based on this, sensitivity analysis is carried out on the influencing factors such as the degree of complementarity, willingness to share, random interference and moral hazard. With the help of numerical simulation, the stochastic evolutionary game model is mainly processed by $Milstein$ method combined with stochastic $Taylor$ expansion and $It\hat o$ stochastic formula. Refer to Huang ^[20] and Sun ^[22] for specific algorithms. See Table 3 for initial values of parameters.

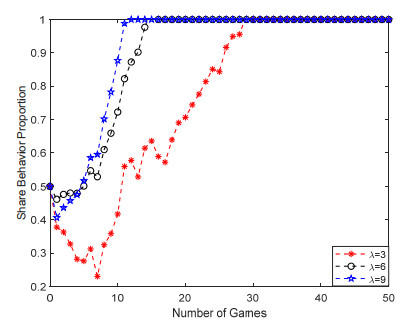
A. Complementarity

In the era of big science, the interdisciplinary integration makes any scientific research group only obtain limited information resources in limited time, space and discipline. Scientific data sharing is to allow massive information resources to flow in scientific research activities and maximize the role of scientific data resources. However, due to the diversity of scientific data forms, different collection methods and purposes, there are differences in scientific data resources of heterogeneous scientific research groups. Research findings (Figure 2): The degree of complementarity of scientific data can effectively reduce the impact of random interference. The greater the degree of complementarity, the smaller the fluctuation of random interference; The degree of complementarity is in direct proportion to the convergence rate of sharing strategies of scientific research groups. The greater the degree of complementarity, the greater the probability of scientific research groups choosing sharing strategies.

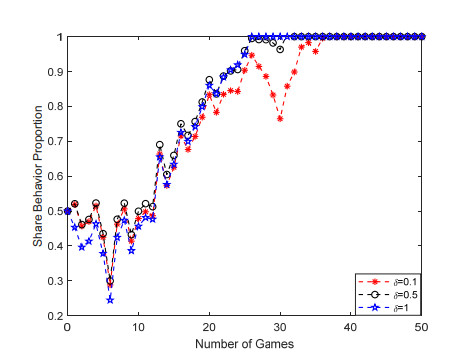
B. Willingness to share

In the face of today's interdisciplinary and integrated development of scientific research environment, scientific data plays an important role in supporting scientific and technological innovation. Scientific researchers want to obtain the original data of others but are not willing to share their own original data, resulting in low willingness to share scientific data and difficulty in sharing scientific data. The belief, reputation and self-worth of scientific researchers are important factors that directly lead to the low willingness to share. The willingness to share is a parameter to describe the psychological contract. The research findings (Figure 3): The sharing intention has no significant impact on group decision-making choices. With the increase of sharing intention, the convergence rate of sharing strategy of scientific research groups has not significantly improved. The main reason is that: the willingness to share is a subjective indicator of individuals, which has no significant impact on group decision-making. Enhancing the willingness to share will not significantly improve the convergence rate of scientific research group sharing strategy.

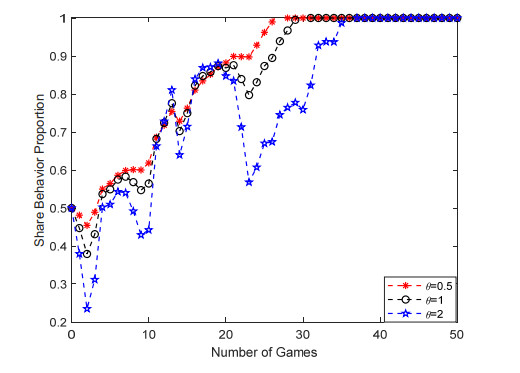
C. Random interference

In the scientific data sharing ecosystem, the complexity of the relationship between scientific research groups and the uncertainty of individual behavior lead to the randomness of sharing behavior selection. Scientific research groups are composed of many individuals, whose behavior choices are affected by their own and environmental factors, and have the characteristics of random evolution. The choice of scientific research group behavior is not a simple superposition of individual behavior choices, but is determined by the evolution of a large number of individual choices, showing some new characteristics and new laws at the group level. If the process of scientific research group selection is regarded as a process of trial and error, random interference is the threshold in trial and error, which can correct or fine-tune the behavior selection of scientific research group according to the surrounding historical information. Research findings (Figure 4): Random interference has a significant impact on individual sharing behavior. The random evolution trajectory shows a non-smooth curve fluctuation. The random interference will only change the local stable state of individual sharing, and will not change the stable state of scientific research group sharing. In addition, random interference will slow down the convergence rate of scientific research groups. The stronger the random interference, the slower the stability rate. In reality, when faced with increasing uncertainty risks, participants need enough time to observe the other party's decision changes to develop their own strategies.

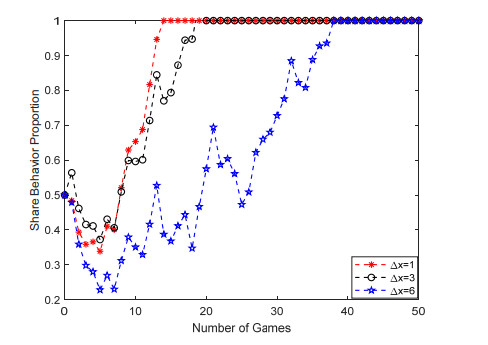
D. Moral hazard

Heterogeneous scientific research groups voluntarily form strategic alliances in order to seek data sharing. Alliance members often take advantage of their own information advantages to adopt strategies that cannot be observed and monitored by the other party, thus causing the objective existence of moral hazard for alliance members. Moral hazard can only reduce the probability of moral hazard by optimizing the shared ecological environment, and cannot completely avoid the occurrence of moral hazard. The study found (Figure 5) that moral hazard was significantly negatively correlated with the rate of group yield. The greater the moral hazard, the slower the convergence rate. The main reason is that moral hazard increases the risk of group selection of sharing strategies. When some individual decisions have a large proportion of non-sharing, group decisions need sufficient time to seek the optimal sharing strategy in the process of trial and error.

To sum up, for the stability of scientific research group sharing evolution, the degree of scientific data complementarity is a positive indicator, while external random interference and network moral hazard are negative indicators, and individual sharing willingness has no significant impact on group sharing behavior; The evolution trajectory of shared strategy under uncertain environment is a non-smooth curve, which is basically consistent with the evolution law under certain environment, but there are differences in stability solution and judgment.

4.   Incentive mechanism of sharing strategy from the perspective of contract

4.1.   A Bidirectional principal-agent analysis of the incentive mechanism of shared strategies

Heterogeneous scientific research groups voluntarily form strategic alliances in order to maximize their individual utility functions, and have their own reserved utility functions to share scientific data with each other, which is a typical two-way principal-agent relationship. The two-way principal-agent relationship of alliance members is constrained by the explicit contract mechanism, and both sides are at a strategic disadvantage in the case of asymmetric information. How to design a sharing strategy incentive mechanism for third parties (governments, platforms, scientific research groups, etc.) to balance benefits and risks? How to maximize the benefits of the alliance?

Following the traditional principal-agent theory paradigm, this paper discusses the optimal incentive contract design from the perspective of principal and agent. Alliance members (scientific research groups) have the dual identities of principal and agent, construct a virtual member to represent the strategic alliance, and ask the alliance members to turn in the right of entrustment to the virtual member. Virtual members (strategic alliances) are called "virtual principals", and alliance members (scientific research groups) who turn in the power of attorney are called "agents". Build a two-way principal-agent model after the introduction of virtual principals:

See Table 1 for the meaning of variables in model (4.1). $F$, ${F_1}$ and ${F_2}$ represent the utility functions of virtual client, scientific research group 1 and scientific research group 2, and the utility functions are concave functions. They represent the utility functions of virtual client, scientific research group 1 and scientific research group 2, and the utility functions are concave functions. For the convenience of discussion, the costs shared by scientific research groups are as follows:${C_1}({x_1}) = \frac{1}{2}{b_1}x_1^2$ and ${C_2}({x_2}) = \frac{1}{2}{b_2}x_2^2$, use $Cobb - Douglas$ production function to describe the overall income of strategic alliance, then virtual principal production function $Y = {x_1}^\alpha {x_2}^{1 - \alpha } + \varepsilon$. Among them, $\varepsilon$ is a normal distribution random variable with zero mean and variance equal to ${\sigma ^2}$, it represents exogenous uncertainties. Then the expected output of the virtual client is $E(Y) = {x_1}^\alpha {x_2}^{1 - \alpha }$. When designing incentive contracts, use Holmstrom et al. ^[23] proposed a linear function as the distribution function of the alliance members' income: ${y_1} = {w_1} + \frac{1}{2}\beta (Y - {w_1} - {w_2})$; ${y_2} = {w_2} + \frac{1}{2}\beta (Y - {w_1} - {w_2})$. Among them, the utility function of the alliance members has an invariable absolute risk aversion, and the risk cost $\frac{1}{2}\rho {\beta ^2}{\sigma ^2}$ proposed by Zhang ^[24] is used to represent the random risk. Then:

Virtual client utility function:

Utility function of scientific research group 1 and 2:

The two-way principal-agent model (4.1) can be converted into model (4.2):

For solving the optimization problem of model (4.2), the optimal solution is obtained by constructing the Lagrange function. Optimize two first-order conditions to obtain:

Formula (4.3) shows that under the optimal solution of model (4.2), the optimal sharing amount of scientific data between scientific research group 1 and scientific research group 2 is linear, inversely proportional to the sharing cost coefficient and directly proportional to the output elasticity coefficient.

4.2.   Optimal contract design of incentive mechanism for sharing strategy

The incentive of scientific researchers is the core issue of scientific data sharing and sharing, and the main explicit constraint mechanism is incentive contract. For the third party, how to design the optimal incentive contract is the key issue of whether the data sharing ecosystem can be healthy and sustainable, and is also an effective means to achieve open data sharing. It is impossible for one member of the alliance to use the mandatory contract to force the other party to adopt the desired strategy, but can only use the incentive contract to induce the other party to choose the desired strategy. For simplicity, suppose ${x_1} = {x_2} = x$. Model (4.2) can be simplified into model (4.4):

The first-order condition of model (4.4) optimization means:

Bring formula (4.5) into the constraint of scientific research group participation:

Formula (4.5) indicates that the Pareto optimal contract under the condition of information symmetry requires the members of the alliance not to bear any risk $({\beta ^*} = 0)$, and the members' income is composed of two parts: the retained wage and the shared cost, which is independent of the amount of scientific data sharing. In the cooperative work of actual alliance members, Pareto optimality under the condition of information symmetry is obviously not achievable. Because: it is impossible for one member of the alliance to completely and truly observe the amount of scientific data shared by the other, the member will choose to maximize their utility function. Given $\beta = 0$, the income of the alliance member is independent of the amount of data shared, then $x = \beta /({b_1} + {b_2}) = 0$. This shows that under the condition that the alliance members do not bear any risks, they will choose to adopt the non-sharing strategy to minimize the sharing costs.

Next, we discuss the optimal incentive contract under the condition of asymmetric information. Given $(x, \beta )$, the incentive compatibility constraint of the alliance members means $x = \beta /({b_1} + {b_2})$ and the problem of the virtual client is to choose the optimal (x, y) solution model (4.6) optimization problem.

The optimal first-order condition of model (4.6) means:

Formula (4.7) indicates that the members of the alliance must bear certain risks, and the size of the risks is inversely proportional to the cost coefficient, risk aversion and output variance. In short, the more members of the alliance are afraid of scientific data sharing, the less risk they will take. Because under a certain cost coefficient, in order to encourage the members of the alliance to choose the same amount of data sharing, the greater the risk, the virtual client would prefer to exchange less data for saving the risk cost.

5.   Conclusions and enlightenment

5.1.   Conclusions

By building a scientific big data sharing ecosystem, this paper proposes the psychological contract and the explicit and implicit constraint mechanism of the contract contract. On this basis, the evolution mechanism of the sharing strategy and the incentive mechanism of the sharing strategy are discussed respectively. The main conclusions are as follows:

A. The alliance of heterogeneous scientific research groups cooperates to carry out innovative research, which is bound by psychological contract and contract contract. The scientific big data sharing and sharing ecosystem includes six links: demand analysis, data collection, data processing, heterogeneous data amplification effect, data configuration and data empowerment. Data is the flowing energy source in the ecosystem.

B. The solution of stochastic evolutionary game equilibrium conditions is more complex than the solution of evolutionary game equilibrium conditions. The former has stronger explanatory power for the evolution of scientific research group sharing behavior. The evolution trajectory of stochastic evolutionary game is a non-smooth curve, which is closer to the actual problem. The degree of complementarity of scientific big data is a positive indicator, while external random interference and network moral hazard are negative indicators. Individual sharing willingness does not affect the evolution and convergence rate of group sharing strategy.

C. The two-way principal-agent theory can explain the mutual principal-agent relationship of alliance cooperation, providing a theoretical basis and research paradigm for the follow-up research. The optimal incentive contract consists of fixed wage and incentive wage, which is an increasing function of risk. Risks must exist and can only be reduced by optimizing the sharing environment. The more researchers are afraid of sharing, the smaller the risk cost they bear. The core problem is to find the optimal solution between incentive cost and risk cost.

5.2.   Enlightenment

At present, there is still a certain gap between China's science big data sharing business and that of developed countries such as Europe and the United States. Although China's science big data collection capacity has been continuously improved, the international policy level is still relatively weak. In view of the weak links in China's science big data sharing, combined with the contents of this paper, the policy implications are as follows:

A. Create a healthy scientific big data sharing ecosystem and improve the conversion efficiency of mobile energy sources. The scientific research community and the shared environment are an inseparable whole, which is called the ecosystem. It can be seen from Figure 1 that the amplification effect of heterogeneous data is the core link of ecosystem health, efficiency and evolution. We should learn from the successful experience of developed countries in Europe and the United States to support the formation of a number of national-level scientific big data sharing centers, and strengthen the standardization of scientific big data collection and production, processing and processing, open sharing and other links.

B. Establish and improve the scientific big data sharing legal system and strengthen the protection of intellectual property rights. This paper believes that it can be carried out from three aspects: first, improve the trading mechanism of scientific big data and make scientific big data realize formal trading. Big data as a resource must have typical trading characteristics; Second, improve the punishment mechanism for scientific big data abuse and protect the rights and interests of the original data owners. Big data as a resource will inevitably have theft, abuse, counterfeiting and other behaviors; Third, improve the scientific big data sharing mechanism, strictly follow the principles of openness, fairness and equity to carry out data sharing and sharing, and minimize the costs caused by random interference and moral hazard.

C. Establish and optimize the incentive mechanism for scientific big data sharing, and incorporate the sharing behavior into the performance evaluation. This paper believes that suitable psychological contract and incentive contract are the two main mechanisms to constrain the sharing behavior of scientific big data. For the special relationship between cooperative work of heterogeneous scientific research groups, new theories should be adopted to explain. The choice of sharing strategies for scientific research groups is ultimately a matter of interest distribution. The government should fully consider the proportion of fixed wages and incentive wages when formulating policies, and should design incentive contracts that change with risk.

5.3.   Future research directions

Application of blockchain technology. Integrate blockchain technology into the system to enhance security, transparency and traceability. Trusted collaboration, where data is available but not visible. The encryption algorithm of blockchain technology enables permission management for different entities involved in data sharing, effectively reducing security risks during the data sharing process, providing users with strong privacy protection and ensuring the security and accuracy of data during transmission. At the same time, the data that needs to be shared is stored on the chain. If there is a data ownership dispute in the future, records can be searched on the chain ^[25]. Authorization on the data chain and sharing off the chain. By building a data sharing blockchain alliance chain, data providers import data information according to settings. Assuming that one party wants to use the data inside, they can view who has the data they want through the blockchain network and then apply on the chain. This operation will also be provided to the data provider synchronously. After the other party sees the application information, they will place the authorization information on the chain to complete data authorization. At this time, the data user can obtain the data from the data provider through offline means. This is the on chain authorization and off chain sharing, which has a wide range of applications, especially in the supply chain field ^[26].

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Social Science Foundation Program of China (No. 22CJY040).

Conflict of interest

The authors declare that they have no conflicts of interest.