Computing mod $\ell$ Galois representations associated to modular forms for small primes

1.   Introduction

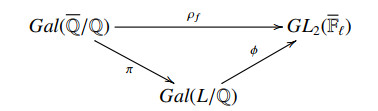
Let $\ell$ be a prime number and $f \in S_{k}(\varGamma_{1}(N))$ be a cusp form of weight $k$ and level $N$. Let $\rho_{f}: Gal(\overline{\mathbb{Q}}/\mathbb{Q}) \rightarrow GL_{2}(\overline{\mathbb{F}}_{\ell})$ be a mod $\ell$ Galois representation associated to $f$. Let $L$ be the fixed field of the kernel of $\rho_{f}$. Then the representation $\rho_{f}$ factors through as:

where $\pi$ is the canonical restriction map and $\phi$ is the isomorphism between Gal$(L/\mathbb{Q})$ and the image ${\rm im}(\rho_{f})$ of $\rho_{f}$. Thus to compute $\rho_{f}$, it suffices to give the Galois extension field $L$ over $\mathbb{Q}$ and the isomorphism $\phi$.

In their book ^[1], Edixhoven et al. propose a polynomial time algorithm to compute $\rho_{f}$ associated to level one modular forms. They prove that $\rho_{f}$ can be described by a certain polynomial $P_{f}\in \mathbb{Q}[x]$ of degree $\ell^{2}-1$ whose splitting field is the fixed field $L$ of ker($\rho_{f}$). One can obtain $L$ by adjoining the roots of $P_{f}$ to $\mathbb{Q}$, and the isomorphism $\phi$ is induced by a bijection between the roots of $P_{f}$ and a $2$-dimensional subspace of the $\ell$-torsion of the Jacobian variety $J_{1}(\ell)$ of the modular curve $X_{1}(\ell)$ associated to $\varGamma_{1}(\ell)$. This algorithm has been generalized to modular forms of arbitrary levels by Bruin ^[2]. Likewise, the associated projective representation $\tilde{\rho}_{f}: Gal(\overline{\mathbb{Q}}/\mathbb{Q}) \rightarrow PGL_{2}(\overline{\mathbb{F}}_{\ell})$ can be described by a suitable polynomial $\tilde P_{f}\in \mathbb{Q}[x]$ of degree $\ell+1$.

The computations depend heavily on $\ell$ and the genus of the modular curve $X_{1}(\ell)$, which is equal to $(\ell-5)(\ell-7)/24$. In practice, the most time-consuming part of the algorithm is to approximate the points of $J_1(\ell)$, and the precision significantly increases when $\ell$ grows. Consequently, the explicit computations have been done only for the primes no bigger than $43$.

Let $\Delta_{k}$ be the unique cusp form of level $1$ and weight $k$ with $k = 12, 16, 18, 20, 22, 26$. In practice, this algorithm has been first implemented by Bosman [1,Chapter 7] to evaluate the projective polynomial $\tilde P_{\Delta_{k}}$ for $\ell\le 23$ and $k\le \ell+1$. In ^[3,4] and the unpublished paper ^[5], this algorithm has been improved and more polynomials $\tilde P_{\Delta_{k}}$ have been explicitly computed for $\ell\le43$.

However, as far as we know, no one has implemented the algorithm to calculate the polynomials for the cases with $\ell < k-1$. In this paper, we shall discuss the algorithms for computing mod $\ell$ Galois representations associated to modular forms of weight $k$ when $\ell < k-1$. We will propose an algorithm of this case and then do explicit computations of the mod $\ell$ projective Galois representations $\tilde{\rho}_{ \Delta_{k}}$ for $k = 16, 20, 22, 26$ and all the unexceptional primes $\ell$ for which $\ell < k-1$.

In the book ^[1], the authors deal with the case with $\ell < k-1$ by twisting the representations and then reduce the computations to the cases with $k\le\ell+1$. In fact, for a form of level one and weight $k$ with $\ell < k-1$, in [1,Proposition 2.5.18] they show a method to obtain a form of weight $k'\le \ell+1$, such that the two Galois representations associated to the two forms are isomorphic. In this paper, we will prove this result also holds for modular forms of levels greater than $1$.

First, in Section 2, we show a generalization of Sturm bound theorem [6,Theorem 2] to mod $\ell$ modular forms, which gives an explicit method to identify two forms by observing a few coefficients of the $q$-expansions. Then in Section 3, we use the generalized result to give an explicit method, for a given modular form of type $(N, k, \varepsilon)$, to obtain a twist form of type $(N, k', \varepsilon)$ with $k'\le \ell+1$, such that the two Galois representations associated to the two forms are isomorphic up to twist. In fact this is a generalization of [1,Proposition 2.5.18] to modular forms of arbitrary levels. Consequently, the computations of the cases with $\ell < k-1$ boil down to the cases with $k\le\ell+1$.

In the end of Section 3, we prove the corresponding results for the projective representations and then present the algorithm for the projective case.

In Section 4, we apply the algorithm in Subsection 3.3 to do explicit computations of the mod $\ell$ projective Galois representations $\tilde{\rho}_{ \Delta_{k}}$ for $k = 16, 20, 22, 26$ and all the unexceptional primes $\ell$ for which $\ell < k-1$. Here $\Delta_{k}$ is the normalized cusp form of level one and weight $k$. The computed projective polynomials $\tilde P_{\Delta_{k}}(x)$ associated to the representations $\tilde{\rho}_{ \Delta_{k}}$ are shown in Table 4.

Lehmer ^[7] conjectures that Ramanujan's tau function $\tau(n)$ is non-vanishing for all $n$ and shows that $\tau(n) \neq 0$ for all $n < 3316799$. Serre ^[8] sums up the congruences of $\tau(p)$ modulo exceptional primes of $\tau(p)$ and obtains a bound of 15 digits for Lehmer's conjecture with respect to $\tau(n)$. Bosman ^[1] first used the results of modular Galois representations to discuss the non-vanishing coefficients of $\tau(n)$ and then this method was developed by others. So far the bound for Lehmer's conjecture with respect to $\tau(n)$ is up to 24 digits ^[5].

In ^[9], the authors discuss non-vanishing Fourier coefficients $a_n(\Delta_k)$ of $\Delta_{k}$ and achieve the bounds $B_k$ of $n$ such that $a_n(\Delta_k)\ne0$ for all $n < B_k$ in the cases with $k = 16, 18, 20, 22, 26$.

In this paper, as an application, we shall discuss the non-vanishing Fourier coefficients of $\Delta_{k}$ using our results. In fact, for $k = 16, 20, 22, 26$, we obtain higher bounds $B_k$ of $n$ such that $a_n(\Delta_k)\ne0$ for all $n < B_k$. We demonstrate how much the bounds $B_k$ have been improved for $k = 16, 20, 22, 26$ in Table 1. Note that the last column of Table 1 is the approximate quotients of the new and old bounds.

The method in this paper is different with that in the previous papers. In ^[4], we compute modular Galois representations only when $\ell\ge k-1$, in which case we say the prime $\ell$ is "large enough". However, in this paper, we discuss the cases when $\ell < k-1$, that is, the prime $\ell$ is small. In this case, we don't have the weight 2 forms by which we can carry out all the computations. Instead, in this paper, we use the twists of the forms by the $\theta$ operator. In ^[9], to obtain the new bounds $B_k$, we discuss the exceptional primes and observe the congruence formulas, and there is none of new modular Galois representation being computed. In this paper, we do computations in the cases with unexceptional primes by using the new modular Galois representations, which are computed in Subsection 4.2.

Throughout this paper, we suppose $\ell\ge5$ to be a prime and denote $\overline{\mathbb{F}}_{\ell}$ the algebraic closure of the finite field $\mathbb{F}_{\ell}$. All the explicit computations of this paper have been done in the open source software SAGE ^[10].

2.   Mod $\ell$ modular forms

2.1.   Modular forms of type $(N, k, \varepsilon)$

The mod $\ell$ modular forms were first developed by Serre ^[11] and Swinnerton-Dyer ^[12], and generalized by Katz ^[13]. In this subsection we give a brief review of the theory of mod $\ell$ modular forms. For the details, we refer to ^[14] and [15,Section 2].

Let $\ell$ be a prime and $N\ge1$ be prime to $\ell$. The congruence subgroup $\varGamma _{1}(N)$ of level $N$ is

Let $X_{1}(\ell)$ be the modular curve associated to $\varGamma_{1}(\ell)$. Let $k > 0$ be an even integer. Let $E$ be a generalized elliptic curve over a scheme $S$ and $\alpha:(\mathbb{Z}/N\mathbb{Z})_{S}\hookrightarrow E$ be an embdedding of group schemes. Denote the relative differentials by $\varOmega^{1}_{E/S}$ and zero section by $0$. Let $\omega_{E/S}: = 0^{*} \varOmega^{1}_{E/S}$. Then a modular form $f$ of type $(N, k)$ over $\overline{\mathbb{F}}_{\ell}$ is a law, that assigns to each pair $(E/S, \alpha)$ a section of $\omega_{E/S}^{\otimes k}$.

The $q$-expansions of mod $\ell$ modular forms $f$ at cusp $\infty$ of $\varGamma_{1}(N)$ have been given by evaluating $f$ on $(E_{q}, \alpha)$, where $q = e^{2\pi iz}$ and $E_{q}$ is the Tate curve over $\overline{\mathbb{F}}_{\ell}[[q]](q^{-1})$. More precisely, the $q$-expansions of $f$ at $\infty$ are the the power series $f(E_{q}, \alpha)/(dt/t)^{\otimes k}\in\overline{\mathbb{F}}_{\ell}[[q]]$, where $dt/t$ is the standard differential on $E_{q}$. This in fact coincides with the usual $q$-expansions of modular forms, since $(E_{q}, \alpha)$ corresponds to a neighbourhood of the cusp $\infty$ in the completed up half plane $\mathcal{H}^{*} = \mathcal{H}\cup \mathbb{Q} \cup \infty$, where $\mathcal{H}$ is the up half plane. As usual, we denote the $n$-th coefficient of the $q$-expansion by $a_{n}(f)$.

Let $\varepsilon:(\mathbb{Z}/(N\ell)\mathbb{Z})^{\ast}\rightarrow \overline{\mathbb{F}}_{\ell}$ be a Dirichlet character. Define an action of $\mathbb{Z}/(N\ell)\mathbb{Z})^{\ast}$ on mod $\ell$ form $f$ by

A modular form $f$ of type $(N, k)$ is called a form of type $(N, k, \varepsilon)$ if it satisfies

One can also define Hecke operators $T_{p}$ that are coincide with the usual Hecke operators. For instance, we have that all the $T_{p}$ commute with each other and the eigenvalues determine the $q$-expansions of $f$ up to a constant factor.

A modular form $f$ is called cusp form if $a_{0}(f) = 0$. A modular form $f$ of type $(N, k, \varepsilon)$ is said to be an eigenform if it is an eigenvector for all the Hecke operators $T_{p}$ with $p \nmid N\ell$. An eigenform $f$ is said to be normalized if $a_{1}(f) = 1$.

2.2.   Operator $\theta$ and Hasse invariant $A$

Let $\theta = q\frac{d}{dq}$ be the classical differential operator $\sum_{n > 0} a_{n} (f) q^{n} \mapsto \sum_{n > 0} n a_{n} (f) q^{n}$. If $f$ is an eigenform of type $(N, k, \varepsilon)$, in [16,Section 2.1], it is shown that $\theta f$ is an eigenform of type $(N, k+\ell+1, \varepsilon)$.

Let $A$ be the Hasse invariant of the Tate curve $E_{q}$ over $\overline{\mathbb{F}}_{\ell}[[q]](q^{-1})$, then we have:

Lemma 2.1. The Hasse invariant $A$ is given by $A = (dt/t)^{\otimes \ell-1}$. Hence, $A$ is a mod $\ell$ modular form of type $(1, \ell-1, 1)$.

Proof. This is Proposition 1.9 $c)$ of ^[14]. □

From this lemma, we know the $q$-expansion of $A$ is $1$. For two forms of types $(N, k_{1}, \varepsilon)$ and $(N, k_{2}, \varepsilon)$ with $k_{1}\equiv k_{2} \mod \ell-1$, we can view the two forms as forms of the same type by multiplying one form by suitable powers of $A$. This can be used to prove the following proposition, which is a generalization of Sturm bound theorem to modular forms of different weights:

Proposition 2.2. Let $f_{1}$ and $f_{2}$ be two normalized eigenforms of type $(N, k_{1}, \varepsilon)$ and $(N, k_{2}, \varepsilon)$, respectively. Let $k = max\{k_{1}, k_{2}\}$. Suppose that $k_{1}\equiv k_{2} \mod \ell-1$ and $a_{m}(f_{1}) = a_{m}(f_{2})$ in $\overline{\mathbb{F}}_{\ell}$ for all $m$ with $m \le \frac{k[SL_{2}(\mathbb{Z}):\varGamma_{1}(N)]}{12}$. Then $f_{1} = f_{2}$.

Proof. Let $A$ be the Hasse invariant. Without loss of generality, we suppose $k_{1}\le k_{2}$. Then by Lemma 2.1, the form $A^{(k_{2}-k_{1})/(\ell-1)} f_{1}$ is an eigenform of type $(N, k_{2}, \varepsilon)$. We know $A = 1$, and this implies that the form $f_{1}$ is also a form of type $(N, k_{2}, \varepsilon)$. Since we have $a_{m}(f_{1}) = a_{m}(f_{2})$ in $\overline{\mathbb{F}}_{\ell}$ for all $m$ with $m \le \frac{k[SL_{2}(\mathbb{Z}):\varGamma_{1}(N)]}{12}$, it follows from Sturm's theorem that $f_{1} = f_{2}$. □

A proof of this result for classical modular forms can be found in ^[17].

The following well-known theorem takes an important role for our computations:

Theorem 2.3. Let $f$ be a normalized eigenform of type $(N, k, \varepsilon)$, then there exist $i$ and $k'$ with $0\le i\le \ell-1, \ k'\le \ell+1$, and a normalized eigenform of type $(N, k', \varepsilon)$, such that $f = \theta^{i}g$.

Proof. See [15,Theorem 3.4]. □

3.   Computing mod $\ell$ Galois representations for small $\ell$

In this section, we shall describe the algorithm for computing mod $\ell$ Galois representations associated to modular forms of weight $k$ when $\ell < k-1$. We also prove the corresponding results for the projective representations and then present the algorithm for the projective case.

3.1.   Modular Galois representations and $\theta$ twists

Deligne ^[18] proves the following well known theorem:

Theorem 3.1 (Deligne). Let $f$ be an eigenform of type $(N, k, \varepsilon)$. Then there exists a continuous semi-simple representation

which is unramified outside $N\ell$, and for all primes $p\nmid N\ell$ the characteristic polynomial of $\rho_{f} (Frob_{p})$ satisfies in $\overline{\mathbb{F}}_{\ell}$

Moreover, $\rho_{f}$ is unique up to isomorphism.

Let $f = \sum_{n > 0} a_{n} (f) q^{n}$ be an eigenform. Then by definition, the eigenform $\theta f$ has $q$-expansion $\sum_{n > 0} na_{n} (f) q^{n}$. It follows from the above theorem that

where $\chi$ is the mod $\ell$ cyclotomic character. Then for an eigenform $f$ of type $(N, k, \varepsilon)$ with $\ell < k-1$, it follows from Theorem 2.3 that there exist an integer $i$ and an eigenform $g$ of type $(N, k', \varepsilon)$ with $k' \le \ell+1$, such that $\rho_{f}$ is a twist of $\rho_{g}$ by $\chi^{i}_{\ell}$, i. e.,

Moreover, we have the following theorem to determine such $i$ and $k'$:

Theorem 3.2. Let $f_{1}$ and $f_{2}$ be two normalized eigenforms of type $(N, k_{1}, \varepsilon)$ and $(N, k_{2}, \varepsilon)$, respectively. Let $i$ be an integer with $0\le i \le \ell-1$. Then $f_1 = \theta^{i}f_2$ if and only if $k_{1}\equiv k_{2}+2i \mod \ell-1$ and $a_{p}(f_{1}) = p^{i}a_{p}(f_{2})$ in $\overline{\mathbb{F}}_{\ell}$ for all primes $p$ with $p \le \frac{\ell(\ell+1)[SL_{2}(\mathbb{Z}):\varGamma_{1}(N)]}{12}$.

Proof. We first assume that $f_1 = \theta^{i}f_2$. By the argument above, it follows that $\rho_{ f_1}$ and $\rho_{f_2} \otimes \chi^{i}_{\ell}$ are isomorphic. Then by (3.2), we have

Hence we have $k_{1}\equiv k_{2}+2i \mod \ell-1$. Since $a_{p}(\theta^i f_{2}) = p^{i}a_{p}(f_{2})$ for all primes $p$, in $\overline{\mathbb{F}}_{\ell}$ we have

for all primes $p$ with $p \le \frac{\ell(\ell+1)[SL_{2}(\mathbb{Z}):\varGamma_{1}(N)]}{12}$.

For the other direction, we assume that

and $a_{p}(f_{1}) = p^{i}a_{p}(f_{2})$ for all primes $p$ with $p \le \frac{\ell(\ell+1)[SL_{2}(\mathbb{Z}):\varGamma_{1}(N)]}{12}$.

It follows from Theorem 2.3 that there exist an integer $j$ with $0\le j \le \ell-1$ and a normalized eigenform $g_{1}$ of type $(N, k_{g_{1}}, \varepsilon)$ with $k_{g_{1}}\le\ell+1$ such that $f_{1} = \theta^{j}g_{1}$ in $\overline{\mathbb{F}}_{\ell}$. This implies that $f_{1} = \theta^{j}g_{1}$ is a form of type $(N, k_{1}, \varepsilon)$ with $k_{1}\le \ell(\ell+1)$.

We set $f'_{2} = \theta^i f_{2}$. Then for the same reason as above, the form $f'_{2}$ is of type $(N, k_{2}', \varepsilon)$ with $k_{2}'\le \ell(\ell+1)$. Moreover, we have that $\rho_{f_2'}$ is isomorphic to $\rho_{f_2} \otimes \chi^{i}_{\ell}$. By the argument in the first paragraph of the proof, we have

Then by the assumption and (3.4), we have

and

for all primes $p$ with $p \le \frac{\ell(\ell+1)[SL_{2}(\mathbb{Z}):\varGamma_{1}(N)]}{12}$.

Since $f_1$ and $f_{2}'$ are normalized eigenforms, this implies that $a_{m}(f_{1}) = a_{m}(f_{2}')$ for all $m\in \mathbb{Z}$ with $m \le \frac{\ell(\ell+1)[SL_{2}(\mathbb{Z}):\varGamma_{1}(N)]}{12}$. By Proposition 2.2, we then have that $f_{1} = f_{2}'$ and therefore $f_1 = \theta^{i}f_2$. This completes the proof. □

This theorem also provides a method to calculate the values of $i$ and $k'$ for which (3.3) is satisfied. From this point of view, this theorem is a generalization of [1,Proposition 2.5.18] from level one to arbitrary levels. In [2,Theorem 3.5], the author gives an elaborate result of the generalization of [1,Proposition 2.5.18], which is used to theoretically prove that the algorithm described in ^[2] is in polynomial time. However, it is quite convenient to apply Theorem 3.2 when we do explicit computations.

3.2.   The algorithm

In this subsection, we shall describe the algorithm for computing the mod $\ell$ Galois representations associated to modular forms. This algorithm was first proposed by Edixhoven and Couveignes ^[1] for modular forms of level one and then generalized to forms of arbitrary levels by Bruin ^[2]. The algorithm that we shall present is slightly different. In fact, we shall apply Theorem 3.2 instead when we reduce the computations to the cases with $2 \le k \leq \ell+1$.

Now let $f$ be a cuspidal normalized eigenform of type $(N, k, \varepsilon)$ with $\ell < k-1$. Theorem 2.3 and 3.2 allow us to explicitly obtain a normalized eigenform $f'$ of type $(N, k', \varepsilon)$ with $2\le k' \le \ell+1$ such that $\rho_{f}$ and $\rho_{f'} \otimes \chi^{i}_{\ell}$ are isomorphic. Thus it suffices to compute $\rho_{f'}$ and the question boils down to the case with $2 \le k' \leq \ell+1$.

In [19,Theorem 2.2], the author shows that if $2 < k \leq \ell+1$ and $\rho_{f, \lambda}$ is ireducible, then there is a cuspidal normalized eigenform $f_{2}$ of type $(N\ell, 2, \varepsilon_2)$ such that $\rho_{f}$ is isomorphic to $\rho_{f_{2}}$. Therefore, for any $p \nmid N\ell$, this reduces the questions to the case with $k = 2$.

Now suppose that $\rho_{f}$ is a mod $\ell$ Galois representation associated to a cuspidal normalized eigenform of type $(N, 2, \varepsilon)$. Let $X_{1}(\ell)$ be the modular curve associated to $\varGamma_{1}(\ell)$ and let $J_{1}(\ell)$ denote its Jacobian. Denote $\mathbb T$ the subring of End$(J_{1}(\ell))$ generated by the Hecke operators $T_p$ over $\mathbb Z$. Then

Define a ring homomorphism

given by

Let $\mathfrak m$ denote the maximal ideal ker$\theta$ and then $\mathbb{T}/\mathfrak{m}\subset \overline{\mathbb{F}}_{\ell}$. Moreover, we let

Then we have:

Theorem 3.3. The set $V$ is a 2-dimensional $\mathbb{T}/\mathfrak{m}$-linear subspace of $J_{1}(\ell)(\overline{\mathbb{Q}})[\ell]$. Moreover, the representation

is isomorphic to the modular Galois representation $\rho_{f}$.

Proof. See [20,Section 3.2 and 3.3]). □

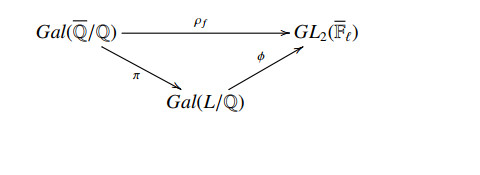
Let $L$ be the fixed field of ${\rm ker}(\rho_{f})$ of the Galois representation $\rho_{f}$. Then the representation $\rho_{f}$ can factor through as:

where $\pi$ is the canonical restriction map and $\phi$ is the isomorphism between Gal$(L/\mathbb{Q})$ and the image ${\rm im}(\rho_{f})$ of $\rho_{f}$. It can be shown that, to compute $\rho_{f}$, it suffices to compute a suitable polynomial $P_{f}(x)\in \mathbb Q[x]$ of degree $\ell^2-1$ with

for some suitable function $h$ in the function field of $X_1(\ell)$. Here $h(P) = \sum_{i = 1}^g h(P_i)$ where $g$ is the genus of $X_1(\ell)$, and $P_i$ are the points on $X_1(\ell)$ such that each divisor $P\in V-\{0\}$ can be written as $\sum_{i = 1}^g (P_i) -gO$.

In fact, it can be shown that the fixed field of $\rho_{f}$ is actually the splitting field of $P_{f}\in \mathbb Q[x]$. Then one can obtain $L$ by adjoining the roots of $P_{f}$ to $\mathbb{Q}$, and the isomorphism $\phi$ is induced by the bijection between the roots of $P_{f}$ and the points of the 2-dimensional $\mathbb{T}/\mathfrak{m}$-linear subspace $V$ of $J_{1}(\ell)(\overline{\mathbb{Q}})[\ell]$.

3.3.   Computations of projective Galois representations

Composed with the canonical projection map $GL_{2}(\mathbb{F}_{\lambda})\rightarrow PGL_{2}(\mathbb{F}_{\lambda})$, the representation $\rho_{f}$ in (3.1) gives a projective representation

Now we apply Theorem 3.2 to the projective representation cases and then we have:

Theorem 3.4. Let $f_{1}$ and $f_{2}$ be two normalized eigenforms of type $(N, k_{1}, \varepsilon)$ and $(N, k_{2}, \varepsilon)$, respectively. Let $i$ be an integer with $0\le i \le \ell-1$. Suppose that $k_{1}\equiv k_{2}+2i \mod \ell-1$ and $a_{p}(f_{1}) = p^{i}a_{p}(f_{2})$ in $\overline{\mathbb{F}}_{\ell}$ for all primes $p$ with $p \le \frac{\ell(\ell+1)[SL_{2}(\mathbb{Z}):\varGamma_{1}(N)]}{12}$. Then $\tilde{\rho}_{ f_1}$ and $\tilde{\rho}_{f_2}$ are isomorphic.

Proof. It follows from Theorem 3.2 that $\tilde{\rho}_{ f_1}$ and $\tilde{\rho}_{f_2} \otimes \chi^{i}_{\ell}$ are isomorphic. For any $\sigma \in$ Gal$(\overline{\mathbb{Q}}/\mathbb{Q})$, we have

In $PGL_{2}(\mathbb{F}_{\lambda})$, we have

where, as usual, the bar denotes the quotient by the subgroup of $GL_{2}(\overline{\mathbb{F}}_{\ell})$ consisting of scalar matrices. Hence we have $\tilde{\rho}_{f_2} \otimes \chi^{i}_{\ell} = \tilde{\rho}_{f_2}$ and this implies $\tilde{\rho}_{ f_1}$ and $\tilde{\rho}_{f_2}$ are isomorphic. □

Now we can describe the algorithm for computing the projective Galois representation $\tilde{\rho}_{f}$ associated to an normalized eigenform of type $(N, k, \varepsilon)$ with $\ell < k-1$.

First, by Theorems 2.3 and 3.4, we can explicitly obtain a normalized eigenform $f'$ of type $(N, k', \varepsilon)$ with $2\le k' \le \ell+1$ such that $\tilde{\rho}_{ f}$ and $\tilde{\rho}_{f'}$ are isomorphic. Thus our computations boil down to the case with $2 \le k' \leq \ell+1$. Then again we can reduce the question to the weight $2$ case using the same arguments in the previous subsection. Finally, we can compute a suitable polynomial instead for the following reason:

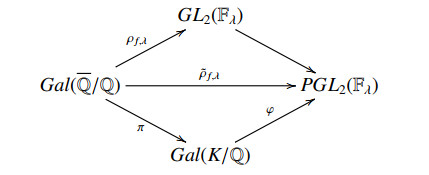
Let $K$ be the fixed field of ${\rm ker}(\tilde{\rho}_{f})$, then the representation $\tilde{\rho}_{f}$ can factor through as:

where $\pi$ is the canonical restriction map and $\varphi$ is the isomorphism between Gal$(L/\mathbb{Q})$ and ${\rm im}(\tilde{\rho}_{f})$.

Let $V = J_{1}(\ell)(\overline{\mathbb{Q}})[\mathfrak{m}]$ be the 2-dimensional $\mathbb{T}/\mathfrak{m}$-linear subspace of $J_{1}(\ell)(\overline{\mathbb{Q}})[\ell]$ as in Theorem 3.3. Then the projective line $\mathbb P(V)$ has $\ell+1$ points, and it follows that the fixed field of $\tilde{\rho}_{f}$ is in fact the splitting field $K$ of a certain polynomial $\tilde P_{f}\in Q[x]$ of degree $\ell+1$, which is given by

Moreover, one can obtain $K$ by adjoining the roots of $\tilde P_{f, \ell}$ to $\mathbb{Q}$ and, the isomorphism $\varphi$ is induced by the bijection between the roots of $\tilde P_{f}$ and the points of the projective line $\mathbb P(V)$. This implies that the projective representation $\tilde{\rho}_{f}$ can be described by the polynomial $\tilde P_{f}$.

4.   Explicit computations

For $k = 16, 18, 20, 22$ and $26$, let $\Delta_k = \sum_{n > 0}^{\infty}a_{n}q^{n}$ denote the unique cusp form of level $1$ and weight $k$. A prime $\ell$ is said to be exceptional if the image of $\rho_{\Delta_k, \ell}$ does not contain $SL_{2}(\mathbb{F}_{\ell})$. Otherwise, a prime $\ell$ is called unexceptional.

Bosman ^[1] first does practical computations and obtains $\tilde P_{\Delta_{k}}$ for modular forms $\Delta_{k}$ of level 1 and of weight $k\le 22$, with $\ell \leq 23$. Others improve the algorithm and computed the polynomials for more cases. See ^[4] and ^[5] for instance. As far as we know, all the polynomials $\tilde P_{\Delta_{k}}$ that have been computed in this method are shown in [1,Section 7.5] and [5,Table 4].

Note that all the computed polynomials are of the cases with $k\le \ell+1$. In this section, we shall apply the algorithm described in Subsection 3.3 to explicitly compute the polynomials $\tilde P_{\Delta_{k}}$ associated to the mod $\ell$ projective Galois representations $\tilde{\rho}_{ \Delta_{k}}$ for $k = 16, 20, 22, 26$ and all the unexceptional primes $\ell$, with $\ell < k-1$.

As an application, we shall discuss the non-vanishing Fourier coefficients of $\Delta_{k}$ using our results.

4.1.   Reducing to the cases with $k\le \ell+1$.

For a prime $\ell$, we let $\tilde{\Delta}_k = \sum_{n > 0}^{\infty}\tilde{a}_{n}q^{n}$, where $\tilde{a}_{n}$ means the reduction of $a_{n}$ mod $\ell$. Then $\tilde{\Delta}_k$ is a normalized cuspidal eigenform of type $(1, k, 1)$. We denote by $\tilde P_{\Delta_{k}, \ell}$ the polynomial $\tilde P_{\Delta_k}(x)$ defined in (3.5) which describes the mod $\ell$ projective Galois representation $\tilde{\rho}_{\Delta_k}$ associated to $\tilde{\Delta}_k$.

A prime $\ell$ is said to be exceptional if the image of $\rho_{f}$ does not contain $SL_{2}(\mathbb{F}_{\ell})$. In Table 2 we list the all unexceptional primes for $\Delta_k$ with $\ell < k-1$. Then for the $(k, \ell)$ in Table 2, we shall compute the polynomials $\tilde P_{\Delta_{k}, \ell}$.

For $\Delta_{k}$ and unexceptional prime $\ell$, with $(k, \ell)$ in Table 2, we apply Theorem 3.4 to find normalized eigenforms $f$ of type $(1, k', 1)$ with $k' < \ell-1$ such that $\tilde{\rho}_{\Delta_{k}}$ and $\tilde{\rho}_{f}$ are isomorphic. More precisely, we first obtain all pairs $(i, k')$ such that

Then we take a pair $(i, k')$ such that $a_{p}(f_{1}) \equiv p^{i}a_{p}(f_{2}) \mod \ell$ for all primes $p$ with $p \le \frac{\ell(\ell+1)}{12}$. This condition can be verified quickly in SAGE. In fact, by Theorem 2.3, such $k'$ and $i$ do exist and after doing some simple calculations we explicitly obtain the forms that satisfy the conditions in Theorem 3.2. Then by Theorem 3.4, we finally reduce the computations to the cases with $k\le \ell+1$. Thus it gives:

Proposition 4.1. We take values of $k, \ell, i, k'$ in each row of Table 3. Then we have the congruences

and moreover, we have $\tilde{\rho}_{ \Delta_{k}}\cong\tilde{\rho}_{\Delta_{k'}}$.

4.2.   The polynomials $\tilde{P}_{\varDelta_{k}, \ell}$

We take values of $k, \ell, i, k'$ in each row of Table 3. Since $\tilde{\rho}_{ \Delta_{k}}$ and $\tilde{\rho}_{\Delta_{k'}}$ are isomorphic, we have

Fortunately, all the corresponding polynomials $\tilde P_{\Delta_{k'}, \ell}(x)$ have been computed and shown in [1,Section 7.5]. As a result, the polynomials $\tilde P_{\Delta_{k}, \ell}(x)$ associated to the mod $\ell$ projective Galois representation $\tilde{\rho}_{ \Delta_{k}}$ are shown in Table 4.

4.3.   An application for the non-vanishing Fourier coefficients of $\Delta_{k}$

In ^[9], the authors discuss the non-vanishing Fourier coefficients of $\Delta_{k}$ with $k = 16, 18, 20, 22, 26$ and achieve the explicit bounds $B_k$ of $n$ such that the Fourier coefficients $a_n(\Delta_k)\ne0$ for all $n < B_k$. They first prove that the smallest $n$ for which $a_n(\Delta_k) = 0$ must be a prime. Then, for each prime $p$ with $a_p(\Delta_k) = 0$, they obtain the formulations that such $p$ must satisfy. In addition, the congruence

can be verified by the polynomials $\tilde P_{\Delta_k, \ell}$ associated to the projective Galois representations. Precisely, when the polynomial $\tilde P_{\Delta_k, \ell}\in \mathbb{Z}[x]$, it can be shown that $a_{p}(\Delta_k)\equiv 0 \mod \ell$ is equivalent to $\tilde P_{\Delta_k, \ell} \mod{p}$ having an irreducible factor of degree $2$ in $\mathbb{F}_{p}[x]$. Consequently, one can systematically search for the smallest prime $p$ satisfying the formulations, as well as $a_{p}(\Delta_k)\equiv 0 \mod \ell$.

Now we can add the polynomials $\tilde P_{\Delta_k, \ell}$ in Table 4 to the searching computations. That is, for $k = 16, 20, 22, 26$ and all the small unexceptional primes $\ell$ in Table 2, we can efficiently verify the additional searching conditions

As a result, for $k = 16, 20, 22, 26$, we are able to obtain the new bounds $B_k$ of $n$ such that $a_n(\Delta_k)\ne0$ for all $n < B_k$.

Proposition 4.2. Let the pair ($k, B_k$) take the values as in Table 5. Then the coefficients $a_n(\Delta_{k})$ are non-vanishing for all $n$ with $n < B_k$ in Table 5.

5.   Further work and applications

The computational results of modular Galois representations can be applied to compute the Fourier coefficients of modular forms $f$ according to (3.2). More precisely, if we can calculate mod $\ell$ Galois representations for enough primes $\ell$ whose product exceeds $4p^{(k-1)/2}$, the coefficient $a_p(f)$ can be easily computed by Chinese Remainder Theorem. Our results in this paper add the small primes to the list and can be applied to the computations of the Fourier coefficients of modular forms. Besides, for many groups $\mathrm{SL}_2(\mathbb{F}_{\ell ^k})$ and $\mathrm{GL}_2(\mathbb{F}_{\ell ^k})$, it is still unknown whether they are Galois groups of number fields over rational field $\mathbb{Q}$. Our results are expected to answer some of these questions, since our computations also provide number fields and their Galois groups, namely $\mathrm{SL}_2(\mathbb{F}_{\ell ^k})$ and $\mathrm{GL}_2(\mathbb{F}_{\ell ^k})$.

6.   Conclusions

In this paper, we give an explicit method, for a given modular form of type $(N, k, \varepsilon)$, to obtain a twist form of type $(N, k', \varepsilon)$ with $k'\le \ell+1$, such that the two Galois representations associated to the two forms are isomorphic up to twist. Then we prove the corresponding results for the projective representations and present the algorithm for the projective case. Moreover, we apply the algorithm in Subsection 3.3 to do explicit computations of the mod $\ell$ projective Galois representations $\tilde{\rho}_{ \Delta_{k}}$ for $k = 16, 20, 22, 26$ and all the unexceptional primes $\ell$ for which $\ell < k-1$. The computed projective polynomials $\tilde P_{\Delta_{k}}(x)$ associated to the representations $\tilde{\rho}_{ \Delta_{k}}$ are shown in Table 4.

In the end, as an application, we discuss the non-vanishing Fourier coefficients of $\Delta_{k}$ using our results. In fact, for $k = 16, 20, 22, 26$, we obtain new higher bounds $B_k$ of $n$ such that $a_n(\Delta_k)\ne0$ for all $n < B_k$, which are shown in Table 5.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

Peng Tian is supported by NSFC (NOs: 11601153) and Ha T. N. Tran was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) (funding RGPIN-2019-04209 and DGECR-2019-00428).

Conflict of interest

The authors declare that they have no conflicts of interest.