Distinguishing colorings of graphs and their subgraphs

1.   Introduction

Graph distinguishing coloring is a hot issue in the area of graph coloring theory. As an application, graph distinguishing colorings may be connected with the frequency assignment problem in wireless communication. The vertices (nodes) of graphs (networks) represent transmitters, the set $C[u, \pi]$ of colors assigned to a vertex $u$ and the edges (links) incident to $u$ under a total coloring $\pi$ indicates the frequencies usable. For a pair of adjacent vertices $u$ and $v$, the property $C[u, \pi]\neq C[v, \pi]$ ensures the corresponding two stations can operate on a wide range of frequencies without the danger of interfering with each other.

We use standard notation and terminology of graph theory ^[1]. Some additional notations will be used. The shorthand notation $[m, n]$ stands for a set $\{m, m+1, \dots, n\}$, where integers $n$ and $m$ hold $n > m\geq 0$. The set of vertices that are adjacent to a vertex $u$ of $G$ is denoted as $N(u)$, thus, the degree $d _G(u)$ of the vertex $u$ is equal to the cardinality $|N(u)|$. $N(u)$ is also called the neighborhood of the vertex $u$. The edge neighborhood of the vertex $u$ is defined as $N_e(u) = \{uv:v\in N(u)\}$. Let $\Delta(G)$ (or $\Delta$) and $\delta(G)$ denote the maximum degree and minimum degree of $G$, respectively. Let $n_d(G)$ be the number of vertices of degree $d$ in $G$. In a graph, a $k$-degree vertex is a vertex of degree $k$, especially, a $\Delta$-vertex is a vertex of maximum degree; a leaf is a vertex of degree one; a $k$-cycle is a cycle of $k$ vertices.

Graphs mentioned here are undirected, connected and simple, and all graph colorings are proper. A $k$-total coloring $\pi$ of a graph $G$ from a nonempty subset $S\subset V(G)\cup E(G)$ to $[1, k]$ (also, $[1, k]$ is called a color set) satisfies that $\pi(x)\neq \pi(y)$ for any two adjacent/incident elements $x, y\in S$. The set $\{\pi(ux): ux\in N_e(u)\}$ is called the edge-color set of the vertex $u$, and denoted by $C(u, \pi)$. Notice that an edge-color set $C(u, \pi)$ is never a multiset, that is, $|C(u, \pi)| = d _G(u)$. Let $\pi$ be a total coloring of $G$, the set $C[u, \pi] = C(u, \pi)\cup \{\pi(u)\}$ is called a closed color set of vertex $u$. Clearly, $|C[u, \pi]| = d _G(u)+1$. The following distinguishing constraints will be used in the following Definitions:

(A1) $C(u, \pi)\neq C(v, \pi)$ for distinct vertices $u, v\in V(G)$;

(A2) $C(u, \pi)\neq C(v, \pi)$ for each edge $uv\in E(G)$;

(A3) $C[u, \pi]\neq C[v, \pi]$ for distinct vertices $u, v\in V(G)$;

(A4) $C[u, \pi]\neq C[v, \pi]$ for each edge $uv\in E(G)$.

For the purpose of simplicity, two notations $\pi(V(G)) = \{\pi(x):x\in V(G)\}$ and $\pi(E(G)) = \{\pi(xy):xy\in E(G)\}$ will be used here. We reformulate the definitions of several known distinguishing colorings of graphs occurred in literature.

Definition 1.1. ^[2,3] Let $\pi:E(G)\rightarrow [1, k]$ be an edge coloring of $G$. If (A1) holds, then $\pi$ is called a vertex distinguishing edge $k$-coloring ($k$-vdec) of $G$. The vdec chromatic number of $G$ is the minimum number of $k$ colors required for which $G$ admits a $k$-vdec, and denoted by $\chi\, '_{s}(G)$.

Definition 1.2. ^[4] Let $\pi:E(G)\rightarrow [1, k]$ be an edge coloring of $G$. If (A2) holds, then $\pi$ is called an adjacent vertex distinguishing edge $k$-coloring ($k$-avdec) of $G$. The avdec chromatic number of $G$ is the minimum number of $k$ colors required for which $G$ admits a $k$-avdec, and denoted by $\chi\, '_{as}(G)$.

Definition 1.3. ^[5] Let $\pi:V(G)\cup E(G)\rightarrow [1, k]$ be a total coloring of $G$. If (A3) holds, then $\pi$ is called a vertex distinguishing total $k$-coloring ($k$-vdtc) of $G$. The vdtc chromatic number of $G$ is the minimum number of $k$ colors required for which $G$ admits a $k$-vdtc, and denoted by $\chi\, ''_{s}(G)$.

Definition 1.4. ^[6] Let $\pi:V(G)\cup E(G)\rightarrow [1, k]$ be a total coloring of $G$. If (A4) holds, then $\pi$ is called an adjacent vertex distinguishing total $k$-coloring ($k$-avdtc) of $G$. The avdtc chromatic number of $G$ is the minimum number of $k$ colors required for which $G$ admits a $k$-avdtc, and denoted by $\chi\, ''_{as}(G)$.

A graph $G$ is called a vdec no-covered graph (resp. a vdtc no-covered graph) if there exists a proper subgraph $H$ of $G$ such that $\chi\, '_{s}(H) > \chi\, '_{s}(G)$ (resp. $\chi\, ''_{s}(H) > \chi\, ''_{s}(G)$). Similarly, a graph $G$ is called an avdec no-covered graph (resp. an avdtc no-covered graph) if $G$ contains a proper subgraph $H$ with $\chi\, '_{as}(H) > \chi\, '_{as}(G)$ (resp. $\chi\, ''_{as}(H) > \chi\, ''_{as}(G)$).

The following three lemmas will be used.

Lemma 1.1. ^[7] For a graph $G$ of order at least three, $\chi\, '_s(G)\leq |V(G)|+1$.

Lemma 1.2. ^[8] For integers $n, m\geq 3$, $\chi\, '_{s}(C_m) = n$ if and only if either $n$ is odd and $m\in\Big [\frac{n^2-4n+5}{2}$, $\frac{n^2-n-6}{2}\Big ]$ $\bigcup \left \{\frac{n^2-n}{2}\right \}$, or $n$ is even and $m\in \left [\frac{n^2-3n-2}{2}, \frac{n^2-3n}{2}\right ]$$\bigcup \left [\frac{n^2-3n+4}{2}, \frac{n^2-n}{2}\right ].$

Lemma 1.3. Let $K_n$, $P_n$ and $C_n$ be a complete graph, path and cycle on $n$ vertices, respectively; and let $K_{m, n}$ be a complete bipartite graph on $m+n$ vertices. Then

$(1)$ ^[4] $\chi \, '_{as}(K_{m, n}) = n$ for $n > m > 0$ and $\chi \, '_{as}(K_{n, n}) = n+2$ for $n\geq 2$.

$(2)$ ^[5] $\chi \, ''_{s}(K_{m, n}) = n+1$ for $n > m\geq 2$, and $\chi \, ''_{s}(K_{n, n}) = n+3$ for $n\geq 3$.

$(3)$ ^[9] $\chi \, ''_{as}(K_{2m+2}) = \chi \, ''_{as}(K_{2m+1}) = 2m+3$ for all integers $m\geq 1$.

$(4)$ ^[6] $\chi \, ''_{as}(P_{n}) = 4$ for $n\geq 4$; $\chi \, ''_{as}(C_{n}) = 4$ for $n\geq 6$.

In 1997, Burris and Schelp ^[2] studied the vertex distinguishing edge colorings (vdec) on graphs. Independently, as "observability" of a graph, the concept of the vdec was proposed by Černý, Horňák and Soták ^[3]. This graph coloring has absorbed researchers' intentions. Surprisingly, determining the vdec chromatic numbers of graphs seems to be quite difficult, even for some special graphs. In 2002, Balister, Bollobás and Schelp ^[10] proved that $k\leq \chi \, '_{s}(G)\leq k+5$ for a graph $G$ with $\Delta(G) = 2$, $n_1(G)\leq k$ and $n_2(G)\leq {k \choose 2}$. Zhang, Liu and Wang ^[4] introduced the adjacent vertex distinguishing edge colorings (avdec) of graphs, a weaker version of a vdec. However, finding avdec chromatic number of graphs is not easy, even for special planar graphs ^[11]. Three conjectures on graph distinguishing colorings are listed as follows.

Conjecture 1.1. ^[2] For a graph $G$ of order at least three, if $k$ is the minimal integer such that $\left (^k_d\right)\geq n_d(G)$ for all $d$ with $\delta(G)\leq d\leq \Delta(G)$, then $\chi \, '_{s}(G) = k \ or\ k+1$.

Conjecture 1.2. ^[4] For a graph $G$ of order at least three, if $G$ is not a cycle on five vertices, then $\chi\, '_{as}(G)\leq \Delta(G)+2$.

Conjecture 1.3. ^[6] For a graph $G$ of order at least three, $\chi\, ''_{as}(G)\leq \Delta(G)+3$.

In ^{[10,12,13,14,15]}, some results on Conjecture 1.1 were obtained. Conjecture 1.2 was partially answered in ^[16] and ^[17]. A good result on Conjecture 1.2, due to Hatami ^[18], is that if $G$ has no isolated edges and $\Delta(G) > 10\, ^{20}$, then $\chi \, '_{as}(G)\leq \Delta (G)+300$. Since $\Delta (G)\leq \chi \, '_{as}(G)$, the Hatami's result implies that $\lim \limits_{\Delta (G)\rightarrow \infty}\frac{\chi \, '_{as}(G)}{\Delta (G)} = 1$. Conjecture 1.3 has been verified for some special graphs in ^[6] and ^[19]. It is noticeable, Conjecture 1.2 implies that $G$ is not an avdec no-covered graph if $\chi\, '_{as}(G) = \Delta(G)+2$; and Conjecture 1.3 implies that $G$ is not an avdtc no-covered graph if $\chi\, ''_{as}(G) = \Delta(G)+3$.

2.   Vertex distinguishing edge and total colorings

Theorem 2.1. Each connected graph is a proper subgraph of a vdec no-covered Hamilton graph.

Proof. First of all, we prove the following claim.

Claim. Let $G$ be a Hamilton graph with $\delta(G)\geq 3$. Then $G$ has a vdec no-covered Hamilton graph with $|E(G)|-1$ edges.

The proof of Claim. Suppose that a Hamilton graph $G$ on $n$ vertices admits a $k$-vdec $\pi$ with $k = \chi\, '_{s}(G)$. Without loss of generality, $\pi(uv) = 1$ for a certain edge $uv$ of a Hamilton cycle of $G$. By Lemma 1.1, two cases appear as follows:

For $k < n+1$ we take a cycle $C_{m}$ on $m = {n \choose 2}$ vertices. Clearly, $\chi\, '_{s}(C_m) = n$ by Lemma 1.2. Let $\phi$ be a $n$-vdec of $C_m$, and $\phi(xy) = 1$ for a certain edge $xy\in E(C_m)$. We construct a new graph $G\, ^*$ by deleting two edges $uv$ and $xy$ from $G$ and $C_m$ respectively, and then join $u$ with $x$, $v$ with $y$ together. Next, we define an edge coloring $\psi$ of $G\, ^*$ as: $\psi(st) = \pi(st)$ if $st\in (E(G)\setminus \{uv\})\subset E(G\, ^*)$; $\psi(st) = \phi(st)$ if $st\in (E(C_m)\setminus \{xy\})\subset E(G\, ^*)$, and $\psi(ux) = \psi(vy) = 1$. It is easy to see that $C(a, \psi)\neq C(b, \psi)$ for distinct vertices $a, b\in V(G\, ^*)$, since degrees $d _{G\, ^*}(x)\geq 3$ for $x\in V(G\, ^*)\setminus V(C_{m})$. Immediately, $\chi\, '_{s}(G\, ^*)\leq n$, and furthermore $\chi\, '_{s}(G\, ^*) = n$ since $G\, ^*$ has ${n \choose 2}$ vertices of degree two. Notice that $C_{m+n}\subset G\, ^*$, and $m+n = {n \choose 2}+n = {n+1 \choose 2}$ as well as $\chi\, '_{s}(C_{m+n}) = n+1$ according to Lemma 1.2. Therefore, $G\, ^*$ is a vdec no-covered graph.

If $k = n+1$, we take a cycle $C_{m}$ on $m = {n+1 \choose 2}$ vertices, and then we still have a graph $H\, ^*$ obtained from $G$ and $C_{m}$ by the same construction as the above one. Clearly, $\chi\, '_{s}(H\, ^*) = n+1$, and $H\, ^*$ is vdec no-covered, since $H\, ^*$ contains a Hamilton cycle $C_{m+n}$ with $m+n = {n+1 \choose 2}+n > {n+1 \choose 2}$, which means $\chi\, '_{s}(C_{m+n}) > n+1$. The proof of the claim is finished.

By adding vertices and edges to a given connected graph $H$, we can obtain a Hamilton graph $G$ with $\delta(G)\geq 3$ and $G$ has a Hamilton cycle containing an edge $uv\not \in E(H)$ and $\pi(uv) = 1$ under a $k$-vdec $\pi$ of $G$. The theorem follows from the above claim. □

The construction of the graph $G\, ^*$ in the proof of Theorem 2.1 enables us to obtain the following result:

Corollary 2.1. For given positive integers $M$ and $N$, there is a vdec no-covered Hamilton graph $G$ having $\Delta(G)\geq M$ and $|V(G)|\geq N$.

Theorem 2.2. There exist Hamilton graphs $H_0, H_1, \dots, H_m$ with $m\geq 1$ such that $H_{i}$ is a proper subgraph of $H_{i-1}$ and $\chi\, '_s(H_i) > \chi\, '_s(H_{i-1})$ for $i\in [1, m]$.

Proof. For $m = 1$, the conclusion is deduced by Theorem 2.1. The case $m\geq 2$ is discussed as follows. Let $N$ be a positive integer, and let $G_1, G_2, \dots, G_m$ be $m$ vertex-disjoint Hamilton graphs with $|G_i| = N+i-1$, $2\leq k_i = \chi\, '_s(G_i)\leq N$, $\Delta(G_{j-1}) < \delta(G_{j})$ for $j\in [2, m]$, and $\delta(G_1)\geq 3$. Suppose that $\pi_i$ is a $k_i$-vdec of $G_i$ for $i\in [1, m]$. Since $k_i\geq 2$, we have two edges $x_{i}y_{i}$ and $u_{i}v_{i}$ of a Hamilton cycle $T_i$ of $G_i$ with $\pi_i(x_{i}y_{i}) = 1$ and $\pi_i(u_{i}v_{i}) = 2$, $i\in [1, m]$. We construct a graph $G$ by means of $G_1, G_2, \dots, G_m$ in the following two steps.

Step 1. Delete edges $u_{1}v_{1}$ of $G_1$, $u_{m}v_{m}$ of $G_m$, and $x_{i}y_{i}$ and $u_{i}v_{i}$ of $G_i$ for $i\in [2, m-1]$, respectively.

Step 2. Join $x_{i}$ with $y_{i-1}$, $y_{i}$ with $x_{i-1}$, $u_{i}$ with $v_{i-1}$ and $v_{i}$ with $u_{i-1}$, respectively, $i\in [3, m-1]$; join $u_{2}$ with $v_{1}$, $v_{2}$ with $u_{1}$; and join $u_{m}$ with $v_{m-1}$, $v_{m}$ with $u_{m-1}$.

Let $C_n$ be a cycle on $n = {N \choose 2}$ vertices. Suppose that an edge $x_0y_0$ of $C_n$ is labelled as $\pi(x_0y_0) = 1$ under a $N$-vdec $\pi$ of $C_n$ from Lemma 1.2. Now, we have a graph $H_0$ obtained by joining $x_0\in V(C_n)$ with $y_1\in V(G)$, $y_0\in V(C_n)$ with $x_1\in V(G)$, and removing the edge $x_0y_0$. Clearly, $H_0$ is hamiltonian by the above construction. We define an edge coloring $\theta$ of $H_0$ as: $\theta(wz) = \pi_i(wz)$ when $wz\in E(G_i)\setminus \{x_{i}y_{i}, u_{i}v_{i}\}$ for $i\in [2, m-1]$; $\theta(x_{i}y_{i-1}) = \theta(y_{i}x_{i-1}) = 1$ for $i\in [3, m-1]$; $\theta(u_{i}v_{i-1}) = \theta(v_{i}u_{i-1}) = 2$ for $i\in [2, m]$; $\theta(x_{1}y_{0}) = \theta(y_{1}x_{0}) = 1$ and $\theta(wz) = \pi(wz)$ when $wz\in E(C_n)\setminus \{x_0y_0\}$; $\theta(u_{m}v_{m-1}) = \theta(v_{m}u_{m-1}) = 2$ and $\theta(wz) = \pi_m(wz)$ for $wz\in E(G_m)\setminus \{u_mv_m\}$. By the choices of $C_n$ and $G_1, G_2, \dots, G_m$, we have $C(w, \theta)\neq C(z, \theta)$ for distinct vertices $w, z\in V(H_0)$ and $\chi\, '_s(H_0)\leq N$.

Deleting every edge of $S_1 = E(H_0)\cap \big (E(G_1)\setminus E(T_1)\big)$ from $H_0$ results in a graph $H_1$. Notice that $H_1$ is hamiltonian and has $|G_1|+n = N+{N \choose 2} = {N+1 \choose 2}$ vertices of degree 2 that form a set $X^{(2)}_1$, which implies $\chi\, '_s(H_1)\geq N+1\geq 1+\chi\, '_s(H_0)$. By Lemm 1.2 we have $\chi\, '_s(H_1) = N+1$, since $d_{H_1}(z)\geq 3$ for $z\in V(H_1)\setminus X^{(2)}_1$. In general, we have Hamilton graphs $H_i = H_{i-1}-S_i$, where $S_i = E(H_{i-1})\cap \big (E(G_i)\setminus E(T_i)\big)$ with $\chi\, '_s(H_i) = N+i$, since $H_i$ has $|G_i|+{N+i-1 \choose 2} = (N+i-1)+{N+i-1 \choose 2} = {N+i \choose 2}$ vertices of degree $2$ that form a set $X^{(2)}_i$ such that $d_{H_i}(z)\geq 3$ for $z\in V(H_i)\setminus X^{(2)}_i$, $i\in [1, m]$. Continue with this method, finally, we obtain $H_m$ that is a cycle of order $M = |G_m|+{N+m-1 \choose 2} = (N+m-1)+{N+m-1 \choose 2} = {N+m \choose 2}$ with $\chi \, ''_{s}(H_m) = N+m$. The proof is completed. □

Theorem 2.3. Each Hamilton graph is a proper subgraph of some vdtc no-covered Hamilton graph.

Proof. By Lemma 1.3, $\chi \, ''_{s}(K_{n, n-1}) = n+1$ and $\chi \, ''_{s}(K_{n-1, n-1}) = n+2$ for $n\geq 4$. Let $G$ be a graph having a Hamilton cycle $C_m = x_1x_2\cdots x_mx_1$ and let $n$ be so large such that $n-1\geq \max\{\Delta(G), 7\}$ and $n-5\geq k = \chi\, ''_s(G)$. Since $K_{n-1, n-1} = K_{n, n-1}-\{u\}$ is hamiltonian, we have a Hamilton cycle $C_{2n-2} = u_1v_1u_2v_2\cdots u_{n-1}v_{n-1}u_1$ of $K_{n-1, n-1}$, where $u$ is adjacent to $v_i$ for $i\in [1, n-1]$ in $K_{n, n-1}$. Let $H = C_4+\{w_2w_4\}$, where $C_4 = w_1w_2w_3w_4w_1$.

Let $f$ be a $(n+1)$-vdtc of $K_{n, n-1}$, without loss of generality, $f(v_1u_2) = 1$, $f(u_1v_1) = 2$ and $f(u_1v_{n-1}) = 3$; and let $g$ be a $k$-vdtc of $G$. Select an edge $u_iv_i$ with $2\leq i\leq n-1$. We can modify the colors of elements of $V(G)\cup E(G)$ under the coloring $g$ such that some edge $x_jx_{j+1}$ of $C_m$ holds $g(x_j)\neq f(v_i)$, $g(x_{j+1})\neq f(u_i)$, $g(x_jx_{j+1}) = f(u_iv_i)$ (if $k < f(u_iv_i)$, we set $g(x_jx_{j+1}) = f(u_iv_i)$ directly). Now, we define a total coloring $h$ of $H$ as: $\{h(w_i):i\in [1, 4]\} = \{n-2, n-1, n, n+1\}$ with $h(w_1)\neq f(v_1)$, $h(w_2)\neq f(u_2)$, $h(w_3)\neq f(v_{n-1})$ and $h(w_4)\neq f(u_1)$; $h(w_1w_2) = 1$, $h(w_2w_3) = 2$, $h(w_3w_4) = 3$, $h(w_1w_4) = 4$ and $h(w_2w_4) = 5$.

We do: (1) delete $w_1w_2$ of $H$ and $v_1u_2$ of $K_{n, n-1}$, and join $w_2$ with $u_2$, join $w_1$ with $v_1$; (2) delete $w_3w_4$ of $H$ and $u_1v_{n-1}$ of $K_{n, n-1}$, and join $w_3$ with $v_{n-1}$, join $w_4$ with $u_1$; (3) delete the edge $x_jx_{j+1}$ of $G$ and the edge $u_iv_i$ of $K_{n, n-1}$, and join $x_j$ with $u_i$, join $x_{j+1}$ with $v_i$. Through the above measures, we get a connected graph $G^*$ and $G^*$ has a total coloring $\theta$ as folows: $\theta(V(G^*)) = f(V(K_{n, n-1}))\cup g(V(G))\cup h(V(H))$,

and $\theta(w_2u_2) = 1$, $\theta(w_1v_1) = 1$, $\theta(w_3v_{n-1}) = 3$, $\theta(w_4u_1) = 3$, $\theta(x_ju_i) = f(u_iv_i)$ and $\theta(x_{j+1}v_i) = f(u_iv_i)$. Notice that $C(a, \theta)\neq C(b, \theta)$ for distinct vertices $a, b\in V(G\, ^*)$ according to the definitions of the total colorings $f$, $g$, $h$ and $\theta$. We conclude that $\theta$ is a $(n+1)$-vdtc of $G^*$. Clearly, $\chi\, ''_s(G\, ^*)\leq n+1$ and, $G^*$ has a Hamilton cycle $uu_1v_1w_1w_4w_2w_3v_{n-1}u_{n-1}\cdots v_jx_{j+1}x_{j+2}\cdots x_mx_1\cdots x_ju_iv_{i-1}\cdots v_2u_2u$.

Since $G$ and $K_{n-1, n-1}$ both are the proper subgraphs of $G\, ^*$, the theorem is covered. □

3.   Adjacent vertex distinguishing edge and total colorings

Theorem 3.1. For given integers $M\geq 3$ and $N\geq 5$, there is a connected graph $G$ with $\Delta\geq M$ and $n\geq N$ vertices such that $G$ contains a proper subgraph $H$ with $\chi \, '_{as}(H) > \chi\, '_{as}(G)$.

Proof. First of all, we define the avd-linking operation on two graphs. Suppose that each connected graph $G_i$ has a $k_i$-avdec $\pi_i$ with $k_i = \chi\, '_{as}(G_i)$ for $i = 1, 2$, and furthermore $\pi_1(u_1v_1) = \pi_2(u_2v_2)$ for $u_iv_i\in E(G_i)$, and $C(u_i, \pi_i)\neq C(v_{3-i}, \pi_{3-i})$, $i = 1, 2$. We obtain a new graph $H\, ^*$ by deleting edges $u_iv_i$ from $G_i$, and join $u_i$ to $v_{3-i}$ for $i = 1, 2$. Clearly, $H\, ^*$ admits a $k_0$-avdec $\pi$, where $k_0 = \max\{k_1, k_2\}$, by defining an edge-coloring $\pi$ as: $\pi (uv) = \pi_i(uv)$ for $uv\in E(G_i)\setminus\{u_iv_i\}$, and $\pi(u_iv_{3-i}) = \pi_i(u_iv_i)$ for $i = 1, 2$.

There are many ways to construct the desired graph $G$ mentioned in this theorem. Here, we take a complete graph $K_{\Delta+1, \Delta}$ with $\Delta\geq M\geq 3$. Clearly, a proper subgraph $K_{\Delta, \Delta}\subset K_{\Delta+1, \Delta}$ holds $\chi \, '_{as}(K_{\Delta, \Delta}) = \Delta+2 > \Delta+1 = \chi\, '_{as}(K_{\Delta+1, \Delta})$.

Let $K\, '_{\Delta+1, \Delta}$ be a copy of $K_{\Delta+1, \Delta}$, and let the edge $u\, 'v\, '\in E(K\, '_{\Delta+1, \Delta})$ be isomorphic to an edge $uv\in E(K_{\Delta+1, \Delta})$. By the avd-linking operation on two graphs $K_{\Delta+1, \Delta}$ and $K\, '_{\Delta+1, \Delta}$, we obtain a connected graph $H_1(2(2\Delta+1))$ that contains two copies of $K_{\Delta, \Delta}$ and has $2(2\Delta+1)$ vertices. Since $\chi\, '_{as}(H_1(2(2\Delta+1))) = \chi\, '_{as}(K_{\Delta+1, \Delta}) = \Delta+1$, so $\chi\, '_{as}(K_{\Delta, \Delta}) > \chi\, '_{as}(H_1(2(2\Delta+1)))$. Consequently, by implementing the avd-linking operation, we take a copy $H\, '_1(2(2\Delta+1))$ of $H_1(2(2\Delta+1))$, and then construct a connected graph $H_2(2^2(2\Delta+1))$ such that $\chi\, '_{as}(K_{\Delta, \Delta}) = \Delta+2 > \Delta+1 = \chi\, '_{as}(H_2(2^2(2\Delta+1)))$ for a proper subgraph $K_{\Delta, \Delta}$ of $H_2(2^2(2\Delta+1))$. Go on in this way, we can construct a connected graph $H_k(2^k(2\Delta+1))$ having a proper subgraph $K_{\Delta, \Delta}$, and furthermore, $\chi\, '_{as}(H_k(2^k(2\Delta+1))) = \Delta+1$ and $2^k(2\Delta+1)\geq N\geq 5$. □

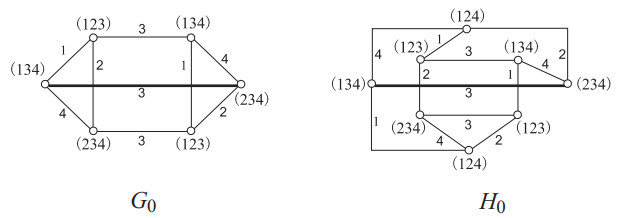
An example for illustrating the avd-linking operation used in the proof of Theorem 3.1 is given in Figures 1 and 2.

Theorem 3.2. Each connected graph is a proper subgraph of an avdec no-covered graph.

Proof. Let the bipartition $(X, Y)$ of vertex set of $K_{n+1, n}$ for $n\geq 3$ be defined as $X = \{u_i:i\in [1, n+1]\}$ and $Y = \{v_i:i\in [1, n]\}$, and let $f$ be a $(n+1)$-avdec of $K_{n+1, n}$ by Lemma 1.3. Suppose that each given connected graph $H_j$ has a $k_j$-avdec $g_j$ with $k_j = \chi\, '_{as}(H_j)\leq n-2$ and $\Delta(H_j)\leq n-2$ for $j = 1, 2$.

We delete the edge $u_1v_1$ from $K_{n+1, n}$, without loss of generality, set $f(u_1v_1) = n+1$. Next we join $u_1$ with a vertex $w_1$ of $H_1$, join $v_1$ with a vertex $w_2$ of $H_2$, the resultant graph is denoted by $G$. Notice that $\chi\, '_{as}(G)\geq n+1$ since $d_G(v_{i}) = n+1$ for $i\in [2, n]$. We define an edge coloring $h$ of $G$ as: $h(xy) = f(xy)$ for $xy\in \big (E(K_{n+1, n})\setminus \{u_1v_1\}\big)\subset E(G)$; $h(u_1w_1) = f(u_1v_1)$ and $h(v_1w_2) = f(u_1v_1)$; $h(xy) = g_j(xy)$ for $xy\in E(H_j)$, $j = 1, 2$. Furthermore, $\Delta(G) = n+1\leq \chi\, '_{as}(G)\leq n+1 = \max\{\chi\, '_{as}(K_{n+1, n}), k_1, k_2\}$. However, $\chi\, '_{as}(K_{n, n}) = n+2 > n+1 = \chi\, '_{as}(G)$ since $K_{n, n}\subset G$. The theorem is covered since each given connected graph $H_j$ is a proper subgraph of $G$ for $j = 1, 2$. □

Theorem 3.3. There are infinitely many connected 3-regular graphs $G$ on $n (\geq 6)$ vertices that are avdec no-covered, planar and hamiltonian, and furthermore $\chi\, '_{as}(G) = \chi\, ''(G) = 4$.

Proof. For the sake of simplicity, we define Property (Ⅰ) as follows: A graph $G$ has Property (Ⅰ) if (i) $G$ is connected, 3-regular, planar and hamiltonian; (ii) $G$ is embedded well in the plane; (iii) $G$ has a particular edge $uv$ locating in the bound of the outer-face and a Hamilton cycle of $G$, $G-\{uv\}$ contains at least a $5$-cycle; and (iv) $\chi\, '_{as}(G) = 4$.

Obviously, a graph having Property (Ⅰ) is avdec no-covered. Let $G_0$ and $H_0$ be two vertex-disjoint graphs shown in Figure 1. Clearly, $G_0$ and $H_0$ both possess Property (Ⅰ). Let $u_0v_0\in E(G_0)$ and $x_0y_0\in E(H_0)$ be the particular edges described in Property (Ⅰ). And let $C_0$ be a Hamilton cycle of $G_0$ such that $u_0v_0\in E(C_0)$ and $C\, '_0$ be a Hamilton cycle of $H_0$ such that $x_0y_0\in E(C\, '_0)$. Since $\chi\, '_{as}(G_0) = 4 = \chi\, '_{as}(H_0)$, we have a $4$-avdec $\pi_0$ of $G_0$ and a $4$-avdec $\pi\, '_0$ of $H_0$ such that $\pi_0(u_0v_0) = \pi\, '_0(x_0y_0)$ (we can modify the colors used in $\pi\, '_0$ to achieve the desired requirement, since $G_0$ and $H_0$ are vertex-disjoint). We construct a graph $G_1$ by deleting the edges $u_0v_0$ and $x_0y_0$ from $G_0$ and $H_0$, respectively, and then join $u_0$ with $y_0$, join $v_0$ with $x_0$. Clearly, $G_1$ has a Hamilton cycle $(C_0-u_0v_0)+u_0y_0+(C\, '_0-x_0y_0)+x_0v_0$, and has Property (Ⅰ). We select another graph $H_1$ having Property (Ⅰ), and then construct a graph $G_2$ from $G_1$ and $H_1$ by the above way such that $G_2$ has Property (Ⅰ). Go on in this way, we have graphs $G_m$ having Property (Ⅰ) for all integers $m\geq 1$. Notice that $C(s, f_i)\neq C(t, f_i)$ for every edge $st\in E(G_i)$ under a $4$-avdec $f_i$ of $G_i$, so $[1, 4]\setminus C(s, f_i)\neq [1, 4]\setminus C(t, f_i)$, $i\geq 1$. We can use one color in $[1, 4]\setminus C(s, f_i)$ to color the vertex $s$, and use one color in $[1, 4]\setminus C(t, f_i)$ to color the vertex $t$ for every edge $st$ of $G_i$, thus, $\chi\, ''(G_i) = 4$ for $i\geq 1$, as desired. □

For a graph $G$ with $\Delta(G) = 3$, let $P = ux_1x_2\cdots x_mv$ be a $(u, v)$-path of $G$ if $d_G(v) = 3$ and $d_G(x_i) = 2$ for $i\in [1, m]$. We call $P$ a $(k, 3;m)$-path if $d_G(u) = k$ for $k = 1, 3$.

Lemma 3.1. If $\chi\, ''_{as}(G) = 3$, then $G$ contains no proper subgraph $H$ such that $\chi\, ''_{as}(H)\geq 4$.

Proof. Since $\chi\, ''_{as}(G) = 3$, we have $\Delta(G)\leq 2$. By Lemma 1.3, $G$ is a path of length at most two, which implies that $G$ has no proper subgraph $H$ with $\chi\, ''_{as}(H)\geq 4$. □

Lemma 3.2. Suppose that a graph $H$ has maximum degree $\Delta = 3$ and no adjacent $\Delta$-vertices. If each $2$-degree vertex is adjacent to two $3$-degree vertices in $H$, then $\chi\, ''_{as}(H) = 4$.

Proof. It is trivial for $|V(H)| = 4$. For $|V(H)| = 5$, $H = K_{2, 3}$ and $\chi\, ''_{as}(K_{2, 3}) = 4$. The case $|V(H)|\geq 6$ is considered as follows. Notice that $d_H(x)\neq d_H(y)$ for every edge $xy$ of $H$, which means that each proper total coloring of $H$ is also an avdtc, and vice versa. Thereby, we can use the induction on orders of graphs.

Case 1. $H$ has leaves.

Let $N(w) = \{w_1, w_2, w_3\}$ be the neighborhood of a $3$-degree vertex $w$ of $H$. If $w_1, w_2$ both are leaves, and $w_3$ is adjacent to two $3$-degree vertices $w$ and $v$. We know that $\chi\, ''_{as}(H-\{w_1, w_2, w\}) = 4$ by induction hypothesis. Suppose that $H-\{w_1, w_2, w\}$ has a $4$-avdtc $f$ such that $f(v) = 1$, $f(w_3v) = 2$ and $f(w_3) = 3$. We can extend $f$ to a $4$-avdtc of $H$ described in Figure 3(a).

If $w_1, w_2$ both are $2$-degree vertices, where $w_1$ is adjacent to a $3$-degree vertex $x$, $w_2$ is adjacent to a $3$-degree vertex $y$, and $w_3$ is a leaf. We have a graph $G_1$ obtained by deleting $w$ and all vertices in $N(w)$, and adding a new vertex $u$ to join $x$ and $y$ respectively. Clearly, $G_1$ is a graph holding the hypothesis of the lemma. Let $f_1$ be a $4$-avdtc of $G_1$ by induction hypothesis. Without loss of generality, $f_1(xu) = 1$, $f_1(u) = 2$ and $f_1(uy) = 3$. Thereby, we can extend $f_1$ to a $4$-avdtc of $H$, see Figure 3(b).

Case 2. $H$ has no leaves.

Subcase 2.1. $H$ has $4$-cycles. $H\neq K_{2, 3}$ since $|V(H)|\geq 6$. Let $u_1u_2u_3u_4$ be a $4$-cycle of $H$. Notice that $\delta(H) = 2$ and each $2$-degree vertex of $H$ is adjacent to two $3$-degree vertices. Hence, a local part of $H$ that contains the $4$-cycle $u_1u_2u_3u_4$ is shown in Figure 3(c). Let $X = \{u_1, u_2, u_3, u_4, u_5, u_6\}$. Thereby, a graph $G_2$ can be obtained by deleting every vertex of $X$ and add a new vertex $w\, '$ to join $u$ and $v$, respectively. Clearly, $G_2$ is a graph holding the hypothesis of the lemma. By induction hypothesis, $G_2$ has a $4$-avdtc $f_2$ such that $f_2(uw\, ') = 1$, $f_2(w\, ') = 2$ and $f_2(w\, 'v) = 3$. It is not hard to extend $f_2$ to a $4$-avdtc of $H$ (see Figure 3(c)).

If $u$ is adjacent to $u_6$, refereing Figure 3(c), we have a graph $G'_2 = H-\{u_1, u_2, u_3, u_4\}$ having leaves. So $\chi\, ''_{as}(G'_2) = 4$ by the proof in Case 1. Then we can extend a $4$-avdtc of $G'_2$ to a $4$-avdtc of $G$.

Subcase 2.2. $H$ has no $4$-cycles. If $H$ has the exact four $3$-degree vertices, then it is an edge-subdivision of $K_4$, so we are done, see Figure 4(a). We, now, consider that $H$ has at least six $3$-degree vertices in the following. $H$ has a subgraph $H\, ^*$ with vertex set $V(H\, ^*) = \{u, v, w, u_1, u_2, v_1, v_2\}$ by referring to Figure 4(b). In $H$, two vertices $u, v$ both have $3$-degree, each vertex of $V(H\, ^*)\setminus \{u, v\}$ has $2$-degree, where $N(u_1) = \{u, x\}$, $N(u_2) = \{u, y\}$, $N(v_1) = \{v, s\}$ and $N(v_2) = \{v, t\}$ (see Figure 4(b)). Now, we have a graph $G_3$ obtained by deleting $V(H\, ^*)$ from $H$ and adding a new vertex $x_0$ to join $x$ and $y$, and adding another new vertex $s_0$ to join $s$ and $t$, respectively. So $G_3$ has a $4$-avdtc $f_3$ by induction hypothesis, since $G_3$ satisfies the lemma's hypothesis. Without loss of generality, $f_3(xx_0) = 1$, $f_3(x_0) = 2$, $f_3(x_0y) = 3$. We define a proper total coloring $h_3$ of $H$ in the following two steps.

Step 1. (1) Set $h_3(z) = f_3(z)$ for $z\in \big (V(G_3)\cup E(G_3)\big)\setminus \{xx_0, x_0, x_0y, ss_0, s_0, s_0t\}$; (2) $h_3(xu_1) = 1$, $h_3(u_1) = 2$, $h_3(yu_2) = 3$, $h_3(u_2) = 2$; (3) $h_3(u_1u) = 3$, $h_3(u) = 4$, $h_3(u_2u) = 1$ and $h_3(uw) = 2$ (see Figure 4(c)).

Step 2. To color every element of $S = \{sv_1, v_1, v_1v, tv_2, v_2, v_2v, v, vw, w\}$, we consider the colors on $ss_0, s_0, s_0t$ under $f_3$. Let $f_3(ss_0) = a$, $f_3(s_0) = b$, $f_3(s_0t) = c$ (see Figure 4(c)).

Step 2.1. $(a, b, c) = (1, 2, 3)$. Thus, we need to consider two cases $f_3(t) = 4$ and $f_3(t) = 1$, respectively.

(i) When $f_3(t) = 4$, we set $h_3(sv_1) = 1$, $h_3(v_1) = 2$, $h_3(v_1v) = 3$, $h_3(tv_2) = 3$, $h_3(v_2) = 1$, $h_3(v_2v) = 2$, $h_3(v) = 4$ and $h_3(vw) = 1$ and $h_3(w) = 3$. Thereby, $h_3$ is a desired $4$-avdtc of $H$.

(ii) If $f_3(t) = 1$, we set $h_3(sv_1) = 1$, $h_3(v_1) = 2$, $h_3(v_1v) = 3$, $h_3(tv_2) = 3$, $h_3(v_2) = 4$, $h_3(v_2v) = 2$, $h_3(v) = 1$ and $h_3(vw) = 4$ and $h_3(w) = 3$. In this situation, $h_3$ is a desired $4$-avdtc of $H$.

Step 2.2. $(a, b, c) = (a, 2, c)$ and $(a, b, c)\neq (1, 2, 3)$, where distinct $a, c\in [1, 4]\setminus \{2\}$. The procedure of coloring properly every element of $S$ is very similar to that in Step 2.1. We still obtain a desired $4$-avdtc of $H$.

Step 2.3. $b\neq 2$. We set $h_3(sv_1) = a$, $h_3(v_1) = b$, $h_3(tv_2) = c$, $h_3(v_2) = b$, $h_3(vw) = b$, $h_3(v) = 2$ and $h_3(w)\in [1, 4]\setminus \{2, b, 4\}$ (see Figure 3(c)). For the last two edges $v_1v$ and $v_2v$, we set $h_3(v_1v) = c$ and $h_3(v_2v) = a$ if $a, c\in [1, 4]\setminus \{2, b\}$; and if $a = 2$, without loss of generality, we set $h_3(v_1v) = c$ and $h_3(v_2v)\in [1, 4]\setminus \{2, b, c\}$. Eventually, we can get a desired $4$-avdtc of $H$.

The proof is completed. □

Since $\chi \, ''_{as}(P_{n}) = 4$ for $n\geq 4$, it is not hard to get the following result.

Lemma 3.3. Let $H$ be a graph with $\Delta(H) = 3$, no adjacent $\Delta$-vertices and $\chi\, ''_{as}(H) = 4$. If $H$ has an edge $uv$ with $d_H(u) = 1$ and $d_H(v) = 3$, replace the edge $uv$ with a path $P = ux_1x_2\cdots x_mv$ $(m\geq 1)$, where each $x_i$ is out of $H$ for $i\in [1, m]$, the resultant graph is denoted by $H_2$, then $\chi\, ''_{as}(H_2) = 4$.

Theorem 3.4. For a graph $G$ with $\Delta = 3$ and no adjacent $\Delta$-vertices, $\chi\, ''_{as}(G) = 4$.

Proof. Obviously, the conclusion holds when $|E(G)| = 3$. Next we consider the case that $|E(G)|\geq 4$. If $G$ contains some $(3, 3;m)$-$(u, v)$-paths with $m\geq 2$. For every $(3, 3;m)$-$(u, v)$-path $P = ux_1x_2\cdots x_mv$ of $G$, we delete $x_i$ for $i\in [1, m]$, and add a new vertex $w$ out of $G$ by joining $w$ with $u, v$ respectively. The resulting graph is denoted as $G'$. If $G'$ contains some $(1, 3;m)$-paths $Q = uy_1y_2\cdots y_mv$ with $m\geq 1$, $d_G(u) = 1$ and $d_G(v) = 3$. To each $(1, 3;m)$-path $Q$ of $G'$, we delete $y_j$ for $j\in [1, m]$ and then join $u$ with $v$. Eventually, we obtain a graph $G''$ that contains no adjacent $\Delta$-vertices, and each $2$-degree vertex is adjacent to two $3$-degree vertices.

According to Lemma 3.2, $\chi\, ''_{as}(G'') = 4$, and then $\chi\, ''_{as}(G') = 4$ by Lemma 3.3. Thereby, we can use the induction on orders of $G'$ in the following argument.

Let $G'$ have a $2$-degree vertex $w$ that is adjacent to two $3$-degree vertices $u, v$, after replacing some $(3, 3;m)$-$(u, v)$-path $P = ux_1x_2\cdots x_mv$ of $G$ with $m\geq 2$ by a path $uwv$.

Case 1. Replace the path $uwv$ by a path $ux_1x_2v$.

If one of two vertices $u, v$ is in a $4$-cycle of $G'$, without loss of generality, $G'$ has a $4$-cycle $vu_1u_2u_3v$ shown in Figure 5(a). We delete the set $\{w, v, u_1, u_2, u_3, u_4\}$ from $G'$, and then add a new vertex $s$ out of $G'$ by joining $s$ with $u, u_5$, respectively. The resulting graph is written as $H_1$. Clearly, $H_1$ admits $4$-avdtcs by induction hypothesis, since $H_1$ has $\Delta(H_1) = 3$ and no adjacent $\Delta$-vertices. Next, we substitute by a path $ux_1x_2v$ the path $uwv$ of $G'$ to obtain another graph $H_2$. By means of a $4$-avdtc of $H_1$, we can get a desired $4$-avdtc of $H_2$ shown in Figure 5(a).

Suppose that two vertices $u, v$ are not in any $4$-cycle of $G'$. If $G'$ is the graph shown in Figure 4(a), we are done. Otherwise, $G'$ has a part shown in Figure 5(b) (no dashing lines and black vertices).

We have a graph $H_3$ obtained by deleting every vertex of $\{u_1, u_2, u, w, v, v_1, v_2\}$ from $G'$ and adding a new vertex $x_0$ out of $G'$ to join $x$ and $y$, and adding another new vertex $s_0$ out of $G'$ to join $s$ and $t$, respectively. Since $H_3$ has $\Delta(H_3) = 3$ and no adjacent $\Delta$-vertices that is a $4$-avdtc $f_3$ of $H_3$ by induction hypothesis. Thus, we construct a graph $H_4$ in the way of replacing by a path $ux_1x_2v$ the path $uwv$ of $G'$, and extend $f_3$ to a proper total coloring $h_4$ of $H_4$. Clearly, $H_4$ has maximum degree 3 and no adjacent $\Delta$-vertices.

Except $h_4(x_1) = 1$, $h_4(x_1x_2) = 2$ and $h_4(x_2) = 3$, each $h_4(z)$ for $z\in \big (V(H_4)\cup E(H_4)\big)\setminus \{x_1, x_1x_2, x_2\}$ are determined well based on $f_3$ (see Figure 5(b)) such that $h_4(u)\neq h_4(v)$ since $h_4(u_1u) = c$ or $d$, and $h_4(u) = d$ or $c$, where $d\in [1, 4]\setminus \{a, b, c\}$. Notice that $d'\in [1, 4]\setminus \{a', b', c'\}$. By exhaustion we can select appropriately colors $1, 2, 3$ such that $h_4$ is a $4$-avdtc of $H_4$.

Case 2. Let $H'$ be a graph having maximum degree 3, a $(3, 3;m)$-path $P = ux_1x_2\cdots x_mv$ with $m\geq 2$ and no adjacent $\Delta$-vertices as well as $\chi\, ''_{as}(H') = 4$. Our goal is to construct a new graph $G^*$ having maximum degree 3 and no adjacent $\Delta$-vertices by replacing an edge $x_ix_{i+1}$ of the path $P$ for some $i\in [1, m-1]$ by a path $x_iyx_{i+1}$, where $y$ is a new vertex out of $H'$, and then show $\chi\, ''_{as}(G^*) = 4$. Note that $G^*$ contains a path $(3, 3;m)$-path $Q = ux_1x_2\cdots x_iyx_{i+1}\cdots x_mv$ with $m\geq 2$ and $|G^*| > |G|$.

Subcase 2.1. For $m = 2$, $H'$ contains a $(3, 3;2)$-path $ux_1x_2v$.

Let $\eta_{21}$ be a $4$-avdtc of $H'$. Without loss of generality, $\eta_{21}(ux_1) = 2$, $\eta_{21}(x_1) = 1$, $\eta_{21}(x_1x_2) = 3$. Hence, $\eta_{21}(x_2)\in \{2, 4\}$ and $\eta_{21}(x_2v)\in \{1, 2, 4\}$, since $C(x, \eta_{21})\neq C(y, \eta_{21})$ for each edge $xy$ of $H'$. Now, we delete the edge $x_1x_2$ from $H'$ and add a new vertex $z$ out of $H'$ and two edges $zx_1$, $zx_2$. The resulting graph is denoted as $H_{21}$. We can define a $4$-avdtc $\lambda_{21}$ of $H_{21}$ by means of $\eta_{21}$. Let $Z = \{x_1z, zx_2, x_2v\}\cup \{z, x_2\}$. We define $\lambda_{21}(s) = \eta_{21}(s)$ for $s\in (V(H_{21})\cup E(H_{21}))\setminus Z$; and $\lambda_{21}(x_2) = \eta_{21}(x_2)$, $\lambda_{21}(x_2v) = \eta_{21}(x_2v)$.

If $\eta_{21}(x_2) = 2$ and $\eta_{21}(x_2v) = 4$, set $\lambda_{21}(x_1z) = 4$, $\lambda_{21}(z) = 3$ and $\lambda_{21}(zx_2) = 1$.

If $\eta_{21}(x_2) = 4$ and $\eta_{21}(x_2v) = 2$, define $\lambda_{21}(x_1z) = 4$, $\lambda_{21}(z) = 1$ and $\lambda_{21}(zx_2) = 3$.

If $\eta_{21}(x_2) = 4$ and $\eta_{21}(x_2v) = 1$, then let $\lambda_{21}(x_1z) = 4$, $\lambda_{21}(z) = 3$ and $\lambda_{21}(zx_2) = 2$.

If $\eta_{21}(x_2) = 2$ and $\eta_{21}(x_2v) = 1$, so $\eta_{21}(v)\in \{3, 4\}$. If $\eta_{21}(v) = 3$, we reset $\lambda_{21}(x_2) = 4$, and let $\lambda_{21}(x_2z) = 2$, $\lambda_{21}(z) = 3$ and $\lambda_{21}(zx_1) = 4$; if $\eta_{21}(v) = 4$, we reset $\lambda_{21}(x_2) = 3$, and let $\lambda_{21}(x_2z) = 2$, $\lambda_{21}(z) = 4$ and $\lambda_{21}(zx_1) = 3$. Thereby, $\lambda_{21}$ is really a $4$-avdtc of $H_{21}$.

Subcase 2.2. For $m = 3$, let $N(u) = \{u\, ', u\, '', x_1\}$ and $N(v) = \{x_3, v\, ', v\, ''\}$. Let $\eta_{22}$ be a $4$-avdtc of $H'$. Without loss of generality, assume that $\eta_{22}(u\, 'u) = 2$, $\eta_{22}(u\, ''u) = 3$, $\eta_{22}(u) = 4$, $\eta_{22}(ux_1) = 1$, $\eta_{22}(x_1) = 2$, $\eta_{22}(x_1x_2) = 3$. So, $\eta_{22}(x_2)\in \{1, 4\}$ and $\eta_{22}(x_2x_3)\in \{1, 2, 4\}$. We replace the edge $ux_1$ of $H'$ by a path $uzx_1$, where $z$ is a new vertex out of $H'$, and the resulting graph is denoted as $H_{22}$. We will extend $\eta_{22}$ to a $4$-avdtc $\lambda_{22}$ of $H_{22}$.

First, we define $\lambda_{22}(s) = \eta_{22}(s)$ for $s\in (V(H_{22})\cup E(H_{22}))\setminus Z\, '$, where $Z\, ' = \{z$, $zx_1$, $x_1$, $x_1x_2$, $x_2$, $x_2x_3\}$. If $\eta_{22}(x_2) = 4$ and $\eta_{22}(x_2x_3) = 2$, we define $\lambda_{22}(z) = 2$, $\lambda_{22}(zx_1) = 4$, $\lambda_{22}(x_1) = 1$; $\lambda_{22}(y) = \eta_{22}(y)$ for $y\in \{x_1x_2$, $x_2$, $x_2x_3\}$.

We have two subcases for colors $\eta_{22}(x_2)$ and $\eta_{22}(x_2x_3)$ in the following. (i) If $\eta_{22}(x_3) = 2$ and $\eta_{22}(x_3v) = 4$, then define $\lambda_{22}(z) = 3$, $\lambda_{22}(zx_1) = 4$, $\lambda_{22}(x_1) = 2$, $\lambda_{22}(x_1x_2) = 1$, $\lambda_{22}(x_2) = 4$ and $\lambda_{22}(x_2x_3) = 3$. If $\eta_{22}(x_3) = 3$ and $\eta_{22}(x_3v) = 2$ (resp. $\eta_{22}(x_3) = 2$ and $\eta_{22}(x_3v) = 3$), thus, we set $\lambda_{22}(z) = 2$, $\lambda_{22}(zx_1) = 4$, $\lambda_{22}(x_1) = 3$, $\lambda_{22}(x_1x_2) = 2$, $\lambda_{22}(x_2) = 4$ and $\lambda_{22}(x_2x_3) = 1$. (ii) If $\eta_{22}(x_2) = 1$ and $\eta_{22}(x_3) = 2$ or $4$, we can extend $\eta_{22}$ to a $4$-avdtc $\lambda_{22}$ of $H_{22}$ by the way similarly to the above one.

Subcase 2.3. For $m\geq 4$, we let $N(u) = \{u\, ', u\, '', x_1\}$ and let $\eta_{23}$ be a $4$-avdtc of $H'$. Without loss of generality, we assume that $\eta_{23}(u\, 'u) = 2$, $\eta_{23}(u\, ''u) = 3$, $\eta_{23}(u) = 4$, $\eta_{23}(ux_1) = 1$, $\eta_{23}(x_1) = 2$, $\eta_{23}(x_1x_2) = 3$. So, $\eta_{23}(x_2)\in \{1, 4\}$ and $\eta_{23}(x_2x_3)\in \{1, 2, 4\}$, since $C(x, \eta_{23})\neq C(y, \eta_{23})$ for each edge $xy\in E(H')$.

In order to obtain a new graph $H_{23}$ we replace the edge $ux_1$ of $H'$ by a path $uzx_1$, where $z$ is a new vertex out of $H'$. Next, we extend $\eta_{23}$ to a $4$-avdtc $\lambda_{23}$ of $H_{23}$. We set $\lambda_{23}(s) = \eta_{23}(s)$ for $s\in (V(H_{23})\cup E(H_{23}))\setminus Z\, ''$, where $Z\, '' = \{z$, $zx_1$, $x_1$, $x_1x_2, x_2\}$. Suppose that $\eta_{23}(x_2) = 4$, $\eta_{23}(x_2x_3) = 1$ (resp. $\eta_{23}(x_2x_3) = 2$). If $\eta_{23}(x_3) = 2$ and $\eta_{23}(x_3x_4) = 4$, define $\lambda_{23}(z) = 2$, $\lambda_{23}(zx_1) = 3$, $\lambda_{23}(x_1) = 4$, $\lambda_{23}(x_1x_2) = 2$ and $\lambda_{23}(x_2) = 3$. So $C(s, \lambda_{23})\neq C(t, \lambda_{23})$ for every edge $st\in E(H_{23})$. If $\eta_{23}(x_3) = 2$ and $\eta_{23}(x_3x_4) = 3$ (resp. $\eta_{23}(x_3) = 3$ and $\eta_{23}(x_3x_4) = 4$), which imply $\eta_{23}(x_2x_3) = 1$ or $4$, so we define $\lambda_{23}(z) = 2$, $\lambda_{23}(zx_1) = 4$, $\lambda_{23}(x_1) = 3$, $\lambda_{23}(x_1x_2) = 2$, and $\lambda_{23}(x_2) = 4$ when $\eta_{23}(x_2x_3) = 1$, or $\lambda_{23}(x_2) = 1$ if $\eta_{23}(x_2x_3) = 4$.

For the other choices of colors $\eta_{23}(u\, 'u)$, $\eta_{23}(u\, ''u)$, $\eta_{23}(u)$, $\eta_{23}(ux_1)$, $\eta_{23}(x_1)$ and $\eta_{23}(x_1x_2)$ under the distinguishing constraint $C(s, \eta_{23})\neq C(t, \eta_{23})$ for each edge $st\in E(H')$, by the above ways we can obtain a $4$-avdtc of $H_{23}$.

Based on the proofs in Case 1 and Case 2 above, we can reconstruct $G$ from $G'$ step by step such that $\chi\, ''_{as}(G) = 4$. The proof is covered. □

Theorem 3.4 implies that a connected graph $G$ with $\Delta = 3$ and no adjacent $\Delta$-vertices holds $\chi\, ''_{as}(G) = \chi\, ''(G) = 4$ and $\chi\, '_{as}(G) = \chi\, '(G) = 3$, and furthermore $\chi(G) = 3$ if $G$ contains odd-cycles.

Corollary 3.1. There are infinitely many avdtc no-covered graphs.

Proof. The result follows from Lemmas 3.1, 3.2, 3.3 and Theorem 3.4. □

4.   Further works

Motivated from the avd-linking operation introduced in the proof of Theorem 3.1, we define the avd-equivalent operation on a graph as below. Let $\pi$ be a $k$-avdec of graph $G$. If there are two edges $u_1v_1, u_2v_2$ of $G$ such that $\pi(u_1v_1) = \pi(u_2v_2)$, $C(u_i, \pi)\neq C(v_{3-i}, \pi)$ and $u_iv_{3-i}\not \in E(G)$ for $i = 1, 2$, then we have an avd-equivalent graph $G\, '$ obtained by deleting $u_1v_1, u_2v_2$ from $G$ and join $u_i$ to $v_{3-i}$ for $i = 1, 2$. Clearly, the avd-equivalent graph $G\, '$ has a $k$-avdec generated from $\pi$. Notice that $V(G) = V(G\, ')$, $|E(G)| = |E(G\, ')|$, and $\chi\, '_{as}(G\, ')\leq \chi\, '_{as}(G)$. The avd-equivalent class $\mathcal {G}_{as}(G)$ is the set of avd-equivalent graphs generated from $G$. In other words, each $H\in \mathcal {G}_{as}(G)$ is an avd-equivalent graph of a certain graph of $\mathcal {G}_{as}(G)$, and $\chi\, '_{as}(H)\leq \chi\, '_{as}(G)$. It is noticeable, $|\mathcal {G}_{as}(G_0)| = 1$, where $G_0$ is the graph shown in Figure 1. We want to figure out $\mathcal {G}_{as}(G)$ for a simple and connected graph $G$.

Observe that some connected graph $G$ having a proper subgraph $H$ with $\chi\, '_s(H) > \chi\, '_s(G)$ may hold $|\Delta(G)-\Delta(H)|\geq M$ for given integers $M\geq 1$. However, for cases $\chi\, '_{as}(H) > \chi\, '_{as}(G)$ and $\chi\, ''_{as}(H) > \chi\, ''_{as}(G)$, can we say $|\Delta(G)-\Delta(H)|\leq 1$?

In ^[9], the author point out that no simple graph $G$ having maximum degree three and $\chi\, ''_{as}(G) = 6$ has been discovered, although all graphs $H$ of maximum degree three obey $\chi\, ''_{as}(H)\leq 6$. For a graph $G$ with $\Delta(G)\geq 4$, we do not find a proper subgraph $H$ of $G$ such that $\chi\, ''_{as}(G) < \chi\, ''_{as}(H)$. Therefore, we propose:

Conjecture 4.1. $(1)$ Let $H$ be a proper subgraph of $G$. Then $\chi\, '_{as}(H)\leq \chi\, '_{as}(G)+1$ and $\chi\, ''_{as}(H)\leq \chi\, ''_{as}(G)+1$.

$(2)$ Let $H$ be a proper subgraph of $G$. Then there is no proper subgraph $H\, ^*$ of $H$ such that $\chi\, '_{as}(H\, ^*) > \chi\, '_{as}(H) > \chi\, '_{as}(G)$, or $\chi\, ''_{as}(H\, ^*) > \chi\, ''_{as}(H) > \chi\, ''_{as}(G)$.

$(3)$ Let $H$ be a common proper subgraph of two graphs $G_1$ and $G_2$. If $\chi\, '_{as}(H) > \chi\, '_{as}(G_i)$ for $i = 1, 2$, then $\chi\, '_{as}(G_1) = \chi\, '_{as}(G_2)$.

$(4)$ Let $G$ be a graph having adjacent $\Delta$-vertices and $\Delta = 3$. Then $G$ is not avdtc no-covered.

As known, $\chi'(G)\leq \chi''(G)$ is true in the traditional colorings of graph theory. But we can see $\chi\, ''_{as}(C_5) = 4 < 5 = \chi\, '_{as}(C_5)$ and $\chi\, ''_{s}(C_{13}) = 6 < 7 = \chi\, '_{s}(C_{13})$. We call $G$ an avdtc no-covering avdec (resp. vdtc no-covering vdec) if $\chi\, ''_{as}(G) < \chi\, '_{as}(G)$ (resp. $\chi\, ''_{s}(G) < \chi\, '_{s}(G)$). It may be interesting to characterize avdtc no-covering avdec graphs or vdtc no-covering vdec graphs.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to thank all the reviewers for their very helpful comments and constructive suggestions. This work was supported by the National Natural Science Foundation of China under Grant Nos. 62072296 and 61662066.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.