1.
Introduction
Von Neumann gave the idea of regularity in rings in 1935 [1] and showed that if the semigroup, (S,⋅) is regular, then the ring (S,+,⋅) is also regular [1]. In 1951, Bourne showed if ∀x∈S there exist a,b∈S such that x+xax=xbx, then semiring (S,+,⋅) is also regular [2]. In structure theory of semirings, ideals play a vital role[3]. In [4], Xueling Ma and Jianming Zhan used the concept of h-ideals. They used the basic and main concept of h-ideals to prove many properties and results. Similarly, Jianming Zhan et al., in [5] also used h-ideals in their researches. This class of h-ideals has been used in many researches by different researchers. Ideals of semirings used in the structure theory play an important role in many aspects. Some properties of ideals are discussed in [6,7,8]. Gan and Jiang [9] studied the ordered semirings containing 0. Han and others in [10] discussed also the ordered semirings. Iizuka [11] introduced a new type of ideals namely h-ideals. In [12,13,14] they used h-ideals for many purposes related to their researches.
Main and basic concepts related to ordered semirings are given by Gan and Jiang [9]. The authors also derived some ideas related to minimal ideal, maximal ideal, ordered ideal of an ordered semiring and simple ordered semirings. Han, Kim and Neggers [10] also worked on semirings by partial ordered set. Munir and Shafiq [19] characterized the regular semirings through m-ideals. Satyt Patchakhieo and Bundit Pibalijommee [15] gave the basic definition of ordered semirings and left and right ordered ideal of the ordered semirings. They used two definitions in their properties and applications to prove their result.
Keeping in view the different characterizations of the regular semirings by the properties of the h-ideals, we were motivated to characterize the ordered h-regualr semirings by the properties of their ordered h-ideals. For this purpose, this paper represents ordered h-regular semirings along with their ordered h-ideals. In Section 2, we give some basic definitions which will be used in our further course of work. In Section 3, we characterize the ordered h-ideals semirings by their ordered h-ideals. In Section 4, we characterize the ordered h-regular semirings, and in Section 5, the characterization of the ordered h-weakly regular semirings is given. The conclusion of the paper is presented in the final Section 6.
2.
Preliminaries
Definition 1. A non-empty set S together with two binary operations + and ⋅ satisfying the following properties:
(C1) (S,+) is a semigroup,
(C2) (S,⋅) is a semigroup,
(C3) Distributive laws hold in S, that is
and
is called a semiring, which is denoted by (S,+,⋅).
Definition 2. (S,+,⋅) is additively commutative iff for all x1,y1∈S,x1+y1=y1+x1. S is multiplicatively commutative iff for all x1,y1∈S,x1⋅y1=y1⋅x1.(S,+,⋅) is called a commutative semiring iff it is both additively commutative and multiplicatively commutative. Suppose (S,+,⋅) is a semiring, if ∀a∈S;a+0=a=0+a and a⋅0=0=0⋅a, then 0∈S is called absorbing zero in S.
Definition 3. [15] Let E≠∅ and (S,+,⋅) is a semiring, E⊆S, is a left ideal or right ideal if these properties are satisfied:
(I1) t1+t2∈E for all t1,t2∈E.
(I2) SE⊆E or ES⊆E.
If E is left ideal and right ideal of S, then E is an ideal of S.
Definition 4. [15] Suppose (S,≤) is a partially ordered set satisfying the following properties:
(T1) (S,+,⋅) is semiring,
(T2) if x1≤x2, then x1+e≤x2+e,
(T3) if x1≤x2, then x1e≤x2e and ex1≤ex2,
for all x1,x2,e∈S, then, (S,+,⋅,≤) is an ordered semiring.
Definition 5. [15] Suppose (S,+,⋅,≤) is an ordered semiring. Let E≠∅, F≠∅ be subsets of S, then we denote (E]={g∈S|g≤r for some r∈E} and EF={gh|g∈E,h∈F}.
We can write (S,+,⋅,≤) as S.
Definition 6. [15] Suppose S is an ordered semiring, E≠∅ and E⊆S satisfies the following properties:
(T1) E is left ideal or right ideal of S;
(T2) if g≤w for some w∈E, then g∈E.
Then E is a left ordered ideal or right ordered ideal.
If E is both left ordered ideal and right ordered ideal of S, then E is ordered ideal of S.
Definition 7. Suppose S is an ordered semiring, if x1∈S, there exist t∈S such that x1≤x1tx1, then S is called a regular ordered semiring.
3.
Ordered h-ideals semirings
In this section, we characterize the ordered h-ideals semirings by their ordered h-ideals.
Definition 8. Suppose E is a nonempty subset of an ordered semiring S, then E is a left ordered h-ideal of S if the following properties are satisfied:
(1) E is a left ordered ideal of S,
(2) if e+x1+t=x2+t for some x1,x2∈E,t∈E, then e∈E.
Similarly, we define the right ordered h-ideal.
If E is both a left ordered h-ideal and a right ordered h-ideal of S, then E is said to be an ordered h-ideal of S.
Definition 9. Suppose E≠∅, E⊆S and S is an ordered semiring, then the h-closure of E, denoted by ¯E, is defined by
Definition 10. Suppose S is an ordered semiring. If for every x1∈S, there exist e,h,c∈S such that x1+x1ex1+c≤x1hx1+c,. Then S is called h-regular ordered semiring.
Definition 11. Suppose S is an ordered semiring then x1∈S is said to an ordered h
-regular if x1∈¯(x1Sx1]. If each element of S is ordered h-regular, then S is said to be an ordered h-regular semiring.
It is easy to see that each h-regular ordered semiring is an ordered h-regular semiring but converse does not hold. We see this by the following example.
Example 1. Suppose S={t1,t2,t3}. Define binary operations ⋅ and + on S as:
We define order relation ≤ on S as follows :
Then (S,+,⋅,≤) is an ordered semiring. Furthermore, forall a∈S (1) a+t1+c≤t2+c, c∈S (2) t1,t2∈(aSa] i.e. t1≤asa, t2≤asa, for some asa∈aSa. Hence S is an ordered h-regular semiring. On the other hand t3+t3at3+t2≤t3ct3+t2 has no solution, so S is not an h-regular ordered semiring.
Lemma 1. Suppose S is an ordered semiring and E⊆S and F⊆S, where E and F are nonempty, then
(1) (¯E]⊆¯(E].
(2) If E⊆F, then ¯E⊆¯F.
(3) ¯(E]F⊆¯(EF] and E¯(F]⊆¯(EF].
Proof. (1) Let g∈(¯E]. Then there exists h∈¯E such that g≤h. Since h∈¯E, then there exist r1,r2∈E such that h+r1+k≤r2+k, k∈E. It follows that g+r1+k≤h+r1+k≤r2+k. Since E⊆(E],r1,r2∈(E], k∈(E], g∈¯(E], i.e. (¯E]⊆¯(E].
(2) Consider E⊆F. Let g∈¯E. Then, there exist r1,r2∈E such that g+r1+k≤r2+k, k∈E. By the assumption, we get r1,r2,k∈F. This implies g∈¯F, so ¯E⊆¯F.
(3) Let g∈¯(E] and w∈F. So, there exist p,q∈(E] such that g+p+s≤q+s,s∈(E]. So, gw+pw+sw≤qw+sw. Since p,q,s∈(E], p≤r1 and q≤r/1 and s≤r//1,for some r1,r/1,r//1∈E, so pw≤r1w∈EF and qw≤r/1w∈EF and sw≤r//1w∈EF. This implies that gw∈¯(EF]. So ¯(E]F⊆¯(EF]. Similarly we get E¯(F]⊆¯(EF].
Lemma 2. [15] Suppose E⊆S, where E is nonempty and S is an ordered semiring. If E is closed under addition, then so are (E], ¯(E].
Now we will use further throughout the section N (set of all positive integers). Let S be ordered semiring, E≠∅ and E⊆S, suppose ∑finiteE be set of all finite sum of elements of E, and for x∈S, let Nx={nx|n∈N}.
Lemma 3. Suppose E and F are nonempty subsets of an ordered semiring S, with E+E⊆E and F+F⊆F. Then
(1) E⊆(E]⊆¯E⊆¯(E],
(2) ¯(E] = ¯¯(E], if E is left ordered h-ideal (or right ordered h-ideal) of S,
(3) E+F⊆¯E+¯F⊆¯E+F,
(4) ¯(E]+¯(F]⊆¯¯(E]+¯(F]⊆¯(E+F],
(5) ¯E¯F⊆¯(E]¯(F],
(6) If E and F are two left ordered h-ideal and right ordered h-ideal of S, respectively then ¯(E]¯(F]⊆¯(∑finiteEF].
Proof. (1) We see that E⊆(E].
Let g∈(E], so by definition of “(]
”, there exists r∈E such that
This implies that g∈¯E⟹(E]⊆¯E.
Since E⊆(E],
(2) Let E is left ordered h-ideal (or right ordered h-ideal) of S.
By(ⅰ), (E]⊆¯(E];⟹¯(E]⊆¯¯(E].
Let g∈¯¯(E], then by definition of h -closure, there exist h,k∈¯(E] such that
Since h,k,s∈¯(E], then by definition of h -closure, there exist r1,r2,r3,r4,r5,r6∈(E], such that
⟹
⟹
Since s1,s2,s3∈(E], then by definition of “(]”, there exist s/1,s/2,s/3∈E such that s1≤s/1 and s2≤s/2 and s3≤s/3.
As E is a left ordered h-ideal (or right ordered h-ideal) of S, so E is a left ordered ideal (or right ordered ideal) of S.
Then by definition of left ordered ideal or right ordered ideal, we get
Now, since r1,r4,r6∈(E], so by using definition of “(]”, there exist r/1,r/4,r/6∈E, such that r1≤r/1 and r4≤r/4 and r6≤r/6
Then by definition of left ordered ideal or right ordered ideal, we get
Then by definition of left ordered ideal or right ordered ideal, we get r1,r2,r5,r6,s1,s3∈E
where s1+s2+s3∈E, then by definition of h-closure, we get g∈¯E, then by (1), we get g∈¯E⊆¯(E]⟹g∈¯(E], ⟹¯¯(E]⊆¯(E]
(3) From (1), we have E⊆¯E and F⊆¯F
Now we show ¯E+¯F⊆¯E+F. Suppose g∈¯E+¯F, so there exists h∈¯E and k∈¯F such that g=h+k.
Since h∈¯E, k∈¯F, so by using definition of h-closure, there exist r,r/∈E and w,w/∈F such that
and
⟹
As (s1+s2)∈E+F, then by definition of h-closure, we get g∈¯E+F,
(4) Let g∈¯(E]+¯(F], then there exists p∈¯(E],q∈¯(F], such that g=p+q.
Now,
Since p+p∈¯(E] and q+q∈¯(F], then by definition of h-closure, we get g∈¯¯(E]+¯(F],
Suppose g∈¯(E]+¯(F], so there exists p∈¯(E],q∈¯(F], such that g=p+q.
Since p∈¯(E] and q∈¯(F], so by using definition of h-closure, there exist r,r/∈(E] and w,w/∈(F] such that
and
Since (r+w),(r/+w/)∈(E+F],
This implies g∈¯(E+F], ⟹
(5) By Lemma 1, we get
(6) Let E, F are two left ordered h-ideal or right ordered h
-ideal of S. We will prove that ¯(E]¯(F]⊆¯(∑fijEF].
For this, let g∈¯(E]¯(F] then g=hk, as h∈¯(E],k∈¯(F], then by definition of h-closure, there exist p,p/∈(E] and q,q/∈(F] such that
and
As
Also
As
Since E and F are left ordered ideal and right ordered ideal of S respectively, therefore,
and
This implies that
So
Example 2. (i) Every regular ordered semiring is an ordered h-regular semiring.
(ii) Consider the semiring (N,+,⋅,≤), where N is the set of natural numbers. We define the relation ⪯ on N by g⪯h⇔g≥h for all g,h∈N. Then, (N,⪯) is a partially ordered set, furthermore (N,+,⋅,⪯) is an ordered semiring. Since g+ghg+s⪯ghg+s for all g,h∈N,s∈N, (N,+,⋅,⪯) is an ordered h-regular semiring. Moreover, since 2∈N,2⋠2h2=4h for all h∈N, (N,+,⋅,⪯) is not a regular ordered semiring. In addition, we get (2N] is an ordered ideal of (N,+,⋅,⪯) which is not an h-ideal, for the reason that 2+4+1=3+4as1∉(2N].
Theorem 1. Suppose S is an ordered semiring and E be left ideal or right ideal or ideal, then conditions given below are equivalent:
(1) E is left ordered h-ideal or right ordered h-ideal or ordered h-ideal of S;
(2) Let g∈S,g+r1+h≤r2+h for some r1,r2∈E, h∈E then g∈E;
(3) ¯E=E.
Proof. (1) ⟹(2) Suppose E is a left ordered h
-ideal. Suppose g∈S such that g+r1+h≤r2+h for some r1,r2∈E, h∈E then by using definition of left ordered h
-ideal, we get g∈E.
(2) ⟹(3) Suppose (2) is true. Consider g∈¯E, then there exist r1,r2∈E such that g+r1+h≤r2+h, h∈E. By condition (2), we get g∈E. So, ¯E⊆E. Since E⊆¯E, therefore ¯E=E.
(3) ⟹(1) Assume that ¯E=E. Let g∈S be such that g+r1+h≤r2+h for some r1,r2∈E, h∈E. Then g∈¯E. Since ¯E=E, so g∈¯E=E. Thus g∈E. Since g+r1+h≤r2+h for some r1,r2∈E, h∈E, then g∈E, so by the definition of left ordered h-ideal or right ordered h-ideal or ordered h-ideal, we get E is left ordered h-ideal or right ordered h-ideal or ordered h-ideal of S.
Theorem 2. Suppose S is an ordered semiring, then:
(1) Intersection of any family of left ordered h-ideals of S is a left ordered h-ideal.
(2) Intersection of any family of right ordered h-ideals of S is a right ordered h-ideal.
(3) Intersection of any family of ordered h-ideals of S is an ordered h-ideal.
Proof. (1) Suppose En is a left ordered h-ideal of S for all n∈J, as ∩n∈JEn≠∅. Since En is a left ordered h-ideal, we get En is a left ordered ideal for all n∈J. Then ∩n∈JEn is left ordered ideal. Consider there exist g∈S and r1,r2∈∩n∈JEn,h∈∩n∈JEn is such that g+r1+h=r2+h. Since ∩n∈JEn⊆En for all n∈J, we get, r1,r2,h∈En. Since En is a left ordered h-ideal and r1,r2∈En,g+r1+h=r2+h,h∈En for all n∈J, so by using definition of left ordered h
-ideal, we get g∈En for all n∈J. So g∈∩n∈JEn. Therefore, r1,r2∈∩n∈JEn,g+r1+h=r2+h,h∈∩n∈JEn. Then g∈∩n∈JEn. By definition of left ordered h-ideal, we get ∩n∈JEn is a left ordered h-idealof S.
(2) Suppose that En is a right ordered h-ideal of S for all n∈J, as ∩n∈JEn≠∅. Since En is right ordered h-ideal, we get, En is right ordered ideal for all n∈J. Then ∩n∈JEn is right ordered ideal. Consider that there exist g∈S and r1,r2∈∩n∈JEn,h∈∩n∈JEn such that g+r1+h=r2+h. Since ∩n∈JEn⊆En for all n∈J, we have r1,r2,h∈En. Since En is a right ordered h-ideal and r1,r2∈En,g+r1+h=r2+h,h∈En for all n∈J. So by using the definition of right ordered h-ideal, we get g∈En for all n∈J. So g∈∩n∈JEn. Therefore, r1,r2∈∩n∈JEn,g+r1+h=r2+h,h∈∩n∈JEn. Then g∈∩n∈JEn. By definition of right ordered h-ideal, we have ∩n∈JEn is a right ordered h-idealof S.
(3) From (1) and (2), we get ∩n∈JEn is a left and right ordered h-ideal of S. Therefore, ∩n∈JEn is an ordered h-ideal of S. Hence proved.
Remark 1. (1) The sum of two left ordered h-ideals or right ordered h-ideals is a left ordered h-ideal or right ordered h-ideal.
(2) The sum of two left ordered ideals or right ordered ideals is a left ordered ideal or right ordered ideal.
(3) The sum of two left ideals or right ideals is a left ideal or right ideal.
Theorem 3. Suppose S is an ordered semiring and E≠∅,F≠∅,E⊆S,F⊆S.
(1) Consider E,F be two left ordered h-ideals, then ¯(E+F] is smallest left ordered h-ideal containing E∪F.
(2) Consider E,F be two right ordered h-ideals, then ¯(E+F] is smallest right ordered h-ideal containing E∪F.
(3) Consider E,F be two ordered h-ideals, then ¯(E+F] is smallest ordered h-ideal containing E∪F.
Proof. (1) Suppose E, F are two left ordered h-ideal of S. Suppose g,h∈¯(E+F], s∈S.
By the definition of h-closure, there exist r,r/,w,w/∈(E+F] such that
and
Hence
and
As (sf1)∈(E+F], so by using the definition of h-closure, we get (g+h)∈¯(E+F] and (sg)∈¯(E+F].
This implies
Let g∈¯¯(E+F], then by definition of h-closure, there exist i,v∈¯(E+F] such that
Since i,v,f∈¯(E+F], then by definition of h
-closure, there exist r,r/,w,w/,d,d/∈(E+F], such that
and
Now,
Since (r+w/+d/),(i+f+r+w+d)∈E+F and (f1+f2+f3)∈E+F, then by definition of h-closure, we get g∈¯E+F⊆¯(E+F]⟹¯¯(E+F]⊆¯(E+F].
So, we get ¯¯(E+F]=¯(E+F].
This shows that ¯(E+F] is a left ordered h-ideal.
Suppose g∈E∪F, then g∈E or g∈F
As g∈E, then g+(g+w)=(g+g)+w∈E+F, for all w∈F. Thus g∈¯(E+F]
As g∈F, then (r+g)+g=r+(g+g)∈E+F, for all r∈E. Thus g∈¯(E+F]
Hence,
Suppose L is a left ordered h-ideal containing E∪F.
Then E+F⊆L and hence (E+F]⊆(L]=L implies that ¯(E+F]⊆¯L=L
Therefore, ¯(E+F] is the smallest left ordered h
-ideal containing E∪F.
(2) This is similar to (1).
(3) From (1) and (2), we prove that ¯(E+F] is smallest left and right ordered h-ideal containing E∪F. Therefore, ¯(E+F] is smallest ordered h-ideal containing E∪F.
Theorem 4. Suppose S is an ordered semiring and E≠∅, E⊆S. Then these properties hold.
(1) Consider E a left ideal, then ¯(E] is the smallest left ordered h-ideal containing E.
(2) Consider E a right ideal, then ¯(E] is the smallest right ordered h-ideal containing E.
(3) Consdier E an ideal, then ¯(E] is the smallest ordered h-ideal containing E.
Proof. Suppose E is a left ideal. We know that ¯(E] is closed with respect to the operation of addition.
Suppose g∈¯(E], and k∈E, then by using definition of h -closure, there exist r,w∈(E] such that
Hence
So by using definition of “(]”, we have kh∈(E]. Since (kr),(kw)∈(E], kg+(kr)+(kh)≤(kw)+(kh),(kh)∈(E].
Then by definition of h-clousre, we get kg∈¯(E]. Therefore, ¯(E] is a left ordered h-ideal.
We know that ¯(E] is a left ordered h-ideal containing E.
Suppose Q is a left ordered h-ideal containing E. So (E]⊆(Q]=Q. Then, ¯(E]⊆¯Q=Q. Therefore, ¯(E] is the smallest left ordered h-ideal containing E.
(2) This is similar to (1).
(3) From (1) and (2), we prove that ¯(E] is the smallest left and right ordered h-ideal containing E. Therefore, ¯(E] is the smallest ordered h
-ideal containing E.
Corollary 1. Suppose S is an ordered semiring, let ∅≠E⊆S. We denote the smallest left ordered h-ideal containing E by Lh(E), the smallest right ordered h-ideal containing E by Rh(E), and the smallest ordered h-ideal of S containing E by Mh(E). Then, the following results follows:
(1) Lh(E)=¯(∑finiteE+∑finiteSE],
(2) Rh(E)=¯(∑finiteE+∑finiteES],
(3) Mh(E)=¯(∑finiteE+∑finiteSE+∑finiteES+∑finiteSES].
Proof. We want to prove ∑finiteE+∑finiteSE is a left ideal.
For this,
(I1) Let a,b∈∑finiteE+∑finiteSE. Then
(I2) Let a∈∑finiteE+∑finiteSE,r∈S
⟹
Therefore, ∑finiteE+∑finiteSE is a left ideal. By Theorem 4, we get
We see that the proofs of (2) and (3) are similar to that of (1).
Corollary 2. Suppose S is an ordered semiring, let r∈S. Then
(1) Lh(r)=¯(Nr+Sr];
(2) Rh(r)=¯(Nr+rS];
(3) Mh(r)=(Nr+Sr+rS+∑finiteSrS], where N = Set of natural numbers.
4.
Ordered h-regular semirings
We now give the characterization of ordered h-regular semirings by their ordered h-ideals.
Theorem 5. Consider S is an ordered semiring. Then S is an ordered h-regular iff E∩F=¯(EF], for all right ordered h-ideals E, left ordered h-ideals F of S.
Proof. Suppose S is an ordered h-regular semiring and E is right ordered h-ideal, F is left ordered h-ideal of S. Then, we have EF⊆E and EF⊆F. Thus, (EF]⊆(E]=E and (EF]⊆(F]=F.
This implies ¯(EF]⊆¯E=E and ¯(EF]⊆¯F=¯F. Thus ¯(EF]⊆E∩F
Let p∈E∩F. As S is an ordered h-regular, there exist h,k∈(pSp], such that
Since h,k,o∈(pSp], then by definition of “(]”, there exist s,j,j1∈S such that
Since E is a right ordered h-ideal, F is a left ordered h-ideal, we have psp,pjp,pj1p∈EF. Since h≤psp∈EF,k≤pjp∈EF,o≤pj1p∈EF, so by using definition of “(] ”, we have h,k,o∈(EF] so p∈¯(EF]⟹E∩F⊆¯(EF]
Conversely, Consider E∩F=¯(EF] for all right ordered h-ideals E of S, left ordered h-ideals F of S. Suppose d∈S, then by above Corollary 2 we get
By assumption, (Rh(d)∩Lh(d)=¯(Rh(d)Lh(d)]). Now we show that Rh(d)Lh(d)⊆¯(Sd]∩¯(dS]
Let p∈Rh(d) and h∈Lh(d).
Since p∈Rh(d), then by the definition of h-closure,
Since h∈Lh(d), then by the definition of h-closure,
Since h,k,o∈(pSp], then by definition of “(]”, there exist s,j,j1∈S such that
It follows that
Then by definition of “(]”, we get ih,i/h,o1h∈(dS]. Since ih,i/h∈(dS],
Then by definition of h-closure, we get ph∈¯(dS]. So,
Similarly, we can show that
Therefore,
Since ¯(dS] is a right ordered h-ideal, ¯(Sd] is a left ordered h-ideal and by assumption, we have,
Now we will show that ¯(dS]¯(Sd]⊆¯(dSd]. For this let m∈¯(dS] and k∈¯(Sd], then by definition of h-closure, there exist l,l1∈(dS] and q,q1∈(Sd], such that
and
From above equations we get,
Since S is a multiplicatively commutative ordered semiring,
Since l,l1,o3∈(dS],q,q1,o4∈(Sd], then by definition of “(]”, there exist s1,s2,s3,l/,l//,l///∈S, such that
Hence, we obtained,
⟹
and
Then by definition of “(]”,
⟹
So, mk∈¯(dSd]. Hence ¯(dS]¯(Sd]⊆¯(dSd].
Hence
Thus,
It turns out, d∈¯(dSd]. Hence, S is an ordered h
-regular.
Corollary 3. Suppose S is a commutative ordered semiring. Then S is an ordered h-regular iff for each ordered h-ideal E of S, E=¯(E2].
Proof. Suppose S is an ordered h-regular. Consider E is an ordered h-ideal of S. Obviously we have E=E∩E=¯(E2].
Conversely, Suppose that for each ordered h-ideal E of S, E=¯(E2]. Consider r∈S. As S is a commutatively multiplication ordered semiring, we get
So,
Since S is commutative i.e., ¯(rS]=¯(Sr], and ¯(rS] is an ordered h-ideal, therefore
Thus, S is an ordered h-regular.
Definition 12. Suppose S is an ordered semiring, let r∈S. Suppose r∈¯(Sr2], then r is said to be left ordered h-regular. Suppose r∈¯(r2S], then r is called right ordered h-regular. Suppose each element of S is left or right ordered h-regular. Then, ordered semiring S is said to be a left or right ordered h-regular.
Theorem 6. Suppose S is left ordered h-regular semiring. Then
(1) for each left ordered h-ideal E of S, ¯(E2]=E;
(2) Q∩E=¯(QE], for each left ordered h-ideal E and each ordered h-ideal Q of S.
Proof. (1) Suppose E is left ordered h-ideal of S. Then, we get ¯(E2]⊆¯(E]=E.
Suppose r∈E. As S is a left ordered h-regular, so r∈¯(Sr2].
Since ¯(Sr2]⊆¯(SE2]⊆¯(E2],⟹r∈¯(E2]. Hence, E⊆¯(E2]⟹¯(E2]=E.
(2) Let E is left ordered h-ideal and Q is ordered h-ideal of S. Then, we get, ¯(QE]⊆¯(Q]=Q and ¯(QE]⊆¯(E]=E. Hence, ¯(QE]⊆Q∩E. Let a∈Q∩E. As S is left ordered h-regular,
⟹a∈¯(QE]. Hence, Q∩E⊆¯(QE]. Thus,
Theorem 7. Suppose S is a right ordered h-regular semiring. Then
(1) for each right ordered h-ideal E of S, ¯(E2]=E;
(2) E∩Q=¯(EQ], for each right ordered h-ideal E and each ordered h-ideal Q of S.
Theorem 8. Suppose S is an ordered semiring, then the conditions given below are equivalent:
(1) for each left ordered h-ideal E, F of S, E∩F=¯(EF].
(2) for each left ordered h-ideal E and each ordered h-ideal Q of S, E∩Q=¯(EQ].
(3) S is left ordered h-regular and Rh(E)⊆Lh(E) for all ∅≠E⊆S
Proof. (1) ⇒(2) Let E is left ordered h-ideal of S and F is ordered h-ideal of S. Then E∩F=¯(EF],F being left ordered h-ideal of S, we get E∩F=¯(EF].
(2) ⇒(3) Let ∅≠E⊆S. By assumption, we get Lh(E)=Lh(E)∩S=¯(Lh(E)S]. We have
Moreover, we show that Lh(E)=Mh(Lh(E)). Since Rh(E)⊆Lh(E), we get, Lh(E)⊆Rh(Lh(E))⊆Lh(Lh(E))=Lh(E).
Hence, Lh(E)=Rh(Lh(E)). It follows that Lh(E)=Mh(Lh(E))
Let p∈S. From assumption, we get
⟹
Since p∈¯(Np2+Sp2], then by definition of h-closure, there exist v,v/∈(Np2+Sp2], such that
Since v,v/,t1∈(Np2+Sp2], then by definition of “(]”, there exist e,f,g∈N and s,r,r1∈S such that
In a similar way, we obtain
Then by definition of h-closure, there exist u,u/∈(Np4+Sp4], such that
Since u,u/,t2∈(Np4+Sp4], then by definition of “(]”, there exist e/,f/,g/∈N and s/,r/,r/1∈S such that
From p2+u+t2≤u/+t2 we get
Now we have
Then by definition of “(]”, v+eu+et2+fu+ft2∈(Sp2].
Now
Then by definition of “(]”,
Now,
Then by definition of “(]”,
Now
Hence, S is a left ordered h-regular.
(3) ⇒ (1)
Let E, F are left ordered h-ideals of S, then we get ¯(EF]⊆¯(F]=F We see that E⊆Rh(E)⊆Lh(E)=E. Hence, E is an ordered h-ideal. Thus ¯(EF]⊆¯(E]=E. So, ¯(EF]⊆E∩F
Suppose p∈E∩F. By assumption, we get p∈¯(Sp2]. Since ¯(Sp2]⊆¯(SEF]⊆¯(EF],p∈(EF]. It turns out that E∩F⊆¯(EF].
Therefore,
Theorem 9. Suppose S is an ordered semiring. Then the conditions given below are equivalent:
(1) for each right ordered h-ideal E, F of S, E∩F=¯(EF].
(2) for each right ordered h-ideal E of S, each ordered h
-ideal Q of S, Q∩E=¯(QE].
(3) S is right ordered h-regular, Lh(E)⊆Rh(E) for all ∅≠E⊆S.
5.
Ordered h-weakly regular semirings
Definition 13. Suppose S is an ordered semiring, let r∈S. Suppose r∈¯(∑finite(Sr)2], then r is said to be a left ordered h-weakly regular. Suppose r∈¯(∑finite(rS)2], then r is said to be a right ordered h-weakly regular. Suppose each element in S is left or right ordered h-weakly regular, then ordered semiring S is said to be left or right ordered h-weakly regular.
Theorem 10. Suppose S is an ordered semiring, then the conditions given below are equivalent:
(1) S is a left ordered h-weakly regular.
(2) for each left ordered h-ideal E of S, ¯(∑finiteE2]=E.
(3) for each left ordered h-ideal E of S and each ordered h
-ideal Q of S, Q∩E=¯(∑finiteQE].
Proof. (1) ⇒(2) Suppose E is a left ordered h-ideal of S. Then, we get, ¯(∑finiteE2]⊆¯(E]=E
Let a∈E. By assumption, we have
Hence,
Thus,
(2) ⇒(1) Let r∈S. From assumption, Lemma 3, and Corollary 2. We get,
Since ¯(Sr] is left ordered h-ideal, we get r∈¯(Sr]=¯(∑finite¯(Sr]2].
By Lemma 2 and Theorem 4, we have
Hence,
Therefore, S is a left ordered h-weakly regular.
(2) ⇒ (3) Suppose E is a left ordered h-ideal of S and Q is an ordered h-ideal of S. Then,
and
Hence, ¯(∑finiteQE]⊆Q∩E.
Let a∈Q∩E. By assumption, we get,
Hence,
Thus
(3) ⇒(2) Suppose E is a left ordered h-ideal of S, then, we get ¯(∑finiteE2]⊆¯(E]=E.
By Lemma 1, 2, Theorem 4 and Corollary 1, we get
Thus,
Theorem 11. Suppose S is an ordered semiring, then the conditions given below are equivalent:
(1) S is a right ordered h-weakly regular.
(2) for each right ordered h-ideal E of S, ¯(∑finiteE2]=E.
(3) for each right ordered h-ideal E of S and each ordered h
-ideal Q of S, E∩Q=¯(∑finiteEQ].
Proof. Straightforward.
6.
Conclusions
Concepts of the ordered h- ideals in semirings, alongside their essential properties, were presented. The classes of the semirings like ordered h-regular and ordered h-weakly regular semirings were characterized by the properties of the ordered h-ideals.
The ideas of the ordered h-ideals can be extended to the non associative structures like the ones in ([16,17,18,20,21,22]). Moreover, ordered h-ideals can be extended for fuzzification in semiring theory.
Acknowledgments
The research was supported by the National Natural Science Foundation of China (Grant Nos. 11971142, 11871202, 61673169, 11701176, 11626101, 11601485).
Conflict of interest
The authors declare no conflict of interest.









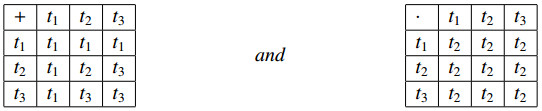




 DownLoad:
DownLoad: