Stochastic comparisons of extreme order statistic from dependent and heterogeneous lower-truncated Weibull variables under Archimedean copula

1.   Introduction

The dengue fever caused by mosquitoes is one of the most dangerous transmissible disease. More than 100 countries are effectively facing challenges from this disease. After malaria, dengue is scrutinized as the most life-threatening disease in recent times. It has been shown in WHO reports that every year 50 to 100 million cases of dengue are being observed. Earlier, dengue was considered a disease of hot regions, but now it has spread to the other regions of the world due to global warming. In the past 30 years, dengue infection has increased almost five fold. The symptoms of this disease are identified by high fever, frontal headache, pain behind the eyes, joint pain, nausea, vomiting and some other symptoms. The human population is mainly affected by the bites of the female mosquitoes carrying the dengue virus. The infection occurs when a mosquito sucks the blood from an infected person and transfers the virus to other healthy individuals by biting them. The symptoms do not appear in infected individuals for approximately 4 to 7 days (on average) before they begin to experience a sudden onset of fever.

There is no specific cure for dengue fever, but some precautions can be suggested to avoid or reduce the effect of disease. They include hospital treatments, with complete bed rest in support of medication to prevent fever and to give relief in pain. In addition, mosquito repellent must be used, wearing long-sleeved shirts and pants. Outdoors must be avoided without having proper preventive measures at dawn and dusk. It is highly recommended to clean uncovered stagnant water properly indoors and outdoors and to avoid camping near still water. According to conventional wisdom, the human body's natural immune system eliminates dengue virus within 7 days of infection ^[1].

A useful tool for forecasting the dynamics of communicable diseases with preventive measures is the mathematical modeling technique. Many epidemic models consisting of ordinary, stochastic or delay differential equations have been suggested and investigated to analyze the dynamics of a variety of vector-host infectious diseases. The transmission dynamics of dengue fever can be understood with the help of the variety of models given in ^{[2,3,4,5,6,7,8,9,10,11,12,13]}. Researchers have conducted several studies to investigate the transmission of dengue fever to control the disease and to compare various theories to eradicate it from the society. For example, in ^[6], a compartmental deterministic model including human prevention and vector control interventions for the dynamics of dengue fever spread is presented to analyze the impact of various control strategies on disease control. An optimal control model of dengue infection with partial immune and asymptomatic individuals is analyzed in ^[13], where the authors introduced four time-dependent control measures and performed a cost-effective analysis by suggesting five strategies for controlling dengue fever. The various modeling approaches used in formulating these models are limited because of the local nature of integer order derivatives. Recently, many researchers have started converting these mathematical models to fractional models in order to add memory effects for the best analysis of dengue fever disease. For example, the authors in ^[14,15] consider a compartmental model for the transmission dynamics of dengue fever with nonlinear forces of infection through the fractional derivative and show that the biting rate, recruitment rate of mosquitoes and index of memory are the most sensitive factors to lower the level of dengue fever. Vaccination effect on the proposed system's threshold is also explored here.

Fractional modeling for epidemiology is more productive than integer order with reference to the memory as the past is required to explain the present. Classical integer order models consisting of autonomous differential equations have no memory, as their solution does not depend on previous instant. This means, given an initial value, the solution is determined uniquely for any point of the domain. However, this claim is not true for fractional-order differential equations. Thus, to introduce the memory effect into a mathematical model, the order of the derivative of the classical model is changed to the noninteger order ^[16,17]. In the recent past, fractional calculus has been considered a key tool to design epidemic models to obtain better results to eradicate diseases from society. Recent literature on fractional modeling ^{[18,19,20,21,22,23,24,25,26]} shows that the mathematical models constructed by using fractional operators behave more accurately and provide a better fit to the real data.

A variety of fractional derivative operators have been suggested in the last few decades, but recently the fractional operators, namely, the Caputo ^[27,28], Caputo-Fabrizio (CF) ^[29,30,31] and Atangana-Baleanu-Caputo (ABC) ^[32,33,34] have obtained more attraction of the researchers. The main disadvantage of the Caputo operator is the singularity property of its kernel. Although the CF derivative has a nonsingular kernel, the function space of CF derivative is not clear and has no memory effects ^[35]. The ABC fractional derivative operator, proposed by Atangana and Baleanu, uses a Mittag-Leffler (ML) kernel with one parameter. The ML function is a generalization of the exponential function in the context of fractional calculus, and the main advantage of this kernel is its nonlocal and nonsingular behavior. The ABC fractional operator is thus considered to be superior and is chosen as the best option for modeling real world phenomena, including epidemic diseases. The applicability of this operator to models can be found in ^[36,37,38]. Some more attributes of this operator were later reported by Losada and Nieto in ^[39]. Since then, many mathematical models have been formulated by researchers by using this operator. The results associated with these models have shown both the efficiency and suitability of the ABC operator.

Optimal control analysis is considered to be a very effective tool to provide reasonable control strategies to eradicate or to minimize an infection in the human population. Moreover, such an analysis gives better understanding of the disease flow pattern. Therefore, conveniently, the optimal control problems involving fractional calculus are called fractional optimal control problems (FOCPs) and are considered to be the general form of classical optimal control problems (OCPs). Many researchers have applied FOCPs for better understanding and for speedy results about the behavior of eradicating diseases ^[41,42,43]. We can say that by using FOCPs, we are able to do some new analysis to remove the dengue disease from the face of earth. Hence, FOCPs have become potentially the most flexible tool in modeling and analyzing biological systems related to time memory. The main objective of this study is also to design a fractional optimal control problem of eradicating dengue disease from society.

To demonstrate the usefulness of the ABC fractional operator, we have developed a new ABC fractional-order system of ordinary differential equations to explore the dynamics of dengue fever for optimal control in the context of treated travelers. The choice of ABC operator is due to its nonlocal and nonsingular kernel; moreover, the crossover attribute of epidemic models can be described in a better way via this operator. Another advantage of this operator is its capability to capture more susceptibilities and fewer infections than that of the other fractional operators such as Caputo and Caputo-Fabrizio ^[34]. The purpose of developing this fractional model is to examine the impact of fractional order on disease dynamics and to determine the possible control strategy. For this, we first present some important features of the suggested model, such as the existence and uniqueness of the solution, positivity, invariant regions, reproduction number and stability analysis. An important feature of this study is to use Toufik-Atangana numerical scheme for the first time to optimally analyze the proposed ABC fractional dengue fever model.

The remaining sections of this paper are structured as follows: In Section $2$, we formulate a $S_hE_hI_hT_hR_hP_h$ host population and $S_vI_v$ vector population integer order model by introducing two compartments in the host population, i.e., treatment and protected travelers. Corresponding to this integer-order model, a nonlinear fractional model is formulated with the help of the Atangana-Baleanu fractional derivative in Section 3 for better analysis of the memory effects. Sections $4$ and $5$ address the theoretical view of the proposed fractional model where the existence of the unique solution, the positivity and boundedness of solutions, the calculations of the equilibrium points and the basic reproduction number are presented. Section $6$ presents the stability analysis of the model, where we analyze the behavior of the model locally as well as globally. In Section $7$, a numerical scheme is presented to simulate the effect of order as well as the effect of various treatments levels on the suggested model. In this section, we present sensitivity analysis to determine highly sensitive parameters to reproduction number $\mathcal{R}_0$. The model is then adjusted with time-dependent control to formulate an optimal control problem in Section 8. Associated optimality conditions resulting from the Pontryagin principle are numerically solved by using the Toufik-Atangana scheme to determine the best treatment strategy for dengue fever control. Conclusions drawn from numerical simulations are presented in Section 9.

2.   Description of dengue fever model

The central idea about transmission models is to describe the transmission of infected individuals in a mechanical way. This approach makes it easy to transform the evolution of an epidemic in mathematical form. Therefore, designing a mathematical model requires focusing on necessary processes needed in formulating the epidemiology of an infectious disease and discerning the most significant and tractable parameters for control. Consequently, in this section, we formulate a basic $S_hE_hI_hR_h$ host and $S_vI_v$ vector population model with the addition of two new classes, treatment class $T_h$ and protected travelers class $P_h$ to make it more realistic. In the treatment class, the infectious subjects receives proper treatment along with some preventive measures, and after treatment, they move to the recovered class and finally become protected travelers. Protected travelers are free to move anywhere in the society without being afraid of becoming infected again^[44].

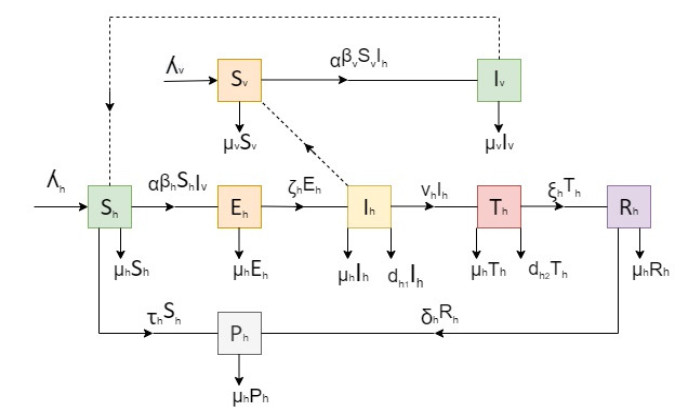
This model is represented by two populations, i.e., the human population and the vector (mosquitoes) population. The total population is denoted by $\mathcal{P}(t)$, which is further partitioned into various compartments, i.e., susceptible human population denoted by $S_h(t)$, the exposed individuals $E_h(t)$ after being bitten by mosquitoes, infected humans denoted with $I_h(t)$, humans under treatment represented by $T_h(t)$, $R_h(t)$ are the recovered or removed individuals and the protected travelers represented by $P_h(t)$. The vector (mosquito) population is subdivided into two classes, i.e., susceptible mosquitoes denoted by $S_v(t)$ and the infected mosquitoes represented by $I_v(t)$. The human population recruitment rate is denoted by $\lambda_{h}$. Susceptible humans are bitten by the mosquitoes at the rate of $\alpha$. The probabilities of contact between an infectious mosquito and a susceptible person and between an infectious person and a susceptible mosquito are given by $\beta_{h}$ and $\beta_{v}$, respectively. Humans in the exposed class become infectious at a rate $\zeta_{h}$. Infected people receiving treatment from the hospital are recruited to the treatment class at the rate $v_h$, and they recover from dengue fever at a rate $\xi_h$ to move into the class of protected travelers at the rate of $\delta_h$. Humans die naturally at a rate $\mu_h$ in all compartments and die due to disease at the rates $d_{h_{1}}, \ d_{h_{2}}$ in the compartments $I_h$ and $T_h$, respectively. The mosquitoes are recruited at rate $\lambda_{v}$ to the susceptible class $S_v$ and become infected when they have interaction with the infected humans. The mosquitoes die naturally at a rate $\mu_v$. The real-valued state variables $S_h, \ E_h, \ I_h, \ T_h, \ R_h, \ P_h, \ S_v, \ I_v$ are considered as time dependent functions that belong to class $C^1[0, \infty)$. Figure 1 describes the disease flow pattern through the population compartments together with the model assumptions and the parameters for the considered compartments.

The disease flow pattern given in Figure 1 is described in the form of the following nonlinear coupled ordinary differential equations, called the $S_hE_hI_hT_hR_hP_hS_vI_v$ model.

with the initial conditions

where $S_h(0), \ E_h(0), \ I_h(0), \ T_h(0), \ R_h(0), \ P_h(0), \ S_v(0), \ I_v(0)$ represent the initial population sizes. The parameters of this dynamical system for the human population and the vector population are given in Table 1.

3.   Atangana-Baleanu fractional order model

Fractional-order derivatives are very useful in the field of mathematical epidemiology, as they give very versatile results as compared to those of classical derivatives. Before applying the Atangana-Baleanu fractional derivative to our proposed dengue model, we first describe some basic concepts regarding the Atangana-Baleanu fractional derivative and other associated results.

Definition 3.1. Let $\Omega\subseteq\mathbb{R}$ be open and $p$ $\epsilon$ $[1, \infty)$, so $\mathbb{H}^{p}(\Omega)$ can be defined as

Definition 3.2. ^[45,46] The Caputo derivative of fractional order $\rho$ with $n - 1 < \rho < n, \ n\in \mathbb{N}$, for an integrable function $g\in C^n$, can be presented as

For either of the cases $n = 1$ or $n = 2$, the Caputo fractional derivative $^{C}_aD^{\rho}_t g(t)$ tends to $g'(t)$ as its order $\rho$ tends to $1$.

Definition 3.3. ^[32] The Atangana-Baleanu fractional derivative of a differentiable function $g(t)$, i.e., $g:[a, b]\rightarrow \mathbb{R}$ of order $\rho$ where $\rho$ $\in(0, 1)$, $b > a$, is denoted by $^{ABC}_{a}{D}^{\rho}g(t)$, where $g$ $\in$ $\mathbb{H}^{1}(a, b)$ is defined as:

where $M(\rho)$ represents the normalization function satisfying $M(0)$ = $M(1)$ = 1 and $E_{\rho}$ is known to be the Mittag-Leffler (ML) function defined as

Definition 3.4. ^[32] The Laplace transform of the Atangana-Baleanu fractional derivative is defined as:

Definition 3.5. ^[32,46] The fractional integral with a nonlocal kernel can be defined as:

Definition 3.6. The fractional derivatives and integrals satisfy the following useful relation:

Fractional order models are very widely used compared to the integer order models due to hereditary and the description of memory. Therefore, to observe the internal memory effects of the dengue fever biological model, we replace the first-order ordinary derivatives in (2.1) by the Atangana-Baleanu fractional derivative of order $\rho$ where $0 < \rho < 1$ to obtain:

with the initial conditions:

where $0\leq t \leq t_f < \infty$. We suppose that

The compact form of the above model is

Since the given system of differential equations is an autonomous system, it can be written as:

where $\eta(t) = \big(S_h(t), E_h(t), I_h(t), T_h(t), R_h(t), P_h(t), S_v(t), I_v(t)\big)^{T}\in \mathbb{R}^{8}$ and $\eta_{0}(t) = \big(S_h(0), \ E_h(0), \ I_h(0), \ T_h(0), \ R_h(0), P_h(0), \ S_v(0), \ I_v(0)\big)^{T}$ is the initial vector.

4.   Existence and uniqueness of solutions

In this section, we prove the existence and uniqueness of solutions with the help of theorems from functional analysis and fractional calculus. Some relevant material in the form of definitions and theorems from fractional calculus and functional analysis is also given in this section to assist in proving the stated theorems.

Definition 4.1. ^[48] A sequence $(x_n)$ in a metric space $X = (X, d)$ is said to be convergent to $x$ if for every $\epsilon > 0$, there is an $N = N(\epsilon)$ such that

Definition 4.2. ^[48] A sequence $(x_n)$ in a metric space $X = (X, d)$ is said to be a Cauchy sequence if for every $\epsilon > 0$, there is an $N = N(\epsilon)$ such that

Definition 4.3. ^[48] A metric space $X$ is known as a complete metric space if every Cauchy sequence is convergent in $X$.

Definition 4.4. ^[48] The space of bounded and continuous functions C[a, b] is a complete metric space with the metric defined as:

Definition 4.5. ^[48] A sequence $(x_n)$ is contractive in a metric space X if a constant $C\in(0, 1)$ such that

for all $n\in N$. C is called the contractive constant of the sequence.

Theorem 4.1. ^[48] A sequence is convergent in a complete metric space X if and only if it is Cauchy sequence.

Theorem 4.2. ^[51] Every contractive sequence is a Cauchy sequence, and therefore, convergent in complete metric space.

Theorem 4.3. ^[49] Let $\phi:{D}\rightarrow R^n$ with $\phi\in C^1(D)$ and $x\in {D}\subseteq R$. Then $\phi$ fulfills a Lipschitz condition on each convex compact set $\mathcal{D}\subseteq{D}$ with Lipchitz constant $K > 0$ such that

Theorem 4.4. The function $\chi(\eta)$ in Eq (3.3) is Lipschitz continuous.

Proof. Let ${S} = \{(t, \eta)|\ 0\leq t\leq t_f, \ \eta\in R_+^8\}$ and $U\subseteq S$ be convex compact.

Let $\eta_1, \eta_2\in S$, then by $Mean \ Value \ Theorem$ $\exists$ $\gamma\in(\eta_1, \eta_2)$ such that

or

Since $\chi\in C^1[0, t_f]$, over convex compact set $U$, $\exists$ a constant $\theta > 0$ such that

hence,

Hence, $\chi(\eta)$ is Lipschitz. □

Theorem 4.5. We suppose that the function $\chi(\eta)$ satisfies the Lipschitz condition

then the problem (3.3) has a unique solution for

Proof. We prove that the function $\eta(t)$ satisfies Eq (3.3) if and only if the equation

is satisfied by it.

Let $\eta(t)$ satisfy Eq (3.3). Applying the Atangana-Baleanu fractional integral to Eq (3.3), that is,

After simplification, we obtain the following integral equation:

For the converse implication, we let $\eta_n$ be a sequence of solutions which converges to the solution (4.1) with Picard successive iteration, defined as follows:

First, we show that the sequence (4.2) is contractive if:

where $T^* = t_f\Upsilon$ and $\Upsilon = \sup_{t\in[0, t_f]}(t-\gamma)^{\rho-1}$.

Using the Lipchitz property of function $\chi(\eta)$, we obtain the following expression:

which implies

Thus, from Eq (4.3), the sequence (4.2) is contractive; hence, Theorem 4.2 implies that the sequence is Cauchy sequence. Now for $m, n\in N$ and $m > n$,

where

Hence, the right-hand side is a geometric series that is always convergent for $0 < k < 1$.

Since $0 < k < 1$, $lim(k^n) = 0$. Therefore, we infer that the sequence $(\eta_n)$ is Cauchy, and hence, from Theorem 4.1, it is convergent. Let $lim(\eta_n) = y$; then, Eq (4.2) gives

Equation (4.4) is the required solution.

Uniqueness: To prove the uniqueness of the solution, we suppose on contrary that the sequence $(\eta_n)$ converges to two different limits $\eta_1$ and $\eta_2$. Then, there exist $n_1 \ and \ n_2\in N$ such that

Let $n = max\{n_1, n_2\}$

which implies,

Hence, we have proved that solution (4.4) is a unique solution of (3.3). □

4.1.   Invariant region

In this subsection, we determine the feasible region of solutions $(S_h, E_h, I_h, T_h, R_h, P_h, S_v, I_v)$ of the system of Eq (3.1) with initial data having nonnegative values. Here, our focus is to prove that the feasible region lies in $\mathbb{R}_{+}^{8}$, which is a positive invariant region with respect to the model (3.1).

Theorem 4.6. For the Atangana-Baleanu fractional model (3.1), the epidemiological feasible region is given by

where $\lambda = \lambda_h+\lambda_v$ and $\mu = \min\left(\mu_h, \mu_v\right).$

We have already proven the existence and uniqueness of solutions of model (3.1) in the last section; it remains to be proven that the set $\Pi$ is positively invariant with respect to initial data $S_h(0) > 0$, $E_h(0)\geq0$, $I_h(0)\geq0$, $T_h(0)\geq0$, $R_h(0)\geq0$, $P_h(0)\geq0$, $S_v(0) > 0$, $I_v(0)\geq0$. The following Lemma proves Theorem 4.6.

Lemma 4.1. System (3.1) has bounded solutions.

Proof. Adding equations of the fractional model (3.1), we have

where $\mathcal{P}(t)$ is the total of the host and vector populations. Clearly,

where $\lambda = \lambda_h+\lambda_v$ and $\mu = min(\mu_h, \mu_v)$. Therefore, it follows that

By applying the Laplace transform on both sides:

or

where $\mathcal{P}(s) = \mathscr[\mathcal{P}(t)](s)$ and $\mathcal{P}(0)$ is the total initial population. Solving inequality (4.6) for $\mathcal{P}(s)$, we obtain the following expanded expression:

Applying the inverse Laplace, we obtain

where $\Omega = \dfrac{\rho\mu}{M(\rho)+(1-\rho)\mu}$, and $E_{\alpha, \beta}$ is the ML function with two nonnegative parameters $\alpha$ and $\beta$, which are defined by

The following Laplace transform exists:

provided that $s > |\Lambda|^{1/\alpha}$. For nonnegative $\alpha, \ \beta$, the ML function satisfies

and in the case $\alpha = \rho$, $\beta = \rho+1$ and $z = -\Omega t^{\rho}$, we obtain

The ML function is bounded for all $t > 0$ and behaves asymptotically ^[32]. By using the expression (4.8) in inequality (4.7), so we obtain $\mathcal{P}(t)\leq\dfrac{\lambda}{\mu}$ as $t\rightarrow \infty$. Thus, $\mathcal{P}(t)$ is bounded in a region $\Pi$, and hence, all the state variables of model (3.1) are bounded. □

Thus, for any set of nonnegative initial data in $\Pi$, the corresponding solution $y(t)$ of model (3.1) in $\mathbb{R}_{+}^{8}$

approach asymptotically in finite time $t$ to enter and remain in $\Pi$. This means that the region $\Pi$ attracts all solutions in $\mathbb{R}^{8}_{+}$. Therefore, the region $\Pi$ is a positively invariant ^[34,50] for the model (3.1) and hence, the proposed model (3.1) is epidemiologically correct.

4.2.   Positivity of solutions

In this subsection, we prove that the state variables $S_h$, $E_h$, $I_h$, $T_h$, $R_h$, $P_h$, $S_v$, and $I_v$ are greater than or equal to zero for any $t\in R_{+}$. This implies that solution $y(t)$ of model (3.1) remains positive corresponding to any initial data in $\mathbb{R}^{8}_{+}$. The proof of this property shows that model (3.1) is physically realizable.

Theorem 4.7. The solution $y(t) = (S_h, E_h, I_h, T_h, R_h, P_h, S_v, I_v)$ of the model (3.1) always remains positive against any positive initial data.

Proof. Let Eq (3.1a) be rearranged to write

Since all the solutions are bounded, Eq (4.9) can be rewritten as

where we take $c = \alpha\beta_hI_v+(\tau_h+\mu_h)$ as a constant. With the Laplace transform, inequality (4.10) reduces to

Applying the inverse Laplace transform to the above inequality, we obtain

Since both terms on the right-hand side of (4.11) are positive, the solution $S_h(t)$ remains positive for all $t\geq0$. Following a similar technique, it can be proven that other states are positive for all $t\geq0$ against any initial data in $\Pi$. Thus, the solutions in $\mathbb{R}^{8}_{+}$ always remain positive. □

5.   Existence of equilibrium points

In this section, we describe the existence of disease-free and endemic points for our Atangana-Baleanu fractional order dengue fever model (3.1) to discuss the stability and dynamical behavior of the epidemic.

5.1.   Dengue fever free equilibrium point

The human population and the vector population free of dengue fever virus can be represented by the disease-free point, which is obtained by considering $^{ABC}_0 \mathcal{D}_{t}^{\rho}\eta_i(t) = 0$ for each state variable $\eta_i, \ i = 1, 2, \ldots, 8$ and substituting $E_h^{0} = I_{h}^{0} = R_h^{0} = P_{h}^{0} = I_{v}^{0} = 0$. Therefore, with these substitutions, model (3.1) gives:

Thus, the disease-free point, denoted by $Q_h^{0}$, can be written as:

Before describing the dynamics of model (3.1), we first determine the reproduction number in the next subsection.

5.2.   Computation of threshold parameter $\mathcal{R}_0$

The reproduction number, denoted by $\mathcal{R}_{0}$, is a basic measure in epidemiology that shows the total number of secondary cases produced by a single infected person in a fully susceptible population during an infectious period. We focus on fractional differential equations associated with the compartments of exposed $E_h$, infected $I_h$ and receiving treatment $T_h$ human population and the infected vector (mosquitoes) population $I_v$. Here, we used the next generation method strategy to compute the value of $\mathcal{R}_{0}$. The column matrix of the rate of arrival of new infections denoted by $F$ is written as

and the column matrix of transitional terms in $E_h$, $I_h$, $T_h$ and $I_v$ compartments is given by

Jacobian of the matrices $F$ and $V$ at point $Q_h^{0}$ are calculated to give

Then,

where $L_1 = \frac{(\alpha\beta_h)\lambda_h}{\tau_h+\mu_h}$ and $L_2 = \frac{(\alpha\beta_v)\lambda_v}{\mu_v}$ and $C_2 = \zeta_h+\mu_h$ and $C_3 = v_h+\mu_h+d_{h_{1}}$ and $C_4 = \xi_h +\mu_h+d_{h_{2}}$.

After multiplication, we compute the reproduction number $\mathcal{R}_{0}$ as the spectral radius of the matrix $\mathcal{F}\mathcal{V}^{-1}$, which is given as:

5.3.   Dengue fever endemic equilibrium point

Endemic equilibrium point of the fractional order model (3.1), denoted by $Q_h^{1}$, is obtained by considering $^{ABC}_0 \mathcal{D}_{t}^{\rho}\eta_i(t) = 0$ for each state variable $\eta_i, \ i = 1, 2, \ldots, 8$ and by solving the resultant equations to produce:

where

where $N_{1} = \frac{C_3}{\zeta_h}$, $N_{2} = \frac{v_h}{C_4}$, $N_{3} = \frac{\xi_h}{C_5}$.

6.   Stability investigation

In this section, we describe the dynamics of the model (3.1) at disease-free equilibrium point and the endemic equilibrium point with the help of the following analysis. In that analysis, we present the local and global stabilities of model (3.1) at both equilibrium points with the help of reproduction number $\mathcal{R}_{0}$.

6.1.   Local behavior

Theorem 6.1. The equilibrium point $Q_h^{0}$ is locally asymptotically stable (LAS) when $\mathcal{R}_{0} < 1$ and unstable otherwise provided $\mathcal{R}_{0}\neq 1$.

Proof. We compute the Jacobian of system (3.1) at $Q_h^{0}$ to obtain

The disease-free Jacobian matrix (6.1) has the following eigenvalues:

$\bar{\lambda}_{1} = -\mu_v$, $\bar{\lambda}_{2} = -\mu_h$, $\bar{\lambda}_{3} = -C_3$, $\bar{\lambda}_{4} = -C_2$, $\bar{\lambda}_{5} = -\frac{C_2C_3\mu_v-L_1L_2\zeta_h}{C_2C_3}$, $\bar{\lambda}_{6} = -C_5$, $\bar{\lambda}_{7} = -C_4$, $\bar{\lambda}_{8} = -C_1$. As we can see that $C_1, C_2, C_3, C_4, C_5$ are positive so $\bar{\lambda}_{1}, \bar{\lambda}_{2}, \bar{\lambda}_{3}, \bar{\lambda}_{4}, \bar{\lambda}_{6}, \bar{\lambda}_{7}, \bar{\lambda}_{8}$ are negative. $\bar{\lambda}_{5}$ can be written as $\bar{\lambda}_{5} = \mu_v(\mathcal{R}_0 -1) < 0$. Therefore, $\bar{\lambda}_{5} < 0$ as $\mathcal{R}_0 < 1$. Therefore, the proposed model is locally asymptotically stable where all the eigenvalues are negative when $\mathcal{R}_0 < 1$. □

Theorem 6.2. A dengue fever present equilibrium $Q_h^{1}$ is LAS whenever $\mathcal{R}_{0} > 1$ and unstable whenever $\mathcal{R}_{0} < 1$.

Proof. Jacobian for the system (3.1) at $Q_h^{1}$ is computed to obtain

The following eigenvalues have been computed for matrix $J(Q_h^{1})$.

where $M_1 = \alpha\beta_hI^{1}_v$, $M_2 = \alpha\beta_vI^{1}_h$, $L_1 = \alpha\beta_hS^{1}_h$ and $L_2 = \alpha\beta_vS^{1}_v$. Therefore, $\bar{\lambda}_{1}$ is negative and $\bar{\lambda}_{2} = -\alpha\beta_vI_h-\mu_v$ which is negative. We observe that $\bar{\lambda}_{3}, \bar{\lambda}_{4}, \bar{\lambda}_{7}, \bar{\lambda}_{8}$ are all negative as $C_2, C_3, C_4, C_5$ are positive. Therefore, $\bar{\lambda}_{6} = -\mu_v+\frac{\mu_vC_1C_2L_2\zeta_h}{C_1M_2+C_1\mu_v+M_1M_2+M_1\mu_v}$ which is negative if and only if $\frac{\mu_vC_1C_2L_2\zeta_h}{C_1M_2+C_1\mu_v+M_1M_2+M_1\mu_v}$ is Positive that is true. Thus, all the eigenvalues of the Jacobian matrix $J(Q_h^{1})$ are less than zero, so the system is LAS at $Q_h^{1} = (S^{1}_{h}, E^{1}_{h}, I^{1}_{h}, T^{1}_{h}, R^{1}_{h}, P^{1}_{h}, S^{1}_{v}, I^{1}_{v}$).□

6.2.   Global behavior

Theorem 6.3. A dengue fever free equilibrium $Q_h^{0}$ is globally asymptotically stable (GAS) in the region $\Pi$ when $\mathcal{R}_{0} < 1$.

Proof. Here, we use the disease-free value $S_h^{0} = \dfrac{\lambda_h}{\tau_h+\mu_h}$ and construct a candidate Lyapunov function $Y_{0}:\Pi\rightarrow \mathbb{R}$ ^[50,51,52] such that

By applying the Atangana-Baleanu fractional derivative, i.e., $^{ABC}_{0}D^{\rho}_{t}$, we have

Now, from system (3.1), we substitute the values of all fractional derivatives to have

This implies that

Clearly, $S^{0}_{h}(\alpha\beta_vI_v+\tau_h)\geq 0$; therefore,

Then, $^{ABC}_{0}\mathcal{D}_{t}^{\rho}Y_{0}\leq 0$. We see that $^{ABC}_{0}\mathcal{D}_{t}^{\rho}Y_{0} = 0$ if and only if $S_h = S^{0}_{h}$, $E_h = E^{0}_{h} = 0$, $I_h = I^{0}_{h} = 0$, $T_h = T^{0}_{h}$, $R_h = R^{0}_{h}$, $P_h = P^{0}_{h}$, $S_v = S^{0}_{v}$, $I_v = I^{0}_{v}$. Hence, by LaSalle's invariance principle ^[58,59], $Q^{0}_{h}$ is globally asymptotically stable in $\Pi$. Therefore, we have the result that the very dangerous virus disappears from the human population. □

Theorem 6.4. Dengue fever present steady state $Q^{1}_{h}$ is GAS in the positively invariant region $\Pi$ if $\mathcal{R}_{0} > 1$.

Proof. To show the global stability at $Q^{1}_{h}$, we consider a Lyapunov function $Y_{1}: \Pi \rightarrow \mathbb{R}$ ^[50,51,52] such that

The Atangana-Baleanu fractional derivative of $Y_{1}$ can be written as

Utilizing the equations of model (3.1), we obtain

Rearrangement of the terms yields us

where

and

As each parameter of the model (3.1) is positive, $^{ABC}_0D_{t}^{\rho}Y_{1}\leq0$ for $\sigma_{1}\leq \sigma_{2}$. The equality $^{ABC}_0D_{t}^{\rho}Y_{1} = 0$ holds if and only if $S_h = S^{1}_{h}$, $E_h = E^{1}_{h}$, $I_h = I^{1}_{h}$, $T_h = T^{1}_{h}$, $R_h = R^{1}_{h}$, $P_h = P^{1}_{h}$, $S_v = S^{1}_{v}$, $I_v = I^{1}_{v}$. Implies $\{Q^{1}_{h}\}$ is the maximum invariant set contained in

Hence, by LaSalle's invariance principle ^[50], the disease present point $Q^{1}_{h}$ is GAS in $\Pi$. □

7.   Numerical study

To obtain a numerical solution for the Atangana-Baleanu fractional order model of dengue fever for the various values of $\rho$, we implement the Toufik-Atangana scheme ^[53,54] with the help of MATLAB code. We use the scheme to study the dynamical behavior of The dengue fever epidemic over time $t$ for various values of fractional order $\rho$. Furthermore, the validity of treatment program given to infected people is analyzed numerically for various treatment levels.

7.1.   Toufik-Atangana method for the fractional-order model

To discuss the numerical stability of the dengue fractional model (3.1), we present here a finite difference scheme that is based on the Toufik-Atangana scheme ^[53] for fractional models. First, we present the development of the iterative method for fractional differential equations in brief and then write each fractional equation of the model (3.1) in discrete form. We apply the fundamental theorem of fractional calculus to system (3.2) to obtain:

In discrete form, we have

where $t = t_{q+1}, \ q = 0, 1, \ldots, N\ \text{with}\ h = \frac{T_f}{N}$. Equivalently,

The function $\chi(\gamma, \eta(\gamma))$ can be approximated over $[t_{p}, t_{p+1}]$, by using the interpolation polynomial

Putting in (7.1), we obtain

Evaluation of the integrals results in the following numerical scheme for solving equations of type (3.2).

Hence, the discrete form of the equations of the model (3.1) are given as:

7.2.   Effect of fractional order on disease dynamics

We use the above approximations to present the graphical picture of the proposed fractional model (3.1) and to observe the impact of memory on the dynamics of the disease, particularly on affected individuals.

Figure 2 shows the graphical behavior of the state variables under the influence of arbitrary fractional order $\rho$. We observe that all of the state variables of the host and the vector populations except the susceptibles decrease when the fractional order $\rho$ increases. Initially, the exposed humans increase with order but later on start decreasing. Therefore, we conclude that the number of affected individuals reduce with an increase in the fractional order from $0.6$ to 1. However, we notice a significant increase in the vector susceptible population with an increase in fractional order $\rho$.

7.3.   Disease control with different treatment rates

In this section, we quantitatively investigate the influence of different treatment rates on the dynamics of the dengue fever model (3.1). Figures 3–6 show the impact of different treatment rates to control the disease for fractional order $\rho$ taken as $0.4, \ 0.6, \ 0.8,$ and $1.0$.

It is obvious from Figures 3–6 that the exposed humans $E_h$ and the infected humans $I_h$ decrease with the rise in the treatment rate $v_h$ from 0.1 to 0.9. However, the reduction in infected humans is comparatively higher than that in the exposed individuals. We also observe that the curve for infected humans approaches its disease-free state when the fractional order $\rho$ is increased along with the treatment rate. A decrease in the infected vector population is also noticed when the treatment rate is increased. For $\rho = 0.4$, the susceptible humans decrease by increasing the treatment rate, but this behavior shifts to a rise in susceptibles when the fractional order moves to the higher value i. e., $\rho = 1$. This analysis reveals that the infected host population decrease significantly to approach disease free with a high treatment rate. However, the disease does not die out completely under the considered treatment rates.

7.4.   Sensitivity analysis

Sensitivity analysis is used to determine those parameters of the model, which are highly sensitive to $\mathcal{R}_0$. The parameters having a high sensitivity index are highly sensitive to $\mathcal{R}_0$. The approach is very useful to design disease control strategies. The sensitivity index of a parameter $\mathcal{\omega}$ is determined by using the formula

where $\mathcal{R}_0$ is the basic reproduction number.

The sensitivity indices of each of the parameters of $\mathcal{R}_0$ have been determined by using this formula and are listed in Table 2. Figure 7 shows the graphical representation of these values where the upward and downward bars show, respectively the direct and indirect relationship of parameters with reproduction number $\mathcal{R}_0$. Ignoring the sensitivity indices of parameters representing birth and death rates, we observe that the parameters $\alpha$, $\beta_v$ and $\zeta_h$ have high positive sensitivity impact on $\mathcal{R}_0$. This means that a unit increase or decrease in the value of $\zeta_h$ causes an increase or decrease of 0.6250 in the value of $\mathcal{R}_0$. The same logic applies to the parameters $\alpha$ and $\beta_v$. The parameter $\nu_h$ has a negative high sensitivity index of -0.3333. Thus, a unit increase in the value of $\nu_h$ causes a decrease of 0.3333 in the value of $\mathcal{R}_0$.

From the above observations, we conclude that the disease can be controlled significantly if it is possible to reduce the values of the parameters $\alpha, \ \beta_v, \ \zeta_h$ by some optimal strategy. However, practically, it appears difficult to control these values. On the other hand, the treatment rate $\nu_h$ of humans can be increased to reduce the impact of disease. Thus, this analysis suggests that we choose the treatment rate $\nu_h$ as the control variable to control the disease optimally.

8.   Optimization of the dengue fever model

In this section, we optimize the dengue fever model. For optimization, we update the dengue fever model (3.1) to adjust the control variable, and we define an optimal control problem by defining an objective functional. Then, the adjoint variables are introduced to attach the updated system of fractional differential equations to the objective functional, resulting in the formation of a function called the Hamiltonian. We consider the treatment rate denoted by $v_h$ as a time-dependent control variable denoted by $u_1(t)$ and develop optimality conditions from the Hamiltonian function by using Pontryagin's principle ^[55,56,57]. The conditions are calculated numerically to produce solutions of the optimal control problem.

8.1.   Optimal control problem and optimality conditions

The main purpose of introducing an optimal control problem is to optimally explore the effect of the treatment on the spread of dengue fever by implementing the best optimal control strategy. Therefore, we apply a control strategy for the maximization of recovered individuals and for the minimization of exposed or infected individuals at a minimal cost of control.

The suggested epidemic model of FODEs with the inclusion of control is given by

and the initial conditions are

The objective cost functional that consists of state and control variables may be defined as

where $T_{f}$ is the fixed terminal time, and $u_{1}(t)$ is the control variable.

The optimal control problem is then defined as:

where $\mathcal{U}$ is the control space.

To apply Pontryagin's maximum principle for optimality conditions, we constructed the Hamiltonian for the control problem (8.3) as follows:

where ${\Theta} = (S_h, E_h, I_h, T_h, R_h, P_h, S_v, I_v)$ is a vector of state variables, $G_i, \ i = 1, \ldots, 8$ are adjoint variables associated with the state equations given in (8.1) and $\hat{G} = (G_1, G_2, G_3, G_4, G_5, G_6, G_7, G_8)$ is called the adjoint vector.

Theorem 8.1. Let $\bar{S}_h$, $\bar{E}_h$, $\bar{I}_h$, $\bar{T}_h$, $\bar{R}_h$, $\bar{P}_h$, $\bar{S}_v$ and $\bar{I}_v$ be optimal state solutions for model (8.1) associated with the optimal control variable $u^{*}_{1}$ for the optimal control problem (8.3). Then, there exist an adjoint system such that

along with transversally conditions

and a control variable $u^{*}_{1}$ characterized by

□

Differentiating the Hamiltonian (8.4) with respect to the state variables and then using (8.5), the adjoint system of fractional-order differential equations is obtained as

with transversality conditions

Using the first condition of Pontryagin's principle, we obtain an equation for the control, i.e.,

Thus, the optimal control characterization for $u^{*}$ with bounds is given as

For an approximate solution of the state system (8.1), we implement the Toufik-Atangana scheme developed and explained in Subsection 7.1, and for the adjoint system (8.6), we make use of the Toufik-Atangana method backward in time $t$, together with the transversality conditions (8.6i).

8.2.   Solution algorithm

We implement steps of the following algorithm to calculate the optimality conditions for the optimal control problem (8.3). Here, $\Theta$ represents each of the state variables, the adjoint variables, the control variable, and $\sigma > 0$ is the tolerance parameter.

8.3.   Optimal solutions

In this section, we describe the simulation results obtained by solving the necessary optimality conditions derived from the fractional order optimal control problem (8.3). Steps of the algorithm are implemented through MATLAB code. To implement the Toufik-Atangana scheme for approximating solutions of state and adjoint equations, we discretize the domain $[0, T_f]$ into $N+1$ discrete points $t_j = jh, \ j = 0, 1, \ldots, N$ where $h = \frac{T_f}{N}$. The cost functional (8.2) is approximated at these discrete points by using Simpson's one by three rule. Simulation results are presented for different values of fractional order, i.e., for $\rho = 0.7, \ 0.8, \ 0.9, \ 1$.

The main purpose of the study was to determine the optimal treatment rate $v_h(t)$ (control variable) that minimizes the cost functional (dengue fever infection in the society). Figure 8 shows the plots of optimal control variable and the corresponding cost functional for various values of fractional order $\rho$. From the figure, we observe that each curve for the cost functional reaches its minimum corresponding to each time-dependent optimal treatment rate $v_h(t)$ (control). We notice that the number of solution iterations increases with the fractional order $\rho$.

Figure 9 shows the solution curves for the state variables before and after optimization at final time $T_f$. Solid lines represent the optimal solution curves for state variables, whereas the dashed lines represent the curves before optimization. A remarkable decrease in exposed and infected humans is observed after optimization for each of the fractional order $\rho = 0.7, \ 0.8, \ 0.9, \ 1$. Each of the optimal curves for recovered and protected individuals rise after optimization. The number of susceptible and treated humans also increases with time under the optimal treatment rate. With the given control strategy, we also observe a significant decrease in the infected mosquitoes for each of the fractional orders $\rho$. The decline in the infected mosquitoes is another achievement of the implemented control strategy. Thus, we conclude that the fractional order $\rho$ affects the dynamical behavior of the disease for a longer time. The study also reveals that the cost of implementing a treatment strategy reduces continuously with an increase in the value of fractional order $\rho$. This analysis gives us the importance of considering a fractional order dengue fever model over an integer order model. Further analysis can be done to see the impact of other fractional operators on dengue fever model in comparison to Atangana-Baleanu fractional operator.

9.   Conclusions

In this study, we proposed a new ABC fractional-order model for dengue fever to analyze the disease flow in the situation of protected travelers with proper treatment. We have proved that there exist a unique solution of the proposed fractional model that lies in a feasibly invariant region. The model also satisfies both the local and global stability properties at the disease free and endemic equilibrium points. All of these proofs conclude that the newly designed fractional model is well-posed. The main objective of this study was to control the disease by minimizing the number of infected humans. For this, we considered treatment rate $v_h$ as the control variable. First, we study the impact of the memory index and the effect of different constant treatment rates on the control of disease. We noticed that infected humans decrease by increasing the memory index (fractional order) and by increasing the treatment rate of infected humans. The infected humans vanish with treatment rate $v_h = 0.5$ for fractional order $\rho = 1$. Later, we considered treatment rate $v_h(t)$ as the time-dependent control in the proposed fractional model. We designed an optimal control problem by defining the objective functional. Pontryagin's maximum principle is used to establish optimality conditions for the solution of the optimal control problem. Graphical results show the effectiveness of the strategy to determine optimal treatment rates for various fractional orders that minimize the cost functional and significantly reduce the number of exposed and infected humans. Numerical analysis of the study revealed that the index of memory and the treatment rate can play a significant role in minimizing the impact of disease. We also conclude that the time dependent control is more cost effective than the time independent control. In future, we plan to consider different nonpharmaceutical control strategies to adjust in the existing ABC fractional model for more reliable optimal control analysis. We are also working on a dengue and COVID-19 coinfection model with an ABC derivative operator to develop various control strategies with cost-effective analysis.

Acknowledgments

The authors would like to acknowledge the support from King Faisal University, Saudi Arabia, Project No. GRANT2397. This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Project No. GRANT2397].

Conflict of interest

The authors declare no conflict of interest.