The method of fundamental solutions for analytic functions in complex analysis

1.   Introduction

It is known that the complex analysis plays an important role in the fields of science and engineering. An analytic function is composed by two real conjugate harmonic functions. Therefore, the problems involve harmonic and biharmonic equations e.g., electromagnetic fields, heat transfer, fluid flow, elastic and anti-plane fracture mechanics etc, can be studied in complex domain. Theodore and Lai ^[1] developed a method called complex variable boundary element method (CV-BEM), which is different from the traditional boundary element method (BEM). It was discussed in the complex domain, and could be easily implemented to two-dimensional potential problems. Lavrentiev and Shabat ^[2] discussed the problems of heat transfer, fluid flow and fracture mechanics etc, in complex domain. Muskhelishvili ^[3] proposed an elegant complex analysis in elastic mechanics. The above literatures reveal that the complex analysis is a powerful tool in solving the boundary value problems (BVPs) of harmonic and biharmonic equations.

The method of fundamental solutions (MFS) is a true boundary meshless method for the BVPs. It merely depends on the discrete nodes on the boundaries, and has been used as an approximate solutions for BVPs of harmonic or biharmonic functions ^[4,5]. The MFS is different from BEM, which need integral on the boundaries. The MFS also has the advantages of less digital inputting and minor computational consumption over the other mesh type method, and is regarded as a competing method to BEM and finite element method (FEM).

The MFS is widely use to solved the BVPs of linear differential equations, which have fundamental solutions. The MFS has been successfully implemented to elastic problems ^{[6,7,8,9,10,11,12,13]}, crack problems ^[14,15,16], wave and vibration problems ^{[17,18,19,20]}, bending of plates ^[21,22], fluid flows ^{[23,24,25,26]}, heat transfers ^[27,28], numerical conformal mappings ^[29,30,31] and inverse problems ^[32,33,34]. Additionally, the properties of stability and convergence of the MFS have been studied by many researchers. Dou and Zhang et al. ^[35] established the robust error and stability analysis for solving Laplace's equation. They provided a criteria for evaluating numerical techniques, and gave some strategies for choosing pseudo-boundaries. Kitagawa ^[36] gave an asymptotic evaluation for the stability of the MFS in the numerical solution of Laplace's equation based on the number of collocation points and developed a practical scheme to examine the stability of the method by singular value decomposition (SVD). Gaspar ^[37] built a simple multi-level method by using the gradient iteration, which could greatly reduce the computational complexity. Based on the MFS, Chen and Wang ^[38] developed a meshless boundary method called singular boundary method (SBM) with the source and collocation points being located on the physical boundary. Chen et al. ^[39] presented an extended meshfree method to treat the BVPs by a combination of particular and homogeneous solutions. Their numerical results revealed that this extended meshfree approach significantly improved the solution accuracy. The above citations are not intended to be exhaustive. One can be referred to Cheng and Hong et al. ^[40] for additional reviews. In their paper, they gave a excellent overview of the MFS on its solvability, uniqueness, convergence and stability. It can be concluded that fundamental solutions can be used in various forms for different purposes ^[40].

It is noted that the analytical solutions for analytic functions can not be found in many general cases. The numerical solutions of BVPs by real analysis have been studied much further than the ones by complex analysis. It is necessary to give the numerical solutions for the complex functions in an alternative way. Therefore, it is our purpose to develop a method by complex analysis based on the MFS. In this paper, we extend the MFS in solving the analytic functions by considering the Cauchy-Riemann equations and the properties of the harmonic functions. Additionally, the conformal mapping technique is also applied to deduce the singularities of the approximate analytic functions and reconstruct the fundamental solutions. The developed method can naturally introduce the informations of homogeneous boundary conditions and singularity properties by the conformal mapping technique and (or) the reconstructed fundamental solutions. The proposed method shares the merits of traditional MFS, and can be used to solve the BVPs of the analytic functions.

The rest of paper is organized as follows. In Section 2, the basic equations of analytic functions are given. The equations for complex analysis based the MFS is introduced in Section 3. The reconstructed fundamental solutions for the special cases are built by conformal mapping technique in Section 4. Four typical numerical examples are given and discussed to verify the validation of the developed method in Section 5. Some conclusions are drawn in the last section.

2.   Basic equations of analytic functions

2.1.   Analytic function and Cauchy-Riemann equations

The complex variable is composed of points of the form $z = x_1+i x_2$, where $\boldsymbol{x} = (x_1, x_2)$ is the group of real variables in Cartesian coordinate and $i = \sqrt{-1}$. Let $w(z)$ be an analytic function defined in domain $S$. We can write $w(z)$ in terms of two functions $\varphi(\boldsymbol{x})$ and $\phi(\boldsymbol{x})$ of real variables, which is

The functions $\varphi(\boldsymbol{x})$ and $\phi(\boldsymbol{x})$ are called potential and stream functions, which can be widely used in the fields of electrostatics, fluid mechanics, torsion, etc ^[2]. The two functions in Eq (2.1) satisfy Cauchy-Riemann equations as follow

It is noted that the functions $\varphi(\boldsymbol{x})$ and $\phi(\boldsymbol{x})$ are conjugate to each other, and either function could be directly determined by the other with the help of Cauchy-Riemann equations (Eq (2.2)). If the second partial derivatives exist and be continuous in $S$, the functions $\varphi(\boldsymbol{x})$ and $\phi(\boldsymbol{x})$ satisfy Laplace's equations

Therefore, $\varphi(\boldsymbol{x})$ and $\phi(\boldsymbol{x})$ are the harmonic functions in the domain $S$. By using the differential relation $\mathrm{d}z = \mathrm{d}x_1+i \mathrm{d}x_2$, the derivative of the analytic function $w(z)$ can be written as

It is noted that the derivative of the analytic function $w(z)$ of every order is analytic in the domain $S$. The integrals of $w(z)$ can be given by

In addition, there are generalized Cauchy-Riemann equations, which can be given in the following forms ^[2]

where $n_n$ and $n_s$ are the two unit vectors perpendicular to each other, and have the relationship of $n_n = i n_s$.

The corresponding derivative of $w(z)$ is ^[2]

The Eqs (2.6) and (2.7) are useful in the following analysis of the boundary conditions.

2.2.   Boundary conditions of analytic functions

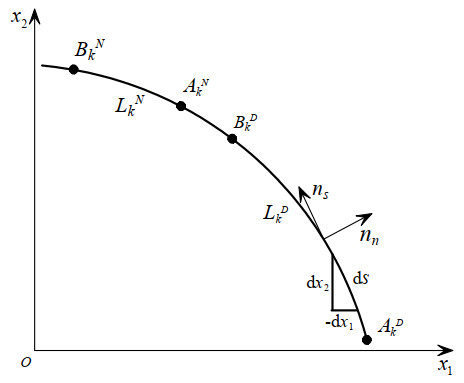
Let simple continuous, piecewise smooth curves $L_k$ ($k = 1, 2, ...$), with no point of intersection, be the boundaries of domain $S$ in the complex domain. The total boundary is $L = \Sigma L_k$, and the boundary $L_k$ is defined by

where $t$ is the point on the boundary $L_k$.

Consider a curve $L_k = L_k^D+L_k^N$ in the discussing plane $O-x_1x_2$ (as shown in Figure 1) contains the boundary $L_k^D$($A_k^DB_k^D$, $k = 1, 2, ...$) and the boundary $L_k^N$($A_k^NB_k^N$, $k = 1, 2, ...$). The positive direction of $L_k$ is defined that the domain keeps on the left side of it, with outward normal $n_n$ and the tangent $n_s$. Then, the positive direction of $n_n$ and $n_s$ are orientated with respect to the axes $Ox_1$ and $Ox_2$. We have

where $\mathrm{d}s = \sqrt{(\mathrm{d}x_1)^2+(\mathrm{d}x_2)^2}$.

If the function $w(z)$ in the domain $S$ has definite solution, the boundary conditions can be given as follows

or

where $\mathrm{Re}$ is the real part operator, the superscript "-" represents the complex conjugate, $L = L^D+L^N = \Sigma L_k^D+\Sigma L_k^N$, $w_0(t)$, $w_n(t)$ and $w_s(t)$ are the given functions on the corresponding boundaries.

It is seen that there are two types of the boundary conditions. One is the function itself, and the other is the derivatives of the function. In general, the first type boundary of Eq (2.10) is called Dirichlet boundary, the other types in Eqs (2.11) and (2.12) are called Neumann boundaries. Since that the analytic function $w(z)$ is rigorously related to the harmonic function $\varphi (x_1, x_2)$, we can derive the substitutes of the boundary conditions in Eqs (2.10)–(2.12) as follows. From Eq (2.1), Eq (2.10) can be rewritten as

where $\varphi_0(t)$ is the boundary value of function $\varphi (x_1, x_2)$.

After using Eq (2.4), we have

By considering Eqs (2.9) and (2.14), the function $\partial \varphi/\partial n_n$ on the boundary $L^N$ can be given as

Integrating Eq (2.15) on the boundary, we have the following boundary condition

where $\varphi_n (t)$ is the given function on the corresponding boundary.

The function $\partial \varphi/\partial n_s$ on the boundary $L_k^N$ can also be given as

where $\varphi_s (t)$ is another given function on the corresponding boundary.

It is obviously that the Eqs (2.13) and (2.17) are equivalent to each other, since that

on boundary $L_k^N$.

From Eqs (2.16) and (2.17), one can conclude that the boundary conditions of second type can be transformed to the ones of first type. Furthermore, the boundaries of two real conjugate functions $\varphi(\boldsymbol{x})$ and $\phi(\boldsymbol{x})$ can also be given as

where $\phi_0 (t)$ is the given boundary value of $\phi(\boldsymbol{x})$.

The Dirichlet boundary in Eq (2.10) only defines the real part $\varphi(\boldsymbol{x})$ of the function $w(z)$, and does not concern the imaginary part. Based on the generalized Cauchy-Riemann equations in Eq (2.6), the Dirichlet boundary of $\phi(\boldsymbol{x})$ could be given by the loosened boundary condition $\partial \phi(t)/\partial n_s$. Therefore, the alternative boundary condition of Eq (2.19) can be written in forms of

Additionally, the Neumann boundary can be given as follows

or

2.3.   The degree of the arbitrariness of the determined function $w(z)$

One can see that, the function $w(z)$ can only be determined by the real part based on the boundary in Eq (2.10). Hence, it is mentioned that the solution of function $w(z)$ could be determined apart from the terms of imaginary constants. If the boundaries are defined by Neumann boundaries in Eqs (2.11) or (2.12), the solutions will also be determined apart from a complex constant terms.

On the other hand, the treatment of loosened boundary of the second equation in Eq (2.20) reveals that the harmonic function $\phi(\boldsymbol{x})$ could also be determined apart from the term of real constant, which induces an imaginary constant in the function $w(z)$. Therefore, the Neumann boundaries of Eqs (2.21) or (2.22) will introduce a complex constant for the function $w(z)$. To determine the above constants, one can use a definite value of $w(z)$ to solve the constants, e.g., the value $w(z_0)$ is known at the point $z_0$. In most cases, the derivative $\mathrm{d}w(z)/\mathrm{d}z$ is more interested than the value of $w(z)$ itself, and the constants will not be concerned in analysis.

3.   Interpolation equations for the MFS

In order to solve the BVPs of $w(z)$ defined by Eqs (2.13), (2.16) and (2.17), we can apply two approaches to given the approximate solutions of the analytic functions. For method 1, the analytic function $w(z)$ is decomposed into two real harmonic functions $\varphi(\boldsymbol{x})$ and $\phi(\boldsymbol{x})$ to be solved. We call this method real functions of method of the fundamental solutions for analytic functions (RF-MFS). For method 2, we solve the analytic function $w(z)$ only depending on the real harmonic function $\varphi(\boldsymbol{x})$ by using the conjugate properties of the complex functions. We call this method conjugate analysis of method of the fundamental solutions for analytic functions (CA-MFS). These two approaches (RF-MFS and CA-MFS) have the merits that there are not such problems that the multi-values and branches to be considered. Therefore, it is convenient to be applied in single-connected and multiply-connected domain.

3.1.   Basic formulas for RF-MFS

From the equations derived in Section 2, the boundary conditions of Eqs (2.13), (2.16) and (2.17) can be treated as the weak forms of the Eqs (2.3) and (2.20)–(2.22). Therefore, one can solve the harmonic functions $\varphi(\boldsymbol{x})$ or $\phi(\boldsymbol{x})$ in the real plane instead of solving the BVPs of the analytic function $w(z)$ in the complex domain.

The approximate solutions $\hat{\varphi}(\boldsymbol{x})$ and $\hat{\phi}(\boldsymbol{x})$ of the harmonic functions $\varphi(\boldsymbol{x})$ and $\phi(\boldsymbol{x})$ in Eq (2.3) for the MFS read^[4,5]

where $\boldsymbol{x}$ is the node in the discussed plane, and $\boldsymbol{x}'_m$ ($m = 1, 2, ..., N$) is the source node on the fictitious boundary located outside the boundary $L$. $N$ is the number of the source nodes. $\alpha_m$ and $\beta_m$ are the real constants to be determined by boundary conditions, respectively. $G(\boldsymbol{x}, \boldsymbol{x}'_m)$ is the fundamental solution for harmonic equation. It can be expressed by

where $r = \|\boldsymbol{x}-\boldsymbol{x}'\|_2$, is the distance between nodes $\boldsymbol{x}$ and $\boldsymbol{x}'$.

Assume a multiply-connected domain $S$ with $n$ simple closed contours $L_1, L2, ..., L_n$, and the contour $L_0$ contains all the closed contours which is shown in Figure 2. The contour $L_k (k = 0, 1, 2, ..., n)$ is either Dirichlet boundary $L^D$ or Neumann boundary $L^N$, that is $L = \Sigma^n_{k = 0}L_k = \Sigma L^D+\Sigma L^N$. The numbers of boundary nodes on contour $L_k$ are $M_k$, and the numbers of source nodes outside or inside $L_k$ are $N_k$. The total numbers of the boundary and source nodes are $M = \Sigma^n_{k = 0}M_k$ and $N = \Sigma^n_{k = 0}N_k$. By using the boundary condition of Eqs (2.20)–(2.22), the constants and could be solved by

or

where $\boldsymbol{x}_j (j = 1, 2, ..., M)$ is the boundary node located on the boundary $L = L^D+L^N$. In the calculating system, the number $M$ of collection nodes should be no less than the number $N$ (the source nodes), that is $M \ge N$.

From Eqs (3.3)–(3.5), it is noted that there are two interpolation matrices (with $M$ nodes on the boundary $L$) to determine the constants $\alpha_m$ and $\beta_m$. After the constants being solved, the approximate solution $\hat{w}(z)$ can be given by the combination of $\varphi(\boldsymbol{x})$ and $\phi(\boldsymbol{x})$ as follow

3.2.   Basic formulas for CA-MFS

Since that analytic function has conjugate properties of Cauchy-Riemann equations, $w(z)$ can be determined by solving the harmonic function $\varphi(\boldsymbol{x})$ only. The formulas to solve $w(z)$ in CA-MFS merely depend on the first equation in Eqs (3.1) and (3.3)–(3.5), these are

or

If the approximate solution $\hat{\varphi}(\boldsymbol{x})$ is solved, the function $\hat{w}(z)$ can be give by the theorem of the uniquely determined analytic function as follows. Let $L_s$ be a line segment of $\mathrm{Im} z = x_2^p$ in the analytic domain $S$. One can define an analytic function $\kappa(z)$ by

Consider $L_s = [x_2^q, x_2^p]$ in the domain $S$, and assume that there is a point $z_0$ on $L_s$, and let $l_{\min} = \min \{ |x_2^q-z_0|, |x_2^p-z_0| \}$. One can get a sequence of points $z_k (k = 1, 2, ...)$, which is $z_1 \in (z_0-l_{\min}/2, z_0+l_{\min}/2)$, $z_2 \in (z_0-l_{\min}/3, z_0+l_{\min}/3)$, ..., $z_n \in (z_0-l_{\min}/(n+1), z_0+l_{\min}/(n+1))$. Therefore, the point $z_k$ converges to $z_0$, i.e $\lim_{n\to \infty}z = z_0$. Let $z_k = x_1^k+i x_2^p$, $(k = 1, 2, ...)$, the function $\kappa(z_k)$ can be given by

According to the theorem of the uniquely determined analytic functions, one have $w(z) = \kappa(z)$. If $x_2^p = 0$, we can get

We have $w(x_1) = \kappa(x_1)$ i.e $w(z) = \kappa(z)$.

As mentioned before, the derivative $\mathrm{d}w(z)/\mathrm{d} z$ is analytic in the domain $S$ since that $w(z)$ is analytic. Considering Eq (2.4), we can get

where $\kappa_\xi(x_1)$ is the known function in the domain. We have $\mathrm{d}w(z)/\mathrm{d} z = \kappa_\xi(z)$. Consequently, the the function $w(z)$ can be determined by

where $\nu$ is a real constant.

For any component of $\hat{\varphi}_k(\boldsymbol{x})$ expressed by Eq (3.7), it can be written as

where $k = 1, 2, ..., M$, $x'_{k1}$ and $x'_{k2}$ are the locations nodes on the fictitious boundary.

Therefore, the approximate solution of $\hat{w}(z)$ can be given as follow

where $z'_k = x'_{k1}+i x'_{k2}$, $V$ is an arbitrary real constants.

From Eq (3.17), we can conclude that the fundamental solution $G(z, z')$ of analytic function $w(z)$ in infinite complex domain is naturally $-\ln (z-z')/(2\pi)$, which can be found in the reference ^[2]. In addition, the relationship of the fundamental solution between real and complex plane can be given by

3.3.   Some discussions of the approximate solutions

Since that the fundamental solution $G(z, z')$ is multi-valued function, we cut the whole complex plane by negative real axis, and use $-\pi < \mathrm{arg}(z-z')\le \pi$ as the principle branch in the following discussion. It is shown that function $\varphi(\boldsymbol{x}) = \mathrm{Re}[w(z)]$ is a potential function that the curl of it degenerates to zero. In practice, the integral of $\partial\varphi(\boldsymbol{x})/\partial n_s$ must be

on the every closed contour $L_k (k = 0, 1, 2, ..., n)$ as shown in Figure 2.

From Eq (2.16), the imaginary part of will have an increasement on the contour $L_k$, which can be written as

on the every closed contour $L_k (k = 0, 1, 2, ..., n)$. Consider that the real part of $\ln (z, z')$ has no increasement and the imaginary one has the increasement $2\pi i$ on the closed contour $L_k$, which gives

where $V_k$ is the resultant of $\varphi_n(t)$ on any closed contour $L_k$.

Furthermore, we also have

where $V$ is the undetermined constant in Eq (3.17).

Since that the function $w(z)$ is solved by RF-MFS and CA-MFS in the real domain, the approximate solution $\hat{w}(z)$ in Eq (3.17) satisfies Eqs (3.19)–(3.22), automatically.

It is necessary to discuss the solutions in the infinite domain, when the closed contour $L_0$ in Figure 2 disappears. The value of fundamental solution $G(\infty, z')$ is infinity, whereas the real part of the approximate solution $\hat{w}(\infty)$ degenerates to zero. When Eq (3.21) is considered, the approximate solution $\hat{w}(z)$ given before can solve the problem of $w(\infty) = 0$. In more general cases, the solutions for $w_m(z)$, which have nonzero value at the infinity, can be defined by

where $w(z)$ is analytic in the discussed domain, and has the property of $w_(\infty) = 0$, and $\gamma_k$ is nonzero complex constant.

It is obviously that $w_m(z)$ is not an analytic function with pole of $m$ -order at infinity. We can solve the function $w_m(z)$ by introducing a new function

where $W(z)$ is analytic in the discussed domain, and degenerates to zero at infinity.

The methods of RF-MFS and CA-MFS can then be valid for $W(z)$. Furthermore, the boundary conditions should be transformed to the derivatives corresponding to $\varphi_0(t)$, $\varphi_n(t)$ and $\varphi_s(t)$. For example, the Dirichlet boundary conditions should be given by

Thus, the approximate solution of the actual solution $w_m(z)$ is

after the function $W(z)$ being solved.

4.   The fundamental solutions in some special cases

The fundamental solution $G(z, z')$ in Eq (3.18) does not satisfy the boundary conditions of $L_k$ in Figure 2, generally. In some special cases, we can reconstruct the new fundamental solutions, which satisfies the specific boundaries. The reconstructed fundamental solutions applied in the computations can help to reduce the computing costs and the singularities of the interpolation matrices.

4.1.   The fundamental solutions for symmetrical problems

Suppose that the discussed problem be symmetric about real axis $x_1$, there exists

or

where $t$ is the point on boundary.

The fundamental solution $-\ln (z-z')/(2\pi)$ in Eq (3.18) does not satisfy Eqs (4.1) and (4.2), obviously. We introduce a new fundamental solution $G(z, z')$ by

where $\mathrm{Im}z' > 0$, $w^*(z)$ is an analytic function to be determined in $\mathrm{Im}z > 0$.

Substituting Eq (4.3) into Eq (4.1), we have

By applying Schwarz's reflection principle, we define a new analytic function $\Omega (z)$ by

If $\mathrm{Im}t = 0$, we have $t = \bar{t}$. Thus, Eq (4.5) yields

Eq (4.6) implies that $\Omega (z)$ is continuous on ${Im}t = 0$, and is analytic in the whole domain. According to Liouville's theorem, $\Omega (z)$ must be a constant (we can let this constant be zero for convenience). Therefore, the function $w^*(z)$ becomes

Then, the new fundamental solution can be obtained by

By the similar analysis, the fundamental solution for Eq (4.2) is

According to Eq (3.18), the reconstructed fundamental solution in real plane for $\varphi(\boldsymbol{x})$ can be given as

and

It is noted that Eqs (4.10) or (4.11) can also be used in the half plane problem with homogeneous boundary of $\varphi_0(t)$ or $\varphi_n(t)$. The deduced fundamental solutions in Eqs (4.8)–(4.11) contain not only the source node information at $z'$ but also the information at $\bar{z}'$. We can locate the source nodes merely in the upper half domain without setting the source nodes on $\mathrm{Re}z'\le 0$.

4.2.   The fundamental solutions for hole boundaries

Consider that there exists a hole in an infinite domain, the conformal mapping technique can be used to find the specific fundamental solutions. It is noted that the complex functions take the great advantages in solving the problems in an infinite domain.

Let the function of the conformal mapping be $z = \varpi(\zeta)$, which maps $z$-plane to $\zeta = \eta_1+i \eta_2$ plane (as shown in Figure 3). It is convenient to map the discussed domain outside the hole in $z$-plane to the domain outside the unit circle in $\zeta$-plane. In general, the mapping function is

where $R$ and $c_k$ are complex constants in general.

The fundamental solution in Eq (3.18) can be transformed as

Since the second term in Eq (4.13) has a finite value if $\zeta = \zeta'$, the fundamental solution in $\zeta$-plane can then be written by

In addition, the mapped normal $n_n(\boldsymbol{\eta})$ and tangent vector $n_s(\boldsymbol{\eta})$ in $\zeta$-plane can be given as

where $\boldsymbol{\eta} = (\eta_1, \eta_2)$.

The analytic function $w(z)$ and its derivatives can be given as follows

When the hole is in the shape of ellipse $(x_1/a)^2+(x_2/b)^2 = 1$ with major axis and minor axis of $a$ and $b$, the mapping that transforms the domain outside the ellipse in $z$-plane to the domain outside the unit circle in $\zeta$-plane, is

where $R = (a+b)/2$, $c_1 = (a-b)/(a+b)$. It is seen that the ellipse degenerates to circle with radius $R$ if $c_1 = 0$, or crack with length $2R$ if $c_1 = 1$.

When $\varphi_0(t) = 0$ or $\varphi_n(t) = 0$ on the boundary of the unit circle ($|t| = 1$) in $\zeta$-plane, we can give the boundary conditions by Eqs (4.1) or (4.2). To reconstruct the fundamental solution, we introduce a new function $G(\zeta, \zeta')$ by

where $|\zeta'| > 1$, $w^*(\zeta)$ is an analytic function to be determined in the domain $|\zeta| > 1$.

Similar to the deduction in the last subsection, we have

for Eq (4.1).

Introducing a new analytic function $\Omega(\zeta)$ by

If $|t| = 1$, we have $\bar{t} = 1/t$, which ensure that $\Omega(\zeta)$ is continuous on $|t| = 1$, and is analytic in the whole domain. According to Liouville's theorem, $\Omega(\zeta)$ should be a constant. Therefore, the function $w^*(\zeta)$ is

Thus, the new fundamental solution in $\zeta$-plane is

We can also obtain the fundamental solution

for Eq (4.2).

According to the Eqs (4.24) and (4.25), the reconstructed fundamental solutions for $\varphi(\boldsymbol{\eta})$ in $\zeta$-plane can be given as

and

By substituting Eq (4.19) into Eqs (4.24) and (4.25), the reconstructed fundamental solutions $G(z, z')$ in-plane can be given by

and

It is noted that Eqs (4.28) and (4.29) have branch points at $z_0 = \pm2R\sqrt{c_1}$. To be easily used, the analytic function $w(z)$ is suggested to be solved by $w(\zeta)$ in transformed $\zeta$-plane, firstly.

We have $c_1 = 0$, when the elliptical hole degenerates to circle with radius $R$. The fundamental solutions for $G(\boldsymbol{x}, \boldsymbol{x}')$ in $z$-plane can be simplified to

and

The singularities of $w(z)$ or $\mathrm{d}w(z)/\mathrm{d}z$ are another important topics to be discussed. As mentioned before, the conformal mapping $\varpi(\zeta)$ can naturally give the explicit formulas of properties of the singularity. In $\zeta$-plane, it is obviously that the fundamental solution $G(\zeta, \zeta')$ has branch points at $\zeta_0 = \pm\sqrt{c_1}$. With the help of Eqs (4.17) and (4.19), $\mathrm{d}G(z, z')/\mathrm{d}z$ in (4.24) and (4.25) can be expanded by Laurent series

and

at the isolated singular point $\zeta_0 = \sqrt{c_1}$ ($z_0 = 2R\sqrt{c_1}$).

Therefore, the singularity parts of the approximate solution $\mathrm{d}\hat{w}(z)/\mathrm{d}z$ for the Diriclet boundary $\varphi_0(t) = 0$ and Neumann boundary $\varphi_n(t) = 0$ in $z$-plane, can be given as follows

and

It is noted that, the singularities would not be obviously induced, if the traditional MFS is used. When the mapping technique is used, the singular property can be induced naturally.

4.3.   The fundamental solutions for parabola boundaries

Consider there exists a parabola boundary $(x_2)^2 = -2\varepsilon x_1+\varepsilon^2$ ($\varepsilon > 0$) with the vertex at ($\varepsilon/2, 0$) and the focus at the origin, in an infinite domain (as shown in Figure 4). If $\varepsilon = 0$, the parabola boundary degenerates to a half line ($x_1\le 0, x_2 = 0$) on the negative real axis with principle branch $-\pi < \mathrm{arg}z\le \pi$.

The mapping function is[^[2]]

which transforms the domain outside parabola in $z$-plane to the upper half plane $\mathrm{Im}\zeta > 0$ in $\zeta$-plane.

The fundamental solution in Eq (3.18) can be written as

Since the second and third terms in Eq (4.37) has no singular value if $\zeta = \zeta'$, the fundamental solution in $\zeta$-plane can also be written by Eq (4.14). For the Dirichlet boundary $\varphi_0(t)$ and Neumann boundary $\varphi_n(t)$ on the parabola boundaries, the boundary conditions can be given by Eqs (4.1) and (4.2). In the mapped plane, the reconstructed fundamental solution in $\zeta$-plane, can also be written by the same expressions in Eqs (4.8) and (4.9) as follows

and

The differences between Eqs (4.8), (4.9), (4.38) and (4.39) are that these be in the $z$-plane, the others be in the $\zeta$-plane. Additionally, the fundamental solution for $\varphi(\boldsymbol(\eta))$ in $\zeta$-plane can be given as

and

which are in the same forms of Eqs (4.10) and (4.11).

According to Eqs (4.38) and (4.39), we can induce the corresponding fundamental solution in $z$-plane by

and

where the constant $i\pi/2$ is neglected.

In $\zeta$-plane, the mapping function $\varpi(\zeta)$ have branch points at $\zeta_0 = -i\sqrt(\varepsilon/2)$. Thus, $\mathrm{d}G(z, z')/\mathrm{d}z$ corresponding to Eqs (4.38) and (4.39), can be expanded as follows

and

Thus, the singularity parts of the approximate solution $\mathrm{d}\hat{w}(z)/\mathrm{d}z$ for the Dirichlet boundary $\varphi_0(t)$ and Neumann boundary $\varphi_n(t)$ in $z$-plane are

and

Therefore, most of the original BVPs can be transformed to the regular domain in the $\zeta$-plane by utilizing mapping technique. We can use the reconstructed fundamental solutions to solve these problems in the mapped plane. Furthermore, the singularities of the functions can be naturally given in our method.

5.   Numerical examples and discussions

To verify the validation of the developed method in this paper, 4 typical numerical examples for the simply-connected and the multiply-connected domain are studied. In the numerical computations, the truncated singular value decomposition (TSVD) technique is used to solve the constants $\alpha_k$ and $\beta_k$. The relative errors $e_r$ in this section are defined by

where $\chi_{num}$ is the numerical result, $\chi_{ana}$ is the analytical solution of the discussed problem.

5.1.   Numerical example 1: a BVP in simply-connected domain

We consider a BVP of an irregular simply-connected domain with $a = 10, h = 12$, which is shown in Figure 5. The boundary conditions are given by

The analytical solution is

where $\Gamma_c$ is an arbitrary real constant.

We test the RF-MFS and CA-MFS to show the validation of the proposed method, firstly. In the numerical calculating, the numbers of boundary and the source nodes are $M = 100$ and $N = 100$. To construct the interpolation matrices, the CA-MFS and RF-MFS utilize Eqs (3.3)–(3.5) and (3.8)–(3.10) with the fundamental solution of Eq (3.2).

As shown in Tables 1 and 2, the results $\mathrm{Re}\hat{w}(z)$ agree well with those of the analytical solutions $\mathrm{Re}w(z)$. The imaginary parts have the different constants about $2.247\times 10^6$ and $1.985\times 10^4$ in CA-MFS and RF-MFS, respectively. As mentioned before, the numerical results of the imaginary part of $w(z)$ naturally induce a constants $\Gamma_c$ when the boundary conditions of the Eqs (5.3)–(5.5) are used. To avoid this problem, one can obtain the imaginary part by using the given complex value at the specify point $z_0$. From Tables 3 and 4, the maximum error is about $10^{-4}$ order. The results obtained here using CA-MFS and RF-MFS have great availability for the simply-connected system.

5.2.   Numerical example 2: a BVP in infinite multiply-connected domain

Consider an infinite multiply-connected domain containing an circle with radius $r$, which is shown in Figure 6. The boundary conditions are given by

where $\Gamma_{-1}$, $\Gamma_1$ and $\Gamma_0$ are the complex constants, respectively.

The analytical solution for the corresponding boundary conditions is

When $\Gamma_1$ and $\Gamma_0$ degenerate to zero, the BVP can be solved by the traditional MFS. If they are not zero, the problem should be solved by Eqs (3.25) and (3.26), alternatively. To verify the validation of the presented method, we use traditional MFS and Eq (3.25) to construct the interpolation matrices, respectively. In the numerical calculating, $\Gamma_{-1} = 1+2i$, $\Gamma_1 = 5+6i$, $\Gamma_0 = 3+4i$ and $r = 3$ are used. The numbers of boundary and source nodes are $M = 50$ and $N = 50$ based on the CA-MFS.

As shown in Tables 5 and 6, the numerical results are failed to approach the analytical solutions. The reason is that the interpolation matrices constructed by Eqs (3.8)–(3.10) do not satisfy the boundary conditions at infinite. From Tables 7 and 8, it is shown that the numerical results are accurate to analytical solutions when the modified boundary of Eq (3.25) are used. The order of error for the numerical results is with maximum magnitude $10^{-5}$, and decreases when the $z$ is far away from the inner circle.

5.3.   Numerical example 3: a BVP in finite multiply-connected domain

Consider a finite square domain with a circular hole, which is shown in Figure 7. Let the side length of the square and radius of the circle be $2a$ and $r$. The boundary conditions are given as follows

where $\Gamma$ is complex constant.

It is obviously that the boundary conditions are all Neumann types. The corresponding numerical solutions of the approximate function $\hat{w}(z)$ can be only determined to the term $z$ and highers. The analytical solution for the corresponding boundary conditions can be written as

where the complex constant is neglected.

The boundary condition in Eq (5.9) reveals that we can use the reconstructed fundamental solution of Eq (4.31) to solve this BVP. To compare the validations between the reconstructed and the traditional fundamental solutions, we use Eqs (3.2) and (4.31) to construct the interpolation matrices, respectively. In the numerical calculating, $\Gamma = 1+2i$, $a = 10$ and $r = 3$ are used, the numbers of boundary and source nodes are $M = 100$ and $N = 100$ for the traditional fundamental solution in Eq (3.2), and $M = 50$, $N = 50$ for the reconstructed fundamental solution in Eq (4.31), respectively.

From Tables 9 and 10, one can see that numerical results derived by the traditional and reconstructed fundamental solutions in Eqs (3.2) and (4.31), both have good accuracy in the calculations. The difference between these two approaches, is that the numbers of the boundary and fictitious nodes. The order of the interpolation matrix utilizing the reconstructed fundamental solution is only the half of the traditional fundamental solution. We also find that the errors of the reconstructed fundamental solution, are slightly larger than the ones of the traditional fundamental solutions. The magnitudes of errors are tolerable, compared with the cost of calculation.

Compared to the analytical solution $\partial \varphi/\partial n$ along the circular boundary $z = r e^{i \theta}$, the numerical results $\partial \hat{\varphi}^{(1)}/\partial n$ (the traditional fundamental solution is used) and $\partial \hat{\varphi}^{(2)}/\partial n$ (the reconstructed fundamental solution is used) are also given in Table 11. As mentioned before, the boundary condition $\partial \hat{\varphi}^{(2)}/\partial n$ will be automatically satisfied when the reconstructed fundamental solution is used. Therefore, we can use the reconstructed fundamental solution to solve these type of BVPs without considering the circular boundary condition in which, calculating cost can be greatly reduced.

5.4.   Numerical example 4: a BVP in finite domain with a line crack

As shown in Figure 8, a BVP of circular plate with radius $r$ which contains a line crack situated on the segment $[-r, 0]$, is presented to verify the validation of the conformal mapping in the numerical solution of an analytic function. The parameter $\varepsilon$ in Eq (4.36) degenerates to zero in this case, and the mapping function is $\zeta = i\sqrt{z}$. The whole domain can then be transformed to a semicircle domain with the radius $\sqrt{r}$. Furthermore, the crack in the physical plane is transformed to a line $[-\sqrt{r}, \sqrt{r}]$ located on the real axis $\eta_1$ in $\zeta$-plane. The boundary conditions are set to be mixed types as follows

where $\theta = \mathrm{arg}z$, $\Gamma_1$ and $\Gamma_2$ are real constants.

The corresponding analytical solution is

It is noted that the crack also has the boundary information, where the boundary nodes must be set. On the other hand, the corresponding source nodes should be placed inside the crack based on the MFS. Unfortunately, there is no place to locate the source nodes. Chen and Wang ^[38] suggested a method named SBM to located the fictitious node on the boundary. We propose another way to avoid this problem by conformal mapping. In the mapped plane, the boundary conditions can be written as follows

where $\theta = \mathrm{arg}\zeta$.

According to the boundary conditions in Eq.(5.16), the reconstructed fundamental solution Eq (4.39) can be applied to solve this BVP in the mapped plane. The numbers of boundary and source nodes are $M = 100$ and $N = 100$, and $\Gamma_1 = 1$, $\Gamma_2 = 4$, $r = 25$ are used for the numerical example, respectively. After the BVP being solved in transformed plane, the numerical results in the physical plane can then be given by Eqs (4.16) and (4.17).

As shown in Tables 12 and 13, the relatively maximum error is about $10^{-12}$, which shows that the numerical results agree well with the analytical solution. It is also noted that the boundary nodes are only set on the semicircle except on the crack by using the reconstructed fundamental solution Eq (4.39), which satisfies the boundaries of the crack automatically.

With the help of Eq (4.47), the approximate singularity factor $\mathrm{d}\hat{w}(z)/\mathrm{d}z$ can also be given as $2.00i/\sqrt{z}$, which satisfies the the singularity of analytical solution $i\Gamma_2/(2\sqrt{z}) = 2i/\sqrt{z}$. Therefore, it is shown that the proposed method based on the conformal mapping technique is effective in solving the BVPs of cracks.

6.   Conclusions

This study extends the traditional MFS to RF-MFS and CA-MFS in solving the analytic functions by considering the Cauchy-Riemann equations and the properties of the harmonic functions. The method developed in this paper shares the merits of traditional MFS, and does not induce the multi-valuedness problem, which simplifies the analysis of the BVPs for analytic functions. The RF-MFS utilizes the boundary conditions of real and imaginary parts of $w(z)$ to solve analytic functions in real domain. The CA-MFS only involves the boundary condition of $w(z)$ directly, by considering the conjugate properties of harmonic functions. These two methods are both valid for the BVPs of analytic function $w(z)$, which can meet the requirement of conciseness and reliability. It is suggested that the CA-MFS is preferred to be used for efficiency and easy-using.

Furthermore, the conformal mapping technique is introduced to solve the BVPs. Based on this technique, it is more convenient to solve the crack BVPs and give more information of the numerical results (e.g., singularity properties), whereas the traditional MFS can't. In addition, the conformal mapping technique can easily give the reconstructed fundamental solutions, which can be used in solving the specified BVPs (e.g., symmetric and hole boundaries).

Four numerical examples are given to illustrate the validity and accuracy of the developed method. The obtained numerical solutions agree pretty well with the analytical functions. As an extension of the traditional MFS, the RF-MFS and CA-MFS can be applied to solve the BVPs of analytic functions for two dimensional problems.

Acknowledgments

We would like to thank the Editor and Reviewers for giving valuable improvements to the paper. This work was supported by the National Natural Science Foundation of China under grant No. 11802145 and Jiangsu Provincial Natural Science Foundation of China under grant No. BK20191450. We also thank Mr. Jicheng Jiang for his patience and help on our work.

Conflict of interest

The authors declare no potential conflict of interests.