Heat and mass transfer of fractional second grade fluid with slippage and ramped wall temperature using Caputo-Fabrizio fractional derivative approach

Sami Ul Haq; Saeed Ullah Jan; Syed Inayat Ali Shah; Ilyas Khan; Jagdev Singh; Sami Ul Haq; Saeed Ullah Jan; Syed Inayat Ali Shah; Ilyas Khan; Jagdev Singh

doi:10.3934/math.2020198

AIMS Mathematics

2020, Volume 5, Issue 4: 3056-3088. doi: 10.3934/math.2020198

Previous Article Next Article

Research article Special Issues

Heat and mass transfer of fractional second grade fluid with slippage and ramped wall temperature using Caputo-Fabrizio fractional derivative approach

1.
Department of Mathematics, Islamia College University, Peshawar 25000, Pakistan
2.
Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam
3.
Department of Mathematics, JECRC University, Jaipur-303905, Rajasthan, India

Unsteady free convection slip flow of second grade fluid over an infinite heated inclined plate is discussed. The effects of mass diffusions in the flow are also eligible. Caputo-Fabrizio fractional derivative is used in the constitutive equations of heat and mass transfer respectively. Laplace transform is utilized to operate the set of fractional governing equations for both ramped and stepped wall temperature. Expression for Sherwood number and Nusselt number with non-integer order are found by differentiating the analytical solutions of fluid concentration and temperature. Numerical results of Sherwood number, Nusselt number and skin friction are demonstrated in tables. Solutions are plotted graphically to analyze the impact of distinct parameters i.e. Caputo-Fabrizio fractional parameter, second grade parameter, slip parameter, Prandtl number, Schmidt number, thermal Grashof number and mass Grashof number to observe the physical behavior of the flow.

Keywords:

Citation: Sami Ul Haq, Saeed Ullah Jan, Syed Inayat Ali Shah, Ilyas Khan, Jagdev Singh. Heat and mass transfer of fractional second grade fluid with slippage and ramped wall temperature using Caputo-Fabrizio fractional derivative approach[J]. AIMS Mathematics, 2020, 5(4): 3056-3088. doi: 10.3934/math.2020198

Related Papers:

[1]	Asifa, Poom Kumam, Talha Anwar, Zahir Shah, Wiboonsak Watthayu . Analysis and modeling of fractional electro-osmotic ramped flow of chemically reactive and heat absorptive/generative Walters'B fluid with ramped heat and mass transfer rates. AIMS Mathematics, 2021, 6(6): 5942-5976. doi: 10.3934/math.2021352
[2]	Zehba Raizah, Arshad Khan, Saadat Hussain Awan, Anwar Saeed, Ahmed M. Galal, Wajaree Weera . Time-dependent fractional second-grade fluid flow through a channel influenced by unsteady motion of a bottom plate. AIMS Mathematics, 2023, 8(1): 423-446. doi: 10.3934/math.2023020
[3]	Imran Siddique, Yasir Khan, Muhammad Nadeem, Jan Awrejcewicz, Muhammad Bilal . Significance of heat transfer for second-grade fuzzy hybrid nanofluid flow over a stretching/shrinking Riga wedge. AIMS Mathematics, 2023, 8(1): 295-316. doi: 10.3934/math.2023014
[4]	W. Abbas, Ahmed M. Megahed, Osama M. Morsy, M. A. Ibrahim, Ahmed A. M. Said . Dissipative Williamson fluid flow with double diffusive Cattaneo-Christov model due to a slippery stretching sheet embedded in a porous medium. AIMS Mathematics, 2022, 7(12): 20781-20796. doi: 10.3934/math.20221139
[5]	Bengisen Pekmen Geridonmez . RBF simulation of natural convection in a nanofluid-filled cavity. AIMS Mathematics, 2016, 1(3): 195-207. doi: 10.3934/Math.2016.3.195
[6]	Mushtaq Ahmad, Muhammad Imran Asjad, Ali Akgül, Dumitru Baleanu . Analytical solutions for free convection flow of Casson nanofluid over an infinite vertical plate. AIMS Mathematics, 2021, 6(3): 2344-2358. doi: 10.3934/math.2021142
[7]	Saleh Mousa Alzahrani . Enhancing thermal performance: A numerical study of MHD double diffusive natural convection in a hybrid nanofluid-filled quadrantal enclosure. AIMS Mathematics, 2024, 9(4): 9267-9286. doi: 10.3934/math.2024451
[8]	Taqi A. M. Shatnawi, Nadeem Abbas, Wasfi Shatanawi . Comparative study of Casson hybrid nanofluid models with induced magnetic radiative flow over a vertical permeable exponentially stretching sheet. AIMS Mathematics, 2022, 7(12): 20545-20564. doi: 10.3934/math.20221126
[9]	Nadeem Abbas, Wasfi Shatanawi, Taqi A. M. Shatnawi . Innovation of prescribe conditions for radiative Casson micropolar hybrid nanofluid flow with inclined MHD over a stretching sheet/cylinder. AIMS Mathematics, 2025, 10(2): 3561-3580. doi: 10.3934/math.2025164
[10]	J. Kayalvizhi, A. G. Vijaya Kumar, Ndolane Sene, Ali Akgül, Mustafa Inc, Hanaa Abu-Zinadah, S. Abdel-Khalek . An exact solution of heat and mass transfer analysis on hydrodynamic magneto nanofluid over an infinite inclined plate using Caputo fractional derivative model. AIMS Mathematics, 2023, 8(2): 3542-3560. doi: 10.3934/math.2023180

Abstract

Nomenclature
$u^{'}$	Fluid velocity $[LT^{-1}]$
$T^{'}$	Fluid temperature $[\theta]$
$C^{'}$	Fluid concentration $[(MOL)L^{-3}]$
$t^{'}$	Time $[T]$
$C_{p}$	Specific heat at a constant pressure $[L^{2}T^{-1}\theta^{-1}]$
$D$	The mass diffusion coefficient $[L^{2}T^{-1}]$
$g$	Acceleration because of gravity $[LT^{-2}]$
$k$	The thermal conductivity of the fluid $[MLT^{-3}\theta^{-1}]$
$\alpha$	Second grade parameter
$\beta$	Non-integer order fractional parameter
$\mu$	Dynamic viscosity $[ML^{-1}T^{-1}]$
$\nu$	Kinematic viscosity $[L^{2}T^{-1}]$
$\rho$	Fluid density $[ML^{-3}]$
$\beta$	The volumetric coefficient of thermal expansion $[\theta^{-1}]$
$\beta^{*}$	The volumetric coefficient of mass expansion $[MOL]^{-1}$
$j^{''}$	Mass flux per unit area on the plate
$T^{'}_{w}$	The temperature at the plate
$T^{'}_{\infty}$	Fluid Temperature far away from the plate
$C^{'}_{w}$	The concentration at the plate
$C^{'}_{\infty}$	Fluid concentration far away from the plate
$t_{0}$	Characteristics time
$Gm$	Grashof number of mass
$Gr$	Grashof number of thermal
$Nu$	Nusselt number
$Sh$	Sherwood number
$\lambda$	Dimensional slip parameter
$s$	Laplace transforms parameter
$\eta$	Non-dimensional slip parameter

1. Introduction

Non-Newtonian fluids consist of three main groups which depend on their performance in the shear. The second grade fluid is one of the popular in the common models of non-Newtonian fluids. Firstly Coleman and Noll ^[1] configured the mathematical model of second grade fluid. Later this scheme was carrying out to interpret various problems that have approximately simple construction. To explain the pattern of non- Newtonian fluids, the second order Rivlin-Ericksen equation has been applied by Erdogan and Imrak ^[2]. In this research article they discussed about unsteady Poiseuille flux, unsteady flow across a float sheet and the coquette flow.

Nevertheless, all the researchers are more on vertical plates. Many researchers worked on the flow nearby inclined plates or surfaces, though in real application, such as crystal growth and solar energy collection. Chamkha ^[3] has discussed the Hydromagnetic free convection flow through an isothermal inclined plate under the impact of the thermal porous sheet. The heat transfer of an inner rotational flow over an inclined sheet has been explored by kimura et al. ^[4]. The analytical solution of free convection flow, which is unsteady in nature flowing over an inclined rotating plate was scrutinized by Toki ^[5].

The field of fractional calculus (FC) is that branch of applied analysis that is, in a certain sense, as old as classical calculus as it well known at present time. Leibniz and Newton formed the bases of integral and differential calculus in the seventeenth century. In 1695, when Leibniz notice the symbol which is employed for the nth derivative of a function $f$ in a letter to de l'Hospital. De l'Hospital arise a question that what does the nth derivative of a function $f$ mean if $n = \frac{1}{2}$ . Now a days this important letter from de L'Hospital as commonly accepted as the first instant which is known as fractional derivative ^[6]. In particular, fractional derivative of certain substantial problems are more appropriate than regular derivative. This is because of two key reasons firstly, we have the freedom to select any order for the differential and integral operators, and not be restricted to integer-order only. Secondly, fractional derivatives depend not only at the present time but also at the past, so they are very suitable and accurate when the system has a long-term memory. It has several applications not only in engineering and physical sciences but also in other areas such as geology, ecology, biology and chemistry etc ^[7]. In fluid dynamics fractional calculus has been expanded in the opposite direction. To interpret the viscoelastic nature of materials, fractional calculus has been used. Friedrich ^[8] successfully applied the fractional approach to explain the viscoelastic of material. The utilization of fractional derivative in viscoelasticity has been proposed by Gemant ^[9]. It has several uses in natural science and engineering like as geology, physics, ecology, biology and chemistry, etc. This tool efficiency to generalize some physical concept was used by Palade et al. ^[10]. Transport phenomena exhibit is sub diffusion for and super diffusion for $\beta\in (0, 1)$ and super diffusion for $\beta > 1$ , where $\beta$ is the fractional parameter.

Among the recently published article, the fractional derivative of free convection flow on a vertical sheet with mass diffusion and heating of Newtonian fluid was explored by Vieru et al. ^[11]. Zafar and Fetecau ^[12] studied the motion of a viscous fluid involving fractional operator without singular kernel on infinite sheet. The free convection flow of a fractional viscous fluid over the vertical sheet by applying shear stress to the fluid has been explored by Nehad et al. ^[13]. Imran et al. ^[14] reported the second grade fluid with Caputo fractional approach. An extended second grade fluid model with double convection flow with MHD on an exponentially increasing infinite perpendicular plate has been investigated by Nazar et al. ^[15]. Imran et al. ^[7] have analyzed comparatively the flow of second grade fluid with fractional approaches (Caputo and Caputo-Fabrizio (CF)) and Newtonian heating. The free convection second grade fluid flow with ramped wall temperature has been explored by Samiulhaq et al. ^[16]. The second grade fluid with MHD among two parallel walls normal to the plate under the effects of porous medium has been scrutinized by Samiulhaq et al. ^[17]. The MHD flow of Williamson nanofluid with the impacts of distinct parameters is studied by Gupta et al. ^[18]. MHD 3-D boundary layer flow and heat transfer of nanofluid induced by convective conditions is examined by Gupta et al. ^[19]. In an another article Gupta et al. ^[20] reported a study on MHD mixed convective stagnation point flow and heat transfer of an incompressible fluid containing nanoparticles through an inclined stretching surface having different kind of effects. In the last few years, many authors used the fractional operators in scientific applications ^{[21,22,23,24,25,26,27,28,29,30,31,32,33,34,35]}.

The purpose of the present note is to study the unsteady natural convection second grade fluid over an infinite heated inclined plate with the impact of slip condition. CF operator is used in the constitutive equations of heat and mass transfer respectively. Integral transform method (Laplace transformation) is utilized to operate the set of fractional governing equations for both ramped and stepped wall temperature. The effects of memory parameters, i.e. CF fractional parameter $\beta$ are graphically studied. Following are main contribution in this article.

1. The impact of slip boundary condition over an infinite heated inclined plate.

2. CF fractional derivative of second grade fluid with the impact of wall slip condition.

3. Laplace transform method is employed the set of fractional governing equations for constant as well as ramped wall temperature.

2. Analysis of the governing problem

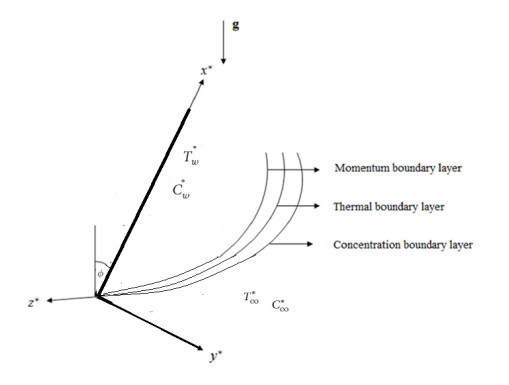
Here we assume the unsteady free convection slip flow of second grade fluid over an infinite heated inclined plate. Taking $x-$ axis in upward direction along the plate while $y-$ axis is perpendicular to it. Initially for $t'\leq 0$ , both the fluid and the plate are at rest position at the constant temperature $T^{'}_{\infty}$ and concentration $C^{'}_{\infty}$ . When $0 < t'\leq t_{0}$ the plate temperature is elevated or declined to $\{T^{'}_{\infty}+(T_{w}^{'}-T_{\infty}')\frac{t'}{t_{0}}$ and for $t' > t_{0}$ the plate temperature is kept at uniform temperature $T_{w}$ and the level of concentration at the plate is elevated to $C_{w}'$ or concentrations is accrued to the plate at fixed rate. It is assumed that temperature, concentration and velocity are dependent over t and y only. By Boussinesq's approximation, the governing equations of the problem are ^[36,37].

Figure 1. Physical configuration of the problem.

DownLoad: Full-Size Img PowerPoint

$\begin{eqnarray} \frac{{\partial u^{'}}}{{\partial t^{'}}} = \left(\mu+{\alpha_{1} }\frac{\partial}{\partial t^{'}}\right)\frac{{{\partial ^2}u^{'}}}{{\partial {y'^2}}}+\rho g\beta_{t}\cos\phi (T^{'} - {T^{'}_\infty })+\rho g\beta^{*}\cos\phi(C^{'}-C^{'}_{\infty}), \end{eqnarray}$

(2.1)

$\begin{eqnarray} \rho c_{p}\frac{\partial T^{'}}{\partial t^{'}} = k\frac{\partial ^{2}T^{'}}{\partial y'^{2}}, \end{eqnarray}$

(2.2)

$\begin{eqnarray} \frac{\partial C^{'}}{\partial t^{'}} = D\frac{\partial^2 C^{'}}{\partial y'^2}. \end{eqnarray}$

(2.3)

The corresponding initial conditions (ICs) and boundary conditions (BCs)are under as:

$\begin{align} \begin{split} &{u^{'}(y', 0)} = 0, \quad {T^{'}(y', 0) = T^{'}_{\infty}}, \quad {C'(y', 0) = C^{'}_{\infty}} \quad \quad for\quad t' = 0\quad and\quad y^{'}\geq0\\ &{u^{'}(y', t')} = \lambda\frac{\partial {u'(y', t')}}{\partial y^{'}} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad for\quad t' \gt 0 \quad and\quad y^{'} = 0\\ &{T^{'}(0, t')} = \begin{cases} T^{'}_{\infty}+(T^{'}_{w}-T^{'}_{\infty})\frac{t^{'}}{t_{0}}\quad \quad \quad \quad for\quad 0 \lt t^{'}\leq t_{0}\\ {T^{'}_{w}} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad for\quad t^{'} \gt t_{0}\\ \end{cases}\\ &{C^{'}(0, t')} = {C^{'}_{w}} \quad \quad \quad \quad \quad\quad\quad \quad \quad \quad \, \, \quad for\quad t' \gt 0\\ &{u^{'}}\rightarrow0, \quad {T^{'}\rightarrow T^{'}_{\infty}}, \quad {C^{'}\rightarrow C^{'}_{\infty}} \quad as \quad y^{'}\rightarrow \infty\\ \end{split} \end{align}$

(2.4)

In the above equation $\lambda$ is the slip parameter.

In order to reduce the number of variables involved in the governing equation, we introduce dimensionless variables as follows

$\begin{align} \begin{split} &{y^*} = \frac{y^{'}}{\frac{\nu}{U_{0}}} = \frac{y^{'}}{\sqrt{\nu t_{0}}}, \quad t^* = \frac{t^{'}}{\frac{\nu}{U^{2}_{0}}} = \frac{t^{'}}{t_{0}}, \quad {u^*} = \frac{u^{'}}{U_{0}} = \frac{u^{'}}{t_{0}g\beta_{T}(T_{w}-T_{\infty})} = \frac{u^{'}}{Gr}\sqrt{\frac{t_{0}}{\nu}}, \\ &{\theta^*} = \frac{(T^{'}-T^{'}_{\infty})}{(T^{'}_{w}-T^{'}_{\infty})}, \quad {\Pr} = \frac{\mu C_{p}}{k}, \quad {Gr} = \frac{g\beta_{T}(T_{w}-T_{\infty})t^{\frac{3}{2}}_{0}}{\sqrt{\nu}}, \quad{C^*} = \frac{C^{'}-C^{'}_{\infty}}{C^{'}_{w}-C^{'}_{\infty}}\\ &\text{or} \quad {C^*} = \frac{C^{'}-C^{'}_{\infty}}{\frac{j''\sqrt{\nu t_{0}}}{D}}, \quad{Sc} = \frac{\nu}{D}, \quad{\eta} = \frac{\lambda}{\sqrt{\nu t_{0}}} \quad \quad {Gm} = \frac{g\beta_{C}(C^{'}_{w}-C^{'}_{\infty})t^{\frac{3}{2}}_{0}}{\sqrt{\nu}}, \\ &\text{or} \quad {Gm} = \frac{g\beta_{C}j'' t^{2}_{0}}{D}\quad \text{and}\quad {\alpha} = \frac{{\alpha _1}U^{2}_{0}}{\mu\nu}\\ \end{split} \end{align}$

(2.5)

Using these non-dimensional variables (2.5) in Eq. (2.1), and removing the star notation the Eq. (2.1) take the simplest form as

$\begin{eqnarray} \frac{\partial{u(y, t)}}{\partial{t}} = \left(1+{\alpha}\frac{\partial}{\partial t}\right)\frac{{{\partial ^2}u}}{{\partial {y^2}}}+{Gr\cos\phi}\theta(y, t)+{Gm\cos\phi}{C(y, t)}, \end{eqnarray}$

(2.6)

The equation of the thermal balance in local form explained the diffusion phenomenon of heat as

$\begin{eqnarray} \rho {c_p}\frac{{\partial T}}{{\partial t}}{\rm{ }} = -{\nabla}.\overrightarrow{q}, \end{eqnarray}$

(2.7)

Where $\rho$ represent the fixed fluid density, ${c_p}$ represent the specific heat, ${\nabla}$ represent the gradient operator and $q(y, t)$ represent the thermal flux density.

Henry et al. ^[38] and Hristov ^[39,40] suggested the fractional generalization Fourier law which is consider for the thermal heat flux as

$\begin{eqnarray} q(y, t){\rm{ }} = -kD^{\beta}_{t}\left[{\nabla}T(y, t)\right]. \end{eqnarray}$

(2.8)

In the above equation $D^{\beta}_{t}$ is the CF operator and their definition can be seen in appendix.

Using Eq. (2.8) in Eq. (2.7) we get,

$\begin{eqnarray} \rho {c_p}\frac{{\partial T}}{{\partial t}}{\rm{ }} = -{\nabla}.\left[-kD^{\beta}_{t}\left({\nabla}T(y, t)\right)\right]. \end{eqnarray}$

(2.9)

Using the dimensionless parameters (2.5) in Eq. (2.9) and dropping out the star notation, Eq. (2.9) take the simplest form as

$\begin{eqnarray} \Pr\frac{\partial{\theta\left(y, t\right)}}{\partial{t}} = D^{\beta}_{t}\frac{\partial^{2} \theta\left(y, t\right)}{\partial y^{2}}, \end{eqnarray}$

(2.10)

Consider the Fick's law,

$\begin{eqnarray} \frac{\partial{C\left(y, t\right)}}{\partial{t}} = -{\nabla}.j \end{eqnarray}$

(2.11)

Where $j$ represent the flux of particles and ${\nabla}$ represent the gradient operator.

To eliminate flux from Fick's law, we can use the conservation equation

$\begin{eqnarray} j{\rm{ }} = -DD^{\beta}_{t}\left[{\nabla}C(y, t)\right], \end{eqnarray}$

(2.12)

Making use of Eq. (2.12) in Eq. (2.11), we get

$\begin{eqnarray} \frac{\partial{C\left(y, t\right)}}{\partial{t}} = -{\nabla}.\left[-DD^{\beta}_{t}\left({\nabla}C(y, t)\right)\right] \end{eqnarray}$

(2.13)

Using the dimensionless variables (2.5) in Eq. (2.13) and dropping out the star notation, Eq. (2.13) take the simplest form as

$\begin{eqnarray} Sc\frac{\partial{C\left(y, t\right)}}{\partial{t}} = D^{\beta}_{t}\frac{\partial^{2} C\left(y, t\right)}{\partial y^{2}}, \end{eqnarray}$

(2.14)

where Eq. (2.6) is in classical form, and Eqs. (2.10) and (2.14) are in CF time fractional operator model of order $\beta\in(0, 1)$ .

In the above expressions $u$ , $y$ , $t$ , $C$ , $\theta$ , $Gr$ , $Gm$ , $Sc$ and $\Pr$ denote the velocity, coordinate axis, time, concentration, temperature, thermal Grashof number, mass Grashof number, Schmidt number and Prandtl number respectively. Moreover, characteristics time $t_{0}$ can be define as

$\begin{align} t_{0}& = [\frac{\nu}{g^{2}\beta^{2}(T^{'}_{w}-T^{'}_{\infty})^{2}}]^{\frac{1}{3}}. \end{align}$

(2.15)

The associated initial and boundary condition (2.4) are given below:

$\begin{align} \begin{split} &u(y, 0) = 0, \quad T(y, 0) = 0, \quad C(y, 0) = 0 \quad for \quad y\geq0 \\ &u(0, t) = \eta\frac{\partial{u(0, t)}}{\partial{y}} \quad \quad \quad \quad for \quad t \gt 0 \quad \\ &T(0, t) = \begin{cases} t \quad for \quad t\leq1\\ 1 \quad for \quad t \gt 1 \quad for \quad \quad \quad t \gt 0\\ \end{cases}\\ &C(0, t) = 1 \quad \quad for \quad t \gt 0\\ &u(y, t)\rightarrow 0, \quad T(y, t)\rightarrow 0, \quad C(y, t)\rightarrow0 \quad as \quad y\rightarrow\infty \quad for \quad t \gt 0. \end{split} \end{align}$

(2.16)

In the above equation $\eta$ indicates the slip parameter.

3. Analytical solutions

We know propose to solve equations (2.6), (2.10) and (2.14) having the ICs and BCs (2.16) with the aid of Laplace transform (LT) algorithm. Since the velocity equation depends upon the temperature and concentration, so we first find the solutions for temperature and concentration.

3.1. Solution for ramped temperature

Using the LT technique to Eq. (2.10) and the utilizing the initial and boundary condition (2.16), we have

$\begin{align} \frac{d^{2} \theta(y, s)}{dy^{2}}-\frac{\Pr}{\xi}\left(s+\beta\xi\right)\theta(y, s) = 0, \end{align}$

(3.1)

$\begin{align} \theta(0, s)& = \left(\frac{1-\exp(-s)}{s^{2}}\right), \, \, \, \theta(y, s)\rightarrow 0\, \, as \, \, y\rightarrow \infty \end{align}$

(3.2)

The solution of Eq. (3.1) with BCs (3.2) is

$\begin{align} \theta(y, s)& = \left(\frac{1-\exp(-s)}{s^{2}}\right)\exp\left(-y\sqrt{\frac{\Pr}{\xi}}\sqrt{s+\beta\xi}\right), \end{align}$

(3.3)

The inverse LT of Eq. (3.3) is

$\begin{align} \theta(y, t)& = \psi(y, t)-H(t-1)\psi(y, t-1). \end{align}$

(3.4)

In the above expression,

$\begin{align*} \begin{split} \psi(y, t)& = \left(\frac{2t\sqrt{\beta\xi}+y\sqrt{\frac{\Pr}{\xi}}}{4\sqrt{\beta\xi}}\right)\exp\left(y\sqrt{\Pr\beta}\right)\text{erfc}\left(\frac{y}{2}\sqrt{\frac{\Pr}{\xi t}}+\sqrt{\beta\xi t}\right)+\\ &\left(\frac{2t\sqrt{\beta\xi}-y\sqrt{\frac{\Pr}{\xi}}}{4\sqrt{\beta\xi}}\right)\exp\left(-y\sqrt{\Pr\beta}\right)\text{erfc}\left(\frac{y}{2}\sqrt{\frac{\Pr}{\xi t}}-\sqrt{\beta\xi t}\right), \\ \xi& = \frac{1}{1-\beta}. \end{split} \end{align*}$

And the unit step function $H(t-1)$ is presented as

$\begin{align} \begin{split} H(t-r) = \begin{cases} t \quad for \quad 0\leq t \lt r\\ 1 \quad for \quad t\geq r \\ \end{cases}\\ \end{split} \end{align}$

(3.5)

Where r is any constant.

3.2. Solution for concentration profile

Applying LT technique to Eq. (2.14) and utilizing the ICs and BCs (2.16), we have

$\begin{align} \frac{d^{2} C(y, s)}{dy^{2}}-\frac{Sc}{\xi}\left(s+\beta\xi\right)C(y, s)& = 0, \end{align}$

(3.6)

$\begin{align} C(0, s)& = \frac{1}{s}, \, \, \, C(y, s)\rightarrow 0\, \, as \, \, y\rightarrow \infty \end{align}$

(3.7)

The solution of Eq. (3.6) with boundary condition (3.7) is

$\begin{align} C(y, s)& = \frac{1}{s}\exp\left(-y\sqrt{\frac{Sc}{\xi}}\sqrt{s+\beta\xi}\right), \end{align}$

(3.8)

Using the inverse LT, the solution for concentration is obtained as

$\begin{equation} \begin{split} C(y, t) = &\frac{1}{2}\bigg[\text{erfc}\left(\frac{y}{2}\sqrt{\frac{Sc}{\xi t}}+\sqrt{\beta\xi t}\right)\exp\left(y\sqrt{Sc\beta}\right)\\ &+\text{erfc}\left(\frac{y}{2}\sqrt{\frac{Sc}{\xi t}}-\sqrt{\beta\xi t}\right)\exp\left(-y\sqrt{Sc\beta}\right)\bigg]. \end{split} \end{equation}$

(3.9)

3.3. Solution for ramped velocity

Applying LT technique to Eq. (2.6), and utilizing ICs and BCs (2.16), we obtain

$\begin{equation} s{u}\left(y, s\right)-\alpha s\frac{d^{2} {u}\left(y, s\right)}{dy^{2}}-\frac{d^{2} {u}\left(y, s\right)}{dy^{2}} = {Gr}\cos\phi\theta\left(y, s\right)+{Gm}\cos\phi C\left(y, s\right), \end{equation}$

(3.10)

$\begin{equation} u(0, s) = \eta\frac{\partial{u(0, s)}}{\partial{y}} \end{equation}$

(3.11)

The solution of (3.10) with BCs (3.11) is

$\begin{eqnarray} \begin{array}{c} {u}\left(y, s\right) = u_{1}\left(y, s\right)+u_{2}\left(y, s\right)+u_{3}\left(y, s\right)+u_{4}\left(y, s\right)+u_{5}\left(y, s\right)+u_{6}\left(y, s\right). \end{array} \end{eqnarray}$

(3.12)

where

$\begin{align*} \begin{split} u_{1}(y, s) = &\left[\frac{-\left(1-\exp\left(-s\right)\right)Gr\xi\cos\phi\left(\exp\left(-y\sqrt{\frac{s}{1+\alpha s}}\right)\right)}{\left(1+\eta\sqrt{\frac{s}{1+\alpha s}}\right)}\right]\left[\frac{(1+\alpha s)}{s^{2}\Pr\left(s+\beta\xi\right)\left(1+\alpha s\right)-s^{3}\beta}\right], \\ u_{2}(y, s) = &\left[\frac{-Gm\xi\cos\phi\left(\exp\left(-y\sqrt{\frac{s}{1+\alpha s}}\right)\right)}{\left(1+\eta\sqrt{\frac{s}{1+\alpha s}}\right)}\right]\left[\frac{(1+\alpha s)}{Scs\left(s+\beta\xi\right)\left(1+\alpha s\right)-\xi s^{2}}\right], \end{split} \end{align*}$

$\begin{align*} \begin{split} u_{3}(y, s) = &\left[\frac{-\left(1-\exp\left(-s\right)\right)Gr\xi\eta\cos\phi\sqrt{\frac{\Pr}{\xi}}\sqrt{s+\beta\xi}\left(\exp\left(-y\sqrt{\frac{s}{1+\alpha s}}\right)\right)}{\left(1+\eta\sqrt{\frac{s}{1+\alpha s}}\right)}\right]\\ &\left[\frac{(1+\alpha s)}{s^{2}\Pr\left(s+\beta\xi\right)\left(1+\alpha s\right)-s^{3}\beta}\right], \\ u_{4}(y, s) = &\left[\frac{-Gm\xi\eta\cos\phi\sqrt{\frac{Sc}{\xi}}\sqrt{s+\beta\xi}\left(\exp\left(-y\sqrt{\frac{s}{1+\alpha s}}\right)\right)}{\left(1+\eta\sqrt{\frac{s}{1+\alpha s}}\right)}\right]\left[\frac{(1+\alpha s)}{Scs\left(s+\beta\xi\right)\left(1+\alpha s\right)-\xi s^{2}}\right], \\ u_{5}(y, s) = &\left[\left(1-\exp\left(-s\right)\right)Gr\xi\cos\phi\exp\left(-y\sqrt{\frac{\Pr}{\xi}}\sqrt{s+\beta\xi}\right)\right]\\ &\left[\frac{(1+\alpha s)}{s^{2}\Pr\left(s+\beta\xi\right)\left(1+\alpha s\right)-s^{3}\beta}\right], \\ u_{6}(y, s) = &\left[Gm\xi\cos\phi\exp\left(-y\sqrt{\frac{Sc}{\xi}}\sqrt{s+\beta\xi}\right)\right]\left[\frac{(1+\alpha s)}{Scs\left(s+\beta\xi\right)\left(1+\alpha s\right)-\xi s^{2}}\right].\\ \end{split} \end{align*}$

Equation (3.12) can be written in inverse LT as

$\begin{eqnarray} {u}\left(y, t\right) = u_{1}\left(y, t\right)+u_{2}\left(y, t\right)+u_{3}\left(y, t\right)+u_{4}\left(y, t\right)+u_{5}\left(y, t\right)+u_{6}\left(y, t\right). \end{eqnarray}$

(3.13)

where

$\begin{align*} \begin{split} &u_{1}\left(y, t\right) = A_{11}M_{15}\left(y, t\right)+A_{12}M_{16}\left(y, t\right)-A_{12}B_{8}M_{17}\left(y, t\right)+A_{13}M_{17}\left(y, t\right), \\ &u_{2}\left(y, t\right) = A_{21}m_{9}\left(y, t\right)+A_{22}m_{10}\left(y, t\right), \\ &u_{3}\left(y, t\right) = A_{31}M_{18}\left(y, t\right)+A_{32}M_{19}\left(y, t\right)-A_{32}B_{8}M_{20}\left(y, t\right)+A_{33}M_{20}\left(y, t\right), \\ &u_{4}\left(y, t\right) = A_{41}m_{14}\left(y, t\right)+A_{42}m_{15}\left(y, t\right), \\ &u_{5}\left(y, t\right) = -A_{11}M_{21}\left(y, t\right)-A_{12}M_{22}\left(y, t\right)+A_{12}B_{8}M_{23}\left(y, t\right)-A_{13}M_{23}\left(y, t\right), \\ &u_{6}\left(y, t\right) = A_{21}m_{19}\left(y, t\right)+A_{22}m_{20}\left(y, t\right), \\ &M_{15}\left(y, t\right) = m_{6}\left(y, t\right)-m_{6}\left(y, t-1\right)H(t-1), \\ &m_{6}\left(y, t\right) = \int_{0}^{t}E_{\eta}\left(y, \tau\right)d\tau, \\ &E_{\eta}\left(y, t\right) = b_{4}\left(\frac{\exp\left(-y\sqrt{b_{1}}\right)}{b_{4}+\sqrt{b_{1}}}\right)\delta(t)+b_{4}\left(\frac{b_{1}\exp\left(-b_{1}t\right)}{\sqrt{\pi t}}\right)\\ &\int_{0}^{\infty}\exp\left(-b_{1}x-\left(\frac{y^{2}}{4x}\right)\right)J_0\left(2b_{1}\sqrt{xt}\right)dx\\ &-\left(\frac{b_{1}\exp\left(-b_{1}t\right)}{\sqrt{t}}\right)b^{2}_{4}\exp(b_{4}y)\int_{0}^{\infty}\exp\left((b^{2}_{4}-b_{1})x\right)\\ &\sqrt{x}J_0\left(2b_{1}\sqrt{xt}\right)\text{erfc}\left(\frac{y}{2\sqrt{x}}+b_{4}\sqrt{x}\right)dx\\ \end{split} \end{align*}$

$\begin{align*} \begin{split} \text {where}\\ &b_{4} = \frac{1}{\alpha}, \\ &M_{16}\left(y, t\right) = m_{7}\left(y, t\right)-m_{7}\left(y, t-1\right)H(t-1), \\ &m_{7}\left(y, t\right) = \int_{0}^{t}\exp(-B_{8}\tau)\cos\sqrt{B_{9}}\tau E_{\eta}\left(y, t-\tau\right)d\tau, \\ \text {where} \\ &B_{8} = \frac{\Pr+\Pr\beta\xi\alpha-\xi}{2B_{7}}, \, B_{9} = \frac{\Pr\beta\xi}{B_{7}}-\left(\frac{\Pr+\Pr\beta\xi\alpha-\xi}{2B_{7}}\right)^{2}, \\ &\text {and}\, \, B_{7} = \Pr\alpha.\\ &M_{17}\left(y, t\right) = m_{8}\left(y, t\right)-m_{8}\left(y, t-1\right)H(t-1), \\ &m_{8}\left(y, t\right) = \frac{1}{\sqrt{B_{9}}}\int_{0}^{t}\exp(-B_{8}\tau)\sin\sqrt{B_{9}}\tau E_{\eta}\left(y, t-\tau\right)d\tau, \\ &m_{9}\left(y, t\right) = \int_{0}^{t}D_{0}\left(y, \tau\right)E_{\eta}\left(y, t-\tau\right)d\tau, \\ &D_{0}\left(y, t\right) = -\frac{1}{B^{2}_{11}+B_{12}}\exp(-B_{11}t)\cos\sqrt{B_{12}}t+\frac{1}{B^{2}_{11}+B_{12}}\\ &+\frac{B_{11}}{\sqrt{B_{12}}\left(B^{2}_{11}+B_{12}\right)}\exp(-B_{11}t)\sin\sqrt{B_{12}}t, \\ \text {where}\\ &B_{11} = \frac{Sc+Sc\beta\xi\alpha-\xi}{2B_{10}}, \, B_{12} = \frac{Sc\beta\xi}{B_{10}}-\left(\frac{Sc+Sc\beta\xi\alpha-\xi}{2B_{10}}\right)^{2}\\ &\text {and}\, \, B_{10} = Sc\alpha.\\ &m_{10}\left(y, t\right) = \frac{1}{\sqrt{B_{12}}}\int_{0}^{t}\exp(-B_{11}\tau)\sin\sqrt{B_{12}}\tau E_{\eta}\left(y, t-\tau\right)d\tau, \\ &M_{18}\left(y, t\right) = m_{11}\left(y, t\right)-m_{11}\left(y, t-1\right)H(t-1), \\ &m_{11}\left(y, t\right) = \int_{0}^{t}D_{1}\left(y, \tau\right)E_{\eta}\left(y, t-\tau\right)d\tau, \\ &D_{1}\left(y, \tau\right) = -\int_{0}^{t}\frac{\exp\left(-B_{11}\xi\tau\right)}{2\tau\sqrt{\pi\tau}}d\tau, \\ &M_{19}\left(y, t\right) = m_{12}\left(y, t\right)-m_{12}\left(y, t-1\right)H(t-1), \\ &m_{12}\left(y, t\right) = \int_{0}^{t}D_{2}\left(y, \tau\right)E_{\eta}\left(y, t-\tau\right)d\tau, \\ &D_{2}\left(y, t\right) = \exp(-B_{8}t)\cos\sqrt{B_{9}}t\int_{0}^{t}\frac{\exp\left(\left(B_{8}-\beta\xi\right)\tau\right)}{2\tau\sqrt{\pi\tau}}\cos\sqrt{B_{9}}\tau d\tau-\\ &\exp(-B_{8}t)\sin\sqrt{B_{9}}t\int_{0}^{t}\frac{\exp\left(\left(B_{8}-\beta\xi\right)\tau\right)}{2\tau\sqrt{\pi\tau}}\sin\sqrt{B_{9}}\tau d\tau, \\ &M_{20}\left(y, t\right) = m_{13}\left(y, t\right)-m_{13}\left(y, t-1\right)H(t-1), \\ &m_{13}\left(y, t\right) = \int_{0}^{t}D_{3}\left(y, \tau\right)E_{\eta}\left(y, t-\tau\right)d\tau, \\ \end{split} \end{align*}$

$\begin{align*} \begin{split} D_{3}\left(y, t\right) = &\frac{-\exp(-B_{8}t)\sin\sqrt{B_{9}}t}{\sqrt{B_{9}}}\int_{0}^{t}\frac{\exp\left(\left(B_{8}-\beta\xi\right)\tau\right)}{2\tau\sqrt{\pi\tau}}\cos\sqrt{B_{9}}\tau d\tau-\\ &\frac{\exp(-B_{8}t)\cos\sqrt{B_{9}}t}{\sqrt{B_{9}}}\int_{0}^{t}\frac{\exp\left(\left(B_{8}-\beta\xi\right)\tau\right)}{2\tau\sqrt{\pi\tau}}\sin\sqrt{B_{9}}\tau d\tau, \\ m_{14}\left(y, t\right) = &\int_{0}^{t}D_{4}\left(y, \tau\right)E_{\eta}\left(y, t-\tau\right)d\tau, \\ D_{4}\left(y, t\right) = &\int_{0}^{t}\left[D_{0}(\tau)\left(\frac{-\exp\left(-\beta\xi(t-\tau)\right)}{2\sqrt{\pi}\left(t-\tau\right)^{\frac{3}{2}}}\right)\right]d\tau\\ m_{15}\left(y, t\right) = &\int_{0}^{t}D_{5}\left(y, \tau\right)E_{\eta}\left(y, t-\tau\right)d\tau, \\ D_{5}\left(y, t\right) = &\frac{-\exp(-B_{11}t)\sin\sqrt{B_{12}}t}{\sqrt{B_{12}}}\int_{0}^{t}\frac{\exp\left(\left(B_{11}-\beta\xi\right)\tau\right)}{2\tau\sqrt{\pi\tau}}\cos\sqrt{B_{12}}\tau d\tau-\\ &\frac{\exp(-B_{11}t)\cos\sqrt{B_{12}}t}{\sqrt{B_{12}}}\int_{0}^{t}\frac{\exp\left(\left(B_{11}-\beta\xi\right)\tau\right)}{2\tau\sqrt{\pi\tau}}\sin\sqrt{B_{12}}\tau d\tau\\ M_{21}\left(y, t\right) = &m_{16}\left(y, t\right)-m_{16}\left(y, t-1\right)H(t-1), \\ m_{16}\left(y, t\right) = &\int_{0}^{t}\frac{y\sqrt{\frac{\Pr}{\xi}}\exp\left(-\beta\xi\tau-\frac{\Pr y^{2}}{4\xi\tau}\right)}{2\tau\sqrt{\pi\tau}}d\tau, \\ M_{22}\left(y, t\right) = &m_{17}\left(y, t\right)-m_{17}\left(y, t-1\right)H(t-1), \\ m_{17}\left(y, t\right) = &\int_{0}^{t}\exp(-B_{8}\tau)\cos\sqrt{B_{9}}\tau N_{1}(y, t-\tau)d\tau, \\ N_{1}\left(y, t\right) = &\frac{y\sqrt{\frac{\Pr}{\xi}}\exp\left(-\beta\xi\tau-\frac{\Pr y^{2}}{4\xi\tau}\right)}{2\tau\sqrt{\pi\tau}}, \\ M_{23}\left(y, t\right) = &m_{18}\left(y, t\right)-m_{18}\left(y, t-1\right)H(t-1), \\ m_{18}\left(y, t\right) = &\frac{1}{\sqrt{B_{9}}}\int_{0}^{t}\exp(-B_{8}\tau)\sin\sqrt{B_{9}}\tau N_{1}(y, t-\tau)d\tau, \\ m_{19}\left(y, t\right) = &\int_{0}^{t}D_{0}(\tau)N_{2}\left(y, t-\tau\right)d\tau, \\ N_{2}\left(y, t\right) = &\frac{y\sqrt{\frac{Sc}{\xi}}\exp\left(-\beta\xi\tau-\frac{Sc y^{2}}{4\xi\tau}\right)}{2\tau\sqrt{\pi\tau}}, \\ m_{20}\left(y, t\right) = &\frac{1}{\sqrt{B_{12}}}\int_{0}^{t}\exp(-B_{11}\tau)\sin\sqrt{B_{12}}\tau N_{2}(y, t-\tau)d\tau, \\ \text{where}\\ A_{11} = &-Gr\xi\cos\phi\left[\frac{-2B_{8}+B_{7}B^{2}_{8}+B_{7}B_{9}+\alpha B_{7}B^{2}_{8}+\alpha B_{7}B_{9}}{B_{7}\left(B^{2}_{8}+B_{9}\right)^{2}}\right], \end{split} \end{align*}$

$\begin{align*} \begin{split} A_{12} = &-Gr\xi\cos\phi\left[\frac{-2B_{8}-\alpha B_{7}B^{2}_{8}-\alpha B_{7}B_{9}}{B_{7}\left(B^{2}_{8}+B_{9}\right)^{2}}\right], \\ A_{13} = &-Gr\xi\cos\phi\left[\frac{3B^{2}_{8}-B_{9}-2 \alpha B_{7}B^{3}_{8}-2 \alpha B_{7}B_{8}B_{9}}{B_{7}\left(B^{2}_{8}+B_{9}\right)^{2}}\right], \\ A_{21} = &\frac{-Gm\xi\cos\phi}{B_{10}}, \, A_{22} = \frac{-Gm\xi\alpha\cos\phi}{B_{10}}, \\ A_{31} = &-Gr\xi\eta\cos\phi\sqrt{\frac{\Pr}{\xi}}\left[\frac{-2B_{8}+B_{7}B^{2}_{8}+B_{7}B_{9}+\alpha B_{7}B^{2}_{8}+\alpha B_{7}B_{9}}{B_{7}\left(B^{2}_{8}+B_{9}\right)^{2}}\right], \\ A_{32} = &-Gr\xi\eta\cos\phi\sqrt{\frac{\Pr}{\xi}}\left[\frac{-2B_{8}-\alpha B_{7}B^{2}_{8}-\alpha B_{7}B_{9}}{B_{7}\left(B^{2}_{8}+B_{9}\right)^{2}}\right], \\ A_{33} = &-Gr\xi\eta\cos\phi\sqrt{\frac{\Pr}{\xi}}\left[\frac{3B^{2}_{8}-B_{9}-2 \alpha B_{7}B^{3}_{8}-2 \alpha B_{7}B_{8}B_{9}}{B_{7}\left(B^{2}_{8}+B_{9}\right)^{2}}\right], \\ A_{41} = &\frac{-Gm\xi\eta\cos\phi\sqrt{\frac{Sc}{\xi}}}{B_{10}}, \, \text {and}\, \, A_{42} = \frac{-Gm\xi\eta\alpha\cos\phi\sqrt{\frac{Sc}{\xi}}}{B_{10}}. \end{split} \end{align*}$

3.4. Solution for constant Temperature

Now using LT technique to Eq. (2.10) and employing ICs and BCs (2.16), we get

$\begin{align} \frac{d^{2} \theta(y, s)}{dy^{2}}-\frac{\Pr}{\xi}\left(s+\beta\xi\right)\theta(y, s) = 0, \end{align}$

(3.14)

$\begin{align} \theta(0, s) = \frac{1}{s}, \, \, \, \theta(y, s)\rightarrow 0 \, \, as\, \, y\rightarrow\infty \end{align}$

(3.15)

The solution of (3.14) with boundary condition (3.15) is

$\begin{align} \theta(y, s)& = \left(\frac{1}{s}\right)\exp\left(-y\sqrt{\frac{\Pr}{\xi}}\sqrt{s+\beta\xi}\right), \end{align}$

(3.16)

Now using the inverse LT to Eq. (3.16), we have

$\begin{equation} \begin{split} \theta(y, t) = &\frac{1}{2}\bigg[\exp\left(y\sqrt{\Pr\beta}\right)\text{erfc}\left(\frac{y}{2}\sqrt{\frac{\Pr}{\xi t}}+\sqrt{\beta\xi t}\right)\\ &+\exp\left(-y\sqrt{\Pr\beta}\right)\text{erfc}\left(\frac{y}{2}\sqrt{\frac{\Pr}{\xi t}}-\sqrt{\beta\xi t}\right)\bigg]. \end{split} \end{equation}$

(3.17)

3.5. Solution for constant Velocity

Applying LT technique to Eq. (2.6), and employing ICs and BCs (2.16), we obtain

(3.18)

The solution of (3.18) with BCs (3.11) is

$\begin{eqnarray} \begin{array}{c} {u}\left(y, s\right) = u_{7}\left(y, s\right)+u_{2}\left(y, s\right)+u_{8}\left(y, s\right)+u_{4}\left(y, s\right)+u_{9}\left(y, s\right)+u_{6}\left(y, s\right). \end{array} \end{eqnarray}$

(3.19)

where

$\begin{align*} \begin{split} &u_{7}(y, s) = \left[\frac{-Gr\xi\cos\phi\left(\exp\left(-y\sqrt{\frac{s}{1+\alpha s}}\right)\right)}{\left(1+\eta\sqrt{\frac{s}{1+\alpha s}}\right)}\right]\left[\frac{(1+\alpha s)}{s\Pr\left(s+\beta\xi\right)\left(1+\alpha s\right)-s^{2}\beta}\right], \\ &u_{8}(y, s) = \left[\frac{-Gr\xi\eta\cos\phi\sqrt{\frac{\Pr}{\xi}}\sqrt{s+\beta\xi}\left(\exp\left(-y\sqrt{\frac{s}{1+\alpha s}}\right)\right)}{\left(1+\eta\sqrt{\frac{s}{1+\alpha s}}\right)}\right]\left[\frac{(1+\alpha s)}{s\Pr\left(s+\beta\xi\right)\left(1+\alpha s\right)-s^{2}\beta}\right], \\ &u_{9}(y, s) = \left[Gr\xi\cos\phi\exp\left(-y\sqrt{\frac{\Pr}{\xi}}\sqrt{s+\beta\xi}\right)\right]\left[\frac{(1+\alpha s)}{s\Pr\left(s+\beta\xi\right)\left(1+\alpha s\right)-s^{2}\beta}\right], \\ \end{split} \end{align*}$

Equation (3.19) can be written in inverse LT as

$\begin{eqnarray} \begin{array}{c} {u}\left(y, t\right) = u_{7}\left(y, t\right)+u_{2}\left(y, t\right)+u_{8}\left(y, t\right)+u_{4}\left(y, t\right)+u_{9}\left(y, t\right)+u_{6}\left(y, t\right). \end{array} \end{eqnarray}$

(3.20)

$\begin{align*} \begin{split} u_{7}\left(y, t\right) = &A_{71}m_{21}\left(y, t\right)+A_{72}m_{22}\left(y, t\right), \\ u_{8}\left(y, t\right) = &A_{81}m_{23}\left(y, t\right)+A_{82}m_{24}\left(y, t\right), \\ u_{9}\left(y, t\right) = &-A_{71}m_{25}\left(y, t\right)-A_{72}m_{26}\left(y, t\right), \\ where\\ m_{21}\left(y, t\right) = &\int_{0}^{t}\bigg[\frac{-\exp(-B_{8}\tau)\cos\sqrt{B_{9}}\tau}{\left(B^{2}_{8}+B_{9}\right)}+\frac{1}{\left(B^{2}_{8}+B_{9}\right)}\\ &+\frac{B_{8}\exp(-B_{8}\tau)\sin\sqrt{B_{9}}\tau}{\sqrt{B_{9}}\left(B^{2}_{8}+B_{9}\right)}\bigg]E_{\eta}\left(y, t-\tau\right)d\tau, \\ m_{22}\left(y, t\right) = &\frac{1}{\sqrt{B_{9}}}\int_{0}^{t}\exp(-B_{8}\tau)\sin\sqrt{B_{9}}\tau E_{\eta}\left(y, t-\tau\right)d\tau, \\ m_{23}\left(y, t\right) = &\int_{0}^{t}D_{6}\left(y, \tau\right)E_{\eta}\left(y, t-\tau\right)d\tau, \\ D_{6}\left(y, t\right) = &\int_{0}^{t}\bigg[\bigg(\frac{-\exp(-B_{8}\tau)\cos\sqrt{B_{9}}\tau}{\left(B^{2}_{8}+B_{9}\right)}+\frac{1}{\left(B^{2}_{8}+B_{9}\right)}\\ &+\frac{B_{8}\exp(-B_{8}\tau)\sin\sqrt{B_{9}}\tau}{\sqrt{B_{9}}\left(B^{2}_{8}+ B_{9}\right)}\bigg)\left(\frac{-\exp\left(-\beta\xi(t-\tau)\right)}{2\sqrt{\pi}\left(t-\tau\right)^{\frac{3}{2}}}\right)\bigg]d\tau, \\ \end{split} \end{align*}$

$\begin{align*} \begin{split} m_{24}\left(y, t\right) = &\int_{0}^{t}\bigg[\frac{-\exp(-B_{8}t)\sin\sqrt{B_{9}}t}{\sqrt{B_{9}}}\int_{0}^{t}\frac{\exp(\left(B_{8}-\beta\xi\right)\tau)\cos\sqrt{B_{9}}\tau}{2\tau\sqrt{\pi\tau}}d\tau-\\ &\frac{\exp(-B_{8}t)\cos\sqrt{B_{9}}t}{\sqrt{B_{9}}}\int_{0}^{t}\frac{\exp(\left(B_{8}-\beta\xi\right)\tau)\sin\sqrt{B_{9}}\tau}{2\tau\sqrt{\pi\tau}}d\tau\bigg]E_{\eta}\left(y, t-\tau\right)d\tau. \end{split} \end{align*}$

3.6. Nusselt number

The rate of heat transfer can be computed in terms of Nusselt number as

$\begin{equation*} Nu = -\left. \frac{\partial \theta }{\partial y}\right \vert _{y = 0}, \end{equation*}$

$\begin{equation} \begin{split} {Nu(t)} = &\bigg[\frac{\exp\left(-t\beta\xi\right)\sqrt{\Pr}}{\sqrt{\pi\xi}}+ \left(\frac{\sqrt{\frac{\Pr}{\xi}}}{4\sqrt{\beta\xi}}+\frac{1}{2}t\sqrt{\Pr\beta}\right)\\ &\left(\text{erfc}\left(-\sqrt{t\beta\xi}\right)-\text{erfc}\left(\sqrt{t\beta\xi}\right)\right)\bigg]+\\ &\bigg[\frac{\exp\left(-(t-1)\beta\xi\right)\sqrt{\Pr}}{\sqrt{\pi\xi}}+ \left(\frac{\sqrt{\frac{\Pr}{\xi}}}{4\sqrt{\beta\xi}}+\frac{1}{2}(t-1)\sqrt{\Pr\beta}\right)\\ &\left(\text{erfc}\left(-\sqrt{(t-1)\beta\xi}\right)-\text{erfc}\left(\sqrt{(t-1)\beta\xi}\right)\right)\bigg]H(t-1). \end{split} \end{equation}$

(3.21)

3.7. Sherwood number

The rate of mass transfer can be computed in terms of Sherwood number as

$\begin{equation*} Sh = -\left. \frac{\partial C }{\partial y}\right \vert _{y = 0}, \end{equation*}$

$\begin{equation} {Sh(t)} = \frac{\sqrt{Sc}\exp\left(-t\beta\xi\right)}{\sqrt{\pi\xi t}}+\frac{\sqrt{Sc\beta}}{2}\left[\text{erfc}\left(-\sqrt{Rt}\right)-erfc\left(\sqrt{Rt}\right)\right]. \end{equation}$

(3.22)

4. Result and discussion

The unsteady free convection slip flow of an incompressible second grade fluid over an infinite heated inclined plate with fractional parameter $\beta$ is studied. The solutions of dimensionless velocity, concentration and temperature are evaluated with the aid of Laplace transform technique. Expression for Sherwood number and Nusselt number with fractional parameter $\beta$ are obtained by differentiating the solutions of fluid concentration and temperature.

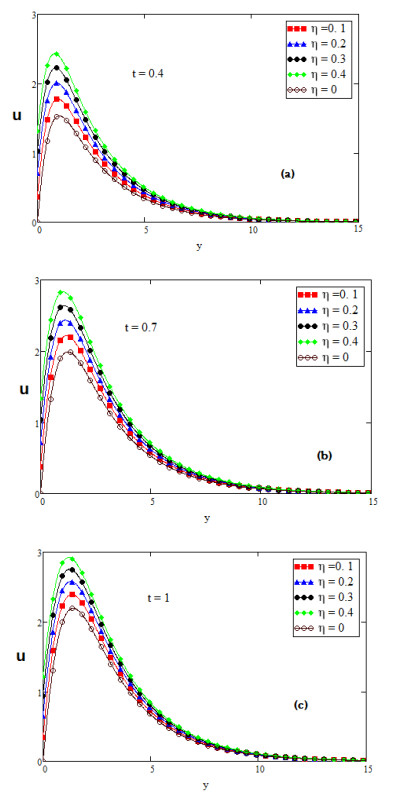
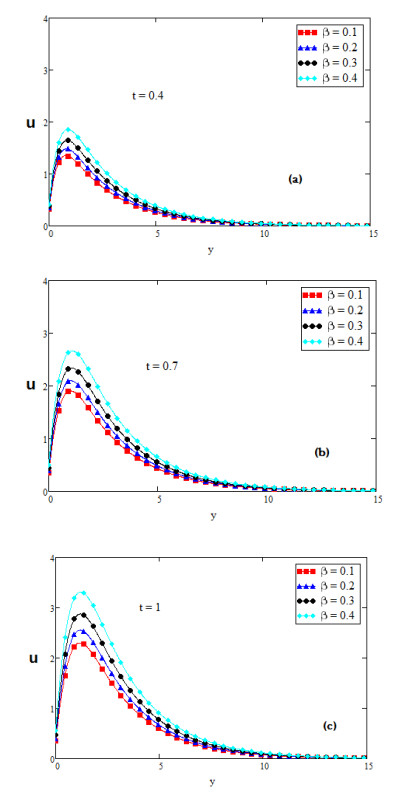
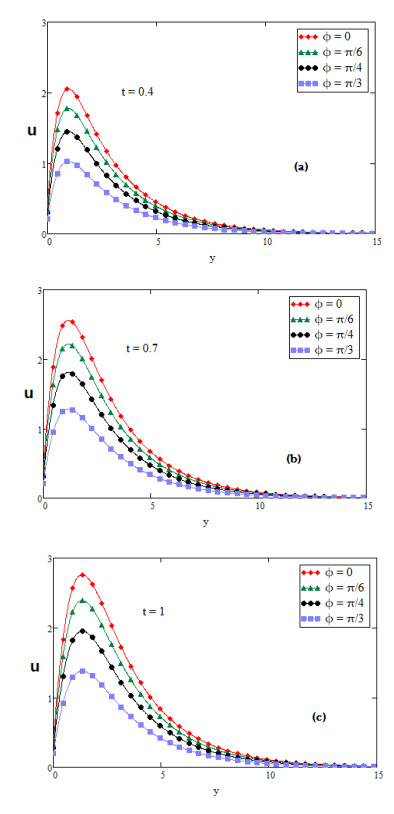
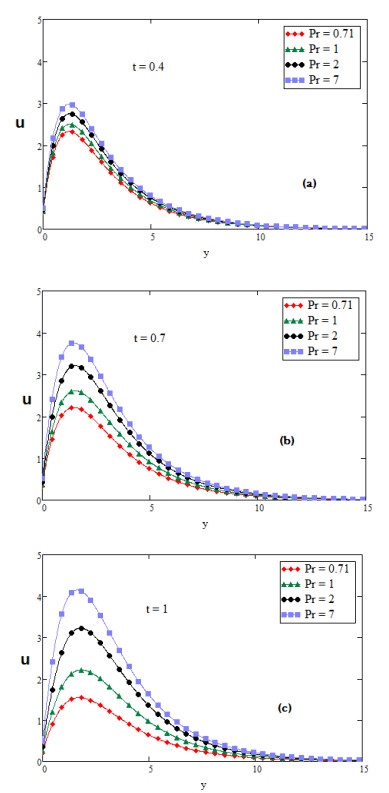
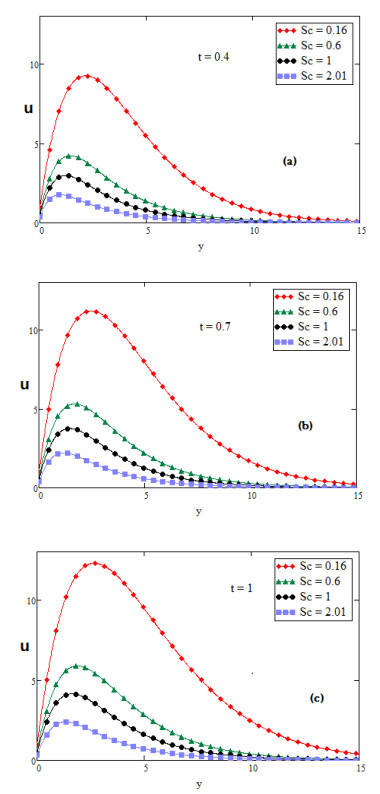
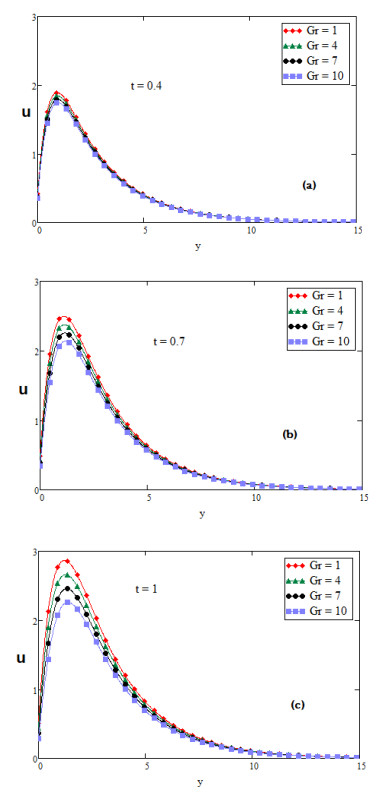
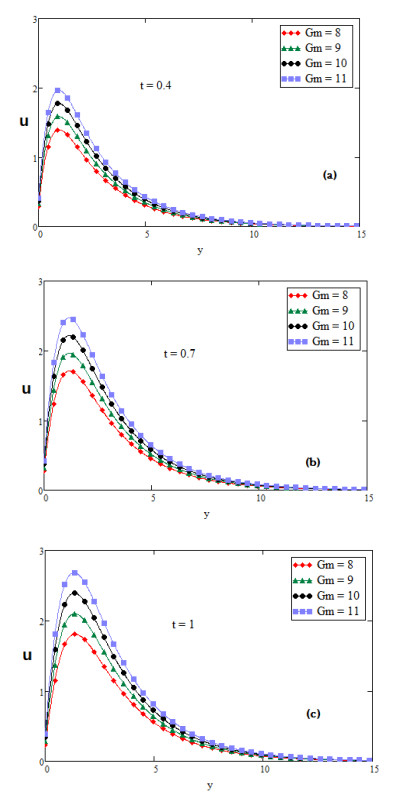
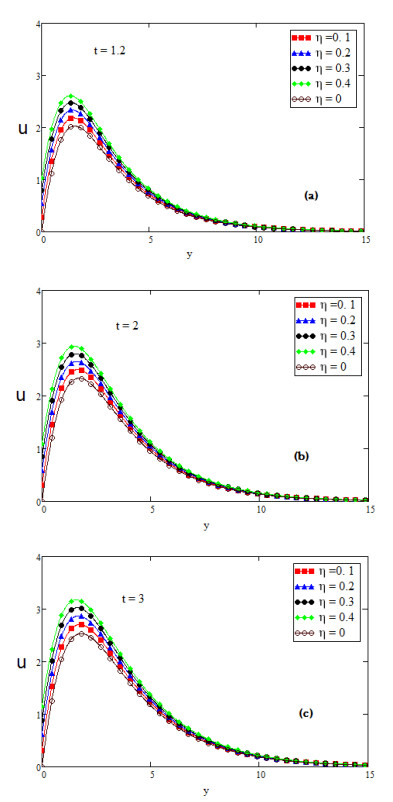
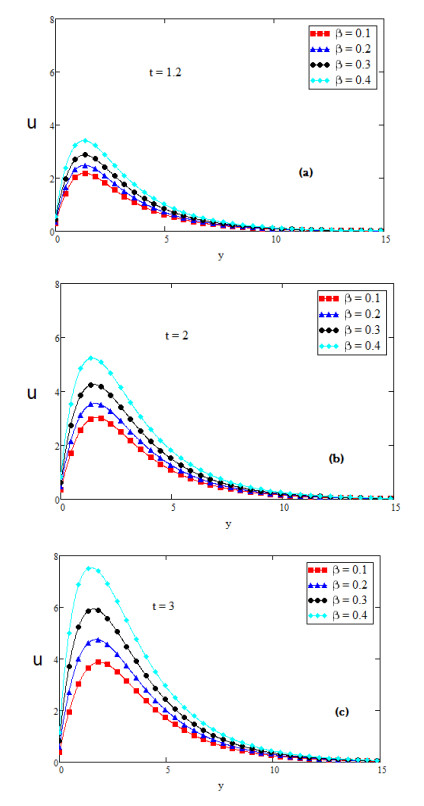
For the physical illustration of the studied problem, the values of temperature, velocity and concentration profiles are calculated, and displayed graphically for several values of distinct parameters such as Prandtl number $\Pr$ , second grade parameter $\alpha$ , inclination parameter $\phi$ , fractional parameter $\beta$ , Schmidt number $Sc$ , thermal Grashof number $Gr$ , mass Grashof number $Gm$ and slip parameter $\eta$ . In Figures (2-14); graphs (a), (b) and (c) discuss the nature of temperature, concentration, velocity, nusselt number and Sherwood number for diverse values of time $t$ . The effect of slip parameter is shown in . The fluid velocity is accelerated if the value of slip parameter $\eta$ is increased. The speed of fluid is high near the plate and the boundary layer thickness rises for large value of $t$ . It is also depicted in that the fluid velocity with slip at the wall is higher than the fluid velocity with no slip at the wall. is plotted to perceive the effect of fractional parameter $\beta$ . It has been seen that the motion of Fluid rises and displays maximum value near the plate for large values of fractional parameter $\beta$ . It is obvious from that growing values of inclination parameter $\phi$ decelerates the motion of fluid. It is observed from that the fluid velocity rises for large value of Prandtl number $(\Pr)$ . shows that viscous forces overcome the diffusional effects for large value of Schmidt number $Sc$ . Mass transfer by diffusion and the relative effectiveness momentum in the concentration and velocity in free convection flow regimes are represented by Schmidt number. If we increase the value of $Sc$ then momentum diffusion will counteract, molecular diffusivity will be reduced and viscosity effects will accelerated. Therefore the flow will be decreased for large value of $Sc$ as shown in . Ramping of the enclosing channel walls can help to decelerate velocities, which is an important feature, for example in achieving better flow control in nuclear engineering applications. The effect of thermal Grashof number $Gr$ is shown in . It is perceived that the fluid velocity is falling, if we increase the value of thermal Grashof number $Gm$ . The thermal Grashof number is the ratio of thermal buoyancy force to viscous force, which causes free convection. shows the influence of mass Grashof number $Gm$ . The mass Grashof number is the ratio of mass buoyancy force to viscous force, which causes free convection. It is perceived that the fluid velocity is increasing, if we increase the value of mass Grashof number $Gm$ . In Figure 2 to Figure 8 we discussed the behavior of velocity with different values of physical parameters for ramped wall temperature. It is clearly seen from and that growing values of fractional parameter $\beta$ and slip parameter $\eta$ , increases the motion of fluid in case of constant wall temperature. Furthermore, it has been analyzed that the motion of fluid is increasing by increasing time $t$ .

Figure 2. Velocity outline for distinct values of slip parameter

$\eta$ and time

$t$ , (a)

$t = 0.4$ , (b)

$t = 0.7$ and (c)

$t = 1$ with

$Pr = 7$ and

$Sc = 2.01$ corresponding to ramped wall temperature.

DownLoad: Full-Size Img PowerPoint

Figure 3. Plots of velocity for distinct values of fractional parameter

$\beta$ and time

$t$ , (a)

$t = 0.4$ , (b)

$t = 0.7$ and (c)

$t = 1$ with

$Pr = 7$ and

$Sc = 2.01$ corresponding to ramped wall temperature.

DownLoad: Full-Size Img PowerPoint

Figure 4. Velocity profile for distinct values of inclination parameter

$\phi$ and time

$t$ , (a)

$t = 0.4$ , (b)

$t = 0.7$ and (c)

$t = 1$ with

$Pr = 7$ and

$Sc = 2.01$ corresponding to ramped wall temperature.

DownLoad: Full-Size Img PowerPoint

Figure 5. Variations in velocity outline for distinct values of Prandtl number

$\Pr$ and time

$t$ , (a)

$t = 0.4$ , (b)

$t = 0.7$ and (c)

$t = 1$ with

$Sc = 1$ with respect to ramped wall temperature.

DownLoad: Full-Size Img PowerPoint

Figure 6. Nature of velocity profile for distinct values of Schmidt number

$Sc$ and time

$t$ , (a)

$t = 0.4$ , (b)

$t = 0.7$ and (c)

$t = 1$ with

$Pr = 7$ with respect to ramped wall temperature.

DownLoad: Full-Size Img PowerPoint

Figure 7. Velocity outline for distinct values of Grashof number of thermal

$Gr$ and time

$t$ , (a)

$t = 0.4$ , (b)

$t = 0.7$ and (c)

$t = 1$ with

$Pr = 7$ and

$Sc = 2.01$ with respect to ramped wall temperature.

DownLoad: Full-Size Img PowerPoint

Figure 8. Velocity outline for distinct values of Grashof number of mass

$Gm$ and time

$t$ , (a)

$t = 0.4$ , (b)

$t = 0.7$ and (c)

$t = 1$ with

$Pr = 7$ and

$Sc = 2.01$ with respect to ramped wall temperature.

DownLoad: Full-Size Img PowerPoint

Figure 9. Plots of velocity for diverse values of slip parameter

$\eta$ and time

$t$ , (a)

$t = 1.2$ , (b)

$t = 2.0$ and (c)

$t = 3$ with

$Pr = 7$ and

$Sc = 2.01$ with respect to stepped temperature of the plate.

DownLoad: Full-Size Img PowerPoint

Figure 10. Velocity profile for distinct values of fractional parameter

$\beta$ and time

$t$ , (a)

$t = 1.2$ , (b)

$t = 2.0$ and (c)

$t = 3$ with

$Pr = 7$ and

$Sc = 2.01$ with respect to ramped temperature of the plate.

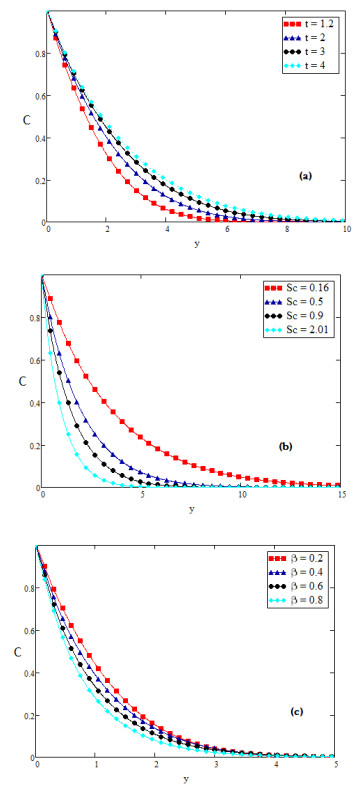
DownLoad: Full-Size Img PowerPoint

demonstrates the variants in temperature portrayal for numerous values of $\Pr$ and fractional parameter $\beta$ . It has been perceived that growing values of $\Pr$ decay the variations of temperature while increases for large value of fractional parameter $\beta$ . Physically, it is true due to the fact that if we increase the $\Pr$ then viscosity of the fluid is increasing and thermal conductivity is decreasing and hence decreases the thickness of thermal boundary-layer. It is evident from that temperature is accelerated for growing value of time $t$ . In we discussed the nature of concentration for distinct values of fractional parameter $\beta$ , time $t$ and Schmidt number $Sc$ . It is clear from that for large value of Schmidt number $Sc$ and fractional parameter $\beta$ , concentration is decreasing while increasing for greater value of time $t$ .

Figure 11. Temperature outline for distinct values of Prandtl number

$\Pr$ , fractional parameter

$\beta$ and time

$t$ with respect to ramped temperature of the plate.

DownLoad: Full-Size Img PowerPoint

Figure 12. Concentration outline for different value fractional parameter

$\beta$ , Schmidt number

$Sc$ and

$t$ of with respect to isothermal temperature of plate.

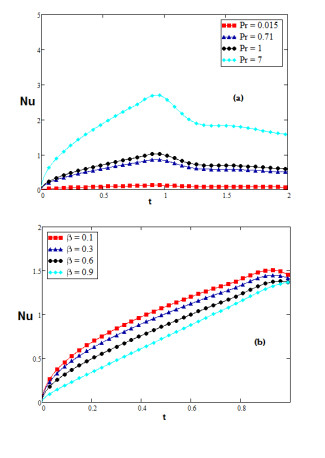
DownLoad: Full-Size Img PowerPoint

displays the modification of Nusselt number for diverse values of $\beta$ and $\Pr$ . It also perceived that Nusselt number accelerates for higher value of $\Pr$ and decelerates for higher value of fractional parameter $\beta$ .

Figure 13. Modification of Nusselt number for numerous values of fractional parameter

$\beta$ and Prandtl number

$\Pr$ with respect to ramped temperature of the plate.

DownLoad: Full-Size Img PowerPoint

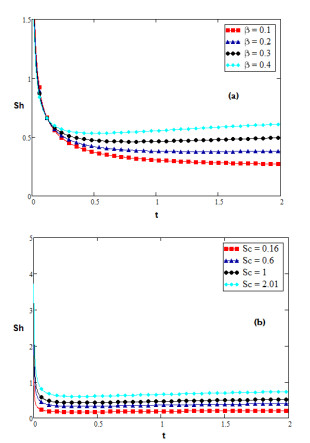
displays the modification of Sherwood number for distinct values of $\beta$ and $\Pr$ . It is clearly noted from that Sherwood number is enhancing for large value of $\Pr$ and fractional parameter $\beta$ .

Figure 14. Modification of Sherwood number

$Sh$ for distinct values of fractional parameter

$\beta$ and Schmidt number

$SC$ with respect to ramped temperature of the plate.

DownLoad: Full-Size Img PowerPoint

5. Numerical tables

Numerical results of the rate of shear stress (skin friction $\tau$ ), heat transfer (Nusselt number $Nu$ ) and mass transfer (Sherwood number $Sh$ ) at the plate are expressed in to for different values of $(\eta)$ , $(\Pr)$ , $(Sc)$ , $(Gm)$ , $(Gr)$ , $(\alpha)$ , $(\beta)$ , $(\phi)$ and $(t)$ in case of ramped wall temperature. It is noted from that growing values of $(Gm)$ , $(Gr)$ , $(\beta)$ and $(t)$ accelerates the skin friction $(\tau)$ , while decelerates for growing values of $(\eta)$ , $(\Pr)$ , $(\alpha)$ , $(\phi)$ and $(Sc)$ . It is detected from that growing values of $(\Pr)$ and $(t)$ accelerates the Nusselt number $(Nu)$ , while decelerates for growing values of $(\beta)$ . It is noticeable from that Sherwood number $(Sh)$ enhances for growing value of $(Sc)$ and $(\beta)$ , while decreases for large value of $(t)$ .

Table 1. Skin-friction.

$t$	$\alpha$	$\beta$	$\eta$	$\Pr$	$Sc$	$Gm$	$Gr$	$\phi$	$\tau$
$0.3$	$5$	$0.6$	$0.5$	$7$	$2.01$	$2$	$4$	$\frac{\pi}{6}$	$0.645$
$0.3$	$5$	$0.6$	$0.5$	$7$	$2.01$	$2$	$4$	$\frac{\pi}{3}$	$0.373$
$0.3$	$5$	$0.6$	$0.5$	$7$	$2.01$	$2$	$5$	$\frac{\pi}{6}$	$0.689$
$0.3$	$5$	$0.6$	$0.5$	$7$	$2.01$	$3$	$4$	$\frac{\pi}{6}$	$0.88$
$0.3$	$5$	$0.6$	$0.5$	$7$	$0.6$	$2$	$4$	$\frac{\pi}{6}$	$1.371$
$0.3$	$5$	$0.6$	$0.5$	$0.015$	$2.01$	$2$	$4$	$\frac{\pi}{6}$	$1.818$
$0.3$	$5$	$0.6$	$0.7$	$7$	$2.01$	$2$	$4$	$\frac{\pi}{6}$	$0.598$
$0.3$	$5$	$0.8$	$0.5$	$7$	$2.01$	$2$	$4$	$\frac{\pi}{6}$	$1.445$
$0.3$	$6$	$0.6$	$0.5$	$7$	$2.01$	$2$	$4$	$\frac{\pi}{6}$	$0.637$
$0.8$	$5$	$0.6$	$0.5$	$7$	$2.01$	$2$	$4$	$\frac{\pi}{6}$	$1.179$

| Show Table

DownLoad: CSV

Table 2. Nusselt number.

$t$	$\beta$	$Nu$	$Nu$	$Nu$	$Nu$
		$\Pr = 0.015$	$\Pr = 0.71$	$\Pr = 1$	$\Pr = 7$
$0.1$	$0.1$	$0.042$	$0.287$	$0.34$	$0.9$
$0.1$	$0.4$	$0.035$	$0.238$	$0.283$	$0.748$
$0.1$	$0.7$	$0.026$	$0.177$	$0.21$	$0.557$
$0.4$	$0.1$	$0.084$	$0.579$	$0.688$	$1.819$
$0.4$	$0.4$	$0.074$	$0.507$	$0.601$	$1.591$
$0.4$	$0.7$	$0.062$	$0.424$	$0.503$	$1.33$
$0.7$	$0.1$	$0.113$	$0.774$	$0.919$	$2.431$
$0.7$	$0.4$	$0.103$	$0.708$	$0.84$	$2.223$
$0.7$	$0.7$	$0.093$	$0.642$	$0.762$	$2.015$

| Show Table

DownLoad: CSV

Table 3. Sherwood number.

$t$	$\beta$	$Sh$	$Sh$	$Sh$	$Sh$
		$Sc = 0.16$	$Sc = 0.6$	$Sc = 1$	$Sc = 2.01$
$1.2$	$0.1$	$0.082$	$0.16$	$0.206$	$0.292$
$1.2$	$0.4$	$0.16$	$0.309$	$0.399$	$0.566$
$1.2$	$0.7$	$0.256$	$0.495$	$0.64$	$0.907$
$1.5$	$0.1$	$0.079$	$0.154$	$0.198$	$0.281$
$1.5$	$0.4$	$0.165$	$0.319$	$0.412$	$0.584$
$1.5$	$0.7$	$0.264$	$0.511$	$0.659$	$0.935$
$1.8$	$0.1$	$0.077$	$0.15$	$0.194$	$0.274$
$1.8$	$0.4$	$0.169$	$0.328$	$0.423$	$0.6$
$1.8$	$0.7$	$0.27$	$0.523$	$0.675$	$0.956$

| Show Table

DownLoad: CSV

6. Conclusions

The second grade fluid which is unsteady and incompressible in nature flowing over an infinite heated inclined plate under the influence of slip condition are studied. CF derivative is used in the constitutive equations of heat and mass transfer respectively. An analytical solution is obtained by integral transform method (Laplace transformation) for velocity, concentration and temperature fields for both stepped and ramped wall temperature. Expression for Sherwood and Nusselt numbers with fractional parameter are obtained by differentiating the analytical solutions of fluid temperature and concentration. The effect of different parameters i.e. Caputo-Fabrizio fractional parameter $\beta$ , second grade parameter $\alpha$ , slip parameter $\eta$ , Prandtl number $\Pr$ , Schmidt number $Sc$ , thermal Grashof number $Gr$ and mass Grashof number $Gm$ are graphically studied. Following are the some observations and concluding remarks :

1. The motion of fluid accelerates for growing value of slip parameter $\eta$ in case of ramped as well as stepped wall temperature.

2. The motion of fluid is increasing and displays maximum value near the plate for large values of fractional parameter $\beta$ in case of ramped as well as stepped wall temperature.

3. Growing values of inclination parameter $\phi$ and thermal Grashof number $Gr$ decelerates the motion of fluid.

4. viscous forces overcome the diffusional effects for large value of Schmidt number $Sc$ . Mass transfer by diffusion and the relative effectiveness momentum in the concentration and velocity in free convection flow regimes are represented by Schmidt number. Effectively, therefore momentum diffusion will counteract for large value of $Sc$ , since molecular diffusivity will be decelerated and viscosity effects will accelerated. Therefore the flow will be decreased for large value of $Sc$ . Ramping of the enclosing channel walls can help to decelerate velocities, which is an important feature, for example in achieving better flow control in nuclear engineering processes.

5. The fluid velocity is accelerated for large value of Prandtl number $\Pr$ and Grashof number of mass $Gm$ .

6. Growing values of Prandtl number $\Pr$ decay the variations of temperature and Nusselt number.

7. Temperature, Concentration and Nusselt number are decreasing for large value of fractional parameter $\beta$ .

Conflict of interest

The authors declare no conflict of interest.

Appendix

1. The Caputo-Fabrizio (CF) fractional operator ^[41,42] can be written as

$\begin{equation*} D^{\beta}_{t}T\left(y, t\right) = \frac{1}{1-\beta}\int_{0}^{t}\exp\left(\frac{-\beta(t-\tau)}{1-\beta}\right)\frac{\partial{T\left(y, \tau\right)}}{\partial{\tau}}d\tau \end{equation*}$

The laplace transform of $D^{\beta}_{t}T(y, t)$ can be given as

$\begin{equation*} {\cal L}{{D^{\beta}_{t}T\left(y, t\right)}} = \frac{sT\left(y, s\right)}{\left(1-\beta\right)s+\beta} \end{equation*}$

2. The Caputo fractional derivative ^[41] can be written as

$\begin{equation*} {D^{(\beta)}_{t}f\left(t\right)} = \frac{1}{\Gamma(1-\beta)}\int_{a}^{t}\frac{f\dot(\tau)}{(t-\tau)^{\beta}}d\tau \end{equation*}$

Where $\beta\in [0, 1]$ and $a\in [-\infty, t]$ , $f\in H^{1}\left(a, b\right), b>a$

The new definition of Caputo fractional time derivative ^[41] is

$\begin{equation*} {D^{(\beta)}_{t}f\left(t\right)} = \frac{M(\beta)}{(1-\beta)}\int_{a}^{t}f\dot(\tau)\exp[\frac{-\beta(t-\tau)}{1-\beta}]d\tau. \end{equation*}$

In the above equation $M(\beta)$ is a normalization function such that $M(0) = M(1) = 1$ .

3. The Riemann-Liuville fractional derivative ^[43] can be written as:

If n is a positive integer and $\beta\in [n-1, n)$ , the $\beta$ derivative of a function $f$ is given by

$\begin{equation*} {D^{\beta}_{a}f\left(t\right)} = \frac{1}{\Gamma(n-a)}\frac{d^{n}}{dt^{n}}\int_{a}^{t}\frac{f(\tau)}{(t-\tau)^{a-n+1}}d\tau \end{equation*}$

References

[1]	B. D. Coleman and W. Noll, An approximation theorem for functionals, with applications in continuum mechanics, Arch. Ration. Mech. Anal., 6 (1960), 355-370. doi: 10.1007/BF00276168
[2]	M. E. Erdoğan and C. E. Imrak, On some unsteady flows of a non-Newtonian fluid, App. Math. Mod., 31 (2007), 170-180. doi: 10.1016/j.apm.2005.08.019
[3]	A. J. Chamkha, Hydromagnetic natural convection from an isothermal inclined surface adjacent to a thermally stratified porous medium, Int. J. Eng. Sci., 35 (1997), 975-986. doi: 10.1016/S0020-7225(96)00122-X
[4]	T. Kimura, M. Takeuchi, N. Nagai, et al. Heat transfer in an inclined enclosure with an inner rotating plate, Heat Transfer-Asian Research: Co-sponsored by the Society of Chemical Engineers of Japan and the Heat Transfer Division of ASME, 30 (2001), 331-340.
[5]	C. J. Toki, An analytical solution for the unsteady free convection flow near an inclined plate in a rotating system, Differential Equations and Control Proc., 3 (2009), 35-43.
[6]	K. Diethelm, The analysis of fractional differential equations: An application-oriented exposition using differential operators of Caputo type, Springer Science & Business Media, 2010.
[7]	M. A. Imran, N. A. Shah, M. Aleem, et al. Heat transfer analysis of fractional second-grade fluid subject to Newtonian heating with Caputo and Caputo-Fabrizio fractional derivatives: A comparison, Eur. Phys. J. Plus., 132 (2017), 340-358. doi: 10.1140/epjp/i2017-11606-6
[8]	C. H. R. Friedrich, Relaxation and retardation functions of the Maxwell model with fractional derivatives, Rheol. Acta, 30 (1991), 151-158. doi: 10.1007/BF01134604
[9]	A. Gemant, XLV. On fractional differentials, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 25 (1938), 540-549. doi: 10.1080/14786443808562036
[10]	L. I. Palade, P. Attane, R. R. Huilgol, et al. Anomalous stability behavior of a properly invariant constitutive equation which generalises fractional derivative models, Int. J. Eng. Sci., 37 (1999), 315-329. doi: 10.1016/S0020-7225(98)00080-9
[11]	D. Vieru, C. Fetecau and C. Fetecau, Time-fractional free convection flow near a vertical plate with Newtonian heating and mass diffusion, Therm. Sci., 19 (2015), 85-98. doi: 10.2298/TSCI15S1S85V
[12]	A. A. Zafar and C. Fetecau, Flow over an infinite plate of a viscous fluid with non-integer order derivative without singular kernel, Alexandria Eng. J., 55 (2016), 2789-2796. doi: 10.1016/j.aej.2016.07.022
[13]	N. A. Shah, A. A. Zafar and C. Fetecau, Free convection flows over a vertical plate that applies shear stress to a fractional viscous fluid, Alexandria Eng. J., 57 (2017), 2529-2540. doi: 10.1016/j.aej.2017.08.023
[14]	M. A. Imran, I. Khan, M. Ahmad, et al. Heat and mass transport of differential type fluid with non-integer order time-fractional Caputo derivatives, J. Mol. Liq., 229 (2017), 67-75. doi: 10.1016/j.molliq.2016.11.095
[15]	M. Nazar, M. Ahmad, M. A. Imran, et al. Double convection of heat and mass transfer flow of MHD generalized second grade fluid over an exponentially accelerated infinite vertical plate with heat absorption, J. Math. Anal., 8 (2017), 28-44.
[16]	S. U. Haq, I. Khan, F. Ali, et al. Free convection flow of a second-grade fluid with ramped wall temperature, Heat Transf. Res., 45 (2014), 579-588. doi: 10.1615/HeatTransRes.2014007241
[17]	S. U. Haq, S. Ahmad, D. Vieru, et al. Unsteady magnetohydrodynamic free convection flow of a second grade fluid in a porous medium with ramped wall temperature, PLoS One, 9 (2014), e88766.
[18]	S. Gupta, D. Kumar and J. Singh, Analytical study for MHD flow of Williamson nanofluid with the effects of variable thickness, nonlinear thermal radiation and improved Fourier's and Fick's laws, SN Appl. Sci., 2 (2020), 438.
[19]	S. Gupta, D. Kumar and J. Singh, MHD three dimensional boundary layer flow and heat transfer of Water driven Copper and Alumina nanoparticles induced by convective conditions, Int. J. Modern Phys. B, 33 (2019), 1950307.
[20]	S. Gupta, D. Kumar and J. Singh, MHD mixed convective stagnation point flow and heat transfer of an incompressible nanofluid over an inclined stretching sheet with chemical reaction and radiation, Int. J. Heat Mass Tran., 118 (2018), 378-387. doi: 10.1016/j.ijheatmasstransfer.2017.11.007
[21]	J. Losada and J. J. Nieto, Properties of a New Fractional Derivative without Singular Kernel, Progr. Fract. Differ. Appl., 1 (2015), 87-92.
[22]	Y. Cenesiz, D. Baleanu, A. Kurt, et al. New exact solutions of Burger's type equations with conformable derivative, WAVE RANDOM COMPLEX, 27 (2017), 103-116. doi: 10.1080/17455030.2016.1205237
[23]	Q. Al-Mdallal, K. A. Abro and I. Khan, Analytical Solutions of Fractional Walter's B Fluid with Applications, Complexity, 2018 (2018), 1-10. doi: 10.1155/2018/8131329
[24]	T. Abdeljawad, Fractional operators with exponential kernels and a Lyapunov type inequality, Adv. Differ. Equ-NY, 2017 (2017), 313.
[25]	T. Abdeljawad, Q. Al-Mdallal and M. A. Hajji, Arbitrary order fractional difference operators with discrete exponential kernels and applications, Discrete Dyn. Nat. Soc., 2017.
[26]	A. Shaikh, A. Tassaddiq, K. S. Nisar, et al. Analysis of differential equations involving CaputoFabrizio fractional operator and its applications to reaction-diffusion equations, Adv. Differ. EquNY, 2019 (2019), 178.
[27]	A. Atangana, The Caputo-Fabrizio fractional derivative applied to a singular perturbation problem, Int. J. Math. Mod. Num. Opt., 9 (2019), 241-253.
[28]	M. Yavuz and N. Ozdemir, Comparing the new fractional derivative operators involving exponential and Mittag-Leffler kernel, Discrete Cont. Dyn-S, 13 (2020), 995-1006.
[29]	D. Kumar, J. Singh, K. Tanwar, et al. A new fractional exothermic reactions model having constant heat source in porous media with power, exponential and Mittag-Leffler laws, Int. J. Heat Mass Tran., 138 (2019), 1222-1227. doi: 10.1016/j.ijheatmasstransfer.2019.04.094
[30]	D. Kumar, J. Singh, M. A. Qurashi, et al. A new fractional SIRS-SI malaria disease model with application of vaccines, anti-malarial drugs, and spraying, Adv. Differ. Equ., 2019 (2019), 278.
[31]	D. Kumar, J. Singh and D. Baleanu, A new numerical algorithm for fractional Fitzhugh-Nagumo equation arising in transmission of nerve impulses, Nonlinear Dyn., 1 (2018), 307-317. doi: 10.1007/s11071-017-3870-x
[32]	J. Singh, D. Kumar and D. Baleanu, New aspects of fractional Biswas-Milovic model with MittagLeffler law, Math. Model. Nat. Phenom., 14 (2019), 303. doi: 10.1051/mmnp/2018068
[33]	S. Bhatter, A. Mathur, D. Kumar, et al. A new analysis of fractional Drinfeld-Sokolov-Wilson model with exponential memory, Phys. A, 537 (2020), 122578. doi: 10.1016/j.physa.2019.122578
[34]	J. Singh, A new analysis for fractional rumor spreading dynamical model in a social network with Mittag-Leffler law, Chaos, 29 (2019), 013137. doi: 10.1063/1.5080691
[35]	D. Kumar, J. Singh and D. Baleanu, On the analysis of vibration equation involving a fractional derivative with Mittag-Leffler law, Math. Meth. Appl. Sci., 43 (2019), 443-457. doi: 10.1002/mma.5903
[36]	M. A. Abd EL-NABY, E. M. E. Elbarbary and N. Y. Abdelazem, Finite difference solution of radiation effects on MHD unsteady free-convection flow over vertical plate with variable surface temperature, J. Appl. Math., 2003 (2003), 65-86. doi: 10.1155/S1110757X0320509X
[37]	M. E. Erdogan, On unsteady motions of a second-order fluid over a plane wall, Int. J. NonLin. Mech., 38 (2003), 1045-1051. doi: 10.1016/S0020-7462(02)00051-3
[38]	B. I. Henry, T. A. M. Langlands and P. Straka, An introduction to fractional diffusion, Complex Physical, Biophysical and Econophysical Systems, (2010), 37-89.
[39]	J. Hristov, Transient heat diffusion with a non-singular fading memory, Therm. Sci., 20 (2016), 757-762. doi: 10.2298/TSCI160112019H
[40]	J. Hristov, Derivatives with non-singular kernels from the Caputo-Fabrizio definition and beyond: Appraising analysis with emphasis on diffusion models, Front. Fract. Calc., 1 (2017), 270-342.
[41]	M. Caputo and M. Fabrizio, A new Definition of Fractional Derivative without Singular Kernel, Prog. Fract. Differ. Appl., 2 (2015), 73-85.
[42]	S. Aman, Q. Al-Mdallal and I. Khan, Heat transfer and second order slip effect on MHD flow of fractional Maxwell fluid in a porous medium, J. King Saud Univ. Sci., 2018.
[43]	A. Kurt, Y. Cenesiz, O. Tasbozan, On the Solution of Burgers Equation with the New Fractional Derivative, Open Phys., 13 (2015), 355-360. doi: 10.1515/phys-2015-0045

This article has been cited by:

1.	Talha Anwar, Poom Kumam, Ilyas Khan, Phatiphat Thounthong, An exact analysis of radiative heat transfer and unsteady MHD convective flow of a second‐grade fluid with ramped wall motion and temperature, 2021, 50, 2688-4534, 196, 10.1002/htj.21871
2.	Poom Kumam, Asifa Tassaddiq, Wiboonsak Watthayu, Zahir Shah, Talha Anwar, Modeling and simulation based investigation of unsteady MHD radiative flow of rate type fluid; a comparative fractional analysis, 2021, 03784754, 10.1016/j.matcom.2021.02.005
3.	Talha Anwar, Poom Kumam, Phatiphat Thounthong, Fractional Modeling and Exact Solutions to Analyze Thermal Performance of Fe3O4-MoS2-Water Hybrid Nanofluid Flow Over an Inclined Surface With Ramped Heating and Ramped Boundary Motion, 2021, 9, 2169-3536, 12389, 10.1109/ACCESS.2021.3051740
4.	Talha Anwar, Poom Kumam, Ilyas Khan, Phatiphat Thounthong, Generalized Unsteady MHD Natural Convective Flow of Jeffery Model with ramped wall velocity and Newtonian heating; A Caputo-Fabrizio Approach, 2020, 68, 05779073, 849, 10.1016/j.cjph.2020.10.018
5.	T Mehta, R Mehta, M Kumar, Mathematical Analysis of Radiating Viscoelastic Unsteady MHD Fluid Flow through an Absorbent Media between Upstanding Equidistant plates with Joule Heating Impact, 2021, 1099, 1757-8981, 012045, 10.1088/1757-899X/1099/1/012045
6.	Talha Anwar, Poom Kumam, Ilyas Khan, Phatiphat Thounthong, Thermal analysis of MHD convective slip transport of fractional Oldroyd-B fluid over a plate, 2021, 1385-2000, 10.1007/s11043-021-09495-z
7.	TALHA ANWAR, POOM KUMAM, ILYAS KHAN, PHATIPHAT THOUNTHONG, FRACTIONAL MAGNETOHYDRODYNAMIC FLOW OF A SECOND GRADE FLUID IN A POROUS MEDIUM WITH VARIABLE WALL VELOCITY AND NEWTONIAN HEATING, 2021, 29, 0218-348X, 2150060, 10.1142/S0218348X21500602
8.	S. Das, A.S. Banu, R.N. Jana, Delineating impacts of non-uniform wall temperature and concentration on time-dependent radiation-convection of Casson fluid under magnetic field and chemical reaction, 2021, ahead-of-print, 1708-5284, 10.1108/WJE-11-2020-0607
9.	Talha Anwar, Poom Kumam, Phatiphat Thounthong, Kanokwan Sitthithakerngkiet, Nanoparticles shape effects on thermal performance of Brinkman-type ferrofluid under heat injection/consumption and thermal radiation: A fractional model with non-singular kernel and non-uniform temperature and velocity conditions, 2021, 335, 01677322, 116107, 10.1016/j.molliq.2021.116107
10.	Mehmet Yavuz, Ndolane Sene, Mustafa Yıldız, Analysis of the Influences of Parameters in the Fractional Second-Grade Fluid Dynamics, 2022, 10, 2227-7390, 1125, 10.3390/math10071125
11.	Talha Anwar, Poom Kumam, Phatiphat Thounthong, A comparative fractional study to evaluate thermal performance of NaAlg–MoS2–Co hybrid nanofluid subject to shape factor and dual ramped conditions, 2022, 61, 11100168, 2166, 10.1016/j.aej.2021.06.085
12.	Wajeeha Iftikhar, Sami Ul Haq, Saeed Ullah Jan, Ilyas Khan, Abdullah Mohamed, Caputo–Fabrizio fractional model of MHD second grade fluid with Newtonian heating and heat generation, 2022, 12, 2045-2322, 10.1038/s41598-022-26080-7
13.	Talha Anwar, Poom Kumam, A fractal fractional model for thermal analysis of GO − NaAlg − Gr hybrid nanofluid flow in a channel considering shape effects, 2022, 31, 2214157X, 101828, 10.1016/j.csite.2022.101828
14.	Imran Siddique, Sehrish Ayaz, Fahd Jarad, Marcus Aguiar, Dufour Effect on Transient MHD Double Convection Flow of Fractionalized Second-Grade Fluid with Caputo–Fabrizio Derivative, 2021, 2021, 1099-0526, 1, 10.1155/2021/7625031
15.	Talha Anwar, Poom Kumam, Shah Muhammad, New fractional model to analyze impacts of Newtonian heating, shape factor and ramped flow function on MgO–SiO2–Kerosene oil hybrid nanofluid, 2022, 38, 2214157X, 102361, 10.1016/j.csite.2022.102361
16.	Muhammad Arif, Poom Kumam, Wiyada Kumam, Ilyas Khan, Muhammad Ramzan, A fractional model of Casson fluid with ramped wall temperature: Engineering applications of engine oil, 2021, 3, 2577-7408, 10.1002/cmm4.1162
17.	Asima Razzaque, Anam Rani, Mudassar Nazar, Dumitru Vieru, Generalization of Thermal and Mass Fluxes for the Flow of Differential Type Fluid with Caputo–Fabrizio Approach of Fractional Derivative, 2021, 2021, 1099-0526, 1, 10.1155/2021/6052437
18.	Talha Anwar, Poom Kumam, Zahir Shah, Kanokwan Sitthithakerngkiet, Significance of Shape Factor in Heat Transfer Performance of Molybdenum-Disulfide Nanofluid in Multiple Flow Situations; A Comparative Fractional Study, 2021, 26, 1420-3049, 3711, 10.3390/molecules26123711
19.	Nazish Iftikhar, Muhammad Bilal Riaz, Jan Awrejcewicz, Ali Akgül, Effect of Magnetic Field with Parabolic Motion on Fractional Second Grade Fluid, 2021, 5, 2504-3110, 163, 10.3390/fractalfract5040163
20.	Mushtaq Ahmad, Muhammad I Asjad, Kottakkaran S Nisar, Ilyas Khan, Mechanical and thermal energies transport flow of a second grade fluid with novel fractional derivative, 2021, 0954-4089, 095440892110535, 10.1177/09544089211053561
21.	Zaib Nisa, Ahmad Shafique, Mudassar Nazar, Muhammad Asjad, Khaled Mahmoud, Abdullah Alsubai, Mustafa Inc, A novel fractional study on free convection flow of Brinkmann hybrid nanofluid over an inclined plate, 2022, 26, 0354-9836, 229, 10.2298/TSCI22S1229N
22.	Anwar Ali, Sami Ul Haq, Syed Inayat Ali Shah, Ilyas Khan, Amnah S. Aljohani, Saeed Ullah Jan, Mulugeta Andualem, Ardashir Mohammadzadeh, Heat Transfer Analysis of Generalized Nanofluid with MHD and Ramped Wall Temperature Using Caputo–Fabrizio Derivative Approach, 2023, 2023, 1563-5147, 1, 10.1155/2023/8834891
23.	Mudassar Nazar, Shajar Abbas, Sumbal Asghar, Salman Saleem, Hajar Abutuqayqah, Hakim AL Garalleh, Zuhair Jastaneyah, Comparison of unsteady MHD flow of second grade fluid by two fractional derivatives, 2024, 1040-7782, 1, 10.1080/10407782.2024.2374536
24.	Ikram Ullah, Sami Ul Haq, Zar Ali Khan, Unsteady MHD flow of a fractional second grade fluid in a channel passing through a porous medium subject to a time-dependent motion of the bottom plate, 2024, 38, 0217-9792, 10.1142/S0217979224502138
25.	Zafar H Khan, Oluwole D Makinde, Muhammad Usman, Rashid Ahmad, Waqar A Khan, Zaitang Huang, Inherent irreversibility in unsteady magnetohydrodynamic nanofluid flow past a slippery permeable vertical plate with fractional-order derivative, 2023, 10, 2288-5048, 2049, 10.1093/jcde/qwad090
26.	Muhammad Atif khan, Sami Ul Haq, Farhad Ali, Analysis of Newtonian heating in fractional hybrid nanofluid with the influence of transverse magnetic field, 2024, 106, 0142727X, 109293, 10.1016/j.ijheatfluidflow.2024.109293
27.	P. Chinnasamy, R. Sivajothi, S. Sathish, Mohamed Abbas, V. Jeyakrishnan, Rajat Goel, Mohammed S. Alqahtani, K. Loganathan, Peristaltic transport of Sutterby nanofluid flow in an inclined tapered channel with an artificial neural network model and biomedical engineering application, 2024, 14, 2045-2322, 10.1038/s41598-023-49480-9
28.	Qasim Ali, Aziz Ullah Awan, Rajai S. Alassar, Muhammad Amir, Usman Younas, Muhammad Farman, Comprehensive study of tri-hybrid nanofluid flow in a vertical channel with Cu, Al2O3, and TiO2 nanoparticles via fractional dynamics and non-local kernel approach, 2024, 0217-9849, 10.1142/S0217984924504013
29.	Saeed Ullah Jan, Sami Ul Haq, Naseeb Ullah, Wasi Ullah, Ilyas Khan, Heat transfer analysis of generalized second-grade fluid with exponential heating and thermal heat flux, 2023, 13, 2045-2322, 10.1038/s41598-023-44007-8
30.	Amal Al-Hanaya, Munirah Alotaibi, Mohammed Shqair, Ahmed Eissa Hagag, MHD effects on Casson fluid flow squeezing between parallel plates, 2023, 8, 2473-6988, 29440, 10.3934/math.20231507

Reader Comments

Your name:*

Email:*
© 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(4949) PDF downloads(402) Cited by(30)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(14) / Tables(3)

AIMS Mathematics

Heat and mass transfer of fractional second grade fluid with slippage and ramped wall temperature using Caputo-Fabrizio fractional derivative approach

Related Papers:

Abstract

1. Introduction

2. Analysis of the governing problem

3. Analytical solutions

3.1. Solution for ramped temperature

3.2. Solution for concentration profile

3.3. Solution for ramped velocity

3.4. Solution for constant Temperature

3.5. Solution for constant Velocity

3.6. Nusselt number

3.7. Sherwood number

4. Result and discussion

5. Numerical tables

6. Conclusions

Conflict of interest

Appendix

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

Heat and mass transfer of fractional second grade fluid with slippage and ramped wall temperature using Caputo-Fabrizio fractional derivative approach

Related Papers:

Abstract

1. Introduction

2. Analysis of the governing problem

3. Analytical solutions

3.1. Solution for ramped temperature

3.2. Solution for concentration profile

3.3. Solution for ramped velocity

3.4. Solution for constant Temperature

3.5. Solution for constant Velocity

3.6. Nusselt number

3.7. Sherwood number

4. Result and discussion

5. Numerical tables

6. Conclusions

Conflict of interest

Appendix

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog