Low-cost piezoelectric sensors and gamma ray attenuation fabricated from novel polymeric nanocomposites

1.   Introduction

In nature, the collective migration of bird flocks, the gathering migration of fish and cooperation of ant colonies are relatively common. The movement of biological groups has shown that, under conditions of limited environmental information and simple rules, the group system organizes itself into an orderly movement in which all individuals move at the same speed and maintain cohesion or geometric formation. Since the second half of the 20th century, the flocking behavior of multi-agent systems has attracted the attention of a large number of biologists, physicists and mathematicians. They take bird flocks as research objects and establish various flock models by observing and analyzing the activities of flock groups in real time (see ^[1,2,3,4]). The most influential and well-studied model is the Cucker–Smale model proposed by Cucker and Smale ^[1,2] in 2007. It is described as follows:

where $x_{i} \in \mathbb{R}^{d}$ denotes the position of the $i$-th particle and $v_{i} \in \mathbb{R}^{d}$ stands for velocity. The parameter $K > 0$ measures the alignment strength. The communication rate $\phi(\cdot):[0, \infty) \rightarrow (0, \infty)$ quantifies the influence between the $i$-th and $j$-th particles, and $\|\cdot\|$ denotes the Euclidean norm in $\mathbb{R}^{d}$. The communication rate is represented as

Note that unconditional flocking occurs if $\beta < \frac{1}{2}$, and conditional flocking occurs if $\beta \ge \frac{1}{2}$. For more in-depth discussions, refer to ^[5,6]. Furthermore, unconditional flocking can also be obtained in the case of $\beta = \frac{1}{2}$ (see ^[7]). Recently, various modifications of the classical Cucker–Smale model have been proposed. For example, the Cucker–Smale model with hierarchical leadership (see ^{[8,9,10,11,12,13]}, etc.), finite time and fixed time (see ^[14,15], etc.), random noise (see ^{[9,10,11,12,16,17,18,19]}, etc.), communication failure (see ^{[10,11,12,19,20,21]}, etc.), switching topologies (see ^[22,23], etc.) and time delay (see ^{[5,17,24,25,26,27,28,29,30,31,32]}, etc.), and, for contributions in an overview, one can refer to ^[33,34].

In practical applications, time delays and communication failures are important factors that influence the dynamical behavior and stability of the system (see ^[35,36], etc.). This paper introduces some studies on the flocking of Cucker–Smale models with time delays. Liu and Wu first introduced the time-delay factor into the Cucker–Smale model in ^[30]. Based on this, Choi and Haškovec ^[27] studied the Cucker–Smale model with fixed transmission delay. However, their analysis is only valid for some re-normalized systems. Furthermore, the Cucker–Smale model with time-varying delays was studied in ^[31], where a strictly positive lower bound is assumed for $\phi$. Erban, Haškovec and Sun ^[17] considered the randomness or imperfection of individual behavior and the delayed response of individuals to signals in the environment of the Cucker–Smale model. The numerical simulation results reveal that the introduction of time delays contributes to collective behaviors. Moreover, Haškovec and Markou ^[29] studied Cucker–Smale models with processing delays. They used the Lyapunov functional method, where the general communication function $\phi$ is considered and some assumptions are given. For other flocking results of delay Cucker–Smale systems, see ^{[5,24,25,26,28,32]}, etc. In particular, Chen and Yin ^[25] studied the non-flocking and flocking behaviors of the Cucker–Smale model with time-varying delays and a short-range interaction rate. The model is as follows:

where $N \in \mathbb{N}$ is the number of agents, $\left(x_i, v_i\right) \in {{\mathbb{R}}^{d} \times {\mathbb{R}}^{d}}$ denotes the phase-space coordinates of the $i$-th agent at the time $t$ and $d \ge 1$ is the physical space dimension. Here, $\widetilde{x}_{i}: = x_{i}(t-\tau (t))$ and $\widetilde{v}_{i}: = v_{i}(t-\tau (t))$, and the variable time delay $\tau (t) \ge 0$ is uniformly bounded, i.e., $\bar{\tau}: = \sup_{t \ge 0} {\tau (t)} < +\infty$. The authors of ^[25] generalized the results of ^[29] and obtained a flocking result for a more general communication rate, which also depends on the initial data in the short-range communication. This paper will present the application of some key inequalities and lemmas in ^[25] (see Lemma 2.1–2.2).

The agent's movement can be affected by obstacles, interference, noise, etc., so interaction failures are common. Martin et al. addressed interaction failures due to a limited communication range in ^[21]. The authors of ^[10] and ^[19] considered the hierarchical Cucker–Smale model under random interactions and the Cucker–Smale model with a random failure under root leadership. In these two studies, the random failures are independent and the probability of the interaction failure is fixed. Meanwhile, the overall leader or root leader of the group moves at a constant rate. Moreover, Mu and He presented a hierarchical Cucker–Smale model with time-varying failure probability under a random interaction and a Cucker–Smale model with random failures on a general graph in ^[11] and ^[12], respectively. Both ^[11] and ^[12] demonstrate that flocking behaviors often occur under certain conditions that depend exclusively on the initial state. However, the models with communication failures in the above literature are all discrete Cucker–Smale models and not continuous Cucker–Smale models. Recently, Bonnet and Flayac ^[20] studied continuous Cucker–Smale models with interaction failures. They emphasized that communication failures in the system are represented by time-varying interaction topologies, which differ from several other known contributions in the literature, such as ^[16,18,37]. The Cucker–Smale-type system with time-varying topological structures in ^[20] is shown below.

where $\left(x_{1}, \ldots, x_{N}\right) \in\left(\mathbb{R}^{d}\right)^{N}$ and $\left(v_{1}, \ldots, v_{N}\right) \in\left(\mathbb{R}^{d}\right)^{N}$ respectively represent the positions and velocities of the agents, while $\phi(\cdot)$ is a positive nonlinear kernel representing the extent of their mutual interactions. The functions $\xi_{i j}(\cdot) \in L^{\infty}\left(\mathbb{R}_{+}, [0, 1]\right)$ are communication weights that may lead to potential interaction failures in the system (e.g., when $\xi_{i j}(t) = 0$). The authors of ^[20] formulated a suitable persistence condition for the system (1.3), and they pointed out that a collection of weights $(\xi_{ij}(\cdot))$ satisfies the persistence condition (PE) (see Definition 2.3). The authors of ^[20] proved that the system (1.3) exhibits non-uniform exponential flocking with the strong fat tail condition (see Hypotheses (K)) in ^[20]) by constructing time-varying trajectory-based strict Lyapunov functions. In this paper, the strong fat tail condition of $\phi$ is improved, and the strong fat tail condition (1.6) is presented.

This paper focuses on the Cucker–Smale model with time-varying topological structures and reaction-type delay. Let $x_i(t) \in {\mathbb{R}}^{d}$ and $v_i(t) \in {\mathbb{R}}^{d}$ respectively be time-dependent position and velocity vectors of the $i$-th agent for $i = 1, 2, \ldots, N$. Let $\, \widetilde{}\,$ signify the value of a variable at time $t-\tau(t)$. For example, $\widetilde{x}_{i} = x_{i}(t-\tau (t))$ and $\widetilde{v}_{i}: = v_{i}(t-\tau (t))$, where the variable time delay $\tau (t) \ge 0$ is uniformly bounded, i.e., $\bar{\tau}: = \sup_{t \ge 0}{\tau (t)} < +\infty$. Then, the delayed Cucker–Smale-type model studied in this paper is described by

The initial position and velocity trajectories are prescribed for $i = 1, 2, \ldots, N$:

with $\left (x^{0}_{i}(t), v^{0}_{i}(t) \right) \in C \left (\left[-\bar{\tau}, 0 \right]; \mathbb{R}^{2d} \right).$ The communication rate $\phi$ quantifies the influence between the $i$-th particle and the $j$-th particle. The same as ^[20], the communication weight is no longer a fixed constant, but is represented by a time-varying communication weight $\widetilde{\xi}_{ij}(t)$. The communication weights $\xi_{ij}(t):\left[-\bar{\tau}, +\infty\right)\rightarrow \left[0, 1 \right]$ are symmetric about the subscript, i.e., $\xi_{ij}(t) = \xi_{ji}(t)$ for any $i, j \in \{ 1, 2, \ldots, N\}$. Obviously, $\xi_{ij}(t) = 0$ indicates that the communication between agent $j$ and agent $i$ is disconnected at time $t$.

This paper aims to provide sufficient conditions for the flocking behavior of Cucker–Smale systems with time-varying topological structures and reaction-type delay (see Theorem 3.1). For the case where no-delay occurs (i.e., $\bar{\tau} = 0$), the critical exponent of unconditional flocking in ^[20] is raised from $\beta = \frac{1}{4}$ to $\beta = \frac{1}{2}$ by replacing the strong fat tail condition with the weak light tail condition (1.6). For the case where no communication fails (i.e., $\xi_{ij}(t)\equiv 1$ for any $i, j \in \{ 1, 2, \ldots, N\}$), our result has a wider upper bound on the time delay than that in ^[25] (see Remark (3.1)). Finally, it is found that the introduction of time delay can deal with the problem of a low flocking convergence rate caused by the time-varying topology structure.

Below, the assumptions for $\phi = \phi(r)$ and $\xi_{ij}(t)$ are presented.

Assumption 1.1. $\phi$ is bounded, positive, non-increasing and Lipschitz continuous on $\mathbb{R}^{+}$. Without loss of generality, we have

Assumption 1.2. $\phi$ satisfies the {weak light tail} condition if there are two constants $\sigma, \kappa > 0$ and a parameter $\eta > \frac{1}{2}$ such that

Assumption 1.3 (Haškovec and Markou ^[29]). Assume $\phi(r)$ is differentiable on $\mathbb{R}^{+}$; then, there is a constant $\alpha > 0$ such that

For the classical communication rate (1.1) in (CS), if $\sigma = 1, \beta \le \eta$ is chosen, Assumption 1.2 is verified; if $\alpha = 2\beta$, Assumption 1.3 is satisfied for all $\beta \ge 0$.

Remark 1.1. Assumption 1.2 implies two cases, namely, $\phi \in L^{1}\left(\mathbb{R}^{+}, \mathbb{R}_{*}^{+}\right)$ if $\beta = \eta > \frac{1}{2}$ and $\phi \notin L^{1}\left(\mathbb{R}^{+}, \mathbb{R}_{*}^{+}\right)$ if $\beta \le \frac{1}{2}$, i.e., long-range communication weight and short-range communication weight.

Assumption 1.4. The communication weights $(\xi_{ij}(t))$ are continuously differentiable over the interval $[0, +\infty)$, and there exists a constant $\gamma > 0$ such that

for any $t \ge 0$ and $i, j \in \{ 1, 2, \ldots, N\}$.

Based on the above arguments, this paper mainly studies the asymptotic behavior of the model (1.4). The structure of the paper is as follows. In Section 2, some preliminary properties of the model (1.4) are established. Given important inequalities for position and velocity fluctuations, it is proved that the set of velocity fluctuations is uniformly bounded. In Section 3, the local time-dependent and global strict Lyapunov methods are respectively applied to prove the existence of a critical time delay for asymptotic flocking in the system (1.4). Finally, some numerical simulations are presented in Section 4.

2.   Preliminaries

In this section, the main tools and propositions used in this paper are introduced. For convenience, two notations of $\phi$ are given as follows:

Below, the model (1.4) is rewritten in a matrix form as

where $\mathit{\boldsymbol{x}} = (x_{1}, x_{2}, \ldots, x_{N})$ and $\mathit{\boldsymbol{v}} = (v_{1}, v_{2}, \ldots, v_{N})$. $\widetilde{\mathit{\boldsymbol{x}}}$ and $\widetilde{\mathit{\boldsymbol{v}}}$ are similar. In addition, ${\mathit{\boldsymbol{L}}}: \mathbb{R} \times {(\mathbb{R}{^d})^N} \to {\mathbb{R}^{dN \times dN}}$ is called the graph-Laplacian operator of the system (2.1). For almost every $t \ge 0$ and any $\mathit{\boldsymbol{v}} \in (\mathbb{R}^{d})^{N}$,

Further, for almost every $t \ge 0$ and any $\mathit{\boldsymbol{v}} \in (\mathbb{R}^{d})^{N}$, the partial graph-Laplacian operator ${\mathit{\boldsymbol{L}}_{\xi}}: \mathbb{R} \to \mathbb{R}^{{dN}\times{dN}}$ related to the weights $(\xi _{ij}(t))$ is defined as

This reformulation of multi-agent dynamics in terms of semi-linear ordinary differential equations in the phase space is fairly general and allows a comprehensive study of flocking problems via the Lyapunov method. With this goal, the so-called bilinear form of variance is introduced below.

Definition 2.1 (see section 1.2 in ^[38]). For any $\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{v}} \in (\mathbb{R}^{d})^{N}$, the variance bilinear form $B:{(\mathbb{R}^d)^N} \times {(\mathbb{R}^d)^N} \to \mathbb{R}$ is defined as:

where

Obviously, it is symmetric positive semi-definite and supports the following Cauchy-Schwarz inequality

For simplicity, this paper defines the position and velocity fluctuations as ($t \ge -\bar{\tau}$):

which can be evaluated based on the solutions of the system (2.1).

Note that any solution $\left({{x\mathit{\boldsymbol{}}}}, {{v\mathit{\boldsymbol{}}}}\right)$ of the model (2.1) satisfies

This in turn implies that $\bar{\mathit{\boldsymbol{v}}}(t) = \bar{\mathit{\boldsymbol{v}}}(0)$ and $\bar{\mathit{\boldsymbol{x}}}(t) = \bar{\mathit{\boldsymbol{x}}}(0) + \bar{\mathit{\boldsymbol{v}}}(0)t$ for any $t \ge 0$. Since the model (1.5a) is Galilean invariant, without loss of generality, it is assumed that $\bar{\mathit{\boldsymbol{x}}} = \bar{\mathit{\boldsymbol{v}}}\equiv 0$; otherwise, $x_{i}- \bar{\mathit{\boldsymbol{x}}}$ and $v_{i}- \bar{\mathit{\boldsymbol{v}}}$ are replaced with $x_{i}$ and $v_{i}$, respectively. The lead-up to this work has been to follow the above assumptions, no longer described. Note that it does not hold for $t \in [-\bar{\tau}, 0)$ generally. Hence, for any $t \ge 0$,

Now, this paper gives the definition of the asymptotic flocking behavior of the model (1.4) and our notion of presistence of excitation for the system (2.1), subject to multiplicative communication failures, respectively.

Definition 2.2. System (1.4) exhibits asymptotic flocking if the position and velocity fluctuations along the classical solution $\left\{\left(x_{i}, v_{i}\right)\right\}_{i = 1}^{N}$ of System (1.4) satisfy

Definition 2.3 (see Definition $3$ in ^[20]). The weight functions $\left(\xi_{ij}(\cdot) \right)$ satisfy the presistence of excitation condition if there exists a pair $(T, \mu)\in \mathbb{R}^{+}_{*} \times (0, 1]$ such that, for all times $t \ge 0$ and every $\mathit{\boldsymbol{v}} \in (\mathbb{R}^{d})^{N}$,

Remark 2.1. (PE) can be interpreted as a lower bound on the so-called algebraic connectivity (see ^[3,39,40]) of the average of the interaction graph with the weights $(\xi_{ij}(\cdot))$ over every time window of length $T > 0$, because $\frac{B({{L\mathit{\boldsymbol{}}}}_{\xi}{{v\mathit{\boldsymbol{}}}}, {{v\mathit{\boldsymbol{}}}}) }{B({{v\mathit{\boldsymbol{}}}}, {{v\mathit{\boldsymbol{}}}})} > \mu > 0$ cannot hold: set $\xi_{ij} = 0$; then, $\mu = 0$, which is a contradiction. The (2.8) requires the system to be persistently exciting in terms of the agents that have not yet reached flocking. Meanwhile, it only involves the communication weights $(\xi_{ij}(\cdot))$, not the kernel $\phi(\cdot)$. For more characteristics and significance of the presistence of excitation condition, see Remark 1 and Section 4 in ^[20].

Next, two lemmas are introduced (see Lemma $2.3$ and Remark $4$ in ^[25]). To distinguish, this paper uses

For convenience, define that

Lemma 2.1 (see Lemma $2.3$ in ^[25]). Let $0 \leq \phi \in C_{b}\left(\mathbb{R}^{+}\right)$ and $V(0) \neq 0$. Assume that $\bar{\tau} > 0$ satisfies $e^{k\bar{\tau}} \leq 2$. Then, the classical solution $\left\{\left(x_{i}, v_{i}\right)\right\}_{i = 1}^{N}$ of the model (1.2) satisfies

and

Lemma 2.2 (see Remark $4$ in ^[25]). Let $0 \leq \phi \in C_{b}\left(\mathbb{R}^{+}\right)$ and $V_{1}(0) \neq 0$. Assume that $\bar{\tau} > 0$ satisfies $e^{k \bar{\tau}} \leq 2$; then, the classical solution $\left\{\left(x_{i}, v_{i}\right)\right\}_{i = 1}^{N}$ of the model (1.2) satisfies that

Lemma 2.3. Let $V(0) \neq 0$ and the communication $\phi$ satisfy Assumption 1. Assume that $\bar{\tau} > 0$ satisfies $e^{ k \bar{\tau} } \leq 2$; then, the classical solution $\left\{\left(x_{i}, v_{i}\right)\right\}_{i = 1}^{N}$ of the model (1.4) satisfies that

and

where $k_{0}$, $k$ and $c$ are defined as in (2.8) and (2.9), respectively.

Proof. This paper first proves the first part of (2.11). Taking the derivative of $X^{2}(t)$ along the solution curve of System (1.4), for almost every $t \ge 0$, according to (2.5), we have

Then, it is easy to obtain $\dot{X}(t) \le \sqrt{V(t)}$ for almost every $t \ge 0$. Comparing our model (1.4) with the model (1.2), $\xi_{ij}(t)\phi$ in the model (1.4) can be recorded as a whole, which satisfies the condition $0 \leq \phi \in C_{b}\left(\mathbb{R}^{+}\right)$, and $2N^{2}V(t) = V^{2}_{1}(t)$. By Lemma 2.1 and Lemma 2.2, Lemma 2.3 is easy to be obtained.

For convenience, some notations are presented here. Most of them come from ^[20] and will be used in subsequent chapters.

Notation. The original function of $\phi(\cdot)$ in $[X(\bar{\tau}), X]$ is defined as

This paper uses the rescaled interaction kernel defined by

where any $r \ge 0$. Define $\mathit{\boldsymbol{\Phi}}_{T}(\cdot)$ by its uniquely determined primitive that vanishes at $X(\bar{\tau})$, i.e.,

This paper introduces the time-state dependent family of $\psi_{ T}(t) : \mathbb{R}^{+} \to \mathbb{R}^{{dN}\times{dN}}$, which is defined by

where

and $\rm{Id}$ denotes the identity matrix of $(\mathbb{R}^{d})^{N}$. Its pointwise derivative is given explicitly by

This paper also gives some symbolic marks that will appear in some conditions and conclusions, i.e.,

At the end of this section, a critical lemma depending on the (PE) is introduced, which is derived from ^[20].

Lemma 2.4. Let $(\mathit{\boldsymbol{x}}(\cdot), \mathit{\boldsymbol{v}}(\cdot))$ be a solution of the system (2.1). Assume that $\bar{\tau} > 0$ satisfies $e^{ k \bar{\tau} } \leq 2$. If (2.8) holds with $(T, \mu)\in \mathbb{R}^{+}_{*} \times (0, 1]$, then, for any $t \ge 0$, we have

where $\mathit{\boldsymbol{\phi}}_{T}(\cdot)$ is defined by (2.13).

Proof. By the definition (2.2) of ${\mathit{\boldsymbol{L}}}: \mathbb{R}^{+} \times {(\mathbb{R}{^d})^N} \to {\mathbb{R}^{dN}} \times {\mathbb{R}^{dN}}$, we have

where $\phi(\cdot)$ is non-increasing. As a consequence of (2.11) in Lemma 2.3, for all $s \in [t, t+T]$, it further holds that

According to (2.18) and the fact that $\phi(\cdot)$ is non-increasing, we have

where the definitions of $\mathit{\boldsymbol{L}}_{\xi }(\cdot)$ in (2.4), $\mathit{\boldsymbol{\phi}}_{T}(\cdot)$ in (2.13) and (PE) in the last inequality are used.

Finally, some common inequalities that will be used in the proofs of subsequent contents are presented as follows:

where $(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{v}})$ is the solution of the system (2.1) and all $t \ge 0.$

Proof. The left-hand side of the inequality (2.19) obviously holds, and it will be proved below that the right-hand side also holds. By Definition (2.2) of $\mathit{\boldsymbol{L}}(t, \mathit{\boldsymbol{x}}(t))\mathit{\boldsymbol{v}}$ and Assumption 1.1, we have

and, thereby, (2.19a) holds. Combining (2.19a) and the linearity of the integral, the estimates (2.19b) can be easily derived:

Then, according to the definition (2.15) of $\psi_{T} (t)$, we have (2.19c). Similarly, our estimate for the inequality (2.19d) is as follows:

where the discrete Cauchy-Schwarz inequality is used in the first inequality, and $0\le \xi_{ij}(t)\phi_{ij}(t) \le 1$ in the second inequality. Next, by applying the integral Cauchy-Schwartz inequality, we have

where the second inequality uses (2.19d) and the third inequality uses (2.19b).

3.   Emergent behavior

The previous section has shown some preparatory work. In the following section, it will be argued that the asymptotic flocking behavior for System (1.4) with both long-range and short-range communication rates.

Theorem 3.1. Let $V(0) \neq 0$ and Assumptions 1.1–1.4 and (PE) be satisfied by the communication rate $\phi$ and the communication weights $(\xi_{ij}(\cdot))$, respectively. If

and

then there exist a radius $\bar{X}_{M} > 0$ and two positive constants $\alpha_{M}, \gamma_{M}$ given by (3.51) such that the classical solutions $\left\{\left(x_{i}, v_{i}\right)\right\}_{i = 1}^{N}$ of the system (1.4) satisfy

where $k$, $c$, $a_{3}$ and $\mathit{\boldsymbol{\Phi}}_{T}(\cdot)$ are defined by (2.8), (2.9), (2.16c) and (2.14), respectively.

Remark 3.1. It is worthy to note that there are very few restrictions on the time delays, and that the convergence rate of flocking is related to the communication weights $(\xi_{ij}(\cdot))$ and time delay $\tau(t)$. Besides, the (PE) condition is independent of the initial configuration. When $\phi(r) = (1+r^{2})^{-\beta}$ with $\beta \in \left[0, \frac{1}{2}\right]$, the second part of Condition (3.1) is equivalent to $c\sqrt{V(0)} < +\infty$, which obviously holds for any initial data. When $\phi(r) = (1+r^{2})^{-\beta}$ with $\beta = \eta > \frac{1}{2}$, the system (1.4) may exhibit flocking behavior if the initial data satisfy Condition (3.1).

If $\xi_{ij}(t)\equiv 1$ for any $i, j \in \{ 1, 2, \ldots, N\}$, then the system (1.4) degenerates into the system (1.3). However, the time-delay in Theorem 3.1 requires only $e^{k\bar{\tau}} \le 2$, which weakens the time delay requirement (see Theorem $3.1$ in ^[25]). If $\bar{\tau} = 0$, then the system (1.4) exhibits unconditionnal flocking and $\beta = \frac{1}{2}$ is a critical exponent, which improves the results of ^[20] and is consistent with the observations of the classic Cucker–Smale model (CS). Therefore, it is easy to get the following corollary.

Corollary 3.1. Let $V(0) \neq 0$ and Assumptions 1.1–1.2 and (PE) be satisfied by the communication rate $\phi$ and the communication weights $(\xi_{ij}(\cdot))$, respectively. If the condition (3.1b) is satisfied, then there exist a radius $\bar{X}_{M} > 0$ and two positive constants $\alpha_{M}, \gamma_{M}$ given by (3.51) such that the classical solutions $\left\{\left(x_{i}, v_{i}\right)\right\}_{i = 1}^{N}$ of the system (1.3) satisfy

for all times $t \ge 0$. Additionally, $k$, $c$, $a_{3}$ and $\mathit{\boldsymbol{\Phi}}_{T}(\cdot)$ are defined by (2.8), (2.9), (2.16c) and (2.14), respectively.

Remark 3.2. When $\bar{\tau} = 0$, Assumptions 1.3–1.4 are unnecessary because the inequalities (3.27)–(3.28) obviously hold.

To prove Theorem 3.1, it is split into a series of lemmas. Let $\psi_{T} (t)$ be defined as in (2.15), and consider the candidate Lyapunov functional defined by

where $t \ge \bar{\tau}$ and $\lambda(t)$ is a smooth differentiable tuning curve. $\lambda(t)$ monotonically decreases with the positive lower bound, i.e., $\dot{\lambda}(t) < 0,$ $\lambda(t) \ge 1.$

Lemma 3.1. Let $V(0) \neq 0$ and Assumption 1.1 and (PE) be satisfied by the communication rate $\phi$ and the communication weights $(\xi_{ij}(\cdot))$, respectively. If the condition (3.1a) is verified, then, for the solution $\left({{x\mathit{\boldsymbol{}}}}(\cdot), {{v\mathit{\boldsymbol{}}}}(\cdot)\right)$ of the system (2.1) and every real number $\lambda_{\bar{\tau}} \ge 1$, there exists a time horizon $T_{\lambda_{\bar{\tau}}} > 0$ such that

where, for almost every time $t \in \left[\bar{\tau}, \bar{\tau}+T_{\lambda_{\bar{\tau}}}\right].$

Proof. Taking the derivative of $\mathcal{L}_{T}(t)$ along the solution curve of System (2.1) on $\left(\bar{\tau}, \infty \right)$, we have

where the first inequality holds because $\dot{\lambda}(t) < 0$, and (2.10a) and (2.19a) are used in the second inequality. Then, go further to a more refined estimate. By (2.15) and the definition of $\psi_{T}(t)$, we have

Estimate $I_{1}$ first:

For the last term, this work uses (2.5), Young's inequality and Assumption 1.1, in turn,

where, following (1.4a) and the $\mathrm{H\ddot{o}lder}$ inequality, we have

Hence, combining (3.6) and (3.5), we have

Next, estimate $I_{2}$, and, following from (2.5) and (2.10a), we obtain that

where (2.19d) and (2.19e) are used in the second inequality. Combining (3.4) with (3.7) and (3.8), we have

where $t > \bar{\tau}$. Choose the curve $\lambda(\cdot)$ as a solution of the ODE for a given constant $\lambda_{\bar{\tau}} \ge 1$:

where $a_{1}$ is defined as that in (2.16a). The latter is uniquely determined and can be written explicitly as

for any $t \in [\bar{\tau}, \bar{\tau}+\frac{\ln {\lambda_{\bar{\tau}}}}{a_{1}}]$. Let $T_{\lambda_{\bar{\tau}}} = \frac{\ln {\lambda_{\bar{\tau}}}}{a_{1}}$, and substituting the analysis expression (3.10) for the curve $\lambda(\cdot)$ into (3.9) yields that (3.3) holds for almost every time $t \in \left[\bar{\tau}, \bar{\tau}+T_{\lambda_{\bar{\tau}}} \right]$.

Note that (3.3) involves both the variance $V(\cdot)$ and the Lyapunov functional $\mathcal{L}_{T}(\cdot)$. However, to prove Theorem 3.1, only the estimate of $V(\cdot)$ needs to be involved.

Lemma 3.2. Let $V(0) \neq 0$ and Assumption 1.1 and (PE) be satisfied by the communication rate $\phi$ and the communication weights $(\xi_{ij}(\cdot))$, respectively. If the conditions of (3.1) hold, then there is a mapping $\lambda_{\bar{\tau}} \in [1, \infty) \mapsto X_{M}(\lambda_{\bar{\tau}}) \in \mathbb{R}^{+}$ along the solution $\left({{x\mathit{\boldsymbol{}}}}(\cdot), {{v\mathit{\boldsymbol{}}}}(\cdot)\right)$ of the system (2.1) such that

In particular, for every $\lambda_{\bar{\tau}} \ge 1$, the following local, strictly dissipative inequality holds:

where $a_{1}, a_{2}$ and $a_{3}$ are positive constants defined as those in (2.16), and $T_{\lambda_{\bar{\tau}}}$ is defined in Lemma 3.1.

Proof. Choose $\lambda_{\bar{\tau}}$ and let $\lambda(\cdot)$ denote the corresponding tuning functions given by (3.10). By (2.19c) and (2.10), for any solution $\left({{x\mathit{\boldsymbol{}}}}(\cdot), {{v\mathit{\boldsymbol{}}}}(\cdot)\right)$ of the system (2.1), we have

where $t \in \left[\bar{\tau}, \bar{\tau}+T_{\lambda_{\bar{\tau}}}\right].$ Because $1 \le \lambda(t) \le \lambda_{\bar{\tau}}$, the following inequality holds:

for any $t \in \left[\bar{\tau}, \bar{\tau}+T_{\lambda_{\bar{\tau}}}\right].$ Then, by (3.3), we have

Now, this paper first proves the first part of Lemma 3.2. By integrating (3.3) on $[\bar{\tau}, t]$ for any $t \in \left[\bar{\tau}, \bar{\tau}+T_{\lambda_{\bar{\tau}}}\right]$, we have

which, together with (3.13), yields

where $t \in \left[\bar{\tau}, \bar{\tau}+T_{\lambda_{\bar{\tau}}}\right]$. Since $\dot{X}(s) \le \sqrt{V(s)}$ and $V(s) \le c^2 V(0)$ by (3.1a), applying the chance of variable $r = X(s)$ in (3.15), the integral estimate can be obtained for all times $t \in \left[\bar{\tau}, \bar{\tau}+T_{\lambda_{\bar{\tau}}}\right]$:

Due to $V(t) \ge 0$, according to (3.16), for any $t \in \left[\bar{\tau}, \bar{\tau}+T_{\lambda_{\bar{\tau}}}\right]$,

Since $\phi(\cdot)$ is a non-increasing positive function, its primitive ${\mathit{\boldsymbol{\Phi}}}_{T}(\cdot)$ is a strictly increasing map. Then, by (3.1b), there exists a constant $X_{M}(\lambda_{\bar{\tau}})$ with $X_{M}(\lambda_{\bar{\tau}}) > X(\bar{\tau})$ such that

This paper claims that (3.11) holds. For contradiction, assume that there exists $t_{*} \in \left[\bar{\tau}, \bar{\tau}+T_{\lambda_{\bar{\tau}}}\right]$ such that $X(t^{*}) > X_{M}(\lambda_{\bar{\tau}})$. By the strict monotonically increasing property of ${\mathit{\boldsymbol{\Phi}}}_{T}(\cdot)$, we have ${\mathit{\boldsymbol{\Phi}}}_{T}(X(t^{*})) > {\mathit{\boldsymbol{\Phi}}}_{T}(X_{M}(\lambda_{\bar{\tau}}))$. Combining this with (3.17) and (3.18) implies

which is a contradiction. Consequently, (3.11) holds.

Finally, this paper proves that (3.12) holds. Applying the Gronwall inequality to (3.14) with (3.11), we have

for all $t \in \left[\bar{\tau}, \bar{\tau}+T_{\lambda_{\bar{\tau}}}\right].$ This, together with (3.13), implies

for all $t \in \left[\bar{\tau}, \bar{\tau}+T_{\lambda_{\bar{\tau}}}\right].$ According to $t = \bar{\tau}+T_{\lambda_{\bar{\tau}}}$ in (3.19), (3.12) holds immediately.

Using the dissipative inequality (3.12) obtained in Lemma 3.2, an upper bound on the standard deviation $X(\cdot)$ can be obtained with respect to $\lambda_{\bar{\tau}}\ge 1$.

Proposition 3.1. Let $V(0) \neq 0$ and Assumptions 1.1–1.2 and (PE) be satisfied by the communication rate $\phi$ and the communication weights $(\xi_{ij}(\cdot))$, respectively. If the conditions of (3.1) are satisfied, then there is a radius $\bar{X}_{M} > 0$ such that $X(t) \le \bar{X}_{M}$ along the classical solution $\left({{x\mathit{\boldsymbol{}}}}(\cdot), {{v\mathit{\boldsymbol{}}}}(\cdot)\right)$ of the system (2.1) for $t \ge 0$.

Proof. From the expression of (3.18), we have

where " $\circ$ " denotes the standard composition operation between functions. In addition, by integrating (1.7) with respect to $r \in [X(\bar{\tau}), X]$ for some $X > X(\bar{\tau})$, it also holds that

which can be reformulated as

for every $X \ge X(\bar{\tau})$. $\Phi(\cdot)$ is defined in (2.12) to represent the primitive function of $\phi(\cdot)$. Next, applying variable substitution to (2.14) yields

so that $X: = X_{M}(\lambda_{\bar{\tau}}) = {\boldsymbol \Phi}_{T}^{-1}\left(\frac{a_{3} \lambda_{\bar{\tau}}}{\mu c\sqrt{V(0)}} V(\bar{\tau}) \right)$. Recalling that ${\mathit{\boldsymbol{\phi}}}_{T}(\cdot)$ is non-increasing, according to (3.20) and (3.21), and together with Assumption 1.2, we have

where $C_{1}, C_{2} < 0$ only depend on $\left(N, T, \mu, \bar{\tau}, k_{0}, \eta, \kappa \right).$ Substituting the inequality in (3.22) into (3.12) while recalling that $T_{\lambda_{\bar{\tau}}} = \frac{\ln \lambda_{\bar{\tau}}}{a_{1}}$, we have

where $C_{3} = \frac{\mu \kappa}{a_{3}}{C_{2}^{\frac{2\eta }{2\eta -1}}} > 0.$ Observe that $\lambda_{\bar{\tau}}$ is free over the interval $[1, +\infty)$ and $T_{\lambda_{\bar{\tau}}}$ is a continuous monotone increasing function of $\lambda_{\bar{\tau}} \in [1, +\infty)$. Since $T_{\lambda_{\bar{\tau}}}$ spans $[0, +\infty)$, a time reparametrization can be defined by using $S: = \bar{\tau}+T_{\lambda_{\bar{\tau}}}$. Then, by (3.23) and (2.11), this new time variable can be expressed as

for any $t\ge\bar{\tau}$. The integral on the right-hand side is uniformly bounded because of $\eta > \frac{1}{2}$. Thus, there exists a constant $\bar{X}_{M} > 0$ such that $X(t) \le \bar{X}_{M}$ for all $t \ge 0$, which proves our claim.

For convenience, it is defined that

Here $\alpha$, $\gamma$ and $c$ are defined in (1.6), (1.8) and (2.11), respectively. Now, this paper provides a mutual-direction estimate for the quantum $D(t)$ defined in (3.25).

Lemma 3.3. Let $V(0)\neq 0$ and Assumptions 1.1, 1.3 and 1.4 be satisfied by the communication rate $\phi$ and the communication weights $\xi_{ij}(t)$, respectively. If (3.1a) holds, then the solution $\left({{x\mathit{\boldsymbol{}}}}(\cdot), {{v\mathit{\boldsymbol{}}}}(\cdot)\right)$ of the system (2.1) satisfies that

for all $t, s \ge 0$. In particular, we have

for all $t \ge \bar{\tau}$.

Proof. The proof is completed in two steps. In the first step, the inequality is proved:

For any $t\ge 0$, $D(t)$ is differentiated in time:

By Assumption 1.1 and Assumption 1.4, $\xi_{ij}'(t) \ge -\gamma$ for $t \ge 0$; for the first term on the right-hand side of (3.30), we have

where (2.6) is used in the last equality. For the second term on the right-hand side of (3.30), the symmetrization trick is applied:

Then, the term is estimated by using the Cauchy-Schwartz inequality:

where $\xi_{ij}(t) \le 1, \, \phi(t) \le 1$ is used. In the last inequality, (2.10a) and (2.10b) in Lemma 2.3 are applied. By Assumption 1.3, for the third term on the right-hand side of (3.30), we have

where, in the second inequality, the bound provided by (2.12) in Lemma 2.3 is used:

By combining the estimates (3.31)–(3.33), we get (3.29).

In the second step, this paper proves (3.27) and (3.28). Integrating (3.29) from $s$ to $t$ yields

This paper claims that, for any $t, s \ge 0$,

In fact, by (2.10a), we have

Combining (3.37) and (3.38) gives (3.35), and (3.36) can be obtained in the same way. According to (3.35) and (3.36), for any $t, s \ge 0$, (3.34) can be scaled to

where (3.39) is the right-hand side of (3.27). Next, exchanging $s$ with $t$ in (3.40), we have

Combining (3.39) and (3.41), we obtain (3.27). In particular, let $s = t-\tau(t)$ in (3.27), which gives (3.28).

Based on the uniform estimate obtained in Proposition 3.1, we shall prove the second part of Theorem 3.1.

Proof of Theorem 3.1. Since $X(\cdot)$ is uniformly bounded in Proposition 3.1, this paper only needs to prove that the exponential convergence of $V(\cdot)$ is toward 0. Combining (2.17) and Proposition 3.1, recalling that ${\mathit{\boldsymbol{\phi}}}_{T}(\cdot)$ is non-increasing, we have

for any $t \ge 0$, where $\mathit{\boldsymbol{\phi}}_{T}(\cdot)$ is defined by (2.13).

Let $\psi_{T}(t)$ be defined as that in (2.15), and consider the Lyapunov functional defined by

for all times $t \ge \bar{\tau}$, where $\lambda > 0$ is a tuning parameter and $(\mathit{\boldsymbol{x}}(t), \mathit{\boldsymbol{v}}(t))$ solves (2.1). Note that, by (2.19) and (2.10), we have

for all times $t \ge \bar{\tau}$, where $a_{4} = \lambda + T$ and $a_{5} = \lambda+2T+(2\lambda+T)\bar{\tau}^{3}e^{4k\bar{\tau}}$. Now, this paper proves that the following strictly dissipative inequality holds for $t \ge \bar{\tau}$:

where $\gamma_{M} > 0$ is a given constant. With this goal in mind, this paper takes the derivative of $\mathfrak{L}_{T}(t)$ along the solution curve of the system (2.1) on $\left(\bar{\tau}, \infty \right)$:

where (3.42) is used. This work uses Young's inequality with $\delta = 2$ and the inequality (2.19d):

The second inequality in (3.46) is the Cauchy-Schwartz inequality (2.5), and the last term is given by (3.6). According to (3.8), we have

where (2.19d) is used in the second inequality and Young's inequality with $\epsilon > 0$ is used in the last inequality. Substituting (3.46) and (3.47) into the inequality (3.45), we have

for any $t \ge \bar{\tau}$ and given $\lambda, \epsilon > 0$. Below, for the right side of (3.48), this paper uses (3.1a) and (3.28):

Therefore, the following parameters are chosen:

According to the condition (3.1a) in Theorem 3.1, we have $\epsilon, \lambda > 0$. Using the inequality (3.44), the following inequality can be obtained:

for any $t \ge \bar{\tau}$. By applying the Gronwall inequality together with (3.44), we have

for all times $t\ge\bar{\tau}$, where $\alpha_{M}, \gamma_{M} > 0$ are given by

with $\lambda > 0$ as that in (3.49). By combining Proposition 3.1 and (3.50), it is concluded that the solution $\left({{x\mathit{\boldsymbol{}}}}(\cdot), {{v\mathit{\boldsymbol{}}}}(\cdot)\right)$ of the system (2.1) converges to flocking with an exponential rate in the velocity variable.

Remark 3.3. Assumptions 1.3–1.4 cannot be removed because it provides a key inequality (3.28) that is needed in the time-delay system (1.4), which is a restriction of Theorem 3.1. However, if $\bar{\tau} = 0$, then Assumptions 1.3–1.4 can be removed because the inequalities (3.27)–(3.28) obviously hold.

4.   Numerical experiments

In this section, numerical simulation examples of the dynamic behavior are provided for the system (1.4) with regard to particle positions and velocities under Condition (3.1). The flocking behavior in Section 3 is simulated and the effect of interaction failure and time lag on the flocking convergence rate is analyzed.

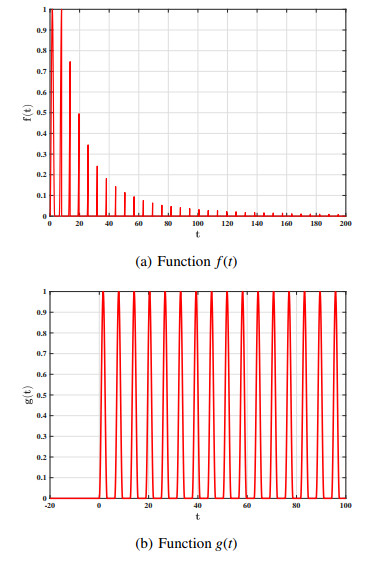
First, for the convenience of the following discussion, two functions and their respective images are given. These two functions are inspired by the forced harmonic vibration equation for any $k \in \mathbb{N}$:

The images are shown in Fig. 1, which shows that the continuous zero set $E_{k}\left(t:f(t) = 0, t \in [2k\pi, 2(k+1)\pi)\right)$ increases over time, while the continuous zero set $F_{k}\left(t: g(t) = 0, t \in [2k\pi, 2(k+1)\pi)\right)$ maintains $\pi$ units over time.

Example 4.1. Let $N = 10$, $\phi(r) = \frac{1}{(1+r)^{\beta}}$, $\tau(t) = \frac{1}{4} \sin t$ and $\xi_{ij}(t) = g(t)$ for any $i, j \in \{ 1, 2, \ldots, N\}$, which satisfies the (PE) condition because $T = 2\pi$ and $\mu \leq \frac{1}{4}$ are chosen; we have

for any $t \ge 0$ and $i, j \in \{ 1, 2, \ldots, N\}$. For the initial data, ${{x\mathit{\boldsymbol{}}}}(t)$ and ${{v\mathit{\boldsymbol{}}}}(t)$ are set to be constant for $t \in [-\bar{\tau}, 0]$. By a direct calculation, $\bar{\tau} = \frac{1}{4}$, $k_0 = 1$, $c = \sqrt{17} / {2}$, $a_3 = 4\pi+\frac{\pi e^2}{16}$ and $e^{k\bar{\tau}} = e^{\frac{1}{2}}\thickapprox 1.65 < 2$ are obtained. Moreover, if $\beta = \frac{1}{2}$, then $\mathit{\boldsymbol{\Phi}}_{T}(+\infty) = +\infty$, which implies that Condition (3.1) in Theorem 3.1 holds. So, according to Theorem 3.1, the flocking occurs. We set the initial position

and the initial velocity

As described in Fig. 2, numerical simulations confirm that position fluctuations are uniformly bounded and velocity fluctuations converge exponentially to zero.

If $\beta = 1$, we set the initial position

and the initial velocity

Then, $V(0) = X(0) = 3.825 \times 10^{-7}$ and $X(0) > X(\bar{\tau})$, which can be seen from Fig. 3(a). Thus, we have

which implies that Condition (3.1) in Theorem 3.1 holds. The numerical simulations are shown in Fig. 3. The results confirm that position fluctuations are uniformly bounded, and that velocity fluctuations converge exponentially to zero, indicating that the system 1.4 exhibits flocking behavior.

It can be seen in Figs. 2 and 3 that the relative velocity between particles is stepped attenuation, and that it finally converges to zero, which is guaranteed by the selection of communication weights satisfying the (PE) condition. Next, another communication weight function is selected, which does not meet the (PE) condition, to analyze the flocking behavior of the system (1.4).

Example 4.2. Let $\xi_{ij}(t) = f(t)$ for any $i, j \in \{ 1, 2, \ldots, N\}$; the remaining parameters and variables are the same as those in Example 1. Obviously, $\xi_{ij}(t)$ does not satisfy the (2.8) condition since $\lim_{t \to \infty} f(t) = 0.$ The numerical simulations are shown in Figs. 4 and 5. It can be seen that the relative positions between the particles are unbounded. Although the relative velocity also decreases in a step-like manner, it does not converge to zero in the end but maintains a uniform velocity. Therefore, when the system 1.4 encounters a communication fault with the communication weight $f(t)$, the flocking behavior will fail.

Example 4.3. To analyze the influence of the time-varying topological structure and time lag $\tau(t)$ on the flocking convergence rate, this paper investigates the evolution of velocity fluctuations with time for four different situations. $\xi_{ij}(t) = g(t)$ for any $i, j \in \{ 1, 2, \ldots, N\}$ and $\tau(t) = \frac{1}{4} \sin t$ is the first case; $\xi_{ij}(t) \equiv 1$ and $\tau(t) = \frac{1}{4} \sin t$ is the second case; $\xi_{ij}(t) = g(t)$ for any $i, j \in \{ 1, 2, \ldots, N\}$ and $\tau(t) = 0$ is the third case; $\xi_{ij}(t) \equiv 1$ and $\tau(t) = 0$ is the fourth case. They are respectively represented in Fig. 6 by a red solid line, a blue dashed line, a magenta dashed line and a green dashed line. Other configurations were chosen in the same way as in Example 4.1. Figure 6 illustrates the numerical simulation, where (a) and (b) represent the flocking convergence rate for long-range communication and short-range communication, respectively. It can be seen that the communication failure caused by the time-varying topological structure slows down the flocking convergence in both situations, whereas the small delay speeds up the flocking convergence. So, it is advantageous to introduce time delays to the general Cucker–Smale system with the time-varying topological structure, which allows the system to initiate flocking more quickly.

5.   Conclusions

The phenomena of communication failure and time delay are often observed in nature. This paper mainly studies the influence of communication failures caused by a time-varying topology and reaction-type delay on the flocking behavior of multi-particle systems. Two main problems are discussed in this paper. One is as follows: what conditions do time-varying topologies need to meet to avoid communication failure without affecting the final flocking behavior? The other is the question of how the influence of time delay affects the flocking behavior of time-varying systems? This paper gives the corresponding (PE) condition for the first problem. Under this condition, the flocking behavior of the Cucker–Smale system (1.3) with a time-varying topological structure will occur, which proves that, when there is long-range interaction, the system will have unconditional flocking behavior, and when there is short-range interaction, the system will have flocking behavior when the initial value satisfies certain conditions. But, inevitably, communication failure slows down the convergence rate of flocking behavior. In addition, it was found in the numerical simulation that, if the (PE) condition given in this paper is not satisfied, the flocking behavior of the system will fail. For the second problem, this paper gives the corresponding delay condition (3.1) to maintain the stability of the system (1.4) flocking behavior, and through numerical simulation analysis, it was found that the delay is conducive to accelerating the convergence rate of the flocking behavior, which improves the slow convergence rate problem caused by communication failure. In addition, it is worth mentioning that the Lyapunov functional constructed in this paper is more refined than that in ^[20], and that the conclusion obtained includes and extends the conclusion in ^[20]. The assumption of communication weight selected in this work is a fixed function, but, in reality, the change of communication weight is often random, which cannot be described by a function. At this time, we need to introduce random time variables and establish corresponding random persistent excitation conditions, which is our next focus of study.

Acknowledgment

The authors would like to thank all of the reviewers who participated in the review and MJEditor (www.mjeditor.com) for its linguistic assistance during the preparation of this manuscript. This research was supported by the National Natural Science Foundation of China (11671011) and Natural Science Foundation for General Program of Hunan Province (2022JJ30655).

Conflict of interest

The authors have no conflict of interest to declare that is relevant to the content of this paper.