Effective thermal properties of a magnetite-polyester composite conformed in the presence of a constant magnetic field

1.   Introduction

Commonly used polymers like polyamide and polypropylene are used as insulators because of their low conductivity. Nevertheless, new applications, such as heatsinks, electromagnetic armors ^[1], and heat exchangers ^[2], require manufacturing new materials with high thermal conductivity.

With the goal of improving the thermal behavior of composite materials, different types of "filling" materials, such as silica, alumina, aluminum ^[3], carbon fibers, graphite, graphene, aluminum nitrides, nickel or silver ^[4], and calcium carbonate ^[5], have been used. It is true that the term "filler" is unattractive to use for these particles; however, it is important to highlight the fundamental role that these particles play in composite materials and in their response to thermal, mechanical, electrical, magnetic, and optical stimuli, among others. This is why they are known as functional fillers ^[6]. Each kind of filling material provides unique properties for every material used as a matrix, such as the effective thermophysical properties of a composite material, which depend on the volumetric fraction, thermal properties of each phase (matrix, fill), the geometry and distribution of the filler particles in the matrix, and the temperature ^[7].

A fundamental response to extend the lifetime and guarantee the performance and reliability of solid-phase devices is the dissipation of heat, which is a difficult problem in materials science ^[8] owing to the miniaturization and development of new architectures, for example, the manufacture of chips, light-emitting diodes, and flexible electronics ^[9]. Thus, it is important to know the thermal conductivity of materials in the design of new technologies, especially in the aerospace, aeronautics, and electronics industry ^[10].

One commonly use of functional filler is magnetite (Fe₃O₄). Mixes with thermoplastic polymers are relatively new ^[11]. On the other hand, on the nanometer scale, the application of an external magnetic field for the alignment of carbon nanotubes and nanofibers submerged in liquids and resins ^[12] as well as carbon nanotubes coated with nickel ^[13], allows the formation of chains and clusters of particles in the direction of the lines of the magnetic field, hence improving the thermal and mechanical properties of the formed materials ^[14]. The effect of magnetic alignment on the heat transfer in fluids containing iron and copper oxide nanoparticles has also been studied, and it has been observed that the applied external magnetic field strengthens the alignment ^[15]. Likewise, analysis of the magnetic structure of nanometric magnetite particles subjected to external magnetic fields using finite micromagnetic elements has been studied, where it was reported that the domain structure is uniform at 100 mT; at 300 mT, it saturates, and the magnetization direction aligns with the field ^[16].

In this study, we report the thermophysical properties (at room temperature) and the morphology of a polyester resin filled by micrometric magnetite particles, where a constant magnetic field of 300 mT is applied during the curing process of the resin.

2.   Materials and methods

Magnetite powders with a particle distribution smaller than 75 µm were used as raw materials, which were supplied by Green Magnetite S.A reference G-Mag A^®, whereas the polyester resin used was a thermostable terephthalic supplied by NovaSuin reference P-115A^®, preaccelerated, with a gelation time of 9–12 min and an exothermic temperature of 145–165 ℃.

Samples were prepared in three configurations: randomly dispersed particles, particles oriented parallel to a constant magnetic field, and particles oriented perpendicular to a constant magnetic field ^[17]. Hence, an experimental design was used, in which, during the resin curing process, the sample is placed between two neodymium magnets (magnetic field: 300 mT, diameter: 50 mm) separated by 90 mm. This process was carried out for 1 h, during which the sample solidified completely. The concentration by weight of the magnetite in the polymer matrix was defined according to that reported in ^[18,19] as 10, 20, and 30%. The samples were prepared at room temperature by means of a manual casting process ^[20] using a PVC cylindrical mold with a 25.4 mm diameter and 50 mm height. In order to mix the Fe₃O₄ particles in the resin, a DLAB OS20-S agitator was used for 5 min at 100 rpm. For the resin curing process, the SuperCat S-960^® catalyst was used, in the proportion of 1% w/w, according to the supplier's specifications, maintaining the agitation for an additional 2 min. Finally, the sample was placed in the center between the two magnets while the resin was cured in the three configurations described: randomly scattered particles, particles oriented parallel to the constant magnetic field produced by the magnets, and particles oriented perpendicular to the constant magnetic field produced by the magnets.

The thermophysical properties of the samples at room temperature were assessed using a KD2 Pro^® system, which uses the physical principle of linear transient heat flow. The sensor used was the dual sensor SH-1, which consists of two needles (ϕ = 1.3 mm), separated by 6 mm from one another, one working as a heat source and the other as a sensor, which register the temperature as a function of time, which propagates through the material with a constant voltage ^[21].

The theoretical fundamentals of the KD2 Pro^® system are described by the solution of the differential equation of heat conduction in a homogeneous and isotropic medium, which is given by the following expression ^[22]:

where T is the temperature (℃), t is the time (s), D is the thermal diffusivity (m²/s), and r is the radial distance (m). One solution to the previous equation for the variation of temperature (ΔT) is given by ^[22]:

where q (W/m) is the heat per unit length and time that goes through the material, λ is the effective thermal conductivity of the sample (W/mK), and E_i is the exponential integral function defined by ^[22]:

With α = r²/4Dt and γ = 0.5772 (Euler's constant). For high values of t, the terms of superior order in the Eq 3 can be despised. Combining Eqs 2 and 3, we get ^[22]:

Equation 4 represents the temperature variation as a function of time for a finite position (r) between the heat source and the temperature sensor, which depends on the thermophysical parameters (λ, D) of the sample. The effective thermal conductivity of the sample (λ) is determined from the slope of the ΔT behavior as a function of the natural logarithm of time. On the other hand, the thermal diffusivity (D) is found registering the intersection of the lineal regression of ΔT as a function of ln(t). At last, the specific heat per volume unit (ρc) and thermal effusivity (ε) of the sample are found using the values of λ and D through the relations $\rho c = \frac{\lambda}{D}$ and ε = λD^{-1/2 [23]}.

The morphology of the samples was studied using a scanning electron microscope (SEM, FEI Quanta 650 FEG), whereas a microanalysis was performed using energy-dispersive X-ray spectroscopy (EDS) with a probe series SDD-Apollo X.

3.   Results and discussion

The microanalysis results of the magnetite powders, which were obtained using ZAF correction (Z: atomic number; A: absorption; F: fluorescence) with EDS, is presented in Table 1. It can be appreciated that the weight percentage of iron (Fe) was 75.74%, whereas that of oxygen was 22.93%. The carbon percentage (1.53%) possibly corresponds to the graphite coating applied on the sample to avoid the charge effects.

Table 1.  Elementary chemical composition (microanalysis) of the magnetite powders.

Element	Weight (%)	Atomic (%)
C	1.53	4.38
O	22.93	49.19
Fe	75.54	46.43
Total	100.00	100.00

---

 | Show Table

DownLoad: CSV

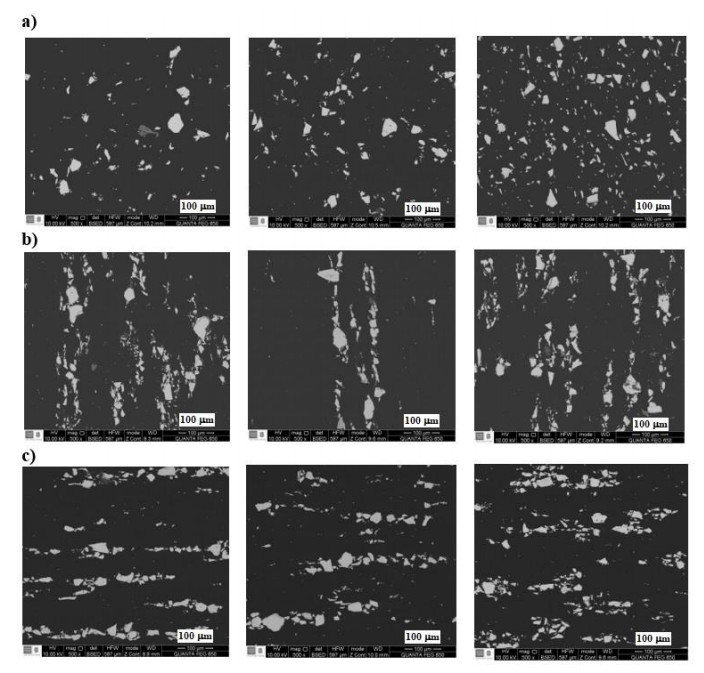
Figure 1 shows the morphology of the samples using an SEM. From this, the effect of the magnetic field is observed, which aligns the magnetite particles according to the direction of the field lines (see Figure 1b, c). This behavior was not observed in samples on which no magnetic field was applied (see Figure 1a). This is consistent with what was reported by Varga et al. ^[17], who suggested that if a polymer with ferromagnetic particles is cured in the presence of a magnetic field, the magnetizable particles will form a column-shaped chain in the direction of the field, producing a polymer under the magnetorheological effect. On the other hand, using the ImageJ^® software, an average particle size of 29.28 ± 6.23 µm for magnetite was detected. It was also seen that, as expected, the average surface density increases with the increase of the concentration of magnetite in the sample, reporting values of 31, 36 and 40 particles/mm². In general, good integration between the resin and the magnetite particles was observed, showing that there is no continuous interaction between the magnetite particles despite their orientation due to the presence of a magnetic field.

Figure 1.  SEM images (magnification: 500×) of the samples: 90-10%, 80-20%, and 70-30%. (a) Randomly dispersed particles, (b) particles oriented parallel to the magnetic field and (c) particles oriented perpendicular to the magnetic field.

DownLoad: Full-Size Img PowerPoint

Tables 2–4 show the experimental values, found using the KD2 Pro^® system through the SH-1 sensor, of the conductivity (λ), diffusivity (D), thermal effusivity (ε) as well as the specific heat per unit volume (ρc) at room temperature for the samples in the three aforementioned configurations.

Table 2.  Effective thermophysical properties of samples with filling particles randomly dispersed.

Sample	ρ (kg/m3)	λ (W/mK)	D (×10−6) (m2/s)	ρc (MJ/m3K)	ε (Ws1/2/m2K)
90-10%	1313.56 ± 39.0	0.277 ± 0.003	0.207 ± 0.01	1.337 ± 0.02	608.973 ± 13.15
80-20%	1463.41 ± 48.6	0.302 ± 0.002	0.211 ± 0.01	1.427 ± 0.03	656.325 ± 16.23
70-30%	1570.75 ± 31.3	0.345 ± 0.003	0.226 ± 0.01	1.530 ± 0.02	726.463 ± 28.17

---

 | Show Table

DownLoad: CSV

Table 3.  Effective thermophysical properties of samples with filling particles aligned parallel to the magnetic field.

Sample	ρ (kg/m3)	λ (W/mK)	D (×10−6) (m2/s)	ρc (MJ/m3K)	ε (Ws1/2/m2K)
90-10%	1337.88 ± 23.4	0.264 ± 0.003	0.225 ± 0.01	1.172 ± 0.02	555.812 ± 17.5
80-20%	1489.13 ± 18.2	0.312 ± 0.002	0.248 ± 0.02	1.258 ± 0.04	626.437 ± 14.3
70-30%	1611.39 ± 35.2	0.351 ± 0.002	0.211 ± 0.01	1.665 ± 0.03	763.896 ± 22.5

---

 | Show Table

DownLoad: CSV

Table 4.  Effective thermophysical properties of samples with filling particles aligned perpendicular to the magnetic field.

Sample	ρ (kg/m3)	λ (W/mK)	D (×10−6) (m2/s)	ρc (MJ/m3K)	ε (Ws1/2/m2K)
90-10%	1356.17 ± 25.2	0.254 ± 0.002	0.207 ± 0.02	1.225 ± 0.03	557.770 ± 15.6
80-20%	1430.53 ± 32.4	0.310 ± 0.003	0.219 ± 0.01	1.416 ± 0.02	662.079 ± 25.7
70-30%	1610.79 ± 21.1	0.345 ± 0.004	0.217 ± 0.03	1.587 ± 0.05	739.452 ± 32.5

---

 | Show Table

DownLoad: CSV

Considering a compound material formed by two phases, the first (Phase 1) being a homogeneous polymer matrix (resin), with thermal conductivity (λ₁) of 0.1635 W/mK ^[24] and volumetric fraction φ₁ = (1 - φ₂). The second (Phase 2) being the filling magnetite particles, with spherical form and thermal conductivity (λ₂) of 9.7 W/mK ^[25] and volumetric fraction φ₂, where there is no interaction between them, with λ₂ > λ₁, the self-consistent model of Hashin and Shtrikman ^[26] provides the upper and lower limits between which the effective thermal conductivity of the composite material can be found, defined using the following expressions ^[27]:

These equations are similar to those reported in Maxwell-Eucken models ^[28] and the new effective medium theory ^[29].

In Table 5, the calculated values of λ_lower and λ_upper are presented using Eqs 5 and 6 with the values of the volumetric fractions (φ₁, φ₂) that were calculated using Eq 7, taking into account the weight percentages of the resin and magnetite (90-10%, 80-20%, and 70-30%) and the density values of the resin (ρ = 1198 kg/m³) ^[24] and magnetite (ρ = 5100 kg/m³), as well as the values λ₁ (0.1635 W/mK) ^[24] and λ₂ (9.7 W/mK) ^[25].

Table 5.  Upper and lower limits using Eqs 5 and 6 for the effective thermal conductivity of the samples, according to the self-consistent model of Hashin and Shtrikman ^[26].

Samples	φ1	φ2	λlower (W/mK)	λupper (W/mK)
90-10%	0.9746	0.0254	0.1757	0.3280
80-20%	0.9445	0.0555	0.1908	0.5258
70-30%	0.9085	0.0915	0.2102	0.7682

---

 | Show Table

DownLoad: CSV

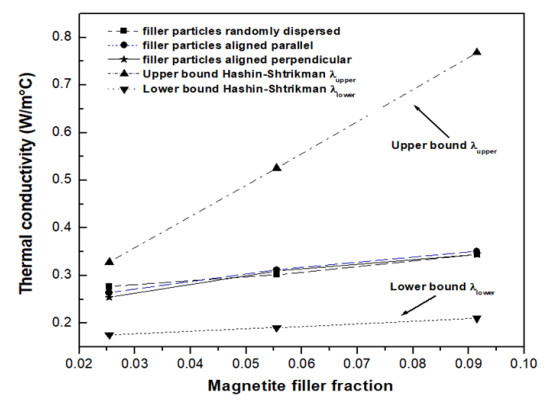
Comparing the results found for λ (see Tables 2–4) with the values in Table 5, it was observed that they are consistent and are within the upper and lower limits defined according to the Hashin-Shtrikman model ^[21]. This behavior is observed in Figure 2, in which it can be seen that there is no significant difference in this thermophysical parameter due to the effect of the magnetic field during curing the resin, which is explained by the fact that the volumetric fractions of the filling (φ₂) are very low (~2 to 9%), less than the percolation threshold, a value that oscillates between 23 and 30% for this compound ^[20]. Therefore, there will be clusters and noncontiguous chains of particles oriented according to the lines of the magnetic field due to the magnetic dipole interactions between the particles ^[24], in the whole volume of the material, a behavior that is observed in the morphology of the samples studied using an SEM (see Figure 1). From the previous results, the existence of a slight increase in the thermal conductivity of the samples due to an increase in the magnetite percentage was evidenced, showing that the values found are closer to the Hashin-Shtrikman lower limit. On the other hand, comparing the values of λ (see Tables 2–4) of the composite samples with the λ value of the resin (0.1635 W/mK) ^[19], an increase between 55 and 115% was observed due to an increase in the magnetite percentage in the sample, transforming it from an insulating to a resistive material ^[24].

Figure 2.  Experimental thermal conductivity of the samples as a function of the magnetite volumetric fraction and lower and upper Hashin-Shtrikman limit.

DownLoad: Full-Size Img PowerPoint

4.   Conclusion

In this study, we obtained a composite material based on a polyester resin and magnetite particles in three configurations, that is, randomly dispersed particles, particles oriented parallel to a constant 300 mT magnetic field, and particles oriented perpendicular to a constant 300 mT magnetic field, applied during the curing process of the resin.

The morphology of the samples allowed the observation of the effect provoked by the application of a magnetic field during the curing process, where the noncontinuous chains and clusters of the magnetite particles in the direction of the magnetic field lines are appreciated. It was found that there was no significant difference in the thermophysical properties of the samples measured in the absence of an external magnetic field, which was used only during the curing process of the resin. This can be due to the fact that the volumetric fractions of the filler material (magnetite) were very low, being lower than the percolation threshold. Likewise, a slight increase in the thermal conductivity of the samples due to an increase in the magnetite concentration was evidenced. It was also found that the values were within the limits of Hashin-Shtrikman models, with a tendency to the lower limit. On the other hand, when comparing the value of the effective thermal conductivity of the composite samples with that of the resin, an increase of 55–115% was found as a result of an increase in the magnetite concentration, transforming the sample from an insulator to a resistive material.

Conflicts of interests

There are no conflicts to declare.