Note on control for hybrid stochastic systems by intermittent feedback rooted in discrete observations of state and mode with delays

1.   Introduction

Stochastic systems have occupied significant positions in diverse fields. Hybrid stochastic differential equations (SDEs) are an important class of stochastic systems, which can effectively describe sudden changes in structures and parameters. Therefore, many scholars have conducted research on hybrid SDEs.

In the study of hybrid SDEs, stability analysis is one of the important research topics ^{[1,2,3,4,5,6,7,8]}. Feedback control is referred to as an important approach to ensure the stability of stochastic systems. However, conventional feedback controllers are rooted in the continuous observations of the system's states. Due to practical limitations, data can only be observed at discrete moments, even if the underlying system is continuous. To address this issue and reduce control costs, Mao ^[9] proposed a feedback control approach for stabilizing a hybrid SDE through discrete-time state observations. Unlike continuous-time controllers, feedback controllers rooted in discrete-time state observations have significant advantages in terms of accuracy and cost. Therefore, discrete-time control strategies ^{[10,11,12,13,14,15,16,17]} have been widely studied. Moreover, a delay is frequently present between the state observed moment and its actual time. Thus, delayed feedback control strategy ^{[18,19,20,21,22,23,24,25,26,27]} has also received extensive attention. Therein, Zhu et al. ^[22] considered both discrete and time-delay issues in designing the controller. They studied exponential stabilization for hybrid SDEs through feedback control rooted in delayed and discrete observations of the state. In addition, Li et al. ^[26] developed a delayed feedback controller for stabilizing the switching diffusion system by discrete observations of state and mode.

Moreover, intermittent control strategy has attracted extensive attention from scholars ^{[28,29,30,31,32,33,34,35]}, particularly been applied in multiagent systems ^[32,33], complex networks ^[34] and other fields. Intermittent control splits time into work and rest periods. The controller switches on during the work period and turns off during the rest period, effectively switching the controlled system between closed-loop and open-loop modes. Compared to classical continuous control strategies, intermittent control strategy is more easily acceptable, which can reduce controller wear, extend the controller's lifespan, and lower costs.

To enhance control performance, a growing number of scholars have used hybrid control strategies, which involves the simultaneous use of multiple control strategies. In particular, Jiang et al. ^[35] considered discrete delayed observations of state and intermittent control method to design the controller. Inspired by these aforementioned works, this paper employs a hybrid control strategy to achieve stabilization, which involves discrete, time-delayed and intermittent components in controller design. Particularly, in this paper, not only the state but also the mode is observed at discrete times. When designing a controller, if the mode is readily apparent (meaning it can be observed without any cost), it can be observed in continuous time. For instance, within a financial system where the mode is referred to as interest rate, this is entirely feasible. However, in most cases, the mode is not evident, and identifying it incurs costs. To lower control expenses, observations pertaining to the state and mode should occur at discrete times. Therefore, our aim is to develop an intermittent feedback controller, rooted in discrete delayed observations related to state and mode, to stabilize an unstable hybrid SDE.

2.   Model description and main results

2.1.   Symbol explanation

Consider a complete probability space $(\varOmega , \mathscr{F}, \{{\mathscr{F}}_{\mu }{{\}}_{\mu }}_{\ge 0}, P)$ satisfying the usual conditions. Let $w\left(\mu \right) = {\left({w}_{1}\left(\mu \right)\cdots {w}_{I}\left(\mu \right)\right)}^{T}$ be an $I$ dimensional Brownian motion defined on the aforementioned probability space. In this probability space, consider a continuous-time Markov chain $\varGamma :{\mathbb{R}}_{+}\to S = \left\{\mathrm{1, 2},\cdots N\right\}$, whose generator $\varLambda = {\left({\gamma }_{uv}\right)}_{N\times N}$ is provided by

in which $\mathit{\Delta} > 0$, ${\gamma }_{uv}$ represents the rate of transition from state $u$ to state $v$, and ${\gamma }_{uu} = -{\sum }_{v\ne u}{\gamma }_{uv}$. Let $w\left(\mu \right)$ be independent of $\varGamma \left(\mu \right)$.

Let ${\upsilon }_{0}$ be a positive number, $C\left(\left[-{\upsilon }_{0}, 0\right], {\mathbb{R}}^{n}\right)$ represent the family of continuous real-valued functions $\xi :\left[-{\upsilon }_{0}, 0\right]\to {\mathbb{R}}^{n}$ with $||\xi || = {\mathrm{sup}}_{-{\upsilon }_{0}\le \theta \le 0}\left|\xi \left(\theta \right)\right|$. ${L}_{{\mathscr{F}}_{\mu }}^{p}(\left[-{\upsilon }_{0}, 0\right];{\mathbb{R}}^{n})$ denotes the family of all ${\mathscr{F}}_{\mu }$ measurable $C\left(\left[-{\upsilon }_{0}, 0\right], {\mathbb{R}}^{n}\right)$ valued random variables $\gamma = \left\{\gamma \left(\theta \right):-{\upsilon }_{0}\le \theta \le 0\right\}$ with $E{||\gamma ||}^{p} <$$\infty$, where $E$ represents the expectation for probability $P$.

2.2.   Model description

Consider an unstable hybrid SDE

on $\mu \ge 0$ along with initial data $\eta \left(0\right) = {\eta }_{0}\ne 0$ and $\varGamma \left(0\right) = {\varGamma }_{0}$, where $h:{\mathbb{R}}^{n}\times S\times {\mathbb{R}}_{+}\to {\mathbb{R}}^{n}$ and $k:$${\mathbb{R}}^{n}\times S\times {\mathbb{R}}_{+}\to {\mathbb{R}}^{n\times I}$. For system (2.1), our objective is to develop a discrete controller $\varpi :{\mathbb{R}}^{n}\times S\times \mathbb{R}\to {\mathbb{R}}^{n}$ with a time delay ${\upsilon }_{0}$ in the drift term to achieve stabilization. Additionally, an intermittent control strategy is incorporated. Thus, the controlled system is as follows:

in which ${\delta }_{\mu } = \left[\mu /\upsilon \right]\upsilon -{\upsilon }_{0}$, $\upsilon > 0$ is the duration separating two consecutive discrete observations, $\left[\mu /\upsilon \right]$ represents the integer part of $\mu /\upsilon$, and ${\mathrm{I}}\left(\mu \right) = {\sum }_{l = 0}^{\infty }{{\mathrm{I}}}_{\left[{\mu }_{l}, {\mu }_{l}+\varphi \mathit{\Delta} \right]}\left(\mu \right)$, ${\mu }_{l} = l\mathit{\Delta}$, $l = \mathrm{0, 1}, 2, \cdots$, $\mathit{\Delta} > 0$ represents the control period, $\varphi \in \left[\mathrm{0, 1}\right]$ represents the control width, and ${{\mathrm{I}}}_{\left[{\mu }_{l}, {\mu }_{l+1}\right]}\left(\mu \right) = \left\{\begin{array}{c}1, \;\;\mu \in [\left.{\mu }_{l}, {\mu }_{l}+\varphi \mathit{\Delta} \right)\\ 0, \mu \in [\left.{\mu }_{l}+\varphi \mathit{\Delta} , {\mu }_{l+1}\right)\end{array}\right.$. Namely, the controller will switch on during $\left.\left[0\right., \varphi \mathit{\Delta} \right),$ $\left.\left[\mathit{\Delta} \right., \left(1+\varphi \right)\mathit{\Delta} \right),$ $\left.\left[2\mathit{\Delta} \right., \left(2+\varphi \right)\mathit{\Delta} \right), \cdots$, switch off during $\left.\left[\varphi \mathit{\Delta} \right., \mathit{\Delta} \right),$ $\left.\left[\left(1+\varphi \right)\mathit{\Delta} \right., 2\mathit{\Delta} \right), \left.\left[\left(2+\varphi \right)\mathit{\Delta} \right., 3\mathit{\Delta} \right), \cdots$.

The original system (2.1) has initial data only at $\mu = 0$, while the controlled system (2.2) requires initial data

To address this issue, set $\lambda \left(\theta \right) = \eta \left(0\right),$ $\varGamma \left(\theta \right) = \varGamma \left(0\right),$ $\theta \in \left[-{\upsilon }_{0}, 0\right]$.

To study the properties of system (2.2), we introduce the auxiliary system as follows:

The system (2.4) is continuous and has no delay term with initial values $\sigma \left(0\right) = {\sigma }_{0} = {\eta }_{0}\ne 0$ and $\varGamma \left(0\right) = {\varGamma }_{0}$.

2.3.   Preliminary knowledge and main result

Assumption 1. There are three positive constants ${K}_{1},$ ${K}_{2}$ and ${K}_{3}$ such that

for $\forall \left(\lambda , \sigma , u, \mu \right)\in {\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\times S\times {\mathbb{R}}_{+}$. Additionally,

for $\forall \left(u, \mu \right)\in S\times {\mathbb{R}}_{+}$.

This assumption implies the linear growth condition

for $\forall \left(\lambda , u, \mu \right)\in {\mathbb{R}}^{n}\times S\times {\mathbb{R}}_{+}$.

Remark 1: Under Assumption 1, from the reference ^[3], it can be inferred that the system (2.2) has a unique solution $\lambda \left(\mu ;\xi , \varsigma , 0\right)$ on $\mu \ge 0$ and

Similarly, under Assumption 1, the auxiliary system (2.4) also has a unique solution denoted by $\sigma \left(\mu ;{\sigma }_{0}, {\varGamma }_{0}, 0\right)$ for $\mu \ge 0$.

Remark 2: Under Assumption 1, here we emphasize the important property from Lemma 2.1 of ^[1], for $\forall {\sigma }_{0}\ne 0$, $P\left\{\sigma \left(\mu ;{\sigma }_{0}, {\varGamma }_{0}, 0\right)\ne 0:\mu \ge 0\right\} = 1.$ Specifically speaking, when any initial data of system (2.4) is nonzero, almost all trajectories will never reach the origin.

Assumption 2. There exist $m > 0$, non-negative numbers ${\tau }_{u},$ ${\beta }_{u}$ and ${c}_{u}$, $u\in S$, satisfying

and

for $\forall \left(\lambda , u, \mu \right)\in \left({\mathbb{R}}^{n}-\left\{0\right\}\right)\times S\times {\mathbb{R}}_{+}$, and ${\beta }_{u}-{\tau }_{u}\le -{c}_{u}.$

Assumption 3. Let $m$ be a positive constant, and $N\times N$ matrix

be a non-singular M-matrix, in which ${\alpha }_{u}\left(m\right) = {c}_{u}m$.

Define

and let

Theorem 1. For a free parameter $\varepsilon \in \left(\mathrm{0, 1}\right)$, let $\varTheta = \frac{1}{{\chi }_{1}}\mathit{log}\frac{{2}^{2{m}_{3}}{b}_{max}}{{b}_{min}\varepsilon } > 0$, and ${\upsilon }^{*} > 0$ be the unique root of Eq (2.9) with respect to ${\upsilon }_{0}\ge 0$,

where ${\chi }_{1} = -\left(m\chi -\frac{1}{{b}_{max}}-m\chi \varphi \right)$, $m > 0$, ${m}_{1} = 2\vee m$, ${m}_{3} = 0\vee \left(m-1\right),$

Under Assumptions 1–3, let ${N}^{+}$ be a positive integer, for $\forall {\upsilon }_{0}\in \left(0, {\upsilon }^{*}\right)$, an intermittent control period $\mathit{\Delta} = \left(\varTheta +2{\upsilon }_{0}\right)/{N}^{+}{\upsilon }_{0}$ and a control width $\varphi \in \left(1-\frac{1}{m\chi {b}_{max}}, 1\right)$ can be selected to make the controlled system (2.2) almost surely exponentially stable.

Remark 3: It is easy to see that the function

on the left side of Eq (2.9) is continuous and increasing. Moreover, $h\left(0\right) < 1$ and $h\left(+\infty \right) = +\infty$. Therefore, Eq (2.9) has a unique positive root.

To prove Theorem 1, a series of lemmas will be introduced in the following section.

3.   Lemmas

Lemma 1. For $\forall \mu \ge 0$, $j > 0$ and $u\in S$, if $s\in \left[\mu , \mu +j\right]$, then

where $\widehat{\gamma } = \underset{u\in S}{max}\left(-{\gamma }_{uu}\right)$.

As for the proof, please refer to the Appendix.

Lemma 2. Under Assumptions 1–3, when $0\le 1-\frac{1}{m\chi {b}_{max}} < \varphi < 1$, the solution of the auxiliary system (2.4) has

where ${\chi }_{1} = -\left(m\chi -\frac{1}{{b}_{max}}-m\chi \varphi \right) > 0$.

As for the proof, please refer to the Appendix.

Lemma 3. Under Assumption 1, for $\forall \varTheta > 0$,

where ${L}_{1}\left(m, {\upsilon }_{0}, \varTheta \right) = \left\{\begin{array}{c}{\left(1+{K}_{2}{\upsilon }_{0}\right)}^{\frac{m}{2}}{e}^{\left(\varTheta +{\upsilon }_{0}\right)m\left({K}_{1}+\frac{1}{2}{{K}_{3}}^{2}+{K}_{2}\right)}, m\in \left(\mathrm{0, 2}\right), \\ \left(1+{K}_{2}{\upsilon }_{0}\right){e}^{\left(\varTheta +{\upsilon }_{0}\right)m\left({K}_{1}+\frac{1}{2}\left(m-1\right){{K}_{3}}^{2}+{K}_{2}\right)}, m\in \left.\left[2, \right.\infty \right).\end{array}\right.$

Proof. For simplicity, denote ${L}_{1}\left(m, {\upsilon }_{0}, \varTheta \right) = {L}_{1}$. When $m\ge 2$, for initial data $\xi \in C\left(\left[-{\upsilon }_{0}, 0\right], {\mathbb{R}}^{n}\right)$, apply the $\mathrm{I}\mathrm{t}\widehat{\mathrm{o}}$ formula to ${\left|\lambda \left(\mu \right)\right|}^{m}$, and have that

By Assumption 1, derive that

Substitute ${\int }_{0}^{\mu }E{\left|\lambda \left({\delta }_{s}\right)\right|}^{m}ds\le {\int }_{0}^{\mu }\underset{-{\upsilon }_{0}\le \theta \le s}{\mathrm{s}\mathrm{u}\mathrm{p}}E{\left|\lambda \left(\theta \right)\right|}^{m}ds\le {\upsilon }_{0}E{||\lambda \left(0\right)||}^{m}+{\int }_{0}^{\mu }\underset{0\le \theta \le s}{\mathrm{s}\mathrm{u}\mathrm{p}}E{\left|\lambda \left(\theta \right)\right|}^{m}ds$ into the above, then

Using the $\mathrm{G}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}$ inequality,

When $m\in \left(\mathrm{0, 2}\right)$,

Therefore, the inequality (3.4) is proven.

Lemma 4. Under Assumption 1, for $\forall \varTheta > 0$,

where

Proof. Denote ${L}_{2}\left(m, {\upsilon }_{0}, \varTheta \right) = {L}_{2}$. When $m\ge 2$,

By (3.5), have that

When $m \in \left( {0, 2} \right)$,

Inequality (3.6) has been proven.

Lemma 5. Under Assumption 1, for $\forall \varTheta > 0$,

where ${L}_{3}\left(m, {\upsilon }_{0}, \varTheta \right)$ can be seen from Theorem 1.

Proof. Denote ${L}_{3}\left(m, {\upsilon }_{0}, \varTheta \right) = {L}_{3}$, when $m\ge 2$,

For $\forall \mu \le s\le \mu +{\upsilon }_{0}$, by (3.5), obtain that

Therefore,

Furthermore,

For $m\in \left(\mathrm{0, 2}\right)$,

Inequality (3.7) has been proven.

Lemma 6. Under Assumption 1, and $\varTheta > 0$, for $\mu \in \left[0, \varTheta +{\upsilon }_{0}\right]$,

where ${L}_{4}\left(m, {\upsilon }_{0}, \varTheta \right)$ can be seen from Theorem 1.

Proof. Let ${L}_{4}\left(m, {\upsilon }_{0}, \varTheta \right) = {L}_{4}$, $\sigma \left(\mu ;{\sigma }_{0}, {\varGamma }_{0}, 0\right) = \sigma \left(\mu \right)$. Taking the difference between system (2.2) and system (2.4), obtain that

when $m\ge 2$. Taking the expectation, yield that

where

and ${T}_{2} = {{\int }_{0}^{\mu }E\left|\varpi \left(\lambda \left({\delta }_{s}\right), \varGamma \left({\delta }_{s}\right), s\right)-\varpi \left(\lambda \left({\delta }_{s}\right), \varGamma \left(s\right), s\right)\right|}^{m}ds.$

By Assumption 1, for $l\upsilon \le s\le \mu \wedge \left(l+1\right)\upsilon$, derive that

By Lemma 1 and inequality (3.4), have that

Hence, for $\mu \in \left[0, \varTheta +{\upsilon }_{0}\right]$,

Furthermore,

By Gronwall inequality, we have that

When $m\in \left(\mathrm{0, 2}\right)$, by $\mathrm{H}\ddot{\mathrm{o}}\mathrm{l}\mathrm{d}\mathrm{e}\mathrm{r}$ inequality, we have that

4.   Proof of Theorem 1

Proof. Write $\lambda \left(\mu ;\xi , \varsigma , 0\right) = \lambda \left(\mu \right)$, $\varGamma \left(\mu ;\varsigma , 0\right) = \varGamma \left(\mu \right)$ for $\mu \ge 0$. Similarly, let

By Lemmas 2 and 3, have that

where ${m}_{2} = 2\wedge m$. By the elementary inequality ${\left(a+b\right)}^{m}\le {2}^{{m}_{3}}\left({a}^{m}+{b}^{m}\right)$ for any $a, b\ge 0$ and Lemma 6,

Using Lemma 5, obtain that

where $\varepsilon = {2}^{2{m}_{3}}M{e}^{-{\chi }_{1}\varTheta }$. Since ${\upsilon }_{0} < {\upsilon }^{*}$, it is obtained from the definition of ${\upsilon }^{*}$ that

Therefore, there exists $\zeta > 0$ such that

It is concluded from (4.3) that

Further considering the solution $\lambda \left(\mu \right)$ on $\mu \ge \varTheta +2{\upsilon }_{0}$, there is a ${N}^{+}$ such that $\varTheta +2{\upsilon }_{0} = {N}^{+}\mathit{\Delta} {\upsilon }_{0}$. Meanwhile, $\lambda \left(\mu \right)$ can be referred to as the solution of the Eq (2.2) with the initial value $\lambda \left({N}^{+}\mathit{\Delta} {\upsilon }_{0}\right),$ $\varGamma \left({N}^{+}\mathit{\Delta} {\upsilon }_{0}\right)$. By following the same procedure as mentioned above, show that

Repeating the above procedure, have that

By Lemma 4, have that

From the Markov inequality and inequality (4.4), it can be concluded that, for all $z\ge 0$,

According to the $\mathrm{B}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{l}-\mathrm{C}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{l}\mathrm{l}\mathrm{i}$ lemma, there is a set ${\varOmega }_{0}\in \mathscr{F}$ with $P\left({\varOmega }_{0}\right) = 1$, then for almost all $\omega \in {\varOmega }_{0}$, there is an integer ${z}_{0} = {z}_{0}\left(\omega \right)$ such that for $\forall z > {z}_{0}\left(\omega \right)$,

Hence,

The proof is completed.

5.   Numerical example

Consider a stochastic differential equation

in which $\varGamma \left(\mu \right)$ represents a Markov chain that takes values in $S = \left\{\mathrm{1, 2}\right\}$ with the generator $\varLambda = \left(\begin{array}{cc}-2& 2\\ 1& -1\end{array}\right),$ and

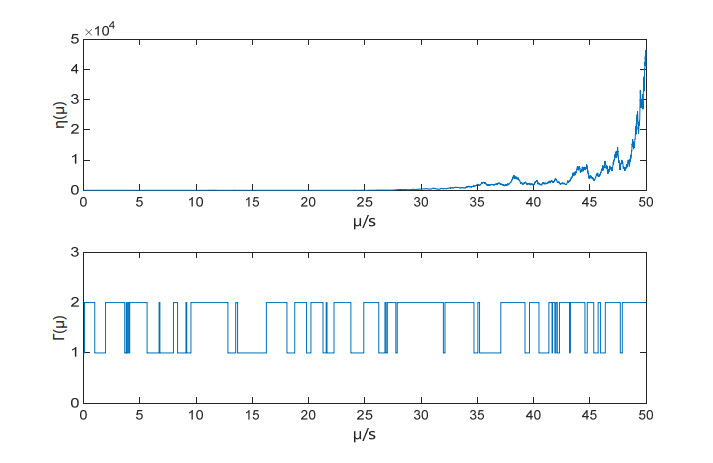
Using the Euler-Maruyama numerical method, with $\eta \left(0\right) = 1$, $\varGamma \left(0\right) = 1$ and the step size ${10^{ - 5}}$, it is seen that the system (5.1) is unstable, as shown in Figure 1.

In order to stabilize the system (5.1), the control function is designed as follows:

By simple calculations, Assumption 1 is satisfied with ${K}_{1} = 0.4,$ ${K}_{2} = 0.5$ and ${K}_{3} = 0.5$. Choosing $m = 1$, we can infer from Assumption 2 that

From (2.6), obtain a non-singular M-matrix.

By (2.7) and (2.8), we have

By Lemma 2, it is known that if $\varphi \in \left(\mathrm{0.7375, 1}\right)$, then the auxiliary controlled stochastic system $d\sigma \left(\mu \right) = \left(h\left(\sigma \right(\mu ), \varGamma (\mu ), \mu )+\varpi \left(\sigma \left(\mu \right), \varGamma \left(\mu \right), \mu \right){\mathrm{I}}\left(\mu \right)\right)d\mu +k\left(\sigma \right(\mu ), \varGamma (\mu ), t)dw\left(\mu \right)$ is almost surely exponentially stable.

This paper aims to develop an intermittent feedback controller with discrete observations of both state and mode with delays for stabilizing system (5.1). The controlled system becomes

We choose $\varphi = 0.95,$ $\varepsilon = 0.9$, and it can be obtained that ${\chi }_{1} = 0.1062,$ $\varTheta = 1.0126$. Then (2.9) becomes

and its unique root is ${\upsilon }^{*} = 4.6436\times 1{0}^{-5}$. Taking $\upsilon = 1{0}^{-4},$ ${\upsilon }_{0} = 1{0}^{-5},$ $\mathit{\Delta} = 1{0}^{-5}$, from Theorem 1, we can get that the system (5.4) is almost surely exponentially stable. The simulated trajectory is shown in Figure 2 with the step size $1{0}^{-5}$.

6.   Conclusions

This paper delves into the issue of exponential stabilization for hybrid stochastic systems by employing an intermittent feedback control with discrete delayed observations related to both state and mode. Compared to state discrete observations of the feedback controller, model observations are also performed at discrete times, which is more practical and cost-saving. Using M-matrix theory and intermittent control approach, the feedback stabilization theory of hybrid stochastic systems is established. However, this study focuses on the stabilization for hybrid stochastic systems and the underlying systems do not consider some important practical factors, such as time delay, which will be addressed in future work.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to thank Humanities and Social Science Fund of Ministry of Education of China (No. 23YJAZH031), Natural Science Foundation of Hebei Province of China (Nos. A2023209002, A2019209005), China Postdoctoral Science Foundation (No. 2017M621588), Tangshan Science and Technology Bureau Program of Hebei Province of China (No. 19130222g) for their financial support.

Conflict of interest

The authors declare there is no conflict of interest.

Appendix

Proof of Lemma 1.

Given $\varGamma \left(\mu \right) = u$, define stopping time ${\stackrel{̄}{\kappa }}_{u} = \mathit{inf}\left\{s\ge \mu :\varGamma \left(s\right)\ne u\right\}$. Let $i\mathrm{nf}\Phi = \infty$. Since ${\stackrel{̄}{\kappa }}_{u}-\mu$ conforms to an exponential distribution with the parameter $-{\gamma }_{uu}$, one has that, for $s\in \left[\mu , \mu +j\right]$,

Thus, assertion (3.1) is obtained.

Proof of Lemma 2.

Define $H\left(\sigma , u, \mu \right) = {b}_{u}{\left|\sigma \right|}^{m},$ $\left(\sigma , u, \mu \right)\in \left({\mathbb{R}}^{n}-\left\{0\right\}\right)\times S\times {\mathbb{R}}_{+}$, then

where generalized $\mathrm{I}\mathrm{t}\widehat{\mathrm{o}}$ operator $LH:\left({\mathbb{R}}^{n}-\left\{0\right\}\right)\times {\mathbb{R}}_{+}\times S\to \mathbb{R}$ is given by

As $\mu \in [\left.{\mu }_{l}, {\mu }_{l}+\varphi \mathit{\Delta} \right)$, ${\mathrm{I}}\left(\mu \right) = 1$. By Assumptions 2 and 3, conclude that

By (2.6) and (2.7), have that

hence,

As $\mu \in [\left.{\mu }_{l}+\varphi \mathit{\Delta} , {\mu }_{l+1}\right)$, ${\mathrm{I}}\left(\mu \right) = 0$, then

Since ${b}_{u}{\alpha }_{u}\left(m\right)-{\sum }_{v = 1}^{N}{\gamma }_{uv}{b}_{v} = 1$,

From (A4) and (A5),

For any integer $\iota \ge 1$, define stopping time ${\kappa }_{\iota } = \mathit{inf}\left\{\mu \ge {\mu }_{0}:\left|\sigma \left(\mu \right)\right|\ge \iota \right\}$. It is evident that when $\iota \to \infty$, ${\kappa }_{\iota }\to \infty$. When $\mu \ge 0$, by utilizing the $\mathrm{I}\mathrm{t}\widehat{\mathrm{o}}$ formula, yield that

When $\iota \to \infty$, get that

which means that

By $0\le 1-\frac{1}{m\chi {b}_{max}} < \varphi < 1$, ${\mu }_{l} = l\mathit{\Delta}$,

Let $l > {N}^{+}$, when $\mu \in [\left.{\mu }_{l}, {\mu }_{l}+\varphi \mathit{\Delta} \right)$,

When $\mu \in \left[ {{\mu _l} + \varphi \mathit{\Delta} , {\mu _{l + 1}}} \right)$,

Substituting this into (A6), yield that

hence $E{\left|\sigma \left(\mu \right)\right|}^{m}\le ME{\left|{\sigma }_{0}\right|}^{m}{e}^{-{\chi }_{1}\mu }$. Inequality (3.2) has been proven.

Next, we start to prove inequality (3.3). Similarly to (A3), employing the $\mathrm{I}\mathrm{t}\widehat{\mathrm{o}}$ formula to ${\left|\sigma \left(\mu \right)\right|}^{m}$, obtain that

As $\mu \in [\left.{\mu }_{l}, {\mu }_{l}+\varphi \mathit{\Delta} \right)$, ${\mathrm{I}}\left(\mu \right) = 1$. By Assumption 2,

As $\mu \in \left.\left[{\mu }_{l}+\varphi \mathit{\Delta} \right., {\mu }_{l+1}\right)$, ${\mathrm{I}}\left(\mu \right) = 0,$

By (2.8), we have that

${\rm{Gronwall}}$ inequality leads to

Hence,

If $m = 2$,

For a non-negative integer $l$, we have that

Under Assumption 1 and utilizing the $\mathrm{B}\mathrm{u}\mathrm{r}\mathrm{k}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{d}\mathrm{e}\mathrm{r}-\mathrm{D}\mathrm{a}\mathrm{v}\mathrm{i}\mathrm{s}-\mathrm{G}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{y}$ inequality, we yield that

Substituting (A7) into the above inequality, we obtain that

For $m\in \left(\mathrm{0, 2}\right)$, by $\mathrm{H}\ddot{\mathrm{o}}\mathrm{l}\mathrm{d}\mathrm{e}\mathrm{r}$ inequality, we get that

where $J = 3+\left(6\mathit{\Delta} {{K}_{1}}^{2}+12{{K}_{3}}^{2}+6\mathit{\Delta} {{K}_{2}}^{2}\right)\frac{1}{2\chi }\left({e}^{2\chi \mathit{\Delta} }-1\right)$.

Repeating the above process, we have that

Using Chebyshev's inequality, have we that

According to the $\mathrm{B}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{l}-\mathrm{C}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{l}\mathrm{l}\mathrm{i}$ lemma, there is a set ${\varOmega }_{0}\in \mathscr{F}$ with $P\left({\varOmega }_{0}\right) = 1$, then for almost all $\omega \in {\varOmega }_{0}$, there exists an integer ${q}_{0} = {q}_{0}\left(\omega \right)$ such that for $\forall q\ge {q}_{0}$,

Therefore, for $q\mathit{\Delta} \le \mu \le \left(q+1\right)\mathit{\Delta}$,

Letting $\mu \to \infty$, obtain that

This completes the proof.