Transition characteristics of the dynamic behavior of a vehicle wheel-rail vibro-impact system

1.   Introduction

With the rapid development of railway technology in China, there are higher requirements for the speed and comfort of the train. The vertical vibration problem caused by the speed increase of the train is becoming more and more prominent. The rail is connected by welding, which eliminates the impact of rail joints and maintains the continuity and integrity of the line to the greatest extent. However, due to the influence of welding materials, welding process level and other factors, under the action of repeated rolling of wheels and wear between wheels and rails, various defects will appear at the welded joints of the rails, which will aggravate the irregularity of the rails. Its existence will cause the deterioration of the dynamic response of the wheels and rails, cause the impact vibration of the wheels and rails and have a great influence on the vibration of the wheels and rails. There is even a safety hazard of wheel-rail detachment ^[1].

In recent years, the theoretical research on vehicle system dynamics has attracted the attention of scholars at home and abroad. The average comfort approach and the Sperling method were used in reference ^[2] to assess the comfort of riding railway vehicles subjected to vertical vibration. Reference ^[3] developed a three-dimensional coupled dynamic model of the vehicle-track, and to find the wheel-flat signal, employed two techniques based on Variational modal analysis and envelope spectrum. Comparing the concurrent existence of wheel planarity and wheel eccentricity provided more evidence of the viability of the suggested strategy. To forecast how the vehicle body and equipment will react to tracking failures, reference ^[4] developed a 3D rigid-flexible coupled vehicle system dynamics model. The suspension parameters were designed using the DVA theory. Reference ^[5] employed numerical simulation to examine how the anti-winding damping affected the vertical vibration and ride quality of the vehicle body. On the vehicle body vertical acceleration power spectral density and ride comfort index, the impacts of damping, stiffness and damper installation angle were primarily studied. Reference ^[6] presented a tangential contact theory based on the FastSim algorithm. With calculation speed an order lower than the Variational Theory, the recommended technique offers errors for creep forces of around 4%. The disturbance rejection and force tracking damper controller algorithms were used in reference ^[7] to manage the required force of the MR damper. This study demonstrated that the proposed semi-active suspension methods may greatly minimize a vehicle's vertical vibrations. Reference ^[8] described an alternative analytical approach based on an analogous VBI model under resonant excitations. The main causes of the excessive damping issue were then identified. The proposed method provided insights that enable a precise estimation of the extra damping amount needed to take into account VBI effects on short railway bridges with simple supports, as shown by the provided numerical demonstrations. A classifier for track defects has been created to automatically detect track faults, according to reference ^[9]. The findings demonstrated how carbody vibration was used to extract the feature of track defects, which are then categorized using the suggested feature space and machine learning approaches. Reference ^[10] gave a summary of the assessment standards relating to feelable vibrations and ground-borne noise, experimental and numerical forecasting methods, the main vehicle and track parameters that may have an impact on vibration levels, and various suggested mitigation solutions. Reference ^[11] suggested calculating the Root-Mean-Square acceleration for various carbody areas using the bond graph approach and Sperling's Riding Index for a low-to-medium speed vehicle. Using ISO 2631, the physiological consequences of the vibrations on the human body were examined. Reference ^[12] used NP versus λ3mm scatter plots from the ECF database to examine how track maintenance operations affect vehicle dynamics. In reference ^[13], the vertical dynamic model of the railway vehicle bogie-carbody-seat coupled system was established, and the numerical analysis method of the vertical dynamic model of the railway vehicle bogie-carbody-seat coupled system was given by variable transformation. In reference ^[14], the free vibration and forced vibration problems of four-axle vehicles with double spring suspension were studied, and the vertical dynamics problem of the vehicle was simplified using the Lagrange equation, which greatly simplified their solution. The relationship between random vibration and motion characteristics of railway vehicles was studied in reference ^[15], and a correlation between random vibration and vertical acceleration of railway vehicles was discovered. In reference ^[16], the impact vibration response features of rail vehicles under different shock excitation sources were classified and analyzed in detail, and some attempts and possible mitigation measures of using rail vehicle vibration to detect rail defects were summarized. In reference ^[17], a two-degree-of-freedom numerical model of 1/2 vehicle with a two-stage Ruzicka model was established, and the multi-objective optimization genetic algorithm was used to verify that the optimized damping parameters could effectively improve the vibration level of the target. The wheel-rail interaction characteristics under the effect of flat scar were simulated by modifying the wheel radius in reference ^[18], and the wheel-rail impact dynamic load characteristics were investigated. In reference ^[19], a three-dimensional finite element model of wheel-rail rolling contact was created. The mechanical response of a wheel-rail impact generated by a flat tire was examined using the explicit finite element approach. The change in the wheel-rail contact state was explained during the process of wheel flat impact on the rail. The effects of fatigue damage and strain rate effect of wheel-rail material on wheel-rail impact reaction were investigated, as well as the influence of critical parameters such as train speed, flat length and axle load. Reference ^[20] investigated the dynamic characteristics of the vehicle wheel-rail impact vibration in crosswind. The rapid Fourier transform harmonic synthesis method and the Davenport coherence function were used to create a wind load model, and the lateral displacement of the high-speed train wheelset under crosswind was then calculated. The dynamic model of the vehicle wheel-rail collision vibration system under crosswind conditions was developed. The impacts of vibration frequency, wheel-rail gap and lateral damping on the characteristics of the vehicle wheel-rail lateral gap impact vibration system were studied.

The application research of non-smooth dynamical systems and collision-shock vibration systems is also rapidly developing. The classic Melnikov approach was utilized in reference ^[21] to investigate the hybrid piecewise smooth system model with impulse effect and noise excitation. The stochastic Melnikov process of the system was developed by measuring the distance between the stable and unstable manifolds after the disturbance, and the criterion for the occurrence of chaos in the system with or without noise stimulation was established. Finally, the algorithm's correctness was validated using this new extension approach and numerical simulation. The Jacobi stability of the five-dimensional self-excited monopole disk generator system was extensively studied in reference ^[22] based on the Kosambii-Cartan-Chern theory. The Jacobi stability of the equilibrium point under specified parameter values was discussed using the eigenvalues of the second KCC invariant matrix. The periodic orbit was shown to be Jacobi unstable. The pulse control problem in a five-dimensional self-excited homopolar disk generator was also studied, and the hidden attractor was efficiently suppressed. Reference ^[23] analyzed the impact gap value's effect on the mean translating velocity of the robot's wheel platform and made recommendations for designers as well as scholars of similar robotic devices. Reference ^[24] studied the influence of important system characteristics, such as the change of size gap term, load resistance and electromagnetic coupling coefficient, on the vibration and energy behavior of electromagnetic shock damping. A study of VCM of mechanical and electrical devices used in the HPS was presented in reference ^[25], along with an introduction of problems caused by vibration based on earlier research from roughly 30 years ago. There have been investigations on the sources of vibrations of HPS spinning and non-rotating machines, as well as vibration measuring standards. A two-degree-of-freedom vibratory mechanism engaging a single stiff stop was examined in reference ^[26]. Some unusual paths to chaos are investigated, including Period-doubling bifurcations of periodic movements with a single impact. The paths to chaos identified in vibro-impact systems were found to be fundamentally distinct from the standard Period-doubling route to chaos observed in conventional sequential maps. In reference ^[27], using a mechanical model of a two-degree-of-freedom forced vibration system with clearance-elastic constraints, the diversity and bifurcation characteristics of periodic impulsive vibration of this type of non-smooth vibration system were investigated. In reference ^[28], the Poincaré map equation of vibration systems with gaps was established, and the stability and local bifurcation of the fixed point of the map was examined. The equation described the symmetric periodic impact motion of a two-degree-of-freedom gap vibration system. Through numerical simulation, the Fork bifurcation, the Period-doubling bifurcation and the "Grazing" singularity transition to chaos were examined as part of the overall bifurcation process of the symmetric periodic collision motion of the vibration system with gaps. Reference ^[29] considered a two-degree-of-freedom vibro-impact system with two-sided clearances. It was shown that the system's periodic motion has a variety of pattern types and transitional properties. There was a relationship between the presence of a saddle-node bifurcation around the grazing bifurcation and the variance in displacement amplitude.

The existing research works show that there were few studies on the vehicle vertical system dynamics from the perspective of bifurcation and chaos characteristics, and these research works considered the theoretical analysis and numerical simulation when the connection stiffness and damping are linear in the system, and the research on the complex vibro-impact system with nonlinear stiffness is limited. Thus, in a dynamical system, with the increase of nonlinear factors, the system will appear more complex with bifurcation and singularity problems. For example, when considering the strong nonlinear factors of the air spring in the secondary suspension of the vehicle, there are more complex nonlinear dynamic behaviors contained in the vehicle impact vibration system, and there are also complex roads leading to the chaotic motion of the system: The quasi-periodic road contains Hopf bifurcation, Neimark-Sacker bifurcation, torus doubling and so on.

Furthermore, in an existing dynamic characteristics analysis of the wheel-rail impact vibration system, the rails were frequently treated as a rigid body to deal with the wheel-rail dynamics problem, rather than as a flexible body to calculate the vertical impact stiffness and damping value between the wheel and rail for dynamic analysis. By integrating the qualitative analysis approach of nonlinear dynamics with the vehicle wheel-rail impact vibration system in engineering practice, a two-degree-of-freedom flexible impact vibration model with high and low uneven clearances of welded joints of rails has been produced. It is demonstrated that there is a process of transition from the vehicle wheel-rail impact vibration system to chaos due to Hopf bifurcation and Neimark-Sacker bifurcation through utilizing an impact interface as the section of the Poincaré map and the fourth-order Runge-Kutta numerical method with variable step size. The detailed examination of its bifurcation and chaotic behavior offers a theoretical foundation for the best design of vehicle stability in practical running.

2.   Uneven model of the welded joint of a rail

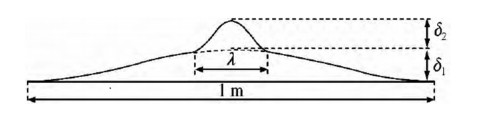
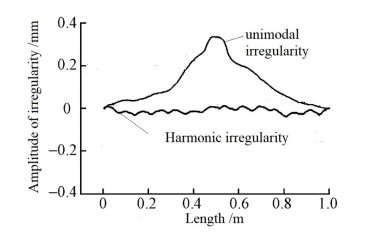
There are some differences in the waveform types of rail joint irregularity, but in general, they can be summarized into 3 types: Convex irregularity, concave irregularity and harmonic irregularity. The harmonic irregularity contains periodic irregularities with wavelengths of tens to one hundred millimeters and usually superposes convex, concave or step-type waveforms, as shown in Figure 1. Among them, the unimodal irregularity is usually composed of half-period cosine wave superposition of weld irregularity with a wavelength of about 0.1 m. The range of joint irregularity is usually between 0.2 and 0.4 mm, accounting for 82% of the total number of samples of range distribution statistical results, and the samples larger than 0.4 mm account for 15% ^[30]. A unimodal rail joint irregularity model is used as the main external excitation to study the nonlinear dynamic response of the vehicle vertical system.

Figure 2 shows a convex welded joint irregularity model, which can be described by a three-segment cosine function and can be expressed as the following displacement function:

In Eq (1):

t—time taken for the vehicle to pass the welded joint irregularity /(s);

v—Vehicle running speed /(km/h);

δ₁, δ₂—long wave and short wave depth /mm respectively for rail welded joints /(mm);

λ—wavelength of short wave irregularity of welded joint /(m).

The research showed that the wheat-rail impact at the welded joint is mainly controlled by short-wave irregularity (wavelength less than 0.2 m) ^[31], and the maximum safety limit of short-wave irregularity amplitude is 0.2 mm, which is ${\delta _2}$ < = 0.2 mm. The maximum safety limit for long-wave irregularity is 0.3 mm.

3.   The impact stiffness and damping were calculated by finite element fitting

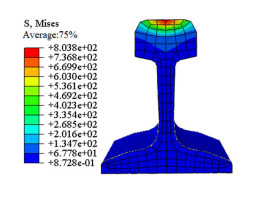
In this paper, U7lMn-rail used in high-speed railways was taken as the calculation model ^[32]. The three-dimensional spatial entity method is adopted to solve the model. After modeling through CATIA, the model was imported into ABAQUS for finite element calculation, as shown in Figure 3. If the axle weight of the vehicle is 150 kN and the wheel-rail force is 1.5 times the static wheel load ^[33], the vertical impact force of the wheel-rail can be 115 kN and the impact force is applied directly above the middle of the model. Table 1 shows the calculation parameters.

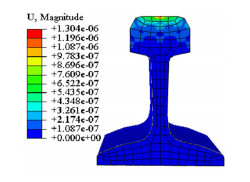
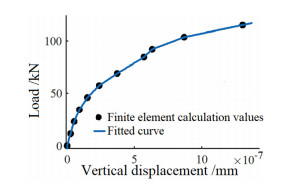
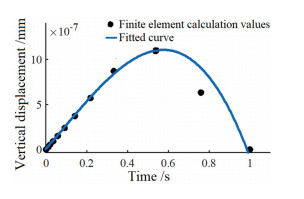
The stress contour and vertical displacement diagram of U7lMn-rail obtained by finite element simulation are shown in Figures 4 and 5. To find the equivalent impact stiffness and damping values, the finite element calculation results were fitted into an approximate curve by MATLAB for calculation purposes as shown in Figures 6 and 7.

The maximum vertical displacement and load of the load-displacement curve are respectively taken as calculation values:

According to Hooke's theorem, the equivalent impact stiffness can be obtained:

The curve of rail deformation and displacement is fitted with the following function:

The fitting load-displacement curve is calculated by applying a vertical dynamic load with a maximum value of 115 kN to the rail, which can reflect the damping characteristics of the material ^[34,35]. That is, the area S enclosed by the curve of vertical deformation displacement of the rail with load is equal to the negative work done by the equivalent damping force of the rail in a cycle:

By substituting Eq (2) into Eq (3), the equivalent impact damping can be obtained as:

4.   Vehicle impact vibration system and its dynamic equation

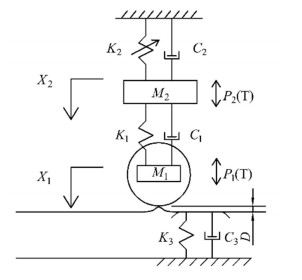
Based on the 1/4 vehicle system model, assuming that the vertical displacement of the vehicle body is 0, the vehicle impact vibration system model is abstracted from the maximum safety amplitude ${\delta _2}$ of short-wave irregularity of the welded rail joint as the wheel-rail impact clearance, and the nonlinear dynamic behavior of the vehicle impact vibration system near the safety critical value of short-wave along amplitude of the welded joint was studied.

As shown in Figure 8, ${M_1}$ is half of the wheelset mass, ${M_2}$ is half of the bogie mass, ${K_1}$ is the suspension stiffness of the first series, ${K_2}$ is the vertical stiffness of the air spring of the second series, ${K_3}$ is the equivalent impact stiffness of the rail, ${C_1}$ is the damping of the first series of suspension, ${C_2}$ is the damping of the second series of suspension, ${C_3}$ is the equivalent impact damping of the rail and $D$ is the impact clearance of the wheel and rail.

The vertical stiffness of vehicle air spring can be fitted as a quadratic function ^[36], and the excitation amplitude and nonlinear stiffness are the major factors affecting the nonlinear characteristics of air spring suspension, and among the nonlinear forces, only the cubic nonlinear force plays a role ^[37], ${K_{22}}$ is the nonlinear stiffness coefficient, so the vertical stiffness of air spring is taken as:

The periodic wheel-rail impact force at the irregularity of the welded joint of the rail:${P_i}(T) = {P_i}\sin (\Omega T + \tau)$ is taken as the external excitation acting on the wheelset and bogie, where:${P_i} = {K_3} \times {\delta _i}/2$, ($i = 1, 2$), $\Omega = v/100$, respectively takes the centroid of the wheelset and bogie as the origin of coordinates, and takes the vertical downward movement as the positive direction to establish a two-dimensional coordinate system as shown in Figure 8. The fixed length of the rail ^[38] is 100 m, that is, the longitudinal distance of each welded joint along the rail. Assuming that the vehicle running speed is v = 246 km/h ~ 263 km/h, the vertical system parameters of a certain type of vehicle are taken as the calculation parameters of the system, as shown in Table 2.

When a wheel-rail collides, the system's kinetic energy (T), potential energy (V) and dissipated energy (D) are as follows:

In Eq (5):

${X_1}$- Wheelset vertical vibration displacement /mm;

${X_2}$- Vertical vibration displacement of bogie /mm;

${\dot X_1}$- Wheelset and track impact instantaneous velocity /(mm/s);

${\dot X_2}$- Vertical vibration speed of bogie /(mm/s);

The motion differential equation of the system is established by using the Hamiltonian principle and Lagrange equation:

In Eq (6):

${q_i}$- Generalized displacement vector;

${\dot q_i}$- Generalized velocity vector;

${Q_i}$- Generalized force vector;

The differential equation of motion of the system may be found by inserting Eqs (4) and (5) into Eq (6):

Given ${M_1} \ne 0$, ${K_1} \ne 0$, the dimensionless form of Eq (7) is:

In Eq (8): "${\ddot x_i}$" represents the two-order derivative of the ${M_i}$ oscillator's displacement concerning dimensionless time $t$, and "${\dot x_i}$" stands for the first-order derivative of the ${M_i}$ oscillator's displacement ${x_i}$ concerning dimensionless time $t$.

5.   Bifurcation of periodic motion of the system and transition to chaos

Assuming that the vehicle running speed is: v = 246 km/h ~ 263 km/h, the corresponding dimensionless excitation frequency is: $\omega \in [1.08, {\text{ }}1.15]$. The Poincaré map $T$ of the periodic impact of the system is constructed to compute the dynamic response of the vehicle wheel-rail system when the impact vibration occurs to analyze the variety, existence area and local bifurcation problems of the periodic motion of the system.

5.1.   Hopf bifurcation and the quasi-periodic road to chaos

Reference ^[39] studies that the critical speed of railway passenger cars is as follows. Chaos is observed when the system experiences nonlinear vibration events like Hopf bifurcation, and the change from chaos to quasi-periodic solution may be associated. Reference ^[40] uses a numerical method to study Hopf bifurcation and the limit cycle of railway passenger cars and verifies the results by full-scale roller stage test.

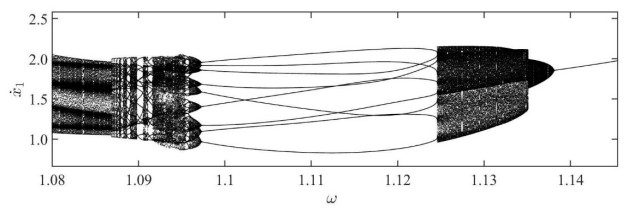
The system parameters in Table 2 are converted to the dimensionless parameters of the system:$b = 0.055$, $\zeta = 0.013$, ${\mu _m} = 1.39$, ${\mu _{c2}} = 0.714$, ${\mu _{c3}} = 0.039$, ${\mu _k}_{21} = 0.9125$, ${\mu _k}_{22} = 1091$, ${\mu _k}_3 = 34125$, ${p_2} = 0.4$. The fourth-order Runge-Kutta numerical method is used to solve the dynamic system, and the bifurcation diagram when $\omega \in [1.08, {\text{ }}1.15]$ is obtained, as shown in Figure 9. In this figure, the abscissa represents the dimensionless excitation frequency, and the dimensionless instantaneous speed when the wheelset ${M_1}$ goes downward and impacts with the rail is represented by the ordinate. The Hopf bifurcation occurs as the excitation frequency of the system decreases.

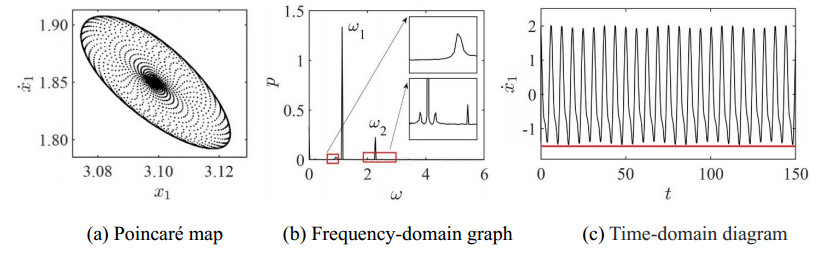
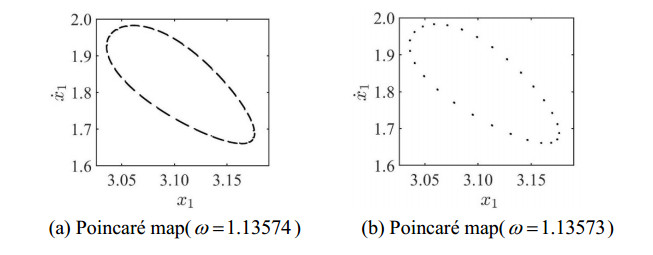
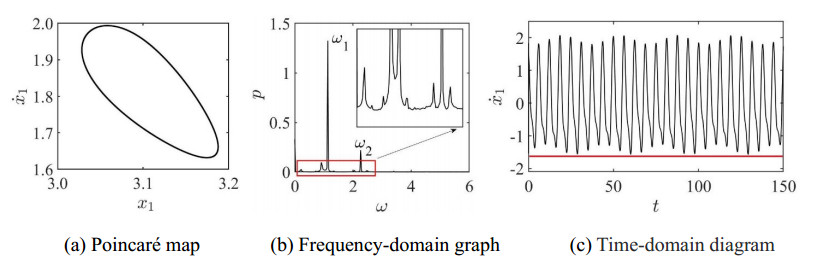
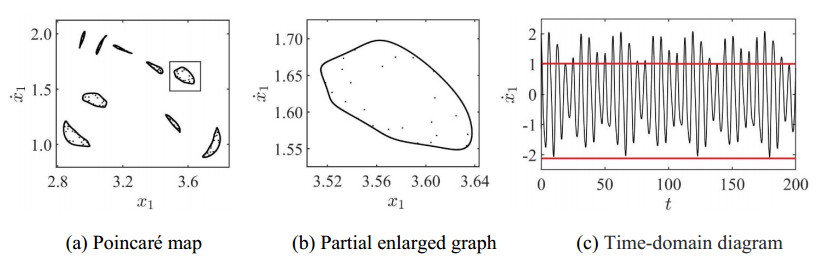
In Figure 10(a), the abscissa represents the dimensionless displacement of the $q = p/n$ periodic motion of the wheelset on the Poincaré section, and the dimensionless instantaneous speed when the wheelset ${M_1}$ goes downward and impacts with the rail is represented by the ordinate. The periodic motion of the impact vibration system is usually expressed by $q = p/n$ ^[41], $n$ denotes the number of force cycles and $p$ denotes the number of collisions between the wheelset and the rail. At that time, the Poincaré map of the system is a fixed point, then the system has stable $q = 1/1$ periodic motion, and no modulation phenomenon occurs. Only the vibration frequency of the fundamental frequency appears in the frequency domain diagram, as shown in Figure 10(b). The Time-domain diagram of the system presents an approximate sinusoidal periodic stable state and has an equal maximum value periodically. The comparison of the red isolines in Figure 10(c) is shown.

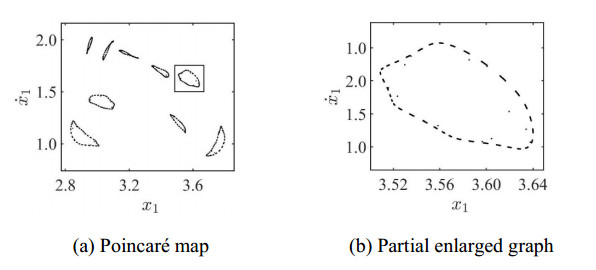
When $\omega$ gradually decreases through 1.38105, the system undergoes Hopf bifurcation, and the $q = 1/1$ periodic motion gradually destabilizes and bifurcates out of the quasi-periodic oscillatory state, forming a closed invariant cycle on the projected Poincaré section. It is worth noting that the attractive invariant cycle near the bifurcation point has smoothness, as shown in Figure 11(a).

In the frequency domain diagram, there are two primary frequency vibration frequencies, ${\omega _1}$ and ${\omega _2}$, and their ratio is irrational. In addition, there are secondary frequency vibration frequencies, as shown in Figure 11(b). The Time-domain diagram of the system transitions from an approximately single-period to a multi-period oscillatory state, as shown in Figure 11(c).

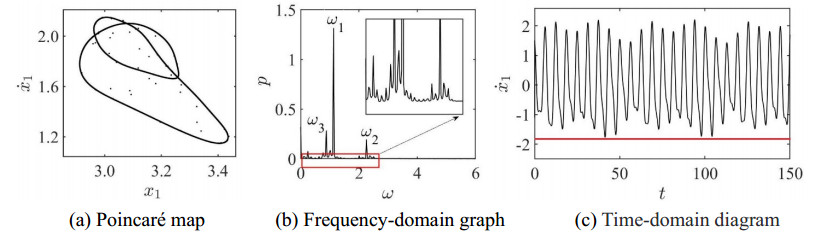
As the excitation frequency $\omega$ gradually decreases, the attractive invariant ring gradually breaks and becomes larger and its smoothness is also destroyed. The system is in a quasi-periodic oscillatory state, as shown in Figure 12(a). With the further decrease of the parameter $\omega$, the system enters the quasi-periodic oscillatory state after phase locking ($q = 27/27$ periodic motion) as shown in Figure 12(b). At this time, the Poincaré map of the system is a closed smooth invariant cycle. There are two major frequency vibration frequencies and it is worth noting that their secondary frequency vibration frequencies gradually increase. As shown in Figure 13(a), (b). The difference in the peak amplitude of the Time-domain diagram of the system is larger than before, as shown in Figure 13(c).

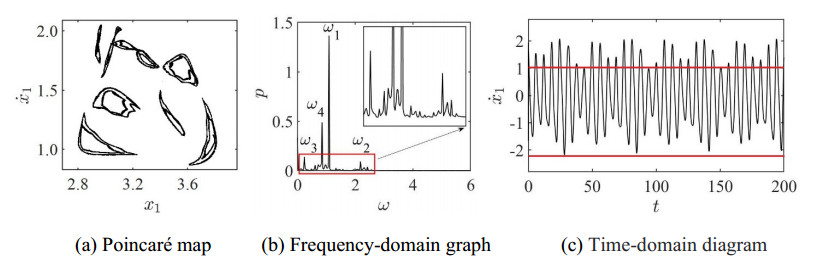
When the $\omega$ goes through 1.13415, the Neimark-Sacker bifurcation occurs, and the system is in the quasi-periodic oscillatory state. At this time, three major frequency vibration frequencies, ${\omega _1}$, ${\omega _2}$ and ${\omega _3}$, appear in the frequency domain diagram, and their secondary frequency vibration frequencies become more, as shown in Figure 14(a), (b). The difference between the peak amplitude of the Time-domain diagram of the system is larger, and the oscillation period is increased, as shown in Figure 14(c).

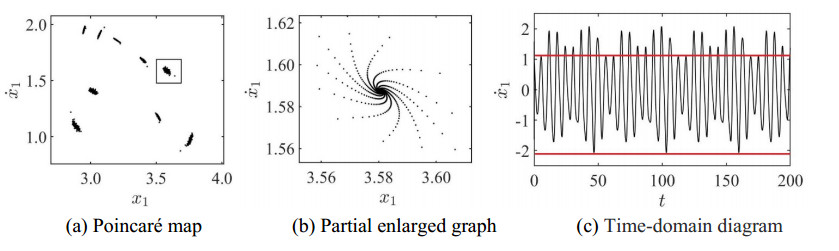
However, as $\omega$ continues to decrease, when $\omega = 1.0972$, as illustrated in Figure 15(a), the system's Poincaré map has 9 fixed points and is in periodic motion with $q = 9/9$, and Figure 15(b) shows the partially enlarged drawing of one of the fixed points. At this time, the Time-domain diagram of the system changes and is in the state of 9-period oscillation, as shown in Figure 15(c).

Here, $T_{p/n}^1$ is used to denote the p attracting invariant cycles generated on the Poincaré map by Hopf bifurcation of $q = p/n$ fixed points in the impact vibration system ^[19]. When $\omega = 1.0961$, 9 attracting invariant cycles $T_{9/9}^1$ are generated by projection in the Poincaré map. At this time, the system enters the quasi-periodic oscillatory state due to Hopf bifurcation, as shown in Figure 16(a), and the partially enlarged drawing is shown in Figure 16(b). The Time-domain diagram of the system is shown in Figure 16(c)

As the parameter $\omega$ gradually decreases, the 9 attracting invariant circles gradually deform and the system then enters a multi-period oscillation, as shown in Figure 17(a), (b).

When $\omega$ crosses 1.0945, the system undergoes $2T_{9/9}^1$ tori doubling, as shown in Figure 18(a), which indicates that the system may enter a chaotic state with further changes of $\omega$. In the frequency domain diagram, there are four major frequency vibration frequencies, and the size of the main frequency has increased compared with before. The system contains abundant secondary frequency vibration frequencies, as shown in Figure 18(b). The Time-domain diagram of the system is still in the state of multi-period oscillation, as shown in Figure18(c).

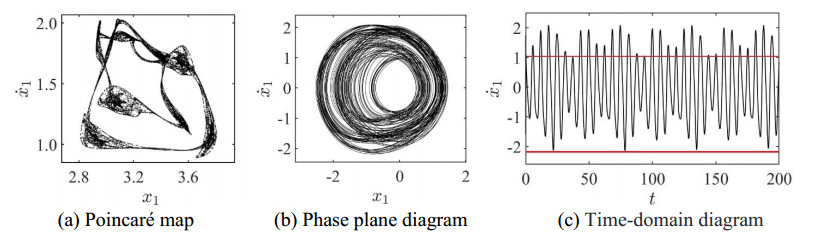
Continue to decrease $\omega$ to 1.0935, the system finally enters the chaotic state that should be avoided. Figure 19(a) shows the strange attractor with a very complex unique and self-similar structure, and the phase plane diagram of the system is shown in Figure 19(b). At this time, the Time-domain diagram shows an aperiodic oscillatory state, as shown in Figure 19(c). The system's motion state follows deterministic law yet exhibits random motion.

5.2.   The road of period-doubling bifurcation to chaos

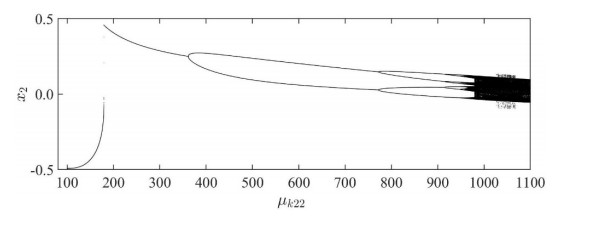
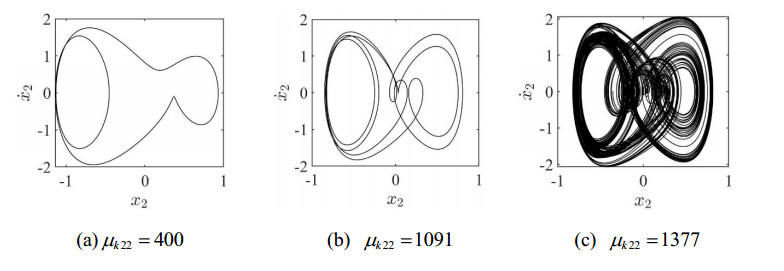
Taking the parameters of the same vehicle impact vibration system in the previous chapter: $b = 0.55$, $\zeta = 0.013$, ${\mu _m} = 1.39$, ${\mu _{c2}} = 0.714$, ${\mu _{c3}} = 0.039$, ${\mu _k}_{21} = 0.9125$, ${\mu _k}_3 = 34125$ and ${p_2} = 0.4$. Continue to use the fourth-order Runge-Kutta numerical method to simulate the system, and obtain the bifurcation diagram when ${\mu _{k22}} \in [100, {\text{ 1100}}]$ as shown in Figure 20. The abscissa in the diagram represents the dimensionless nonlinear stiffness ratio of the system, and the ordinate represents the dimensionless vertical vibration displacement of the bogie. It can be seen that with the increase of the dimensionless nonlinear stiffness ratio of the system, the system transits to the chaotic motion state through the period-doubling bifurcation, and the existence domain of the chaotic motion is gradually dense. The increase of the nonlinear stiffness of the air spring in the system may lead to the occurrence of chaotic motion of the system.

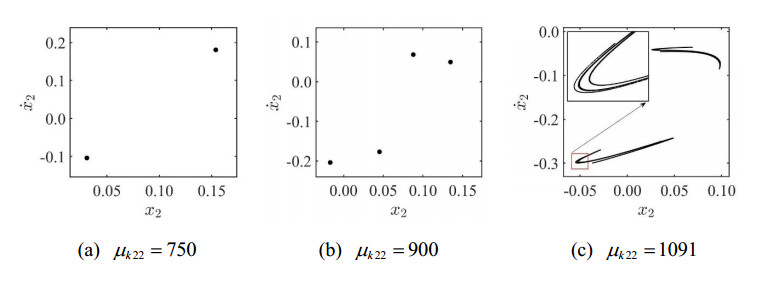
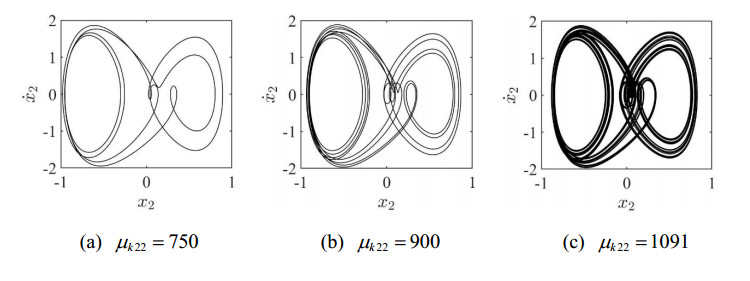
The numerical simulation shows that the nonlinear stiffness ratio is 750. As illustrated in Figure 22(a), the system's phase plane diagram has 2 closed circles. the Poincaré map of the system is two stable fixed points, as shown in Figure 21(a). The abscissa represents the dimensionless vertical vibration displacement of the bogie ${M_2}$, and the ordinate represents the dimensionless vertical vibration velocity of the bogie ${M_2}$. At this time, the system has a stable $q = 2/2$ periodic motion. When the nonlinear stiffness ratio is ${\mu _{k22}} = 900$, the Poincaré map of the system increases to four stable fixed points by Period-doubling bifurcation, as shown in Figure 21(b). As illustrated in Figure 22(b), the system's phase plane diagram has 4 closed circles. At this time, the system is in a stable $q = 4/4$ periodic motion state. When the nonlinear stiffness ratio continues to increase to ${\mu _{k22}} = {\text{1091}}$, the periodic motion state of the system disappears and gradually becomes unstable, as shown in Figure 22(c). At this time, the system enters the chaotic oscillatory state through the period-doubling bifurcation. The fractal structure with a self-similar structure can be seen in Figure 21(c).

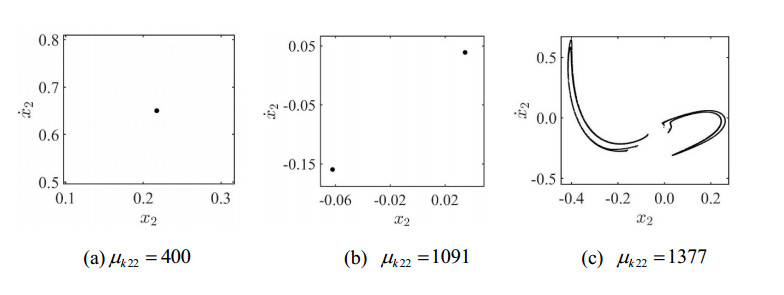
5.3.   The road of boundary crisis to chaos

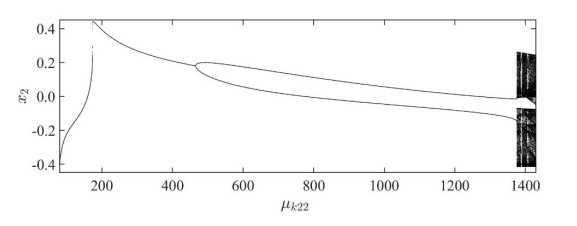
Keep the above system simulation parameters unchanged, increase the system damping ratio to: $\zeta = 0.023$, and obtain the system bifurcation diagram when the nonlinear stiffness ratio is ${\mu _{k22}} \in [100, {\text{ }}1450]$ as shown in Figure 23. It can be seen that with the increase of the nonlinear stiffness ratio ${\mu _{k22}}$, the system enters chaotic motion after the boundary crisis occurs nearby.

When the nonlinear stiffness ratio is ${\mu _{k22}} = 400$, the Poincaré map of the system is a stable fixed point, as shown in Figure 24(a). As illustrated in Figure 25(a), the system's phase plane diagram has 1 closed circle. At this time, the system has a stable $q = 1/1$ periodic motion. When the nonlinear stiffness ratio is ${\mu _{k22}} = 1091$, the system enters the $q = 2/2$ periodic motion state through the Period-doubling bifurcation. As illustrated in Figure 25(b), the system's phase plane diagram has 2 closed circles. The Poincaré map of the system is two stable fixed points, as shown in Figure 24(b).

As the nonlinear stiffness ratio increases to 1377, there is a boundary crisis in the system, and the system suddenly enters a chaotic motion state, as shown in Figure 25(c). The shape of the chaotic attractor can be observed from the Poincaré map of the system, as shown in Figure 24(c).

6.   Conclusions

1) In this paper, the theoretical analysis and numerical simulation of the vehicle wheel-rail impact vibration system at v = 245 km/h ~ 260 km/h show that when the wheelset and rail impact vibration occur near the critical value of the short-wave depth of the rail welded joint (0.2 mm), the system has Hopf bifurcation and Neimark-Sacker bifurcation, and there are multiple complex roads leading to chaotic motion. With the increase of the nonlinear stiffness ratio ${\mu _{k22}}$ of the air spring in the secondary suspension of the vehicle, the system has a transition from Period-doubling bifurcation and Boundary crisis to chaotic motion.

2) When the dimensionless excitation frequency is in the interval $\omega \in [1.1382, {\text{ 1}}{\text{.15]}}$, the vehicle wheel-rail impact vibration system is a stable $q = 1/1$ periodic motion, and the vehicle system is relatively stable at this time (v = 259 km/h ~ 263 km/h). When the non-dimensional excitation frequency is in the range $\omega \in [1.0972, {\text{ 1}}{\text{.1245]}}$, multiple impact collisions (v = 250 km/h ~ 256 km/h) occur between the wheel and rail, and the system is $q = 9/9$ periodic motion. When $\omega \in [1.08, {\text{ 1}}{\text{.0972]}}$, the excitation frequency of the system crosses $\omega = 1.0945$ (v = 249.4 km/h), it enters the chaotic state by $2T_{9/9}^1$ tori doubling.

3) When more nonlinear elements of the vehicle wheel-rail impact vibration system are examined, the system exhibits more complicated and rich nonlinear dynamic behavior. The system analysis results differ when rail flexibility is taken into account. The research on bifurcation and chaos behavior of vehicle wheel-rail shock vibration systems provides a reference for preventing the chatter of bogie components and improving the safe environment of vehicle operation.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The work was supported by the Special Funds for Guiding Local Scientific and Technological Development by the Central Government of China: (22ZY1QA005). The authors are grateful for the financial support. The authors also would like to thank the editors and reviewers for their valuable comments. Finally, we would like to thank Dr. Chen and Dr. Bai who helped with the writing of the paper.

Conflict of interest

The authors declare that there are no conflicts of interest.