Barycentric rational interpolation method for solving time-dependent fractional convection-diffusion equation

1.   Introduction

In this paper, we consider the time-dependent fractional convection-diffusion (TFCD) equation

where $1 \ < \alpha < 2$ and $\Omega$ are bounded domains in $\mathbb{R}^n$ with $n = 1, 2$ and $\Omega = [a, b]$ or $\Omega = [a, b]\times[c, d]$, $\Gamma$ is the boundary of $\Omega$. $f(\mathbf{t}, s), \varphi_{0}(\mathbf{t}), \varphi_{1}(\mathbf{t}), g(\mathbf{t}, s)$ are given functions and

The fractional derivative $C_{s}^{\alpha} = \frac{\partial^{\alpha} \phi(\mathbf{t}, s)}{\partial t^{\alpha}}$ denotes the Caputo fractional derivative.

The Caputo fractional derivative of time is defined as

and $\Gamma(\alpha)$ is the $\Gamma$ function. The time fractional convection-diffusion equation has been widely applied in the modeling of the anomalous diffusive processes and in the description of viscoelastic damping materials.

In ^[1], a class of time fractional reaction diffusion equations with variable coefficients and the nonhomogeneous Neumann problem was solved by a compact finite difference method. It was proven that the method was unconditionally stable for the general case of variable coefficients, and the optimal error estimate for the numerical solution under the discrete $L_2$ norm was also given. In ^[2], by using Legendre spectral squares to discretize spatial variables, a high order numerical scheme for solving nonlinear time fractional reaction diffusion equations was proposed. Then, a priori estimate, existence, and uniqueness of the numerical solution were given, and the unconditional stability and convergence was proven. In ^[3] a fast and accurate numerical method for fractional reaction diffusion equations in unbounded domains using Fourier spectral method was constructed. In ^[4], an immersed finite element (IFE) method for solving time fractional diffusion equations with discontinuous coefficients was proposed. The singularity of the Caputo fractional derivative is approximated by the non-uniform $L_1$ scheme. In ^[5], a numerical method for diffusion problems with fractional derivatives in a bilateral Riemannian Liouville space was proposed. Under appropriate constraints, the monotonicity, positive retention, and linear stability of the method were proven. In ^[6], a locally discontinuous Galerkin and finite difference method for solving multiple variable order time fractional diffusion equations with variable order fractional derivatives was proposed, which proven that the scheme was unconditionally stable. In ^[7], a finite difference method for solving time fractional wave equations (TFWE) was proposed. For $\alpha \in (1, 2)$, the proposed difference scheme was of a second order accuracy in space and time, and the stability of the H-1-norm of the method was given. In ^[8], an hp discontinuous Galerkin method for solving nonlinear fractional differential equations with Caputo type fractional derivatives was proposed. This method converts fractional differential equations into either nonlinear Volterra or Fredholm integral equations, and then uses the hp discontinuous Galerkin method to solve the equivalent integral equations. Time-fractional diffusion equation ^[9] and nonlinear Caputo fractional differential equation ^[10] were studied by the finite difference scheme and optimal adaptive grid method.

The above methods such as the finite difference method, the Legendre spectral method, the Fourier spectral method, the finite element, and the discontinuous Galerkin method had been used to solve fractional partial equation with the time direction and space direction solved separatively in different directions. Different from the above methods, we construct the barycentric rational interpolation method (BRIM) to solve the time-dependent fractional convection-diffusion (TFCD) equation with time direction and space direction at the same time. For the barycentric interpolation method (BIM), there are BRIM and the barycentric Lagrange interpolation method (BLIM) which can be used to avoid the Runge phenomenon. In the recent years, linear rational interpolation (LRI) was proposed by Floater ^[14,15,16] and the error of linear rational interpolation ^[11,12,13] was also proven. BIM has been developed by Wang et al.^[17] and the algorithm of BIM has been used to linear/non-linear problems ^[18,19]. In recent research, the Volterra integro-differential equation (VIDE) ^[20], heat equation (HE) ^[21], biharmonic equation (BE) ^[22,23], telegraph equation (TE) ^[24], generalized Poisson equations ^[25], semi-infinite domain problems^[27], fractional reaction-diffusion equation ^[28], and KPP equation ^[29] have been studied by linear BRIM and their convergence rate are also proven.

In this paper, BRIM has been used to solve the TFCD equation. As the fractional derivative is the nonlocal operator, spectral methods are developed to solve the TFCD equation and the coefficient matrix is a full matrix. The fractional derivative of the TFCD equation is changed to nonsingular integral by integral with order of density function plus one. The new Gauss formula is constructed to compute it simply and the matrix equation of discrete the TFCD equation is obtained by the unknown function replaced by the barycentric rational interpolation basis function. Then, the convergence rate of BRIM is proven.

2.   Calculation of time fractional derivative

By the definition of (1.3), there are certain kinds of singularities in (1.1). Solving the TDFC equation is needed to efficiently calculate the Caputo fractional derivative. There are some methods to overcome the difficulty of singularity, we adopt the fractional integration as follow:

where $\Gamma_{\alpha}^{\xi} = \frac{1}{(\xi-\alpha)\Gamma(\xi-\alpha)}$.

Combining Eqs (2.1) and (1.1), we have

The discrete formula of TFCD equation is obtained as

where

and

is the basis function, see ^[20]. Taking (2.3) into (2.2), we get

Then we get

As for the discrete of $t$ and $s$, we get

where $\phi_{i}(s_{j}) = \phi(t_{i}, s_{j}) = \phi_{ij}, i = 1, \cdots, m; j = 1, \cdots, n$ and

is the basis function.

Combining (2.6) and (2.7),

where

and

The term of (2.9) can be written as

The integral (2.9) is calculated by

where $G_{i}^{\theta, \alpha}$ is Gauss weight and $\tau_{i}^{\theta, \alpha}$ is Gauss points with weights $(s-\tau)^{\xi-\alpha}$, see reference ^[25].

3.   Matrix equation of TFCD equation

3.1.   Matrix equation of (1+1) dimensional TFCD equation

For the (1+1) dimensional TFCD equation with $\Omega^{1} = [a, b]$, (2.9) can be written as

Taking $a = t_{11} < t_{12} < \cdots < t_{1m_{1}} = b, 0 = s_{1} < s_{2} < \cdots < s_{n} = T$ with $h_{t} = (b-a)/m_{1}, h_{s} = T/n$ as either a uniform partition or uninform as a Chebychev point, $(t_{1i}, s_{l}), 1i = 1, 2, \cdots, m_{1}, l = 1, 2, \cdots, n$, we get

By introducing the notation, $R_{j_{1}}(t_{1i}) = \delta_{j_{1}i}, R_{k}(s_{l}) = \delta_{kl}, R'_{j_{1}}(t_{1i}) = R_{ij_{1}}^{(1, 0)}, R'_{k}(s_{l}) = R_{ij}^{(0, 1)}, R''_{j_{1}}(t_{1i}) = R_{ij_{1}}^{(2, 0)}, R''_{k}(s_{l}) = R_{kl}^{(0, 2)}$ where $R_{il}^{(0, 2)}$ is the second order of the barycentric matrix.

by taking (2.11),

then we get

Systems of (3.5) can be written as

where $I_{m_{1}}$ and $I_{n}$ are identity matrices, and $\otimes$ is Kronecker product.

Then, we get Eq (3.6) as

and

with $M = \Gamma_{\alpha}^{\xi} \left(diag(s^{\xi-\alpha}){M}_{1}^{(\xi0)}\otimes {I}_{n}+ {I}_{m_{1}}\otimes {Q^{\alpha_{2}}} \right)- \left({M}^{(2, 0)}\otimes {I}_{n}+ {I}_{m_{1}}\otimes{M}^{(0, 2)} -{M}^{(1, 0)}\otimes {I}_{n}- {I}_{m_{1}}\otimes{M}^{(0, 1)} \right)$ and $\Phi = [{{\phi}_{11}} {\dots} {{\phi}_{1n} } {\dots} {{\phi}_{m_{1}1}} {\dots} {{\phi}_{m_{1}n}}]^{T}, F = [{{f}_{11}} {\dots} {{f}_{1n} } {\dots} {{f}_{m_{1}1}} {\dots} {{f}_{m_{1}n}}]^{T}$.

3.2.   Matrix equation of (2+1) dimensional TFCD equation

For the (2+1) dimensional TFCD equation with $\Omega^{2} = [a, b]\times [c, d]$, then we have

By $a = t_{11} < t_{12} < \cdots < t_{1m_{1}} = b, c = t_{21} < t_{22} < \cdots < t_{2m_{1}} = d, 0 = s_{1} < s_{2} < \cdots < s_{n} = T$ with $h_{t_{1}} = (b-a)/m_{1}, h_{t_{2}} = (d-c)/m_{2}, h_{s} = T/n$ or uninform as a Chebychev point, $(t_{1i}, t_{2i}, s_{l}), 1i = 1, 2, \cdots, m_{1}, 2i = 1, 2, \cdots, m_{2}, l = 1, 2, \cdots, n$, we get

By introducing the notation, $R_{j_{1}}(t_{1i}) = \delta_{j_{1}i}, R_{j_{2}}(t_{1j}) = \delta_{j_{2}j}, R_{k}(s_{l}) = \delta_{kl}, R'_{j_{1}}(t_{1i}) = R_{ij_{1}}^{(1, 0, 0)}, R'_{j_{2}}(t_{1j}) = R_{ij_{1}}^{(0, 1, 0)}, R'_{k}(s_{l}) = R_{ij}^{(0, 0, 1)}, R''_{j_{1}}(t_{1i}) = R_{ij_{1}}^{(2, 0, 0)}, R''_{j_{2}}(t_{1j}) = R_{ij_{1}}^{(0, 2, 0)}, R''_{k}(s_{l}) = R_{ij}^{(0, 0, 2)}$, we get

Then, Eq (3.6) can be written as

and

with $M = \Gamma_{\alpha}^{\xi} \left(diag(s^{\xi-\alpha}){M}_{1}^{(\xi0)}\otimes {I}_{m_{1}}\otimes {I}_{m_{2}}+ {I}_{m_{1}}\otimes {I}_{m_{2}}\otimes {Q^{\alpha_{2}}} \right) - \left({M}^{(2, 0, 0)}\otimes {I}_{m_{2}}\otimes {I}_{n}+ {I}_{m_{1}}\otimes {M}^{(0, 2, 0)}\otimes {I}_{n} + {I}_{m_{1}}\otimes {I}_{m_{2}}\otimes {M}^{(0, 0, 2)} \right) +$ $\left({M}^{(1, 0, 0)}\otimes {I}_{m_{2}}\otimes {I}_{n}+ {I}_{m_{1}}\otimes {M}^{(0, 1, 0)}\otimes {I}_{n} +{I}_{m_{1}}\otimes {I}_{m_{2}}\otimes {M}^{(0, 0, 1)} \right)$ and $\Phi = [{{\phi}_{111}} {{\phi}_{112}} {\dots} {{\phi}_{11n} }, {{\phi}_{121}} {{\phi}_{122}} {\dots} {{\phi}_{12n} }, {\dots}, {{\phi}_{m_{1}m_{2}1}} {{\phi}_{m_{1}m_{2}2}} {\dots} {{\phi}_{m_{1}m_{2}n}}]^{T}$, $F = [{{f}_{111}} {{f}_{112}} {\dots} {{f}_{11n} }, {{f}_{121}} {{f}_{122}} {\dots} {{f}_{12n} }, {\dots},$ ${{f}_{m_{1}m_{2}1}} {{f}_{m_{1}m_{2}2}} {\dots} {{f}_{m_{1}m_{2}n}}]^{T}$.

The boundary condition can be solved by the substitution method, the additional method or the elimination method, see ^[17]. In the following, we adopt the substitution method and the additional method to add the boundary condition.

4.   Convergence rate of TFCD equation

In this part, the error estimate of the TFCD equation is given with $r_n(s) = \sum\limits_{i = 1}^{n} r_{i}(s) \phi_{i}$ to replace $\phi(s)$, where $r_{i}(s)$ is defined as (2.8) and $\phi_{i} = \phi(s_{i})$. We also define

see reference ^[20].

Then, we have

Lemma 1. For $e(s)$ be defined by (4.1) and $\phi(s)\in C^{d+2}[a, b], d = 1, 2, \cdots$, there

For the TFCD equation, the rational interpolation function of $\phi(t, s)$ is defined as $r_{mn}(t, s)$

where

We define $e(t, s)$ be the error of $\phi(t, s)$ as

With a similar analysis of Lemma 1, we have

Theorem 1. For $e(t, s)$ defined as (4.5) and $\phi(t, s) \in C^{d_{s}+2}[a, b]\times C^{d_{t}+2}[0, T]$, then we have

Let $\phi(s_{m}, t_{n})$ be the approximate function of $\phi(t, s)$ and $L$ to be bounded operator, there holds

and

Then, we get

Theorem 2. For $\phi(t_{m}, s_{n}):L\phi(t_{m}, s_{n}) = \phi(t, s)$ and $L$ defined as (4.7), there

Proof. By the definition of (4.7), we have

here

As for $E_{1}(t, s)$, we get

and

where

Now we estimate $E_{11}(t, s)$ and $E_{12}(t, s)$ part by part, for the second part we have

then we have

For $E_{11}(t, s)$, we get

Similarly as $E_{2}(t, s)$, for $E_{3}(t, s)$ we have

Combining (4.9), (4.13), and (4.15) together, the proof of theorem 4.2 is completed.

5.   Numerical examples

In this part, two examples are presented to test the theorem.

Example 1. Consider the time-dependent fractional convection-diffusion equation

with the analysis solution is

with the initial condition

and boundary condition

and

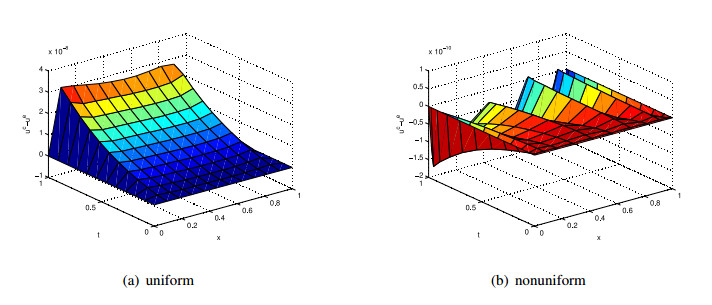
In Figures 1 and 2, errors of $m = n = 12$, $\Omega^{1} = [0, 1], \alpha = 1.2$ and $m = n = 12, d_{t} = d_{s} = 8$, $\Omega^{1} = [0, 1], \alpha = 1.2$ in Example 1 with uniform and nonuniform partition for the TFCD equation by BRIM are presented, respectively. From the Figure, we know that the precision can reach to $10^{-8}$ for both the uniform and nonuniform partition.

In Figures 3 and 4, errors of $m = n = 12$, $\Omega^{1} = [0, 1], \alpha = 1.8$ and $m = n = 12, d_{t} = d_{s} = 8, \alpha = 1.8$, $\Omega^{1} = [0, 1]$ in Example 1 with uniform and nonuniform partition for the TFCD equation by BRIM are presented, respectively. From the Figure, we know that the precision can reach to $10^{-8}$ for both uniform and nonuniform partition. For different value of $\alpha$, BRIM can be used to solve the TFCD equation efficiently.

In Table 1, errors of the TFCD equation for $\alpha_1 = 1.8, d_{t} = d_{s} = 5$ with $t = 0.1, 0.9, 1, 5, 10, 15$ are presented under the uniform and nonuniform partition with BRIM and BLIM. As the time variable increases from $0.5$ to $15$, there is still high accuracy. For BRIM, we can choose the parameters $d_{t}, d_{s}$ and $m, n$ approximately to get high accuracy. Under the same partition of $m, n$, the accuracy of BLIM is higher than BRIM.

In Table 2, for BRIM, the errors of different $\alpha_1 = 1.05, 1.1, 1.3, 1.5, 1.6, 1.8, 1.9, 1.99$ under uniform with $m = n = 10, d_{t} = 5, d_{s} = 5$ are presented under the uniform and nonuniform partition. From the table, we know that for different $\alpha$, BRIM has a high accuracy with decreased values for $m$ and $n$.

In the following table, numerical results are presented to test our theorem.

From Tables 3 and 4, the error of BRIM under uniform for $\alpha = 1.8, d_{s} = 5$ with different $d_{t}$ are given, and the convergence rate is $O(h^{d_{t}})$. From Table 4, with space variable uniform for $\alpha = 1.8, d_{t} = 5$, the convergence rate is $O(h^{7})$, which we will investigate in future paper.

For Tables 5 and 6, the errors of Chebyshev partition for $s$ and $t$ are presented. For $\alpha = 1.8, d_{t} = 5$, the convergence rate is $O(h^{d_{s}})$ in Table 5, while in Table 6, the convergence rate is $O(h^{d_{t}})$, which agrees with our theorem.

In the following table, $\alpha = 1.2$ is chosen to present numerical results. From Tables 7 and 8, the error of BRIM under uniform for $d_{t} = 5$ with different $d_{s}$ is given, and the convergence rate is $O(h^{7})$. From Table 7, with space variable $s, d_{s} = 5$, the convergence rate is $O(h^{d_{t}})$, which agrees with our theorem.

For Tables 9 and 10, the errors of BRIM under the Chebyshev partition for with $\alpha = 1.2$ are presented. For $d_{t} = 5$, the convergence rate is $O(h^{7})$ in Table 9, while in Table 10, the convergence rate is $O(h^{d_{t}})$, which agrees with our theorem.

Example 2. Consider the time-dependent fractional convection-diffusion equation

with the analysis solution is

with the initial condition

and

In Figures 5 and 6, errors of $m = n = 13$, $\Omega^{2} = [0, 1]\times[0, 1], \alpha = 1.2$ and $m = n = 13, d_{t} = d_{s} = 7$, $\Omega^{2} = [0, 1]\times[0, 1], \alpha = 1.2$ in Example 2(a) uniform and 2(b) nonuniform for the TFCD equation by the rational interpolation collocation methods are presented, respectively. From the Figure, we know that the precision can reach to $10^{-6}$ for both the uniform and nonuniform partition.

In Figures 7 and 8, the errors of $m = n = 13$, $\Omega^{2} = [0, 1]\times[0, 1], \alpha = 1.9$ and $m = n = 13, d_{t} = d_{s} = 6, \alpha = 1.9$, $\Omega^{2} = [0, 1]\times[0, 1]$ in Example 2(a) uniform and 2(b) nonuniform for the TFCD equation by rational interpolation collocation methods are presented, respectively. From the figure, we know that the precision can reach to $10^{-6}$ for both the uniform and nonuniform partition.

In Table 11, the errors of the TFCD equation with $d_{t1} = d_{t2} = d_{s} = 5, \alpha = 1.9$ for substitution methods and additional methods are presented, and there are nearly no differences for the two methods. Compared with two methods, the additional method is more simple than the substitution methods. In the following, we chose the substitution method to deal with the boundary condition.

From Tables 12 and 13, the error of BRIM under non-uniform for $\alpha = 1.2, d_{s} = 5$ with different $d_{t1}, d_{t2}$ are given, and the convergence rate is $O(h^{d_{1}})$. From Table 13, with space variable uniform for $\alpha = 1.2, d_{t1} = d_{t2} = 5$, the convergence rate is $O(h^{d_{s}})$, which we will investigate in future paper.

For Tables 14 and 15, the errors of the uniform partition for $s$ and $t$ are presented. For $\alpha = 1.2, d_{s} = 5$, the convergence rate is $O(h^{d_{s}})$ in Table 14, while in Table 15, the convergence rate is $O(h^{d_{t1}})$, which agrees with our theorem.

In the following table, $\alpha = 1.9$ is chosen to present numerical results. From Tables 16 and 17, the error of BRIM under uniform for $d_{s} = 5$ with different $d_{t1}, d_{t2}$ are given, and the convergence rate is $O(h^{d_{t1}})$. From Table 17, with space variable $d_{t1} = d_{t2} = 5$, the convergence rate is $O(h^{d_{s}-1})$, which agrees with our theorem.

For Tables 18 and 19, the errors of BRIM under thev Chebyshev partition for with $\alpha = 1.9$ are presented. For $d_{s} = 5$, the convergence rate is $O(h^{t1})$ in Table 18, while in Table 19, the convergence rate is $O(h^{d_{s}})$, which agrees with our theorem.

6.   Concluding remarks

In this paper, BRIM is used to solve the TFCD equation. The singularity of fractional derivative is overcome by thre integral to the density function from the singular kernel. For arbitrary fractional derivative new Gauss formula is constructed to simply calculate it. For the Diriclet boundary condition, the TFCD equation is changed to discrete the TFCD equation and the matrix equation. In the future, the TFCD equation with the Nuemann condition can be solved by BRIM, and a high dimensional TFCD equation can be studied by our methods.

Acknowledgments

The work of Jin Li was supported by Natural Science Foundation of Shandong Province (Grant No. ZR2022MA003).

Conflicts of interest

The authors declare that they have no conflicts of interest.