Structural optimization study based on crushing of semi-rigid base

1.   Introduction

Semi-rigid base materials are known for high strength and excellent integrity. Therefore, these materials are extensively used in all grades of pavements ^[1]. At present, there are many semi-rigid road base layers that require maintenance and repair; however, the full lifespan of these materials have not been reached, thus the remaining load-bearing capacity of these materials can still be used. To reach maximum life span, this study analyzes the effect of the both rubblization and crushing methods to repair asphalt. Of these two methods, the crushing method has previously been shown to be more feasible ^[2]. In particular, crushing technology is used for the rehabilitation of old concrete roads composed of cement, with the overall service life of the pavement greatly extended over that of a direct pavement method ^[3,4]. During the application of cement concrete pavement, crushing is used as an important tool for overhauling old concrete cement panels ^[5,6]. Old cement concrete treatment techniques that are commonly used include: crack, crack and set, break and set. Cement concrete crushing technology yields small particles similar to those of graded and crushed rock. Crushing technology reduces old pavement to approximately 7.5–30 cm in size. The generated particles are thin on the upper layer and thicker on the bottom later ^[7]. On the other hand, structure rigidity post-rubblization is approximately 3000–5000 MPa. This type of crushing technology has previously been used on Interstate 76 in Sterling, Colorado, using two types of crushing equipment for the construction process (i.e., multiple-head breaker and resonance machines) ^[8,9]. Furthermore, approximately 200 miles of concrete in Arkansas has been treated via crushing. Crushing technology has the potential to successfully eliminate reflective cracks in the overlay and improve its' service life ^[10]. Results of comprehensive petrochemical treatment methods show that the use of petrochemical treatment has the potential to delay occurrence of reflective cracks in the overlay for at least 3 years ^[11].

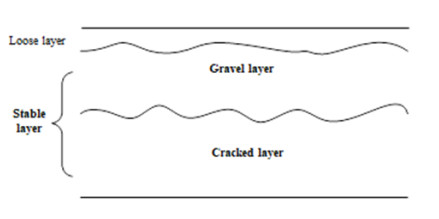
In the present study, a multi-hammer head crusher was used to crush semi-rigid base panels through impaction with high-amplitude, low-frequency falling hammers ^[12]. A qualitative analysis of the composition of the crushed layers was performed by dividing the crushed structure into three structural layers according to particle size distribution which include: loose layer, crushed stone layer, and cracked layer. The top of the semi-rigid base was the most affected by the multi-hammer head and expressed sever damage due to the high-pressure stress. There was no embedded capacity between the particles, which formed a "loose layer". The bottom of the semi-rigid base was the least damaged due to the lowest stress level being applied here. The bottom of the semi-rigid base was broken into large particles, and was defined as a "cracked layer". The layer between the loose layer and cracked layer was defined as a "gravel layer". The layers of the semi-rigid base post-crushing are shown in Figure 1.

Figure 1.  Layer levels post-crushing of the semi-rigid base.

DownLoad: Full-Size Img PowerPoint

The loose layer contained no cement material and it was neglected during the simulation. Appropriate adjustment of the crushing parameters for the equipment has the potential to reduce the need for excess crushing while simultaneously ensuring a complete crush of the semi-rigid base, thus reducing overall thickness of the loose layer. The strength of the gravel layer was mainly comprised of an internal friction angle and pre-compressive stress. A smaller particle size in the crushed layer corresponded to greater volume expansion and pre-compressive stress. The shear strength between the cracked layer and the split layer was mainly determined from block capacity and the "arch effect", which generates horizontal pressure on surrounding blocks as shown in Figure 2. A higher load lead to higher horizontal pressure and a faster load spread. These data indicated that the cracked layer converts vertical compressive stresses applied to the upper part of the block into horizontal pressure, thus spreading the overall load.

Figure 2.  Horizontal forces.

DownLoad: Full-Size Img PowerPoint

In these studies, finite element software was used to analyze the sensitivity of mechanical indicators of the pavement post-crushing. The mechanical indexes with high sensitivity were used as structural damage control indexes and used to optimize pavement structure. These studies also provided thickness and modulus parameters for the structural design of asphalt pavement after post-cracking of a semi-rigid base.

2.   Test design

2.1.   Overlay parameters

The thickness of the gravel layer and cracked layer were each measured at 20 cm, with a modulus of 400 MPa for the gravel layer and 1000 MPa for the cracked layer respectively. The structural design parameters of the original pavement post-crushing are shown in Table 1.

Table 1.  Structural parameters for inverted base layers.

Items	Thickness (cm)	Modulus (MPa)
The gravel layer	20	400
The cracked layer	20	1000
Foundation	60	40/70/100/130

---

 | Show Table

DownLoad: CSV

There were two main types of pavement structure post-crushing of the base layer. One structure was a graded gravel base layer, while the other was an asphalt-stabilized gravel base layer. Based on the modulus of the semi-rigid base post-lithification, the first paving method was defined as inverted base pavement, with the second paving method defined as mixed base pavement. The overlay parameters for the inverted base pavement are shown in Table 1, and the overlay parameters for the mixed base pavement structure are shown in Table 2.

Table 2.  The overlay layer parameters for inverted base pavement.

Items		Group 1	Group 2
Asphalt layer	Thickness(cm)	15/20/25/30/35/40/45	25
	Modulus (MPa)	1000/1300/1600/1900	1500
Graded gravel layer	Thickness(cm)	20	15/20/25/30/35/40/45
	Modulus (MPa)	500	300/400/500/600

---

 | Show Table

DownLoad: CSV

Table 3.  The overlay layer parameters for mixed base pavement.

Items		Group 3	Group 4
Asphalt layer	Thickness(cm)	15/20/25/20/35/40/45	20
	Modulus (MPa)	1000/1300/1600/1900	1500
Asphalt stabilized gravel	Thickness(cm)	20	15/20/25/20/35/40/45
	Modulus (MPa)	1400	900/1200/1500/1800

---

 | Show Table

DownLoad: CSV

Sensitivity analyses were carried out using relevant parameters.

2.2.   Finite element model

The model was based on the Abacus dynamic analysis method. The pavement structure consists of a soil base layer, a cracked layer, a gravel layer, and an additional pavement layer ^[13]. The model parameters and assumptions were as following.

1) The materials of each structural layer were elastic, homogeneous, and isotropic.

2) The contact between the structural layers was continuously and the displacement was continuous in all directions.

3) The effect of gravity on each structural layer of the pavement was neglected.

2.3.   Structure indicators

The modulus post-crushing of the semi-rigid subgrade was between that of graded crushed stone and semi-rigid subgrade ^[14]. A flexible subgrade and asphalt surface layer were subsequently added to avoid the occurrence of reflective cracks. Damage forms and control indicators of the pavement structure post-paving are listed in Table 4.

Table 4.  Damage types and control indicators of pavement structure post-paving.

Type of damage	Mechanical control indicators
Asphalt layer fatigue damage/reflection cracking	Asphalt layer tensile strain/stress
Shear damage in the graded gravel layer	Shear stress in the graded gravel layer
Structural rutting	Top-down compressive strain, surface deflection
Top-down cracking	Asphalt layer shear stress

---

 | Show Table

DownLoad: CSV

2.4.   Structure indicators

An overlay in the form of a graded crushed stone base layer and an asphalt surface layer was generated and is considered equal to an inverted base pavement structure. In terms of pavement structure and materials, the main considerations for these studies were thickness/modulus of the asphalt surface layer, the modulus/thickness of the graded gravel base, modulus of the soil base, the coefficient of friction between the asphalt surface layer and graded gravel layer, as well as the coefficient of friction between the graded gravel layer and cracked layer. These seven factors were subsequently analyzed orthogonally using the extreme difference and variance methods. The extreme difference method was used because of its comprehensiveness and rapid turnaround for time sensitivity, The variance method was employed to determine each factors degree of influence on each mechanical control index. For these studies, the level of factors selected and corresponding values for each influence factor are shown in Tables 5 and 6, and are based on each factors' influence on the control indicators.

Table 5.  Factors for orthogonal analysis of inverted asphalt pavements.

Items	Asphalt layer		Graded gravel layer		Foundation ${E}_{3}$(MPa)	Coefficient of friction
	${h}_{1}$cm)	${E}_{1}$(MPa)	${h}_{2}$cm)	${E}_{2}$(MPa)		${f}_{1}$	${f}_{2}$
1	15	1000	15	300	40	0.3	0.3
2	25	1300	25	400	70	0.5	0.5
3	35	1600	35	500	100	0.7	0.7
4	45	1900	45	600	130	0.9	0.9

---

 | Show Table

DownLoad: CSV

Table 6.  Factors for orthogonal analysis of mixed base pavement.

Items	Asphalt layer		Asphalt stabilized gravel		Foundation ${E}_{3}$(MPa)	Coefficient of friction
	${h}_{1}$cm)	${E}_{1}$(MPa)	${h}_{2}$cm)	${E}_{2}$(MPa)		${f}_{1}$	${f}_{2}$
1	15	1000	15	900	40	0.3	0.3
2	25	1300	25	1200	70	0.5	0.5
3	35	1600	35	1500	100	0.7	0.7
4	45	1900	45	1800	130	0.9	0.9

---

 | Show Table

DownLoad: CSV

According to factor levels shown in Table 5, the L32 (49) orthogonal table was selected to perform analysis. The orthogonal table was specifically designed to test each influencing factor. The test scheme used for these analyses are detailed in Appendix 1.

3.   Results and discussion

3.1.   Overlay pavement sensitivity

3.1.1.   Visual analysis

The experimental designs and results of the visual analyses foreach control indicator are detailed in Appendix I. The test scenarios in Appendix I were simulated using ABAQUS software and each of the required mechanical controls were subsequently extracted from simulation. Extreme difference values outlined in Appendix I were analyzed via a series of diagrams. In each diagram, the extreme difference in asphalt layer thickness was taken as a standard value of 1. The extreme difference ratio for each diagram was calculated by taking the extreme different values for each influencing factor and dividing them by the extreme difference value of asphalt layer thickness. These results were processed using polar ratio and visual schematics of this data are shown in Figures 3 and 4.

Figure 3.  Orthogonal ratios for an inverted base.

DownLoad: Full-Size Img PowerPoint

Figure 4.  Orthogonal ratios for a mixed base.

DownLoad: Full-Size Img PowerPoint

For inverted and mixed base asphalt pavements, asphalt layer thickness was found to have the greatest effect on tensile strain, shear stress, and tensile stress, which was followed by asphalt layer modulus. Therefore, increasing asphalt layer thickness and modulus has the potential to effectively control fatigue damage of asphalt layers and improve overall fatigue life. Asphalt layer thickness and modulus were both found to have a significant effect on road surface deflection and top surface compressive strain of the road base during structural pavement rutting. Therefore, increasing asphalt thickness as well as the modulus of base soil has the potential to effectively improve the load-carrying capacity of pavement structure as well as control structural rutting of the pavement. Additionally, the thickness of asphalt-stabilized aggregates in the mixed structure was also found to have a significant effect on both of these control indexes. Furthermore, in terms of asphalt layer fatigue damage and top-down cracking, priority should be given to increasing overall thickness. This will ensure appropriate structural performance of the pavement and can be modulated through reduction or addition when appropriate to meet economic needs.

3.1.2.   Analysis of variance (ANOVA) studies

ANOVA was used to determine the F-value by calculating the deviation of each influence factor and subsequent mean square deviation, which were then used to perform an F-value test ^[15]. More specifically, ANOVA was used to determine which of the influencing factors had a negligible effect on the control indicators ^[16]. The table containing the ANOVAs for each control indicator is shown in Appendix II, and the impact of the influencing factors on each of the paving structure control indicators are shown in Tables 7 and 8.

Table 7.  F-values for each factor of the inverted base structure.

Factor	Asphalt layer			Shear stress in graded gravel layer	Compressive strain at top surface of road base	Road surface deflection
	Tensile strain	Tensile stress	Shear stress
${h}_{1}$	151.22	97.03	50.88	152.07	124.63	70.03
${E}_{1}$	22.87	11.99	4.89	4.10	15.75	19.18
${h}_{2}$	1.50	1.56	1.31	8.54	39.20	3.46
${E}_{2}$	1.76	3.29	2.58	9.69	0.93	2.72
${E}_{3}$	1.51	1.21	0.50	0.70	72.20	75.78
${f}_{1}$	0.25	0.07	0.36	0.50	4.24	0.96
${f}_{2}$	0.53	0.08	0.22	0.29	4.81	1.31

---

 | Show Table

DownLoad: CSV

Table 8.  F-values for each factor of the mixed base structure.

Factor	Asphalt layer			Compressive strain at the top surface of the road base	Road surface deflection
	Tensile strain	Tensile stress	Shear stress
${h}_{1}$	105.30	42.15	10.28	31.97	54.21
${E}_{1}$	21.96	15.12	3.49	7.96	37.54
${h}_{2}$	7.12	14.04	3.40	44.61	31.91
${E}_{2}$	1.83	4.67	2.57	4.49	6.00
${E}_{3}$	1.80	2.14	0.61	51.25	125.17
${f}_{1}$	0.34	0.04	0.54	0.96	2.01
${f}_{2}$	1.01	0.56	1.78	3.20	5.55

---

 | Show Table

DownLoad: CSV

F-value tests were conducted based on the above tables, and the results are presented in Tables 9 and 10.

Table 9.  Impact factor of inverted base structure.

Indicators		$\text{α = 0.1}$	$\text{α = 0.05}$	$\text{α = 0.01}$
Asphalt layer	Tensile strain	${h}_{1}$ > ${E}_{1}$	${h}_{1}$ > ${E}_{1}$	${h}_{1}$
	Tensile stress	${h}_{1}$ > ${E}_{1}$	${h}_{1}$ > ${E}_{1}$	${h}_{1}$
	Shear stress	${h}_{1}$	${h}_{1}$	-
Shear stress in graded gravel layer		${h}_{1}$ > ${E}_{2}$ > ${h}_{2}$	${h}_{1}$ > ${E}_{2}$	${h}_{1}$
Compressive strain at top surface of road base		${h}_{1}$ > ${E}_{3}$ > ${h}_{2}$ > ${E}_{1}$	${h}_{1}$ > ${E}_{3}$ > ${h}_{2}$ > ${E}_{1}$	${h}_{1}$ > ${E}_{3}$ > ${h}_{2}$
Road surface deflection		${E}_{3}$ > ${h}_{1}$ > ${E}_{1}$	${E}_{3}$ > ${h}_{1}$ > ${E}_{1}$	${E}_{3}$ > ${h}_{1}$

---

 | Show Table

DownLoad: CSV

Table 10.  Impact factors of mixed base structure.

Indicators		$\text{α = 0.1}$	$\text{α = 0.05}$	$\text{α = 0.01}$
Asphalt layer	Tensile strain	${h}_{1}$ > ${E}_{1}$ > ${h}_{2}$	${h}_{1}$ > ${E}_{1}$	${h}_{1}$
	Tensile stress	${h}_{1}$ > ${E}_{1}$ > ${h}_{2}$	${h}_{1}$ > ${E}_{1}$ > ${h}_{2}$	${h}_{1}$
	Shear stress	${h}_{1}$	${h}_{1}$	-
Compressive strain at top surface of road base		${E}_{3}$ > ${h}_{2}$ > ${h}_{1}$ > ${E}_{1}$	${E}_{3}$ > ${h}_{2}$ > ${h}_{1}$ > ${E}_{1}$	${E}_{3}$ > ${h}_{2}$ > ${h}_{1}$ > ${E}_{1}$
Road surface deflection		${E}_{3}$ > ${h}_{1}$ > ${E}_{1}$ > ${h}_{2}$ > ${E}_{2}$ > ${f}_{2}$	${E}_{3}$ > ${h}_{1}$ > ${E}_{1}$ > ${E}_{2}$	${E}_{3}$ > ${h}_{1}$ > ${E}_{1}$

---

 | Show Table

DownLoad: CSV

From the results of this study, the factors that influenced asphalt bottom layer tensile strain and stress were found to be the same for both structures. Therefore, bottom tensile strain was used as the main mechanical control index to manage fatigue damage. For the inverted structure, asphalt layer thickness was found to have a significant effect on shear stress (p < 0.01). Furthermore, the graded gravel layer modulus and thickness was also found to have a significant effect on shear stress (P < 0.01). Asphalt layer thickness and the soil base modulus were both found to have effects on road surface deflection and compressive strain on the top surface of the roadbed upon rutting. For the mixed structure, the soil base modulus, asphalt stabilized aggregates thickness, asphalt layer thickness, and asphalt layer modulus were all found to have significant effects on top surface compressive strain (P < 0.01). Furthermore, the results of these studies showed that the soil base modulus, asphalt layer thickness, and asphalt layer modulus all had effects on road surface deflection settlement (P < 0.01). Asphalt layer thickness and modulus was found to have a significant effect on each control index, and increasing the asphalt layer thickness appropriately for inverted base asphalt pavement structures reduced this effect on each of these indexes. To improve load-carrying capacity of the pavement structure, the modulus of the soil base has the potential to be increased based on need. To improve the load carrying capacity and increase the life-span for mixed subgrade, the soil base modulus, asphalt thickness, and aggregate thickness of the asphalt stabilized should be increased appropriately.

3.2.   Analysis of structural optimization factors

3.2.1.   Asphalt layer thickness and modulus

1) Tensile strain

As shown in Figures 5 and 6, the tensile strain on the bottom layer of asphalt was reduced as ply thickness increased for both inverted and combining substrates. Additionally, increasing the modulus of the asphalt layer simultaneously reduced the subgrade tensile strain of the asphalt layer.

Figure 5.  Variation of tensile strain versus asphalt thickness for inverted base.

DownLoad: Full-Size Img PowerPoint

Figure 6.  Variation of tensile strain versus asphalt thickness for mixed base.

DownLoad: Full-Size Img PowerPoint

For pavement in which the base was inverted, the reduction of the layer bottom tensile strain of the asphalt was approximately 14.7–20.4% for every 5cm increase in layer thickness (i.e., 1000 MPa). These results suggest that increasing asphalt thickness can effectively reduce tensile strain on the bottom layer of asphalt. For mixed subgrade pavement, the reduction in asphalt sub-strain was approximately 14.1–19.3% for every 5 cm increase in asphalt thickness. This indicates that pavement thickness has the potential to directly affect tensile strain of the mixed subgrade and inverted base pavement. Additionally, by increasing the modulus of the pavement, the overall bottom tensile strain was reduced by approximately 15.8–17.4% for each 300 MPa increase in the asphalt layer, and by approximately 12.7–16.8% for the mixed subgrade. These results demonstrate how thickness and modulus of the asphalt layer have a significant impact on the tensile strain of the bottom layer that can be applied to both inverted and mixed layers. Due to differences in materials and construction processes, fatigue tensile strains for asphalt were found to vary greatly and generally ranged from 160 –220 με. Taking the lower limit of these numbers into consideration, it can be concluded than an asphalt layer modulus of 1200 MPa requires a thickness of at least 25 and 20 cm in the inverted base structure and mixed base structure respectively.

2) Shear stress

As shown in Figures 7 and 8, the shear stress on the bottom layer of asphalt was reduced as ply thickness increased for both inverted and combining substrates. Additionally, increasing the thickness of the asphalt layer simultaneously decreased the subgrade shears stress of the asphalt layer, and increasing the layer modulus of the asphalt layer simultaneously increased the subgrade shears stress of the asphalt layer

Figure 7.  Variation of shear stress in asphalt with a inverted base.

DownLoad: Full-Size Img PowerPoint

Figure 8.  Variation of shear stress in asphalt with a mixed base.

DownLoad: Full-Size Img PowerPoint

For inverted subgrade pavements, the shear stress in the asphalt layer was found to decrease by 0.4 to 4.5% for every 5cm increase asphalt thickness. As the asphalt thickness increased, the rate of reduction corresponding to asphalt shear stress gradually decreased. For mixed subgrade pavements, shear stress decreased by 0.1 to 3.1% for each 5cm increase in thickness. As the modulus of the asphalt layer increased, the quicker shear stress was reduced. Additionally, the results show an increase in asphalt layer with an increase in asphalt modulus. For every 300 MPa increase in modulus, an increase in shear stress of the inverted base layer was determined to be 0.5 to 4.1%. The increase in sheer stress for the mixed base layer was determined to be 0.5 to 3.1%. It is well known in the field that the shear stress tolerance value of asphalt is 280 kPa, with both pavement structures meeting requirements when asphalt thickness was greater than 15 cm. Additionally, Figure 9 shows that shear stress in the graded gravel layer of the inverted subgrade is related to both the thickness and modulus of the asphalt layer, and that increasing the thickness of asphalt or increasing the modulus of asphalt has the potential to reduce shear stress in the graded gravel layer.

Figure 9.  Variation of shear stress in the graded gravel layer and asphalt thickness for an inverted base.

DownLoad: Full-Size Img PowerPoint

For every 5cm increase in asphalt thickness of the inverted base, shear stress of the graded gravel layer increased from 22.1 to 31.8%. The results show that by increasing the thickness of the asphalt layer, it is possible to effectively reduce shear stress within the graded gravel layer. As asphalt thickness increased, the rate of shear stress reduction in the graded gravel layer gradually decreased. Additionally, increasing asphalt modulus led to a reduction in shear stress in the graded gravel layer, with a total reduction of 6.8 to 14.8% for each 300 MPa increase in modulus. These results suggest that asphalt thickness had a more significant effect on the shear stress in the graded gravel layer than asphalt modulus.

3) Compressive strain

As shown in Figures 10 and 11, the top surface compressive strain was reduced as ply thickness increased for both inverted and combining substrates. Additionally, increasing the modulus of the asphalt layer simultaneously reduced the vertical compressive strain of the top of the subgrade.

Figure 10.  Variation of top surface compressive strain versus asphalt thickness for an inverted base.

DownLoad: Full-Size Img PowerPoint

Figure 11.  Variation of top surface compressive strain versus asphalt thickness for a mixed base.

DownLoad: Full-Size Img PowerPoint

For inverted subgrade pavements, the top surface compressive strain of the roadbed decreased by 7.9 to 11.2% for every 5cm increase in asphalt thickness (i.e., 1000 MPa). The results show that increasing the thickness of asphalt has the potential to effectively reduce top surface compressive strain of the roadbed. For mixed subgrade pavements, the top surface compressive strain decreased by 7.8–10.5% for each 5cm increase in asphalt thickness. These data indicate that asphalt thickness has a significant effect on top surface compressive strain of the mixed subgrade. Additionally, increasing the modulus of the asphalt layer has the potential to reduce top surface compressive strain of the roadbed. For every 300 MPa of increase in asphalt layer, top surface compressive strain of the inverted subgrade was reduced by 2 to 10.3%. Moreover, top surface compressive strain of the mixed subgrade leaching roadbed was reduced by 0.9 to 8.5%. The data suggest that the top surface of the roadbed allows for a compressive strain of approximately 200 με. Furthermore, the data show that ideal number for an inverted base structure include: an asphalt layer modulus of 1300 MPa, a surface layer thickness of at least 25cm or more, and a surface layer thickness of at least more than 15cm for the mixed base layer.

4) Surface deflection

As shown in Figures 12 and 13, the thickness of the asphalt layer and the modulus of the asphalt layer influenced the surface deflection of the pavement structure for both inverted and combining substrates.

Figure 12.  Variation of surface deflection versus asphalt thickness for an invert base.

DownLoad: Full-Size Img PowerPoint

Figure 13.  Variation of surface deflection versus asphalt thickness for a mixed base.

DownLoad: Full-Size Img PowerPoint

For inverted base pavements, the reduction in road surface deflection settlement was approximately 5.1 to 6.2% for every 5cm increase in asphalt thickness (i.e., 1000 MPa). For mixed subgrade pavements, the reduction in road surface deflection was approximately 3.3 to 4.5% for every 5 cm increase in asphalt thickness, indicating that asphalt layer thickness did not have a significant effect on road surface deflection. Additionally, increasing the modulus of the asphalt layer also reduced road surface deflection. For each 300 MPa increase in asphalt layer, the reduction in road surface deflection settlement was approximately 3.8–12.1% for inverted subgrade and 3.5–13.8% for mixed subgrade.

3.2.2.   Substrate thickness and modulus

1) Tensile strain

As shown in Figures 14 and 15, the tensile strain was reduced as ply thickness increased for both inverted and combining substrates. Additionally, increasing the modulus of the subgrade simultaneously reduced the tensile strain of the asphalt layer subgrade.

Figure 14.  Variation of tensile strain on the bottom asphalt layer versus thickness of the graded gravel layer for an inverted base.

DownLoad: Full-Size Img PowerPoint

Figure 15.  Variation of tensile strain on the bottom asphalt layer versus thickness of the graded gravel layer for mixed base.

DownLoad: Full-Size Img PowerPoint

For inverted subgrade pavement, every 5 cm increase in graded gravel thickness caused a decrease in tensile strain of the bottom asphalt layer by approximately 0.3 to 0.6% (i.e., 300 MPa). A larger modulus led to a more pronounced variation in asphalt layer tensile strain. Therefore, graded aggregates should be between 500 and 600 MPa. For mixed subgrade pavements, increasing the thickness of asphalt aggregates by 5cm has the potential to reduce tensile strain of the bottom asphalt layer by approximately 2%. Additionally, increasing the modulus of the subgrade has the potential to reduce subgrade tensile strain in asphalt. For every 100 MPa increase in graded aggregates, asphalt strain is reduced by approximately 0.9 to 4.9%. For each 300 MPa increase in asphalt aggregates, asphalt subgrade tensile strain was reduced by approximately 1.1 to 5.4%. Under further analysis, a modulus of graded aggregates above 400 MPa significantly changed asphalt layer sub-strain. These data suggest that the aggregates layer should not be too thick. Therefore, this data recommends that a 500 MPa graded gravel layer with a thickness greater than 20cm be used. A larger modulus leads to a more pronounced change in strain with regards to asphalt thickness. Therefore, these data recommended 1200 MPa asphalt stabilized aggregates with a thickness greater than 20 cm to be used in these instances.

2) Shear stress

As shown in Figures 16 and 17, shear stresses in the asphalt layer varied significantly with asphalt thickness for both inverted and mixed base layers. As base layer thickness increased, shear stress in the asphalt layer decreased. When the modulus of the subgrade increased, asphalt layer shear stress decreased.

Figure 16.  Variation of shear stress on the bottom asphalt layer versus thickness of the graded gravel layer for an inverted base.

DownLoad: Full-Size Img PowerPoint

Figure 17.  Variation of shear stress on the bottom asphalt layer versus thickness of the graded gravel layer for a mixed base.

DownLoad: Full-Size Img PowerPoint

For inverted subgrade pavement, shear stress in the asphalt layer decreased by approximately 0.23 to 1.95% when thickness of the graded crushed stone layer varied from a value of 1545 cm. This data indicated that graded crushed stone layer thickness had minimal effect on asphalt layer shear stress. For mixed subgrade pavement, asphalt layer shear stress decreased by approximately 3.1–4.9% when asphalt stabilized crushed stone thickness varied from 15–45 cm. These results indicate that asphalt stabilized crushed stone thickness had little effect on asphalt shear stress. Additionally, the data suggest that as the modulus of the subgrade increases, asphalt layer shear stress gradually decreased. Furthermore, a change in modulus of the asphalt stabilized crushed stone layer from 900–1800 MPa was found to reduce asphalt layer shear stress of the mixed base layer by approximately 1.8–3.8%. As the modulus of graded aggregates changed from 300–600 MPa, asphalt shear stress of the inverted subgrade was reduced by approximately 1.1–2.8%. The data suggest that the effect of subgrade modulus on asphalt shear stress was very small for both mixed and inverted subgrade. In Figure 18, the data shows the relationship the thickness and modulus of the graded grave layer and shear stress in the graded gravel layer. In Figure 18 the data also shows that shear stress in the graded gravel layer can be increased if thickness or modulus are increased.

Figure 18.  Variation of shear stress and thickness of graded aggregates in an inverted base.

DownLoad: Full-Size Img PowerPoint

For inverted subgrade pavements, shear stress in the graded gravel layer increased by 1.7 to 11% for every 5 cm increase in graded gravel thickness. Additionally, for every 100 MPa increase in graded aggregates, shear stress in the graded gravel layer of the inverted subgrade increased by approximately 9.8–10.7%.

3) Compressive strain

As shown in Figures 19 and 20, the compressive strain at the top surface of base was reduced as ply thickness increased for both inverted and combining substrates.

Figure 19.  Variation of top surface compressive strain versus thickness of graded gravel layer for an inverted base.

DownLoad: Full-Size Img PowerPoint

Figure 20.  Variation of top surface compressive strain versus thickness of graded gravel layer for a mixed base.

DownLoad: Full-Size Img PowerPoint

For inverted subgrade pavement, the top surface compressive strain decreased by 4.1–5.9% for every 5 cm increase in asphalt thickness. A larger modulus of graded aggregates correlated to faster variation in top surface compressive strain that was associated with overall thickness. For mixed subgrade pavements, top surface compressive strain decreased by 5.4 to 10.7% for each 5cm increase in asphalt thickness. Additionally, increasing the modulus of the subgrade reduced top surface compressive strain. For each 300 MPa increase in the modulus of asphalt aggregates, the reduction in top surface compressive strain of the mixed subgrade leachate was approximately 0.2 to 7.8%. The modulus of graded aggregates did not have any significant effect on top surface compressive strain of the roadbed. It was determined that top surface compressive strain of the roadbed was approximately 200 με. Therefore, when the thickness of the subgrade was greater than 15cm, both subgrade structures met requirements.

4) Surface deflection

As shown in Figures 20 and 21, that subgrade thickness and modulus had an effect on affected the road surface deflection of the pavement structure for both inverted and combining substrates.

Figure 21.  Variation of surface deflection versus graded gravel layer thickness of an inverted base.

DownLoad: Full-Size Img PowerPoint

Figure 22.  Variation of surface deflection versus graded gravel layer thickness of a mixed base.

DownLoad: Full-Size Img PowerPoint

For inverted subgrade pavement, every 5 cm increase in the graded gravel layer led to a road surface deflection reduction between 0.4 to 1.2%. For mixed subgrade pavement, every 5 cm increase in thickness led to a decrease in road surface deflection between 1.4 to 3.8%. These data suggest that asphalt thickness stabilized the gravel layer and had a significant effect on road surface deflection compared to graded gravel thickness. It further suggests that increasing the modulus of the subgrade is capable of reducing road surface deflection. For every 300 MPa increase in stabilized and crushed asphalt stone, reduction in road surface deflection of the mixed subgrade was found to be between 0.5 to 5.3%. For every 100 MPa increase in graded aggregates, reduction in road surface deflection of the inverted subgrade was found to be between 0.5 to 4.3%. In conclusion, we found that 500–600 MPa of graded gravel, a 20 cm thickness, and a surface modulus of greater than 1300 MPa should be used for inverted subgrade layer structures based on the data. A total thickness of 25 cm for the entire project would be ideal. For mixed subgrade structures, the data recommended using 1200 MPa of asphalt stabilized gravel, with a thickness greater than 20cm and a surface layer thickness greater than 20 cm.

4.   Conclusions

1) Orthogonal analysis was conducted to investigate the sensitivity of structural pavement mechanical control indexes for inverted and mixed base layers. The influence of thickness, modulus, and interlayer contact for each structural layer based on design indexes were investigated using extreme difference and variance analysis of calculated results.

2) For further analysis, design indicators such as: asphalt bottom layer tensile strain and shear stress, graded gravel layer shear stress, top surface compressive strain, and road surface deflection were selected as structural control indexes.

3) For inverted subgrade, thickness and modulus of the asphalt layer had a significant effect on each mechanical control index. More specifically, the road base modulus was found to have the greatest effect on deflection of the road surface. With regards to the inverted subgrade structure, the results of these studies recommended to use 500–600 MPa of graded gravel, with a thickness greater than 20 cm, a modulus of the surface layer greater than 1300 MPa, and a total thickness greater than 25 cm.

4) For the mixed base layer, asphalt layer thickness and modulus had a significant effect on asphalt layer bottom tensile strain and shear stress, while the road base modulus and thickness were determined to have the greatest influence on road surface deflection and top surface compressive strain. For the mixed subgrade paving layer structure, the data from these studies recommended 1200 MPa asphalt stabilized gravel with a thickness greater than 20 cm, with the overall thickness of the surface layer greater than 20 cm.

Conflict of interest

We declare that we have no conflict of interest.