A review of the key sensitive parameters on the aerodynamic performance of a horizontal wind turbine using Computational Fluid Dynamics modelling

1.   Introduction

Energy demands are increasing as the world’s population and industrial growth continue to expand ^[1]. The world’s consumption of energy is predicted to increase by 56% from 524 quadrillion BTUs in 2010 to 820 quadrillion BTUs in 2040 ^[2]. The extensive consumption of fossil fuels is the primary source of carbon dioxide emissions in the atmosphere. The CO₂ released from fossil fuel burning is estimated to increase from 1,000 million metric tons in 2010 to 36,000 million metric tons in 2020 and may reach 45 billion metric tons by the end of 2040 ^[3].

The demands for clean energy sources have risen dramatically and rapidly due to environmental awareness, decreasing reliance on traditional fuel sources, and strict environmental policies ^[4]. Amongst all renewable energy sources, wind energy seems to be one of the more popular rising technologies due to its low price and speedy global development ^[5]. The world’s total installed power from wind energy increased from 296,581 MW in 2013 to 597,000 MW at the end of 2018, and it is predicted to reach 817,000 MW by 2021 ^[3].

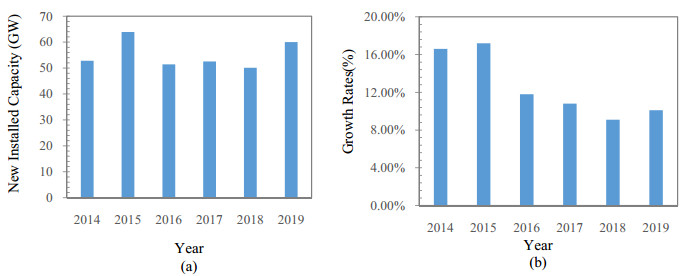
The World Wind Energy Association updated its statistics regarding added wind capacity during 2018 to around 50.1 GW, which is slightly less than the installed wind energy capacity in 2017, as shown in Figure 1(a). The installed wind capacity in 2017 achieved the third largest installation level during one year after record numbers in 2015 and 2014. On the other hand, 2018 exhibited the lowest market growth rate, about 9.1%, since the growth of wind turbine technology at the beginning of the twentieth century, as shown in Figure 1(b). In 2018, the countries making the most contribution to wind turbine energy were China (34.81%), the USA (16.48%), and Germany (10.41%), as shown in Figure 2 ^[3].

There are a few review studies on wind turbine technology. Lydia et al. ^[6] reviewed the modelling of wind turbine power curves using different methodologies. Tchakoua et al. ^[7] presented a general review and classification of wind turbine monitoring methods with focus on trends and future challenges. Infield and Freris ^[8] discussed a study of wake effects on downstream turbines using different fluid dynamics techniques. The study aims to highlight the sensitive parameters that affect the aerodynamic performance of horizontal wind turbines. Understanding the key operating parameters of the wind turbine has significant impacts on the amount of energy output. Optimizing the operating parameters of wind turbine design has significant impacts on the amount of energy output. Atmospheric conditions (wind data models), the shape of the wind turbine blade, wind power curve and tip speed ratio, and airfoil configuration are discussed. Furthermore, this paper examines Computational Fluid Dynamics (CFD) models that are used for solving flow problems around wind turbines.

The paper started with sensitive parameters that affected the performance of horizontal wind turbines and examined the associated aerodynamic characteristics. Furthermore, it highlighted the various turbulence models and their applications in Computation Fluid Dynamic modelling to analyze the aerodynamic characteristic of the horizontal wind turbine.

2.   Sensitive parameters of the aerodynamic performance of the horizontal wind turbine

Several parameters are influencing the aerodynamic characteristic of HAWT, such as atmospheric conditions and shape of the wind blade. Scaling up the capacity of the wind turbine requires an increase in blade length to maximize the energy output. Therefore, understanding the critical operating parameters on the performance of the wind turbine should be considered in the design of the expected power output. This section discusses the key design and operating parameters in the wind turbine.

2.1.   Atmospheric conditions (wind data models)

Wind speed plays a vital role in the performance of the wind turbine since it is the primary source of energy. The wind speeds at a specific site are varying with annual, seasonal, and daily changes. It is crucial, therefore, to describe these variations by different mathematical distribution models ^[9]. A highly accurate analysis of wind data is essential to encourage stakeholders increasing or at least considering their investment in wind energy technology. Statistical analysis methods such as probability distribution function were proposed for studying the potential of wind resources in a specific location.

The probability density distribution describes the occurrence frequency of wind speed using common functions. Nonparametric and parametric models had been used for wind speed probability distribution. Nonparametric kernel density estimation is an important technique in wind data analysis. Kernel density estimators directly take benefit of sample data without using parameter estimation of a theoretical distribution. The following equation is used to express the distribution:

Parametric models such as Rayleigh and Weibull has been popularly used for wind speed analysis ^[10]. Rayleigh probability distribution function requires only the mean wind speed; thus, it is a simplistic probability distribution function f(v) as described by Eq 1:

where v is the wind speed (m/s) and v is the average wind speed (m/s). The Weibull distribution function is considered to be one of the common probability functions used in wind speed probability analysis. The Weibull probability function, as shown in Eq 2, depends on two factors, scale and shape factor ^[11,12]:

where k is the shape factor (dimensionless), and c is the scale factor (m/s). The curvature of the probability distribution function is decided by the shape parameter; any variation in the shape parameter is affected by the estimated wind potential. The Rayleigh distribution is employed when the mean wind speed is only available for the location. Rayleigh distribution is a special type of Weibull distribution when the shape factor is equal to 2, and the scale parameter depends on the mean wind speed. More spread of wind speed probability functions is related to a lower shape factor ^[13].

Determination of the Weibull function requires defining the shape and scale parameters, using different estimation methods. Using the maximum likelihood method, which is a widely accepted formula for defining shape and scale parameters is articulated in the following equations ^[14,15]:

where v_i is the wind speed at time and n is the number of readings of wind speed data. To define the annual energy production of a wind turbine (AEP), probability density distribution f(v) is combined with the power curve of wind turbine P(v) as shown in the following equation:

where v_cut-in is the cut-in wind speed (m/s), and v_cut-out is the cut-out wind speed (m/s).

In the energy market, the values of wind speed at different hub heights of the wind turbine are very desirable, according to unavailable recorded data from wind station measurements. To calculate the wind speed v(h) at different altitude values (h) which depend on the measured wind speeds at reference value using power exponent law, the following equation ^[16] is proposed:

where v_o is the wind speed at reference height (h_ref), and α is a power-law exponent (dimensionless) which varies with time of the day, terrain nature, temperatures, and season of the year ^[17]. The power-law exponent varies from 0.1 in smooth terrains to 0.40 in very rough terrains where a value of 1/7 could be used when no information about specific site formation.

Different studies have analyzed wind data using Weibull and Rayleigh probability distributions functions. For example, Islam et al. ^[18] assessed the potential of wind energy at Kudat and Labuan, Malaysia using Weibull distribution; their results confirmed the unsuitability of these sites for commercial wind energy generation. Krenn et al. ^[19] studied wind data in Austria over a ten-year period, depending on station data combined with a hybrid geostatistical model. The result indicated the feasibility of Weibull distribution in capturing the average annual wind speed with 0.8 m/s standard deviation of error. Celik ^[20] evaluated the potential of wind energy on Turkey’s Mediterranean coast based on Rayleigh and Weibull models. The results showed that the Weibull model gives better accuracy of the power density distribution compared to the Rayleigh model.

In contrast, the Weibull model gives an annual average error of around 4.9% compared with 36.5% for the Rayleigh model when compared to wind speed measured reading. Mentis et al. ^[21] used the daily wind speed at different sites in Africa for one year by Weibull and Rayleigh distributions. Results showed 5% differences along with the findings between Rayleigh and Weibull distribution, but the variation exceeded 100% at specific locations. As such, the Rayleigh model is not valid at those sites, especially on the country level, and it can be used for estimating wind energy probability on a continental level only.

2.2.   The shape of the wind turbine blade

The number of blades in wind turbines varies depending on the design ^[22,23,24]. Currently, the 3-bladed upwind horizontal wind turbine is the most popular modern wind turbine design due to its system efficiency, stability, and the economic feasibility of the wind turbine system. A horizontal wind turbine consists of majors major components. The foundation component of the wind turbine is the tower, which holds the nacelle, while the nacelle contains the transmission system, generator, and control systems. The transmission system transmits the mechanical torque from the rotor to the generator, which includes the gearbox and mechanical brake system ^[25]. The generator uses electromagnetic components to convert mechanical power into electrical power ^{[26,27,28,29]}.

Meanwhile, the rotor component captures the wind power and converts it into mechanical torque. The rotor contains the blade component attached to the nacelle by the hub. Different materials are used in the manufacturing of wind turbine blades such as carbon-hybrid and S-glass ^[30,31]. Various studies demonstrated that decreasing the rotor and nacelle weight will reduce manufacturing costs. It should be noted that this decrease has a dynamic aero-structural limitation, and balancing issues need to be considered in the design ^[32,33].

One of the most design parameters of the shape of the wind turbine is the determination of the airfoil chord length and twist angle distribution along the blade, as seen in Figure 3(a). Discrete radial stations along the blade have been used to describe the shape of the blade, as shown in Figure 3(b). The chord, c(r), and twist angle β(r), which is the angle between tip airfoil and the local airfoil, have been used to define the shape of the blade.

One of the most critical design parameters of the wind turbine is the determination of the airfoil chord length distribution along the wind turbine blade. There are different methods for determining the chord length, where the Betz optimization theory is deemed the most straightforward method and offers reasonable approximation values of the airfoil section’s chord length ^[34]. This method approximates a good optimum value of blade chord length, which has a 6–8 tip speed ratio when neglecting losses from the tip and drag. Consequently, this method is inaccurate in some cases with low tip speeds, blade sections near the hub, and high drag airfoil sections ^[35,36,37]. The blade of the wind turbine is divided into three essential parts; root, mid-span, and tip based on the structural and aerodynamic roles. The larger chord length should be in the root area due to structural loads, while the slender airfoil sections will be in the tip region area. Consequently, the area near the hub is responsible for the required starting torque, while most of the production torque is initiated from the tip region ^{[38,39,40,41,42]}. Research has focused on aerodynamic optimization of the shape of the wind turbine design.

Research has focused on aerodynamic optimization of the shape of the wind turbine design by changing the twist angle and chord length distribution along the blade. The objective of the optimization is maximizing the annual energy output for a specific site, where the wind data model is used to define the wind potential in a particular location. Liu et al. ^[43] studied the novel optimization of fixed speed wind turbines using linearization of twist angle and chord profiles method. They concluded that there is a good increment in annual energy production when designing an optimal blade using novel linearization for wind speed ranging from 4–7 m/s. Blade element momentum theory (BEM) helped in the design the rotor of a 300 kW HAWT based on wind speed data in Semnan, Iran ^[44]. The results defined the optimal shape of the wind turbine, which related to the maximum power coefficient by taking into consideration easy manufacturing. Darwish et al. ^[45] improved the AEP for low wind speed regions by selecting, laying out, and matching the most suitable wind turbine design for a case study conducted in Iraq. Al-Abadi et al. ^[34] optimized the shape of a wind turbine using Blade Element Momentum (BEM) with a gradient-based optimization algorithm. Derakhshan et al. ^[46] tested the effectiveness of the shape optimization in their numerical study of a wind turbine. Their study found that the optimization of chords distribution increased by 3.7% the power of wind turbines at rated speed (10 m/s) while the average amount of power increased by 1.2% for all wind speed. Optimization of the wind turbine blade shape was undertaken at Gökçeada in Turkey using different blade design parameters, i.e., twist angle and chord length. Results showed the highest annual energy production (AEP) of 92,972 kWhr was comparable to the original design ^[47].

2.3.   Wind power curve and tip speed ratio

The power curve gives the power output of the wind turbine at each wind speed. This curve is essential for forecasting the performance of wind speed, which improves grid planning and connecting wind energy to the power systems ^[48]. The least wind speed required to deliver a useful power is called the cut-in speed while the turbine is shut down at the cut-out wind speed for engineering safety reasons to prevent damage caused by massive wind loads ^[49,50]. Some methods used to enhance the aerodynamic performance of the HAWT over different wind speeds include decreasing the cut-in wind speed. For example, Singh et al. ^[51] designed a wind turbine with a better start-up performance at low wind speed using a numerical method, which served to: firstly, reduce the cut-in wind speed; and secondly, achieve a better combination of lift to drag ratios. This was validated against the experimental data.

The tip speed ratio is a key design factor, which affects the calculation of different design parameters of the optimum rotor dimensions. The definition of the tip speed ratio is the ratio between the velocity of the rotor blade and relative wind speed. The aerodynamic design of the wind turbine is sensitive to any changes in the tip speed ratio. Thus, a rotor blade design operated at a relatively high wind speed will generate a lower torque at minimum wind speed. Also, this rotor operating at high wind speed will increase the cut-in speed and self-starting difficulties ^[24].

As shown in Table 1, selecting an appropriate tip speed ratio should take into account the design of different parameters such as output torque, mechanical stress and efficiency, aerodynamic characteristic, and noise ^[52]. Practically, raising the tip speed ratio will increase the noise pollution to the sixth power ^[53]. The tip speed ratio should be six to nine for a modern three-blade wind turbine and nine to ten for a two-blade wind turbine, to yield an efficient mechanical to electrical conversion ^[54].

The main controlled performance parameters in the HAWT are pitch angle and the generator torque. The rotor speed will vary accordingly to undergo maximum power point tracking in the generator torque control system. Conversely, in the pitch-regulated system, the smooth output power will result from controlling the wind input torque. Controlling the optimum blade pitch angle and optimum tip speed ratio will achieve the optimum power coefficient in pitch regulated variable speed horizontal wind speed, especially since there is an optimum power coefficient related to specific wind speed ^[55].

2.4.   Airfoil configuration

2.4.1.   Conventional airfoil

Efficient blade design is formed from different airfoil profiles with a blending at an angle of twist for each airfoil terminating at a circular blade root. Different simplification is used to facilitate industrial production and cut down the manufacturing costs, such as minimizing the number of varying airfoil profiles, linearization of chord width, and decreasing the twist angle ^[56]. The decision to select airfoils plays a critical role in the output torque from a wind turbine. The direct impact of airfoil design defines the aerodynamic performance of wind turbines. The lift to drag ratio is an essential aspect of the aerodynamic characteristics of the airfoil. Over the past decade, several experimental studies tested the lift and drag coefficients of airfoils with different Reynolds number and angles of attack ^[57,58]. The angle of attack is a very sensitive parameter for calculating the drag and lift coefficient of the airfoil. This angle is evaluated as the difference between the flow angle and the rotor plane angle. Therefore, the most important factor in designing the wind turbine is to maximize the lift to drag ratio ^[58,59].

The power output in a horizontal wind turbine is affected mainly by the lift to drag ratio of the airfoil, which is usually designed to operate at a low angle of attack where the lift coefficient is often much higher than the drag coefficient ^[57]. Different airfoil families have been used in the design of modern wind turbines such as NACA sub-families four and five-digit, for example, NACA 65–415, NACA 63–215 ^[60]. NACA is developed by the National Advisory Committee for Aeronautics predecessor of NASA, USA. The NACA airfoils are usually appropriate for situations where the angle of attack is relatively small, and the Reynolds number is high ^[61]. NACA 63 and 44 series are known for their characteristics of stall delay and less sensitivity to roughness in leading-edge than other families ^[62]. Yılmaz et al. ^[63] investigated the aerodynamic efficiency of the wind turbine blade by experiment, and results were compared with a numerical simulation. The study selected NACA 4420 airfoil for analysis and showed that the HAWT’s efficiency depended on the blade profile.

RISØ-A-XX is another family used in the design of the wind turbine blade and has been developed and optimized by RISØ National Laboratory in Denmark ^[64,65,66]. Direct numerical optimization is used to describe the airfoil shape that is optimized with a B-spline representation. The family has contained seven airfoils that varied in relative thickness to chord from 12% to −30%. The DU series airfoil family is another airfoil family, which was developed by the Delft University of Technology, Netherlands. The relative thickness to the chord of DU series airfoil varies from 15% to 40%, for example, DU 91-W2-250 and DU 93-W-210, which has an airfoil thickness of 25% and 21%, respectively ^[67].

There are many airfoils used for wind turbine design; for example, the Aeronautical Research Institute of Sweden has developed the FFA airfoil family ^[60]. Elsewhere, the S airfoil family is developed by the National Renewable Energy Laboratory (NREL) ^[68,69]. Some considerations should be taken in determining the type of airfoil used in wind turbines such as achieving a maximum lift to drag ratio, dynamic and structural requirements, and the sensitivity of airfoil to environmental conditions. Using a single airfoil profile along the whole wind turbine blade results in poorer efficiency of the blade design. In some applications, different airfoil shapes can be used in the design of a wind blade, but blending between these airfoils in the design process would increase the efficiency.

The sections of an airfoil with high thickness to chord length ratio are usually used in the root region according to structural load requirements ^[65]. However, airfoils of high thickness have a lower value of lift to drag ratio. Therefore, significant research has been conducted to increase the lift coefficient of the thick airfoil used in wind turbine design. In the tip regions, the aerodynamic characteristic is critical to maximizing the lift to drag ratio, which explains using a thin airfoil in the tip region.

In large modern wind turbine blades, the inboard and mid-span regions utilize airfoils that had a relative thickness of 25% or above. For example, FFA- W3-241 and FFA-W3-301 airfoils are used for inboard and mid-span regions due to relatively high thickness ^[70]. S809 and S814 airfoils are recommended for the tip region of the wind turbine, which has a blade length that varies from 10 to 15 m ^[71]. Different studies are investigating different airfoils in wind turbine design; for example, Van Rooij et al. ^[72] used Risø, DU, NACA, FFA, and S8xx airfoil families to investigate the performance of those airfoils to meet the aerodynamic and structural requirements. For airfoils of relative thickness to chord ranging between 25% and 30%, the best performing airfoils are S814 (24%), DU 91-W2-250 (25%), and Risø-A1-24 (24%) where the performance differences between those airfoils are relatively small. Meanwhile, for airfoil thickness of 30%, the DU 97-W-300 has the best performance according to restricted requirements.

Recently, a lot of work concentrated on designing blades for wind turbine rotors depending on maximizing the aerodynamic performance ^[73,74,75]. The generated power of a wind turbine varies with the speed and turbulence of the wind. Many countries have low wind speed in some locations. There is a lot of research in the development of small wind turbines to meet the energy needs of such countries. Ahmed et al. ^[76] studied lift, drag coefficient, and flow behavior of SG6043 at low Reynolds number to assess the airfoil aerodynamic characteristics used in wind turbines for regions having wind speeds of 4–6 m/s. The results showed that increasing the freestream turbulence level from 1% up to 10% will not significantly change the lift coefficient. However, with an increasing angle of attack, the separation was delayed from the upper surface, which reflects on increasing the lift coefficient and reducing the drag coefficient. When the angle of attack increases, the lift to drag ratio also increases from 8% to 15% because the turbulence level rises. Sayed et al. ^[77] simulated the aerodynamic performance of different S-series in low wind velocities. The study found that S825, S826, S830, and S831 airfoils are the most efficient in S-series for low and high wind velocities because they give a maximum lift to drag ratio, which achieves maximum power.

Airfoil characteristics such as flow separation vary with the level of wind turbulence ^[78,79,80]. Thus, many models combine the lift coefficient of the airfoil with delay flow separation ^[81]. Hoffmann ^[82] investigated the impact of changing the wind turbulence intensity of NACA 0015 from 0.25% to 9% at Re = 250,000. The analysis found that the effect of delayed flow separation on increasing the maximum lift coefficient increased the angle of attack. It also discovered that the impact on delayed flow separation and increasing the peak lift coefficient was due to changing turbulent intensity. Kamada et al. ^[83] discussed the dynamic and static characteristics at Re = 350,000 for DU93-W-210 at two different turbulent intensity levels. This airfoil had 21% relative thickness, which was tested in a wind tunnel with a turbulence grid that helped to obtain a high turbulent flow. They observed a delay in flow separation when increasing the level of freestream intensity, which reflected an increase in the stall angle of attack.

2.4.2.   Flatback airfoil

Several attempts have been made to improve annual energy production (AEP) by increasing the blade length ^[84]. Manufacturers have also researched reducing the aerodynamic and structural load, which causes a long blade ^[85]. Researchers have proposed flatback airfoils at the inboard section of the blade due to the high lift coefficient and larger sectional area to overcome the disadvantages of the structural load caused by increased blade length ^[86,87]. Kim et al. ^[88] studied the sufficient structural stiffness and safety consideration effect for flatback airfoil that have 20% cross-section areas larger than the non-flatback airfoil. As well, the rigidity of the cross-section area has increased due to a decrease in blade weight ^[89,90].

The wealth of research in wind turbine applications using a flatback airfoil includes aerodynamic characteristics, design process, and simulation methods ^{[91,92,93,94,95]}. Murcia and Pinilla ^[96] investigated the adding thickness and cutting method in the design of a flatback airfoil. Both methods showed an increase in maximum lift coefficient and drag coefficient, where the stall angle is delayed. However, adding thickness method gives a higher maximum lift coefficient when compared with cutting techniques. Standish and Van Dam ^[97] examined the design process used in the flatback airfoil. The study concluded that adding asymmetrical thickness to the baseline of the airfoil improved the aerodynamic characteristics of the flatback airfoil. As such, combined adding asymmetrical thickness design process decreases the negative effect of increasing thickness, which contributed to the cutting method and will improve the aerodynamic characteristics of the airfoil.

Law and Gregorek ^[98] studied a flatback airfoil for a large capacity wind turbine. They found that a higher lift coefficient and the lower drag coefficient is achievable in a flatback airfoil compared to the conventional airfoil. Homsrivaranon found that using flatback airfoils enhanced aerodynamic performance by increasing the lift-to-drag ratio. Chen et al. ^[99] used a genetic algorithm for two desired optimization objectives (maximum lift coefficient and maximum lift to drag coefficient) to produce optimal flatback airfoil that have excellent aerodynamic properties. Zhang et al. ^[100] compared the different numerical parameterization methods used for optimizing the airfoil; the results showed an improvement in the lift-to-drag ratio. Yet there was no improvement in the stall characteristics. Baker et al. ^[101] experimentally verified that insensitivity of trailing edge flatback airfoil to contaminations on the leading edge was evident; the base drag in the wake caused drag to increase. Furthermore, the method of adding asymmetrical thickness on the baseline of airfoil improved the lift coefficient when compared with the conventional airfoil, but the drag coefficient rose.

Some of the drawbacks of the flatback airfoil compared with conventional airfoil are increasing drag at a high angle of attacks due to separation vortex ^[102]. A flatback blade generates separation vortex around the hub in the spanwise direction, so some of the essential research areas in the development of wind turbine blade are adding devices that suppress separation vortex, for example, vortex generator ^{[103,104,105]}. Ceyhan et al. ^[106] looked at the problem of the higher drag coefficient of flatback airfoils, which limits their structural application to inboard parts of the wind turbine’s blade. They suggested the swallowtail concept as a non-conventional flatback airfoil. They analyzed the modified DU 97–300 flatback airfoil experimentally with 10% trailing edge thickness and without the sallow tail. They found that the drag fell by 40%, and hence the output power of the wind blade could increase without any modification done to operating conditions. Therefore, the non-conventional flatback is a promising technology that could be used for the inboard part of the wind turbine. The other drawback of the flatback airfoil is increasing vortex shedding noise and aero-elastic problems ^[107,108]. However, the inboard region in the blade which used flatback airfoil operates at speed lower than tip speed, generated a slight increase in rotor noise.

3.   Computational Fluid Dynamic techniques

In the early 1990s, Computational Fluid Dynamics techniques (CFD) were used for solving flow problems around wind turbines by available commercial software, for example, EllipSys3D and Fluent ^{[109,110,111]}. The environmental conditions, e.g., wind speed and direction, exert a real influence on the lifetime of the wind turbine. Understanding the turbulence model, which simulates the aerodynamics of wind flow around a wind turbine, is essential for obtaining reliable results. In this section, different turbulence models for all flow Navier-Stokes equations will be discussed. In CFD techniques, the method of the finite volume is used for solving the momentum and mass equations in addition to equations of turbulence for each control volume cell.

3.1.   Turbulence models

Until now, there is no one model that can predict all physical characteristics of turbulent flow. Various models are employed in the turbulent flow of wind turbines such as Direct Numerical Simulation (DNS), Reynolds Averaged Navier-Stroke (RANS), and Large Eddy Simulation (LES). DNS has the best accuracy in turbulence solution. However, the required computational time and cost are relatively high ^[112,113]. The most common model used for solving Navier-Stokes equations is RANS ^[114,115]. The mathematical principle concept is based on the calculation method of the Navier–Stokes equation, which divides the flow into a fluctuating part and average part where the average equation is called the Reynolds decomposition. Various turbulence models are used to solve the RANS equation.

Firstly, the k-ε turbulence model series calculates the eddy viscosity by solving two parameters: firstly, the turbulent dissipation rate (ε) parameter; and secondly, a turbulence kinetic energy (k) parameter. Standard k-ε was specified by Launder and Sharma ^[116], which is very popular and widely used; it gives poor results for flow simulation that had a separation phenomenon such as separation at flow around the wind turbine at high wind speed. Another improvement and modification on standard k-ε have been done to attain the Renormalization Group (RNG) k-ε and Realizable k-ε turbulence models ^[117,118]. Both models share the same transport equation as standard k-ε for turbulent kinetic energy (k) and dissipation rate (ε). However, the turbulent viscosity generation and calculation method mark the differences between these models. The renormalization group theory was used as a statistical method for solving the RNG k –ε turbulence model. The RNG k-ε turbulence has different modifications than standard k-ε, for example, considering the impact of rotation in eddy viscosity. The RNG k–ε is more accurate and better able to predict separations flows than standard k-ε ^[119]. The realizable k-ε model is recommended for rotating bodies as the results could be improved when compared with standard k-ε for swirling flow problems under specific Reynolds number ^[120].

The k-ω turbulence model is another RANS that is widely used for simulation flow around the wind turbine. Kolmogorov proposed the first form of the k-ω model ^[121]. The Imperial College group has done a new improvement on this model, but the most distinguished development was undertaken by Wilcox ^[122]. In some applications, the k-ω model has greater accuracy than standard k-ε due to boundary layers with an adverse pressure gradient, and the sublayer could be integrated without the need for any extra damping functions. However, k-ω is still sensitive for some flow with free stream boundaries condition that restricts its implementation. k-ω Shear Stress Transport (SST) is an advanced turbulence model devised by Menter ^[123], and it combines the advantages of the k-ω and k-ε turbulence models. Therefore, the inner part of the boundary layer where is used in the k-ω models and then converted gradually to k-ε in the free shear layer and wake region’s outer layers. The translation between the two models is related to blending functions. The other advantage of this model is the modification of eddy viscosity, which considers the effect of turbulent shear stress transportation. Different modifications of k-ω Shear Stress Transport (SST) had been done to enhance rotation and streamline curvature ^[124].

Another RANS model is the transition SST (γ-Re_θ) model, which was extended based on the k-ω SST ^[125]. It has four-transport equations; the first two equations are identical to k-ω (SST) equations, where the third and fourth equations are intermittency (γ) and transition momentum thickness Reynolds number (Re_θ). The transition SST model is more precise than classical turbulence models due to its ability to deal with the laminar-turbulent transition flow model where the separation of flow and stall phenomena occurs.

The Spalart-Allmaras (SA) is the simplest RANS turbulence model, which uses one transport equation. Here the computational of turbulence quantity is formulated by one transport equation, in which the kinematic eddy turbulent viscosity is the equation’s variable ^[126]. This model was designed and optimized for a compressible flow over airfoils and wings for aerospace applications. It may simply suggest a different type of grid for practical situations with include adverse pressure gradients where it becomes easily stable and converges with the solution ^[127]. In the meantime, the model could enable significant diffusion, especially in regions of 3D vortices flow ^[128]. Different improvement work has been done by Spalart and Shur ^[129], and Rahman et al. ^[130] to take into consideration the effects of rotation, near the wall and reduction of the diffusion effect. The advantage of the fast convergence of this model is the low computation time when compared to other turbulence models ^[127].

Large Eddy Simulation (LES) is another model developed to have less computational demand than the Direct Navier-Stokes model. The first trial of LES in engineering was done by Deardorff ^{[131,132,133,134]}. Unlike the RANS model, the LES turbulence model has wider applicability and more accurate results. Another advantage is decreasing the length of scales in the LES approaches in which turbulence is divided into two parts in the computational domain. The first part concerns the important large scales which was fully resolved, while the second part is the small sub-grid scales are modelled. The superiority of LES models is evident in high Reynolds number turbulence models investigations, and they provide an adequate prediction of complex flow when compared to other turbulence models ^[135,136]. Unfortunately, the required computational time for the LES model is higher than the RANS model.

The Detached-Eddy Simulation (DES) was developed in 1997 ^[137] and applied for high Reynolds number with a massively separated flow ^[138]. The latter method is a model that blends the LES and RANS approaches. Hence, LES is applied with external flow regions with massive separations, whereas the boundary layer is solved by RANS ^[139]. Travin et al. ^[140] described the DES as a single turbulence model that uses unsteady three-dimensional numerical methods. Johansen et al. ^[141] found that using DES approaches does not improve the characteristics of the wind turbine when using the DES method due to the required long computational time.

3.2.   Application of turbulence models used for aerodynamic simulation of the wind turbine

The numerical simulation of flow around the wind turbine is sensitive to the numerical models used for wind turbine design under operating conditions. The literature is abundant with various turbulence models that were used to validate different numerical methods against experimental works. For example, Li et al. ^[142] used CFD Ship-lowa with a sliding mesh for NREL Phase VI to examine the unsteady RANS and DES models. The study found that the results of thrust forces and moments were different from the experimental work. However, using DES did considerably improve the unsteady flow of the wind turbine.

Lanzafame et al. ^[143], Potsdam and Mavriplis ^[144], and Rajvanshi et al. ^[145] studied the numerical simulation of NREL Phase VI using k-ω SST and transition SST. The results demonstrated the better capabilities of transition SST compared to k-ω SST with experimental work. In another study, Moshfeghi et al. ^[146] looked at the effects of near-wall grid treatment on the aerodynamic performance of the wind turbine. NREL Phase VI model with eight cases was examined for a near-wall grid that used k-ω SST and transition SST turbulence models. Different wind speeds are used for predicting thrust forces and pressure coefficients. The thrust force results of k-ω SST did not agree well with the thrust values in test results. In general, the k-ω SST model over-predicts the performance of the wind turbine. However, transition SST behavior is different from the k-ω SST model, particularly in the inboard regions, but the outcomes are close to the experimental work. k-ε turbulence models are used in studying the flow around the wind turbine and wake dynamic behavior. Kasmi and Masson ^[147] and Abelsalam et al. ^[148] performed a full-scale study of three wind turbines based on different k-ε turbulence models and compared results. These showed that the modified k-ε agrees better with previous experimental measurements than standard k-ε. Different studies evaluated the reliability of predicting wind turbine performance using various turbulence models. Rutten et al. ^[149] computed the NREL Phase VI using two RANS models: k-ω, k-ω SST. It emerged that the k-ω SST turbulence model is better at estimating the turbulent kinetic energy value when compared to k-ω. Abdulqadir et al. ^[150] investigated the reliability based on RANS and 12 turbulence models for predicting the NREL Phase VI wind turbine. All RANS numerical key performance coefficients at low tip speed ratios revealed a good value when validated against experimental results. However, during high tip speed ratios, the poorest simulation results were achieved by k-ω SST, whereas realizable k-ε highlighted relatively good results.

You et al. ^[151] investigated the effect of different RANS turbulence models (Spalart-Allmaras, k-ω SST, and transition SST) on estimating the aerodynamic characteristics around the NREL Phase VI blade rotor. Their results demonstrated the ability of transition SST to capture the laminar separation bubbles around the airfoil surface and rotor blade. Thus, the results of the k-ω Transition model agrees well with experimental data due to a good prediction of the boundary layer’s transition area. An investigation into predicting the numerical performance of a New Mexico wind turbine looked at the effect of RANS turbulence models using two different near-wall methods of high and low Reynolds number ^[152]. The RANS models used in the high Reynolds model were the Spalart-Allmaras and k-ε RNG, while the models employed for low Reynolds number were k-ω SST and k-ω transition. All four models, under low wind speeds range, could predict well the wind turbine’s aerodynamic performance. When the wind speeds increased, more differences between the models appeared, and the high Reynolds model had better results compared with the low Reynolds model. A swirl effect was considered with wall function corrections, where the RNG k-ε turbulence model is recommended when wind speed increases ^[152].

The advantages and disadvantages of each turbulence approach are summarised as the following. DNS and LES have higher accuracy for turbulence solutions when compared with RANS. However, the required computational resources and time are relatively high. Thus RANS becomes the most popular due to the balance between accuracy and computational cost. Standard k-ε is very popular and widely used, but it gives poor simulation results for flows with separation phenomenon such as wind turbine at high wind speed. The RNG k–ε is more accurate to predict separation flows than standard k-ε. The realizable k-ε model has improved results for swirling flow problems under specific Reynolds number when compared with standard k-ε, and is thus recommended for rotating bodies. Although k-ω is a simple model used for wind turbine, it is still sensitive for flows with free stream boundaries condition that restricts its implementation. k-ω Shear Stress Transport (SST) had been applied to wind turbine flow problems to enhance rotation and streamline curvature. The transition SST model is more precise than classical RANS turbulence models due to its ability to deal with the laminar-turbulent transition where the separation and stall phenomena occur. The following table summarizes the previous studies on the CFD summary for HAWT.

4.   Conclusion remarks and challenges

The authors proposed a possible research future direction which is to take into account the environmental conditions into blade design. There is a lack of wind turbine experiment data for the validation of CFD models. Therefore, the future work regarding CFD simulations should look at realistic wind speed conditions. The authors find there is still a need for specific research on airfoil configuration, i.e. aerodynamic characteristics of conventional and flatback airfoils. Various challenges emerge when using the wind turbine technology, for instance, there is high competition between industries ^[176], wind measurement devices accuracy ^[177], maintenance and operational problems ^{[178,179,180,181,182,183]}, and power/grid distribution challenges ^{[184,185,186]}. There are different solutions to improve the control system ^[187,188] and wind forecasting devices ^{[189,190,191]}. For more than two centuries, the aerodynamics of the wind turbine have been studied, and previous studies focused mostly on the challenges and solutions using experimental methods. However, 3D simulation work is still in its infancy with many simplifications having to be made due to cost and complexity. This paper reviews the key points in the aerodynamic wind turbine design. The major conclusions of this review are:

●  Accurate wind distribution data is essential in the design of a wind turbine depending on specific site. Weibull and Rayleigh are two probability distribution functions that are commonly used to determine the occurrence frequency of wind speed. Until now, many studies in this field have devised different models to compare the accuracy between these probability density functions.

●  Different parameters affected the design of wind turbines such as the HAWT power curve, tip speed ratio, and blade plane shape. Several analyses have sought to enhance the aerodynamic performance by decreasing cut-in speed, appropriate selection of tip speed ratio and taking into consideration the mechanical stress and noise.

●  There are different families used in a modern wind turbine, and the selection of these airfoils depends on a variety of considerations such as a lift to drag coefficient. Studies have engaged in certain design criteria of mixing airfoil to increase the efficiency of the wind turbine. This is an area requiring further research.

●  The simulation of HAWT using CFD is a very good tool in predicting aerodynamic performance, wherein accuracy depends on selecting suitable turbulence models. Most of the current numerical work focuses on increasing the accuracy of CFD models in predicting aerodynamic performance. They do this by attempting to solve the constraints of cost and time through simulation experiments.

Acknowledgements

The authors would like to sincerely thank Isra University, Jordan for their financial support given through doctoral scholarship to the student Nour Khlaifat.

Conflict of interest

The authors declare no conflict of interest.