The effects of right temporoparietal junction stimulation on embodiment, presence, and performance in teleoperation

Valentina Cesari; Graziella Orrù; Andrea Piarulli; Alessandra Vallefuoco; Franca Melfi; Angelo Gemignani; Danilo Menicucci; Valentina Cesari; Graziella Orrù; Andrea Piarulli; Alessandra Vallefuoco; Franca Melfi; Angelo Gemignani; Danilo Menicucci

doi:10.3934/Neuroscience.2024022

AIMS Neuroscience

2024, Volume 11, Issue 3: 352-373. doi: 10.3934/Neuroscience.2024022

Previous Article Next Article

Research article

The effects of right temporoparietal junction stimulation on embodiment, presence, and performance in teleoperation

1.
Department of Surgical, Medical and Molecular Pathology and Critical Care Medicine, University of Pisa, Pisa, Italy
2.
Clinical Psychology Branch, Azienda Ospedaliero-Universitaria Pisana, Pisa, Italy

Received: 24 July 2024 Revised: 26 August 2024 Accepted: 04 September 2024 Published: 10 September 2024

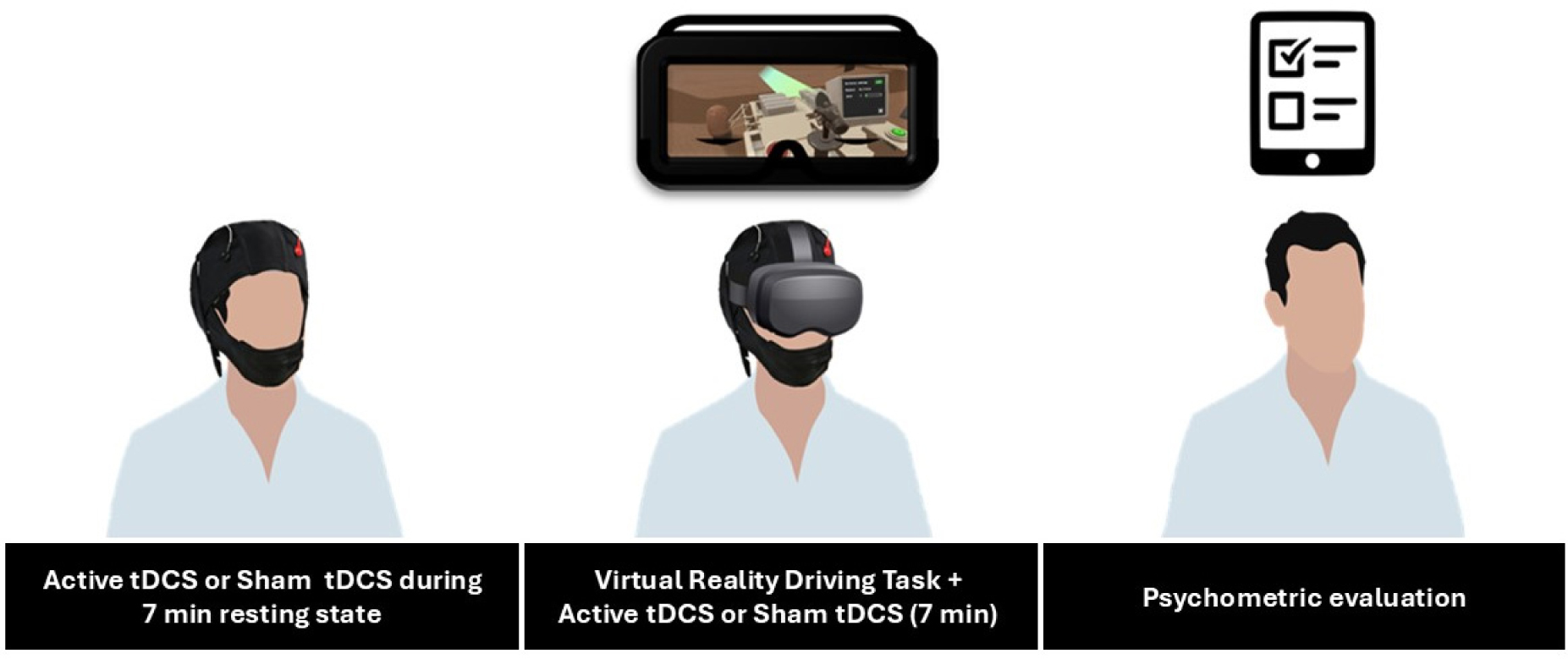
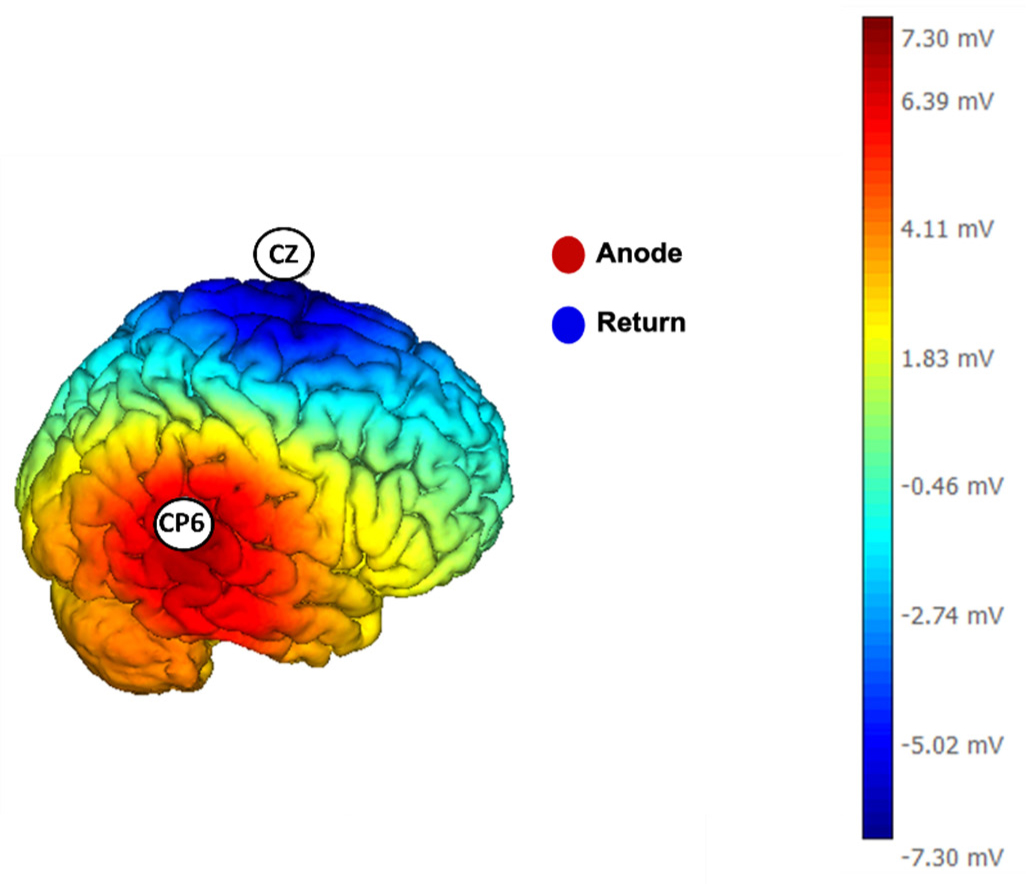
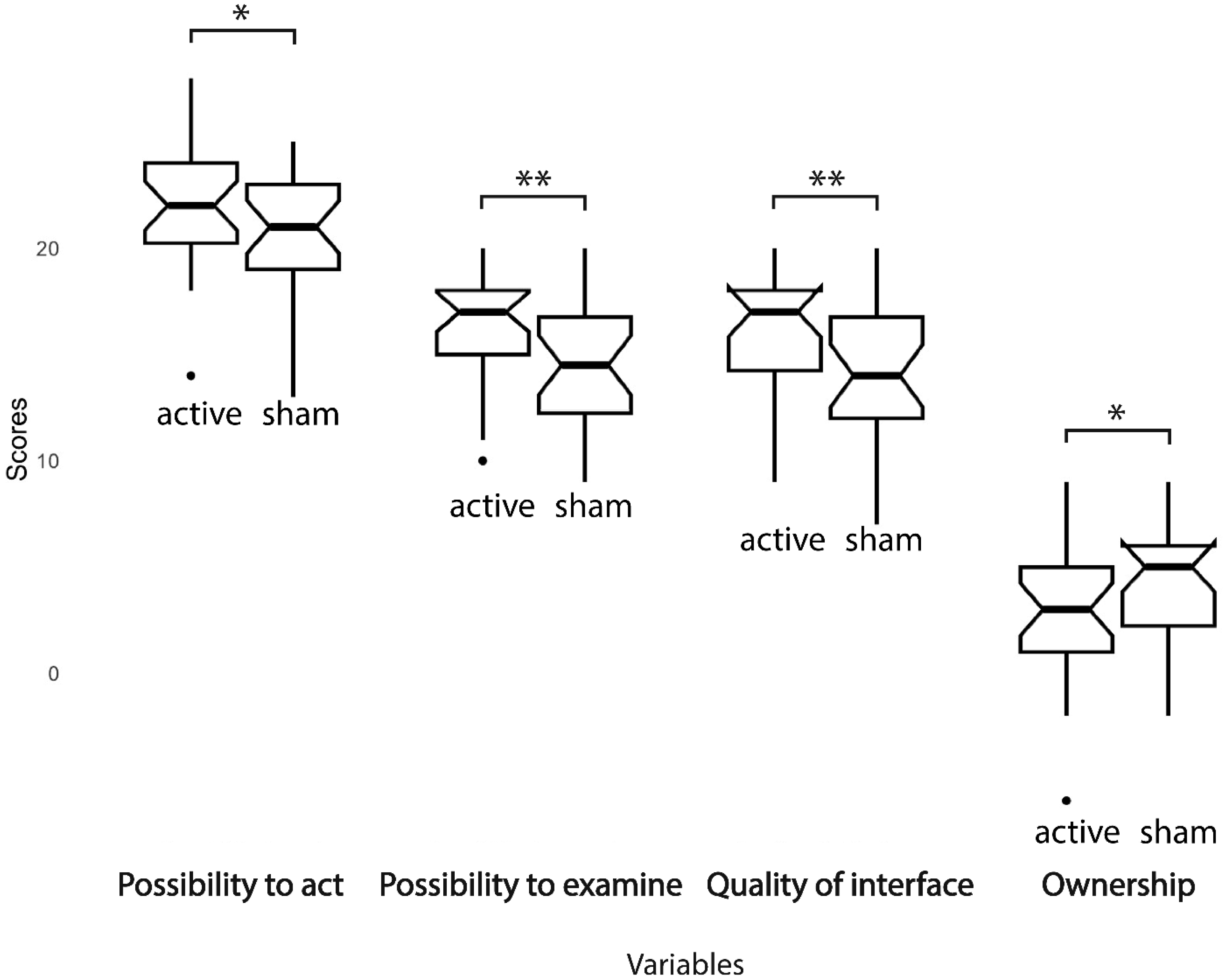
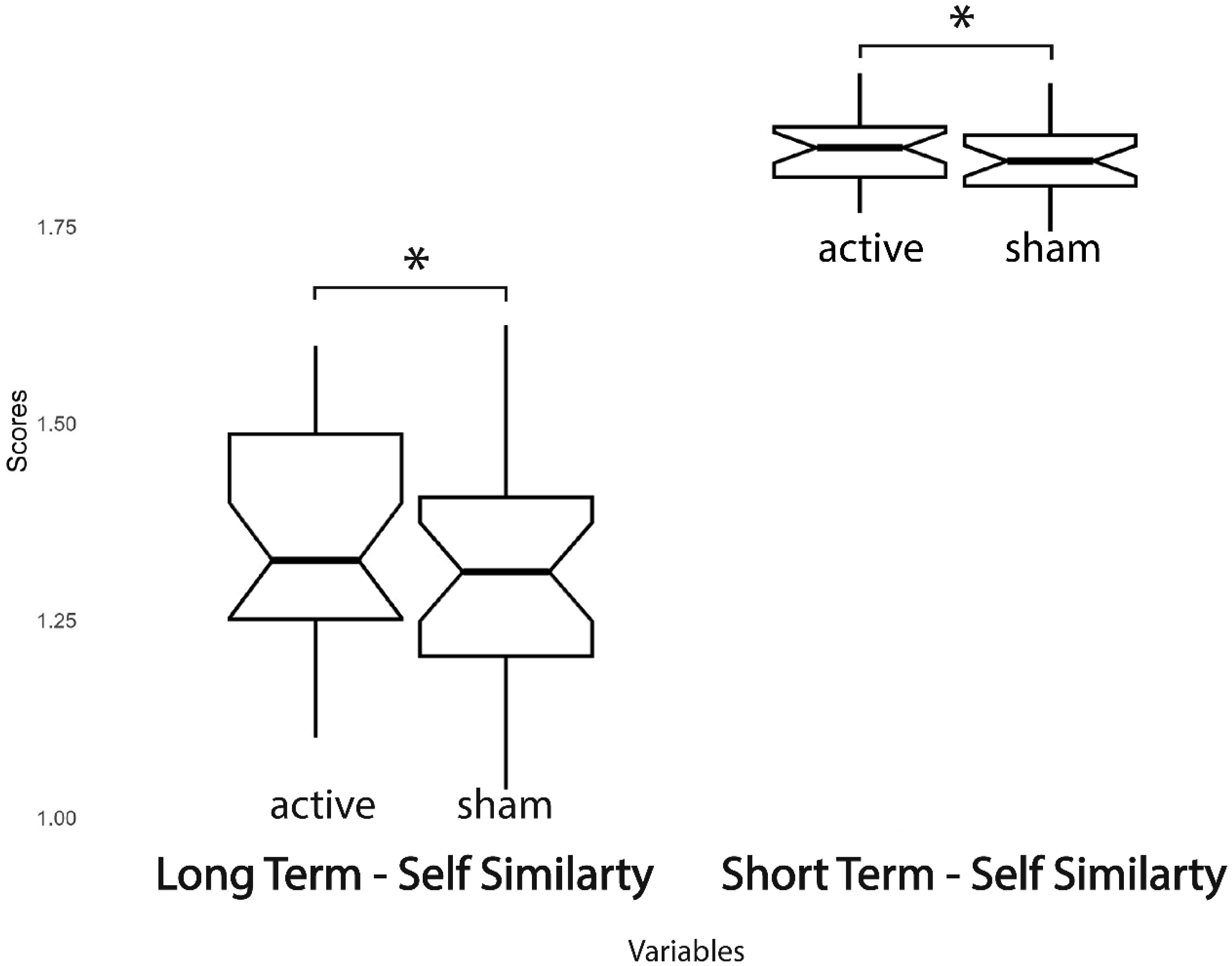
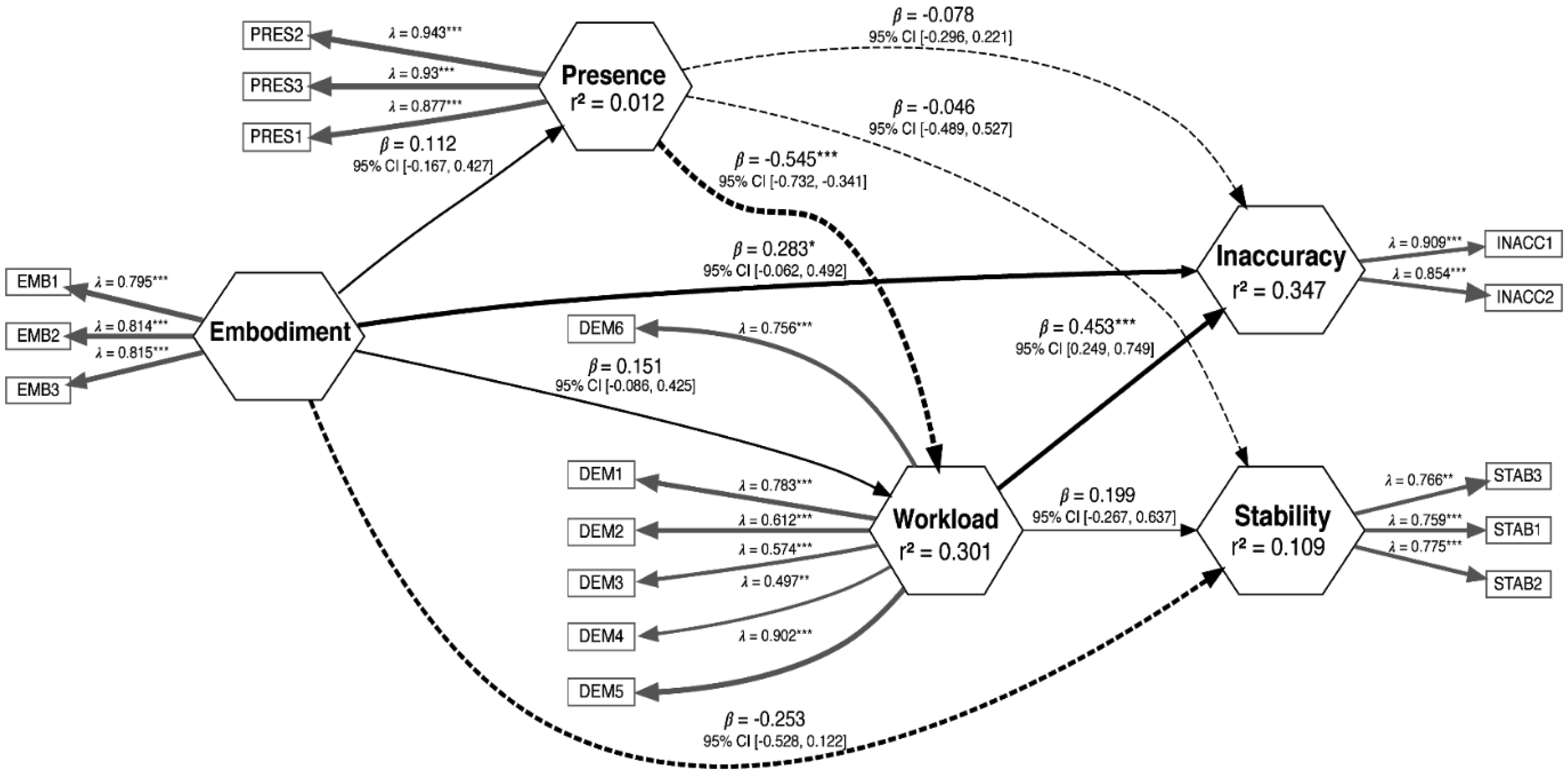
Embodiment (the sensation that arises when the properties of an external instrument are processed as if they are the attributes of one's own biological body) and (tele)presence (the sensation of being fully engaged and immersed in a location other than the physical space occupied by one's body) sustain the perception of the physical self and potentially improve performance in teleoperations (a system that enables human intelligence to control robots and requires implementing an effective human-machine interface). Embodiment and presence may be interdependent and influenced by right temporo-parietal junction (rTPJ) activity. We investigated the interplay between embodiment, (tele)presence, and performance in teleoperation, focusing on the role of the rTPJ. Participants underwent a virtual reality task with transcranial direct current stimulation (tDCS) twice, receiving either active or sham stimulation. Behavioral measures (driving inaccuracy, elapsed time in the lap, time spent in attentional lapses, short-term self-similarity, and long-term self-similarity), perceived workload (mental demand, physical demand, temporal demand, own performance, effort, and frustration), embodiment's components (ownership, agency, tactile sensations, location, and external appearance), and presence's components (realism, possibility to act, quality of interface, possibility to examine, self-evaluation of performance, haptic, and sounds) were assessed. The results showed that rTPJ stimulation decreased perceived ownership but enhanced presence with changes in the complexity of visuomotor adjustments (long and short-term self-similarity indices). Structural equation modeling revealed that embodiment increased visuomotor inaccuracy (a composite variable of overall performance, including deviations from the optimal trajectory and the time taken to complete the task), presence reduced workload, and workload increased inaccuracy. These results suggested a dissociation between embodiment and presence, with embodiment hindering performance. Prioritizing virtual integration may lower human performance, while reduced workload from presence could aid engagement. These findings emphasize the intricate interplay between rTPJ, subjective experiences, and performance in teleoperation.

Keywords:

Citation: Valentina Cesari, Graziella Orrù, Andrea Piarulli, Alessandra Vallefuoco, Franca Melfi, Angelo Gemignani, Danilo Menicucci. The effects of right temporoparietal junction stimulation on embodiment, presence, and performance in teleoperation[J]. AIMS Neuroscience, 2024, 11(3): 352-373. doi: 10.3934/Neuroscience.2024022

Related Papers:

[1]	P. Pirmohabbati, A. H. Refahi Sheikhani, H. Saberi Najafi, A. Abdolahzadeh Ziabari . Numerical solution of full fractional Duffing equations with Cubic-Quintic-Heptic nonlinearities. AIMS Mathematics, 2020, 5(2): 1621-1641. doi: 10.3934/math.2020110
[2]	SAIRA, Wenxiu Ma, Suliman Khan . An efficient numerical method for highly oscillatory logarithmic-algebraic singular integrals. AIMS Mathematics, 2025, 10(3): 4899-4914. doi: 10.3934/math.2025224
[3]	Kai Wang, Guicang Zhang . Curve construction based on quartic Bernstein-like basis. AIMS Mathematics, 2020, 5(5): 5344-5363. doi: 10.3934/math.2020343
[4]	Taher S. Hassan, Amir Abdel Menaem, Hasan Nihal Zaidi, Khalid Alenzi, Bassant M. El-Matary . Improved Kneser-type oscillation criterion for half-linear dynamic equations on time scales. AIMS Mathematics, 2024, 9(10): 29425-29438. doi: 10.3934/math.20241426
[5]	Dexin Meng . Wronskian-type determinant solutions of the nonlocal derivative nonlinear Schrödinger equation. AIMS Mathematics, 2025, 10(2): 2652-2667. doi: 10.3934/math.2025124
[6]	Samia BiBi, Md Yushalify Misro, Muhammad Abbas . Smooth path planning via cubic GHT-Bézier spiral curves based on shortest distance, bending energy and curvature variation energy. AIMS Mathematics, 2021, 6(8): 8625-8641. doi: 10.3934/math.2021501
[7]	Chunli Li, Wenchang Chu . Remarkable series concerning $\binom{3n}{n}$ and harmonic numbers in numerators. AIMS Mathematics, 2024, 9(7): 17234-17258. doi: 10.3934/math.2024837
[8]	Beatriz Campos, Alicia Cordero, Juan R. Torregrosa, Pura Vindel . Dynamical analysis of an iterative method with memory on a family of third-degree polynomials. AIMS Mathematics, 2022, 7(4): 6445-6466. doi: 10.3934/math.2022359
[9]	A. Palanisamy, J. Alzabut, V. Muthulakshmi, S. S. Santra, K. Nonlaopon . Oscillation results for a fractional partial differential system with damping and forcing terms. AIMS Mathematics, 2023, 8(2): 4261-4279. doi: 10.3934/math.2023212
[10]	Tongzhu Li, Ruiyang Lin . Classification of Möbius homogeneous curves in $\mathbb{R}^4$ . AIMS Mathematics, 2024, 9(8): 23027-23046. doi: 10.3934/math.20241119

Abstract

Abbreviations

ANOVA:

Analysis of Variance;

AVE:

Average Variance Extracted;

CFA:

Confirmatory Factor Analysis;

DEM:

Demand;

EMB:

Embodiment;

EFA:

Exploratory Factor Analysis;

INACC:

Inaccuracy;

MGA:

multi-group analysis;

PRES:

Presence;

PLS-SEM:

Partial Least Squares Structural Equation Modeling;

rTPJ:

right temporoparietal junction;

STAB:

Stability;

tDCS:

transcranial direct current stimulation;

VR:

Virtual Reality

1. Introduction

We consider the following family of nonlinear oscillators

$\begin{equation} y_{zz}+k(y)y_{z}^{3}+h(y)y_{z}^{2}+f(y)y_{z}+g(y) = 0, \end{equation}$

(1.1)

where $k$ , $h$ , $f\neq0$ and $g\neq0$ are arbitrary sufficiently smooth functions. Particular members of (1.1) are used for the description of various processes in physics, mechanics and so on and they also appear as invariant reductions of nonlinear partial differential equations ^[1,2,3].

Integrability of (1.1) was studied in a number of works ^{[4,5,6,7,8,9,10,11,12,13,14,15,16]}. In particular, in ^[15] linearization of (1.1) via the following generalized nonlocal transformations

$\begin{equation} w = F(y), \quad d\zeta = (G_{1}(y)y_{z}+G_{2}(y))dz. \end{equation}$

(1.2)

was considered. However, equivalence problems with respect to transformations (1.2) for (1.1) and its integrable nonlinear subcases have not been studied previously. Therefore, in this work we deal with the equivalence problem for (1.1) and its integrable subcase from the Painlevé-Gambier classification. Namely, we construct an equivalence criterion for (1.1) and a non-canonical form of Ince Ⅶ equation ^[17,18]. As a result, we obtain two new integrable subfamilies of (1.1). What is more, we demonstrate that for any equation from (1.1) that satisfy one of these equivalence criteria one can construct an autonomous first integral in the parametric form. Notice that we use Ince Ⅶ equation because it is one of the simplest integrable members of (1.1) with known general solution and known classification of invariant curves.

Moreover, we show that transformations (1.2) preserve autonomous invariant curves for equations from (1.1). Since the considered non-canonical form of Ince Ⅶ equation admits two irreducible polynomial invariant curves, we obtain that any equation from (1.1), which is equivalent to it, also admits two invariant curves. These invariant curves can be used for constructing an integrating factor for equations from (1.1) that are equivalent to Ince Ⅶ equation. If this integrating factor is Darboux one, then the corresponding equation is Liouvillian integrable ^[19]. This demonstrates the connection between nonlocal equivalence approach and Darboux integrability theory and its generalizations, which has been recently discussed for a less general class of nonlocal transformations in ^[20,21,22].

The rest of this work is organized as follows. In the next Section we present an equivalence criterion for (1.1) and a non-canonical form of the Ince Ⅶ equation. In addition, we show how to construct an autonomous first integral for an equation from (1.1) satisfying this equivalence criterion. We also demonstrate that transformations (1.2) preserve autonomous invariant curves for (1.1). In Section 3 we provide two examples of integrable equations from (1.1) and construct their parametric first integrals, invariant curves and integrating factors. In the last Section we briefly discuss and summarize our results.

2. Main results

We begin with the equivalence criterion between (1.1) and a non-canonical form of the Ince Ⅶ equation, that is ^[17,18]

$\begin{equation} w_{\zeta\zeta}+3w_{\zeta}+\epsilon w^{3}+2w = 0. \end{equation}$

(2.1)

Here $\epsilon\neq0$ is an arbitrary parameter, which can be set, without loss of generality, to be equal to $\pm 1$ .

The general solution of (1.1) is

$\begin{equation} w = {\rm e}^{-(\zeta-\zeta_{0})}\rm{cn}\left\{\sqrt{\epsilon}({\rm e}^{-(\zeta-\zeta_{0})}-C_{1}),\frac{1}{\sqrt{2}}\right\}. \end{equation}$

(2.2)

Here $\zeta_{0}$ and $C_{1}$ are arbitrary constants and $\rm{cn}$ is the Jacobian elliptic cosine. Expression (2.2) will be used below for constructing autonomous parametric first integrals for members of (1.1).

The equivalence criterion between (1.1) and (2.1) can be formulated as follows:

Theorem 2.1. Equation (1.1) is equivalent to (2.1) if and only if either

$\begin{equation} \begin{gathered} (I)\quad 25515lgp^{2}q_{y}+2352980l^{10}+\left(3430q-6667920p^{3}\right) l^{5}\\ -14580qp^{3}-10q^{2}-76545lgqpp_{y} = 0, \end{gathered} \end{equation}$

(2.3)

$\begin{equation} \begin{gathered} (II)\quad 343l^{5}-972p^{3} = 0, \end{gathered} \end{equation}$

(2.4)

holds. Here

$\begin{equation} \begin{gathered} l = 9(fg_{y}-gf_{y}+fgh-3kg^{2})-2f^{3}, \quad p = gl_{y}-3lg_{y}+l(f^{2}-3gh),\\ q = 25515g_{y}lp^{2}-5103lgpp_{y}+686l^{5}-8505p^{2}\left( f^{2}-3gh \right) l+6561p^{3}. \end{gathered} \end{equation}$

(2.5)

The expression for $G_{2}$ in each case is either

$\begin{equation} (I) \quad G_{2} = \frac {126 l^{2}qp^{2}}{470596 l^{10}- \left( 1333584 p^{3}+1372 q \right) l^{5}+q^{2}}, \end{equation}$

(2.6)

$\begin{equation} (II) \quad G_{2}^{2} = -\frac{49l^{3}G_{2}+9p^{2}}{189pl}. \end{equation}$

(2.7)

In all cases the functions $F$ and $G_{1}$ are given by

$\begin{equation} F^{2} = \frac{l}{81\epsilon G_{2}^{3}}, \quad G_{1} = \frac{G_{2}(f-3G_{2})}{3g}. \end{equation}$

(2.8)

Proof. We begin with the necessary conditions. Substituting (1.2) into (2.1) we get

$\begin{equation} y_{zz}+k(y)y_{z}^{3}+h(y)y_{z}^{2}+f(y)y_{z}+g(y) = 0, \end{equation}$

(2.9)

where

$\begin{equation} \begin{gathered} k = \frac{FG_{1}^{3}(\epsilon F^{2}+2)+3G_{1}^{2}F_{y}+G_{1}F_{yy}-F_{y}G_{1,y}}{G_{2}F_{y}}, \\ h = \frac{G_{2}F_{yy}+(6G_{1}G_{2}-G_{2,y})F_{y}+3FG_{2}G_{1}^{2}(\epsilon F^{2}+2)}{G_{2}F_{y}},\\ f = \frac{3G_{2}(F_{y}+FG_{1}(\epsilon F^{2}+2))}{F_{y}}, \quad g = \frac{FG_{2}^{2}(\epsilon F^{2}+2)}{F_{y}}. \end{gathered} \end{equation}$

(2.10)

As a consequence, we obtain that (1.1) can be transformed into (2.1) if it is of the form (2.9) (or (1.1)).

Conversely, if the functions $F$ , $G_{1}$ and $G_{2}$ satisfy (2.10) for some values of $k$ , $h$ , $f$ and $g$ , then (1.1) can be mapped into (2.1) via (1.2). Thus, we see that the compatibility conditions for (2.10) as an overdertmined system of equations for $F$ , $G_{1}$ and $G_{2}$ result in the necessary and sufficient conditions for (1.1) to be equivalent to (2.1) via (1.2).

To obtain the compatibility conditions, we simplify system (2.10) as follows. Using the last two equations from (2.10) we find the expression for $G_{1}$ given in (2.8). Then, with the help of this relation, from (2.10) we find that

$\begin{equation} 81\epsilon F^{2}G_{2}^{3}-l = 0, \end{equation}$

(2.11)

and

$\begin{equation} \begin{gathered} 567lG_{2}^{3}+(243lgh-81lf^{2}-81gl_{y}+243lg_{y})G_{2}-7l^{2} = 0,\\ 243lgG_{2,y}+324lG_{2}^{3}-81gl_{y}G_{2}+2l^{2} = 0, \end{gathered} \end{equation}$

(2.12)

Here $l$ is given by (2.5).

As a result, we need to find compatibility conditions only for (2.12). In order to find the generic case of this compatibility conditions, we differentiate the first equation twice and find the expression for $G_{2}^{2}$ and condition (2.3). Differentiating the first equation from (2.12) for the third time, we obtain (2.6). Further differentiation does not lead to any new compatibility conditions. Particular case (2.4) can be treated in the similar way.

Finally, we remark that the cases of $l = 0$ , $p = 0$ and $q = 0$ result in the degeneration of transformations (1.2). This completes the proof.

As an immediate corollary of Theorem 2.1 we get

Corollary 2.1. If coefficients of an equation from (1.1) satisfy either (2.3) or (2.4), then an autonomous first integral of this equation can be presented in the parametric form as follows:

$\begin{equation} y = F^{-1}(w), \quad y_{z} = \frac{G_{2}w_{\zeta}}{F_{y}-G_{1}w_{\zeta}}\,. \end{equation}$

(2.13)

Here $w$ is the general solution of (2.1) given by (2.2). Notice also that, formally, (2.13) contains two arbitrary constants, namely $\zeta_{0}$ and $C_{1}$ . However, without loss of generality, one of them can be set equal to zero.

Now we demonstrate that transformations (1.2) preserve autonomous invariant curves for equations from (1.1).

First, we need to introduce the definition of an invariant curve for (1.1). We recall that Eq (1.1) can be transformed into an equivalent dynamical system

$\begin{equation} y_{z} = P, \quad u_{z} = Q, \quad P = u, \quad Q = -k u^{3}-h u^{2}-f u -g. \end{equation}$

(2.14)

A smooth function $H(y, u)$ is called an invariant curve of (2.14) (or, equivalently, of (1.1)), if it is a nontrivial solution of ^[19]

$\begin{equation} PH_{y}+QH_{u} = \lambda H, \end{equation}$

(2.15)

for some value of the function $\lambda$ , which is called the cofactor of $H$ .

Second, we need to introduce the equation that is equivalent to (1.1) via (1.2). Substituting (1.2) into (1.1) we get

$\begin{equation} w_{\zeta\zeta}+\tilde{k}w_{\zeta}^{3}+\tilde{h}w_{\zeta}^{2}+\tilde{f}w_{\zeta}+\tilde{g} = 0, \end{equation}$

(2.16)

where

$\begin{equation} \begin{gathered} \tilde{k} = \frac{kG_{2}^{3}-gG_{1}^{3}+(G_{1,y}-hG_{1})G_{2}^{2}+(fG_{1}-G_{2,y})G_{1}G_{2}}{F_{y}^{2}G_{2}^{2}},\\ \tilde{h} = \frac{(hF_{y}-F_{yy})G_{2}^{2}-(2fG_{1}-G_{2,y})G_{2}F_{y}+3gG_{1}^{2}F_{y}}{F_{y}^{2}G_{2}^{2}},\\ \tilde{f} = \frac{fG_{2}-3gG_{1}}{G_{2}^{2}}, \quad \tilde{g} = \frac{gF_{y}}{G_{2}^{2}}. \end{gathered} \end{equation}$

(2.17)

An invariant curve for (2.16) can be defined in the same way as that for (1.1). Notice that, further, we will denote $w_{\zeta}$ as $v$ .

Theorem 2.2. Suppose that either (1.1) possess an invariant curve $H(y, u)$ with the cofactor $\lambda(y, u)$ or (2.16) possess an invariant curve $\widetilde{H}(w, v)$ with the cofactor $\tilde{\lambda}(w, v)$ . Then, the other equation also has an invariant curve and the corresponding invariant curves and cofactors are connected via

$\begin{equation} \begin{gathered} H(y,u) = \widetilde{H}\left(F,\frac{F_{y}u}{G_{1}u+G_{2}}\right), \quad \lambda(y,u) = (G_{1}u+G_{2})\tilde{\lambda}\left(F,\frac{F_{y}u}{G_{1}u+G_{2}}\right). \end{gathered} \end{equation}$

(2.18)

Proof. Suppose that $\widetilde{H}(w, v)$ is an invariant curve for (2.16) with the cofactor $\widetilde{\lambda}(w, v)$ . Then it satisfies

$\begin{equation} v\widetilde{H}_{w}+(-\tilde{k} v^{3}-\tilde{h} v^{2}-\tilde{f} v -\tilde{g})\widetilde{H}_{v} = \widetilde{\lambda}\widetilde{H}. \end{equation}$

(2.19)

Substituting (1.2) into (2.19) we get

$\begin{equation} uH_{y}+(-k u^{3}-h u^{2}-f u-g)H = (G_{1}u+G_{2}) \tilde{\lambda}\left(F,\frac{F_{y}u}{G_{1}u+G_{2}}\right) H . \end{equation}$

(2.20)

This completes the proof.

As an immediate consequence of Theorem 2.2 we have that transformations (1.2) preserve autonomous first integrals admitted by members of (1.1), since they are invariant curves with zero cofactors.

Another corollary of Theorem 2.2 is that any equation from (1.1) that is connected to (2.1) admits two invariant curves that correspond to irreducible polynomial invariant curves of (2.1). This invariant curves of (2.1) and the corresponding cofactors are the following (see, ^[23] formulas (3.18) and (3.19) taking into account scaling transformations)

$\begin{equation} \widetilde{H} = \pm i \sqrt{-2\epsilon}(v+w)+w^{2}, \quad \tilde{\lambda} = \pm \sqrt{-2\epsilon}w-2. \end{equation}$

(2.21)

Therefore, we have that the following statement holds:

Corollary 2.2. If coefficients of an equation from (1.1) satisfy either (2.3) or (2.4), then is admits the following invariant curves with the corresponding cofactors

$\begin{equation} H = \pm i \sqrt{-2\epsilon}\left(\frac{F_{y}u}{G_{1}u+G_{2}}+F\right)+F^{2}, \quad \lambda = \left(G_{1}u+G_{2}\right)\left(\pm \sqrt{-2\epsilon}F-2\right). \end{equation}$

(2.22)

Let us remark that connections between (2.1) and non-autonomous variants of (1.1) can be considered via a non-autonomous generalization of transformations (1.2). However, one of two nonlocally related equations should be autonomous since otherwise nonlocal transformations do not map a differential equation into a differential equation ^[5].

In this Section we have obtained the equivalence criterion between (1.1) and (2.1), that defines two new completely integrable subfamilies of (1.1). We have also demonstrated that members of these subfamilies posses an autonomous parametric first integral and two autonomous invariant curves.

3. Examples

In this Section we provide two examples of integrable equations from (1.1) satisfying integrability conditions from Theorem 2.1.

Example 1. One can show that the coefficients of the following cubic oscillator

$\begin{equation} y_{zz}-\frac{12\epsilon \mu y}{(\epsilon \mu^{2}y^{4}+2)^{2}}y_{z}^{3}-6\mu y y_{z}+2\mu^{2}y^{3}(\epsilon\mu^{2}y^{4}+2) = 0, \end{equation}$

(3.1)

satisfy condition (2.3) from Theorem 2.1. Consequently, Eq (3.1) is completely integrable and its general solution can be obtained from (2.2) by inverting transformations (1.2). However, it is more convenient to use Corollary 2.1 and present the autonomous first integral of (3.1) in the parametric form as follows:

$\begin{equation} y = \pm\sqrt{\frac{w}{\mu}}, \quad y_{z} = \frac{w(\epsilon w^{2}+2) w_{\zeta}}{2w_{\zeta}+w(\epsilon w^{2}+2)}, \end{equation}$

(3.2)

where $w$ is given by (2.2), $\zeta$ is considered as a parameter and $\zeta_{0}$ , without loss of generality, can be set equal to zero. As a result, we see that (3.1) is integrable since it has an autonomous first integral.

Moreover, using Corollary 2.2 one can find invariant curves admitted by (3.1)

$\begin{equation} \begin{gathered} H_{1,2} = \frac{y^{4}\left[(\sqrt{2}\pm \sqrt{-\epsilon}\mu y^{2})^{2}(\sqrt{2}\mp\sqrt{-\epsilon}\mu y^{2})+2(\epsilon\mu y^{2}\mp\sqrt{-2\epsilon})u\right]}{2\mu^{2}y^{2}(\epsilon\mu^{2}y^{4}+2)-4u},\\ \lambda_{1,2} = \pm\frac{2(\mu y^{2}(\epsilon\mu^{2}y^{4}+2)-2u)(\sqrt{-2\epsilon}\mu y^{2}\mp 2)}{y(\epsilon\mu^{2}y^{4}+2)} \end{gathered} \end{equation}$

(3.3)

With the help of the standard technique of the Darboux integrability theory ^[19], it is easy to find the corresponding Darboux integrating factor of (3.1)

$\begin{equation} M = \frac{(\epsilon \mu^{2}y^{4}+2)^{\frac{9}{4}}}{(2\epsilon u^{2}+(\epsilon\mu^{2}y^{4}+2)^{2})^{\frac{3}{4}}(\mu y^{2}(\epsilon \mu^{2}y^{4}+2)-2u)^{\frac{3}{2}}}. \end{equation}$

(3.4)

Consequently, equation is (3.1) Liouvillian integrable.

Example 2. Consider the Liénard (1, 9) equation

$\begin{equation} y_{zz}+(b_{i}y^{i}){y_{z}}+a_{j}y^{j} = 0, \quad i = 0,\ldots 4, \quad j = 0,\ldots,9. \end{equation}$

(3.5)

Here summation over repeated indices is assumed. One can show that this equation is equivalent to (2.1) if it is of the form

$\begin{equation} y_{zz}-9(y+\mu)(y+3\mu)^{3}y_{z}+2y(2y+3\mu)(y+3\mu)^{7} = 0, \end{equation}$

(3.6)

where $\mu$ is an arbitrary constant.

With the help of Corollary 2.1 one can present the first integral of (3.6) in the parametric form as follows:

$\begin{equation} y = \frac{3\sqrt{-2\epsilon}\mu w}{2-\sqrt{-2\epsilon}w}, \quad y_{z} = \frac{7776 \sqrt{2} \epsilon \mu^{5} w w_{\zeta}}{(\sqrt{-2\epsilon}w-2)^{5}(2\sqrt{-\epsilon}w_{\zeta}+(\sqrt{2}\epsilon w +2\sqrt{-\epsilon})w)}, \end{equation}$

(3.7)

where $w$ is given by (2.2). Thus, one can see that (3.5) is completely integrable due to the existence of this parametric autonomous first integral.

Using Corollary 2.2 we find two invariant curves of (3.6):

$\begin{equation} H_{1} = \frac{y^{2}[(2y+3\mu)(y+3\mu)^{4}-2u)]}{(y+3\mu)^{2}[(y+3\mu)^{4}y-u]}, \quad \lambda_{1} = \frac{6\mu(u-y(y+3\mu)^{4})}{y(y+3\mu)}, \end{equation}$

(3.8)

and

$\begin{equation} H_{2} = \frac{y^{2}(y+3\mu)^{2}}{y(y+3\mu)^{4}-u}, \quad \lambda_{2} = \frac{2(2y+3\mu)(u-2y(y+3\mu)^{4})}{y(y+3\mu)}. \end{equation}$

(3.9)

The corresponding Darboux integrating factor is

$\begin{equation} M = \left[y(y+3\mu)^{4}-u\right]^{-\frac{3}{2}}\left[(2y+3\mu)(y+3\mu)^{4}-2u\right]^{-\frac{3}{4}}. \end{equation}$

(3.10)

As a consequence, we see that Eq (3.6) is Liouvillian integrable.

Therefore, we see that equations considered in Examples 1 and 2 are completely integrable from two points of view. First, they possess autonomous parametric first integrals. Second, they have Darboux integrating factors.

4. Conclusions and discussion

In this work we have considered the equivalence problem between family of Eqs (1.1) and its integrable member (2.1), with equivalence transformations given by generalized nonlocal transformations (1.2). We construct the corresponding equivalence criterion in the explicit form, which leads to two new integrable subfamilies of (1.1). We have demonstrated that one can explicitly construct a parametric autonomous first integral for each equation that is equivalent to (2.1) via (1.2). We have also shown that transformations (1.2) preserve autonomous invariant curves for (1.1). As a consequence, we have obtained that equations from the obtained integrable subfamilies posses two autonomous invariant curves, which corresponds to the irreducible polynomial invariant curves of (2.1). This fact demonstrate a connection between nonlocal equivalence approach and Darboux and Liouvillian integrability approach. We have illustrate our results by two examples of integrable equations from (1.1).

Acknowledgments

The author was partially supported by Russian Science Foundation grant 19-71-10003.

Conflict of interest

The author declares no conflict of interest in this paper.

Acknowledgments

This work was supported by MUR (Ministry of University and Research), by the University of Pisa, and by European Union - Next Generation EU, in the context of The National Recovery and Resilience Plan, Investment 1.5 Ecosystems of Innovation, Project Tuscany Health Ecosystem (THE), Spoke 3 “Advanced technologies, methods, materials and health analytics” CUP: B83C22003920001.”

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Author contributions

Valentina Cesari: Writing – review & editing, Writing – original draft, Methodology, Investigation, Formal analysis, Visualization, Conceptualization. Graziella Orrù: Writing – original draft, Writing – review & editing, Methodology, Investigation. Andrea Piarulli: Writing – review & editing, Writing – original draft, Data curation. Alessandra Vallefuoco: Writing – review & editing, Investigation, Data curation. Franca Melfi: Writing – review & editing, Conceptualization. Angelo Gemignani: Writing – review & editing, Writing – original draft, Conceptualization, Supervision. Danilo Menicucci Writing – review & editing, Writing – original draft, Supervision, Investigation, Formal analysis, Project administration.

References

[1]	Cui J, Tosunoglu S, Roberts R, et al. (2003) A review of teleoperation system control. In: Proceedings of the Florida conference on recent advances in robotics; Boca Raton, FL. Boca Raton: Florida Atlantic University p. 1-12.
[2]	Pala M, Lorencik D, Sincak P (2012) Towards the robotic teleoperation systems in education. In: 2012 IEEE 10th International Conference on Emerging eLearning Technologies and Applications (ICETA); Stará Lesná, Slovakia. New York: IEEE p. 241-246. https://doi.org/10.1109/ICETA.2012.6418328
[3]	Siciliano B, Khatib O (2016) Springer Handbook of Robotics. Cham: Springer International Publishing. https://doi.org/10.1007/978-3-319-32552-1
[4]	Schinstock DE (1998) Approximate solutions to unreachable commands in teleoperation of a robot. Robot Comput Integr Manuf 3: 219-227. https://doi.org/10.1016/S0736-5845(97)00033-1
[5]	Álvarez B, Iborra A, Alonso A, et al. (2001) Reference architecture for robot teleoperation: development details and practical use. Control Eng Pract 9: 395-402. https://doi.org/10.1016/S0967-0661(00)00121-0
[6]	Toet A, Kuling IA, Krom BN, et al. (2020) Toward Enhanced Teleoperation Through Embodiment. Front Robot AI 7: 14. https://doi.org/10.3389/frobt.2020.00014
[7]	Kilteni K, Groten R, Slater M (2012) The Sense of Embodiment in Virtual Reality. Presence Teleoperators Virtual Environ 21: 373-387. https://doi.org/10.1162/PRES_a_00124
[8]	Slater M (2009) Place illusion and plausibility can lead to realistic behaviour in immersive virtual environments. Philos Trans R Soc Lond B Biol Sci 364: 3549-3557. https://doi.org/10.1098/rstb.2009.0138
[9]	Slater M, Spanlang B, Corominas D (2010) Simulating virtual environments within virtual environments as the basis for a psychophysics of presence. ACM Trans Graph 29: 1-9. https://doi.org/10.1145/1778765.1778829
[10]	Lombard M, Biocca F, Freeman J, et al. (2015) Immersed in Media: Telepresence Theory, Measurement & Technology. Cham: Springer International Publishing. https://doi.org/10.1007/978-3-319-10190-3
[11]	Herbelin B, Salomon R, Serino A, et al. (2016) 5. Neural Mechanisms of Bodily Self-Consciousness and the Experience of Presence in Virtual Reality. Human Computer Confluence: Transforming Human Experience Through Symbiotic Technologies. Warsaw, Poland: De Gruyter Open Poland pp. 80-96. https://doi.org/10.1515/9783110471137-005
[12]	Blanke O, Mohr C, Michel CM, et al. (2005) Linking out-of-body experience and self processing to mental own-body imagery at the temporoparietal junction. J Neurosci Off J Soc Neurosci 25: 550-557. https://doi.org/10.1523/JNEUROSCI.2612-04.2005
[13]	Orrù G, Bertelloni D, Cesari V, et al. (2021) Targeting temporal parietal junction for assessing and treating disembodiment phenomena: a systematic review of TMS effect on depersonalization and derealization disorders (DPD) and body illusions. AIMS Neurosci 8: 181-194. https://doi.org/10.3934/Neuroscience.2021009
[14]	Arzy S, Thut G, Mohr C, et al. (2006) Neural basis of embodiment: distinct contributions of temporoparietal junction and extrastriate body area. J Neurosci Off J Soc Neurosci 26: 8074-8081. https://doi.org/10.1523/JNEUROSCI.0745-06.2006
[15]	Ptak R, Schnider A (2011) The attention network of the human brain: Relating structural damage associated with spatial neglect to functional imaging correlates of spatial attention. Neuropsychologia 49: 3063-3070. https://doi.org/10.1016/j.neuropsychologia.2011.07.008
[16]	Donaldson PH, Rinehart NJ, Enticott PG (2015) Noninvasive stimulation of the temporoparietal junction: A systematic review. Neurosci Biobehav Rev 55: 547-572. https://doi.org/10.1016/j.neubiorev.2015.05.017
[17]	Pascual-Leone A, Amedi A, Fregni F, et al. (2005) The plastic human brain cortex. Annu Rev Neurosci 28: 377-401. https://doi.org/10.1146/annurev.neuro.27.070203.144216
[18]	Polanía R, Nitsche MA, Ruff CC (2018) Studying and modifying brain function with non-invasive brain stimulation. Nat Neurosci 21: 174-187. https://doi.org/10.1038/s41593-017-0054-4
[19]	Santarnecchi E, Brem A-K, Levenbaum E, et al. (2015) Enhancing cognition using transcranial electrical stimulation. Curr Opin Behav Sci 4: 171-178. https://doi.org/10.1016/j.cobeha.2015.06.003
[20]	Škola F, Liarokapis F (2021) Study of Full-body Virtual Embodiment Using noninvasive Brain Stimulation and Imaging. Int J Hum-Comput Interact 37: 1-14. https://doi.org/10.1080/10447318.2020.1870827
[21]	Convento S, Romano D, Maravita A, et al. (2018) Roles of the right temporo-parietal and premotor cortices in self-location and body ownership. Eur J Neurosci 47: 1289-1302. https://doi.org/10.1111/ejn.13937
[22]	Lapenta OM, Fregni F, Oberman LM, et al. (2012) Bilateral temporal cortex transcranial direct current stimulation worsens male performance in a multisensory integration task. Neurosci Lett 527: 105-109. https://doi.org/10.1016/j.neulet.2012.08.076
[23]	Marques LM, Lapenta OM, Merabet LB, et al. (2014) Tuning and disrupting the brain—modulating the McGurk illusion with electrical stimulation. Front Hum Neurosci 8: 533. https://doi.org/10.3389/fnhum.2014.00533
[24]	Lira M, Pantaleão FN, de Souza Ramos CG, et al. (2018) Anodal transcranial direct current stimulation over the posterior parietal cortex reduces the onset time to the rubber hand illusion and increases the body ownership. Exp Brain Res 236: 2935-2943. https://doi.org/10.1007/s00221-018-5353-9
[25]	Abedanzadeh R, Alboghebish S, Barati P (2021) The effect of transcranial direct current stimulation of dorsolateral prefrontal cortex on performing a sequential dual task: a randomized experimental study. Psicol Reflexao E Crit Rev Semest Dep Psicol UFRGS 34: 30. https://doi.org/10.1186/s41155-021-00195-8
[26]	Fregni F, Liguori P, Fecteau S, et al. (2008) Cortical stimulation of the prefrontal cortex with transcranial direct current stimulation reduces cue-provoked smoking craving: a randomized, sham-controlled study. J Clin Psychiatry 69: 32-40. https://doi.org/10.4088/JCP.v69n0105
[27]	Mondino M, Luck D, Grot S, et al. (2018) Effects of repeated transcranial direct current stimulation on smoking, craving and brain reactivity to smoking cues. Sci Rep 8: 8724. https://doi.org/10.1038/s41598-018-27057-1
[28]	Stagg CJ, Jayaram G, Pastor D, et al. (2011) Polarity and timing-dependent effects of transcranial direct current stimulation in explicit motor learning. Neuropsychologia 49: 800-804. https://doi.org/10.1016/j.neuropsychologia.2011.02.009
[29]	Nitsche MA, Paulus W (2000) Excitability changes induced in the human motor cortex by weak transcranial direct current stimulation. J Physiol 527 Pt 3: 633-639. https://doi.org/10.1111/j.1469-7793.2000.t01-1-00633.x
[30]	Khalil R, Karim AA, Godde B (2023) Less might be more: 1 mA but not 1.5 mA of tDCS improves tactile orientation discrimination. IBRO Neurosci Rep 15: 186-192. https://doi.org/10.1016/j.ibneur.2023.08.003
[31]	Santiesteban I, Banissy MJ, Catmur C, et al. (2012) Enhancing Social Ability by Stimulating Right Temporoparietal Junction. Curr Biol 22: 2274-2277. https://doi.org/10.1016/j.cub.2012.10.018
[32]	Santiesteban I, White S, Cook J, et al. (2012) Training social cognition: From imitation to Theory of Mind. Cognition 122: 228-235. https://doi.org/10.1016/j.cognition.2011.11.004
[33]	Bufano P, Albertini N, Chiarelli S, et al. (2022) Weakened Sustained Attention and Increased Cognitive Effort after Total Sleep Deprivation: A Virtual Reality Ecological Study. Int J Human–Computer Interact : 1-10. https://doi.org/10.1080/10447318.2022.2099047
[34]	Cesari V, Marinari E, Laurino M, et al. (2021) Attention-Dependent Physiological Correlates in Sleep-Deprived Young Healthy Humans. Behav Sci Basel Switz 11: 22. https://doi.org/10.3390/bs11020022
[35]	Laurino M, Menicucci D, Mastorci F, et al. (2012) Mind-body relationships in elite apnea divers during breath holding: a study of autonomic responses to acute hypoxemia. Front Neuroengineering 5. https://doi.org/10.3389/fneng.2012.00004
[36]	Peng CK, Havlin S, Stanley HE, et al. (1995) Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos Woodbury N 5: 82-87. https://doi.org/10.1063/1.166141
[37]	Maczák B, Gingl Z, Vadai G (2024) General spectral characteristics of human activity and its inherent scale-free fluctuations. Sci Rep 14: 2604. https://doi.org/10.1038/s41598-024-52905-8
[38]	Gonzalez-Franco M, Peck TC (2018) Avatar Embodiment. Towards a Standardized Questionnaire. Front Robot AI 5. https://doi.org/10.3389/frobt.2018.00074
[39]	Klotz AC, Swider BW, Kwon SH (2023) Back-translation practices in organizational research: Avoiding loss in translation. J Appl Psychol 108: 699-727. https://doi.org/10.1037/apl0001050
[40]	Cyberpsychology Lab of UQO, ‘Welcome to the Cyberpsychology Lab of UQO!’, consulted on 9 May 2024. [Online]. Available from: http://w3.uqo.ca/cyberpsy/index.php/welcome
[41]	Witmer BG, Singer MJ (1998) Measuring presence in virtual environments: A presence questionnaire. Presence Teleoperators Virtual Environ 7: 225-240. https://doi.org/10.1162/105474698565686
[42]	Hart SG, Staveland LE (1988) Development of NASA-TLX (Task Load Index): Results of empirical and theoretical research. Human mental workload. Oxford, England: North-Holland 139-183. https://doi.org/10.1016/S0166-4115(08)62386-9
[43]	Mueller ST, Piper BJ (2014) The Psychology Experiment Building Language (PEBL) and PEBL Test Battery. J Neurosci Methods 222: 250-259. https://doi.org/10.1016/j.jneumeth.2013.10.024
[44]	Poreisz C, Boros K, Antal A, et al. (2007) Safety aspects of transcranial direct current stimulation concerning healthy subjects and patients. Brain Res Bull 72: 208-214. https://doi.org/10.1016/j.brainresbull.2007.01.004
[45]	Harrington D (2009) Confirmatory Factor Analysis. USA: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195339888.001.0001
[46]	Brown TA Confirmatory Factor Analysis for Applied Research, Second Edition, Guilford Publications (2015).
[47]	Gould SJ (2015) Second Order Confirmatory Factor Analysis: An Example. Proceedings of the 1987 Academy of Marketing Science (AMS) Annual Conference. Cham: Springer International Publishing 488-490. https://doi.org/10.1007/978-3-319-17052-7_100
[48]	Jöreskog KG, Wold HOA Systems Under Indirect Observation: Causality, Structure, Prediction, North-Holland (1982).
[49]	Hair JF, Hult GTM, Ringle CM, et al. (2021) The SEMinR Package. Partial Least Squares Structural Equation Modeling (PLS-SEM) Using R: A Workbook. Cham: Springer International Publishing 49-74. https://doi.org/10.1007/978-3-030-80519-7_3
[50]	Dijkstra TK, Henseler J (2015) Consistent Partial Least Squares Path Modeling. MIS Q 39: 297-316. https://doi.org/10.25300/MISQ/2015/39.2.02
[51]	Söllner M, Mishra AN, Becker J-M, et al. (2024) Use IT again? Dynamic roles of habit, intention and their interaction on continued system use by individuals in utilitarian, volitional contexts. Eur J Inf Syst 33: 80-96. https://doi.org/10.1080/0960085X.2022.2115949
[52]	Breves P, Schramm H (2019) Good for the feelings, bad for the memory: the impact of 3D versus 2D movies on persuasion knowledge and brand placement effectiveness. Int J Advert 38: 1264-1285. https://doi.org/10.1080/02650487.2019.1622326
[53]	Buonocore S, Massa F, Di Gironimo G (2023) Does the Embodiment Influence the Success of Visuo-haptic Learning?. Application of Emerging Technologies. AHFE (2023) International Conference. AHFE Open Access, vol 115. USA: AHFE International. https://doi.org/10.54941/ahfe1004350
[54]	Roettl J, Terlutter R (2018) The same video game in 2D, 3D or virtual reality – How does technology impact game evaluation and brand placements?. PLOS ONE 13: e0200724. https://doi.org/10.1371/journal.pone.0200724
[55]	Minsky M (1980) Telepresence. OMNI Magazine : 44-52.
[56]	Rheingold H Virtual Reality: Exploring the Brave New Technologies, Simon & Schuster Adult Publishing Group (1991).
[57]	Koch C, Massimini M, Boly M, et al. (2016) Neural correlates of consciousness: progress and problems. Nat Rev Neurosci 17: 307-321. https://doi.org/10.1038/nrn.2016.22
[58]	Tononi G, Boly M, Gosseries O, et al. The Neurology of Consciousness (2016) 407-461. https://doi.org/10.1016/B978-0-12-800948-2.00025-X
[59]	Dai R, Larkin TE, Huang Z, et al. (2023) Classical and non-classical psychedelic drugs induce common network changes in human cortex. NeuroImage 273: 120097. https://doi.org/10.1016/j.neuroimage.2023.120097
[60]	Tsakiris M, Costantini M, Haggard P (2008) The role of the right temporo-parietal junction in maintaining a coherent sense of one's body. Neuropsychologia 46: 3014-3018. https://doi.org/10.1016/j.neuropsychologia.2008.06.004
[61]	Papeo L, Longo MR, Feurra M, et al. (2010) The role of the right temporoparietal junction in intersensory conflict: detection or resolution?. Exp Brain Res 206: 129-139. https://doi.org/10.1007/s00221-010-2198-2
[62]	Kammers MPM, Longo MR, Tsakiris M, et al. (2009) Specificity and Coherence of Body Representations. Perception 38: 1804-1820. https://doi.org/10.1068/p6389
[63]	Jakobs O, Wang LE, Dafotakis M, et al. (2009) Effects of timing and movement uncertainty implicate the temporo-parietal junction in the prediction of forthcoming motor actions. NeuroImage 47: 667-677. https://doi.org/10.1016/j.neuroimage.2009.04.065
[64]	Wu Q, Chang C-F, Xi S, et al. (2015) A critical role of temporoparietal junction in the integration of top-down and bottom-up attentional control. Hum Brain Mapp 36: 4317-4333. https://doi.org/10.1002/hbm.22919
[65]	Nitsche MA, Nitsche MS, Klein CC, et al. (2003) Level of action of cathodal DC polarisation induced inhibition of the human motor cortex. Clin Neurophysiol Off J Int Fed Clin Neurophysiol 114: 600-604. https://doi.org/10.1016/S1388-2457(02)00412-1
[66]	Berg H (2019) How does evidence-based practice in psychology work? – As an ethical demarcation. Philos Psychol 32: 853-873. https://doi.org/10.1080/09515089.2019.1632424
[67]	Grechuta K, Guga J, Maffei G, et al. (2017) Visuotactile integration modulates motor performance in a perceptual decision-making task. Sci Rep 7: 3333. https://doi.org/10.1038/s41598-017-03488-0
[68]	Kokkinara E, Slater M, Lopez-Moliner J (2015) The Effects of Visuomotor Calibration to the Perceived Space and Body, through Embodiment in Immersive Virtual Reality. ACM Trans Appl Percept 13. https://doi.org/10.1145/2818998
[69]	Tsakiris M, Haggard P (2005) The Rubber Hand Illusion Revisited: Visuotactile Integration and Self-Attribution. J Exp Psychol Hum Percept Perform 31: 80-91. https://doi.org/10.1037/0096-1523.31.1.80
[70]	Botvinick M, Cohen J (1998) Rubber hands ‘feel’ touch that eyes see. Nature 391: 756-756. https://doi.org/10.1038/35784
[71]	Cesari V, D'Aversa S, Piarulli A, et al. (2024) Sense of Agency and Skills Learning in Virtual-Mediated Environment: A Systematic Review. Brain Sci 14: 350. https://doi.org/10.3390/brainsci14040350
[72]	Levac DE, Huber ME, Sternad D (2019) Learning and transfer of complex motor skills in virtual reality: a perspective review. J NeuroEngineering Rehabil 16: 121. https://doi.org/10.1186/s12984-019-0587-8
[73]	El Rassi I, El Rassi J-M (2020) A review of haptic feedback in tele-operated robotic surgery. J Med Eng Technol 44: 247-254. https://doi.org/10.1080/03091902.2020.1772391
[74]	Ma R, Kaber DB (2006) Presence, workload and performance effects of synthetic environment design factors. Int J Hum-Comput Stud 64: 541-552. https://doi.org/10.1016/j.ijhcs.2005.12.003
[75]	Kaber DB, Riley JM (1999) Adaptive automation of a dynamic control task based on secondary task workload measurement. Int J Cogn Ergon 3: 169-187. https://doi.org/10.1207/s15327566ijce0303_1
[76]	Lackey SJ, Salcedo JN, Szalma JL, et al. (2016) The stress and workload of virtual reality training: the effects of presence, immersion and flow. Ergonomics 59: 1060-1072. https://doi.org/10.1080/00140139.2015.1122234

This article has been cited by:

1.	Dmitry I. Sinelshchikov, Linearizabiliy and Lax representations for cubic autonomous and non-autonomous nonlinear oscillators, 2023, 01672789, 133721, 10.1016/j.physd.2023.133721
2.	Jaume Giné, Xavier Santallusia, Integrability via algebraic changes of variables, 2024, 184, 09600779, 115026, 10.1016/j.chaos.2024.115026
3.	Meryem Belattar, Rachid Cheurfa, Ahmed Bendjeddou, Paulo Santana, A class of nonlinear oscillators with non-autonomous first integrals and algebraic limit cycles, 2023, 14173875, 1, 10.14232/ejqtde.2023.1.50
4.	Jaume Giné, Dmitry Sinelshchikov, Integrability of Oscillators and Transcendental Invariant Curves, 2025, 24, 1575-5460, 10.1007/s12346-024-01182-x

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)