A critical review of the impact of uncertainties on green bonds

1.   Introduction

Coronavirus Disease (COVID-19) is a highly contagious and viral disease that spreads easily from person to person through contact ^[1]. It can also be contracted through respiratory droplets released when an infected person coughs, sneezes, breathes, sings or talks ^[2]. The common symptoms of COVID-19 include fever, cough, chills, headache, muscles aches, vomiting and diarrhea ^[3]. Other symptoms include breathing difficulties, loss of speech and in severe cases, pneumonia, stroke and blood clots have been the most common problems in COVID-19 patients ^[4]. The disease affects most people with high blood pressure, cancer, heart failure, overweight, obesity, liver disease and weakened immune systems ^[5]. Evidence from literature shows that old age has high risk of serious illness from COVID-19 and the risk increases with age ^[6].

The World Health Organization (WHO) declared COVID-19 a public health problem on 30th January 2020 ^[7] and a pandemic on 11th March 2020 ^[7,8]. The first case report of COVID-19 in Tanzania was declared in Arusha before spreading to other parts of the country. Then, on 29th April 2020, the Ministry of Health, Community Development, Gender, Elderly and Children reported a total of 480 confirmed cases and 16 deaths from the disease ^[9].

Public health prevention measures, including banning all large gatherings, limiting the number of people attending burials, physical distancing and wearing masks, were implemented all over the world ^[10]. Unlike other East African countries, Tanzania did not enforce lock-down, and people were allowed to continue with income-generating activities normally ^[9]. However, health education campaigns on prevention measures, such as wearing masks, hygiene practices, avoiding public gatherings and keeping physical distance, were intensively encouraged through mass media and social media ^[11]. Despite these prevention measures, vaccination remains the most powerful tool in preventing the spread of COVID-19 in the population ^[12]. Globally, WHO reported that more than $116,135,492$ and $2,581,976$ confirmed cases and deaths, respectively, and $249,160,837$ vaccine doses have been administrated worldwide, including Tanzania ^[9,13]. However, the disease still persists in the population and there are several cases of resurgences globally. Understanding the dynamics of COVID-19 and its control strategies is a substantially important in order to minimize the spread of the disease in the community ^[14,15].

Mathematical models of disease transmission have been widely studied since the work of Kermack and McKendrick ^[16], Greenwood and Yule ^[17], Ross ^[18], Bernoulli ^[19], Brownlee ^[20], Soper ^[21], Greenwood ^[22] and also for the details of history in disease modeling (see, ^[23,24]) and the references therein. Mathematical models with fractional-order differential equations have particulary received greater attention (see, ^{[25,26,27,28,29,30,31]}) and are widely used in disease modeling compared to the integer-order derivatives ^[32,33]. Fractional-order operators are more accurate in modeling dynamical systems than classical operators as fractional-order models allow more degree of freedom ^[34,35]. It is worth mentioning here that fractional-order operators have more advantages than classical-order operators as fractional-order models adequately capture hereditary properties, long-range interactions and memory effects that exist in many biological systems ^{[32,33,34,35]}. In contrast, it has been documented in the literature that models that utilize integer-order derivatives do not adequately capture hereditary properties, and memory effects that exist in many biological systems ^[33]. Besides, when compared to the classical integer-order models, fractional-order models provide a higher level of precision and give a better fit to the actual data ^[36].

Recently, Bushnaq et al. ^[37], Owusu et al. ^[38], Ahmed et al. ^[39], Baba et al. ^[40], Omame et al. ^[41] and Aslam et al. ^[42] utilized the fractional-order derivatives to investigate the effect of memory on COVID-19 disease transmission. Mathematical studies of fractional order differential equations in disease modeling are also found in ^{[43,44,45,46,47,48]} and the references therein. For instance, Singh et al. ^[44] proposed and studied a fractional order model using Atangana-Baleanu Caputo sense to investigate the effect of quarantine on the spread of COVID-19 disease in the population. In conclusion the authors mentioned that quarantine of the infected individuals is effective to minimize the spread of disease in the population. Rehman et al. ^[43] formulated a fractional order model using the Caputo derivative to investigate the dynamics of COVID-19 and dengue co-infections in the population. The authors simulated the graphs of both COVID-19 and dengue co-infection to compare the results in the sense of Caputo, Caputo-Fabrizio and Atangana-Baleanu. From numerical simulations, their results demonstrated that Caputo sense had better results in the form of stability compared to other operators. Anggriani and Beay ^[47], formulated a mathematical model of COVID-19 to study the impact of self-isolation and hospitalization. The authors performed a global sensitivity analysis of the model using Latin Hypercube sampling and partial correlation coefficient methods. Their results revealed that parameters representing self-isolation and hospitalization have negative relations. Lolika and Mlyashimbi ^[48] proposed and studied a COVID-19 epidemic model with incubation delay. The authors computed the basic reproduction number and used to establish the conditions for global stability of equilibrium points. Furthermore, the authors concluded that quarantine of asymptomatic and symptomatic individuals have an impact on minimizing the spread of COVID-19 in the population.

Fractional derivatives have many definitions. In this study, we have chosen to utilize the renowned Caputo fractional operator due to the fact that, the ability to use classical initial conditions in the model formulation is the key benefits of the Caputo fractional derivatives compared to other fractional operators ^{[49,50,51,52,53]}. It is worthwhile to mention that the Caputo fractional derivative of any constant is zero. Furthermore, the Caputo fractional operator has a singular non-kernel, which is missing in other operators ^[54,55,56]. Therefore, we proposed and studied a Caputo fractional-order model of COVID-19 disease transmission to assess the effects of vaccination and quarantine in order to minimize the spread of disease in the population.

The rest of the paper is organized as follows: In Section 2, the proposed model and its analytical results are presented. Results discussion are provided in Section 3. Finally, the concluding remarks are presented in Section 4.

2.   Model formulation

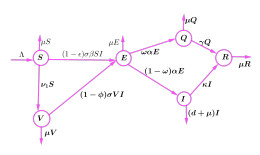
In this section, the Caputo fractional-order derivative has been used to define the model differential equations for COVID-19 transmission. The compartments proposed in this study are used to represent the epidemiological status of each human population. The proposed model consists of six sub-divided compartments: susceptible $S(t)$, exposed $E(t)$, vaccinated $V(t)$, infectious $I(t)$, quarantine $Q(t)$ and recovered $R(t)$ human populations. Thus, the total human population is denoted by $N(t)$ which is, $N(t) = S(t)+E(t)+ V(t)+I_v(t)+Q(t)+R(t)$. Throughout the article, variables and parameters are assumed to be none-negative and are defined as follows: $\Lambda$ and $\nu_1$ represent the rate of new recruitment and transition rate from susceptible to vaccinated classes respectively. Thus; $\phi$ represents the efficacy of vaccination for vaccinated susceptible individuals; $\frac{1}{\alpha}$ denotes the average time humans spend in incubation period; $\omega$ represents the rate of quarantine in the population; following successful treatment, $I(t)$ infected humans recover from disease after $\frac{1}{\kappa}$ days; $\mu$ and $\gamma$ represent the human natural mortality and the transition rate of quarantined people to recovered classes, respectively; $d$ represents the death rate of infected humans. Additionally, it is assumed that once the people become aware of COVID-19 transmission, they change their behavior and take precautions, such as hand-washing, wearing masks, keeping social distances and even quarantining themselves. Thus, the parameter $\epsilon$ represents the reduction rate of COVID-19 transmission of susceptible individuals due to health education campaigns. Furthermore, it was assumed that $\beta$ represents the probability of disease transmission following the successful contact rate $\sigma$ between infected and susceptible individuals.

Our assumptions on the dynamics of COVID-19 in this study are illustrated in figure 1 and the corresponding model differential equations are presented in model (2.1):

2.1.   Preliminaries on the Caputo fractional calculus

We begin by introducing the definition of Caputo fractional derivative and state the related theorems (see, ^{[56,57,58,59]}) that we will utilize to derive important results in this work.

Definition 2.1. Suppose that $\theta > 0, t > b, \theta, b, t\in \mathbb{R},$ the Caputo fractional derivative is given by:

Definition 2.2. (Linearity property ^[56]). Let $f(t), g(t):[b, d]\rightarrow \mathbb{R}$ be such that $^c_bD^{\theta}_tf(t)$ and $^c_bD^{\theta}_tg(t)$ exist almost everywhere and let $c_1, c_2\in\mathbb{R}.$ Then, $^c_bD^{\theta}_t(c_1f(t))+^c_bD^{\theta}_t(c_2g(t))$ exists everywhere, and

Definition 2.3. (Caputo derivative of a constant ^[59]). The fractional derivative for a constant function $f(t) = c$ is zero, that is:

Let us consider the following general type of fractional differential equations involving the Caputo derivative:

with initial condition $x_0 = x(t_0).$

Definition 2.4. (see ^[56]). The constant $x^*$ is an equilibrium point of the Caputo fractional dynamic system (2.5) if and only if $f(t, x^*) = 0.$

In what follows, we present an extension of the Lyapunov direct method for Caputo type fractional order for nonlinear systems ^[56,60].

Theorem 2.1. (Uniform Asymptotic Stability ^[56,60]). Let $x^*$ be an equilibrium point for the non-autonomous fractional order system (2.5) and $\Omega \subset \mathbb{R}^n$ be a domain containing $x^*.$ Let $L:[0, \infty)\times \Omega \rightarrow \mathbb{R}$ be a continuously differentiable function such that:

and:

for all $q\in(0, 1)$ and all $x\in \Omega$, where ${\cal M}_1(x)$, ${\cal M}_2(x)$ and ${\cal M}_3(x)$ are continuous positive definite functions on $\Omega$. Then, the equilibrium point of system (2.5) is uniformly asymptotically stable.

The following theorem summarizes a lemma proved in ^[56], where a Volterra-type Lyapunov function is obtained for fractional-order epidemic systems.

Lemma 2.1. (see ^[56]. Let $x(\cdot)$ be a continuous and differentiable function with $x(t) \in\mathbb{R}_+$. Then, for any time instant $t\geq b,$ one has:

2.2.   Model analysis

2.2.1.   Non-negativity and boundness of model (2.1)

Theorem 2.2. For the model (2.1), there exists a unique solution in $(0, \infty)$; however, the solution is always positive for all values of $t \ge 0$ and remains in ${\cal R}^6_+$.

Proof. From the model (2.1), we first show that

${\cal R}^6_+ =$ $\{ N(t)$ $\in {\cal R}^6_+: N(t)\ge 0\}$ is a positive invariant set. Then, we have to demonstrate that each hyper-plane bounding the positive orthant and the vector field points to ${\cal R}^6_+.$ Now consider the following: let us assume that there exists a $t_* > t_0$ such that $N(t_*) = 0,$ and $N(t) < 0$ for $t \in (t_*, t_1),$ where $t_1$ is sufficiently close to $t_*,$ if $N(t_*) = 0,$ then we have that,

$^c_bD^{\theta}_{t}N(t_*)-\Lambda^{\theta} > 0$. This implies that $^c_bD^{\theta}_{t}N(t) > 0$ for all $t \in [t_*, t_1].$ The above discussion shows that the three hyper-plane bounding the orthants that is the vector field points to ${\cal R}^6_+.$ This shows that all the solutions of the model (2.1) remains positive for all $t \ge 0.$ □

Theorem 2.3. Let $\Phi(t) = N(t)$ be the unique solution of the model (2.1) for all $t \geq 0.$ Then, the solution $\Phi(t)$ is bounded above, that is, $\Phi(t) \in \Omega,$ where $\Omega$ which is the feasible region is defined as,

and its interior denoted by int$(\Omega)$ is given by,

Proof. Here, we prove that the solutions of model (2.1) are bounded for all $t \ge 0$. Biologically, the lowest possible value of each state of model (2.1) is zero. Next, we determine the upper-bound of states. Based on this discussion, it is easy to show that the following condition holds for biological relevance of species. $0 \le N(t) \le C_N.$ From this condition one gets:

From the Laplace transformation condition one gets:

Collecting the likely terms we have:

Using the inverse Laplace transform we have:

Where, $C_N = Max \bigg\{\frac{\Lambda^{\theta}}{\mu^{\theta}}, N(0)\bigg\}$. Therefore, $N(t)$ is bounded above and this completes the proof. □

2.3.   Disease-free equilibrium and the basic reproduction number

Since $R(t)$ does not appear in all the equations in model (2.1), it is sufficient to analyze the solutions of model (2.6) for the behavior of model differential equations (2.1).

In what follows, we compute the threshold quantity, ${\cal R}_0$ which determines the power of the disease to spread in the population. The model (2.6) always has a disease-free equilibrium, ${\cal E}^0$ given by:

Following the next generation matrix approach as used in ^[31,61], the non-negative matrix ${\cal F}$ that denotes the generation of new infections and the non-singular matrix ${\cal V}$ that denotes the disease transfer among compartments evaluated at ${\cal E}^0$ are defined as follows:

Therefore, from (2.7) and (2.8) it can easily be verified that the basic reproduction number ${\cal R}_0$ of model (2.1) is:

The basic reproduction number ${\cal R}_0$ is defined as the expected number of secondary cases of humans produced in a completely susceptible population by one infected individual during its lifetime as infectious. The terms $\frac{\Lambda^{\theta}}{\nu_1^{\theta}+\mu^{\theta}}$, $\frac{\nu_1^{\theta}}{\mu_1^{\theta}}$ and $\frac{(1-\omega^{\theta})\alpha^{\theta}}{\alpha^{\theta}+\mu^{\theta}}$ represent the total life span of humans and the average life span of vaccinated and quarantined individuals respectively.

2.4.   Global stability of the model equilibria

Our goal in this section is to investigate the global stability of the disease-free equilibrium and the endemic equilibrium of the model (2.6).

Theorem 2.4. If ${\cal R}_0 < 1,$ the disease free-equilibrium point of the model (2.1) is locally asymptotically stable and unstable if ${\cal R}_0 > 1$.

Proof. To prove theorem (2.4), we evaluate the Jacobian matrix of the model (2.6) at the disease-free equilibrium and investigate the behavior of eigenvalues. In what follows, the Jacobian matrix of the model (2.6) evaluated at the disease free-equilibrium is given by:

The first three eigenvalues of matrix (2.9) are $\lambda_1 = -(\nu_1^\theta+\mu^\theta), \quad \lambda_2^\theta = -\mu^\theta,$ and $\lambda_3 = -(\gamma^\theta+\mu^\theta)$ which are non-positive. The remaining two eigenvalues are obtained in the following matrix;

It follows that we find the characteristic polynomial of the matrix (2.10) which is given as follows:

Since the coefficients of characteristic polynomial (2.11) are all non-negative for ${\cal R}_0 < 1,$ we conclude that the disease-free equilibrium ${\cal E}^0$ of the model (2.2) is locally asymptotically stable and this completes the proof. □

Theorem 2.5. The disease-free equilibrium ${\cal E}^0$ is globally asymptotically stable if ${\cal R}_0 \leq 1$, otherwise is unstable.

Proof. To prove the theorem (2.5), we first evaluate the model (2.6) at the point ${\cal E}^0$ and this leads to the following model;

In the followings, we consider the following Lyapunov function:

Taking the derivative of ${\cal L}_0(t)$ along the model (2.12) and making simplifications, one gets:

Since all the parameters and variables in system (2.13) are non-negative, it follows that $^c_bD^{\theta}_{t}{\cal L}_0(t) < 0$ holds if $\mathcal{R}_{0} < 1$. Moreover, $^c_bD^{\theta}_{t}{\cal L}_0(t) = 0$ if and only if $S(t) = 0$, $V(t) = 0$, $E(t) = 0$, $Q(t) = 0$, $I(t) = 0$, for all $t\geq 0$. Thus, $\mathcal{L}_0(t)$ is Lyapunov function on $\Omega$. Using Lasalle Invariance principle ^[62] it implies that every solution of the system (2.6) approaches the disease-free equilibrium ${\cal E}^0$ as $t\rightarrow \infty.$ Therefore, we conclude that the disease-free equilibrium of system (2.6) is globally asymptotically stable whenever ${\cal R}_0\leq 1.$ This completes the proof. □

Theorem 2.6. The Model (2.6) has endemic equilibrium ${\cal E}^*$ point which is globally asymptotically stable for ${\cal R}_0 > 1.$

Proof. To prove the theorem (2.6), we consider the following Lyapunov functional:

Differentiating ${\cal L}_1(t)$ one gets the following:

In what follows, we substitute (2.1) in (2.13) and get the following:

Setting the model (2.6) at the endemic equilibrium point,

By substituting (2.15) in (2.14) and solving the constants $A_i$ for $i = 1, 2, ...5,$ one gets the following after simplifications:

Since the arithmetic mean is greater than or equal to the geometrical mean, it follows that, from (2.16) we have the following:

Furthermore, let $\Phi(z) = 1-z-\ln(z)$ for $z > 0$. One can note that $\Phi (z) \leq0$ if and only if $z = 1$. Using the aforementioned properties of $\Phi(z)$, from (2.16) one can note that:

From (2.17), (2.19), (2.18), and (2.20), one can note that $^c_bD^{\theta}_{t}{\cal L}_1(t) \le 0$ whenever ${\cal R}_0 > 1$. Therefore, using Lasalle Invariance principle ^[62], the model (2.1) has a global asymptotically stable equilibrium point for all ${\cal R}_0 \ge 1$ and this completes the proof. □

3.   Results and discussion

In this section, we perform the numerical simulations of the model (2.1) to justify the analytical results. Most of the parameter values that are not available in the literature have been estimated. Additionally, for the simulation initial conditions of the model (2.1), was assumed to be $S(0) = 900, \quad V(0) = 0, \quad E(0) = 200, \quad Q(0) = 0$ and $I(0) = 2.$ Using the similar concept in ^[63], the fractional Adam-Bashforth-Moulton scheme for the model (2.1) has the following form:

Where:

In what follows we have:

Additionally, the quantities:

are the derivatives from (3.3) at the point $t_{n+1}, n = 1, 2, 3, ...m.$.

3.1.   Sensitivity analysis of the model

In this section, the sensitivity analysis of the model (2.1) has been performed to demonstrate the influence of each parameter on the magnitude of the threshold quantity ${\cal R}_0$. Most of the parameters used in this study have been drawn from literature and some are estimated using reasonable ranges for the purpose of simulation.

Definition 3.1. (See, ^[66]) The normalized sensitivity index of ${\cal R}_0,$ which depends on differentiability of parameter, $\omega$ is defined as follows:

Figure 2 demonstrates the relationship between the basic reproduction number ${\cal R}_0$ and the model parameters of the model (2.1). Overall, one can note that the model parameters $\beta$, $\gamma$, $\sigma$ and $\Lambda$ have a positive influence on the ${\cal R}_0$, that is whenever they are increased, the size of ${\cal R}_0$ increases. On the other-hand, parameters with negative index values have a negative influence on ${\cal R}_0$, that is, whenever they increased, the value of ${\cal R}_0$ decreases.

3.2.   Effect of vaccination and quarantine

3.3.   Parameter estimation and model validation using real data

In this section, we use the daily cases of COVID-19 from Wuhan in China as reported in ^[67] and estimate the parameters $(\beta, \sigma)$ that minimize the deviation of real data from prediction of model system (2.1). The main advantage of fractional-order differential equation is that the order of fractional can be any real positive number, so one can choose the one that has best fit of real data to the model and predict the future evolution of the disease in the population. Therefore, in this study, we use both the least squares and Nelder mead algorithm methods as presented in ^[71] to fit and estimate the parameters $(d, \beta, \theta)$ of the model (2.1). The real data used in this study are daily reported cases as shown in table (2), and the commutative new infections predicted by the model (2.1) is obtained using the equation (3.6)

We use the following function to compute the best fitting:

where $\beta, \sigma$ are parameters such that:

(1) For a given $(\beta, \sigma)$, we numerically solve the system (2.1) to get a solution $\hat{Y}_i(t) = (\hat{S}, \hat{V}, \hat{E}, \hat{Q}, \hat{I}, \hat{R}$ which is an estimation of daily reported cases $Y(t)$ of COVID-19 from Wuhan in China.

(2) Set $t_0 = 1$ (the fitting process starts in day $1$) and for $t = 2, 3, ..., 23,$ corresponding to daily in where data are available, evaluate the computed numerical solution for $I(t);$ that is., $\hat{I}(1)$, $\hat{I}(2)$, $\hat{I}(3),$.....$, \hat{I}(23).$

(3) Compute the root mean square (RMSE) of the difference between $\hat{I}(1), \hat{I}_h(2), ...., \hat{I}(23)$ and real data. This function $\mathbb{F}$ returns the root-mean-square error (RMSE) where:

(4) Determine a global minimum for the RMSE using Nelder-Mead algorithm. The function $\mathbb{F}$ takes values in $\mathbb{R}^2$ and returns a positive real number.

Using the formula (3.8), we computed the $RMSE$ that measures the closeness of the model prediction to the real data and was found to be $0.1186$. This shows that the system (2.1) has a good fit to the daily reported cases of COVID-19. On performing the fitting process we set the following initial conditions $S(0) = 9999$, $V(0) = 7990$, $E(0) = 10$, $I(0) = 5$, $Q(0) = 5$ $R(0) = 3$ and the model parameters are in Table (1). Note that since the fractional-order is any positive real number $\theta \in (0, 1]$, one can choose the one that better fits the model to the real data. Based on this assertion, the fractional-order $\theta$ were assumed to be $0.59, \; 0.6, \; 0.61, \; 0.62$ and $0.63$ that had a better fit of model to the real data reported in ^[67].

3.4.   Model fitting and validation with real data

4.   Concluding remarks

The outbreak of the COVID-19 depends on the close contact between infected and susceptible individuals in the community. Vaccination and quarantine are proposed as the most effective control strategies that minimize the spread of the COVID-19 disease in the population. In this study, a fractional-order model for COVID-19 has been proposed and studied to assess the effects of the aforementioned control strategies. To analyze the model, the important threshold parameter, ${\cal R}_0,$ has been computed to investigate the stability analysis of the steady states of the model. The results from the analysis demonstrated that both the disease-free equilibrium and endemic equilibrium points are globally stable whenever the basic reproduction number is less and greater than unity, respectively. A Normalized sensitivity index of the basic reproduction number was been performed to establish the relationship between the threshold and model parameters. Overall, one can note that model parameters with a positive index increased the disease persistence in the population. Furthermore, to support the analytical results, matlab software was used to simulate the proposed model and the results demonstrated that both vaccination and quarantine have the potential to minimize the spread of disease in the population. In particular, the disease can die out from the population by vaccinating $70%$ susceptible people and quarantine $60%$ of suspected individuals. Besides, real data of COVID-19 disease from Wuhan city in China has been used to fit and validate the proposed model. From the numerical findings, it can be deduced$70%$ that the model fits well with reported cases of COVID-19 in China. Additional simulation of the model to assess the effect of memory on the spread of COVID-19 disease has been performed and the results demonstrated that memory effect has an influence on the spread of COVID-19 in the population. In future, the proposed model presented in this study will be improved by incorporating time delay and assessing its effect on the spread of COVID-19 disease in the population.

Acknowledgment

All authors are grateful to their respective institutions for the support during preparation of the manuscript. Paride O. Lolika acknowledges the support from the University of Juba, South Sudan.

Conflict of interest

The authors declare that they have no conflicts of interest in this paper.

Authors contributions

All authors have equal contributions and they read and approved the final version of the paper.