Dynamic tail dependence on China's carbon market and EU carbon market

1.   Introduction

With the rapid development of the Internet in recent years, the total amount of news on the Internet has proliferated. When users receive a large amount of news information, they usually want to filter out the news content of interest quickly. Therefore, a simple and attractive headline for news can significantly increase the number of news views. In traditional news media, headlines are usually generated by human editors. However, in the face of the massive news base on the Internet, it is essential to reduce the cost of human editing and improve the news dissemination rate if a more suitable headline can be automatically generated for given news content.

Automated news headline generation can be addressed using automatic text summary generation methods in natural language processing ^[1]. However, training deep neural network-based news headline generation models often relies on many labeled data ^[2]. In practical application scenarios, it is challenging to train news headline generation models by relying entirely on the labeled data in the target topic domain because of too many news topic domains. Therefore, it is worth further research on effectively training a deep text generation model to achieve better domain generalization in the absence of labeled data in the target domain.

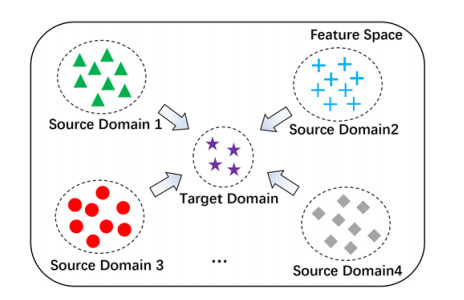
In this regard, existing work often adopts the "Pre-train & Fine-tune" approach in transfer learning to alleviate the limitation of the lack of labeled data in the target domain ^[2]. However, the transfer learning paradigm shown in Figure 1 still has some shortcomings. First, the data differences between the source and target domains are relatively noticeable. In addition to fine-tuning, it is necessary to eliminate further the negative impact of data differences on the domain transfer effect from the data distribution perspective. Second, when it is insufficient, or no labeled data in the target domain for fine-tuning, the given deep text generation model cannot be effectively adapted to the target domain by fine-tuning, which leads to poor performance of the transfer text generation and directly weakens the adaptability of the text generation model to the target domain. In this regard, zero-shot learning provides a good inspiration ^[3] to construct a "domain prototype" for each domain to describe the semantics of the data under the domain through the feature attributes. The semantic correlation between different domain prototypes by the labeled data of the most relevant source domains assists in processing the unlabeled data of the target domain (i.e., semantic prototype transduction). Then for the task of news headline generation, even without any manually labeled data in the target domain, it is still possible to use a deep text generation model to generate domain-adapted news headlines, following the zero-shot learning semantic prototype transduction principle for many news bodies without reference truth summary in the target domain ^[4].

In summary, this paper proposes a cross-domain news headline generation method based on semantic prototype transduction in the intermediate domain, with the following main contributions:

1) Aligning the data representation distribution of source and target domain data in the kernel space to alleviate the negative impact of the distribution difference of data representation between different domains on inter-domain transfer and enhance inter-domain transfer at the data representation level.

2) The source and target domain data are divided into K intermediate transition domain according to the text similarity index, forming an intermediate domain of "new source domain + target domain." In the intermediate domain, the target domain data can refer to the source domain data with more semantic similarity in the generation process through more appropriate domain data selection.

3) To construct semantic prototypes for source and target domain data and improve the internal structure of the deep text generation model to enhance the model encoding and decoding process, so that the improved deep text generation model can receive all elements of the data-level semantic prototypes and improve inter-domain transferability from the model structure.

4) Based on the improved text generation model, the corresponding text generation loss functions are constructed for different elements in the semantic prototypes of the data according to the idea of semantic prototype transduction. In this way, the model is guided to capture the approximate reference relations of cross-domain data on the semantic prototypes so that the model can further learn the semantic association between cross-domain data and thus use the relevant new source domain reference news headlines as the reference truth data of news bodies with no reference truth in the target domain in the intermediate domain.

This paper is organized as follows: Section 1 summarizes the existing work on news headline generation and the current state of research on traditional transfer learning and zero-shot learning approaches in text generation tasks. Section 2 describes the internal mechanism of the proposed approach and the transfer strategy adopted in this paper. Section 3 describes the experimental data, setup, and comparison model and analyzes the experimental results. Finally, a conclusion and an outlook on future work are presented.

2.   Related works

The task of news headline generation is a branch of automatic text summarization ^[1]. The current mainstream automatic text summarization models mainly rely on many reference truth summary data for supervised training of the generative models to obtain a model with good generative performance. However, the problem of missing ground-truth text often occurs in practical application scenarios, and thus transfer learning-related methods are introduced to solve the above problem. The following is summarized the news headline generation task, the traditional transfer learning methods in the text generation task, and the zero-shot learning approach in the text generation task.

2.1.   Automatic text summary generation methods

The news headline generation task aims to output the corresponding news headlines based on the input news body through an automatic text summary generation model. The output headlines need to be semantically fluent and coherent while maintaining the semantic novelty of the headlines ^[1]. Current mainstream automatic text summary generation methods can be divided into Extractive and Abstractive. The extractive methods extract salient sentences or phrases from the original article ^[5]. In contrast, the generative methods generate new words or phrases that may be rewritten or use words that are not in the original article ^[6]. This paper focuses on the generative text summary model to generate corresponding headlines based on a given news body.

Many researchers have recently used Sequence to Sequence structures to build generative text summarization models. For example, Krishna et al. ^[7] use a Recurrent Neural Network (RNN) with an attention mechanism in the "encoder-decoder" form to generate summary content for different topics of interest for a single text. Ma et al. ^[8] proposed a critical sentence selection method combining topic words and TF-IDF to obtain the score of the topic corresponding to each text in the original text data and then select the sentence with the highest score as the summary of the topic. Jadhav et al. ^[9] used a pointer generator network ^[10] to identify salient sentences and keywords in the input document and combine them to form the final summary. In addition, text summary generation models can also be constructed by neural network components based on the Self-Attention mechanism, such as Transformer ^[11]. The Transformer-based text generation model is also built as an "encoder-decoder, " which solves the problem that the traditional RNN architecture cannot compute in parallel and improves the efficiency of text generation. Du et al. ^[12] used the Transformer as a feature extractor to obtain text representations. They realized context-based bidirectional text coding, which embedded the location information of words into text representations according to their different positions in the text by contextual information and distinguished the semantic differences of similar expressions in the context at a fine granularity.

As a result, the mainstream text generation models are still structured as "encoder-decoder." However, the current generative text summarization models built using recurrent neural networks (RNN) or Transformer with an "encoder-decoder" structure are usually trained in a traditional supervised manner ^[13]. They are not suitable for applications where the target domain is missing ground-truth data ^[14], which means that transfer text generation methods for such scenarios need to be investigated to overcome the limitation of sparse ground-truth data in the target domain.

2.2.   Transfer learning methods in text generation tasks

For the application of transfer learning methods in text generation tasks, current research work has shown that models trained using specific corpus data cannot be generalized across domains ^[15]. Currently, traditional transfer learning approaches focus on the source domain data to assist the target domain in accomplishing a specific task through some transfer strategy ^[13]. An example is the use of large-scale pre-trained language models for transfer. Transferring from the source domain to the target domain is achieved by obtaining a pre-trained model using a large-scale corpus and fine-tuning the pre-trained model using a relatively small amount of training data in the target domain ^[16]. Various pre-trained language models have been proposed according to the "pre-train & fine-tune" model. Specifically, Raffel et al. ^[17] proposed a pre-trained text generation model T5 using a large-scale Common Crawl database containing data from multiple domains to pre-train the model for different span masking padding tasks. Lewis et al. ^[18] pre-trained the sequence-to-sequence model BART using a denoising auto-encoder. A noise function was used to mask a random text span during the model's pre-training, guiding the model to learn how to reconstruct the original text. Zhang et al. ^[19] proposed the pre-trained text generation model PEGASUS to learn how to repopulate multiple masked sentences in a corpus for pre-training. Zhang et al. ^[20] proposed a novel encoder-decoder architecture based on a pre-trained language model that integrates contextual representations into Chinese character embeddings to aid the model in semantic understanding for migration. In addition, some researchers have obtained migratory representations of text or features to migrate domain information between domains in different feature spaces. Specifically, Chen et al. ^[21] designed a generalized covariate transfer assumption method to model the unsupervised domain adaptation problem by applying a distribution adaptation function in the subspace and using a convex optimization loss function to adapt the source domain data distribution to the target domain data distribution, thus solving the problem that the traditional feature transformation methods cannot approximate the transformed source domain distribution and the target domain distribution when the domain differences are significant. Li et al. ^[22] proposed a semi-supervised heterogeneous domain adaptation method based on matrix decomposition within the Reproducing Kernel Hilbert Space (RKHS) to learn heterogeneous features in the source and target domains using the nonlinear relationship between features and data instances to compensate for the feature differences between the source and target domains in the kernel space. Zellinger et al. ^[23] proposed a metric-based regularization method, representing similar latent features in different domains by maximizing the similarity between specific activation distributions to achieve unsupervised domain adaptation. In addition, there are also unsupervised domain adaptation methods ^{[24,25,26,27,28,29]} that extend the feature space by connecting common features and specific features of two domains in a cross-filling way to eliminate the heterogeneity of features between domains, making the feature space homogeneous and thus achieving the goal of reducing the variability of features between domains.

Existing research shows that ^[16], on the one hand, fine-tuning the pre-trained language model with a "small amount" of target domain data allows for effective domain adaptation of the language model. On the other hand, when applying the pre-trained language model to the target domain, a certain amount of data is still needed to fine-tune the model to achieve better domain adaptation ^[30]. If the target domain lacks ground-truth data, it will directly affect the generalization effect of the model in the target domain, and the limitation of missing labeled data in the new domain still exists. Therefore, more and more researchers are focusing on more effective methods to transfer text generation models from the source domain to the target domain in the absence of labeled data in the target domain to achieve better text generation results in the target domain.

2.3.   Zero-shot learning methods in text generation tasks

In terms of relationship-based transfer strategies, many researchers have applied zero-shot learning ^[31] related methods to transfer text generation tasks in recent years. The zero-shot learning method is more targeted at solving the problem of missing labeled data in the target domain than the traditional transfer learning method. In the absence of ground-truth data for the target domain, the zero-shot learning approach usually constructs a corresponding "prototype description" for each domain. Thus, even if the input data is unlabeled, the category label of a given input data can be inferred if a set of attributes of the input data is "close" to the "prototype description" of a domain ^[4]. Thus, the problem of the lack of ground-truth data in the target domain can be solved using domain semantic prototype transduction. Specifically, Zhao et al. ^[32] used a cross-domain encoder to encode the domain prototypes shared between the source and target domains by selecting several representative conversation texts from each domain data, using the corresponding ground-truth texts as seeds as well as the critical entity words in the representative conversation texts as annotations, and then generating the conversation texts through a decoder, thereby achieving transfer from the source domain to the target domain based on the similarity of the domain prototypes between different domains. Liu et al. ^[33] first collected semantically similar terms in the source and target languages (including words collected from the target language ground-truth text) as domain semantic prototypes in a multilingual scenario; based on this, the hidden variable model was used to deal with the differences in domain distribution of similar sentences across languages. The transfer text generation model proposed by Shen et al. ^[34] and Duan et al. ^[35] takes the original document of the source domain as input but generates text for the target domain directly and uses the ground-truth text of the target domain to train the generation model. By building a streamlined text generation model with the same structure, the semantic prototype mapping from the source domain to the target domain is established by imitating the above "input→output" process. Finally, the original document of the target domain is used as input to generate the text generation result corresponding to the target domain.

The following aspects still need further research by summarizing the existing transfer text generation methods. First, the language model pre-trained by the large-scale corpus still requires a certain amount of labeled data in the target domain for fine-tuning when applied to the target domain so that the model can be adapted to the target domain. This means the limitation of missing ground-truth data in the target domain still exists. Secondly, the variability in the distribution of data representations across different domains can hurt the model across domains ^[15]. This implies the need to reduce the variability between data representations across domains through practical methods. Finally, in the process of cross-domain model generation, the target domain data should be assisted by the source domain data as much as possible to improve the text generation effect. This means that we need to mine the existing source domain data to find the information that is helpful to the target domain data and find the most valuable source domain data for the target domain data by obtaining the correlation between the data and improving the model's ability to get the correlation information, to assist the generation of the target domain data.

3.   Intermediate domain-based semantic prototype transduction cross-domain news headline generation method

The main challenge of the transferable text generation task using the zero-shot learning approach is how to fully leverage the existing data with reference truth in the source domain to help the text generation of the target domain data without reference truth. This section describes the proposed transferable news headline generation method in four aspects: domain data distribution alignment, intermediate domain redistribution, transferable news headline generation model construction, and semantic prototype transduction, respectively. Table 1 lists the symbols used in this method and the corresponding descriptions.

The problem to be solved in this paper can be defined as when the news body text of the source domain, the news headline text of the source domain, and the news body text of the target domain are given. The proposed method for generating news headlines text based on semantic prototype transduction generates news headlines text for the target domain when there is no reference truth headline text in the target domain.

In this regard, the overall flow of the proposed method is shown in Figure 2:

First, the textual representations of the source and target domain data are projected into the Reproducing Hilbert Kernel Space (RKHS) to align the data distribution of the source domain with the data distribution of the target domain, thus reducing the negative impact caused by the difference in data distribution between different domains and improving inter-domain transferability from the data representation level.

Second, the intermediate domains are established, and the data in the source and target domains are redistributed into several intermediate domains based on the composite index of text similarity, forming a "new source domain + target domain" intermediate domain. This enables more appropriate domain data selection in the intermediate domains and assigns source domain data with more semantic similarity to the target domain data.

Third, the text generation model with the "encoder-decoder" structure is improved for the cross-domain transfer scenario to realize the transfer from the source domain to the target domain by applying the semantic prototype transfer method in zero-shot learning.

Fourth, in each intermediate domain, "semantic prototypes" are constructed for each piece of news data in different domains. Through semantic prototype transduction, the news body without reference truth headline of the target domain in the intermediate domain is semantically associated with the most relevant headlines in the new source domain, and news headlines are generated for the target domain news body in a transferable manner based on the similarity or proximity of the semantic prototypes.

Eventually, in the transferred text generation process, as shown in Figure 2, the news headlines in the relevant source domains will act as ground-truth data for the target domain news headline generation, thus no longer relying on manual annotation of the target domain data.

3.1.   Domain data distribution alignment

In practical application scenarios, the feature spaces of the two domains have similarities and differences. For example, in a news headline generation task, news headlines on different topics will have some common descriptors, such as "good, " "bad, " etc. News on different topics also have specific descriptors, such as "expensive" for cars and "exciting" for sports ^[3]. We, therefore, define these common descriptors as domain common features and these specific descriptors as domain specific features. Specifically, there are some common characteristics among the different domains, but each domain has specific characteristics. In domain adaptation, the variability between data distributions in different domains can be effectively reduced by using the common features of different domains to link them together. As shown in Figure 3, there will be some common features between the two domains ${S}_{c}/{T}_{c}$, where ${S}_{c}$ denotes the common features of the source and target domains contained inside the source domain and ${T}_{c}$ denotes the common features of the source and target domains contained inside the target domain. While each domain has domain-specific features ${S}_{s}/{T}_{t}$, where ${S}_{s}$ denotes the source domain-specific features and ${T}_{t}$ represents the target domain-specific features. Therefore, to achieve better performance metrics on transferable text generation, it is necessary first to align the data distribution representation between the source and target domains to reduce the impact of the distribution differences in data representation between domains on transferable text generation.

In Figure 3, the source domain news body is denoted as ${X}_{src}$, and the embedding of the input features is represented as ${X}_{src} = \left[{S}_{c}; {S}_{s}\right]$, where ${S}_{c}$ represents the feature matrix of the source domain containing $c$ common features and s source domain-specific features. The target domain news body data is represented as ${X}_{tar}$, and the embedding of the input features is represented as ${X}_{tar} = \left[{T}_{c}; {T}_{t}\right]$, where ${T}_{c}$ represents the feature matrix of the target domain containing $c$ common features and the feature matrix of $t$ target domain-specific features ${T}_{t}$. The data distribution between ${X}_{src}$ and ${X}_{tar}$ is first aligned with feature filling using class cross-filling in Figure 3 to reduce the influence of domain-specific features. On this basis, Maximum Mean Discrepancy (MMD) is used to align the filled source and target domain data from the data distribution level by minimizing the maximum mean discrepancy to reduce the difference in the distribution of the filled domain data within the Reproducing Hilbert Kernel Space (RKHS).

Specifically, first, as shown in Eq (1), the feature mapping functions ${\mathrm{\Psi }}_{src}$ and ${\mathrm{\Psi }}_{src}$ map the common features in the source and target domains to associate with features specific to their respective domains. Second, as shown in Eq (2), the resulting feature mappings ${\mathrm{\Psi }}_{src}$ and ${\mathrm{\Psi }}_{tar}$ are cross-acted on ${T}_{c}$ and ${S}_{c}$ for feature filling, i.e., the feature mapping ${\mathrm{\Psi }}_{tar}$ obtained from the target domain is applied to the common feature ${S}_{c}$ in the source domain as shown in Figure 3 to obtain the domain-adapted feature matrix ${S}_{a}$. The same crossover operation is done for the target domain to obtain the domain adaptation-specific feature matrix ${T}_{a}$. Third, as shown in Eq (3), the original feature matrix, the specific feature matrix and the adapted feature matrix of the source and target domains are filled to obtain the filled feature matrices ${X}_{{s}_{f}}$ and ${X}_{{t}_{f}}$, respectively. And the 2 feature mappings ${\mathrm{\Psi }}_{src}$ and ${\mathrm{\Psi }}_{tar}$ in Eq (1) can be expressed respectively as ${\mathrm{\Psi }}_{src}\left({S}_{c}\right) = {\mathrm{W}}_{s}^{\mathrm{\top }}{S}_{c}$ and ${\mathrm{\Psi }}_{tar}\left({T}_{c}\right) = {\mathrm{W}}_{t}^{\mathrm{\top }}{T}_{c}$, then ${S}_{a} = {\mathrm{W}}_{t}^{\mathrm{\top }}{T}_{c}, {T}_{a} = {\mathrm{W}}_{s}^{\mathrm{\top }}{S}_{c}$. Thus Eq (1) can be further derived as Eq (4):

Further, to better adapt the source domain to the target domain, it is also necessary to ensure that the feature matrices ${X}_{{s}_{f}}$ and ${X}_{{t}_{f}}$ (${X}_{{{s}_{f}}_{i}}$ and ${X}_{{t}_{{f}_{i}}}$ is the single instance in the source and target domains, respectively; ${n}_{1}$ and ${n}_{2}$ denote the number of samples input in the source and target domains respectively) of the source and target domains output by Eq (3) are as close as possible in distribution.

As shown in Eq (5), the representation after filling alignment is mapped into the Reproducing Kernel Hilbert Space (RKHS) $H$ using feature mapping $\mathrm{\Phi }:\mathbb{R}\to H$ respectively. In this kernel space, the distribution distance $Dist$ of different domain data after mapping into the kernel space is measured by the maximum mean difference (MMD). By reducing the distribution distance $Dist$ between ${\mathrm{\Phi }}_{\mathrm{s}}\left({X}_{{s}_{f}}\right)$ and ${\mathrm{\Phi }}_{\mathrm{t}}\left({X}_{{t}_{f}}\right)$ mapping results thus reducing the distribution difference between the source and target domain data.

As shown in Figure 4, the source domain text embedding representation and the target domain text embedding representation are output through BERT. Since the maximum number of Tokens input to BERT is 512 ^[36], we consider truncating the excess directly if the length of the input news body exceeds 512. Since we show information about the dataset we used in Section 4.1, most of the news bodies in the dataset we used were less than 512 in length, so taking a direct truncation approach would not have a significant impact on the results.

The source domain text embedding representation is feature transformed through the fully connected layer with the Sigmoid activation function, and then the result is projected into the kernel space $H$, while the target domain text embedding representation is projected directly into the kernel space $H$. Because the textual representation output from the source domain feature mapping is treated as consistent with the target domain distribution after alignment of the domain data distribution, the textual representation of the target domain will be output directly through the updated source domain feature mapping, so only the source domain feature mapping needs to be updated here, and no changes to the target domain feature mapping are required.

By minimizing the objective function $Dist({X}_{{s}_{f}}, {X}_{{t}_{f}})$ in Eq (5), the data distribution of the source domain and the target domain are made close to each other. As a result, the parameters of the fully connected layer in Figure 4 will be updated as ${\mathrm{\Phi }}_{\mathrm{s}}^{'}$ to minimize the objective function of Eq (5).

After training according to Eq (5), the source domain text representation ${X}_{src}^{'}$ output from the source domain fully connected layer mapping ${\mathrm{\Phi }}_{s}^{'}\left(X\right)$ is used as the result of the representation aligned with the target domain distribution as shown in Eq (6). And the text representation ${X}_{tar}^{'}$ of the target domain itself is calculated by inputting the original embedding representation of the target domain into the source domain mapping ${\mathrm{\Phi }}_{s}^{'}\left(X\right)$. When there are multiple source domains, as shown in Eq (6), the text representation of the target domain will be the average representation on multiple source domains. Here, $N$ in Eq (6) denotes the total number of all domains. In summary, the overall process of aligning the domain data distribution for the source domain news body ${X}_{src}$ and the target domain news body ${X}_{tar}$ is shown in Algorithm 1.

3.2.   Intermediate transition domain redistribution

In order to enhance the transferability between source and target domains, improve the relevance of domain data in the transfer process, and find more suitable source domain news headlines for the target domain news body as a reference, all the data in the source and target domains are further reassigned to $K$ intermediate transition domains according to the comprehensive index of text similarity, forming a new intermediate domain of "new source domain + target domain". Thus, a more appropriate source domain data is assigned to the target domain data in the intermediate domain, i.e., a more relevant domain data selection.

Specifically, as shown in Figure 5, each redistributed intermediate domain contains the source and target domain data with the most similarity. Due to the semantic differences between different domain data, an inappropriate intermediate domain division can lead to negative transfer problems between the source and target domain data it contains ^[3]. Therefore, the data within each intermediate domain should have as many similar features as possible. First, as shown in the left side of Figure 5, the distribution alignment representations ${X}_{src}^{'}$ and ${X}_{tar}^{'}$ of each source domain and target domain are obtained from Eq (6), and then the distribution alignment representations of all data in each source domain are averaged to obtain the average distribution alignment representation vector in each source domain. Next, the data point in each source domain that is closest to the average distribution alignment representation vector is used as the starting point of each intermediate domain, and thus the number of source domains N-1 intermediate domain starting points is obtained. Next, this paper investigates and selects four similarity calculation metrics for intermediate domain redistribution in terms of text content similarity:

Word-specific overlap ${\mathit{\boldsymbol{S}}}_{\mathit{\boldsymbol{o}}\mathit{\boldsymbol{v}}\mathit{\boldsymbol{e}}\mathit{\boldsymbol{r}}\mathit{\boldsymbol{l}}\mathit{\boldsymbol{a}}\mathit{\boldsymbol{p}}}$: Calculates the similarity of a given text pair, i.e., the higher the overlap of specific words used in the text, the more similar the main message conveyed by the text. The cosine similarity is used to quantify this metric, as shown in Eq (7). where ${x}_{i}$ and ${y}_{i}$ denote the values of the word frequency vectors $x$ and $y$ phases at the same position $i$, i.e., the number of occurrences of each participle, after the source and target domain texts have been encoded by OneHot.

Word coverage ${\mathit{\boldsymbol{S}}}_{\mathit{\boldsymbol{c}}\mathit{\boldsymbol{o}}\mathit{\boldsymbol{v}}\mathit{\boldsymbol{e}}\mathit{\boldsymbol{r}}\mathit{\boldsymbol{a}}\mathit{\boldsymbol{g}}\mathit{\boldsymbol{e}}}$: the number of overlapping words in each text pair is divided by the number of words in the target domain text, i.e., more identical words in the text indicates that the source domain text is more like the target domain text. The co-occurrence of source and target domain text on a single word was measured using ROUGE-1 ^[37] based on Recall as shown in Eq (8). Where, 1-gram means the co-occurrence word granularity is 1; $\sum _{\text{1-gram}\in \text{S}}\ {\text{Count}}_{\text{match}}\left(\text{1-gram}\right)$ means the number of 1-gram occurring in the source text and the target text at the same time; $\sum _{\text{1-gram}\in \text{S}}\ \text{Count}\left(\text{1-gram}\right)$ means the number of 1-gram occurring in the target text.

Information density ${\mathit{\boldsymbol{S}}}_{\mathit{\boldsymbol{d}}\mathit{\boldsymbol{e}}\mathit{\boldsymbol{n}}\mathit{\boldsymbol{s}}\mathit{\boldsymbol{i}}\mathit{\boldsymbol{t}}\mathit{\boldsymbol{y}}}$: divides the number of overlapping words in each text pair by the number of words in the source domain text, i.e., a high information density indicates that there is a large amount of information in the source domain text that can be transferred to the target domain. Using BLEU₁ ^[37] the similarity between the source and target domain text on a single word is measured according to the Precision as shown in Eq (9). Where 1-gram indicates a co-occurrence word granularity of 1; $\sum _{\text{1-gram}\in \text{C}}\ {\text{Count}}_{\text{clip}}\left(\text{1-gram}\right)$ indicates the number of simultaneous 1-gram in the source text and the target text; $\sum _{\text{1-gram'}\in {\text{C}}^{'}}\ \text{Count}\left({\text{1-gram}}^{'}\right)$ denotes the number of 1-gram appearing in the source domain text.

Text length ${\mathit{\boldsymbol{S}}}_{\mathit{\boldsymbol{l}}\mathit{\boldsymbol{e}}\mathit{\boldsymbol{n}}\mathit{\boldsymbol{g}}\mathit{\boldsymbol{t}}\mathit{\boldsymbol{h}}}$: The text length can reflect the amount of information contained, i.e., the amount of information contained in text pairs having similar length or approximately the same. This metric is quantified using the negative value of the absolute difference between the length of the source and target domain text tokens and the ratio of the text token lengths, as shown in Eq (10). Where, ${S}_{tar\_len}$ denotes the number of words in the word sequence obtained after the target domain text has been split; ${S}_{src\_\mathrm{s}len}$ denotes the number of words in the word sequence obtained after the source domain text has been split.

Finally, as shown in Eq (11), the word-specific overlap, word coverage, information density and text length are summed to obtain the comprehensive index S used to calculate the content similarity between the source domain text and the target domain text:

Then, after obtaining the number of source domains N-1 intermediate domain starts, the number of starts is evaluated using the Silhouette Coefficient ^[38], which is commonly used in clustering methods, to determine the best K intermediate domain starts from the N-1 intermediate domain starts.

Assume that the data in the source and target domains have been divided into several intermediate domains according to the composite index $S$ of text content similarity in the source domain, and for each sample point $i$ in each intermediate domain, its silhouette coefficient is calculated separately. Specifically, the following two metrics need to be calculated for each sample point i: $a\left(i\right)$ denotes the average of the distances from sample point $i$ to other sample points belonging to the same intermediate domain as it; $b\left(i\right)$ denotes the mean ${b}_{ij}$ of the average distance from sample point $i$ to all samples in the other intermediate domains ${C}_{j}$, where $b\left(i\right) = \mathrm{m}\mathrm{i}\mathrm{n}({b}_{i1}, {b}_{i2}, \dots, {b}_{ik})$. Then the Silhouette Coefficient of sample point $i$ is

The average of the silhouette coefficients of all sample points $i$ in the intermediate domain is the total silhouette coefficient $S\in [-\mathrm{1, 1}]$ of the intermediate domain, and the closer $S$ is to 1, the better the intermediate domain partitioning effect is. Then the silhouette coefficients of each intermediate domain are summed and ranked to obtain the combination of intermediate domains with the highest silhouette coefficient sum score, at which the number of combined intermediate domains is the optimal $K$ value for intermediate domain partitioning. Finally, the remaining news bodies in the source and target domains are divided into the intermediate domains with the first scores, and the remaining news bodies in the source and target domains are divided into the intermediate domains with the most similar scores, as shown in Figure 5, forming the $K$ intermediate domains ${D}_{i}^{'}$ of the "new source domain + target domain".

On the other hand, each intermediate domain in Figure 5 contains both the most similar source and target domain data, so that the most relevant new source domain news headlines can be used as the model training reference ground-truth data according to the similarity of semantic prototypes for the target domain news body in the intermediate domain. Finally, the overall process of intermediate domain redistribution based on the text similarity index in Figure 5 is shown in Algorithm 2.

3.3.   Construction of a transfer news headline generation model for semantic prototypes

The transfer text generation model can effectively cope with the problem of missing ground-truth data in the target domain during the generation process. A semantic prototype is a cognitive reference point, i.e., the proto image of all representatives of the meaning of a word or a category. Accordingly, the members of a category can be graded according to their typicality. Accordingly, the correlation between different domains can be obtained indirectly by obtaining similar high-frequency usage keywords between different domains. Based on the distribution-aligned source domain data representation ${X}_{src}^{'}$ and target domain data representation ${X}_{tar}^{'}$ in Figure 4, and the data in $K$ intermediate domains ${D}_{i}^{'}$ redivided in Figure 5, this paper designs a zero-shot learning semantic prototype transduction transfer text generation model based on intermediate domains. Through the semantic prototype transduction strategy, the transfer text generation model can learn the semantic association of texts between different domains.

First, a semantic prototype is constructed for each (news $\mathit{\boldsymbol{x}}$, headline $\mathit{\boldsymbol{y}}$) data in the source and target domains from the news body $\mathit{\boldsymbol{x}}$, the corresponding news headline $\mathit{\boldsymbol{y}}$ and the semantic annotation $\mathit{\boldsymbol{a}}$ obtained based on the news body $x$, denote as $z = \left[{x}^{d}, {y}^{d}, {a}^{d}\right], d\in \left\{src, tar\right\}$. Where $d$ indicates that the data comes from the source domain $src$ or the target domain $tar$. The news body of the source and target domains in the semantic prototype $z$ is denoted as ${x}^{src}$ and ${x}^{tar}$; the news headline of the source domain is denoted as ${y}^{src}$. When it comes to the news headline data ${y}^{tar}$ of the target domain, the top $n$ clauses with the highest scores are selected from the news body ${x}^{tar}$ as the "pseudo-truth data" of the current target domain news body ${x}^{tar}$ (${y}^{tar}$, i.e., the target domain pseudo-news headline) based on the ROUGE-L index score between each clause in the corresponding news body ${x}^{tar}$ and the whole news body ${x}^{tar}$. Here, the number of extracted clauses n = len(headline y)/len(news x) × number of clauses of news x, based on the (news x, headline y) data information of the intermediate domain source domain to which the current target domain news body ${x}^{tar}$ belongs. The semantic annotations ${a}^{sr}$ c and ${a}^{tar}$ of the source and target domains are obtained by converting the news body ${x}^{src}$ and ${x}^{tar}$ of the source and target domains into a keyword sequence in which the lexical properties of each word belong to {noun, verb, adjective, adverb}, and each word is assigned the corresponding sentiment polarity value (i.e., between [-1, 1]). Thus, by the above process, a semantic prototype is constructed for each "news $\mathit{\boldsymbol{x}}$ - (pseudo-)headline $\mathit{\boldsymbol{y}}$" pair in the source and target domains, denoted as $z = \left[{x}^{d}, {y}^{d}, {a}^{d}\right], d\in \{src, tar\}$.

It is worth noting that, on the one hand, the news body ${x}^{d}$, news headline ${y}^{d}$ and semantic annotations ${a}^{d}$ are obtained from their embedding representations by the BERT model. On the other hand, in constructing the semantic prototype $z = \left[{x}^{d}, {y}^{d}, {a}^{d}\right], d\in \{src, tar\}$, all domain data have been divided into $K$ intermediate domains following the domain redistribution principle shown in Figure 5. And the news body representation ${x}^{d}$ has been aligned with the domain data distribution according to Eq (6). Finally, the constructed semantic prototype $z = \left[{x}^{d}, {y}^{d}, {a}^{d}\right], d\in \{src, tar\}$ will be input to the transfer text generation model for semantic prototype transduction as shown in Figure 6.

As shown in Figure 6, the proposed transfer text generation model is built based on the "encoder-decoder" format. Among them, the encoder side consists of two encoder modules ${E}_{T}$ and ${E}_{R}$ with the same structure. The encoder modules ${E}_{T}$ and ${E}_{R}$, and the decoder module ${D}_{T}$ at the decoder side are built by combining the Transformer model ^[11] with a bi-directional long and short-term memory network (Bi-LSTM), which allows the transfer text generation model to integrate a self-attentive mechanism with a recurrent neural network. In addition, a pointer generator network ^[10] was added to the decoding side of the model to address the Out-Of-Vocabulary (OOV) problem in the text generation. It has been shown ^[39] that the combination of recurrent networks and transformers can further improve the model performance of the transformer, and that the bi-directional LSTM in the decoder helps downstream sequential prediction tasks to achieve better accuracy in NLP tasks.

Specifically, first, the encoder module, as well as the decoder module of the transfer text generation model in Figure 6, are designed with reference to the original Transformer model ^[11], and each module includes N stacked sublayers, each of which consists of a Multi-Head Attention mechanism and a fully connected Feed Forward Network, while both employ the residual connection renormalization (Add & Norm) processing. Second, the Bi-LSTM layer is added to each sub-layer of the encoder modules ${E}_{T}$, ${E}_{R}$ and decoder module ${D}_{T}$ to construct the enhanced encoder and decoder. In each sub-layer so designed, the input of the Bi-LSTM layer is the same as the original input of the sub-layer, while the output is added to the original output of the sub-layer before the final normalization of the sub-layer (Add & Norm). In addition, if the Bi-LSTM uses the same number of hidden units $H$ as the Transformer model, a Bi-LSTM output of dimension $2H$ is obtained, so the design adds a Linear layer that projects the output dimension $2H$ of the Bi-LSTM to dimension H to match the output dimension of the Transformer. As a result, the semantic correlation (provided by the self-attention mechanism in the Transformer) and the temporal dependency (provided by the Bi-LSTM) in the input data can be preserved simultaneously. Third, during the model training process the encoder module ${E}_{T}$ at the encoder side is used to receive news body ${x}^{d}$ as input. Another encoder module ${E}_{R}$ is used to receive news headline ${y}^{d}$ or semantic annotation ${a}^{d}$ as input. In contrast, the module ${D}_{T}$ at the decoder side will receive news headline ${y}^{d}$ to participate in the model training. When the news headline ${y}^{d}$ is from the source domain, the ground-truth news headline ${y}^{src}$ from the source domain is used; when the news headline ${y}^{d}$ is from the target domain, the pseudo news headline ${y}^{tar}$ from the target domain is used.

In the above way, the news body ${x}^{d}$ and news headline ${y}^{d}$ of the source and target domains are fed to the encoder and decoder simultaneously, thus establishing the semantic association between the source and target domain data in the zero-shot learning semantic prototype transduction phase. As a result, during the training process of the transferred text generation model, the decoder module performs Multi-head Attention computation ^[11] with the outputs of the two encoder modules at the encoder side, respectively, thus capturing the global dependencies between the news body ${x}^{d}$, the semantic annotation ${a}^{d}$ and the news headline ${y}^{d}$ at the encoder and decoder sides, as shown in Figure 6. In addition, due to the inclusion of the pointer generator network, the decoder uses the "copy mechanism" ^[10] provided by the pointer generator network during the text generation process to decide at each time step of the news headline generation whether to copy words from the input text at the encoder side or to generate words from the word list, thus completing the final News headline generation.

3.4.   Zero-shot learning semantic prototype transduction based on intermediate domains

As shown in Figure 6, the text generation model constructed in this paper applicable to semantic prototype transduction receives semantic prototype $z = \left[{x}^{d}, {y}^{d}, {a}^{d}\right], d\in \left\{src, tar\right\}$ as input and outputs the generated news headline text ${y}^{d\text{'}}$. Specifically, the model encoder receives the semantic prototype $z = \left[{x}^{d}, {y}^{d}, {a}^{d}\right], d\in \{src, tar\}$ as input, and in the encoding stage, the encoder receives the input $v = [{W}_{{v}_{1}}, \dots, {W}_{{v}_{n}}]$ to obtain the encoder hidden state $h = \left[{h}_{1}, {h}_{2}, \dots, {h}_{n}\right]$. In the decoding stage, given the input ${x}_{t}$, the decoded hidden state ${s}_{t}$ at time step $t$ can be derived and the attention distribution ${a}_{t}$ of the encoder hidden state $h$ is calculated to combine the linear transformation of the encoder hidden state $h$ and the decoder state ${s}_{t}$. Next, at time step $t$, a context vector representation ${c}_{t}$ is computed from the weighted sum of the encoder hidden state to the attention distribution. The word distribution ${P}_{vocab}\left({w}_{t}\right)$ can then be obtained, where ${W}_{p}$ and ${b}_{v}$ are learnable parameters, and ${P}_{vocab}\left({w}_{t}\right)$ represents the probability distribution of all words in the word list when words are predicted at time step $t$.

In addition, the pointer generator network is used to employ the pointer ${p}_{gen}^{t}$ as a soft switch at time step $t$ of decoding to choose whether to generate a word from the vocabulary by selecting it with probability ${P}_{vocab}\left({w}_{t}\right)$ or to copy a word from the input text according to the attention weight ${a}_{t}$. Thus, the probability distribution $P\left({w}_{t}\right)$ of the final extended word list is obtained. where ${p}_{gen}^{t}$ is calculated based on the context vector ${c}_{t}$, decoder state ${s}_{t}$ and decoder input ${x}_{t}$. The specific process of generating news headlines ${y}^{d\text{'}}$ by the model shown in Figure 6 is shown in Eq (13):

As a result, in the training process of the model shown in Figure 6, the model receives inputs ${x}^{d}/{y}^{d}/{a}^{d}$ and obtains the final word order distribution probability ${P}_{vocab}$ by weighting and summing the word generation probability distribution ${P}_{vocab}$ and attention probability distribution ${a}_{t}$ with the pointer switch ${p}_{gen}^{t}$ according to Eq (13) to generate the corresponding news headline ${y}^{d}\mathrm{'}$.

Further, based on the generation process shown in Eq (13), the loss function ${L}_{xy}$ is designed for $({x}^{d}, {y}^{d})$ in the semantic prototype z according to Eq (14), so that the news headline ${y}^{d}\mathrm{'}$ generated by the input news body ${x}^{d}$ is "close" to the reference news headline ${y}^{d}$ corresponding to ${x}^{d}$, and thus the semantic prototype transduction relationship among the news body ${x}^{d}$, the truth news headline ${y}^{d}$ and the generated news headline ${y}^{d}\mathrm{'}$ is deduced.

Specifically, as shown in Eq (14), ${E}_{T}\left({x}^{d}\right)$ indicates that the news body ${x}^{d}$ is input into the encoder module ${E}_{T}$ at the encoder end; ${E}_{R}\left({y}^{d}\right)$ indicates that the news headline ${y}^{d}$ is input into another encoder module ${E}_{R}$ at the encoder end. When minimizing the loss function ${L}_{xy}$ defined in Eq (13), $\mathbb{D}\left[{E}_{T}\right({x}^{d}\left)\right|\left|{E}_{R}\left({y}^{d}\right)\right]$ means that the hidden state of ${E}_{T}\left({x}^{d}\right)$ output should be "close" to the hidden state of ${E}_{R}\left({y}^{d}\right)$ output, where $\mathbb{D}$ means that the mean-square error (MSE) is used as the distance measure. In the process of ${x}^{d}$ generating ${y}^{d\text{'}}$, i.e. ${x}^{d}\to {y}^{d}\text{'}$, ${x}^{d}$ and ${y}^{d\text{'}}$ are naturally semantically similar to the reference truth ${y}^{d}\text{'}$, so it can be approximated as ${x}^{d}\approx {y}^{d}$ and ${y}^{d}\approx {y}^{d}\text{'}$, then an implicit semantic prototype transduction relation ${(y}^{d}\approx {x}^{d})\to {y}^{d}\mathrm{'}\approx {y}^{d}$ can be established in the intermediate domain ${D}_{i}^{'}$ by minimizing the loss function ${L}_{xy}$.

Similarly, based on the generation process shown in Eq (13), the loss function ${L}_{ay}$ is designed for $({a}^{d}, {y}^{d})$ in the semantic prototype z according to Eq (15) for the zero-shot learning semantic prototype transduction, so that the headline ${y}^{d\text{'}}$ generated by the input semantic annotation ${a}^{d}$ is "close" to the reference news headline ${y}^{d}$ corresponding to ${a}^{d}$, and thus the semantic prototype transduction relationship among the semantic annotation ${a}^{d}$, the news headline ${y}^{d}$ and the generated news headline ${y}^{d\text{'}}$ is deduced.

Specifically, as shown in Eq (15), after inputting the semantic annotation ${a}^{d}$ corresponding to the news body ${x}^{d}$ to the encoder module ${E}_{R}$, the model is still made to generate the news headline ${{y}^{d}}^{'}$. Meanwhile, by minimizing $\mathbb{D}\left[{E}_{R}\right({a}^{d}\left)\right|\left|{E}_{R}\left({y}^{d}\right)\right]$, the hidden state ${E}_{R}\left({a}^{d}\right)$ of the output of the encoder module ${E}_{R}$ is guided to be "close" to the hidden state of the output of ${E}_{R}\left({y}^{d}\right)$. In the process of ${a}^{d}$ generating ${y}^{d\text{'}}$, i.e. ${a}^{d}\to {y}^{d}\text{'}$, ${a}^{d}$ and ${y}^{d\text{'}}$ are naturally semantically similar to the reference truth ${y}^{d}\text{'}$, so it can be approximated as ${a}^{d}\approx {y}^{d}$ and ${y}^{d}\approx {y}^{d}\text{'}$, then an implicit semantic prototype transduction relation ${(y}^{d}\approx {a}^{d})\to {y}^{d}\mathrm{'}\approx {y}^{d}$ can be established in the intermediate domain ${D}_{i}^{'}$ by minimizing the loss function ${L}_{ay}$.

Finally, as shown in Eq (16), a composite generative loss function ${L}_{main}$ is constructed by combining the loss function ${L}_{xy}$ and ${L}_{ay}$, thus indirectly responding to the principle of transfer text generation based on semantic prototype transduction, i.e., when the input semantic prototype $z = \left[{x}^{d}, {y}^{d}, {a}^{d}\right], d\in \left\{src, tar\right\}$, the parameters of the transfer text generation model in Figure 6 will be trained by the compound loss function ${L}_{main}$ in Eq (16).

As shown in Figure 7, when it comes to semantic prototype transduction between the new source and target domains, based on the similar semantic prototypes $x/a/y$ between different domains, if any semantic prototypes ${z}^{tar} = \left[{x}^{tar}, {y}^{tar}, {a}^{tar}\right]$ in target domain has a semantic association with a semantic prototypes ${z}^{src} = \left[{x}^{src}, {y}^{src}, {a}^{src}\right]$ in source domain, then a ${{(x}^{d}\approx y}^{d}\approx {a}^{d})\to {y}^{d}\mathrm{'}\approx {y}^{d}$ relationship can be established through the association between ${y}^{d}\approx {x}^{d}\to {y}^{d}\mathrm{'}\approx {y}^{d}$ and ${y}^{d}\approx {a}^{d}\to {y}^{d}\mathrm{'}\approx {y}^{d}$, which in turn forms an latent relationship of ${x}^{tar}\to {y}^{src}$. Therefore, when given the target domain news body ${x}^{tar}$, the relevant ground-truth news headlines ${y}^{src}$ in the new source domain can be referred to assist in generating the news headlines ${y}^{tar}$ in the target domain. Thus, even if there is no ground-truth news headline data in the target domain, the news headline can be generated with the help of the news body in the target domain by means of zero-shot learning semantic prototype transduction with the new source domain data. The overall process is shown in Algorithm 3.

4.   Experiment

4.1.   Experimental data and experimental setup

In the experiment, for the task of news headline generation, this paper selects the publicly available dataset PENS (PErsonalized News headlineS) ^[1]. 113,762 news items are included in PENS, which are divided into 15 topics, and each news item contains a headline and body. In this paper, 8 news topics are randomly selected from the PENS dataset, including Sport, Finance, Music, Weather, Auto, Movie, Health, and Kid. 8000 news data are randomly chosen as the training dataset in each domain.

The information about the datasets used in the experiments is described in Table 2. The "Average Length" and "Maximum Length" represent the maximum and average length of the word sequences in each domain after the pre-trained BERT model has been used to split the words of all news bodies and news headlines. The "Compression Ratio" represents the ratio of the average length of the text of news headlines to the average length of the news body in a domain.

In the experiments, the number of sub-layers of both the encoder and decoder modules of the transfer text generation model in Figure 6 is 4, the input and output dimensions of the sub-layers are 512, and the number of attention heads of the multi-head attention is 8; the pre-trained BERT model used to obtain the word embedding representation uses BERT-Medium with dimension size 512; the number of hidden units of Bi-LSTM is 512; the model training was performed using Adam optimizer with custom learning rate ^[11]; the number of iterations (epochs) trained on each domain was 1000; all experiments in this paper were implemented using Python 3.8 and TensorFlow-GPU 2.5.0, and the experimental platform was configured with Windows 10 operating system, NVIDIA 2080Ti GPU graphics card, 32GB RAM, and Intel Core i7-11700K CPU.

4.2.   Evaluation metrics and baseline models

To evaluate the effectiveness of the transfer text generation model proposed in this paper when applied to the task of news headline generation, the transfer text generation model presented in this paper is compared with existing pre-trained language models and text generation models related to zero/few-shot learning that perform well.

For the pre-trained language models, T5 ^[17], BART ^[18], PEGASUS ^[19], and BertSum ^[40] were selected. All these four pre-trained language models used the pre-training parameters as the initial parameters of the models. The training was continued based on the pre-training initial parameters for these four models using the data in Table 2 without changing the other hyperparameters.

For zero/few shot text generation models, TransferRL ^[41], ZSDG ^[32], DAML ^[42], and MTL-ABS ^[43] are chosen. Among them, TransferRL contains a decoder shared among different domains and maximizes the "reward" of generalizing the decoder to different domains by reinforcement learning self-critic strategy to improve the domain adaptation of the model so that it only needs to be fine-tuned on small batches of data for fast adaptation to the target domain. ZSDG uses zero-shot learning to generate transferred text with zero data in the target domain by projecting "seed-level" data descriptions into a subspace and then transferring the semantic descriptions at the domain level. DAML and MTL-ABS build generative models using a sequence-to-sequence format based on Meta-Learning principles. Still, DAML uses Gate Recurrent Neural Network (GRU) as encoder and decoder, while MTL-ABS uses Transformer as encoder and decoder. The above two models search for the most promising parameter fetches for the model from the gradient optimization level using meta-learning, which makes the model more responsive to small data in the target domain and improves the domain generalization of the model. In contrast to the pre-trained language models, both zero/few-shot learning models directly use the data in Table 2 to train the models according to their respective transfer strategies.

The generation effectiveness of the above comparison models was evaluated using the evaluation metrics ROUGE-1/2/L ^[35], BLEU ^[35], and METEOR ^[35], which are commonly used in text generation tasks. The news body in the target domain is input to the trained model. The scores of evaluation metrics between the news headlines generated by the model and the corresponding ground-truth news headlines are calculated. Among them, the ground-truth news headlines in the target domain are only used for evaluation and are not involved in the model training process. Based on the above metrics scores, we investigate whether the proposed transferred text generation model can effectively obtain relevant reference knowledge from the source domain data to effectively assist the target domain in completing the text generation task without giving the reference ground-truth data of the target domain text.

4.3.   Experimental results and analysis

4.3.1.   Data distribution alignment effect

To demonstrate the actual effect of the internal mechanism of each stage of the proposed transfer text generation model more directly, the alignment effect of the data distribution in the domain of Figure 4 is further demonstrated with the "kid" news topic as the target domain, as shown in Figure 8. In Figure 8, the source and target domain data are mapped according to Eq (6); in Figure 8, the original embedding representations ${X}_{src}$ and ${X}_{tar}$ of the source and target domains (Figure 8, left panel), and the aligned representations ${X}_{src}^{'}$ and ${X}_{tar}^{'}$ obtained by Eq (6) (Figure 8, right panel) are represented by Principal Component Analysis (PCA) method for dimensionality reduction.

Specifically, in Figure 8, the data representations for different domains are shown in different colors. The top dark blue area indicates the data distribution when the "kid" news topic is the target domain. In Figure 8, the left panel shows the original representation distribution of the text data of the eight domains, which is output by the pre-trained BERT model without any cross-feature filling and data distribution alignment. It can be found that there are significant differences in the original representation distributions for the given eight domains. After that, the other seven domains, except "kid, " are used as source domains, as shown on the right side of Figure 8. The data in the source domain and the news data in the target domain "kid" are first filled with cross features between the source and target domains according to Eqs (1)–(3); on this basis, the alignment of the domain data distribution is done by Eq (6) according to the process shown in Figure 4, and the result is shown in the right side of Figure 8. After the domain data distribution alignment, although there is still a slight difference between the source and target domain data, the distribution difference between different domains has been significantly reduced. Comparing the left plot and right plot in Figure 8, it can be found that the proposed model involves the alignment of domain data distribution between different domains by first using cross-filling to fill the features for the source and target domain data and then minimizing the maximum mean difference distance metric between the source and target domains, which effectively reduces the data distribution difference between the source and target domains.

4.3.2.   Target domain round-robin experiments

For zero-shot learning semantic prototype transduction, one of the eight domains listed in Table 2 is selected as the target domain, and the remaining seven are used as source domains. The seven source domains and one target domain are formed into $K$ intermediate domains, as shown in Figure 5 for experiments according to the intermediate domain redistribution. In the process of target domain rotation, the silhouette coefficient commonly used in the K-means method ^[38] is used to evaluate the effect of intermediate domain redistribution under different values of $K$ to determine the value of $K$. Currently, the value of $K$ does not exceed the number of source domains. The range of the silhouette coefficient is [-1, 1]; if the value of the silhouette coefficient tends to 1, it means that the cohesion and separation are relatively better and the clustering effect is better, thus determining the number of intermediate domains.

Figure 9 shows that the size of the silhouette coefficients is determined by Algorithm 2 for different values of K for each domain as the target domain. The optimal number of intermediate domains is the point with the most considerable $K$ value of the silhouette coefficient. After obtaining the optimal number of intermediate domains $K$ taken for each domain as the target domain, the scores of ROUGE-1/2/L, BLEU, and METEOR metrics in Table 3 are calculated from the news headlines generated by the model and the corresponding headline ground-truth data under the corresponding intermediate domain redistribution scheme after each target domain is determined in the round-robin experiment. Specifically, the effect of text generation in each target domain is first evaluated. In this case, only the ground-truth news headline data in the source domain are involved in the model training, no headline ground-truth data are involved in the target domain, and only the pseudo news headline text extracted from the news body is used in the target domain. As a result, based on the distribution-aligned representation of domain data obtained by Eq (6) and the zero-shot learning semantic prototype transduction by Eqs (14) and (15), the news body in each target domain can generate news headlines directly without relying on any manually ground-truth values.

Table 3 lists the performance of the transfer text generation model proposed in this paper applicable to semantic prototype transduction for news headline generation in different target domains. As we can see, the performance of indicators in all fields is relatively stable except for "Movie"; "Health", "Car" and "Weather" rank in the top 3 in terms of performance. As a result, although the model does not refer to the headline truth data in the target domain in the process of generating training, the semantic correlation of data between different domains is obtained through the alignment of domain data distribution used according to Eq (6) in Figure 4 and the semantic prototype transduction transfer based on (news $\mathit{\boldsymbol{x}}$, headline $\mathit{\boldsymbol{y}}$) in Figure 7, which results in better scores on each evaluation index in the process of rotating through different target domains. This phenomenon can be attributed to the fact that, firstly, based on Figure 4, the differences in the distribution of data across domains are reduced after the alignment of the domain data distribution. Therefore, the negative impact of the differences in the distribution of data across domains can be reduced during the transfer of the model from the source domain to the target domain. Then, through zero-shot learning semantic prototype transduction, the transfer text generation model proposed in this paper simultaneously acquires the semantic correlations between different domain data through the attention mechanism and temporal dependency in the enhanced encoder and decoder in Figure 6 to adjust the model parameters to improve the model domain transfer effect.

Further, Figure 9 shows the training performance of the text generation model during the zero-shot learning semantic prototype transduction phase when part of the domain is used as the target domain. In this phase, the model is trained through 1000 epochs by the loss function ${L}_{main}$ defined in Eq (16). The accuracy is calculated as the ratio of identical words between the generated text and the ground-truth text at each time step of the generated text. As can be seen from Figure 9, even for the three domains with the lowest evaluation index of text generation, the loss function ${L}_{mian}$ in training is gradually decreasing, which proves that the model can fully parse the semantic prototypes of each domain data by the loss function ${L}_{xy}$ designed for $({x}^{d}, {y}^{d})$ in the semantic prototype $z$ and the loss function ${L}_{ay}$ designed for $({a}^{d}, {y}^{d})$ in the target domain without the ground-truth data, so that the model captures the correlation between the semantic prototypes of different domain data during the generation process, and thus performs effective transfer from the source domain to the target domain. The smooth increase of accuracy proves the accuracy of the text generated by the transfer text generation model proposed in this paper after transfer from the source domain to the target domain, in which the pointer generator network is responsible for handling the out-of-vocabulary (OOV) problem, which further improves the text quality.

4.3.3.   Ablation experiments

From Table 3, we can see that the best performance of transfer text generation is achieved when the three domains of "Health, " "Auto, " and "Weather" are used as target domains. Therefore, further ablation experiments are conducted on the proposed transfer text generation method using these three domains, and the results are shown in Table 4.

In Table 4, "Semantic prototype transduction" indicates that the original representation of the pre-trained BERT model output is directly used without intermediate domain redistribution. The model is directly trained using the semantic prototype transduction based on Eqs (14)–(16) in Figure 7; "Intermediate Domain Redistribution + Semantic prototype transduction" indicates that the original representation of the output of the pre-trained BERT model is directly adopted, and the model is trained using the semantic prototype transduction based on Eqs (14)–(16) in Figure 7, after the intermediate domain redistribution according to the optimal number of intermediate domains, "Distribution Alignment + Intermediate Domain Redistribution + Semantic prototype transduction" indicates that the model is trained with the semantic prototype transduction based on Eqs (14)–(16) in Figure 7 after dividing the intermediate domain by the optimal number of intermediate domains based on the distribution-aligned data representation of Eq (6) in Figure 4.

From the experimental results in Table 4, the text generation effect is better than that of using the original representation directly after adopting the distribution representation alignment method in each target domain, which means that the distribution alignment of domain data can effectively eliminate the data distribution differences between domains and improve the transferability from the source domain to the target domain. In addition, comparing the experimental results in Table 4 with those in the comparison experiments in Table 5 below, the model proposed in this paper can also obtain higher evaluation metric scores compared with most other transfer text generation models using only the semantic prototype transduction method for training. This phenomenon shows that in the transfer scheme proposed in this paper, zero-shot learning semantic prototype transduction explores data semantic correlation between different domains. The enhanced encoder and decoder in the "encoder-decoder" structure correlate the no-ground-truth news text in the target domain with the most relevant news headlines in the source domain and obtain semantic prototype similarity or proximity according to the attention mechanism and temporal dependence and derive the reference of the target domain to the source domain data in text generation, thus improving the text generation effect of transfer.

In addition, it can be seen from the data in the table that the combination of "Intermediate Domain Redistribution + Semantic prototype transduction" achieves higher evaluation index scores than the "Semantic prototype transduction" method only, which indicates that the "intermediate domain redistribution" by the content similarity composite index, the target domain text is generated based on the relevant source domain data with more semantic similarity, achieving the better performance of transferred text generation. Meanwhile, the complete "Distribution Alignment + Intermediate Domain Redistribution + Semantic prototype transduction" approach in Table 4 can achieve the optimal text generation results of the model, which means that the model can obtain the optimal transferred text generation performance on the target domain by getting the composite transfer strategy of distribution alignment representation of domain data and zero-shot learning semantic prototype transduction via Eq (16) while obtaining helpful information from the relevant source domain in the intermediate domain without reference to the ground-truth data in the target domain. The pointer generator network will also improve the accuracy of the generated text.

4.3.4.   Comparison experiment

As the experimental results in Table 3 show, the text generation performance of the model is the worst when the "Movie" domain is the target domain. Therefore, we further compare the performance of the proposed text generation model approach for zero-shot learning semantic prototype transduction with other transfer text generation model approaches in terms of pre-training models (i.e., T5, BART, PEGASUS, BertSum) and "zero/few-shot learning models" (i.e., TransferRL, ZSDG, DAML, MTL-ABS) for the "Movie" domain. The results are shown in Table 5.

All the models in Table 5 are trained with the intermediate domain data shown in Figure 5 after the domain data distribution alignment. All the models do not use the ground-truth data in the target domain during the training process. The performance improvement rate refers to the difference between the proposed "Distribution Alignment + Intermediate Domain Redistribution + Semantic prototype transduction" method in the performance evaluation metric score compared with the highest score in the comparison model.

Specifically, with the "Movie" domain as the target domain, which is the least effective of our approach, the transfer text generation model proposed in this paper achieves the best performance in the comparison based on the evaluation metric scores, followed by the pre-trained language model approach, and finally the zero/few-shot learning model approach. This phenomenon can be attributed to the fact that the transfer scheme proposed in this paper first alleviates the data distribution differences between domains by aligning the domain data distribution at the text representation level according to Eq (6) based on Figure 4 and then improves the text generation model structure based on Figure 6 by making it more applicable to the zero-shot learning semantic prototype transduction according to Eq (15) in Figure 7 so that the model can more effectively acquire a priori knowledge from the relevant source domains that can help transfer and improve the model's text generation performance in the target domain.

Second, furthermore, the pre-trained language models T5, BART, PEGASUS, and BertSum in Table 5 have been pre-trained in a large-scale corpus, so more prior knowledge has been incorporated into the parameters of such pre-trained language models in advance. However, the experimental results in Table 5 show that the scores of T5, BART, PEGASUS and BertSum for each evaluation metric are lower than those of the transfer approach proposed in this paper. This phenomenon can be attributed to the fact that although the pre-trained language model has acquired a large amount of domain prior knowledge through the large-scale corpus pre-training, this knowledge is not specific to the target domain and its underlying tasks. In contrast, the transfer text generation model proposed in this paper first reduces the distribution difference in data representation with other related source domain data from the target domain perspective by domain data distribution alignment, and establishes cross-domain semantic association ${x}^{tar}\approx {y}^{src}\approx {a}^{src}\to {y}^{src}$, i.e., ${x}^{tar}\to {y}^{src}$, based on semantic prototypes ${z}^{src} = \left[{x}^{src}, {y}^{src}, {a}^{src}\right]$ and ${z}^{tar} = \left[{x}^{tar}, {y}^{tar}, {a}^{tar}\right]$ by zero-shot learning semantic prototype transduction, which maximizes the semantic correlation between different domain data and exploits the semantic correlation. It ensures that the target domain can help the target domain generate text with the help of source domain data using semantic prototype transduction even if there is no reference ground-truth data, thus having better domain transfer adaptability for a specific target domain and the tasks under it.

Third, for the zero/few-shot learning models TransferRL, ZSDG, DAML, and MTL-ABS in Table 5, these models use reinforcement learning, zero-shot learning, or meta-learning methods for transfer respectively. However, the results in Table 5 show that the scores of all evaluation metrics of these methods are lower than those of the transferred text generation models proposed in this paper. This phenomenon can be attributed to the structural improvements adopted in this paper for the transferred text generation model in Figure 6. Specifically, as shown in Figure 6, the improved text generation model can explore the semantic meaning of the text to a greater extent by adding a Bi-LSTM layer to resolve the text serialization dependencies. At the same time, the Transformer multi-head attention mechanism increases the internal contextual observation of the text. It processes the out-of-vocabulary (OOV) with the help of the pointer generator network. On this basis, by constructing data-level semantic prototypes, the no ground-truth news body in the target domain is associated with the most relevant news headlines in the source domain, and the semantic relatedness of the cross-domain text is captured according to the approximation on the semantic prototypes; thus, when the news body ${x}^{tar}$ in the target domain is given, the most relevant ground-truth news headlines ${y}^{src}$ in the source domain will be referenced to assist in generating news headlines ${y}^{tar}$ in the target domain, and thus the higher score performance on the evaluation metrics of ROUGE-1/2/L, BLEU, and METEOR.

5.   Conclusions

In this paper, we propose a transfer text generation model based on distribution alignment of domain data and zero-shot learning semantic prototype transduction for the task of news headline generation, whose primary principle is to assist the target domain in text generation with the help of data in the relevant source domain to overcome the problem of missing reference truth in the target domain. When the model is applied to a new domain, even if the data of the target domain (new domain) lacks the reference truth, the method proposed in this paper can fully utilize the existing source domain data information and the data information available in the target domain to solve the problem of model generalization caused by data when the common text generation model is applied in the new domain and realize the excellent application of the model in the new domain. The transfer text generation method proposed in this paper can be effectively applied to the task of news headline generation to solve the reference truth of data missing problems in the target domain by transferring the domain data information.

We believe that the work in this paper still has some limitations in practical applications. First, the proposed method is mainly applied to tasks with several different but similar domains, and the performance of the proposed method may be reduced if the differences between domains are too significant. In addition, the proposed method is since the target domain provides a certain amount of data with no reference truth that can be used in the domain transfer method. The target domain will also affect the proposed method if it does not provide any data. Therefore, through our research, we believe several aspects of future work deserve further exploration. First, we would like to investigate further the effect of the proposed method on transfer text generation between different domains that differ significantly. Second, to further investigate how to supplement new data when there is a lack of available data in a new domain. Third, selecting relevant source domains is crucial to the final transfer generation performance when the target domain is given. More suitable methods for domain data selection need to be further investigated. Fourth, the source domain data often provide noisy information that is not relevant to the target domain during the transfer process, which affects the transfer effect and brings about the negative transfer problem, so avoiding the "negative transfer" problem is also a direction worthy of further research.

Acknowledgments

This work was supported in part by National Science Foundation of China (No. 62102187), Jiangsu Natural Science Foundation (Basic Research Program) (BK20210639) and National Key Research and Development Program (2021YFE0104400). This research project was also supported by a grant from the Research Center of the Female Scientific and Medical Colleges, Deanship of Scientific Research, King Saud University, Saudi Arabia.

Conflict of interest

The authors declare no conflict of interest.

Appendix