1. Introduction
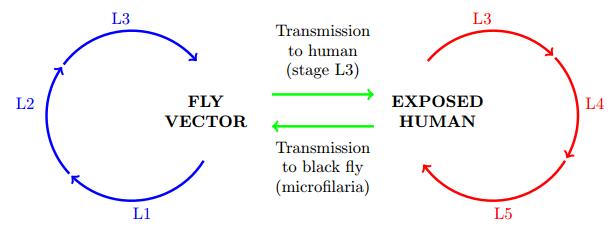
Onchocerciasis (known colloquially as "River Blindness") is a vector-borne disease affecting the skin and eyes of humans. It is endemic in parts of Africa, Central America, and Yemen, with greater than 99% of the burden of onchocerciasis found in sub-Saharan Africa [3]. There are an estimated 125 million people worldwide who are at risk for onchocerciasis [20]. In Central America, Guatemala accounts for the largest at-risk population for onchocerciasis, but the disease has been designated as eradicated there [17]. It is caused by the filarial nematode Onchocerca volvulus, a parasitic worm with a complicated life cycle that includes five larval stages, labeled L1-L5 in Figure 1 [15], some in a human host and some in a black fly host of the genus Simulium. The disease is listed by the World Health Organization as a neglected tropical disease, but it has been targeted by the Carter Center's River Blindness Elimination Program.
Microfilaria are produced by mature adults in the human host, where they can live from 6 to 24 months. Black flies of genus Simulium ingest the microfilariae while biting a human host. It takes 6-12 days for the microfilariae to mature through larval stages L1 through L3. Stage L3 larvae migrate to the fly's mouth, where they are transmitted to a new human host through a bite. These take approximately a week to develop to the final L5 larval stage and an additional 7-15 months to mature into reproductive adults, which have a life span of 10-14 years. At maturity, female worms produce 700-1500 microfilariae per day [8].
The black fly has peak biting times during the daylight hours and largely stays within 5 km of their breeding sites on well-oxygenated water. Communities living near a river are more at risk than those further away, and it happens that the peak biting times of the vector correspond with the times when the exposed class of people are most likely to be at the river for activities such as gathering water or washing [8].
There are several medications that can help treat onchocerciasis, including diethylcarbamazine and ivermectin (which are both microfilaricides) and flubendazole (which is a macrofilaricide). Due to adverse side effects of some of the medications, ivermectin is considered to be the standard in effective treatment of onchocerciasis [8]. Oral administration of ivermectin rapidly kills microfilariae that are present in the human host; it does not kill the adult worms, but it does reduce their reproductive rate for several months [3,13]. In a study spanning 1987-1991, analysis of data from five consecutive annual treatments with ivermectin showed reduced microfilariae production after each treatment. The microfilariae production did gradually increase over a 10 month period, reaching a plateau that was around 32% lower than pre-treatment values [13].
The distribution of ivermectin in sub-Saharan Africa remains a challenge due to many factors, including the more pronounced itching caused by the increase in the number of microfilariae deaths brought on by treatment with ivermectin and the restriction that ivermectin is only approved for adults and children over the age of 5 who are neither pregnant nor chronically ill [15]. In the African Programme for Onchocerciasis Control's (APOC) progress report for 2014-2015, 22 of 26 endemic countries (from a total of 28 endemic countries) reported treatment data showing an average of 65.3% global coverage [1].
A variety of models have been developed to study onchocerciasis. Most recent work has been done using complex simulation software packages ONCHOSIM [14] or SIMON [5] that include all immunological and epidemiological processes believed to be relevant. These can be used to make predictions for specific locations, but the value of the predictions is limited by the difficulty of estimating parameter values. Although predictions from ONCHOSIM closely fit the data for the first five years of ivermectin treatment, the results from the subsequent twelve years of treatment showed the predictions from ONCHOSIM to be overly optimistic with regard to the feasibility of eradication [4,10]. Even if good data is available, simulation models cannot easily be used to characterize the overall effect of each parameter on model behavior, so it is difficult to use them to obtain conclusions of broad applicability.
Another model in common use is EpiOncho [19], a population-based deterministic epidemiological model that incorporates immunological elements, such as the mean number of female adult worms per host, the mean number of microfilaria per milligram of skin, and the mean number of larvae per vector that are at the stage of development to be transmitted to a human host. The complexity of the model again makes it difficult to draw broad conclusions that do not depend strongly on estimated parameter values.
As an alternative to complex models, one can construct simpler models that incorporate only the most important biological features of a setting or focus on some aspects of a setting while oversimplifying others. For example, Basáñez and Boussinesq [2] developed an immunological model that focuses on the population dynamics of O. volvulus within the human hosts, while Remme et al. [16] developed a model that focuses on the force of infection.
Because disease eradication depends on epidemiological factors rather than immunological factors, there should be some value to developing a purely epidemiological deterministic model for onchocerciasis; however, there does not seem to be any such model more recent than 1982 [6]. One reason for this lack may be that the infectivity of human hosts to uninfected flies is not a simple parameter, but is dependent on the microfilarial load, which varies over time from almost nil immediately after ivermectin treatment to about 65% of that in untreated humans by a year after treatment [13]. Nevertheless, it is reasonable to decouple the within-host dynamics from the epidemiological dynamics by assuming an "effective" infectivity factor computed as a weighted average of the infectivities of the individual infected human hosts.
Epidemiology models are classified according to the specific classes of individuals that need to be tracked (see [7] for an overview) and whether the diseases are infectious or vector-borne. In Section 2, we extend the SEIS (susceptible, exposed, infective, susceptible) model for a vector-borne disease to a nonstandard SEIPMS model that distinguishes three classes of infectives: standard infectives who do not participate in a health care system or are ineligible for ivermectin treatment, premedicated infectives who are participants in a health care system but not yet treated, and medicated infectives who have received ivermectin treatment. We show how this model can be approximated as an infectious disease model with nonlinear incidence. A linearized stability analysis provides a complete characterization of the equilibria as functions of a small number of model parameters. In Section 3 we present a more realistic model that assumes health care delivery occurs at discrete times rather than continuously and analyze that model by characterizing endemic periodic solutions, finding a uniqueness condition for the disease-free solution, and showing that the disease-free solution is stable whenever it is unique. Section 4 presents simulations of treatment scenarios and compares the outcomes of annual and continuous delivery of health care.
2. A continuous model
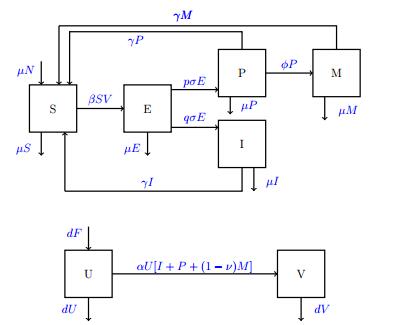
An onchocerciasis model needs to have at least two classes for the black fly host: one for the uninfected flies (U) and one for the infected flies (V). In the absence of treatment, the human population needs to have at least three classes: susceptible (S), exposed (E), and infective (I). The exposed class for the human population is necessary because of the long incubation period for the disease. We omit an exposed class of flies because their incubation period is less than a week.
With treatment, it is necessary to use three infective classes for the humans: standard infectives who do not participate in a health care system or are ineligible for ivermectin treatment (I), premedicated infectives who are participants in a health care system but not yet treated (P), and medicated infectives who have received ivermectin treatment (M) (see Figure 2).
The model includes the following specific assumptions:
1. The human population N and fly population F are constant, as onchocerciasis is not fatal to either and does not inhibit reproduction. These parameters vary widely by region.
2. Human and black fly birth and death rates are proportional to the population numbers, with rate constants μ for humans and d for the flies, respectively. We take typical values to be μ=0.02 and d=12 from lifespan estimates of 50 years for humans (appropriate for the regions where the disease is most prevalent) and 1 month for the flies.
3. The infection rate of humans is proportional to the susceptible population S and the (infected) vector population V, with proportionality constant β. The rate constant β depends on the rate at which humans are bitten by flies and the probability that a given bite transmits the larvae. This value is hard to measure directly.
4. Exposed individuals become infectious at a rate proportional to their number, with rate constant σ that is independent of participation in the health care system. The incubation period for onchocerciasis is about one year, because the larvae that infect humans must develop into a second larval stage and mature into adult worms before the mature adults begin to produce the microfilaria that infect the flies. Hence, a typical value is σ=1.
5. Ivermectin treatment is available to a fraction p of the population, limited by restrictions on who can receive the medication and limited health care coverage and participation. Thus, the rates of progress from class E to classes P and I are pσ and qσ, respectively, where q=1−p. A typical value is p=0.65 [1]; however, this quantity could perhaps be increased through interventions.
6. Individuals move from the premedicated class P to the medicated class M at a rate proportional to the population, with rate constant ϕ taken as the reciprocal of the mean time between the first production of microfilaria and the onset of treatment. The typical health care delivery rate of once per year corresponds to ϕ=2.
7. The effective population of infective humans is W=I+P+(1−ν)M, where ν is the relative decrease in infectivity of a medicated host compared to an untreated host. In reality, ν is 1 shortly after treatment and gradually falls to about 0.35 [13]. For our model that neglects population dynamics within the host, we take ν to be constant, with a typical value of 0.6 to 0.8.
8. The infection rate of the fly vector is proportional to the product of the uninfected fly population F−V and the effective population of infective humans (W), with proportionality constant α. Like β, the factor α is hard to measure directly.
9. Given that ivermectin does not kill the adult worms, patients can only be cured of the disease upon the natural deaths of all the adult worms. The average life span is approximately 12 years, independent of the treatment, so we use a common rate constant γ for the progress of all three infective classes to the S class, with typical value γ=0.08. This assumption ignores the possibility of having the infection reintroduced into human hosts who are already infected, which would restart the clock for clearance of the disease; hence, our model will overestimate the clearance rate.
These assumptions yield a model consisting of differential equations for E, I, H=P+M (the population of infected individuals who are currently or will eventually be treated), M, and V, along with an algebraic equation for S:
where we have used T for time in order to reserve t for dimensionless time. Note that differential equations are not needed for S and U because the populations N and F are constant.
2.1. Nondimensionalization and simplification
We define dimensionless parameters
|
δ=γ+μd,ϵ=μσ,θ=γ+μϕ,η=γ+μσ+μ,a=αNd,b=βFσ(γ+μ)(σ+μ).
|
(7)
|
The parameters δ, ϵ, θ, and η are chosen for convenience from among many possible parameters representing ratios of time scales; specifically, δ, θ, and η represent (approximately) the expected times for fly lifespan, treatment, and larval development relative to the expected duration of the infective stage, respectively, while ϵ represents the ratio of larva development time to human lifespan. The parameters a and b represent the expected number of transmissions from a fully-infective human to a susceptible fly and from an infective fly to a susceptible human, respectively.
The natural scale for all human population groups is the total population N; however, the analysis benefits from scaling groups according to the sizes needed for equilibrium. In particular, the I and H equations establish that E/N=O((γ+μ)/σ), so [(γ+μ)/σ)]N is a better scale for E than is N. We choose the expected time in the infective class for the time scale, so t=(γ+μ)T. With our typical parameter values, one unit of dimensionless time represents about 10 years.
With the substitutions
|
S=Ns,E=γ+μσNx,I=Ni,H=Nh,M=Nm,V=Fv,t=(γ+μ)T,
|
(8)
|
the model becomes
|
s+i+h+ζx=1,w=i+h−νm,
|
(14)
|
where
2.2. Parameter estimation
Using the estimates μ=0.02, d=12, γ=0.08, σ=1, and ϕ=2, all in inverse years, we can estimate the dimensionless time scale parameters as
|
δ≈0.008,ϵ≈0.02,θ≈0.05,η≈0.1,ζ≈0.1.
|
(16)
|
The infectivity parameters a and b are order 1 and can be estimated from known endemic fractions of infected humans and flies in the absence of ivermectin treatment. To do this, we first compute the equilibrium solutions for the SEIS model obtained by taking p=0:
|
i0=1−(ab)−11+b−1+ζ,v0=ai01+ai0.
|
Thus we can calculate the infectivity parameters from values for the endemic equilibrium fractions i0=I/N and v0=V/F as
|
a=i−10v−10−1,b=v−10i−10−(1+ζ).
|
(17)
|
Using field estimates from Cameroon, i0=0.46 and v0=0.30 [10], we obtain parameter estimates a=0.93 and b=3.1. Subsequent examples will use a=0.9 and b=3.0 unless otherwise noted. We will also see that the basic reproductive number is the product of the infectivity parameters; hence, the study data suggests a value of R0=2.7. Eradication of the disease from this population will therefore require that the human-to-fly infectivity rate be reduced by almost three-fold.
2.3. Asymptotic simplification
We will examine asymptotic limits as ϵ, θ, and η go to 0 as needed. For now, we assume
which makes the vector equation (13) quasi-steady, yielding the algebraic equation
The final model, consisting of differential equations (9)-(12) along with algebraic equations (14) and (19), is an SEIPMS infectious disease model with nonlinear incidence.
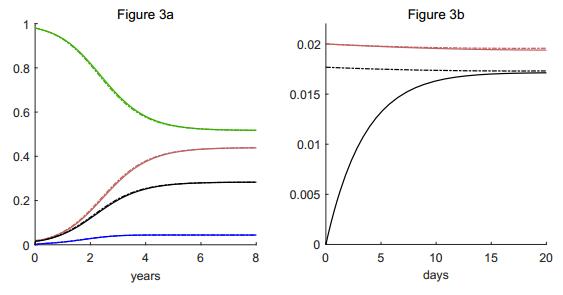
The error in taking δ→0 is only noticeable on a very short time scale. Simulation results in Figure 3 verify this claim for a scenario where a small number of infective humans seed a region where the disease was previously absent. The plot of Figure 3a includes both the solution of the full model ((9)-(14), solid curve) and the simplified model with the quasi-steady approximation for the vector equation ((19) instead of (13), dash-dot); there is no visible difference. In both cases, the numbers of infective humans and flies gradually increase over a six-year period to their stable no-treatment values, with the greatest increase coming between 1 and 3 years. To highlight the actual difference, Figure 3b shows the solution on a much shorter time scale. The infective vector population rises from 0 to 0.018 (1.8% of the total fly population) in the first 20 days, while the quasi-steady approximation jumps to that level instantly. This is the extent of the error caused by the approximation.
2.4. Equilibria and stability
The system (9)-(12), (14), and (19) always has a disease-free equilibrium in which s=1 and all other variables are 0. Any endemic disease equilibria must satisfy the equations
|
i=qx,h=px,m=p1+θx,s=1−(1+ζ)x,w=ρx,
|
(20)
|
where
This leaves the algebraic system
for v and x. Assuming v,x>0, these equations can be rewritten as
and then elimination of v yields the result
|
x=1−R−101+b−1+ζ,provided R0>1,
|
(25)
|
where
is the basic reproductive number.
We can interpret R0 as the product of the number of secondary human infections per infective fly (b) and the number of secondary fly infections per infected human (ρa), where ρ<1 is a weighted average of the relative infectivity for the classes I, P, and M as compared to the infectivity of class Ⅰ.
The stability of the equilibria is determined by the Jacobian matrix, which is
|
J =[−η−1Q1η−1Q3η−1Q3−η−1Q2q−100p0−1000θ−1−θ−1−1],
|
where
|
Q1=1+ζbv,Q2=bsdvdw=abs(1+aw)2,Q3=Q2−bv.
|
(27)
|
The characteristic polynomial can be written as
where
|
P3(λ)=(λ+η−1Q1)(λ+θ−1+1)(λ+1)−η−1Q3(λ+θ−1+1)+η−1θ−1νpQ2.
|
(29)
|
The stability of the equilibria can then be determined from P3 by the Routh-Hurwitz conditions c1>0, c3>0, and c1c2>c3, where cj is the coefficient of λ3−j [12]. Here
|
c1=(θ−1+1)+(η−1Q1+1)>θ−1+1>0,
|
|
c2=η−1Q1+η−1(θ−1+1)Q1+(θ−1+1)−η−1Q3=η−1(Q1+bv)+η−1(θ−1+1)Q1−η−1Q2+(θ−1+1)>η−1(Q1+bv)+η−1[(θ−1+1)Q1−Q2],
|
|
c3=η−1(θ−1+1)Q1−η−1(θ−1+1)Q3+η−1θ−1νpQ2=η−1(θ−1+1)(Q1+bv−ρQ2),
|
and
|
c1c2>η−1(θ−1+1)(Q1+bv)+c1η−1[(θ−1+1)Q1−Q2].
|
The requirement c3>0 yields a necessary condition for stability:
The stronger requirement
is sufficient for c1c2>c3 as well as c3>0 because it implies
|
(θ−1+1)Q1−Q2>(θ−1+1)ρQ2−Q2=[1+θ−1(1−νp)]Q2−Q2>0,
|
whence
|
c1c2>η−1(θ−1+1)(Q1+bv)>c3.
|
The disease-free equilibrium has
so both stability criteria become
confirming that the disease-free equilibrium is stable when R0<1 and unstable when R0>1. The endemic disease equilibrium has (from (22))
then
|
ρQ2=ρa(1+aw)21+awρa=11+aw<1<Q1.
|
Both criteria are always satisfied provided that the existence requirement R0>1 is met.
Proposition 1 summarizes the results.
Proposition 1. The SEIPMS model given by (9)-(12), (14), (19) has
1. a disease-free equilibrium that is stable whenever R0<1 (26), and
2. a stable endemic disease equilibrium given by (25) and (20) whenever R0>1.
3. A pulsed model
The general pulsed model follows from two changes to the SEIPMS model of Section 2:
1. Set ϕ=0 because delivery of health care occurs only at fixed intervals;
2. Introduce a jump condition at times nτ, where τ is the scaled treatment interval (typically 0.1 or 0.05, corresponding to treatment intervals of 1 year or 6 months with a time scale of 10 years). At these points in time, all individuals in the premedicated class become medicated, which means m=h.
Thus, the model (using the δ→0 and ϵ=0 approximations) is
|
ηdxdt=bsv−x,x+=x− at t=nτ,
|
(32)
|
|
didt=qx−i,i+=i− at t=nτ,
|
(33)
|
|
dhdt=px−h,h+=h− at t=nτ,
|
(34)
|
|
dmdt=−m,m+=h− at t=nτ,
|
(35)
|
|
s=1−i−h−ηx,v=aw1+aw,w=i+h−νm.
|
(36)
|
The system can be simplified somewhat by introducing variables y, z, and r to replace h, i, and m and rescaling time to match the treatment interval:
|
y=p−1h,z=i−qy,r=p−1m,t∗=tτ,ξ=τη.
|
(37)
|
The problem for z is then
which can be solved immediately, reducing the system to
|
dxdt∗=ξ(bsv−x),x+=x− at t∗=n,
|
(38)
|
|
dydt∗=τ(x−y),y+=y− at t∗=n,
|
(39)
|
|
drdt∗=−τr,r+=y− at t∗=n,
|
(40)
|
|
s=1−y−z−ηx,v=aw1+aw,w=y+z−νpr,z=z(0)e−τt∗.
|
(41)
|
3.1. Periodic solutions
Periodic solutions are defined by the differential equations of (38-40) along with the periodicity conditions
|
x(0)=x(1),y(0)=y(1),r(0)=y(1)
|
(42)
|
and the auxiliary equations of (41). Clearly any periodic solution must have z=0, and we can solve the r equation analytically; thus, we can recast the problem as that of finding initial conditions (xi,yi) such that the solution of the system defined by
|
dxdt=ξ(bsv−x),x(0)=xi,
|
(43)
|
|
dydt=τ(x−y),y(0)=yi,
|
(44)
|
where
|
s=1−y−τξ−1x,w=y−yiνpe−τt,v=wa−1+w,
|
(45)
|
satisfies the periodicity conditions
|
x(1)=x(0),y(1)=y(0).
|
(46)
|
Obviously there is a disease-free periodic solution with x0=y0=0. Numerical solutions can in principle be found by solving (43-46); in practice, this system is difficult to work with because the presence of the small parameter τ in (44) makes y very nearly constant. As an alternative, we can derive another periodicity condition by combining (43) and (44) into a single equation
integration over the interval [0,1] then yields the condition
Our numerical scheme implements this condition by adding initial value problem components
|
dFdt=bsv,F(0)=0;dYdt=y,Y(0)=0;
|
(48)
|
whence we can compute the correct initial conditions (xi,yi) from
|
x(1)=x(0),F(1)=Y(1).
|
(49)
|
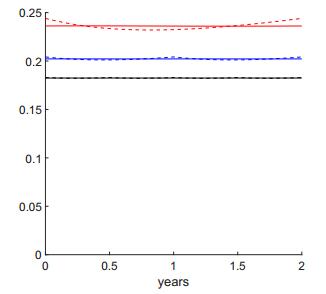
Figure 4 shows some periodic solutions using typical parameter values. The variation over the treatment interval is seen primarily in the exposed populations and not the infective population. The principal driver of this behavior is the sudden drop in infectivity from human to fly each time treatment occurs. This creates a noticeable decrease in the infected fly population, which decreases the rate at which susceptible humans become infected; meanwhile, the rate at which exposed humans become infective changes only slightly during the period. The result is a decline in the exposed population in the first portion of the treatment interval. The subsequent rise is due to the fact that individuals who become infective during the interval between treatments are not medicated and hence more infective to the flies.
3.2. Asymptotic approximation
It is also possible to compute asymptotic approximations for periodic solutions. The leading order approximation is the solution of the reduced problem having τ=0. With
we have
|
s∼s0=1−y0,w∼w0=(1−νp)y0,v∼v0=w0a−1+w0.
|
The integral condition (47) requires
so
|
a−1+w0=w0v−10=bs0w0y−10=b(1−νp−w0),
|
from which we obtain the results
|
w0=1−νp−(ab)−11+b−1,y0=w01−νp,s0=1−y0,v0=w0a−1+w0.
|
(51)
|
The result (50) reduces the x0 equation to
which has the unique periodic solution x0=y0.
To obtain first order corrections to the constant leading order solution, we assume
|
x(t;τ)=y0+τx1(t)+O(τ2),y(t;τ)=y0+τy1+O(τ2),
|
(52)
|
where y1 is constant because the result x0=y0 means y′0=O(τ2); the results are
|
y1=a−1νps0−2ξ−1w0(a−1+w0)2(1−νp)(a−1+1−νp),
|
(53)
|
and
|
x1(t)=y1+ba−1νpy0s0(a−1+w0)2(−12−ξ−1+t+e−ξt1−e−ξ).
|
(54)
|
Details of these calculations appear in the Appendix.
3.3. A necessary condition for an endemic disease equilibrium
If we begin with a set of parameters that yields an endemic disease equilibrium and gradually make the parameters less favorable, the solutions of the fixed point equations (46) gradually converge to (x0,y0)=(0,0). Hence, the critical case can be thought of as corresponding to the limit of the periodic solution problem as y0→0 with x0=O(y0). We can identify the bifurcation hypersurface by assuming
|
(x,y,x0,x1,y1)=(y0X,y0Y,y0X0,y0X1,y0Y1)
|
(55)
|
in (43-46) and taking the asymptotic limit y0→0, resulting in the problem
|
dXdt∗=−ξX+ξabY−ξabνpe−τt∗,X(1)=X(0),
|
(56)
|
|
dYdt∗=τX−τY,Y(0)=Y(1)=1.
|
(57)
|
With three boundary conditions for a system of two differential equations, this problem is overspecified and will have a solution only for a particular relationship among the parameters.
Letting UT=[XY], the system can be written in vector form as
|
dUdt∗=[−ξξabτ−τ]U+[ξab0]νpe−τt∗.
|
(58)
|
The eigenvalues of the matrix in (58) are given by
|
λ1,2=−(ξ+τ)±√ξ2+(4ab−2)ξτ+τ22,
|
(59)
|
which are real for the case where the disease is endemic in the absence of treatment (ab>1). Given a treatment interval that is much shorter than the lifespan of adult worms, we expect τ to be small (τ≈0.1 for annual treatment); hence, we write the eigenvectors as
|
u1=[u11],u2=[u2τ]whereu1=λ1+ττ,u2=λ2+τ.
|
(60)
|
With this notation, the solution of the system of differential equations is
|
X=c1u1eλ1t∗+c2u2eλ2t∗,
|
(61)
|
|
Y=c1eλ1t∗+c2τeλ2t∗+νpe−τt∗.
|
(62)
|
The three boundary conditions yield a linear system for unknowns c1, c2, and νp, leading to the necessary condition (for existence of an endemic periodic solution)
|
νp<(τu1−u2)(eλ1−1)(1−eλ2)τu1(eλ1−1)(e−τ−eλ2)−u2(eλ1−e−τ)(1−eλ2).
|
(63)
|
Asymptotic expansion of this result (included in the Appendix) yields the approximate condition
|
νp<(1−1ab)(1+τ2)+O(τ2),
|
(64)
|
which can be rearranged as
|
R0=ab(1−νp1+τ/2+O(τ2))>1.
|
(65)
|
The quantity on the left side of this inequality is the basic reproductive number for the continuous model (τ/2 is the mean dimensionless time a newly infective person must wait for initial treatment, which was defined as θ in Section 2).
3.4. Stability of the disease-free solution
Consider the case where there is a small perturbation to the disease-free solution owing to a small non-zero initial value z(0)=z0, corresponding to the introduction of a small number of unmedicated infectives. We assume
|
(x,y,r,z)=(z0X,z0Y,z0R,z0Z)
|
and define sequences
|
Xn=X(nτ),Yn=Y(nτ),Zn=Z(nτ)=e−nτ,Kn=νpYn−Zn,
|
along with a shifted time variable on the interval nτ<t∗<(n+1)τ:
With the solution R(ˆt)=Yne−τˆt, we obtain a recursive definition of the sequences Xn and Yn through the system
|
dXdˆt=−ξX+ξabY−ξabKne−τˆt,X(0)=Xn,X(1)=Xn+1,
|
(66)
|
|
dYdˆt=τX−τY,Y(0)=Yn,Y(1)=Yn+1.
|
(67)
|
The eigenvalues and eigenvectors are again given by (59) and (60), leading to the solutions
|
X=c1u1eλ1ˆt+c2u2eλ2ˆt,
|
(68)
|
|
Y=c1eλ1ˆt+c2τeλ2ˆt+Kne−τˆt,
|
(69)
|
where
|
c1=τXn−(1−νp)u2Yn−u2Znτu1−u2,c2=−Xn+(1−νp)u1Yn+u1Znτu1−u2.
|
(70)
|
Evaluating these solutions at ˆt=1 yields a system of difference equations having the form
Since limn→∞Zn=0, the solution vector for this system decays to 0 if the eigenvalues of A have magnitude less than 1, which we can determine directly from the matrix entries
|
a11=τu1eλ1−u2eλ2τu1−u2,a12=−(1−νp)u1u2eλ1−eλ2τu1−u2,
|
(71)
|
|
a21=τeλ1−eλ2τu1−u2,a22=(1−νp)τu1eλ2−u2eλ1τu1−u2+νpe−τ
|
(72)
|
using the Jury conditions [9]
With τ→0, we can quickly see that
from which it is clear that the trace is positive and the determinant is less than 1; hence, the only condition that needs to be satisfied is
Computing and simplifying the trace and determinant yields the inequality
|
(eλ1+eλ2−1)+νpe−τ−νpτu1eλ2−u2eλ1τu1−u2
|
|
<(1−νp)eλ1+λ2+νpτu1eλ1−τ−u2eλ2−ττu1−u2.
|
Multiplying this inequality by the positive quantity τu1−u2 and rearranging leads ultimately to the condition
|
νp>(τu1−u2)(eλ1−1)(1−eλ2)τu1(eλ1−1)(e−τ−eλ2)−u2(eλ1−e−τ)(1−eλ2),
|
(75)
|
which is just the reverse of the inequality needed for existence of the endemic periodic solution.
Proposition 2 summarizes the results of the pulsed model.
Proposition 2.In the limit η→0, the disease-free periodic solution is unique and stable whenever
|
νp>(τu1−u2)(eλ1−1)(1−eλ2)τu1(eλ1−1)(e−τ−eλ2)−u2(eλ1−e−τ)(1−eλ2).
|
When the inequality is reversed, the disease-free periodic solution is unstable and an endemic disease periodic solution can be found numerically by solving the algebraic equations (49) applied to the system (43), (44), (48). In the limit as τ→0, the inequality reduces to
|
R0=ab(1−νp1+τ/2+O(τ2))<1.
|
4. Results and discussion
4.1. Using the continuous model in lieu of the pulsed model
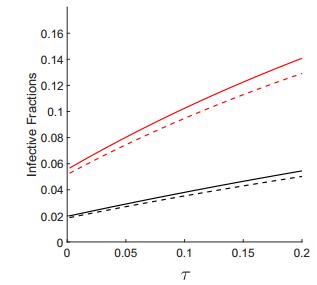
In practice, the treatment protocol for onchocerciasis leads to the pulsed model. As we would predict, the continuous model slightly underestimates the numbers of infectives compared to the pulsed model (see Figure 5), which increases the extent to which the model results are overly optimistic. However, the intervals between treatment events are short compared to the time required for a patient to be cleared of the disease (τ≪1), which means that the results for the continuous model are only slightly better than those of the pulsed model. Certainly the difference between the continuous and pulsed models is small compared to the errors caused by uncertainty in parameter values. Given these considerations, we use the continuous model in the subsequent discussion of our model projections.
4.2. The prognosis for onchocerciasis treatment plans
In the pre-treatment equilibrium, the product ab is given in terms v0 and i0 (from (17)) by
The condition for a basic reproductive number R0<1 is then
|
1−νp1+θ=ρ<1ab=(1−v0)[1−(1+ζ)i0],
|
or
|
νp1+θ>v0+(1+ζ)i0(1−v0).
|
(76)
|
Using estimated parameter values i0=0.46 and v0=0.30 [10], this means that eradication would require νp≈0.69. This is problematic, as the generally accepted treatment fraction is only p=0.65 [1]. With an optimistic value of 0.9 for ν, at best achievable if treatment is more frequent than in the current protocol, a compliance rate higher than p=0.76 would be required. This might be possible, but it would be difficult to achieve since there are people who cannot be given ivermectin treatment, such as pregnant women and children under the age of 5.
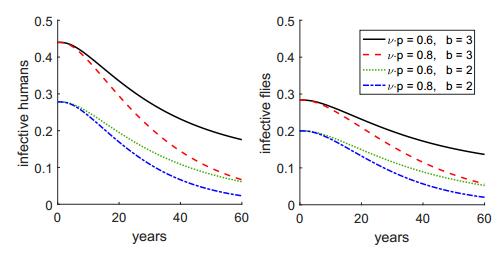
Even if R0 can be brought below 1, the eradication dynamics is unacceptably slow. Figure 6 shows the results of simulations using a=0.9 with optimistic and pessimistic values for b and νp. The combination of a=0.9 and b=3 yields a pre-treatment equilibrium of 44% human infectivity and 28% fly infectivity, which is not quite as much as the reported values given above. The lowest curve in each plot is for the optimistic choices b=2 and νp=0.8, corresponding to R0=0.43. It takes about 60 years in this scenario for the infective populations of humans and flies to be decreased to 10% of their initial values. These disappointing results are due to two key factors:
1. Ivermectin does not kill adult worms, so the expected value of the time needed to eradicate the disease from an individual human host is still half the lifespan of the adult worms, which is about 6 years.
2. Even with optimistic projections for microfilaria suppression and fraction of humans who get treated, the expected transmission rate from an individual human to the black fly population is still 20% of the untreated value.
While our model is overly simple, it should be able to provide an overestimate of the efficacy of onchocerciasis treatment simply by choosing an optimistic value of νp; thus, the results strongly suggest that the current eradication plan is inadequate. The problem cannot be fixed simply by improving parameter values such as the treatment fraction. The more significant reason for the poor results is that ivermectin targets the parasite at the least critical point in its life cycle. From a mathematical point of view, we should apply a treatment plan that targets the adult worms because this would shorten the expected value of the longest time scale. While this might not have a larger effect on the basic reproductive number, it would speed up the approach to the disease-free equilibrium by changing the time scale of that approach.
4.3. Using an analytical model in lieu of a complex simulation
Modeling of onchocerciasis has generally been done using complex simulations such as ONCHOSIM and EpiOncho. One would expect that more detail would provide better results than a simplified model such as ours. This is true in theory, but in practice it is only true if the processes are very well understood, the parameter values are known to a modest degree of accuracy, the models are thoroughly tested against data, and the predictions for hypothetical scenarios viewed skeptically rather than accepted without reservation. Here there is ample reason for caution.
ONCHOSIM predicts eradication of onchocerciasis with 5 to 20 years of treatment, depending on the initial mean population microfilarial load [18]. Given that the adult worm lifespan is 10-12 years, 5 years of treatment is only sufficient to reduce the prevalence of adult worms in the human population by half, and then only with complete suppression of microfilarial production. The actual results must be worse because treatment does not result in complete suppression and coverage is not universal. Perhaps the disease can be temporarily eradicated from the flies in 5 years, but microfilarial production rebounds somewhat after treatment is discontinued and there would be a large number of infective humans available to restart the infection in the fly population. This simple example illustrates the danger of taking the detailed predictions of complex simulations too seriously.
Simpler analytical models can be thought of as sacrificing precision for accuracy, insofar as they can be used to determine a range of reasonable results and the results are robust to changes in parameter values. Of course the accuracy of this range depends on the specific simplifications in the analytical model. Our model has one major omission, which is the assumption that the expected duration of the onchocerciasis infection in humans is the same as the expected lifespan of the adult worm. This is not true if new onchocerca larvae can establish themselves in a human who is already infected from an earlier time. Reintroduction of larvae into an infective human would reset the 12-year timer for clearance of the disease, resulting in a much smaller expected clearance rate. This omission makes our model more optimistic about the conditions needed for local eradication of the disease from any given population. Our results are not so much a projection of what will happen with a particular treatment plan as they are a best case scenario for what could happen with that plan.
Another simplification in our model of onchocerciasis is our assumption that the effect of treatment is to lower the infectivity of humans to flies by a fixed fraction ν. There is a considerable amount of literature showing that this is not the case; instead, the mean infectivity of humans drops to near 0 when the dose of ivermectin is administered but then rises to a level somewhat less than that of untreated patients but still significant. In theory, there should be a particular mean value of infectivity loss ν for any treatment protocol, but the best value for ν should depend on the frequency with which the medication is administered. This could be determined by the overall treatment interval (as represented by τ in the pulsed model and θ=τ/2 in the continuous model) if doses are only administered during the periodic visits by the medical community, but it could also be independent of the frequency of medical visits if it is possible to have permanent members of the population arrange for doses to be administered at any interval prescribed by the treatment plan. These considerations affect the choice of ν for investigations with the model, but the idea of using a fixed value of ν in lieu of a complex simulation is valid in any case.
4.4. The value of asymptotics
Asymptotic approximation can sometimes simplify the analysis of a model without making an appreciable change in the results. This is most clearly seen in Figure 3, where the error caused by the quasi-steady assumption that changes the model from a vector-borne disease with linear incidence to an infectious disease with nonlinear incidence is only visible for the first 15 days of a disease introduction scenario. The duration of the period for which the initial transient is important depends primarily on the time scale of the differential equation being approximated. This time scale is just 30 days in the onchocerciasis model, so we should not expect a transient duration to be significantly longer than that. The extent of the imbalance between the initial conditions of the experiment and the equilibrium solution does not make much difference. For example, a similar experiment with double the initial load of human infectives shows a transient of the same duration.
Asymptotics also has a clear value in characterizing solutions, as for example in the analytical result for the periodic solutions of the pulsed model in the limit τ→0. While the value in this case is modest, there are examples where asymptotic analysis can provide a detailed explanation of complex behavior (see [11] for an example).
Appendix: Asymptotics for the pulsed model
A.1. Periodic solutions
This subsection shows the calculations necessary to obtain the approximations (53) and (54). We begin by defining
and assuming the asymptotic expansions
|
x∼y0+τx1(t)+O(τ2),y∼y0+τy1+O(τ2),
|
(B)
|
where the term y1 is necessarily constant because the leading order solution x∼y0 implies y′=O(τ2). We also define subsidiary expansions, (suppressing the O(τ2) term)
and
|
w∼w0+τw1,w1=w10+w11tv∼v0+τv1,v1=v10+v11tf∼f0+τf1,f1=f10+f11t.
|
The calculation proceeds by using the equations for s, w, v, and f to determine the corresponding first-order corrections in terms of y1 and then use the periodicity condition (47), which reduces to
|
y1=∫10f1(t)dt=f10+12f11,
|
(C)
|
to obtain an algebraic equation for y1. Once y1 is known, then x1 is determined directly from its initial value problem.
From s=1−y−τξ−1x, we obtain
The expansion
|
w=y−νpyie−τt∼(y0+τy1)[1−νp(1−τt)]
|
yields
|
w10=(1−νp)y1,w11=νpy0.
|
(E)
|
The equation v=w/(a−1+w) can be written as
|
(v0+τv1)(a−1+w0+τw1)∼w0+τw1,
|
from which we eventually obtain
|
v10=a−1(1−νp)y1(a−1+w0)2,v11=a−1νpy0(a−1+w0)2.
|
(F)
|
Expansion of (A) then yields
|
f11=bs0v11=ba−1νpy0s0(a−1+w0)2
|
(G)
|
and
Combining this last result with (C), (D), (F), and (G) yields an algebraic equation for y1, with solution
|
y1=a−1νps0−2ξ−1w0(a−1+w0)2(1−νp)(a−1+1−νp).
|
(H)
|
Once this result is known, the differential equation for x1 with the periodicity condition has the solution
|
x1=y1−(12+ξ−1)f11+f11t+f11e−ξt1−e−ξ.
|
(I)
|
A.2. Existence condition for a nontrivial periodic solution
This subsection shows the calculations necessary to obtain the approximation (64)
from the original result (63)
|
νp<(τu1−u2)(eλ1−1)(1−eλ2)τu1(eλ1−1)(e−τ−eλ2)−u2(eλ1−e−τ)(1−eλ2).
|
1. We begin by rewriting the original result as
|
P=(eλ1−1)(1−τu1u2)(eλ1−e−τ)−τu1u2(eλ1−1)e−τ−eλ21−eλ2,
|
or
|
P=eλ1−1eλ1−e−τ⋅1−τu1u21−τu1u2⋅eλ1−1eλ1−e−τ⋅e−τ−eλ21−eλ2.
|
(J)
|
2. The eigenvalue λ2∼−ξ=O(1) as τ→0; hence, the last factor in the denominator of (J) can be expanded as
and u2=λ2+τ∼−ξ. We then have
|
P∼eλ1−1eλ1−e−τ⋅1+ξ−1τu1+O(τ2)1+ξ−1τu1⋅eλ1−1eλ1−e−τ+O(τ2).
|
(K)
|
3. The eigenvalue λ1 is O(τ) as τ→0; hence, the other ratio of exponential functions can be expanded as
|
eλ1−1eλ1−e−τ∼λ1+12λ21+O(τ3)(λ1+12λ21)−(−τ+12τ2)=λ1+12λ21+O(τ3)(λ1+τ)+12(λ21−τ2)=λ1λ1+τ⋅1+12λ1+O(τ2)1+12(λ1−τ)∼λ1λ1+τ⋅(1+12λ1+O(τ2))(1−12(λ1−τ)+O(τ2))∼λ1λ1+τ⋅(1+τ2+O(τ2)).
|
Substituting this result into (K) yields
|
P∼λ1λ1+τ⋅(1+τ2+O(τ2))⋅1+ξ−1τu1+O(τ2)1+ξ−1τu1⋅λ1λ1+τ+O(τ2).
|
(L)
|
4. The denominator in the last factor of (L) can be expanded as a geometric series, yielding
|
P∼λ1λ1+τ⋅(1+τ2+O(τ2))⋅(1+ξ−1τu1⋅τλ1+τ+O(τ2));
|
since τu1=λ1+τ, we have
|
P∼λ1λ1+τ⋅(1+τ2+O(τ2))⋅(1+ξ−1τ+O(τ2)).
|
(M)
|
5. Expansion of the formula for λ1 (59) yields the results
|
λ1∼(ab−1)τ[1−abξ−1τ+O(τ2)],λ1+τ∼abτ[1−(ab−1)ξ−1τ+O(τ2)],
|
so
|
λ1λ1+τ∼ab−1ab⋅[1−abξ−1τ+O(τ2)]⋅[1+(ab−1)ξ−1τ+O(τ2)]∼(1−1ab)[1−ξ−1τ+O(τ2)].
|
Substituting this last result into (M) yields the desired final result
|
P∼(1−1ab)(1+τ2)+O(τ2).
|
(N)
|









 DownLoad:
DownLoad: