Equilibria and control of metabolic networks with enhancers and inhibitors

1.   Introduction

Models in Quantitative Systems Pharmacology (briefly QSP) ^[2,25,26,28] have been used by the pharmaceutical industry in order to discover new drugs at less cost. In modeling metabolic networks, bio-chemical reactions are organized into a graph, with nodes representing metabolites and edges representing fluxes ^[20,22,24]. The dynamics is described by a Stoichiometric matrix encoding the kinetics of the biochemical reactions.

QSP models are commonly used with the assumption that all fluxes are independent or have insignificant correlation ^[1,15,27], which does not recognize the resilience of metabolic networks. Thus, despite the vast knowledge by Systems Biology (as well as other fields ^{[3,8,10,16,18,19,23,24]}), researchers were unable to accurately simulate large metabolic networks ^[12,28] as an inexpensive alternative for clinical trials. A new method called Linear-in-Flux-Expressions (briefly LIFE), where one rewrites the system as linear with respect to the fluxes ^[20], has shown potential to help pharmacology simulators recover crucial characteristics of metabolic networks. This approach has been investigated ^[22] and currently works for mild nonlinearities, however inhibitors, enhancers, and fully nonlinear dynamics are still not included.

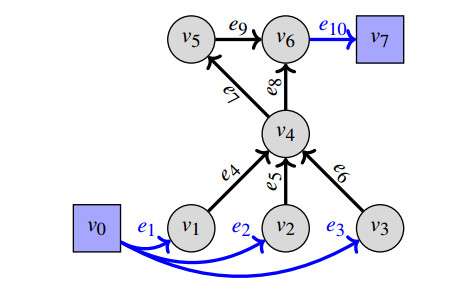
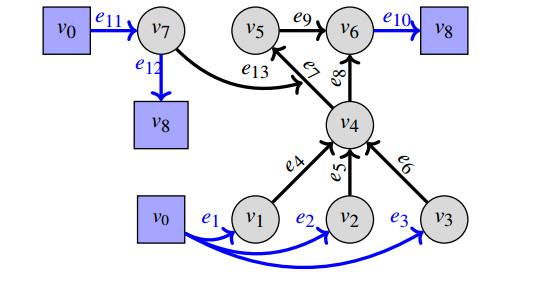
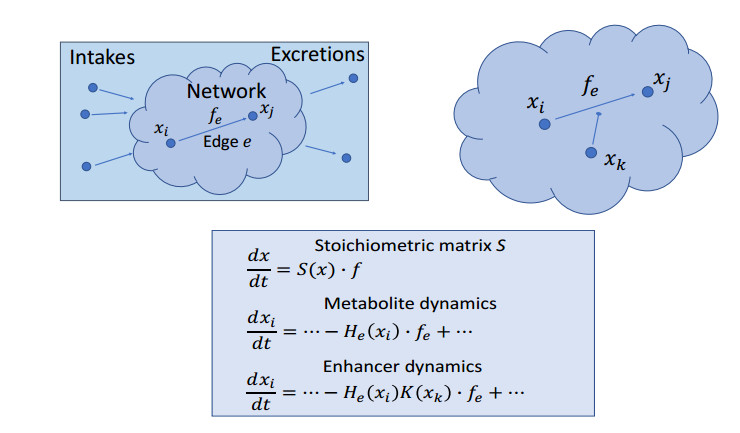
The aim of this work is to apply results from previous studies to actual networks and extend our results to include control of the intakes and enhancer dynamics. Figure 1 depicts the main ideas. Metabolic networks naturally have intakes and excretions, while fluxes $f_e$ are determined by kinetics of bio-chemical reactions. The LIFE approach consists of writing dynamics with Stoichiometric matrix $S(x)$ that describes the mass consumed and produced by the reactions. This matrix is dependent on the metabolites (as opposed to classical $S(f)$ dependent on fluxes) thus allowing nonlinear dynamics in metabolites. A general condition on network topology (connection of every node to excretion, see ^[22]) guarantees existence and uniqueness of an equilibrium $\bar{x}_f$ for every flux vector $f = \{f_e\}$. Thus network dynamics is captured by the map $f\to \bar{x}_f$ with a multivalued inverse $x\to F(x)$ (see [19,Theorem 4]).

We first show various theories applied to a small yet significant part of human cholesterol metabolism, called "Reverse Cholesterol Transport'' (briefly RCT). In particular, nonlinear dynamics implemented on RCT admits a unique stable equilibrium (for fixed fluxes and intakes). This allows to study drug discovery by control methods. More precisely, we consider both control of intakes (corresponding to a diet and/or supplements) and the introduction of enhancers and inhibitors (corresponding to drugs). Also, control of inhibitors/enhancers is compared versus control of the intakes.

The control of intakes is entirely similar to the problem of controlling inputs to compartmental systems. The main difference here is in the assumptions on the specific network dynamics. In particular, choosing Michaelis-Menten kinetic, which gives a nonlinear dynamics in metabolites, one has to face the problem of saturation. The latter may lead to non existence of equilibria. More precisely, since the kinetic can support only a maximal level of discharge for a given metabolite, too high intakes may cause the metabolite levels to increase indefinitely. By analyzing the map from intakes to equilibria, we are able to compute the set of admissible intakes (compatible with saturation levels) and thus reduce optimal control problems to finite-dimensional optimization ones.

The action of inhibitors and enhancers is defined for general networks: Inhibitors and enhancers augment other edges via multiplicative Michaelis-Menten kinetics. Existence, uniqueness and stability of equilibria is proved for the RCT example and conjectures for general networks under suitable assumptions. The latter are entirely similar to the case without enhancers and inhibitors, thus are expected to be satisfied by most natural metabolic networks. Lastly, we describe a process of drug discovery by f augmenting the network with enhancers or inhibitors and finding optimal controls.

The paper is organized as follows. Section 2 introduces the LIFE methods and main definitions. Section 3 describes the Reverse Cholesterol Transport network and provide various results by applying well-established theories. Section 4 considers control problems for intakes, while Section 5 introduces the dynamics with enhancer and inhibitors. Section 6 illustrated drug discovery by mean of enhancer and inhibitors, and, finally, Section 7 contains conclusions.

2.   Linear-In-Flux-Expressions

The most general description of a metabolic network includes the dynamics of the metabolites $x\in\mathbb{R}^n$ and dynamics of fluxes $f\in\mathbb{R}^m$:

where $F:\mathbb{R}^n\times\mathbb{R}^m\rightarrow\mathbb{R}^n$ and $G:\mathbb{R}^n\times\mathbb{R}^m\rightarrow\mathbb{R}^m$. In ^[14,18] the authors show that the dynamics $F$ governing the metabolites typically evolves faster than the dynamics $G$ governing the fluxes. Thus we approximate the dynamics of the system with $G\approx 0$, i.e., the fluxes remain practically constant.

One can define a directed graph related to a metabolic system (see Figure 2), with $n$ metabolites and $m$ reactions. The metabolites are represented by vertices $V = \{v_1, \ldots, v_n\}$. The reactions are represented by a set of edges $E \subset V \times V$. To represent the interactions between the network and the external environment, we introduce two virtual vertices $v_0$ and $v_{n+1}$. The sets of vertices attached to $v_0, v_{n+1}$ are denoted by $I, X$, the vertices in $I$ and $X$ are called intake vertices and excretion vertices, respectively. The intakes are defined as the edges $(v_0, w)$ with $w\in I \subset V$, and the excretions are defined as the edges $(w, v_{n+1})$, $w\in X \subset V$. A graph is strongly connected if there exists a path between every pair of vertices. A strongly connected component of a directed graph is a maximal strongly connected subetaaph. A terminal component of a directed graph $G = (V, E)$ is a strongly connected component $G' = (V', E')$, with $V'\subset V$, $E'\subset E$, such that there exists no edge $e = (v', v)$, with $v'\in V'$ and $v\in V\setminus V'$. We define the parameters of the model: $x \in \mathbb{R}^n_+$, $S(x)$ is $n\times m$, and $f\in \mathbb{R}^m_+$, where $\mathbb{R}^d_+$ is the $d$-dimensional space of vectors with all positive components. Assuming $G\equiv 0$ and $F$ linear in $x$, the usual method of writing the system of Ordinary Differential Equations(ODEs) (2.1) governing metabolism is given by (see ^[14]):

where $J(f)$ is an $n\times n$ matrix depending on the fluxes of the system.

Our method is also based on the assumption $G\equiv 0$, but asks for linearity of $F$ with respect to the fluxes rather than to the metabolites. Such assumption is more often encountered when dealing with metabolic networks ^[20]. We call the Linear-in-Flux-Expressions (LIFE) approach the idea of using linearity with respect to fluxes to write the dynamics as:

where $f$ is the column vector of fluxes and $S(x)$ is the stoichiometric matrix defined as follows. Each row of $S(x)$ corresponds to a metabolite represented by a vertex and each column corresponds to a flux of a reaction, which is represented by an edge in the directed graph. Thus we use the notation $S_{v e}(x)$ for the matrix entry corresponding to vertex $v$ and edge $e$. In simple words, the entry $S_{v e}(x)$ is a function quantifying how much mass moves along edge $e$. We notice that, in systems biology, researchers often refer to $J(f)$ of (2.2) as the stoichiometric matrix, see ^[24].

In this paper, our analysis is organized into sections with different assumptions on the entries $S_{ve}$ of the stoichiometric matrix as function of the values of metabolites and fluxes. The most general class of systems we consider satisfies the following assumption. For $x\in (\mathbb{R}_+)^n$, it holds:

where $H_e:\mathbb{R}^n\to \mathbb{R}_+$ is continuous. Notice that Assumption (A) implies that, for each $v \in V$,

All columns of $S$ have zero sum, except those corresponding to intakes and excretions, which have positive and negative sum, respectively. Under Assumption (A), the dynamics (2.3) can be interpreted as mass conservation law. Here we introduce a special class of systems of type (2.3) with simplified dynamics. We consider Assumption (A), and we impose further restriction on the functions $H_e(x)$: For an edge $e = (v, w)$, we assume $H_e$ to depend on $x_v$ only, and moreover we impose the scalar function $H_e(x_v)$ to be strictly increasing:

where $H_e:{{\mathbb{R}}_{+}} \to \mathbb{R}_+$ is differentiable, strictly increasing, and $H_e(0) = 0$.

A typical example of a system verifying (B) is given by metabolic networks with Hill functions representing reactions, i.e., $H_e(x_v) = \frac{x_v^{p_e}}{K + x_v^{p_e}}$ with $p_e \in \mathbb{N}$, and $K$ is called the dissociation constant. LIFE approach allows a simple description of flux vector $f$ which permits the system to be in equilibrium; such vectors comprise the null space of $S(x)$. In previous work ^[22], the authors showed how the theory of Laplacian dynamics, Markov chains, network flows, and compartmental systems apply to LIFE systems. The results tell us how the structure of the graph of the metabolic network affects existence, uniqueness, and stability of equilibria. An example of structure the authors investigated in ^[22] is a terminal component of a network, which is a part of the network not connected to excretions. The assumptions on $S(x)$ and the structure of the network allow also to compute equilibria related to a given flux vector $f$.

3.   Dynamics theories at work on Reverse Cholesterol Transport

In this section, results from ^[21,22] are applied to the example network of RCT ^[20]. RCT (see Figure 2) represents the mechanism of removal of cholesterol from plaques in arteries. Here, we apply theory from ^[5] to derive equilibria and stability of the RCT. The various mathematical approaches are applicable to this example as follows. Linear systems without intakes nor excretions are related to continuous-time Markov chains ^[9]. Linear systems with intakes and excretions from and to the external environment are known as compartmental systems ^[5,16]. Nonlinear systems are studied using the results from ^[19].

The dynamics of the RCT network can be written as (2.3), with $S: \mathbb{R} \to M_{6\times 10}$. The matrix $S$ is then the concatenation of $S_{1-3}$ and $S_{4-10}$ which are the submatrices given by the first three columns and last seven columns respectively.

and $S_{4-10}$ is given by:

while the flux vector $f \in \mathbb{R}^{10}$ is a $10\times 1$ vector $(f_i)_{i\in \{1, \ldots, 10\}}$.

A further simplification is where $H_e(x_v)$ is the same function $H_v(x_v)$ for all edges $e$ having $v$ as an initial vertex. This gives Assumption (C), as follows. For all $x \in (\mathbb{R}_+)^n$,

and each $H_v:\mathbb{R}_+ \to \mathbb{R}_+,$ with $H_v(0) = 0$ is a differentiable and strictly increasing function. The system can be equivalently re-written as:

where $h(x)$ = $\begin{pmatrix} h_1(x_1), & \cdots, & h_n(x_n)\\ \end{pmatrix}^T$, $J(f) \in M_{n\times n}$ (a $n\times n$ matrix with real entries), and $\phi \in \mathbb{R}^n$. The intake vector $\phi$ is written as a $n\times 1$ vector with a zero if there is no intake flux from the outside environment and $\phi_{e_i}$ the value of the flux if there is an edge to $v_i$. For the RCT network, $J(f)$ and $\phi$ are given by:

The following Proposition 1 (from ^[22]) shows that the existence of nontrivial equilibria implies some network structure. We define the sets $I$, $X$, as the set of vertices attached to $v_0$, $v_{7}$ respectively.

Proposition 1. Consider system (2.3) satisfying (A). Assume there exists an equilibrium $\bar{x}\in (\mathbb{R}_+)^n$ for a flux vector $f$ such that $f_e > 0$ for every $e\in E$. Then for every vertex $v \in V$ for which there exists a path from $I$ to $v$, there exists a path from $v$ to $X$.

The max-flow min-cut theorem ^[11] implies that a positive flux vector exists if there is a path from $v_0$ and $v_{n+1}$ as shown by the following proposition.

Proposition 2. Consider system (2.3) satisfying (A), fix an $x \in (\mathbb{R}_+)^n$ and intake flow vector $\bar{\phi}$ with strictly positive entries. Then there exists $f \in (\mathbb{R}_+)^{m}$ in the null space of $S(x)$ if and only if for each $v \in I$ there exists a path to $X$.

3.1.   Linear RCT without intakes and excretions

Assume the RCT network dynamics is linear, then the flow of mass along an edge is proportional to the mass of the metabolite represented by the initial vertex. This means that Assumption (C) is satisfied with $h(x)$ from (3.1) such that $h(x) = x$. When the network is isolated from the external environment, the dynamics can be written as $\dot x = \bar{J}(f) x$, where $\bar{J}(f)$ is a Metzler matrix (i.e., has non-negative off-diagonal entries), and all its columns sum to zero (${\bf 1}^T \bar{J}(f) = {\bf 0}^T$).

Let $G'$ be a graph associated to RCT network without intakes (remove two virtual vertices $v_0, v_7$ and remove blue edges $e_1, e_2, e_3, e_{10}$ in Figure 2). We assume each edge is associated with a strictly positive weight $f_e > 0$. In the theory of Laplacian dynamics ^[23], the matrix $L = -\bar{J}(f)^T$ can be interpreted as a weighted Laplacian of $G'$. The weighted adjacency matrix $A$ is composed of elements $A_{ij} = f_{(v_i, v_j)}$ if $(v_i, v_j)\in E$, and $A_{ij} = 0$ if there no directed edge from $v_j$ to $v_i$. We defined a diagonal matrix $D$ that contains the row-sum of $A$ indicating the weights leaving from each vertex. The weighted Laplacian is given by $L = D - A$.

In the field of consensus dynamics [5,Theorem 6] systems are modeled using the weighted Laplacian $\dot{x} = -Lx$. The dynamics is different from the linear LIFE dynamics, but $\bar{J}(f)$ and $-L$ have the same eigenvalues. The study of the spectrum of the Laplacian has been investigated in the fields of graph theory and control ^[22]. The results of these fields apply to LIFE systems when we consider the metabolic network with all intakes and excretions removed. Moreover, the RCT network without intakes and excretions is related to a continuous-time Markov chain over a finite state $V = \{v_1, \ldots, v_6\}$. Thus results on Markov chains are applicable to LIFE systems. The spectrum of $\bar{J}(f)$ and the asymptotic behavior of the dynamics are described by the following proposition:

Proposition 3. Assume there are no intakes nor excretions, then:

(1) All eigenvalues of $\bar{J}(f)$ are either $0$ or have strictly negative real part.

(2) The dimension of the nullspace of $\bar{J}(f)$ is equal to the algebraic multiplicity of the $0$ eigenvalue, and is equal to the number of terminal components in the graph.

(3) From any positive initial condition, the system converges to an equilibrium, having strictly positive entries in correspondence of vertices of terminal components, and $0$ elsewhere.

(4) The equilibrium is determined by the initial mass if there is a unique terminal component.

The RCT network without intakes and excretions has a unique terminal component made up of the singular vertex $v_6$. Satisfying (1) and (2) of Proposition 3, the eigenvalues of $\bar{J}(f)$ are: $\{0, -f_{e_{4}},$ $-f_{e_{5}}, -f_{e_{6}}, -f_{e_{9}}, -(f_{e_{7}}+f_{e_{8}})\}$. Furthermore (3) and (4) imply that all the initial mass in the RCT will converge to $v_6$.

3.2.   Linear RCT with intakes and excretions

In the case the linear RCT network interact with the environment via intakes and/or excretions, the dynamics is given by $\dot{x} = J(f)x + \phi$, where $J(f)$ and $\phi$ is defined in (3.2). The associated graph $G$ is given by Figure 2. A directed graph is called weakly connected if there exists an undirected path between each pair of vertices. A weakly connected component of a directed graph is defined as a maximal weakly connected subetaaph. We notice that $G$ is a weakly connected component including $v_0$ and $v_7$. The rows of $J(f)$ no longer sum to $0$ because of a single element in the last column representing excretion. Thus $-J(f)^T$ does not satisfy the definition of weighted Laplacian. In ^[29] a term grounded Laplacian $L_g$ is introduced. $L_g$ can be constructed by deleting the row and column corresponding to a given set of vertices (called grounded vertices) from $L$. For RCT network, $-J(f)^T$ is a grounded Laplacian $L_g$ (see ^[22]). The spectrum of $J(f)$ is described by:

Proposition 4. Consider a linear system with intakes and/or excretions, then the following are equivalent:

(a) For every $v \in V$ there is a path from $v$ to $X$.

(b) $J(f)$ is Hurwitz stable (i.e., all its eigenvalues have strictly negative real part).

(c) $J(f)$ is invertible.

Moreover, when $J(f)$ is invertible, all entries of $-J(f)^{-1}$ are positive; if the graph is strongly connected, all entries of $-J(f)^{-1}$ are strictly positive.

It is clear from Figure 2 that the RCT network with intake and excretion satisfies (a). The Jacobian $J(f)$ can be seen in equation 3.2, and the eigenvalues are: $\{-f_{e_{4}},$ $-f_{e_{5}}, -f_{e_{6}}, -f_{e_{9}}, -f_{e_{10}}, -(f_{e_{7}}+f_{e_{8}})\}$, verifying (b).

3.3.   Non-linear RCT

The non-linear RCT network satisfies Assumption (B) with $h(x)$ may be non-linear, e.g., $h(x) = \frac{Hx}{K_M + x}$ is Michaelis-Menten type of equation, where $H$ is the saturation value, and $K_M$ is the Michaelis constant.

Proposition 5. ([19,Theorem 6]) Consider the non-linear system under Assumption (B) with no intakes and excretions. The following properties hold:

(1) The total mass of the system $m = \sum_{v\in V} x_v$ is constant in time.

(2) From any positive initial condition $x(0)$, the system tends to the equilibrium set.

(3) Moreover, if there is a unique terminal component, then there exists a unique equilibrium with positive entries with the same mass as the initial mass, and the system converges to it.

This means that despite the $h(x)$ functions being non-linear, the RCT network with no intakes and excretions will have constant total mass and the system tends to the equilibrium set. For the general case with intakes and excretions, we recall results from ^[19]:

Proposition 6. ([19,Theorems 2 and 3]) For a system with positive initial condition:

(1) Trajectories are bounded if and only if there exists an equilibrium with positive entries.

(2) If trajectories are bounded, then they approach an equilibrium set for $t \to \infty$. If moreover the equilibrium set consists of isolated points, then they converge to some equilibrium.

The following results concern the existence and uniqueness of equilibria.

Proposition 7. ([19,Theorems 4 and 5]) Under Assumption (B) the following holds,

(1) There exists an equilibrium with positive entries for arbitrary constant intakes if and only if for all $v \in V$ there is a path to $X$ such that all edges in the path have $\lim_{x_v\to \infty} H_e(x_v) = +\infty$.

(2) If there exists an equilibrium with positive entries, and all $v \in V$ connect to $X$, then the equilibrium is unique.

For the RCT network, for every vertex $v \in I$ there is a path from $v$ to $X$, therefore by Proposition 7 there is a unique equilibrium $x_{eq}$ and by Proposition 6 we will approach the equilibrium as $t \to \infty$. Under the stricter Assumption (C) this equilibrium can be calculated analytically using equation 3.1 with $h(x)$ being given by:

The equilibrium $x_{eq}$ can then be calculated by computing the inverse of each $h_i(x_i)$ function.

4.   Control of intakes

In this section, we focus on the special LIFE system under Assumption (C). Typically $f$ is fixed and $x$ cannot be controlled directly, which leaves the intake vector $\phi$ as a natural choice for control targets. We are interested in intakes $\phi$ that lead to an equilibrium. In this section the inequality $x > 0$, respectively $x\geq 0$, with $x\in \mathbb{R}^n$, is to be interpreted as $x_i > 0$, respectively $x_i\geq 0$, for all $i = 1, \ldots, n$.

Proposition 8. Consider system (2.3) satisfying Assumption (C), then the set $\Phi$ of intake vector $\phi$ giving rise to a positive equilibrium $x_{\phi} > 0$ is given by:

Proof. The dynamics of systems under Assumption (C) can be rewritten as (3.1). Thus the equilibrium of the system can be found by solving $J(f)h(x_{\phi}) + \phi = 0$.

The control action is then captured by the map:

However, to obtain admissible equilibria, we need to take into account the saturation effect of nonlinear kinetics such as Michaelis-Menten:

Proposition 9. Consider system (2.3) with Assumption (C) holding true and the function $h(x) = (h_i(x_i))_{i\in \{1, \ldots, n\}}$ in (3.1) with $h_i(x_i): \mathbb{R}_+ \to \mathbb{R}_+$ being strictly increasing and bounded by saturation values $H = (H_i)_{i\in \{1, \ldots, n\}}$,

Then for the system to tend to an equilibrium the intake vector $\phi$ must satisfy

Proof. Under Assumption (C) the system can be written as (3.1). From (3.1) and inequality (4.3), solving for $\phi$ we get (4.4).

We consider the following control problem:

Definition 4.1. For a given system (2.3) satisfying Assumption (C), and a given desired equilibrium $x_{eq}\in (\mathbb{R}_+)^n$, find the optimal intake vector $\phi$ that drives the system as close as possible to $x_{eq}$.

The solution is provided by the intake vector $\phi$ which minimizes the Euclidean distance

An alternative control problem is to minimize the distance of the kinetic vector $h$ instead of the metabolites:

Definition 4.2. For a given system (2.3) satisfying Assumption (C), and a given desired equilibrium $x_{eq}\in (\mathbb{R}_+)^n$, find the optimal intake vector $\phi$ that drives the system kinetic vector $h(x_{\phi})$ as close as possible to $h(x_{eq})$.

The solution is given by the intake vector $\phi$ which minimizes the Euclidean distance

Since $h(x_{eq}) = -J(f)^{-1}\phi$ is linear with respect to $\phi$, for the second problem we can use linear solvers to find the optimized $\phi$. Therefore, the second control problem can be solved much more efficiently. Notice that, in general, the two control problems are not equivalent, since the solution minimizing (4.5) may be different than that minimizing (4.6). However, we do expect the solution to the control problem of Definition 4.2 to provide an ansatz toward the solution to the control problem of Definition 4.2. Indeed, even if the level sets of the two functions (4.5) and (4.6) are different, they are both convex and centered at the same point.

Let us now focus on the RCT network under Assumption (C) and explore the map (4.2): $h(x)$ is a $6\times 1$ vector $h(x) = h_i(x_i)_{i\in \{1, \ldots, 6\}}$. We choose kinetics of Michaelis-Menten type with saturation value $H_i$ (^[17]), $h_i(x_i) = \frac{H_i x_i}{K_M+x_i}$, where $K_M$ is the Michaelis constant. Our intake vector $\phi$ is a $6\times 1$ vector with last three components vanishing. Figure 4 illustrated the bounds on the kinetic and the intakes.

The matrices $\phi, J(f), h$, and $H$ can be written in block form, then (4.4) becomes

So we have

We define $\tilde{\phi} = \phi_{e_1} + \phi_{e_2} + \phi_{e_3}$ as the total mass flows in the system. Then

Observing the structure of Figure 2 and that the total outflow of a vertex must equal the total inflow for an equilibrium state, we have

Having determined the bounds on $\phi$ for existence of an equilibrium, we explore the map (4.2) on the subset describe by the bounds.

Some parameters in the RCT network are chosen a priori, such as the fluxes $f$, the given functions $h(x)$, and the corresponding saturation values $H$. As a proof of concept, we randomly sample $f$ and the initial values for $x$ from the uniform distribution with range $(0, 1)$, randomly sample $H_i$ from the uniform distribution with range $(0, 10)$, and randomly sample the desired equilibrium $x_{eq}$ from uniform distribution $(0, 3)$. We use these randomly generated data to test the effectiveness of the optimization algorithm to drive the state to $x_{eq} = ((x_{eq})_i)_{i \in \{1, \ldots, 6\}}$. $x_{v_4}$ corresponds to the High-density lipoprotein (HDL), $x_{v_5}$ corresponds to the Very low-density lipoprotein (VLDL), and $x_{v_6}$ corresponds to the low-density lipoprotein (LDL). According to ^[13], a high ratio indicates a higher risk of heart attack. A healthy state is considered to have lower ratio of $\frac{HDL+LDL}{LDL}$. The second control problem (Definition 4.2) can be solved using the following optimization algorithm:

Algorithm 1. For assigned fluxes and kinetics:

Step 1: Calculate the Jacobian matrix $J$ in (3.1) and the matrix $-J(f)^{-1}$.

Step 2: Implement linear least-square method to find $\phi_{opti}$ minimizing (4.6) with inequality constraint $-J(f)^{-1}\phi \leq H$ and lower bound $0$.

Step 3: Calculate the cost and run simulation with optimized intakes $\phi_{opti}$ to verify numerically the stability of dynamics.

Notice that not all combinations of sampled parameters lead to equilibrium: Here we show an example leading with stability. To implement Algorithm 1, we use a linear least-square solver in MATLAB (2018b) for Step $2$, finding the optimized $\phi_{opti}$ by minimizing the cost $\frac{1}{2}||h(x_{\phi}) - h(x_{eq})||^2_2 = \frac{1}{2}||-J(f)^{-1}\phi - h(x_{eq})||^2_2$, which is half of the square of (4.6). The flux vector is given by:

and the initial value of metabolites is:

The kinetic $h$ functions for all vertices are given by:

while the saturation levels for $h$ are:

We randomly generate the equilibrium $x_{eq}$ to be matched:

with

The $h(x)_{opti}$ and $(x)_{opti}$ optimized by Algorithm 1 are:

while the optimized intake vector is $\phi_{opti} = \begin{pmatrix} \phi_{e_1}, & \phi_{e_2}, & \phi_{e_3} \end{pmatrix}^T = \begin{pmatrix} 1.73, & 1.24, & 0.24 \end{pmatrix}^T$. In the following, we check the conditions (4.7) and (4.8):

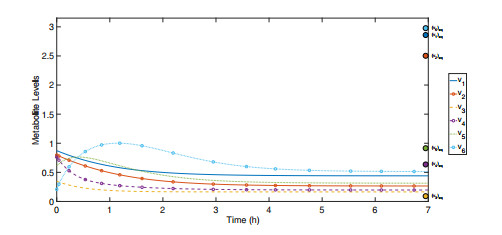
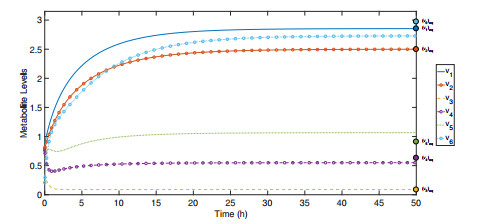
We run the simulation with optimized intakes $\phi_{opti}$ and keep the other parameters constant. Figures 4 and 5 show simulations for the not controlled case and the one with optimized intakes. Notice that well approximate the desired equilibrium.

5.   Metabolic networks with inhibitor and enhancer

In order to include inhibitors and enhancers we introduce a new Assumption (D):

where $H_v: \mathbb{R}^n\to \mathbb{R}_+$ is differentiable and strictly increasing while $H_v(0) = 0$, $K_u:\mathbb{R} \to [0, +\infty)$ is differentiable, monotonic, and $K_u(0) = 1$. Moreover, for enhancers $K_u$ is increasing while for inhibitors $K_u$ is decreasing.

Let us clarify the differences among the assumptions we discuss. Assumption (A) requires the function $H_e(x)$ to be defined for each edge, continuous, and dependent on the entire state $x$. Assumption (B) requires $H_e(x_v)$ to be defined for each edge, continuous, and dependent on the metabolite associated to the initial vertex of edge $e$. Assumption (C) requires $H_v(x_v)$ to be defined for the initial vertex of an edge, differentiable and strictly increasing, $H_v(0) = 0$, and dependent on the metabolite associated to the initial vertex of an edge. Therefore all edges with the same initial vertex will be associated to the same function $H_v(x_v)$. For Assumption (D) the function $H_v(x_v)$ is defined just as in Assumption (C), however entries of $S_{ve}(x)$ consist of a product $H_v(x_v)\cdot K_u(x_u)$. The factor $K_u(x_u)$ models the action of inhibitors or enhancers. This represents nonlocal action, because the inhibitor or enhancer is not necessarily nearby (in topological sense) the affected metabolites. Assumption (A) is the most general with Assumption (B) implying Assumption (A), and Assumption (C) implying (B), i.e., $C \implies B \implies A$. Assumption (D) also implies Assumption (A), but is comparable with (B), i.e., $D \implies A, D \nRightarrow B, B \nRightarrow D$.

To illustrate the effect of enhancers and inhibitors on dynamics under Assumption (D), an example is shown on the RCT network of Figure 2, but with the addition of a single enhancer. It is assumed that the metabolite $v_1$ will act as an enhancer for the edge $f_{e_{7}}$. When the dynamics of this network are written, the stoichiometric matrix $S: \mathbb{R} \to M_{6\times 10}$ where $S = (S_{1-3}|S_{4-10})$ is different from Section 3 only by the non-zero entries of the seventh column, i.e., $S_{4-10}$ is given by

5.1.   Equilibria under Assumption (A) and (B)

The previous research focused on finding necessary and sufficient conditions for equilibria of (2.3), as well as the uniqueness and stability of such solutions, under Assumption (A) or (B). We aim at extending the results to the case of Assumption (D) as well. The Propositions 1 and 2 work also for Assumption (A) and as such are still applicable when inhibitors/enhancers are added as in Assumption (D). Proposition 1 gives necessary structural conditions to obtain an equilibrium $x_{eq}$ for fixed flux vector $f$, specifically that any vertex with a directed path from an intake, also has a directed path to an excretion.

5.2.   Dynamics under Assumption (D)

Without further assumptions on the system, there are few conclusions about these types of equilibria. In Section 3, additional properties summarized in Assumptions (B) and (C) were needed to prove uniqueness and stability for this type of equilibrium (see Propositions 6 and 7). To investigate equilibria for Assumption (D), we consider system (2.2). For a single enhancer or inhibitor, we may write the dynamics as follows,

where $J_1$ is the Jacobian matrix removing the terms which are affected by inhibitors or enhancers, $h(x)$ is a column vector of size $n$ given by $h_i(x) = H_{v_i}(x_{v_i})$, $J_2$ is a matrix with nonzero entries only in the column affected by the enhancer or inhibitor, $k$ is a column vector of size $n$ representing inhibitors and enhancers given by $k_i(x) = K_{v_j}(x_{v_j}) \cdot H_{v_i}(x_{v_i})$ where $v_i$ is the node from which the edge begins and $v_j$ is the node which acts as an inhibitor or enhancer, and $\phi$ is a vector of size $n$ given by $\phi_i = f_{e(v_0, v_i)}$ if ($v_0, v_i) \in \tilde{E}$ and $\phi_i = 0$ otherwise. Note that multiple enhancers or inhibitors may require additional matrices $J_i$. To see the possible necessity of added $J_i$ matrices, consider two edges $e(v_i, v_j)$ and $e(v_i, v_k)$ of a network that are enhanced by $v_m$ and $v_n$ respectively. Since both edges begin at $v_i$ they would be in the same column of $J_2$, however enhancer $v_m$ is represented by $k_i(x) = K_{v_m}(x_{v_m}) \cdot H_{v_i}(x_{v_i})$, and enhancer $v_n$ is represented by $k_i(x) = K_{v_n}(x_{v_n}) \cdot H_{v_i}(x_{v_i})$, because of this an additional $J_3$ matrix and $k_2$ would be necessary.

Proposition 10. Consider system satisfying Assumption (D). For each vertex, if all of the outgoing edges from the vertex are affected by at most one enhancer or inhibitor, then the system can always be written as (5.2).

When all the edges leaving a vertex $v_i$ are affected by the same enhancer or inhibitor $v_m$, then $k_i(x) = K_{v_m}(x_{v_m}) \cdot H_{v_i}(x_{v_i})$, this allows the system to be written as (5.2).

Our main conjecture is the following.

Conjecture 1. For a metabolic network under Assumption (D) containing enhancers and inhibitors, the following holds.

● An equilibrium with positive entries for arbitrary intakes can exist only if for all $v \in V$ there is a path to $X$ such that all edges in the path have $\lim_{x_v\to \infty} H_e(x_v) = +\infty$.

Under Assumption (D) with enhancers but no inhibitors the following hold.

● There exists an equilibrium with positive entries for arbitrary constant intakes if and only if for all $v \in V$ there is a path to $X$ such that all edges in the path have $\lim_{x_v\to \infty} H_e(x_v) = +\infty$.

● If there exists an equilibrium with positive entries, and there is a path from all $v \in V$ to $X$, then the equilibrium is unique.

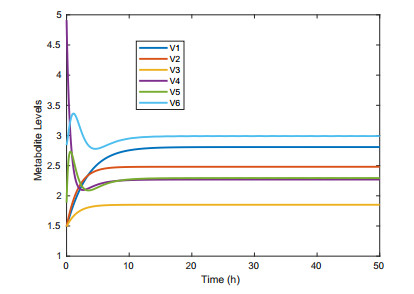
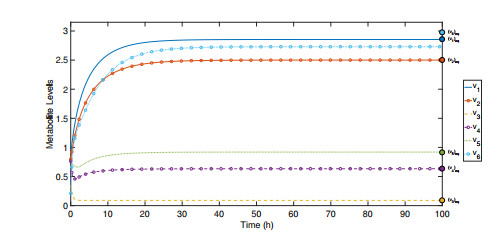
It is expected that under Assumption (D) there exists an equilibrium if several conditions are verified. Here it is shown that the Reverse Cholesterol Transport network with the single enhancer (indicated previously) has a unique equilibrium. In addition, simulations show that this equilibrium is stable.

5.3.   Unique equilibrium of the RCT network with a single enhancer

Consider the RCT network with enhancer, then the system can be written as (5.2) where $J_1(f)$, $J_2(f)$, $h(x)$, $k(x)$ and $\phi$ matrices are given by

We assume that the $H_{v_i}$ functions satisfy the additional condition that

Condition (5.3) is required so that we are able to satisfy equation (4.4).

In order for the system to be at equilibrium it must satisfy

which provides the following system of six equations,

Immediately notice that the first equation gives $-f_{v_0}H_{v_1}(x_{v_1}) = -\phi_1$. Since $H_{v_1}$ is invertible and $f_{e_4}$ and $f_{e_1}$ are constants, this gives $x_{v_1} = H^{-1}_{v_1}(\frac{f_{e_1}}{f_{e_4}})$. Once the equilibrium value of $x_{v_1}$ has been found, the equilibrium of $K_{v_1}(x_{v_1})$ is determined. Now let $f^*_{e_7} = f_{e_7} \times K_{v_1}(x_{v_1})$. Now we rewrite the system as $J(f)h(x)+ \phi$ with,

This system satisfies the assumptions of Proposition 7 and we conclude that the RCT network has a unique equilibrium.

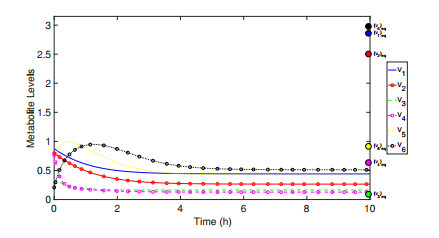
To show that the equilibrium solution for the RCT network is stable, simulations were performed with fixed randomized fluxes (sampled from a uniform distribution on interval [0, 1]). Using the values of the flows the equilibrium was calculated, and then compared with the metabolite levels reached in simulation. The calculated equilibrium was reached in each simulation, suggesting that the RCT network is asymptotically stable. Figure 6 shows the results of one such simulation.

6.   Drug discovery by control methods

Existence and uniqueness of equilibria for networks with enhancer and inhibitors (I-E), as explored in Section 5, is the basis for studying drug discovery. Usually a drug affects a flux as an enhancer or inhibitor, thus a new drug can be represented as a specific extended network and flux vector $f$, see Figure 7. If networks including the drug treatment effect satisfy the assumptions for uniqueness and stability of equilibria, then we can predict the asymptotic state of the metabolic network, which is the unique equilibrium $x_f$ corresponding to the flux vector $f$. In other words, one may reduce the drug discovery problem to an optimization one using the map $f\to x_{f}$ and studying those $f$ corresponding to potential drugs. More precisely we proceed as follows:

Step 1. Consider the extended networks as in Figure 7 and study conditions on uniqueness and stability of equilibria using the methods of previous sections. As shown in Section 5, Step 1 is not trivial. Indeed, the I-E dynamics are non local, which means that the molecule affecting the specific reaction is not necessarily close in the network topology (i.e., may belong to a far away component of the network). For a given network $G = (E, V)$, we consider the extended version $\tilde{G} = (\tilde{E}, \tilde{V})$ as in Figure 7. More precisely, we add a new vertex representing the drug molecule and being both an intake and excretion vertex (assuming the drug is administered and there is a known excretion mechanism). Moreover, we add an edge from the drug molecule to the affected flux edge $e$. We denote by $f_{e, \pm}$ the flux vector corresponding to the extended network, where $\pm$ indicates the enhancer (+) or inhibitor (-) expected effect. Notice that the source flux of the drug molecule depends on the scheduled treatment, which may be given as pills, injections or others. For drug discovery purposes, we use an average flux, while for simulations we may use a time-varying one.

Step 2. Study the map $f_{e, \pm}\to x_{f_{e, \pm}}$ to minimize $\|\bar{x}- x_{f_{e, \pm}}\|$, where $\bar{x}$ is a desired "healthy" state. Step 1 ensures that the map $f_{e, \pm}\to x_{f_{e, \pm}}$ is well defined. Using the method of previous section, we can also compute explicitly this map under suitable assumptions. The set of states $R(x_{f_{e, \pm}})$ that can be reached using the admissible controls $f_{e, \pm}$ is called the reachable set, see ^[4]. In practice, we do not expect a unique desired state to be defined, but rather a set of conditions which determine a desired or target set ${\mathcal X}$ of metabolic states deemed healthy. A successful treatment prescribes the fluxes $f_{e, \pm}$ which will drive the patient's current state $x$ to some state $\bar{x}{\mathcal \in \mathcal X}$. If the reachable set and desired states are disjoint, i.e., $R(x_{f_{e, \pm}}) \cap {\mathcal X} = 0$, then we look for the $x_{f_{e, \pm}}$ realizing the minimum distance from ${\mathcal X}$.

Step 3. Introduce dynamic optimization criteria on the trajectory to $x_{f_{e, \pm}}$ to find the best $f_{e, \pm}$. Consider the problem to minimize $\int_0^T L(t, x) dt$ where $L$ measures the toxicity of the drug, see ^[6,7]. In this case the dynamic of the drug is very important. It also becomes important to take the dosing regimen into consideration, which means using a time varying flux for the drug intake.

In the remainder of this section we give more details on 1-2, while 3 is saved for future work. Let us give an explicit example of our approach:

Example 6.1. Figure 7 shows the RCT network with an added vertex $v_7$ which represents the drug. With the addition of the non-local enhancer or inhibitor the stoichiometric matrix of the RCT needs an additional row and several additional columns, and the flux vector $f$ has the additional components $f_{(v_0, v_7)}$, $f_{(v_7, v_{n+1})}$. The new $S(x)$ matrix is a concatenation given by $S_{1-3}, S_{4-10}$, and $S_{10-12}$, is shown below,

where $k_{v_{7}}: \mathbb{R} \longrightarrow [0, +\infty)$ is differentiable, monotonic and $k_{v_{7}}(0) = 1$. For the enhancer the function $k_{v_{7}}(x_{v_7}) = 1 + \frac{x_{v_7}}{x_{v_7}+1}$ was used and for the inhibitor $k_{v_{7}}(x_{v_7}) = 1 - \frac{x_{v_7}}{x_{v_7}+1}$. The addition of the drug allows a control on the system based on the amount of drug used. It is assumed that the drug acts similarly to an enhancer in that the mass of the drug will not be added to the network, but the drug will facilitate the flow through the network by inhibiting or enhancing individual edges. Whether to use an inhibitor or an enhancer drug, as well as how much drug to use depends on the initial conditions of the network.

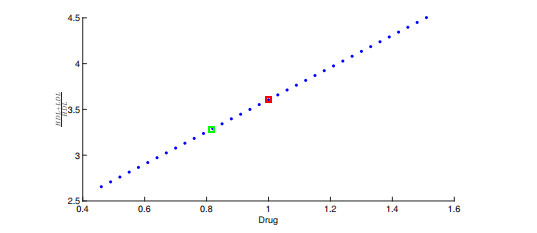
For cholesterol, the healthy state depends mostly on the ratio between total cholesterol and HDL cholesterol. The range of what is considered a healthy ratio depend on factors including age and gender, but in general a lower ratio of total cholesterol to HDL is preferred. In the case of the RCT network the healthy state $x_{f_{e, \pm}}$ depends on the value of $v_4$ (representing HDL) and $v_6$ (representing LDL), more precisely the ratio $\frac{v_4+v_6}{v_4}$. We examine whether an inhibitor or enhancer better lowers this ratio. To do this a set of fluxes were chosen from a uniform distribution so that each flux $f_i \in [0, 1]$. The fluxes $f_{11}$ (corresponding to $e_{11}$) and $f_{12}$ (corresponding to $e_{12}$) directly correspond to the drug and are treated separately, with $f_{12}$ being fixed at 1, and $f_{11}$ being the control variable. The result is rather intuitive, when the edge between $v_4$ and $v_5$ is enhanced the value of $v_4$ is lowered and the ratio increases, and when the edge is inhibited the value of $v_4$ increases and the ratio diminishes as seen in Figure 8. From the result it is clear that an inhibitor is the preferred type of drug for this example.

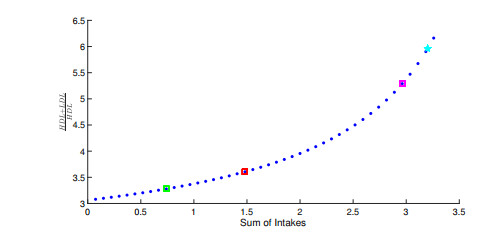
As explored in Section 4 the change in intakes also affects the state $x_{f_{e, \pm}}$. For comparison we also explored the effect of the intakes on the ratio $\frac{v_4+v_6}{v_4}$. Even when the control of intake is possible, large changes may not be realistic. Figure 9 shows how the ratio changes depending on the sum of the intake values. Comparing the control of drug to the control of intakes (see green boxes) we see that the same ratio is obtained by cutting in half intakes o using a drug that provides inhibition of the flow $e_7$ to $0.8$ of its original value.

We show another example, where each metabolite has a desired target.

Example 6.2. Here we use the same initial conditions and target state from the example in Section 4, for a reminder Figure 4 shows an initial simulation with no control and highlights the desired equilibrium. Next, simulations are performed to obtain the desired equilibrium using the added drug from $v_7$ as a control. Two different $k_{v_{7}}$ functions were used, one representing an enhancer drug and the other an inhibitor drug. As in the previous example, the enhancer function $k_{v_{7}}(x_{v_7}) = 1 + \frac{x_{v_7}}{x_{v_7}+1}$ and inhibitor function $k_{v_{7}}(x_{v_7}) = 1 - \frac{x_{v_7}}{x_{v_7}+1}$ were used.

In the simulations it is assumed that the value of $x_{v_7}$ can be easily controlled and kept at a constant value, this would correspond to a dosing regimen having constant intake of drug. Simulations were performed with both enhancers and inhibitors to find the best possible value of $x_{v_7}$ for both types of drug. When only drug control was used it was found that using an inhibitor did not lower the cost between the optimized equilibrium and the desired equilibrium. Using an enhancer function the greater the value of $x_{v_7}$, the lower the cost. The upper bound of $x_{v_7} = 1$ was chosen, which corresponds to enhancement of the edge $e_7$ to 1.5 times its usual value and reduces the total cost to 4.1782. The results of this optimization are shown in Figure 10.

The control of the drug in this simulation has several limitations. For instance, only a single edge was targeted, whereas in pharmacology it is likely that many different targets may be considered and tested. Combining both methods, we control both the intakes and add a drug to act on $e_7$. Using optimized intakes, it was found that the inhibitor drug lowered the total cost between optimized equilibrium and the desired equilibrium. The drugs' optimal value was $x_{v_7} = 0.1765$, which corresponds to inhibition of the edge $e_7$ to 0.85 times its usual value. The results are shown in Figure 11.

Three methods of control are performed; control using intakes (Section 4), control using drug, and finally control using both intakes and drug. The results of all three methods are summarized in Table 1. Controlling intakes rather than adding drug produced better results, although drug targeting of additional edges may further improve the drug results.

7.   Conclusion

LIFE methodology was constructed to provide a new approach to modeling metabolic networks. Previously, in ^[22] the authors gave results which combined portions of several different theories and re-purposed them to shed light on simulating metabolic networks. The focus was on simple LIFE systems.

The intakes of a system are a reasonable target for control, and bio-molecules acting as inhibitors and enhancers are important structure which contributes to the stability of natural networks and often represent drug action. This work expanded the exploration of LIFE by investigating control problems: Controlling the intakes and controlling the inhibitor or enhancers of a network. Moreover, control methods are applied to a toy but significant example network of human metabolism called reverse cholesterol transport. To control the ratio of total cholesterol over HDL, the action of a single inhibitor was equivalent to a dramatic reduction of the intakes (cut by half). Our study on this network lead to conjectures about general networks. Future work will include addressing these conjectures to expand on LIFE methodology.

Acknowledgments

The authors acknowledge the support of the Joseph and Loretta Lopez Chair Professorship endowment, Sanofi via the project "Optimization and Simulation Approaches or Systems Pharmacology in the Pharmaceutical Industry" and the NSF Grant # 1107444 "KI-Net Kinetic description of emerging challenges in multiscale problems of natural sciences".

Conflict of interest

The authors declare no conflict of interest.