Curve construction based on quartic Bernstein-like basis

1.   Introduction

The construction of basis functions has always been an important topic in CAGD, especially the quadratic and cubic basis functions have a wide range of applications. In ^[1], Farin gives a kind of piecewise cubic B-spline curves, which are flexible and used conveniently. However, the shape of given curves are fixed to the related control points. For cubic rational B-spline curves, which possess a weight factor can be used to adjust shape of curves, however, improper use of weighting factors can lead to serious parameterization and even destroy the subsequent curve structure^[2].

In order to improve the shape and the extent of adjustment of the curve, plenty of methods are generated. Where the most easily method is to add shape parameters to classical cubic Bézier and B-spline curves, the partly can be seen ^[3,4]. In recent years, researchers proposed some Bernstein basis possessing tension parameters. Hu et al. ^[5] constructed the developable Bézier-like surfaces using a new kind of cubic Bernstein-like basis with three local shape parameters. In ^[6], Cravero presented a $C^3$ interpolation function, the shape of the related curves can be adjusted by tension parameters. In ^[14], Pelosi et al. proposed the quaternion representation for spatial PH cubics and gave results concerning existence of spatial PH cubic interpolants to given $G^1$ Hermite data. In ^[17], Ait-Haddou et al. proved that the best constrained degree-reduced approximation is qual to the weighted least squares fit of the Bezier coefficients with factored Hahn weights and introduced parameters coming from the Jacobi norm. In ^[7], Wang constructed a new basis possessing denominator shape parameters, which is extended to B-spline curve and triangular domain. In ^[15], González constructed $C^2$ algebraic-trigonometric pythagorean splines with different shape parameters. In order not to increase the computational complexity, some scholars have been studying the method of incorporating shape parameters without increasing the orders in n-order Bernstein basis. In ^[8], Liu gave a set of n-order Bernstein basis with multiple shape parameters in four cases. They have the same order as n-order Bernstein basis. In ^[9], Xiang improved this result. In the case of odd and even, respectively, a homogenous expansion polynomial with multiple shape parameters of n-order Bernstein basis is given. In ^[3], Qin et al. also gave the same expansion scheme of $n$-order Bernstein basis with multiple parameters. In ^[12], Hu et al. presented a novel shape-adjustable generalized Bézier curve with multiple shape parameters. And then, they extended the basis to rectangular domain^[13]. Generally speaking, the extension method which does not increase degree to introduce parameters in Bernstein basis of degree $n$ has faster calculation efficiency, while the extension method which introduces shape parameters by increasing degree of Bernstein basis has stronger ability of adjusting curve. Both of these methods have advantages, so the variable orders as shape parameters is a good choice. In ^[10], Costantini constructed a set of variable order basis functions in space $\{ 1, t, {(1 - t)^m}, {t^n}\}$, and he studied its B-spline form. Subsequently, Costantini ^[11] extended this space to the space ${\rm{\{ }}1, t, {t^2}, \cdots, {t^{n - 2}}, {(1 - t)^p}, {t^q}\}$. In^[16], Zhu et al. constructed a quasi Bernstein basis with two shape parameters in space ${\rm{\{ }}1, 3{t^2} - 2{t^3}, {(1 - t)^\alpha }, {t^\beta }\}$.

The purpose of this paper is to propose a new quartic Bernstein-like basis possessing two exponential shape parameters which serve as a tension parameters. Based on the new basis, a new cubic B-spline-like basis possessing two global and three local shape parameters is presented. And the related cubic B-spline-like curves have ${C^2} \cap F{C^{2l + 3}}$ continuity at each points and include the classical cubic uniform curves as a special case. The rest of this paper are organized as follows: Section 2 gives the definition and properties of the new quartic Bernstein-like basis possessing two exponential shape parameters. And the definition and the connecting conditions of the related curve are shown. Section 3 proposes the cubic B-spline-like basis. And the related properties of connecting, interpolation and locally adjustment of the cubic B-spline-like curves are discussed. The conclusion can be seen in Section 4.

2.   Construction of quartic Bézier-like curves

2.1.   Quartic Bernstein-like basis functions

First, we give the definition of quartic Bernstein-like basis.

Definition 1. For any $t \in [0, 1]$, let $\alpha, \beta \in [2, + \infty)$, we call the following five functions

as quartic Bernstein-like basis with two exponential shape parameters $\alpha$ and $\beta$.

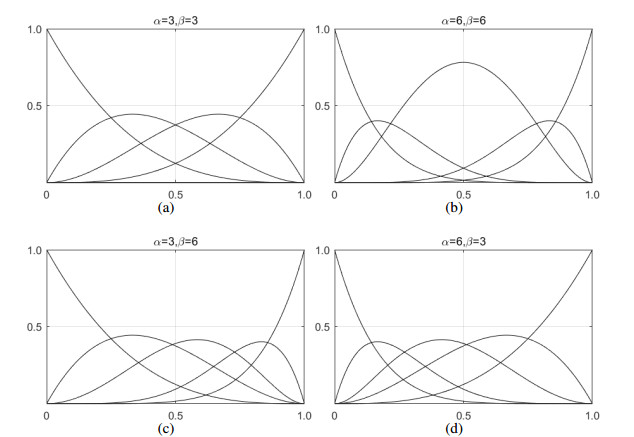
Remark 1. When $\alpha = \beta = 4$, the qqr-basis will degenerate to the classical quartic Bernstein basis.

For the convenience of discussion, we will call the quartic Bernstein-like basis as qqr-basis. Also, we denote the qqr-basis functions as ${A_i}(t; \alpha, \beta)(i = 0, 1, \cdots, 4)$ or ${A_i}(t; \alpha)(i = 0, 1)$ and ${A_i}(t; \beta)(i = 3, 4)$. Next, we will give the following lemma, which is used for the analysis of properties of the basis.

Lemma 1. For any $t \in [0, 1], \lambda \in [2, + \infty)$, the expression $F(t; \lambda) = 1 - 3{t^2} + 2{t^3} - \lambda t{(1 - t)^{\lambda - 1}} - {(1 - t)^\lambda }$ has a globally minimum value of $0$.

Proof. We can easily verify that $F(0, \lambda) = 0, F(1, \lambda) = 0, F(t, 2)$, where $t \in [0, 1], \lambda \in [2, + \infty)$. For any fixed $t \in (0, 1)$, we have

Actually, $f'(t) = \frac{{ - t + 2\ln (1 - t)}}{{{{(1 - t)}^2}}} < 0$ and $g(0) = 0$. Thus, for $t \in (0, 1), t \in [2, + \infty)$, we have

Therefore, for any fixed $t \in (0, 1)$, $F(t, \lambda)$ increases with the increases of $\lambda$. From this, for arbitrary fixed $t \in (0, 1)$, $F(t, \lambda)$ has a minimum value of $F(t, 2)$. Therefore, this lemma holds.

From the above definition of qqr-basis given in (2.1), we have some important properties as follows.

Theorem 1. The qqr-basis given in (2.1) possesses the following properties:

(1) Non-negativity: ${A_i}(t; \alpha, \beta)(i = 0, 1, \cdots, 4) \ge 0$.

(2) Partition of unity: $\sum\limits_{i = 0}^4 {{A_i}(t; \alpha, \beta) = 1}$.

(3) Symmetry: ${A_i}(t; \alpha, \beta) = {A_{4 - i}}(t; \beta, \alpha)(i = 0, 1)$.

(4) Linear independence: For any $(\alpha, \beta) \in [2, + \infty)$ and $t \in [0, 1]$, the qqr-basis ${A_i}(t; \alpha, \beta)(i = 0, 1, \cdots, 4)$ are linear independent.

(5) Endpoint properties: For any $(\alpha, \beta) \in [2, + \infty)$, we have the following endpoint properties:

Also, for any $(\alpha, \beta) \in (2, + \infty)$, we have

Proof. We will proof (1) and (4). The other cases can be easily verified.

(1) We can easily proof that ${A_i}(t; \alpha, \beta) \ge 0, i = 0, 1, 3, 4$. Then, we only consider the basis ${A_2}(t; \alpha, \beta)$. For $\alpha, \beta \in [2, + \infty)$ and $t \in [0, 1]$, from the lemma 1, we have

(4) For $\alpha, \beta \in [2, + \infty), {\lambda _i} \in R(i = 0, 1, 2, 3, 4)$, we have the following linearly combination

Next, we will differentiate on the above linear combination, we can obtain

For $t = 0$, the following linear equations can be obtained from (2.2), (2.3) and (2.4):

Therefore, it can conclude ${\lambda _0} = {\lambda _1} = {\lambda _2} = 0$. For $t = 1$, from (2.2) and (2.3), we can get ${\lambda _3} = {\lambda _4} = 0$, these imply the theorem.

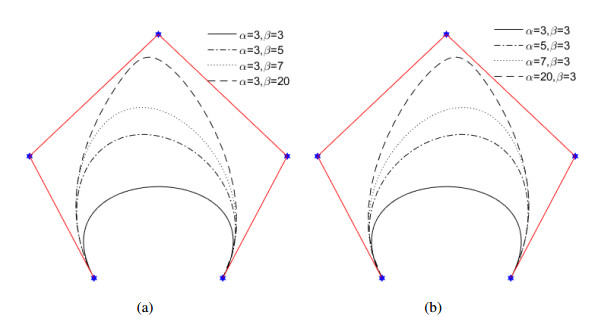
Figure 1 shows the qqr-basis with different shape parameters.

2.2.   Quartic Bézier-like curves

Definition 2. Given control points ${P_i}(i = 0, 1, \cdots, 4)$ in $R^2$ or $R^3$, for any $t \in [0, 1], \alpha, \beta \in [2, + \infty)$, we call the expresiion

as the quartic Bézier-like curves with two exponential shape parameters $\alpha$ and $\beta$, where ${A_i}(t; \alpha, \beta)$ are qqr-basis given in (2.1). For convenience, we also denote the quartic Bézier-like curves as the qqr-curves.

Theorem 2. The qqr-curves given in (2.5) have some important properties as follows.

(1)Endpoint property:

(2)Symmetry: The control points and define a same qqr-curve, i.e.

(3)Geometric invariance: The definition given in (2.5) will meet the folowing rules:

where ${Q^*}$ is an any vector in $R^2$ or $R^3$, and ${M^*}$ is an any $n \times n$ matrix, $n = 2$ or $3$.

(4)Convex hull property: The segments of the qqr-curves must lie inside the control polygon spanned by ${P_0}, {P_1}, {P_2}, {P_3}, {P_4}$.

2.3.   Shape adjustment of qqr-curves

For any $t \in [0, \pi /2]$, we rewrite the expression (2.5) as follows:

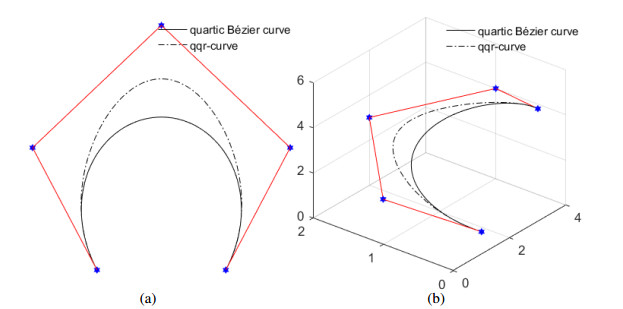
Then, we can easily deduce that the shape parameters $\alpha$ and $\beta$ can influence four edge $\overline {{P_0}{P_2}}, \overline {{P_1}{P_2}}$ and $\overline {{P_2}{P_3}}, \overline {{P_2}{P_4}}$, respectively. We also can predict the behavior of the qqr-curves as follows: The local shape of qqr-curves given in (2.10) can be adjusted by modifing parameters $\alpha$ and $\beta$. With the increase of $\alpha$, the curves will tend to the edge $\overline {{P_0}{P_2}}$ and $\overline {{P_1}{P_2}}$; In contrary, the curves will tend to the opposite direction of edge $\overline {{P_0}{P_2}}$ and $\overline {{P_1}{P_2}}$. The parameter $\beta$ has similar adjustment effect as $\alpha$ concerning edge $\overline {{P_3}{P_2}}$ and $\overline {{P_4}{P_2}}$ as parameter $\alpha$. However, the curves will tend to the control points $P_2$ when the shape parameters $\alpha$ and $\beta$ increase at the same time. Thus, we can conclude that the shape parameters $\alpha$ and $\beta$ serve as tension parameters. In Figure 2, we give some examples about the adjustment effect of parameters on the qqr-curves given in (2.5). Also, the qqr curves have two shape parameters, which can be used to adjust shape of qqr-curves, thus the qqr-curves shows butter approximation ability than classical quartic Bézier curves. Figure 3 illustrates the approximation comparison between qqr-curves and quartic Bézier curves. And the parameters on qqr-curves are set $\alpha = \beta = 5$.

2.4.   Connecting of the qqr-curves

It is not difficult to find that a single qqr-curves cannot express too complicated geometric design. Thus, the importance of connecting of proposed curve is obvious. Let two qqr-curves be respectively defined as follows:

and

Obviously, if the condition ${P_4} = {Q_0}$ holds, then the two curve segments (2.11) and (2.12) will form a $C^0$ curve.

But if we want to obtain a more smooth curve, more constrain conditions are needed. For convenience, we rewrite the expression (2.11) and (2.12) as follows:

where ${u_1} < {u_2} < {u_3}, {h_i} = {u_{i + 1}} - {u_i}, i = 1, 2.$

Theorem 3. For ${\alpha _i}, {\beta _i} \in [2, + \infty), i = 1, 2$, if the target curve $R(u)$ satisfies the following condition:

then, we call $R(u)$ is a $C^1$ continuous curve. And if the target curve $R(u)$ satisfy the condition (2.14) and (2.15) simultaneously, we will call $R(u)$ is a $C^2$ continuous curve.

Proof. According to the formula (2.13), we have

Through simple calculations, we can easily conclude this Theorem holds.

It was points out in ^[18,19] that Frent continuity(FC) is a reasonable smoothness property for practical applications. From the end-point properties (Theorem 2.(1)) of the qqr-curves, we can conclude the following Theorem.

Theorem 4. For ${\alpha _i}, {\beta _i} \in [l + 3, + \infty)$, if the formula (2.14) and (2.15) hold simultaneously, the target curve $R(u)$ is a ${C^2} \cap F{C^{2l + 3}}$ continuous curve at the knot $u_2$, where $i = 1, 2$ and $l \in {Z^ + }$.

Proof. For $k = 3, 4, \cdots, 2l + 3$, it follows that

From (2.1), we have

And from (2.16) and (2.17), we have

Thus, we can conclude

By directly computing, it follows that

These imply the theorem.

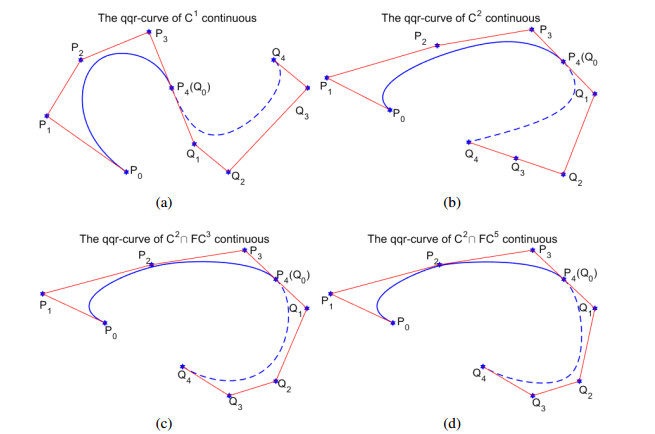
Figure 4. gives some examples of continuous curves with different conditions at the knot $u_2$. For $C^1$ continuous curve, the related parametric values are set ${\alpha _1} = 10, {\beta _1} = 3, {\alpha _2} = 3, \beta = 5$. For $C^2$ continuous curve, the related parametric values are set ${\alpha _1} = 10, {\beta _1} = 2, {\alpha _2} = 2, \beta = 6$. For ${C^2} \cap F{C^3}$ continuous curve, the related parametric values are set ${\alpha _1} = 10, {\beta _1} = 4, {\alpha _2} = 4, \beta = 5.5$. For ${C^2} \cap F{C^5}$ continuous curve, the related parametric values are set ${\alpha _1} = 10, {\beta _1} = 5.5, {\alpha _2} = 5.5, \beta = 5.5$.

3.   Cubic B-spline-like curve

3.1.   Cubic B-spline-like basis

In this subsection, based on the proposed qqr-basis given in (2.1), we will construct a set of cubic B-spline-like basis.

Given a any set of knots ${u_0} < {u_1} < \cdots < {u_{n + 4}}$, we refer to $U = ({u_0}, {u_1}, \cdots, {u_{n + 4}})$ as a knot vector. Let ${h_i} = {u_{i + 1}} - {u_i}, t \in [0, 1]$, for any $i \in {Z^ + }, \alpha, \beta \in [2, + \infty), {x_i}, {y_i}, {z_i} \in R$, we have

where ${A_j}(t; \alpha, \beta)(j = 0, 1, \cdots, 4)$ are the qqr-basis functions given in (2.1).

Definition 3. Given a knot vector $U = ({u_0}, {u_1}, \cdots, {u_{n + 4}})$, let ${t_j}(u) = (u - {u_j})/{h_j}$, where $j = 0, 1, \cdots, n + 3$, the related cubic B-spline-like basis with two global shape parameters $\alpha, \beta$ and three local shape parameters ${x_i}, {y_i}, {z_i}$ are defined as follows

where $i = 0, 1, \cdots, n$.

For convenience, we redefine the cubic B-spline-like basis as qqr B-spline basis. We will also call ${B_i}(u)$ as a uniform basis when given a set of equidistant knots, and the related knot vector $U$ is called as a uniform knot vector. Similarly, for the case of non-equidistant knots, ${B_i}(u)$ and $U$ are called as non-uniform basis and knot vector, respectively.

Remark 2. When the global shape parameters are set $\alpha = \beta = 4$ and all ${x_i}, {y_i}, {z_i}$ satisfy the following rules, then the qqr B-spline basis will degenerate to cubic non-uniform B-spline basis.

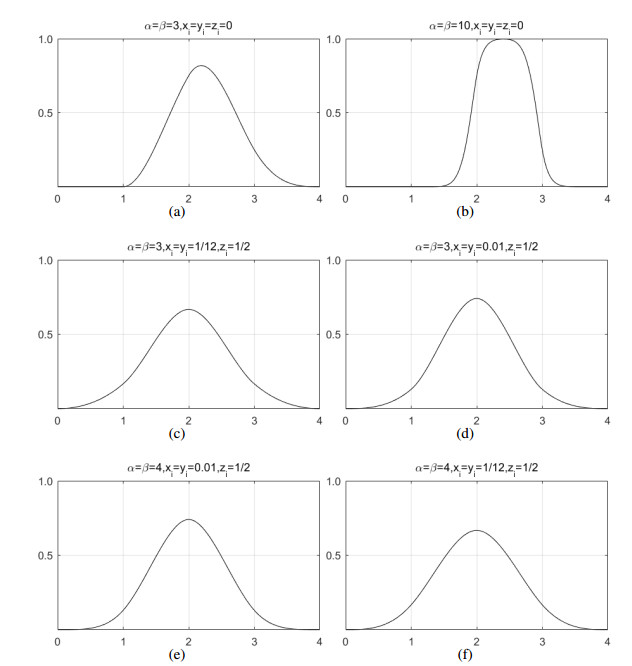
Figure 5. shows the qqr B-spline basis with different global and local shape parameters.

3.2.   Properties of qqr B-spline basis

Theorem 5. For any $u \in [{u_3}, {u_{n + 1}}]$, the qqr B-spline basis functions satisfy the following rule:

Proof. For any $u \in [{u_i}, {u_{i + 1}}), i = 3, 4, \cdots, n$, we have ${B_j}(u) = 0, j \ne i - 3, i - 2, i - 1, i$. Since

It follows that

These imply the theorem.

Theorem 6. For any $\alpha, \beta \in [2, + \infty)$ and ${u_i} < u < {u_{i + 4}}$, if ${x_i}, {y_i}, {z_i}$ satisfy the following rules, then we have ${B_i}(u) > 0$.

Proof. We can easily find that it is direct application of (3.1).

Theorem 7. For any $i \in {Z^ + }, \alpha, \beta \in (2, + \infty)$, if ${x_i}, {y_i}, {z_i}$ satisfy the following form:

then, the system $\{ {B_0}(u), {B_1}(u), \cdots, {B_n}(u)\}$ is linear independent on $[{u_3}, {u_{n + 1}}]$.

Proof. For any ${a_i} \in R(i = 0, 1, \cdots, n), u \in [{u_3}, {u_{n + 1}}]$, we let

For $\alpha, \beta \in (2, + \infty)$, by directly computing, we have

where $i = 3, 4, \cdots, n + 1$. Thus, the linear equations with respect to ${a_{i - 3}}, {a_{i - 2}}, {a_{i - 1}}$ are defined as follows:

Thus, we can easily get the coefficient matrix from the above linear equations. By directly computing, we have ${\upsilon _{i - 1}}[2{\mu _{i - 1}}{y_{i - 1}} + {\upsilon _{i -1}}(1 -{z_{i -2}})] + {\rho _{i - 2}} + {\mu _{i - 1}}({\mu _{i - 1}}{z_{i - 1}} + 2{\upsilon _{i - 1}}{x_{i - 1}}) = 1$. Therefore, the coefficient matrix can be rewrite as follows:

From the formula (3.4), we can get $|{D_i}| \ne 0$. Thus, we have ${a_{i - 3}} = {a_{i - 2}} = {a_{i - 1}} = 0(i = 3, 4, \cdots, n + 1)$. These imply the theorem.

Theorem 8. For any $\alpha = \beta \in (2, + \infty)$, the qqr B-spline basis $B_i(u)$ is $C^2$ continuity.

Proof. For any $\alpha = \beta \in (2, + \infty)$, from Theorem 1(5), we have

By directly computing, it follows that

Moreover, we have

These imply the theorem.

So far, we have been discussing the situation of a single knot, and the conclusion is relatively simple. However, it is relatively important for the case where the knots multiplicity $\lambda \le 4$. Thus, for the case of multiple knots, from Definition 3, we can redefine it as follows:

where ${u_i} = {u_{i + 1}}$ is a double knot.

We give the following theorem, useful for the geometric discussion of the case of multiple knots.

Theorem 9. For any fixed $u$, we suppose that the qqr B-spline basis has a $\lambda$ multiplicity knot, then the continuity of the qqr B-spline basis at point $u$ is reduced from ${C^{j - 1}}$ to ${C^{j - \lambda }}$, where $\lambda = 2, 3, j = 2$, for $\alpha = \beta = 2$ and $\lambda = 2, 3, 4, j = 3$, for $\alpha = \beta \in (2 + \infty)$. In addition, the support interval of the qqr B-spline basis is reduced from 4 segments to $5 - \lambda$ segments.

Proof. That is a direct application of (3.1) and the related expression shown in the previous sections.

3.3.   Definition and properties of cubic B-spline-like curves

Definition 4. Given control points ${P_i}(i = 0, 1, \cdots, n) \in {R^2}or{R^3}$ and a knot vector $U = ({u_0}, {u_1}, \cdots, {u_{n + 4}})$, then for $n \ge 3, u \in [{u_3}, {u_{n + 1}}]$, we call

as a cubic B-spline-like curve with two global shape parameters $\alpha, \beta \in [2, + \infty)$ and three local shape parameters ${x_i}, {y_i}, {z_i}$, where ${B_i}(u)$ is the qqr B-spline basis given in (3.1).

For convenience, we redefine the cubic B-spline-like curve as qqr B-spline curve. Moreover, for $u \in [{u_i}, {u_{i + 1}}], 3 \le i \le n$, the qqr B-spline curve segments can be defined as follows:

Theorem 10. The qqr B-spline curves have the following properties:

(1)When the qqr B-spline basis satisfies the conditions of Remark 2, then the qqr B-spline curve will degenerate to cubic B-spline curve.

(2)For $u \in [{u_i}, {u_{i + 1}}]$, if the Theorem 5 and 6 hold simultaneously, the qqr B-spline curves will lie in the convex hull of the control points ${P_{i - 3}}, {P_{i - 2}}, {P_{i - 1}}, {P_i}$.

(3)Given a non-uniform knots vector, if ${u_i}$ is a vector which has multiplicity $\lambda$, then the qqr B-spline curves are ${C^{j - \lambda }}$ continuous at $u_i$, where $\lambda = 1, 2, 3, j = 2$, for $\alpha = \beta = 2$, and $\lambda = 1, 2, \cdots, 4,$ for $\alpha = \beta \in (2, + \infty)$. Also, for $i = 3, 4, \cdots, n + 1$, if $u_i$ is a single knot, we can get

Proof. We can conclude that the Theorem holds from the result of Theorem 8 and 9. These imply the Theorem.

3.4.   Curve segment of the Bézier form

Based on the qqr B-spline curves, we give the curve segment of the Bézier form, which is useful understanding of role of the shape parameters.

For convenience, we let

where $T_i$ is adjustable interpolation points. Thus, we can rewrite the qqr B-spline segments given in (3.7) as

From the above preparation, we have the following discussion.

We give two knots $u_i$ and ${u_{i + 1}}({u_i} < {u_{i + 1}})$, where $u_i$ is a quadruple point when $i = 3$ and ${u_{i + 1}}$ is a quadruple point when $i = n$, thus, we can get ${h_{i - 2}} = {h_{i - 1}} = {h_{i + 1}} = {h_{i + 2}}$. Also, let ${x_{i - 1}} = 0, {y_i} = 0, {z_{i - 2}} = 0, {z_i} = 1$, for $u \in [{u_i}, {u_{i + 1}}]$, we can get the following basis functions:

Remark 3. Within the framework of qqr B-spline segments given in (3.7), the basis functions given in (3.9) degenerate to the classical cubic Bernstein basis when the global parameters are set $\alpha = \beta = 4$ and the local parameters are set ${x_i} = {y_{i - 1}} = 1/4, {z_{i - 1}} = 1/2$. Thus, the related curves are the classical cubic Bézier curves.

Theorem 11. The basis functions given in (3.9) have the following properties:

(1)For any $u \in [{u_i}, {u_{i + 1}}], \sum\limits_{j = i - 3}^i {{B_j}(u) = 1}$.

(2)For any $u \in [{u_i}, {u_{i + 1}}], {B_j}(u) > 0(j = i - 3, i - 2, \cdots, i)$ when $0 \le {x_i}, {y_{i - 1}}, {c_{i - 1}} \le 1$.

(3)Together with (3.7) and (3.9), we can easily find the following interesting phenomenon. With the decrease of the parameters $x_i$ and $y_{i-1}$, the related curve will moves to the edge $\overline {{P_{i - 2}}{P_{i - 1}}}$ of the control polygon. With the decrease of the parameters $z_{i-1}$, the curve will moves to the point $P_{i-2}$, on the contrary, the curve will moves to the point $P_{i-1}$.

(4)Together with (3.7) and (3.9), we have

Proof. The theorem can be verified from previous discussion.

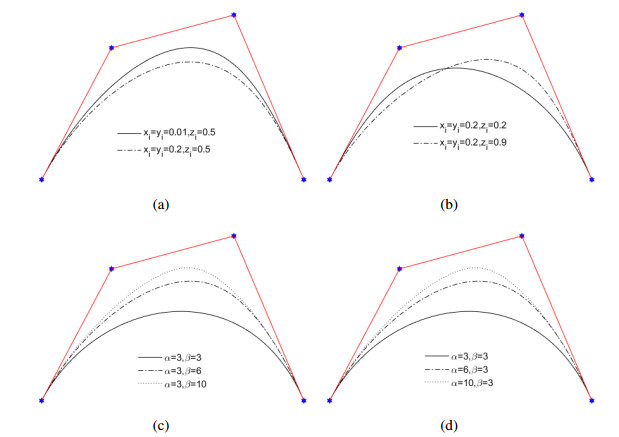
Figure 6. gives some examples of the Bézier form curves of qqr B-spline curves. The first row shows the influence of local shape parameters on curves, where the global shape parameters are fixed, and we set all $\alpha = \beta = 4$. The second row shows the influence of global shape parameters on curves, where the local shape parameters are fixed, and we set all ${x_i} = {y_i} = 0.2, {z_i} = 0.5$.

3.5.   Curves of ${C^2} \cap F{C^{2l + 3}}$ continuity

First, we consider the curve of $C^2$ continuity. Then the following Theorem can be concluded.

Theorem 12. For any $\alpha = \beta \in (2, + \infty)$, the qqr B-spline curves are $C^2$ continuity.

Proof. From Theorem. 8 and 10(3), it is easily conclude that this Theorem holds.

Next, we consider the curve of ${C^2} \cap F{C^{2l + 3}}$, we have the following theorem.

Theorem 13. Let ${x_{i - 1}} = {y_{i - 1}} = 0, {z_{i - 2}} \ne 1$ and ${z_{i - 1}} \ne 0$, for $\alpha = \beta \in [l + 3, + \infty)$, the qqr B-spline curves $Q(u)$ are ${C^2} \cap F{C^{2l + 3}}$ continuous at point $u_i$, where $i = 3, 4, \cdots, n$ and $l \in {Z^ + }$.

Proof. From (3.11) and (3.12), we have

For $j = 3, 4, \cdots, 2l + 3$, by directly computing, we have

From the Theorem 1(5), we can get

Therefore, we have

From (3.13) and (3.14), we have

These imply the theorem.

Let $\alpha = \beta$, for ${C^2} \cap F{C^{2l + 3}}(k \in {Z^ + })$ continuity, with regard to the curve segments given in (3.7), it follows that

By directly computing, we have

From the above formula given in (3.16), we can easily find that $Q'(u)$ is a non-negative linear combination of the $\{ {P_{j + 1}} - {P_j}\}$. Further, for ${C^2} \cap F{C^{2l + 3}}(l \in {Z^ + })$ continuity, we have

In this case, we suppose $Q''(u)$ is a non-negative linear combination concerning the form $\{ ({P_{j + 1}} - {P_j}) - \varphi ({P_j} - {P_{j - 1}})\}$, where $\phi, \varphi \ge 0$. Moreover, from ${z_{i - 1}}({\mu _{i - 1}} - 1) = 0$ and ${\mu _i}(1 - {z_{i - 1}}) = 0$, we will get ${h_i} = 0$. Thus, we refer to the $Q(u)$ as convexity preserving.

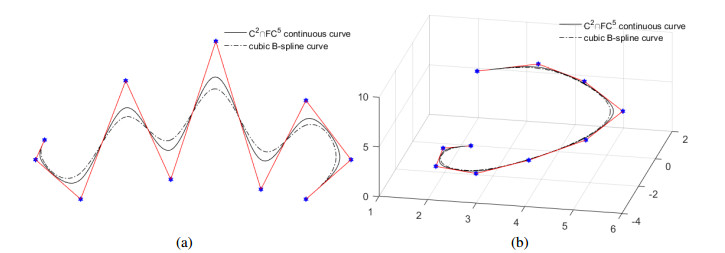
Figure 7. shows the planar and space ${C^2} \cap F{C^5}$ continuous curves (Left) and cubic B-spline curves (Right). All parameters are set $\alpha = \beta = 4, {x_i} = {y_i} = 0, {z_i} = 0.5$. From the figure we can find that ${C^2} \cap F{C^5}$ continuous curves are nearer the control polygon than the cubic B-spline curves.

3.6.   Local interpolations curves

In this subsection, we will use the qqr B-spline curves given in (3.6) to interpolate locally, the resulting curves will have $C^2$ continuity. First, we let

For $i = 3, 4, \cdots, n + 1$, from the Theorem 10(3), we have

In order to obtain a open curve, we will add two additional segments, that is ${P_{ - 1}} = {P_0}, {P_{n + 1}} = {P_n}$. Therefore, by using (3.18), the interpolate points $P_0$ and $P_n$ need to add $i = 2$ and $i = n+2$.

For any $i$, with the conditions (3.18), the resulting curves can be $C^2$ continuity by interpolating all given points. And the resulting curves have two global shape parameters and a local shape parameter. At knot $u_i$, when $\alpha = 4$, based on the formula (3.20), we have

In this case, when ${z_{i - 2}} = {z_{i - 1}} = 0.5$, the interpolation curve has the following tangent

which can generate the Hermite interpolation curves.

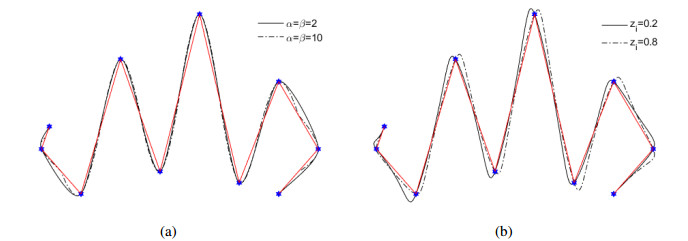
Figure 8. gives some examples of the interpolation qqr B-spline curves with different shape parameters. In the left figure, we show the interpolation qqr B-spline curves with different shape parameters, the global shape parameters are set $\alpha = \beta = 4$. In the right figure, we show the interpolation qqr B-spline curves with different shape parameters, all the local shape parameters are set $z_i = 0.5$.

3.7.   Locally adjustable properties

The qqr B-spline curve have two global shape parameters $\alpha, \beta$ and three local shape parameters ${x_i}, {y_i}, {z_i}$. From the Theorem 13, we can find that the global parameters $\alpha, \beta$ can effectively generate ${C^2} \cap F{C^{2l + 3}}$ continuous curves and can global modify the shape of the curve. When we fix the global shape parameters $\alpha, \beta$, we also locally adjust the shape of the qqr B-spline curves by modifying the local shape parameters ${x_i}, {y_i}, {z_i}$.

From the formula (3.7), the curve segments $Q(u)$ can be adjusted by modifying the local shape parameters ${x_{i - 1}}, {x_i}, {y_{i - 1}}, {y_i}, {z_{i - 2}}, {z_{i - 1}}, {z_i}$ when $u \in [{u_i}, {u_{i + 1}}]$. Thus, we can easily get that the different parameters ${x_i}, {y_i}$ only affect two segments which defined in the interval $u \in [{u_i}, {u_{i + 2}}]$, but the parameters $z_i$ can affect three segments which defined in the interval $u \in [{u_i}, {u_{i + 3}}]$.

From the formula (3.7) and Theorem 10(3), the shape of the proposed qqr B-spline curves can be easily predicted. First, we fix the global shape parameters. Then, the related coefficient values of $P_{i-2}$ and $P_{i-1}$ increase and coefficient values of $P_{i-3}$ and $P_{i}$ decrease with the decrease of the parameter $x_i$ and $y_i$, respectively. With regard to the parameters $y_{i-1}$ and $x_{i-1}$, the curve have the same adjustment effect with the coefficient values of ${P_{i - 3}}, {P_{i - 1}}$ and ${P_{i - 2}}, {P_{i}}$, respectively. Thus, we can find the parameters $x_i$ and $y_i$ have tension effect. With decrease of the parameter $x_i$ and $y_i$, the curve $Q(u)$ will move to the edge $\overline {{P_{i - 2}}{P_{i - 1}}}$ of the control polygon. On the contrary, the curve will move to the opposite direction. Moreover, the shape parameters $z_i$ serves as local control bias. With the decrease of $z_{i-1}$, the end points $Q(u_i)$ and $Q(u_{i+1})$ of the qqr B-spline curve segments will move to the control points $P_{i-2}$. In the opposite case, the curve segments will move to the control points $P_{i-1}$.

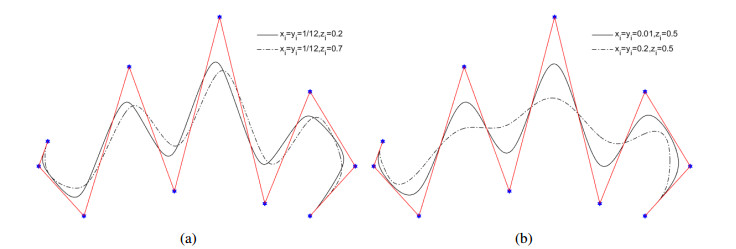
Figure 9. gives some examples of the adjustment effect of the qqr B-spline curves. In the left figure, we show the effect of local shape parameters on qqr B-spline curves, the global shape parameters are set $\alpha = \beta = 4$. In the right figure, we show the effect of global shape parameters on qqr B-spline curves, all the local shape parameters are set ${x_i} = {y_i} = 0.01, {z_i} = 0.5$.

4.   Conclusion

A new quartic Bernstein-like basis possessing two exponential shape parameters is given, which is useful for CAGD. And the conditions of ${C^2} \cap F{C^{2l + 3}}$ continuity and definition of the related curves are discussed. Based on the new basis, a new cubic B-spline-like basis possessing two global and three local shape parameters is presented. And the related cubic B-spline-like curves have ${C^2} \cap F{C^{2l + 3}}$ continuity at each points and include the classical cubic uniform curves as a special case. The related properties of connecting, interpolation and local adjustment of the cubic B-spline-like curves are discussed. How to accurately quantify the influence of each parameter on the shape of the curve will be our future work.

Acknowledgments

This research was supported by National Natural Science Foundation of China (61861040), the Gansu education Department Science and Technology Achievement Transformation project (no. 2017D-09) and Gansu Province Science, technology project funding (no.17YF1FA119) and Lanzhou Science and Technology Plan Project (2018-4-35).

Conflict of interest

The authors declare that they have no conflicts of interest.