1. Introduction

Having an efficient attention span means being capable to select and give priority to a relevant item at a glimpse. But the visual environment combines such a quantity and variety of signals that demands on attention vary when selecting a target. They vary as a function of the target’s physical similarity with neighbouring items, the similarity between these items, as well as the regularity of their dispersion in space, i.e., their spatial organization [1]. Much of research suggests that subcortical structures, such as the superior colliculus (SC) and the pulvinar, contribute to saccadic eye movements and in covert shifts of attention through space [2]. However, some influential theories [2,3] suggest that these structures, especially in the right hemisphere, would also be involved in filtering of irrelevant signals. Neurophysiological studies provided some support to this hypothesis [4,5], but neuropsychological studies in humans did not always provide consistent results [6,7].

Both the SC and the pulvinar are part of the extrageniculate pathways, i.e., they receive information directly from the retina and convey it to the extrastriate cortices, bypassing the lateral geniculate nucleus (LGN) and circumventing the visual striate cortex [8]. Direct retinal input to a monkey’s SC and pulvinar is predominantly contralateral [9,10,11], and imaging techniques suggest that this might also be the case in humans [12,13]. It might be that retinal projections to the SC and the pulvinar coming from the visual field that is on the side of the temple (left field of the left eye and right field of the right eye) are more numerous than those from the visual field that is on the side of the nose (right field of the left eye and left field of the right eye). Such numerical superiority could be reflected in performance of stimuli presented in the temporal field and such a behavioural pattern could be considered a marker of extrageniculate function. Furthermore, presenting the stimulus to the other eye also reverses which hemisphere receives stimulation and would allow investigating hemispheric asymmetries involving the extrageniculate pathways.

In agreement with neurophysiological findings on the extrageniculate pathways, studies have found behavioural nasal-temporal asymmetries in healthy humans in both saccadic eye movements [14] and covert shifts of attention [15,16] in a wide variety of settings. However, since little was done to investigate nasal-temporal asymmetries in tasks of selective attention requiring filtering out irrelevant distractors, evidence is very scarce. For instance, Michael and Ojéda [17] presented participants with a task in which a target was presented among distractors. The physical similarity between the target and distractors varied parametrically to manipulate attention demands. The hypothesis was that a temporal field advantage would appear with increasing demands on attention as a consequence of a stronger involvement of the extrageniculate pathway. No asymmetries between nasal and temporal displays were found. However, a well-marked nasal-temporal asymmetry was found in a more recent investigation with a different visual search paradigm [18]. Attention is thought to progress from the most toward the least salient item until the target is found, making processing efficiency decrease with decreasing salience of the target. In consequence, the smaller this decrement in efficiency, the easier is the processing of one item before moving to the next and vice versa. Concerning accuracy, it was found that processing was quite easier for temporal than nasal displays but only for stimuli projected to the right hemisphere. This tallies well with findings from human and animal studies, suggesting the structures of the right extrageniculate pathways and their cortical targets are more involved in processing targets presented among distractors than their homologues in the left hemisphere [19]. However, in that particular design, spatial orientation was strongly involved, since the task required directing attention serially from one item to the other. It is thus difficult to conclude whether the observed nasal-temporal asymmetry was related to filtering out distractors.

The aim of the present study was to uncover behavioural cues to extrageniculate mediations in filtering irrelevant distractors. Following major theories of attention, neurophysiological data from monkeys and neuropsychological and imaging findings in humans [4,5,7] support the role of the extrageniculate pathway in the filtering of distractors. We might expect that a temporal field advantage would show up in a task where a target has to be detected in a crowd of irrelevant items. Such advantage would be observed with increasing demands on attention. Furthermore, according to previous findings [18], we might expect that the temporal field advantage is a greater marker for stimuli projected to the right cerebral hemisphere than for those projected to the left hemisphere. In the present experiment, participants viewed laterally and tachistoscopically presented sets of 4 identical stimuli, differing only in their spatial rotation, and were required to decide whether a target was present in the set or not. The use of stimuli with such great similarity was dictated by our hypothesis; to induce extrageniculate structures engagement in a large amount of filtering activity, the degree of target-distractor similarity should be high [20]. The manipulation of attention demands was achieved by varying the degree of spatial organization of the stimuli, since behavioural research with humans showed that it is easier to detect a target in spatially-organised sets of stimuli rather in disorganised ones [1].

2. Materials and Methods

2.1. Participants

Twenty-four undergraduates (12 male) from the University of Lyon 2 took part in this experiment for course credits. Their mean age was 21.2 ± 4.6 years and all were right-handers according to the Edinburgh Laterality Inventory [21]; mean laterality quotient = 0.86 ± 0.15). They all reported normal or corrected-to-normal vision, and none of them had strabismus. They all gave their written informed consent for their participation. This study was conducted with respect to the Helsinki Declaration and was approved by the Council of the Laboratory EMC (EA3082-Lyon).

2.2. Stimuli & Apparatus

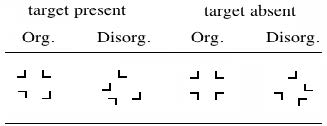
The stimuli were four deep grey (4.04 cd/m²) angles presented on a black background (0.04 cd/m²). From a viewing distance of 57 cm, each one subtended an angular space of 0.3° × 0.3° and all four were presented within the frame of an imaginary square subtending 1.1°× 1.1° of visual angle. An angle stimulus could be rotated 45°, 135°, 225°, and 315° as referred to the vertical. A white “+” sign was used as fixation and subtended 0.3° × 0.3° of visual angle. All stimuli were displayed on the cathodic monitor of a Trinitron Multiscan 20seII computer. All experiments took place in a dimly lit room.

2.3. Procedure

In each trial, the fixation sign was presented in the centre of the screen for 500 ms. The set of four angles was then added for 50 ms and was located randomly at the right or the left side of fixation. The angular distance between the fixation sign and the centre of the stimuli set was 2.5°. The fixation sign remained visible until a response was given followed by an inter-trial interval of 500 ms during which no stimulus was presented. In half the trials, the angles were all arranged to point inwards (target absent trials), and in the remaining half, one of them was pointing outwards (target present trials). Furthermore, in half the trials they were arranged to form a cross-like figure (organised trials; organized configurations promote a kind of perceptual grouping that facilitates target detection by decreasing the need for filtering), and in the remaining half they were arranged randomly (disorganised trials; disorganized configurations make target detection difficult and increase the need for filtering). Participants were required to keep their eyes on the fixation throughout the whole session. Even though no eye tracker was used to ensure this, the short presentation time of the sets (50 ms) ensured that no movements were possible (it was previously shown that no saccades are possible within the first 100 ms of stimuli presentation; see [18] Experiment 4 ). Participants had to decide whether one angle in the set was pointing outwards or not (a “yes-no” detection task) by pressing one of two predefined response buttons as quickly and as accurately as possible. In half the trials, participants responded with the middle and index fingers of the right hand and, in the remaining trials, with the same fingers of the left hand. The order of the hand (right first or left first) was balanced across participants. As mentioned above, differences between the nasal and the temporal fields can be assessed under monocular viewing conditions and reversing the stimulus to the other eye stimulates the alternate hemisphere. Therefore, the experiment was carried out under monocular viewing conditions with half of the participants being tested with the right eye first, and the other half with the left eye first. The session comprised 320 trials (20 trials/target presence/organization/visual field/stimulated hemisphere) and was preceded by a 20-trial training session. In each new trial, the computer randomly chose one of the tested conditions. The arrangement of the angles was different in each trial even in cases where two successive trials were taken within the same condition. Samples from all conditions (see Figure 1) were shown before the session and participants were also asked to describe what they had to do to ensure that the instructions were well understood. A short pause was introduced in the middle of the session. Responses were recorded by the computer.

Figure 1. Sample of each of the four stimuli sets used in the present study. Participants were required to decide whether one angle within each set of four pointed outwards or not (yes/no detection task).

DownLoad: Full-Size ImgPowerPoint

3. Results

Correct Response Times (RT) were submitted to an analysis of variance with the presence of the target (present vs. absent), the stimuli organization (organised vs. disorganised), the visual field of presentation (nasal vs. temporal), and the hemisphere to which the stimuli were projected (left vs. right) as within-subjects factors. The main effect of the presence of the target was significant (F (1, 23) = 38.6; p < 0.0001; η² = 0.76) since RT were faster for target present (820 ms) than target absent (985 ms) trials. The main effect of spatial organization of the stimuli was also significant (F (1, 23) = 14.7; p < 0.0001; η² = 0.1), with shorter RT for organised (874 ms) than disorganised (931 ms) sets. No other significant effects were found.

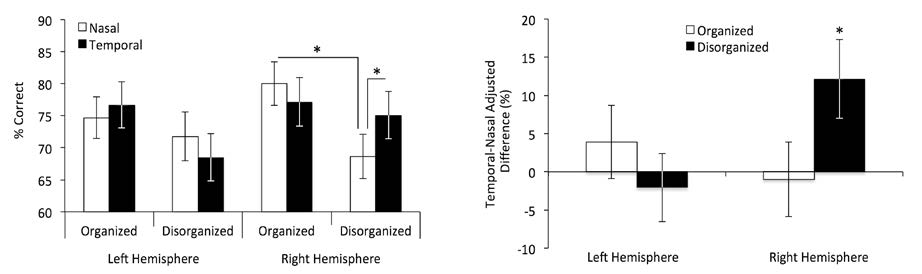
The mean percentage of correct responses was 74% (SD = 24; see Table 1 for accuracy). The percentage of correct responses was submitted to an analysis of variance; the presence of the target (present vs. absent), the stimuli organization (organised vs. disorganised), the visual field of presentation (nasal vs. temporal), and the hemisphere to which the stimuli were projected (left vs. right) were treated as within-subjects factors. The main effect of the presence of the target was significant (F (1, 23) = 9.9; p < 0.005; η² = 0.67); the percentage of correct responses was higher for target present (80.1%) than target absent (67.9%) trials. The main effect of spatial organization of the stimuli was also significant (F(1, 23) = 17.9; p < 0.0001; η² = 0.17), since performance was better with organised (77.1%) than with disorganised (71.0%) sets. Finally, the three-way set organization X visual field X hemisphere interaction reached significance (F (1, 23) = 4.3; p < 0.05; η² = 0.06; Figure 2, left panel). To further understand this interaction, partial analyses of variance were carried out separately for each hemisphere with the remaining factors being the same as before. For stimuli projected to the left hemisphere, the set organization X visual field interaction did not reach significance (F (1, 23) = 2.1; p > 0.15; η² = 0.00), but it was significant for stimuli projected to the right hemisphere (F (1, 23) = 5.5; p < 0.028; η² = 0.05). Newman-Keuls post-hoc comparisons revealed that this interaction was due to a temporal field advantage for disorganised sets (temporal field: 75.0%; nasal field: 68.7%; p < 0.033) but not for organised sets (temporal field: 77.1%; nasal field: 80.0%; p > 0.3). Furthermore, the spatial organization of the stimuli affected performance only when the stimuli were presented in the nasal field (effect of organization = 11.3%; p < 0.003) but not in the temporal field (effect of organization = 2.1%; p > 0.46).

Table 1. Mean (+ SD) accuracy observed in each condition of the present Experiment.

	Left Hemisphere		Right Hemisphere
	Organized	Disorganized	Organized	Disorganized
Temporal Field	76.6 (17.9)	68.4 (18.3)	77.1 (18.9)	75.0 (18.6)
target present	80.0 (21.7)	77.0 (19.9)	82.5 (16.3)	80.2 (17.4)
target absent	73.3 (20.9)	59.7 (29.3)	71.6 (30.2)	69.7 (28.4)
Nasal Field	74.6 (15.9)	71.7 (18.7)	80.0 (16.4)	68.7 (16.9)
target present	81.6 (13.8)	79.3 (15.3)	83.9 (15.6)	76.2 (17.3)
target absent	67.7 (27.3)	64.1 (29.6)	76.0 (21.4)	61.0 (28.0)

 | Show Table

DownLoad: CSV

Figure 2. Left: Mean (± 1 SEM) percentage of correct responses as a function of the spatial organization of the stimuli, the visual field of presentation, and the hemisphere to which the stimuli were projected. Right: Mean (± 1 SEM) adjusted temporal-nasal field difference for spatially organised and disorganised stimuli projected to each hemisphere. Asterisks denote significant effects compared to the 0-value.

DownLoad: Full-Size ImgPowerPoint

In order to complement these analyses, the adjusted percent difference in performance between temporally and nasally presented stimuli was computed ¹ (¹ Adjusted percent difference = (temporal?nasal)/nasal × 100. Since retino-collicular projections from the temporal field are thought to be numerically superior from those coming from the nasal field, extrageniculate mediation is represented by the difference between the temporal and the nasal fields. Therefore, performance for nasally presented stimuli is taken as a baseline, and performance for temporally presented stimuli is the percentage of change from that baseline. This change is adjusted to take into account the individual performance at baseline.) separately for organised and disorganised sets projected to each hemisphere. The 0-value thus represents performance for nasally presented sets and any reliable departure towards positive values is a temporal field advantage. A statistically significant temporal field advantage was found only for disorganised sets projected to the right hemisphere (12.1%; t(23) = 2.34; p < 0.03 bicaudal; Figure 2, right panel). This effect was rather regular across participants since it was present in the performance of 66.7% of them (p < 0.045 binomial). No such field advantage was found for organized sets projected to the same hemisphere (−1%; t(23) = 0.20; p > 0.84; 50% of participants, p > 0.16 binomial). As for sets projected to the left hemisphere, no nasal-temporal asymmetries were observed for disorganized sets (−2%; t(23) = 0.46; p > 0.65, 42% of participants, p > 0.12 binomial) nor for organized ones (4%; t(23) = 0.82; p > 0.42; 50% of participants, p > 0.16 binomial).

4. Discussion

Some theoretical accounts on visual selective attention propose that, in addition to their role in the control of overt and covert spatial shifts of attention, structures such as the SC and the pulvinar that are part of the extrageniculate pathways, especially of the right hemisphere, might participate in filtering irrelevant distractors [2,3,19]. The present study is only the third of its kind and the aim was to collect some behavioural cues in support of these accounts.

4.1. Spotting from the rightmost deep

Participants in this study were required to detect the presence of a target in a briefly presented set of four physically identical stimuli that differed only in their spatial rotation. To assess performance with increasing demands on attention, the four stimuli were either organised or disorganised and randomly dispersed. To assess differences between the temporal and the nasal fields, the task was completed under monocular viewing conditions. The results showed a temporal field advantage in detection performance. But this pattern was observed only for disorganised sets of stimuli, that is, when demands on attention were greater [1]. A closer look at the results (Figure 2, left panel) shows that disorganising the distribution of the stimuli dropped performance in the nasal field by about six times more than in the temporal field (nasal ≈ 11%; temporal ≈ 2%). In addition, the small decrease in performance observed in the temporal field was not statistically reliable. When adjusting temporal performance by taking nasal performance as a baseline, we found that the temporal advantage for disorganised sets had an amplitude of about 12%. Increasing demands on attention decreased processing efficiency for nasally presented stimuli but had virtually no effect on the processing efficiency of stimuli presented in the temporal field. Therefore, filtering distractors in the temporal field was easier. Importantly, this was observed only for stimuli projected to the right cerebral hemisphere. Such a pattern was not observed for stimuli projected to the left hemisphere.

Provided that nasal-temporal behavioural asymmetries rely on the superiority of retino-collicular projections from the temporal field, the whole pattern of results means that signals conveyed through the extrageniculate pathways toward cortical targets in the right cerebral hemisphere allow more efficient filtering of distractors. This provides behavioural support for the hypothesis that structures in the extrageniculate pathways (i.e., the SC and the pulvinar) participate in filtering aspects of selective attention in addition to overt and covert spatial shifts [2,3,19]. It also complements recent evidence from human and animal studies that have supported such accounts [4,5], contrary to neuropsychological studies that produced mixed results [6,7]. Two previous behavioural studies from our laboratory [17,18] tried to investigate this issue in tasks requiring participants to select a target from among distractors. But only one of them successfully showed nasal-temporal asymmetries [18]. Interestingly enough, the asymmetry was also found for stimuli projected to the right hemisphere only, and concerned accuracy. Even though several methodological differences exist between that study and the present one (i.e., a stronger involvement of spatial orientation in the previous investigation and a stronger involvement of filtering in the present one), they share the temporal field advantage for stimuli projected to the right hemisphere.

What are the mechanisms underlying such an asymmetry? Past research demonstrated that decreasing the exposure duration, size, luminance or eccentricity, or increasing the blurring of lateralized visual stimuli produces a concomitant decrement in the performance for those stimuli projected to the left hemisphere, with little or no effect for stimuli projected to the right hemisphere [22]. This effect does not seem to depend on the material used since the same pattern was found for verbal stimuli, non-verbal abstract stimuli, and faces. One interpretation is that the right hemisphere is superior to the left during visual preprocessing, i.e., early and elementary processes that allow a stimulus to be perceived. This might be the reason why stimuli projected to the right hemisphere are less adversely affected by manipulations that make them less perceptible. In one of our previous studies, we showed a similar effect in a task of visual search without manipulating the physical characteristics of the target but its similarity to the neighbouring stimuli [17]. This kind of manipulation influences attention demands to resolve the task and affects the target detectability among distractors. This is consistent with the idea that reduced perceptibility increases the need for attention [20]. It can be argued that the perceptibility of the stimuli used in the present study was low and the target was difficult to detect among distractors because of the use of short exposure duration, low luminance, and the manipulation of the spatial organization of stimuli that increases demands on attention [22]. However, this kind of pattern has been mostly reported under binocular viewing conditions as the lateralized effects emerged at cortical levels. That such an asymmetry may arise at subcortical levels is suggested by the temporal field advantage observed in the present study and in a previous one [18]. It can thus be suggested that it is the extrageniculate pathway of the right hemisphere that is mostly involved in preprocessing of several simultaneously presented stimuli, and this would therefore confer an advantage in filtering distractors.

4.2. Extrageniculate mediation and the temporal field advantage: pros and cons

Is the presence of a temporal field advantage in a behavioural task a marker of extrageniculate mediation? Does this necessarily establish the ultimate validity of the hypothesis of a numerical superiority of projections from the temporal field to the SC and the pulvinar? The very existence of a numerical superiority of temporal field projections in monkeys’ SC has been severely questioned [23]. However, imaging techniques showed that, in humans, the temporal field is indeed over-represented in the contralateral SC, whereas such asymmetry is not observed in the LGN and the primary visual cortex [24]. Furthermore, when the SC is damaged in humans, the advantage of the contralateral temporal field disappears [25]. Finally, the existence of a temporal field advantage in the pulvinar is less controversial since such a numerical superiority was found in monkeys [10] and lesions of the pulvinar in humans also abolish nasal-temporal asymmetries [26]. Thus, even though there are still controversies, there are arguments coming both from animal and human studies suggesting that the temporal field advantage may arise because of asymmetry in the retinal projections toward extrageniculate targets.

5. Conclusions

The present study uncovered a temporal field advantage for stimuli projected to the right hemisphere in a task of selective attention requiring to detect a target among distractors. This suggests that the extrageniculate pathways of the right hemisphere in humans are involved in filtering distractors and may help to better understand a dramatic clinical condition—spatial neglect. Spatial neglect is a neurological disorder that is mostly observed following lesions of the right cerebral hemisphere and is characterized by failures to attend to, explore and react to stimuli located on the left side of space. It was suggested that this conditions results from damage to neural networks that underlie attention functions and which are asymmetrically represented in the brain, that is, predominantly in the right hemisphere [27]. Interestingly though, lesions of the right pulvinar, a structures that is part of the extrageniculate pathway, may result in spatial neglect [28]. Since our results suggest that this pathway is involved in filtering distractors, it might be speculated that patients suffering from spatial neglect not only fail to orient attention, but also that they have difficulties in distinguishing relevant from irrelevant signals within the left side of space. Future research should shed some light on this issue and would also focus on the time course of extrageniculate involvement in filtering distractors.

6. Acknowledgments

This work was supported by the LABEX CORTEX (ANR-11-LABX-0042) of Université de Lyon, within the program "Investissements d'Avenir" (ANR-11-IDEX-0007) operated by the French National Research Agency (ANR). Many thanks to Damien Fernandez and Nathalie Ojéda for their help with data collection.

Conflict of Interest

The authors declare no conflict of interest