Figure 1.
Pie chart to show the number of mouse proteins in each functional type.
Citation: Zoha Deldar, Carlos Gevers-Montoro, Ali Khatibi, Ladan Ghazi-Saidi. The interaction between language and working memory: a systematic review of fMRI studies in the past two decades[J]. AIMS Neuroscience, 2021, 8(1): 1-32. doi: 10.3934/Neuroscience.2021001
| [1] | Lei Chen, Ruyun Qu, Xintong Liu . Improved multi-label classifiers for predicting protein subcellular localization. Mathematical Biosciences and Engineering, 2024, 21(1): 214-236. doi: 10.3934/mbe.2024010 |
| [2] | Hangle Hu, Chunlei Cheng, Qing Ye, Lin Peng, Youzhi Shen . Enhancing traditional Chinese medicine diagnostics: Integrating ontological knowledge for multi-label symptom entity classification. Mathematical Biosciences and Engineering, 2024, 21(1): 369-391. doi: 10.3934/mbe.2024017 |
| [3] | Jiyun Shen, Yiyi Xia, Yiming Lu, Weizhong Lu, Meiling Qian, Hongjie Wu, Qiming Fu, Jing Chen . Identification of membrane protein types via deep residual hypergraph neural network. Mathematical Biosciences and Engineering, 2023, 20(11): 20188-20212. doi: 10.3934/mbe.2023894 |
| [4] | Yanping Xie, Zhaohui Dong, Junhua Du, Xiaoliang Zang, Huihui Guo, Min Liu, Shengwen Shao . The relationship between mouse lung adenocarcinoma at different stages and the expression level of exosomes in serum. Mathematical Biosciences and Engineering, 2020, 17(2): 1548-1557. doi: 10.3934/mbe.2020080 |
| [5] | Cicely K. Macnamara, Mark A. J. Chaplain . Spatio-temporal models of synthetic genetic oscillators. Mathematical Biosciences and Engineering, 2017, 14(1): 249-262. doi: 10.3934/mbe.2017016 |
| [6] | Hacı İsmail Aslan, Hoon Ko, Chang Choi . Classification of vertices on social networks by multiple approaches. Mathematical Biosciences and Engineering, 2022, 19(12): 12146-12159. doi: 10.3934/mbe.2022565 |
| [7] | Yongyin Han, Maolin Liu, Zhixiao Wang . Key protein identification by integrating protein complex information and multi-biological features. Mathematical Biosciences and Engineering, 2023, 20(10): 18191-18206. doi: 10.3934/mbe.2023808 |
| [8] | Wenjun Xu, Zihao Zhao, Hongwei Zhang, Minglei Hu, Ning Yang, Hui Wang, Chao Wang, Jun Jiao, Lichuan Gu . Deep neural learning based protein function prediction. Mathematical Biosciences and Engineering, 2022, 19(3): 2471-2488. doi: 10.3934/mbe.2022114 |
| [9] | Feng Wang, Xiaochen Feng, Ren Kong, Shan Chang . Generating new protein sequences by using dense network and attention mechanism. Mathematical Biosciences and Engineering, 2023, 20(2): 4178-4197. doi: 10.3934/mbe.2023195 |
| [10] | Kunli Zhang, Shuai Zhang, Yu Song, Linkun Cai, Bin Hu . Double decoupled network for imbalanced obstetric intelligent diagnosis. Mathematical Biosciences and Engineering, 2022, 19(10): 10006-10021. doi: 10.3934/mbe.2022467 |
Protein is a major component for almost all living creatures. It is highly related to the maintenance of normal physical functions in cells [1]. Several complicated and essential biological processes need proteins to participate in, such as cell proliferation [2], DNA replication [3], enzyme-mediated metabolic processes [4], etc. Furthermore, protein provides important contributions to construct basic cellular structure, maintain cellular microenvironment and form complex macrostructures. Thus, the research of protein-related problems is quite hot in recent years. Determination of the functions of proteins is one of the essential problems. Experimental determination is a solid method. However, it also has some evident shortcomings, such as high cost and low efficiency. Thus, it is of great urgency to design novel methods with low cost and high efficiency.
In recent years, several computational methods have been designed to identify protein functions. Most of them are data-driven methods. Based on lots of proteins with annotated functions, which can be obtained from some public databases, models were set up by using some existing or newly designed computer algorithms. The basic computational method to identify protein functions is based on protein sequence similarity measured by BLAST [5]. Other methods, such as sequence motif based methods (PROSITE) [6], profile-based methods (PFAM) [7], structure-based methods (FATCAT and ProCAT) [8], were also proposed to identify protein functions. In recent years, network-based methods become more and more popular to tackle some protein-related problems. Two previous studies employed protein network information to design hybrid approaches for the identification of protein functions. The method that adopted protein network information is an important step to identify protein functions [9,10]. Other steps used methods based on protein sequence similarity or biochemical and physicochemical description of proteins. Most established methods always focused on proteins, analyzing their sequences, properties, etc. Few studies considered function labels. As inspired by some studies on drug-related problems [11,12], which considered label information and improved the performance of classifiers, the associations of function labels may also be important information for protein function identification.
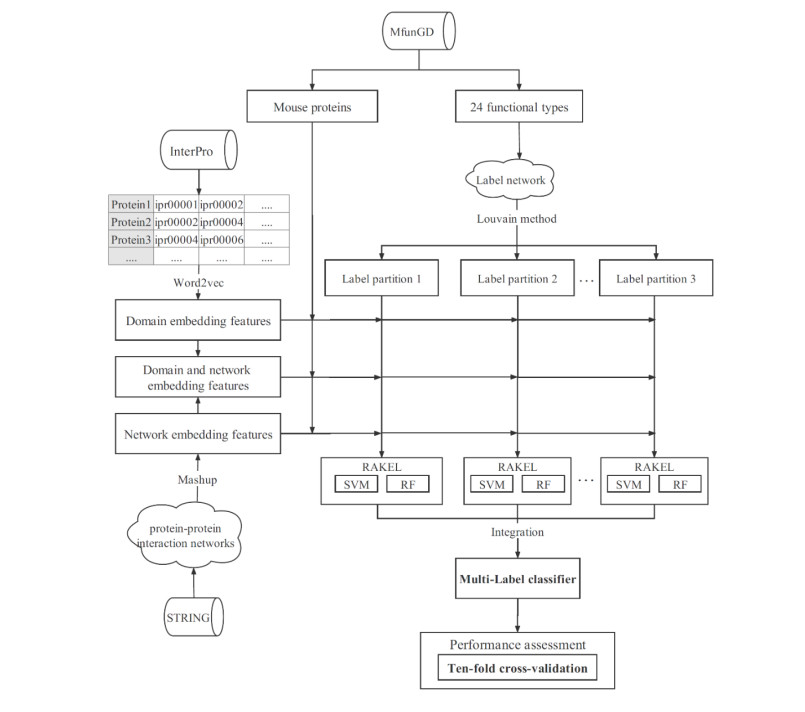
In this study, we constructed a multi-label classifier with a label space partition to identify protein functions. To conduct this investigation, we selected proteins of mouse, one of the most extensively studied organisms, as the research object. Proteins and their function annotations were retrieved from MfunGD [13]. 24 functional types were reported in such database. A label space partition method, incorporating Louvain method [14], was applied to analyze the associations of 24 functional types, resulting in some subsets of types. To prove such partition can improve the performance of classifiers, we set up several classifiers with RAndom k-labELsets (RAKEL) [15], with support vector machine (SVM) [16] or random forest (RF) [17] as the base classifier. On each type subset, a multi-label classifier was set up and they were integrated in the proposed classifiers. The results indicated that classifiers with a label space partition were always superior to those without considering the partition of functional types. Furthermore, these classifiers also provided better performance than those with a random partition of functional types.
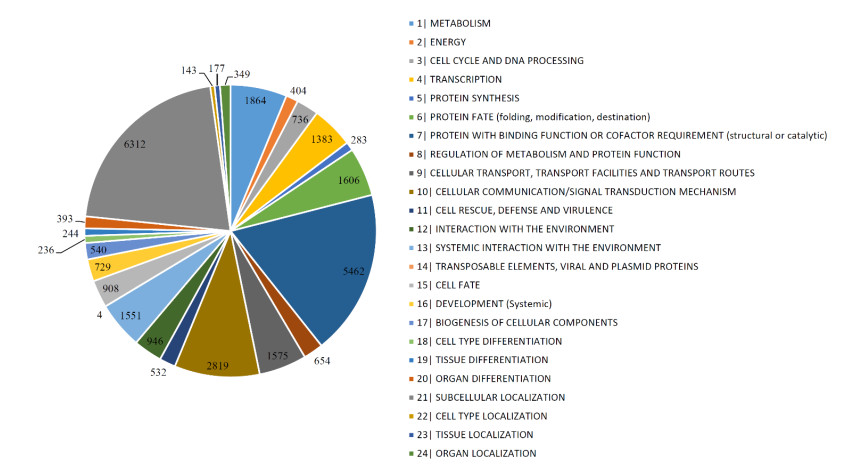
We sourced the mouse proteins and their functional types from one previous study [9]. This information was retrieved from MfunGD (http://mips.gsf.de/genre/proj/mfungd/) [13], a public database collecting annotated mouse proteins and their occurrence in protein networks. In such database, mouse proteins were classified into 24 types, which are illustrated in Figure 1. The types of each mouse protein were determined by manually checking its annotation in the literature and GO annotation [18,19]. Because we encoded mouse proteins according to their functional domain or interaction information, those without these two types of information were excluded. Finally, a dataset consisting of 9655 mouse proteins were constructed. These proteins were also classified into above mentioned 24 functional types. The number of proteins in each functional type is also shown in Figure 1. It was easy to obtain that the sum of protein numbers in all 24 types were 29850, which was much larger than the number of different mouse proteins (9655). This fact implied that several proteins belonged to two or more functional types. Determination of functional types of mouse proteins was evidently a multi-label classification problem if functional types were deemed as labels.
As mentioned above, mouse proteins in MfunGD were classified into 24 functional types and assigning these types to given proteins was a multi-label classification problem, where types were termed as labels. Due to the number of labels, it was difficult to directly build powerful multi-label classifiers. The partition of label set may be helpful to optimize classifiers as inspired by some studies on drug-related problems [11,12]. Thus, this section proposed a label space partition method to divide labels into some label subsets.
To implement this method, a label network was constructed first. Given a training dataset D with h labels (h = 24 in this study), denoted by l1,l2,…,lh, the label set for one sample s was defined as L(s). For each label li(1≤i≤h), samples having such label constituted a sample subset, denoted as SL(li), that is
| SL(li)={s:s∈D and li∈L(s)} | (1) |
The label network defined labels as nodes and two nodes were connected by an edge if and only if their corresponding labels, say li and lj, had common samples, that is SL(li)∩SL(lj)≠∅. Furthermore, a weight was assigned to each edge for indicating the different association strength of labels. For an edge e, its weight was defined by
| w(e)=|SL(li)∩SL(lj)| | (2) |
where li and lj were the endpoints of edge e. For an easy description, let us denoted such label network by NL.
The Louvain method [14], a community detection algorithm, was performed on the label network NL to classify labels into some subsets. Such method adopts a greedy aggregation scheme to detect communities such that nodes in each detected community have strong associations. Initially, each node in the network constitutes a community. A loop procedure is executed. In each round, two communities are selected and merged when such merging can provide highest contribution to modularity. For a node n and community C, the gain in modularity, denoted by ΔQ, by merging n and C is defined as
| ΔQ=[Σin+kn,in2m−(Σtot+kn2m)2]−[Σin2m−(Σtot2m)2−(kn2m)2] | (3) |
where Σin stands for the overall weights of edges inside C, Σtot stands for the overall weights of edges adjacent to nodes in C, kn,in represents the overall weights of edges connecting n and nodes in C, kn denotes the overall weights of edges adjacent to n, m is the overall weights of edges in the network. For each node n, the gain in modularity by merging it and each of its neighbor is computed. The merging producing the highest gain in modularity is selected and a new network is constructed. In details, if such merging involves node n and community C, the new network combines n and community C, producing a new node n′. The weight of an edge connecting n′ and another node n″ in the network is updated as the overall weights of edges connecting n (C) and n″. In the next round, above procedure is executed on the new network. The loop stops until the gain in modularity cannot be positive. The remaining communities in the network indicate a label partition.
In this study, the Louvain method was performed on the label network NL. By refining its outcome, we can access a label partition. Let us denote the label partition as L1,L2,…,Lt.
Efficient classifiers always adopt informative features of samples, which contain essential properties of samples as much as possible. This study employed two schemes to encode each mouse protein. The first scheme extracted features derived from functional domain information of proteins through a natural language processing approach, whereas the second one generated features from several protein-protein interaction (PPI) networks. Their descriptions were as below.
Functional domain information is deemed to be useful to investigate various protein-related problems [20,21,22,23,24]. Here, we also adopted such information to encode each mouse protein.
We retrieved the functional domain information of all mouse proteins from InterPro database (http://www.ebi.ac.uk/interpro/, accessed in October 2020) [25]. This information contained 48739 mouse proteins, covering 16797 domains. Each domain was termed as words, whereas mouse proteins, annotated by domains, were deemed as sentences. Then, such above information was fed into the well-known natural language processing approach, word2vec [26,27], to learn embedding features of domains. As a result, each domain was encoded by a 256-D feature vector. Here, the word2vec program retrieved from https://github.com/RaRe-Technologies/gensim was adopted. It was executed with its default parameters.
The feature vectors of domains were further refined to represent each mouse protein. For each mouse protein, it was encoded by a vector, which was defined as the average of vectors of domains that were annotated on such protein. Thus, each protein was also represented by 256 features. For convenience, such obtained features were called domain embedding features.
Network has been deemed to be a popular research form because it can organize objects at a system level. However, a gap exists between network and traditional machine learning algorithms. This gap promotes the process of network embedding algorithms, which can abstract linkage in one or more networks and learn features for each node in the network(s). In recent years, several network embedding algorithms, such as DeepWalk [28], Node2vec [29], and Mashup [30], etc. have been proposed. Some of them have been applied to tackle different protein-related problems [30,31,32,33,34]. Features obtained by network embedding algorithms are quite different from those extracted from inherent properties of samples and can reflect different aspects of samples. Here, we adopted Mashup to extract features of mouse proteins from several PPI networks.
We used the mouse PPI information collected in STRING (https://www.string-db.org/, Version 10.0) [35], a public database containing interaction of 9, 643, 763 proteins from 2031 organisms. Interactions in this database are derived from five main sources: Genomic context predictions, High-throughput lab experiments, (Conserved) Co-expression, Automated textmining, Previous knowledge in databases. Accordingly, they can widely evaluate the associations of proteins. The mouse PPI information involves 20648 mouse proteins and 5, 109, 107 interactions. Each interaction is assigned eight scores, where the first seven scores measure the association of proteins from some aspect of proteins and they are integrated in the last score. For each of first seven scores, a PPI network was constructed, where proteins were defined as nodes and two nodes were connected by an edge when their corresponding proteins can constitute a PPI with such score larger than zero. In addition, this score was assigned to the edge as its weight. Accordingly, seven PPI networks were built, which can be used to extract informative features of mouse proteins.
The network embedding algorithm, Mashup [30], was executed on above constructed seven PPI networks. To our knowledge, it is the only network embedding algorithm that can process multiple networks. This method contains two stages to extract features for each node. In the first stage, each node in each network is assigned a raw feature vector on the basis of random walk with restart algorithm [36,37]. In this way, several raw feature vectors are produced for the same node. It is necessary to combine them into one vector. At the same time, the dimensionality reduction is also inevitable because of the high dimension of raw feature vectors, which is equal to the node number in the network. All these are done in the second stage. It supposes a uniform vector for each node and a context vector for any node in any network. Based on them, it produces an approximate vector for any node in any network. The optimal components in above two types of vectors were determined by solving an optimized problem such that the produced approximate vectors based on them should be approximate to raw feature vectors as much as possible. For details, please refer to reference [30].
This study adopted the Mashup program downloaded from http://cb.csail.mit.edu/cb/mashup/. Likewise, it was executed with the default parameters. For the dimension of feature vectors, we tried various values between 100 and 300. For convenience, features produced by Mashup were called network embedding features.
Accordingly, each mouse protein can be represented by three forms: (1) domain embedding features; (2) network embedding features; (3) domain and network embedding features.
As mentioned in Section 2.1, several mouse proteins belonged to two or more functional types. A natural way to assign types to given proteins is to design a multi-label classifier. Generally, there are two schemes to construct multi-label classifiers: problem transformation and algorithm adaption [38]. The former one transforms the original multi-label classification problem into some single-label classification problems. The later one generalizes the single-label classification algorithm so that it can process samples with more than one labels. Here, we adopted a widely used problem transformation method, called RAKEL [15], to construct the multi-label classifier.
RAKEL is a generalized method of label powerset (LP) algorithm. Given a dataset with h labels, say l1,l2,…,lh, randomly construct m label subsets, each of which consists of k labels. For each of these label subsets, new labels are defined as the members in its power set. These new labels are assigned to samples based on their original labels. After such operation, each sample is assigned only one new label. Samples with their new labels constitute a new dataset. A classifier is set up by training some single-label classification algorithm on such new dataset. Accordingly, m classifiers can be set up, which are integrated in RAKEL. For a query sample x, each classifier gives a binary prediction result (0 or 1) for each label li. RAKEL calculates the average vote rate for each label li. When the average vote rate is greater than a given threshold (Generally, it is set to 0.5), li is assigned to x. For an easy description, classifiers built by RAKEL were termed RAKEL classifiers in this study. To quickly implement RAKEL, the tool "RAKEL" in Meka (http://waikato.github.io/meka/) [39] was directly employed. The main parameters of RAKEL, m and k, were tuned in this study.
As mentioned in Section 2.2, all labels can be divided into t partitions, say L1,L2,…,Lt. For each partition, a new dataset is constructed by restricting labels of each sample into this partition. For instance, if one sample is assigned three labels, say l1,l2,l3 and l1,l3 belongs to one partition, this sample is assigned l1,l3 as its labels in the new dataset. Accordingly, a RAKEL classifier is built on the new constructed dataset. The final classifier integrates these RAKEL classifiers by collecting their results. In detail, for a query sample, each RAKEL classifier yields its prediction (i.e., a label subset). The final prediction is the union of label subsets yielded by all RAKEL classifiers.
When building the RAKEL classifiers, a single-label classification algorithm is needed. In this study, two powerful classification algorithms were employed: SVM [16] and RF [17].
SVM is a popular classification algorithm based on statistical learning theory [31,34,40,41,42,43,44,45,46]. Its principle is to use a kernel function to map samples from the original space to a higher-dimensional feature space so that samples are linearly separable in the new space. So far, several types of SVM have been designed to process different problems. Here, one type of SVM was adopted. The sequential minimal optimization (SMO) algorithm [47] was employed to optimize the training procedures of this type of SVM. A polynomial kernel or an RBF kernel was set as its kernel.
RF is another powerful classification algorithm, which has been widely applied to tackle various biological problems [48,49,50,51,52,53,54]. In fact, it is an ensemble algorithm, integrating several decision trees. To set up each decision tree, it randomly selects samples from the given dataset, with replacement, and features to extend the tree at each node. For a query sample, all decision trees provide their predictions. These predictions are integrated in RF by majority voting. It is widely accepted that decision tree is a relative weak classifier. However, RF is much more powerful [55].
The above SVM and RF algorithms are all implemented by corresponding tools in Meka [39]. These tools were directly employed in this study.
All multi-label classifiers constructed in this study were assessed by ten-fold cross-validation [56]. Such method first divides the original dataset, denoted by D, into 10 mutually exclusive subsets with similar size, i.e., D=D1∪D2∪…D10,Di∩Dj=∅(i≠j,1≤i,j≤10). Each subset, say Di, is picked up as test dataset and remaining nine subsets constitute the training dataset. The classifier built on the training dataset is applied to the test dataset. Thus, each sample is exactly tested once.
For the results of ten-fold cross-validation, we can compute some measurements to assess the quality of results. In this study, we employed three widely used measurements in multi-label classification: accuracy, exact matching and hamming loss. To list their formulas, some notations are necessary. Given a dataset with n samples and m labels, suppose that Li and L′i are the sets of true labels and predicted labels, respectively, of the ith sample. Above three measurements can be computed by
| {Accuracy=1nn∑i=1(‖Li∩L′i‖‖Li∪L′i‖)Exact match=1nn∑i=1∇(Li,L′i)Hamming loss=1nn∑i=1(‖Li∪L′i−Li∩L′i‖m) | (4) |
where ∇ is defined as below:
| ∇(Li,L′i)={1if Li is identifical to L′i0otherwise | (5) |
Evidently, the high accuracy and exact match indicate the good performance of the classifier, whereas it is on the contrary for hamming loss.
When comparing the performance of different classifiers, different results may be concluded according to different measurements. The ranges of accuracy, exact match and hamming loss are all between 0 and 1. Accuracy and exact match have the same trend to represent the performance of classifiers, that is, higher value represents higher performance; whereas hamming loss suggest the contrary trend, that is, lower value suggests higher performance. Thus, we refined hamming loss as 1-hamming loss to make it having the same trend as accuracy and exact match. In this case, accuracy, exact match and 1-hamming loss can multiply together to define a new measurement, called integrated score in this study, formulated by
| Integrated score=Accuracy∗Exact match∗(1−hamming loss) | (6) |
The higher the integrated score, the higher the performance of the classifier. This measurement has also used in some previous studies [45,57].
In this study, we proposed a multi-label classifier to identify mouse protein functions, incorporating the procedure of analyzing the associations of functional types. Two types of features (domain and network embedding features) were adopted to encode proteins. RAKEL was employed to construct classifiers. The entire procedures are illustrated in Figure 2. In this section, the detailed evaluation results would be given and some comparisons were conducted.
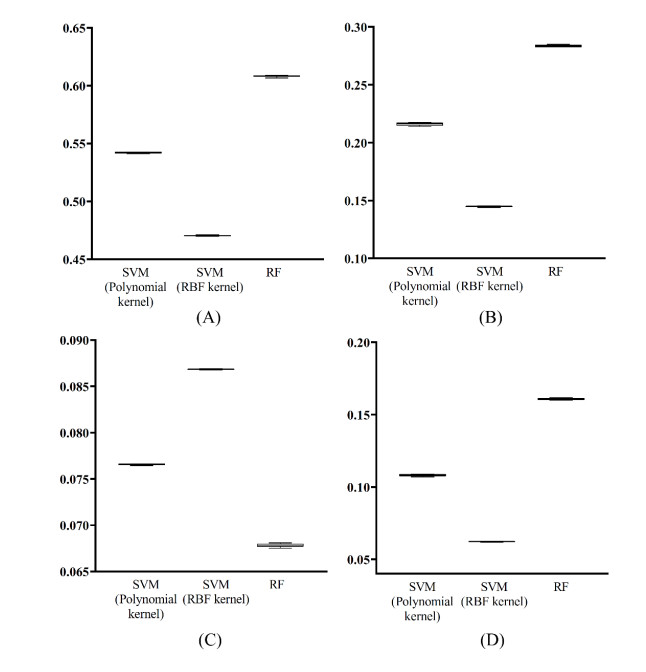
For the protein features derived from its functional domain information, we adopted RAKEL with a certain base classifier to construct multi-label classifiers. Three base classifiers were tried in this study: (1) SVM with polynomial kernel, (2) SVM with RBF kernel, (3) RF. For two types of SVM, the regularization parameter C was set to 0.5, 1 and 2, the exponent of polynomial kernel was set to its default value (one) and the parameter γ of RBF kernel was also set to its default value (0.01). As for RF, its main parameter, number of decision trees, was tuned, including various values between 10 and 300. The main parameter m for RAKEL was set to its default value 10, the other parameter k of RAKEL was wet to 2, 3, 4, 5. The grid search was adopted to set up all RAKEL classifiers, which were assessed by ten-fold cross-validation, and extract the optimum parameters for each base classifier. The best performance, measured by integrated score, for each base classifier is provided in Table 1, in which the best parameters for each base classifier are also provided. The integrated scores for three base classifiers were 0.1026, 0.0611 and 0.1574. Evidently, the RAKEL classifier with RF provided the best performance. Its accuracy, exact match and hamming loss were 0.6025, 0.2806 and 0.0687, respectively, which were all best compared with those of RAKEL classifiers with other two base classifiers. At a glance, these three RAKEL classifiers were not good enough. However, they were better than classifiers without label partition, which would be elaborated in Section 3.4.
| Base classifier | Parameter | Accuracy | Exact match | Hamming loss | Integrated score |
| Support vector machine (Polynomial kernel) |
m = 10, k = 5, C = 2, exponent = 1 | 0.5329 | 0.2087 | 0.0777 | 0.1026 |
| Support vector machine (RBF kernel) |
m = 10, k = 5, C = 2, γ = 0.01 | 0.4643 | 0.1441 | 0.0872 | 0.0611 |
| Random forest | m = 10, k = 3, number of decision trees = 250 | 0.6025 | 0.2806 | 0.0687 | 0.1574 |
DownLoad:
CSV
In addition, to fully evaluate the best RAKEL classifier with a certain base classifier, it was further assessed by ten-fold cross-validation for ten times. The performance under ten-fold cross-validation for ten times is shown in Figure 3, from which we can see that all four measurements yielded by each RAKEL classifier varied in a small range, indicating the classifiers with label partition were quite stable no matter how samples were divided.
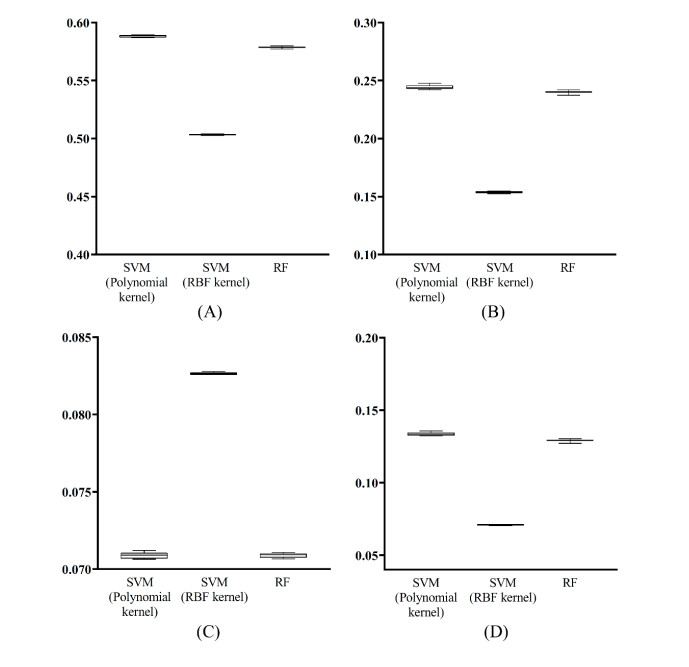
For the network embedding features derived from seven protein networks, a similar procedure was conducted. The same parameters were tried for three base classifiers and RAKEL. Furthermore, the dimension of features was also tuned, including 100, 150, 200, 250 and 300. The grid search was also used to build all RAKEL classifiers, which were further assessed by ten-fold cross-validation. The best RAKEL classifier with a certain base classifier was found and its performance is listed in Table 2. The optimum parameters for each base classifier are also provided in this table. The integrated scores for three base classifiers were 0.1308, 0.0714 and 0.1269, respectively. Clearly, the RAKEL classifier with SVM (polynomial kernel) generated the best performance, where the accuracy, exact match and hamming loss were 0.5853, 0.2407 and 0.0713. These measurements were best among those yielded by three RAKEL classifiers listed in Table 2. Compared with the performance of RAKEL classifiers based on domain embedding features, the superiority of RAKEL classifiers with network embedding features depended on the base classifier. The SVM base classifier gave better performance, whereas RF base classifier yielded lower performance.
| Base classifier | Parameter | Accuracy | Exact match | Hamming loss | Integrated score |
| Support vector machine (Polynomial kernel) |
m = 10, k = 5, C = 2, exponent = 1, feature dimension = 300 | 0.5853 | 0.2407 | 0.0713 | 0.1308 |
| Support vector machine (RBF kernel) |
m = 10, k = 3, C = 2, γ = 0.01, feature dimension=300 | 0.5020 | 0.1551 | 0.0824 | 0.0714 |
| Random forest | m = 10, k = 5, number of decision trees = 250, feature dimension = 150 | 0.5727 | 0.2385 | 0.0714 | 0.1269 |
DownLoad:
CSV
Likewise, for the best RAKEL classifiers with different base classifiers, they were further evaluated by additional ten-fold cross-validation for ten times. A box plot was shown in Figure 4 for each measurement. It is easy to see that each measurement of each classifier was changed in a small range, suggesting the stability of three RAKEL classifiers. This result was almost same as those based on the domain embedding features.
Two types of features were adopted in this study to represent mouse proteins. They indicated essential properties of proteins from different aspects. The combination of these two types of features can be helpful to construct more efficient classifiers. Thus, we constructed RAKEL classifiers using both domain and network embedding features. To save time, we only tried the parameters listed in Tables 1 and 2. The best performance of RAKEL classifiers with different base classifiers are provided in Table 3. The integrated scores for three base classifiers were 0.1619, 0.1096 and 0.1731, respectively. Each of them was higher than the RAKEL classifiers with the same base classifier and domain or network embedding features. Furthermore, it can be observed from Tables 1-3 that given the same base classifier, the classifier with domain and network embedding features always generated higher accuracy, exact match and lower hamming loss than that with only domain or network embedding features. Therefore, the domain and network embedding features can complement each other so that their combination can improve the performance of classifiers.
| Base classifier | Parameter | Accuracy | Exact match | Hamming loss | Integrated score |
| Support vector machine (Polynomial kernel) |
m = 10, k = 5, C = 2, exponent = 1, network embedding feature dimension = 300 | 0.6242 | 0.2777 | 0.0660 | 0.1619 |
| Support vector machine (RBF kernel) |
m = 10, k = 5, C = 2, γ = 0.01, network embedding feature dimension = 300 | 0.5439 | 0.2177 | 0.0743 | 0.1096 |
| Random forest | m = 10, k = 5, number of decision trees = 250, network embedding feature dimension = 150 | 0.6235 | 0.2963 | 0.0633 | 0.1731 |
DownLoad:
CSV
In this study, the label partition was employed to construct multi-label classifiers for identifying functions of mouse proteins. To elaborate the merits of label partition, we also built RAKEL classifiers that did not adopt the label partition. All parameters for three base classifiers and RAKEL were tried for each feature type. All such classifiers were also assessed by ten-fold cross-validation.
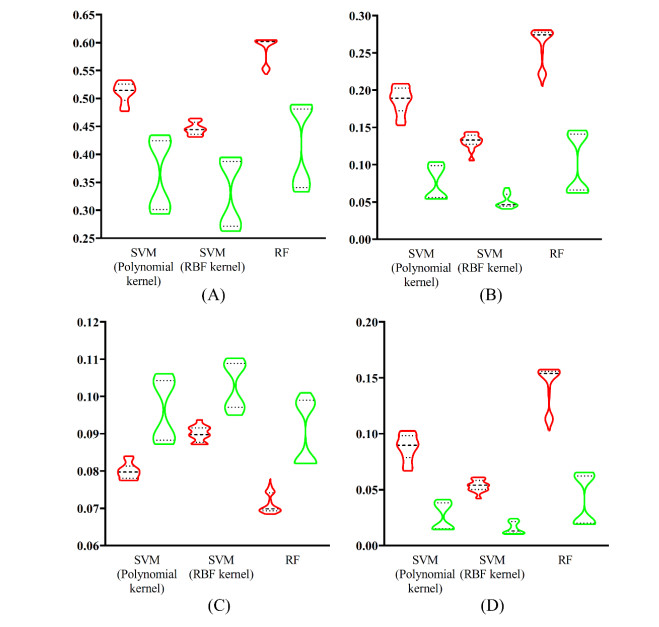
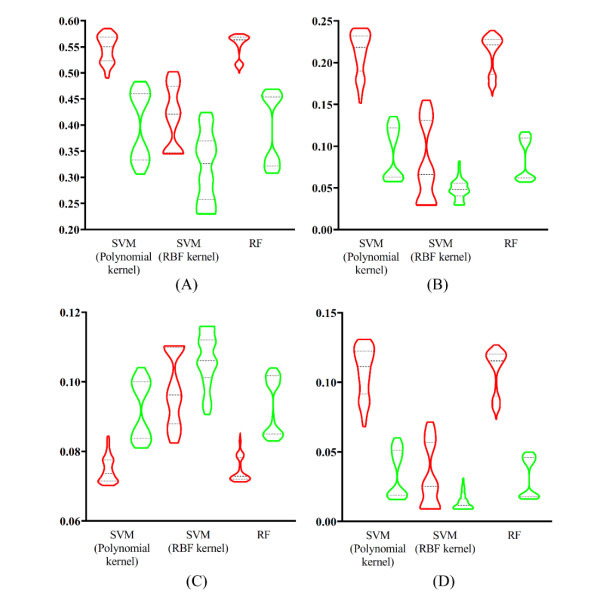
For the classifiers with each base classifier and domain embedding features, we plotted a violin to show their performance on each measurement under different parameters, as shown in Figure 5. For an easy comparison, those yielded by classifiers that employed the label partition were also provided in this figure. It can be observed that the accuracy, exact match and integrated score yielded by classifiers with label partition were all higher than those obtained by classifiers without label partition. As for the hamming loss, it was on the contrary. All these indicated that the employment of label partition can improve the performance of classifiers. For the other feature type, network embedding features, same tests were conducted. The violins of four measurements are illustrated in Figure 6. The same conclusion can be concluded, that is, the classifiers with label partition were generally superior to those without label partition.
For the classifiers using both domain and network embedding features, we tested them with parameters listed in Table 3 when the label space partition procedure was not used. The results of ten-fold cross-validation are listed in Table 4. Evidently, classifiers without label partition were much inferior to those with label partition, suggesting the effectiveness of the label partition.
| Base classifier | Parameter | Accuracy | Exact match | Hamming loss | Integrated score |
| Support vector machine (Polynomial kernel) |
m = 10, k = 5, C = 2, exponent = 1, network embedding feature dimension = 300 | 0.5059 | 0.1507 | 0.0781 | 0.0703 |
| Support vector machine (RBF kernel) |
m = 10, k = 5, C = 2, γ = 0.01, network embedding feature dimension=300 | 0.4485 | 0.1112 | 0.0848 | 0.0456 |
| Random forest | m = 10, k = 5, number of decision trees = 250, network embedding feature dimension = 150 | 0.5069 | 0.1608 | 0.0762 | 0.0753 |
DownLoad:
CSV
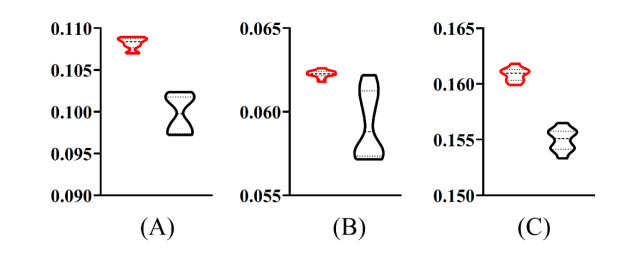
The classifiers proposed in this study adopted the label partition yielded by Louvain method. To confirm such obtained partition was really helpful to improve the performance of classifiers, we employed the random label partition, which randomly divided class labels into some partitions. To give a far comparison, the distribution of partition sizes in random partition was same as that in the partition yielded by Louvain method. On each random partition, the best RAKEL classifier with each base classifier and each feature type was built and assessed by ten-fold cross-validation. Such procedures executed ten times for different random partitions. The performance (integrated score) of each RAKEL classifier on two feature types is shown in Figures 7 and 8, respectively. For easy comparisons, the performance of RAKEL classifiers with partition yielded by Louvain method under ten-fold cross-validation for ten times was also listed in these two figures. It can be observed that when the base classifier was SVM (polynomial kernel) or RF, the RAKEL classifiers with partition yielded by Louvain method always generated better performance. As for the base classifier, SVM (RBF kernel), its superiority was not very obvious. It provided relatively better performance using domain embedding features. However, for network embedding features, classifiers with partition yielded by Louvain method were not always better than those with random partition. As a whole, classifiers with partition yielded by Louvain method were superior to those with random partition. The reasonable partition of class labels can further improve the performance of classifiers.
For the classifiers with both domain and network embedding features, we also compared them with those using random partition. The performance of classifier with each base classifier and random partition is listed in Table 5. Compared with results listed in Table 3, classifiers with partition yielded by Louvain method always produced higher accuracy, exact match and integrated score. As for hamming loss, classifiers with random partition yielded lower values when SVM was the base classifier. However, this cannot change the fact that classifiers with partition yielded by Louvain method were superior to the classifiers with random partition.
| Base classifier | Parameter | Accuracy | Exact match | Hamming loss | Integrated score |
| Support vector machine (Polynomial kernel) |
m = 10, k = 5, C = 2, exponent = 1, network embedding feature dimension = 300 | 0.6177 | 0.2705 | 0.0654 | 0.1562 |
| Support vector machine (RBF kernel) |
m = 10, k = 5, C = 2, γ = 0.01, network embedding feature dimension=300 | 0.5427 | 0.2138 | 0.0737 | 0.1075 |
| Random forest | m = 10, k = 5, number of decision trees = 250, network embedding feature dimension = 150 | 0.6195 | 0.2952 | 0.0635 | 0.1713 |
DownLoad:
CSV
In references [9,10], two hybrid classifiers were proposed to identify functions of mouse proteins. They contained one network-based classifier, which was constructed based on PPI information reported in STRING. For a query protein, this classifier assigned a score to each of 24 functional types. Then, 24 types were sorted by the decreasing order of corresponding scores. Evidently, this classifier cannot determine which types were the predicted types. To compare with our classifiers, we employed a threshold for such score so that this classifier can determine the predicted types. Various thresholds were tried for this classifier, which was assessed by ten-fold cross-validation for ten times. The highest integrated score was only 0.0160, which was much lower than those listed in Tables 1-3. The accuracy was 0.2532, exact match was 0.0706 and hamming loss was 0.1059. Clearly, such performance was much lower than that of any above-mentioned classifier. This result indicated that the classifiers proposed in this study were superior to this previous classifier.
As mentioned above, the usage of label partition improved the performance of multi-label classifiers. The final classifier should use the label partition on the whole dataset. This section gave analyses on 24 functional types (labels).
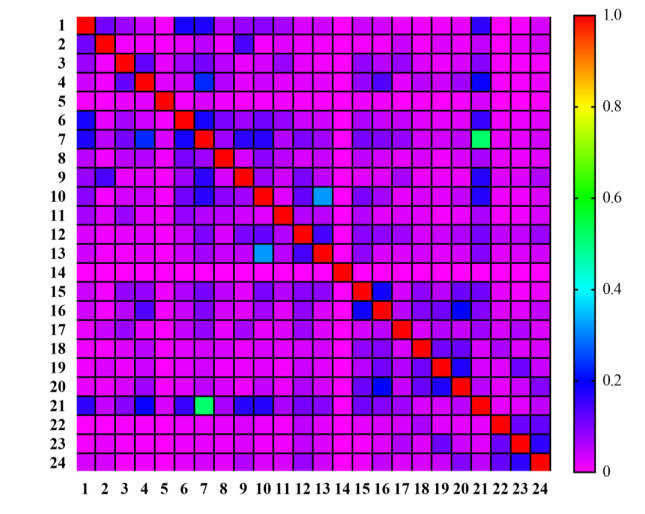
First, we constructed a protein subset for each label, which consisted of all proteins having this label. For any two labels, their associations were evaluated by the Tanimoto coefficient of their corresponding protein subsets. A heat map was plotted to show Tanimoto coefficients for any two functional types, as illustrated in Figure 9. It can be observed that class 14 (TRANSPOSABLE ELEMENTS, VIRAL AND PLASMID PROTEINS) has weak associations with almost all other classes. On the contrary, class 7 (PROTEIN WITH BINDING FUNCTION OR COFACTOR REQUIREMENT (structural or catalytic)) and class 21 (SUBCELLULAR LOCALIZATION) were highly related to other classes. By using the Louvain method, 24 functional types were divided into three partitions, which are listed in Table 6. There were 14 functional types in Partition 1, whereas other two partitions all contained five functional types. Not surprisingly, class 7 and class 21 were classified into the same partition. Given a protein representation, a multi-label classifier can be built on each partition. Classifiers on all three partitions were integrated in the final multi-label classifier.
| Index | Functional type |
| Partition 1 | PROTEIN WITH BINDING FUNCTION OR COFACTOR REQUIREMENT (structural or catalytic) REGULATION OF METABOLISM AND PROTEIN FUNCTION CELLULAR COMMUNICATION/SIGNAL TRANSDUCTION MECHANISM SUBCELLULAR LOCALIZATION CELLULAR TRANSPORT, TRANSPORT FACILITIES AND TRANSPORT ROUTES TRANSCRIPTION ENERGY METABOLISM CELL CYCLE AND DNA PROCESSING PROTEIN FATE (folding, modification, destination) BIOGENESIS OF CELLULAR COMPONENTS SYSTEMIC INTERACTION WITH THE ENVIRONMENT PROTEIN SYNTHESIS CELL RESCUE, DEFENSE AND VIRULENCE |
| Partition 2 | INTERACTION WITH THE ENVIRONMENT CELL TYPE LOCALIZATION TISSUE LOCALIZATION ORGAN LOCALIZATION TRANSPOSABLE ELEMENTS, VIRAL AND PLASMID PROTEINS |
| Partition 3 | CELL FATE DEVELOPMENT (Systemic) TISSUE DIFFERENTIATION ORGAN DIFFERENTIATION CELL TYPE DIFFERENTIATION |
DownLoad:
CSV
By employing the association information of functional types, the performance of the multi-label classifiers for identification of mouse protein functions was improved. However, there still exist rooms for improvement. First, protein features are key factors that can influence the performance of classifiers. Some novel and efficient protein features, such as motif embedding features [58], can be adopted to further improve the classifiers. Second, only one community detection algorithm, Louvain method, was employed to cluster functional types in this study. It was not clear whether this algorithm was optimum to deal with this problem. Some novel community detection algorithms may deeply investigate the associations between functional types, thereby producing a more optimum label partition. Finally, we adopted traditional machine learning algorithms (RAKEL, SVM, RF) to construct classifiers. They can be replaced with more powerful algorithms, such as deep learning algorithms, so that more efficient classifiers can be built. In future, we will continue our study in these aspects.
This study proposed a novel multi-label classifier for identification of functions of mouse proteins. Such classifier considered the associations of functional types (labels) and divided labels into some partitions. By employing the label partition, the performance of classifiers was improved. This classifier can be easily extended to other organisms. It is hopeful that this classifier can be helpful to identify novel functions of mouse proteins. All codes and data are available at https://github.com/LiXuuuu/Mouse-Protein.
The authors declare no conflict of interest.
| [1] | Aitchison J (1999) Linguistics England, UK: The McGraw-Hill Companies, Inc., 50-150. |
| [2] | Fromkin V, Rodman R, Hyams NM (2003) An introduction to language Boston: Thomson, Wadsworth, 69-329. |
| [3] | Parker F, Riley KL (2005) Linguistics for non-linguists: a primer with exercises Boston, Mass: Allyn and Bacon, 12-137. |
| [4] | Finch G (2005) Key concepts in language and linguistics: Palgrave Macmillan. 31-40. |
| [5] | Field J (2003) Psycholinguistics: A resource book for students: Psychology Press London: Routledge. |
| [6] | Fromkin V, Rodman R, Hyams N (2018) An introduction to language Wadsworth: Cengage Learning, 4-270. |
| [7] |
Ghazi Saidi L, Perlbarg V, Marrelec G, et al. (2013) Functional connectivity changes in second language vocabulary learning. Brain Lang 124: 56-65. doi: 10.1016/j.bandl.2012.11.008
|
| [8] |
Ghazi-Saidi L, Ansaldo AI (2017) Second Language Word Learning through Repetition and Imitation: Functional Networks as a Function of Learning Phase and Language Distance. Front Hum Neurosci 11: 463. doi: 10.3389/fnhum.2017.00463
|
| [9] | Parker F, Riley KL, Riley KL (2005) Grammar for grammarians: prescriptive, descriptive, generative, contextual Chicago: Parlay Press, 12-137. |
| [10] | Fromkin V, Rodman R (1988) An introduction to language New York: Holt, Rinehart, and Winston, 69-329. |
| [11] | Yule G (1996) The study of language Cambridge England: Cambridge University Press, 25-156. |
| [12] | Falk JS (1978) ERIC Clearinghouse on Languages and Linguistics. Language and linguistics: bases for a curriculum Arlington Va: Center for Applied Linguistics, 5-12. |
| [13] |
Hickok G, Poeppel D (2007) The cortical organization of speech processing. Nat Rev Neurosci 8: 393-402. doi: 10.1038/nrn2113
|
| [14] |
Poeppel D, Idsardi WJ, Van Wassenhove V (2008) Speech perception at the interface of neurobiology and linguistics. Philos Trans R Soc Lond B Biol Sci 363: 1071-1086. doi: 10.1098/rstb.2007.2160
|
| [15] |
Price CJ (2010) The anatomy of language: a review of 100 fMRI studies published in 2009. Ann N Y Acad Sci 1191: 62-88. doi: 10.1111/j.1749-6632.2010.05444.x
|
| [16] |
Buchweitz A, Mason RA, Tomitch LM, et al. (2009) Brain activation for reading and listening comprehension: An fMRI study of modality effects and individual differences in language comprehension. Psychol Neurosci 2: 111-123. doi: 10.3922/j.psns.2009.2.003
|
| [17] |
Keller TA, Carpenter PA, Just MA (2001) The neural bases of sentence comprehension: a fMRI examination of syntactic and lexical processing. Cereb Cortex 11: 223-237. doi: 10.1093/cercor/11.3.223
|
| [18] | Obler LK, Gjerlow K (1999) Language and the brain Cambridge, UK; New York: Cambridge University Press, 141-156. |
| [19] | Banich MT, Mack MA (2003) Mind, brain, and language: multidisciplinary perspectives Mahwah, NJ: L Erlbaum Associates, 23-61. |
| [20] |
Tan LH, Laird AR, Li K, et al. (2005) Neuroanatomical correlates of phonological processing of Chinese characters and alphabetic words: a meta-analysis. Hum Brain Mapp 25: 83-91. doi: 10.1002/hbm.20134
|
| [21] |
Price CJ (2000) The anatomy of language: contributions from functional neuroimaging. J Anat 197: 335-359. doi: 10.1046/j.1469-7580.2000.19730335.x
|
| [22] |
Hill VB, Cankurtaran CZ, Liu BP, et al. (2019) A Practical Review of Functional MRI Anatomy of the Language and Motor Systems. Am J Neuroradiol 40: 1084-1090. doi: 10.3174/ajnr.A6089
|
| [23] |
Gordon EM, Laumann TO, Marek S, et al. (2020) Default-mode network streams for coupling to language and control systems. Proc Natl Acad Sci U S A 117: 17308-17319. doi: 10.1073/pnas.2005238117
|
| [24] | Liberman P (2000) Human Languages and our brain: The subcortical bases of speech, syntax and thought Cambridge: Harvard University Press. |
| [25] |
Lopes TM, Yasuda CL, Campos BM, et al. (2016) Effects of task complexity on activation of language areas in a semantic decision fMRI protocol. Neuropsychologia 81: 140-148. doi: 10.1016/j.neuropsychologia.2015.12.020
|
| [26] |
Krings T, Topper R, Foltys H, et al. (2000) Cortical activation patterns during complex motor tasks in piano players and control subjects. A functional magnetic resonance imaging study. Neurosci Lett 278: 189-193. doi: 10.1016/S0304-3940(99)00930-1
|
| [27] | Carey JR, Bhatt E, Nagpal A (2005) Neuroplasticity promoted by task complexity. Exerc Sport Sci Rev 33: 24-31. |
| [28] |
van de Ven V, Esposito F, Christoffels IK (2009) Neural network of speech monitoring overlaps with overt speech production and comprehension networks: a sequential spatial and temporal ICA study. Neuroimage 47: 1982-1991. doi: 10.1016/j.neuroimage.2009.05.057
|
| [29] |
Bitan T, Booth JR, Choy J, et al. (2005) Shifts of effective connectivity within a language network during rhyming and spelling. J Neurosci 25: 5397-5403. doi: 10.1523/JNEUROSCI.0864-05.2005
|
| [30] |
Just MA, Newman SD, Keller TA, et al. (2004) Imagery in sentence comprehension: an fMRI study. Neuroimage 21: 112-124. doi: 10.1016/j.neuroimage.2003.08.042
|
| [31] |
Warren JE, Crinion JT, Lambon Ralph MA, et al. (2009) Anterior temporal lobe connectivity correlates with functional outcome after aphasic stroke. Brain 132: 3428-3442. doi: 10.1093/brain/awp270
|
| [32] |
Leff AP, Schofield TM, Stephan KE, et al. (2008) The cortical dynamics of intelligible speech. J Neurosci 28: 13209-13215. doi: 10.1523/JNEUROSCI.2903-08.2008
|
| [33] |
Vitali P, Abutalebi J, Tettamanti M, et al. (2007) Training-induced brain remapping in chronic aphasia: a pilot study. Neurorehabil Neural Repair 21: 152-160. doi: 10.1177/1545968306294735
|
| [34] |
Meinzer M, Flaisch T, Obleser J, et al. (2006) Brain regions essential for improved lexical access in an aged aphasic patient: a case report. BMC Neurol 6: 28. doi: 10.1186/1471-2377-6-28
|
| [35] |
Hillis AE, Kleinman JT, Newhart M, et al. (2006) Restoring cerebral blood flow reveals neural regions critical for naming. J Neurosci 26: 8069-8073. doi: 10.1523/JNEUROSCI.2088-06.2006
|
| [36] |
Marsh EB, Hillis AE (2005) Cognitive and neural mechanisms underlying reading and naming: evidence from letter-by-letter reading and optic aphasia. Neurocase 11: 325-337. doi: 10.1080/13554790591006320
|
| [37] |
Kan IP, Thompson-Schill SL (2004) Effect of name agreement on prefrontal activity during overt and covert picture naming. Cogn Affect Behav Neurosci 4: 43-57. doi: 10.3758/CABN.4.1.43
|
| [38] |
Leger A, Demonet JF, Ruff S, et al. (2002) Neural substrates of spoken language rehabilitation in an aphasic patient: an fMRI study. Neuroimage 17: 174-183. doi: 10.1006/nimg.2002.1238
|
| [39] |
Gotts SJ, della Rocchetta AI, Cipolotti L (2002) Mechanisms underlying perseveration in aphasia: evidence from a single case study. Neuropsychologia 40: 1930-1947. doi: 10.1016/S0028-3932(02)00067-2
|
| [40] |
Arevalo A, Perani D, Cappa SF, et al. (2007) Action and object processing in aphasia: from nouns and verbs to the effect of manipulability. Brain Lang 100: 79-94. doi: 10.1016/j.bandl.2006.06.012
|
| [41] |
Duffau H (2008) The anatomo-functional connectivity of language revisited. New insights provided by electrostimulation and tractography. Neuropsychologia 46: 927-934. doi: 10.1016/j.neuropsychologia.2007.10.025
|
| [42] |
Baddeley A (2012) Working memory: theories, models, and controversies. Annu Rev Psychol 63: 1-29. doi: 10.1146/annurev-psych-120710-100422
|
| [43] |
Diamond A (2013) Executive functions. Annu Rev Psychol 64: 135-168. doi: 10.1146/annurev-psych-113011-143750
|
| [44] |
Baddeley AD, Hitch G (1974) Working memory. Psychology of learning and motivation Elsevier: Academic Press, 47-89. doi: 10.1016/S0079-7421(08)60452-1
|
| [45] |
D'Esposito M, Postle BR (2015) The cognitive neuroscience of working memory. Annu Rev Psychol 66: 115-142. doi: 10.1146/annurev-psych-010814-015031
|
| [46] |
De Fockert JW (2013) Beyond perceptual load and dilution: a review of the role of working memory in selective attention. Front Psychol 4: 287. doi: 10.3389/fpsyg.2013.00287
|
| [47] |
Fougnie D, Marois R (2009) Attentive Tracking Disrupts Feature Binding in Visual Working Memory. Vis Cogn 17: 48-66. doi: 10.1080/13506280802281337
|
| [48] | Dowd EW (2016) Memory-Based Attentional Guidance: A Window to the Relationship between Working Memory and Attention, Doctoral dissertation: Duke University. 6-23. |
| [49] | Pennington BF, Bennetto L, McAleer O, et al. (1996) Executive functions and working memory: Theoretical and measurement issues. |
| [50] | Zillmer E, Spiers M, Culbertson WC (2001) Principles of neuropsychology Belmont CA: Wadsworth Pub Co, 606. |
| [51] | Cowan N (1995) Attention and memory: an integrated framework New York: Oxford University Press. |
| [52] |
Ericsson KA, Kintsch W (1995) Long-term working memory. Psychol Rev 102: 211-245. doi: 10.1037/0033-295X.102.2.211
|
| [53] |
Baddeley A (2003) Working memory: looking back and looking forward. Nat Rev Neurosci 4: 829-839. doi: 10.1038/nrn1201
|
| [54] |
Postle BR (2006) Working memory as an emergent property of the mind and brain. Neuroscience 139: 23-38. doi: 10.1016/j.neuroscience.2005.06.005
|
| [55] |
Woodman GF, Vogel EK (2005) Fractionating working memory: consolidation and maintenance are independent processes. Psychol Sci 16: 106-113. doi: 10.1111/j.0956-7976.2005.00790.x
|
| [56] | Fuster JM (1997) The prefrontal cortex: anatomy, physiology, and neuropsychology of the frontal lobe Philadelphia: Lippincott-Raven. |
| [57] |
Cowan N (2017) The many faces of working memory and short-term storage. Psychon Bull Rev 24: 1158-1170. doi: 10.3758/s13423-016-1191-6
|
| [58] |
Miyake A, Shah P (1999) Models of working memory: mechanisms of active maintenance and executive control New York: Cambridge University Press. doi: 10.1017/CBO9781139174909
|
| [59] |
Awh E, Vogel EK, Oh SH (2006) Interactions between attention and working memory. Neuroscience 139: 201-208. doi: 10.1016/j.neuroscience.2005.08.023
|
| [60] |
Engle RW, Tuholski SW, Laughlin JE, et al. (1999) Working memory, short-term memory, and general fluid intelligence: a latent-variable approach. J Exp Psychol Gen 128: 309-331. doi: 10.1037/0096-3445.128.3.309
|
| [61] |
Heitz RP, Engle RW (2007) Focusing the spotlight: individual differences in visual attention control. J Exp Psychol Gen 136: 217-240. doi: 10.1037/0096-3445.136.2.217
|
| [62] | Baddeley AD (2000) Short-term and working memory. The Oxford handbook of memory Oxford University Press, 77-92. |
| [63] |
Wager TD, Smith EE (2003) Neuroimaging studies of working memory: a meta-analysis. Cogn Affect Behav Neurosci 3: 255-274. doi: 10.3758/CABN.3.4.255
|
| [64] |
Jonides J, Lacey SC, Nee DE (2005) Processes of working memory in mind and brain. Curr Dir Psychol Sci 14: 2-5. doi: 10.1111/j.0963-7214.2005.00323.x
|
| [65] |
Pessoa L, Gutierrez E, Bandettini P, et al. (2002) Neural correlates of visual working memory: fMRI amplitude predicts task performance. Neuron 35: 975-987. doi: 10.1016/S0896-6273(02)00817-6
|
| [66] |
Palva JM, Monto S, Kulashekhar S, et al. (2010) Neuronal synchrony reveals working memory networks and predicts individual memory capacity. Proc Natl Acad Sci U S A 107: 7580-7585. doi: 10.1073/pnas.0913113107
|
| [67] |
Murphy AC, Bertolero MA, Papadopoulos L, et al. (2020) Multimodal network dynamics underpinning working memory. Nat Commun 11: 3035. doi: 10.1038/s41467-020-15541-0
|
| [68] |
Chai WJ, Abd Hamid AI, Abdullah JM (2018) Working Memory From the Psychological and Neurosciences Perspectives: A Review. Front Psychol 9: 401. doi: 10.3389/fpsyg.2018.00401
|
| [69] |
Kim C, Kroger JK, Calhoun VD, et al. (2015) The role of the frontopolar cortex in manipulation of integrated information in working memory. Neurosci Lett 595: 25-29. doi: 10.1016/j.neulet.2015.03.044
|
| [70] |
Jimura K, Chushak MS, Westbrook A, et al. (2018) Intertemporal Decision-Making Involves Prefrontal Control Mechanisms Associated with Working Memory. Cereb Cortex 28: 1105-1116. doi: 10.1093/cercor/bhx015
|
| [71] |
Osaka M, Osaka N, Kondo H, et al. (2003) The neural basis of individual differences in working memory capacity: an fMRI study. Neuroimage 18: 789-797. doi: 10.1016/S1053-8119(02)00032-0
|
| [72] |
Moore AB, Li Z, Tyner CE, et al. (2013) Bilateral basal ganglia activity in verbal working memory. Brain Lang 125: 316-323. doi: 10.1016/j.bandl.2012.05.003
|
| [73] |
Vartanian O, Jobidon ME, Bouak F, et al. (2013) Working memory training is associated with lower prefrontal cortex activation in a divergent thinking task. Neuroscience 236: 186-194. doi: 10.1016/j.neuroscience.2012.12.060
|
| [74] |
Rodriguez Merzagora AC, Izzetoglu M, Onaral B, et al. (2014) Verbal working memory impairments following traumatic brain injury: an fNIRS investigation. Brain Imaging Behav 8: 446-459. doi: 10.1007/s11682-013-9258-8
|
| [75] |
Owen AM, McMillan KM, Laird AR, et al. (2005) N-back working memory paradigm: a meta-analysis of normative functional neuroimaging studies. Hum Brain Mapp 25: 46-59. doi: 10.1002/hbm.20131
|
| [76] |
Andersen RA, Cui H (2009) Intention, action planning, and decision making in parietal-frontal circuits. Neuron 63: 568-583. doi: 10.1016/j.neuron.2009.08.028
|
| [77] |
Kiyonaga A, Egner T (2013) Working memory as internal attention: toward an integrative account of internal and external selection processes. Psychon Bull Rev 20: 228-242. doi: 10.3758/s13423-012-0359-y
|
| [78] |
Sreenivasan KK, Curtis CE, D'Esposito M (2014) Revisiting the role of persistent neural activity during working memory. Trends Cogn Sci 18: 82-89. doi: 10.1016/j.tics.2013.12.001
|
| [79] |
Andrews-Hanna JR (2012) The brain's default network and its adaptive role in internal mentation. Neuroscientist 18: 251-270. doi: 10.1177/1073858411403316
|
| [80] |
Spreng RN, Stevens WD, Chamberlain JP, et al. (2010) Default network activity, coupled with the frontoparietal control network, supports goal-directed cognition. Neuroimage 53: 303-317. doi: 10.1016/j.neuroimage.2010.06.016
|
| [81] |
Cowan N (2001) The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behav Brain Sci 24: 87-114. doi: 10.1017/S0140525X01003922
|
| [82] |
Luck SJ, Vogel EK (1997) The capacity of visual working memory for features and conjunctions. Nature 390: 279-281. doi: 10.1038/36846
|
| [83] |
Cowan N (1999) An Embedded Process Model of Working Memory. Models of Working Memory: Mechanisms of Active Maintenance and Executive Control Cambridge: Cambridge University Press, 62-101. doi: 10.1017/CBO9781139174909.006
|
| [84] |
Van den Berg R, Shin H, Chou WC, et al. (2012) Variability in encoding precision accounts for visual short-term memory limitations. Proc Natl Acad Sci 109: 8780-8785. doi: 10.1073/pnas.1117465109
|
| [85] |
Fougnie D, Suchow JW, Alvarez GA (2012) Variability in the quality of visual working memory. Nat Commun 3: 1229. doi: 10.1038/ncomms2237
|
| [86] |
Klencklen G, Lavenex PB, Brandner C, et al. (2017) Working memory decline in normal aging: Is it really worse in space than in color? Learn Motiv 57: 48-60. doi: 10.1016/j.lmot.2017.01.007
|
| [87] |
Unsworth N, Fukuda K, Awh E, et al. (2014) Working memory and fluid intelligence: capacity, attention control, and secondary memory retrieval. Cogn Psychol 71: 1-26. doi: 10.1016/j.cogpsych.2014.01.003
|
| [88] | Smith EE, Geva A (2000) Verbal working memory and its connections to language processing. In Foundations of Neuropsychology, Language and the Brain Academic Press, 123-141. |
| [89] |
Fan LZ, Li H, Zhuo JJ, et al. (2016) The Human Brainnetome Atlas: A New Brain Atlas Based on Connectional Architecture. Cereb Cortex 26: 3508-3526. doi: 10.1093/cercor/bhw157
|
| [90] |
Bordier C, Hupe JM, Dojat M (2015) Quantitative evaluation of fMRI retinotopic maps, from V1 to V4, for cognitive experiments. Front Hum Neurosci 9: 277. doi: 10.3389/fnhum.2015.00277
|
| [91] |
Fedorenko E, Varley R (2016) Language and thought are not the same thing: evidence from neuroimaging and neurological patients. Ann N Y Acad Sci 1369: 132-153. doi: 10.1111/nyas.13046
|
| [92] |
Emch M, von Bastian CC, Koch K (2019) Neural Correlates of Verbal Working Memory: An fMRI Meta-Analysis. Front Hum Neurosci 13: 180. doi: 10.3389/fnhum.2019.00180
|
| [93] |
Mahdavi A, Azar R, Shoar MH, et al. (2015) Functional MRI in clinical practice: Assessment of language and motor for pre-surgical planning. Neuroradiol J 28: 468-473. doi: 10.1177/1971400915609343
|
| [94] |
Siyanova-Chanturia A, Canal P, Heredia RR (2019) Event-Related Potentials in Monolingual and Bilingual Non-literal Language Processing. The Handbook of the Neuroscience of Multilingualism John Wiley & Sons Ltd, 508-529. doi: 10.1002/9781119387725.ch25
|
| [95] |
Rossi S, Telkemeyer S, Wartenburger I, et al. (2012) Shedding light on words and sentences: near-infrared spectroscopy in language research. Brain Lang 121: 152-163. doi: 10.1016/j.bandl.2011.03.008
|
| [96] | Crosson B (1992) Subcortical functions in language and memory New York: Guilford Press, 374. |
| [97] |
Buchweitz A, Keller TA, Meyler A, et al. (2012) Brain activation for language dual-tasking: listening to two people speak at the same time and a change in network timing. Hum Brain Mapp 33: 1868-1882. doi: 10.1002/hbm.21327
|
| [98] |
Fiebach CJ, Vos SH, Friederici AD (2004) Neural correlates of syntactic ambiguity in sentence comprehension for low and high span readers. J Cogn Neurosci 16: 1562-1575. doi: 10.1162/0898929042568479
|
| [99] |
Mason RA, Just MA (2007) Lexical ambiguity in sentence comprehension. Brain Res 1146: 115-127. doi: 10.1016/j.brainres.2007.02.076
|
| [100] |
Kane MJ, Conway ARA, Miura TK, et al. (2007) Working memory, attention control, and the N-back task: a question of construct validity. J Exp Psychol Learn Mem Cogn 33: 615-622. doi: 10.1037/0278-7393.33.3.615
|
| [101] |
Jaeggi SM, Buschkuehl M, Perrig WJ, et al. (2010) The concurrent validity of the N-back task as a working memory measure. Memory 18: 394-412. doi: 10.1080/09658211003702171
|
| [102] |
Rudner M, Karlsson T, Gunnarsson J, et al. (2013) Levels of processing and language modality specificity in working memory. Neuropsychologia 51: 656-666. doi: 10.1016/j.neuropsychologia.2012.12.011
|
| [103] |
Rudner M, Ronnberg J, Hugdahl K (2005) Reversing spoken items-mind twisting not tongue twisting. Brain Lang 92: 78-90. doi: 10.1016/j.bandl.2004.05.010
|
| [104] |
Newman SD, Malaia E, Seo R, et al. (2013) The effect of individual differences in working memory capacity on sentence comprehension: an FMRI study. Brain Topogr 26: 458-467. doi: 10.1007/s10548-012-0264-8
|
| [105] |
D'Esposito M, Detre JA, Alsop DC, et al. (1995) The neural basis of the central executive system of working memory. Nature 378: 279-281. doi: 10.1038/378279a0
|
| [106] |
Jaeggi SM, Seewer R, Nirkko AC, et al. (2003) Does excessive memory load attenuate activation in the prefrontal cortex? Load-dependent processing in single and dual tasks: functional magnetic resonance imaging study. Neuroimage 19: 210-225. doi: 10.1016/S1053-8119(03)00098-3
|
| [107] |
Taylor JG, Taylor NR (2000) Analysis of recurrent cortico-basal ganglia-thalamic loops for working memory. Biol Cybern 82: 415-432. doi: 10.1007/s004220050595
|
| [108] | Nir-Cohen G, Kessler Y, Egner T (2020) Neural substrates of working memory updating. BioRxiv 853630. |
| [109] |
McNab F, Klingberg T (2008) Prefrontal cortex and basal ganglia control access to working memory. Nat Neurosci 11: 103-107. doi: 10.1038/nn2024
|
| [110] |
Wallentin M, Roepstorff A, Glover R, et al. (2006) Parallel memory systems for talking about location and age in precuneus, caudate and Broca's region. Neuroimage 32: 1850-1864. doi: 10.1016/j.neuroimage.2006.05.002
|
| [111] | Levelt WJ, Roelofs A, Meyer AS (1999) A theory of lexical access in speech production. Behav Brain Sci 22: 1-38. |
| [112] |
Marvel CL, Desmond JE (2012) From storage to manipulation: How the neural correlates of verbal working memory reflect varying demands on inner speech. Brain Lang 120: 42-51. doi: 10.1016/j.bandl.2011.08.005
|
| [113] |
McGettigan C, Warren JE, Eisner F, et al. (2011) Neural correlates of sublexical processing in phonological working memory. J Cogn Neurosci 23: 961-977. doi: 10.1162/jocn.2010.21491
|
| [114] |
Powell JL, Kemp GJ, Garcia-Finana M (2012) Association between language and spatial laterality and cognitive ability: an fMRI study. Neuroimage 59: 1818-1829. doi: 10.1016/j.neuroimage.2011.08.040
|
| [115] |
Sahin NT, Pinker S, Halgren E (2006) Abstract grammatical processing of nouns and verbs in Broca's area: evidence from fMRI. Cortex 42: 540-562. doi: 10.1016/S0010-9452(08)70394-0
|
| [116] | Meyer L, Obleser J, Kiebel SJ, et al. (2012) Spatiotemporal dynamics of argument retrieval and reordering: an FMRI and EEG study on sentence processing. Front Psychol 3: 523. |
| [117] |
Bonhage CE, Fiebach CJ, Bahlmann J, et al. (2014) Brain signature of working memory for sentence structure: enriched encoding and facilitated maintenance. J Cogn Neurosci 26: 1654-1671. doi: 10.1162/jocn_a_00566
|
| [118] |
Bassett DS, Sporns O (2017) Network neuroscience. Nat Neurosci 20: 353-364. doi: 10.1038/nn.4502
|
| [119] |
Meier J, Tewarie P, Hillebrand A, et al. (2016) A Mapping Between Structural and Functional Brain Networks. Brain Connect 6: 298-311. doi: 10.1089/brain.2015.0408
|
| [120] |
Yao Z, Hu B, Xie Y, et al. (2015) A review of structural and functional brain networks: small world and atlas. Brain Inform 2: 45-52. doi: 10.1007/s40708-015-0009-z
|
| [121] |
Makuuchi M, Friederici AD (2013) Hierarchical functional connectivity between the core language system and the working memory system. Cortex 49: 2416-2423. doi: 10.1016/j.cortex.2013.01.007
|
| [122] |
Dehaene S, Cohen L (2011) The unique role of the visual word form area in reading. Trends Cogn Sci 15: 254-262. doi: 10.1016/j.tics.2011.04.003
|
| [123] | Caplan D, Waters GS (1999) Verbal working memory and sentence comprehension. Behav Brain Sci 22: 77-94. |
| [124] |
Perrachione TK, Ghosh SS, Ostrovskaya I, et al. (2017) Phonological Working Memory for Words and Nonwords in Cerebral Cortex. J Speech Lang Hear Res 60: 1959-1979. doi: 10.1044/2017_JSLHR-L-15-0446
|
| [125] |
Newman SD, Just MA, Carpenter PA (2002) The synchronization of the human cortical working memory network. Neuroimage 15: 810-822. doi: 10.1006/nimg.2001.0997
|
| [126] |
Nyberg L, Sandblom J, Jones S, et al. (2003) Neural correlates of training-related memory improvement in adulthood and aging. Proc Natl Acad Sci U S A 100: 13728-13733. doi: 10.1073/pnas.1735487100
|
| [127] |
Cooke A, Grossman M, DeVita C, et al. (2006) Large-scale neural network for sentence processing. Brain Lang 96: 14-36. doi: 10.1016/j.bandl.2005.07.072
|
| [128] |
Tomasi D, Volkow ND (2020) Network connectivity predicts language processing in healthy adults. Hum Brain Mapp 41: 3696-3708. doi: 10.1002/hbm.25042
|
| [129] |
Brownsett SL, Wise RJ (2010) The contribution of the parietal lobes to speaking and writing. Cereb Cortex 20: 517-523. doi: 10.1093/cercor/bhp120
|
| [130] |
Segal E, Petrides M (2013) Functional activation during reading in relation to the sulci of the angular gyrus region. Eur J Neurosci 38: 2793-2801. doi: 10.1111/ejn.12277
|
| [131] |
Tomasi D, Volkow ND (2012) Resting functional connectivity of language networks: characterization and reproducibility. Mol Psychiatry 17: 841-854. doi: 10.1038/mp.2011.177
|
| [132] |
Cunningham SI, Tomasi D, Volkow ND (2017) Structural and functional connectivity of the precuneus and thalamus to the default mode network. Hum Brain Mapp 38: 938-956. doi: 10.1002/hbm.23429
|
| [133] |
Raichle ME, Snyder AZ (2007) A default mode of brain function: a brief history of an evolving idea. Neuroimage 37: 1083-1090. doi: 10.1016/j.neuroimage.2007.02.041
|
| [134] |
Mineroff Z, Blank IA, Mahowald K, et al. (2018) A robust dissociation among the language, multiple demand, and default mode networks: Evidence from inter-region correlations in effect size. Neuropsychologia 119: 501-511. doi: 10.1016/j.neuropsychologia.2018.09.011
|
| [135] |
Ellis Weismer S, Plante E, Jones M, et al. (2005) A functional magnetic resonance imaging investigation of verbal working memory in adolescents with specific language impairment. J Speech Lang Hear Res 48: 405-425. doi: 10.1044/1092-4388(2005/028)
|
| [136] |
Beneventi H, Tonnessen FE, Ersland L (2009) Dyslexic children show short-term memory deficits in phonological storage and serial rehearsal: an fMRI study. Int J Neurosci 119: 2017-2043. doi: 10.1080/00207450903139671
|
| [137] |
Buchsbaum B, Pickell B, Love T, et al. (2005) Neural substrates for verbal working memory in deaf signers: fMRI study and lesion case report. Brain Lang 95: 265-272. doi: 10.1016/j.bandl.2005.01.009
|
| [138] |
Whitwell JL, Jones DT, Duffy JR, et al. (2015) Working memory and language network dysfunctions in logopenic aphasia: a task-free fMRI comparison with Alzheimer's dementia. Neurobiol Aging 36: 1245-1252. doi: 10.1016/j.neurobiolaging.2014.12.013
|
| [139] |
Price CJ (2012) A review and synthesis of the first 20 years of PET and fMRI studies of heard speech, spoken language and reading. Neuroimage 62: 816-847. doi: 10.1016/j.neuroimage.2012.04.062
|
| [140] | Heim S (2005) The structure and dynamics of normal language processing: insights from neuroimaging. Acta Neurobiol Exp (Wars) 65: 95-116. |
| [141] |
Dick AS, Bernal B, Tremblay P (2014) The language connectome: new pathways, new concepts. Neuroscientist 20: 453-467. doi: 10.1177/1073858413513502
|
 neurosci-08-01-001-s001.pdf |
 |
| 1. | FeiMing Huang, Lei Chen, Wei Guo, Tao Huang, Yu-dong Cai, Fan Yang, Identification of Human Cell Cycle Phase Markers Based on Single-Cell RNA-Seq Data by Using Machine Learning Methods, 2022, 2022, 2314-6141, 1, 10.1155/2022/2516653 | |
| 2. | Yu-Hang Zhang, ShiJian Ding, Lei Chen, Tao Huang, Yu-Dong Cai, Andrey Cherstvy, Subcellular Localization Prediction of Human Proteins Using Multifeature Selection Methods, 2022, 2022, 2314-6141, 1, 10.1155/2022/3288527 | |
| 3. | Jian Lu, Mei Meng, XianChao Zhou, Shijian Ding, KaiYan Feng, Zhenbing Zeng, Tao Huang, Yu-Dong Cai, Identification of COVID-19 severity biomarkers based on feature selection on single-cell RNA-Seq data of CD8+ T cells, 2022, 13, 1664-8021, 10.3389/fgene.2022.1053772 | |
| 4. | Yu-Hang Zhang, Zhan Dong Li, Tao Zeng, Lei Chen, Tao Huang, Yu-Dong Cai, Screening gene signatures for clinical response subtypes of lung transplantation, 2022, 297, 1617-4615, 1301, 10.1007/s00438-022-01918-x | |
| 5. | Wenjing Yi, Ao Sun, Manman Liu, Xiaoqing Liu, Wei Zhang, Qi Dai, Lin Lu, Comparative Study on Feature Selection in Protein Structure and Function Prediction, 2022, 2022, 1748-6718, 1, 10.1155/2022/1650693 | |
| 6. | ZhanDong Li, Deling Wang, HuiPing Liao, ShiQi Zhang, Wei Guo, Lei Chen, Lin Lu, Tao Huang, Yu-Dong Cai, Exploring the Genomic Patterns in Human and Mouse Cerebellums Via Single-Cell Sequencing and Machine Learning Method, 2022, 13, 1664-8021, 10.3389/fgene.2022.857851 | |
| 7. | Zhiyang Liu, Mei Meng, ShiJian Ding, XiaoChao Zhou, KaiYan Feng, Tao Huang, Yu-Dong Cai, Identification of methylation signatures and rules for predicting the severity of SARS-CoV-2 infection with machine learning methods, 2022, 13, 1664-302X, 10.3389/fmicb.2022.1007295 | |
| 8. | Feiming Huang, Lei Chen, Wei Guo, Xianchao Zhou, Kaiyan Feng, Tao Huang, Yudong Cai, Identifying COVID-19 Severity-Related SARS-CoV-2 Mutation Using a Machine Learning Method, 2022, 12, 2075-1729, 806, 10.3390/life12060806 | |
| 9. | Qiao Sun, Lin Bai, Shaopin Zhu, Lu Cheng, Yang Xu, Yu-Dong Cai, Hui Chen, Jian Zhang, Ji-Fu Wei, Analysis of Lymphoma-Related Genes with Gene Ontology and Kyoto Encyclopedia of Genes and Genomes Enrichment, 2022, 2022, 2314-6141, 1, 10.1155/2022/8503511 | |
| 10. | Jiwei Song, FeiMing Huang, Lei Chen, KaiYan Feng, Fangfang Jian, Tao Huang, Yu-Dong Cai, Identification of methylation signatures associated with CAR T cell in B-cell acute lymphoblastic leukemia and non-hodgkin’s lymphoma, 2022, 12, 2234-943X, 10.3389/fonc.2022.976262 | |
| 11. | Yaochen Xu, FeiMing Huang, Wei Guo, KaiYan Feng, Lin Zhu, Zhenbing Zeng, Tao Huang, Yu-Dong Cai, Characterization of chromatin accessibility patterns in different mouse cell types using machine learning methods at single-cell resolution, 2023, 14, 1664-8021, 10.3389/fgene.2023.1145647 | |
| 12. | Xiaoqing Liu, Wenjing Yi, Baohang Xi, Qi Dai, Lin Lu, Identification of Drug-Disease Associations Using a Random Walk with Restart Method and Supervised Learning, 2022, 2022, 1748-6718, 1, 10.1155/2022/7035634 | |
| 13. | Zhandong Li, Zi Mei, Shijian Ding, Lei Chen, Hao Li, Kaiyan Feng, Tao Huang, Yu-Dong Cai, Identifying Methylation Signatures and Rules for COVID-19 With Machine Learning Methods, 2022, 9, 2296-889X, 10.3389/fmolb.2022.908080 | |
| 14. | ZhanDong Li, Wei Guo, ShiJian Ding, Lei Chen, KaiYan Feng, Tao Huang, Yu-Dong Cai, Identifying Key MicroRNA Signatures for Neurodegenerative Diseases With Machine Learning Methods, 2022, 13, 1664-8021, 10.3389/fgene.2022.880997 | |
| 15. | Hao Li, Feiming Huang, Huiping Liao, Zhandong Li, Kaiyan Feng, Tao Huang, Yu-Dong Cai, Identification of COVID-19-Specific Immune Markers Using a Machine Learning Method, 2022, 9, 2296-889X, 10.3389/fmolb.2022.952626 | |
| 16. | Jian Lu, JiaRui Li, Jingxin Ren, Shijian Ding, Zhenbing Zeng, Tao Huang, Yu-Dong Cai, Functional and embedding feature analysis for pan-cancer classification, 2022, 12, 2234-943X, 10.3389/fonc.2022.979336 | |
| 17. | ZhanDong Li, FeiMing Huang, Lei Chen, Tao Huang, Yu-Dong Cai, Identifying In Vitro Cultured Human Hepatocytes Markers with Machine Learning Methods Based on Single-Cell RNA-Seq Data, 2022, 10, 2296-4185, 10.3389/fbioe.2022.916309 | |
| 18. | Shiheng Lu, Hui Wang, Jian Zhang, Identification of uveitis-associated functions based on the feature selection analysis of gene ontology and Kyoto Encyclopedia of Genes and Genomes pathway enrichment scores, 2022, 15, 1662-5099, 10.3389/fnmol.2022.1007352 | |
| 19. | Xianchao Zhou, Shijian Ding, Deling Wang, Lei Chen, Kaiyan Feng, Tao Huang, Zhandong Li, Yudong Cai, Identification of Cell Markers and Their Expression Patterns in Skin Based on Single-Cell RNA-Sequencing Profiles, 2022, 12, 2075-1729, 550, 10.3390/life12040550 | |
| 20. | ZhanDong Li, Wei Guo, Tao Zeng, Jie Yin, KaiYan Feng, Tao Huang, Yu-Dong Cai, Detecting Brain Structure-Specific Methylation Signatures and Rules for Alzheimer’s Disease, 2022, 16, 1662-453X, 10.3389/fnins.2022.895181 | |
| 21. | Zhandong Li, Xiaoyong Pan, Yu-Dong Cai, Identification of Type 2 Diabetes Biomarkers From Mixed Single-Cell Sequencing Data With Feature Selection Methods, 2022, 10, 2296-4185, 10.3389/fbioe.2022.890901 | |
| 22. | Xiaohong Li, Xianchao Zhou, Shijian Ding, Lei Chen, Kaiyan Feng, Hao Li, Tao Huang, Yu-Dong Cai, Identification of Transcriptome Biomarkers for Severe COVID-19 with Machine Learning Methods, 2022, 12, 2218-273X, 1735, 10.3390/biom12121735 | |
| 23. | Man Li, Xinyi Zhou, Siyao Qin, Ziyan Bin, Yanhui Wang, Improved RAkEL’s Fault Diagnosis Method for High-Speed Train Traction Transformer, 2023, 23, 1424-8220, 8067, 10.3390/s23198067 | |
| 24. | Hao Wang, Lei Chen, PMPTCE-HNEA: Predicting Metabolic Pathway Types of Chemicals and Enzymes with a Heterogeneous Network Embedding Algorithm, 2023, 18, 15748936, 748, 10.2174/1574893618666230224121633 | |
| 25. | Lei Chen, Linyang Li, Prediction of Drug Pathway-based Disease Classes using Multiple Properties of Drugs, 2024, 19, 15748936, 859, 10.2174/0115748936284973240105115444 | |
| 26. | Jing-Xin Ren, Qian Gao, Xiao-Chao Zhou, Lei Chen, Wei Guo, Kai-Yan Feng, Lin Lu, Tao Huang, Yu-Dong Cai, Identification of Gene Markers Associated with COVID-19 Severity and Recovery in Different Immune Cell Subtypes, 2023, 12, 2079-7737, 947, 10.3390/biology12070947 | |
| 27. | Lei Chen, Ruyun Qu, Xintong Liu, Improved multi-label classifiers for predicting protein subcellular localization, 2023, 21, 1551-0018, 214, 10.3934/mbe.2024010 | |
| 28. | Kailun Sun, Cornelis A. M. van Gestel, Hao Qiu, Two-Dimensional Layered Nano-MoS2 Induces Earthworm Immune Cell Apoptosis by Regulating Lysosomal Maintenance and Function: Toward Unbiased Screening and Validation of Suspicious Pathways, 2024, 58, 0013-936X, 19948, 10.1021/acs.est.4c04512 | |
| 29. | Lei Chen, Huiping Liao, Guohua Huang, Shijian Ding, Wei Guo, Tao Huang, Yudong Cai, Identification of DNA Methylation Signature and Rules for SARS-CoV-2 Associated with Age, 2022, 27, 2768-6701, 10.31083/j.fbl2707204 | |
| 30. | Yuanyuan Luo, Yihan Wang, Lin Liu, Feiming Huang, Shiheng Lu, Yan Yan, Identifying pathological myopia associated genes with GenePlexus in protein-protein interaction network, 2025, 16, 1664-8021, 10.3389/fgene.2025.1533567 |
Figures(1) / Tables(1)
Zoha Deldar, Carlos Gevers-Montoro, Ali Khatibi, Ladan Ghazi-Saidi. The interaction between language and working memory: a systematic review of fMRI studies in the past two decades[J]. AIMS Neuroscience, 2021, 8(1): 1-32. doi: 10.3934/Neuroscience.2021001
| Base classifier | Parameter | Accuracy | Exact match | Hamming loss | Integrated score |
| Support vector machine (Polynomial kernel) |
m = 10, k = 5, C = 2, exponent = 1 | 0.5329 | 0.2087 | 0.0777 | 0.1026 |
| Support vector machine (RBF kernel) |
m = 10, k = 5, C = 2, γ = 0.01 | 0.4643 | 0.1441 | 0.0872 | 0.0611 |
| Random forest | m = 10, k = 3, number of decision trees = 250 | 0.6025 | 0.2806 | 0.0687 | 0.1574 |
DownLoad:
CSV
| Base classifier | Parameter | Accuracy | Exact match | Hamming loss | Integrated score |
| Support vector machine (Polynomial kernel) |
m = 10, k = 5, C = 2, exponent = 1, feature dimension = 300 | 0.5853 | 0.2407 | 0.0713 | 0.1308 |
| Support vector machine (RBF kernel) |
m = 10, k = 3, C = 2, γ = 0.01, feature dimension=300 | 0.5020 | 0.1551 | 0.0824 | 0.0714 |
| Random forest | m = 10, k = 5, number of decision trees = 250, feature dimension = 150 | 0.5727 | 0.2385 | 0.0714 | 0.1269 |
DownLoad:
CSV
| Base classifier | Parameter | Accuracy | Exact match | Hamming loss | Integrated score |
| Support vector machine (Polynomial kernel) |
m = 10, k = 5, C = 2, exponent = 1, network embedding feature dimension = 300 | 0.6242 | 0.2777 | 0.0660 | 0.1619 |
| Support vector machine (RBF kernel) |
m = 10, k = 5, C = 2, γ = 0.01, network embedding feature dimension = 300 | 0.5439 | 0.2177 | 0.0743 | 0.1096 |
| Random forest | m = 10, k = 5, number of decision trees = 250, network embedding feature dimension = 150 | 0.6235 | 0.2963 | 0.0633 | 0.1731 |
DownLoad:
CSV
| Base classifier | Parameter | Accuracy | Exact match | Hamming loss | Integrated score |
| Support vector machine (Polynomial kernel) |
m = 10, k = 5, C = 2, exponent = 1, network embedding feature dimension = 300 | 0.5059 | 0.1507 | 0.0781 | 0.0703 |
| Support vector machine (RBF kernel) |
m = 10, k = 5, C = 2, γ = 0.01, network embedding feature dimension=300 | 0.4485 | 0.1112 | 0.0848 | 0.0456 |
| Random forest | m = 10, k = 5, number of decision trees = 250, network embedding feature dimension = 150 | 0.5069 | 0.1608 | 0.0762 | 0.0753 |
DownLoad:
CSV
| Base classifier | Parameter | Accuracy | Exact match | Hamming loss | Integrated score |
| Support vector machine (Polynomial kernel) |
m = 10, k = 5, C = 2, exponent = 1, network embedding feature dimension = 300 | 0.6177 | 0.2705 | 0.0654 | 0.1562 |
| Support vector machine (RBF kernel) |
m = 10, k = 5, C = 2, γ = 0.01, network embedding feature dimension=300 | 0.5427 | 0.2138 | 0.0737 | 0.1075 |
| Random forest | m = 10, k = 5, number of decision trees = 250, network embedding feature dimension = 150 | 0.6195 | 0.2952 | 0.0635 | 0.1713 |
DownLoad:
CSV
| Index | Functional type |
| Partition 1 | PROTEIN WITH BINDING FUNCTION OR COFACTOR REQUIREMENT (structural or catalytic) REGULATION OF METABOLISM AND PROTEIN FUNCTION CELLULAR COMMUNICATION/SIGNAL TRANSDUCTION MECHANISM SUBCELLULAR LOCALIZATION CELLULAR TRANSPORT, TRANSPORT FACILITIES AND TRANSPORT ROUTES TRANSCRIPTION ENERGY METABOLISM CELL CYCLE AND DNA PROCESSING PROTEIN FATE (folding, modification, destination) BIOGENESIS OF CELLULAR COMPONENTS SYSTEMIC INTERACTION WITH THE ENVIRONMENT PROTEIN SYNTHESIS CELL RESCUE, DEFENSE AND VIRULENCE |
| Partition 2 | INTERACTION WITH THE ENVIRONMENT CELL TYPE LOCALIZATION TISSUE LOCALIZATION ORGAN LOCALIZATION TRANSPOSABLE ELEMENTS, VIRAL AND PLASMID PROTEINS |
| Partition 3 | CELL FATE DEVELOPMENT (Systemic) TISSUE DIFFERENTIATION ORGAN DIFFERENTIATION CELL TYPE DIFFERENTIATION |
DownLoad:
CSV
| Base classifier | Parameter | Accuracy | Exact match | Hamming loss | Integrated score |
| Support vector machine (Polynomial kernel) |
m = 10, k = 5, C = 2, exponent = 1 | 0.5329 | 0.2087 | 0.0777 | 0.1026 |
| Support vector machine (RBF kernel) |
m = 10, k = 5, C = 2, γ = 0.01 | 0.4643 | 0.1441 | 0.0872 | 0.0611 |
| Random forest | m = 10, k = 3, number of decision trees = 250 | 0.6025 | 0.2806 | 0.0687 | 0.1574 |
| Base classifier | Parameter | Accuracy | Exact match | Hamming loss | Integrated score |
| Support vector machine (Polynomial kernel) |
m = 10, k = 5, C = 2, exponent = 1, feature dimension = 300 | 0.5853 | 0.2407 | 0.0713 | 0.1308 |
| Support vector machine (RBF kernel) |
m = 10, k = 3, C = 2, γ = 0.01, feature dimension=300 | 0.5020 | 0.1551 | 0.0824 | 0.0714 |
| Random forest | m = 10, k = 5, number of decision trees = 250, feature dimension = 150 | 0.5727 | 0.2385 | 0.0714 | 0.1269 |
| Base classifier | Parameter | Accuracy | Exact match | Hamming loss | Integrated score |
| Support vector machine (Polynomial kernel) |
m = 10, k = 5, C = 2, exponent = 1, network embedding feature dimension = 300 | 0.6242 | 0.2777 | 0.0660 | 0.1619 |
| Support vector machine (RBF kernel) |
m = 10, k = 5, C = 2, γ = 0.01, network embedding feature dimension = 300 | 0.5439 | 0.2177 | 0.0743 | 0.1096 |
| Random forest | m = 10, k = 5, number of decision trees = 250, network embedding feature dimension = 150 | 0.6235 | 0.2963 | 0.0633 | 0.1731 |
| Base classifier | Parameter | Accuracy | Exact match | Hamming loss | Integrated score |
| Support vector machine (Polynomial kernel) |
m = 10, k = 5, C = 2, exponent = 1, network embedding feature dimension = 300 | 0.5059 | 0.1507 | 0.0781 | 0.0703 |
| Support vector machine (RBF kernel) |
m = 10, k = 5, C = 2, γ = 0.01, network embedding feature dimension=300 | 0.4485 | 0.1112 | 0.0848 | 0.0456 |
| Random forest | m = 10, k = 5, number of decision trees = 250, network embedding feature dimension = 150 | 0.5069 | 0.1608 | 0.0762 | 0.0753 |
| Base classifier | Parameter | Accuracy | Exact match | Hamming loss | Integrated score |
| Support vector machine (Polynomial kernel) |
m = 10, k = 5, C = 2, exponent = 1, network embedding feature dimension = 300 | 0.6177 | 0.2705 | 0.0654 | 0.1562 |
| Support vector machine (RBF kernel) |
m = 10, k = 5, C = 2, γ = 0.01, network embedding feature dimension=300 | 0.5427 | 0.2138 | 0.0737 | 0.1075 |
| Random forest | m = 10, k = 5, number of decision trees = 250, network embedding feature dimension = 150 | 0.6195 | 0.2952 | 0.0635 | 0.1713 |
| Index | Functional type |
| Partition 1 | PROTEIN WITH BINDING FUNCTION OR COFACTOR REQUIREMENT (structural or catalytic) REGULATION OF METABOLISM AND PROTEIN FUNCTION CELLULAR COMMUNICATION/SIGNAL TRANSDUCTION MECHANISM SUBCELLULAR LOCALIZATION CELLULAR TRANSPORT, TRANSPORT FACILITIES AND TRANSPORT ROUTES TRANSCRIPTION ENERGY METABOLISM CELL CYCLE AND DNA PROCESSING PROTEIN FATE (folding, modification, destination) BIOGENESIS OF CELLULAR COMPONENTS SYSTEMIC INTERACTION WITH THE ENVIRONMENT PROTEIN SYNTHESIS CELL RESCUE, DEFENSE AND VIRULENCE |
| Partition 2 | INTERACTION WITH THE ENVIRONMENT CELL TYPE LOCALIZATION TISSUE LOCALIZATION ORGAN LOCALIZATION TRANSPOSABLE ELEMENTS, VIRAL AND PLASMID PROTEINS |
| Partition 3 | CELL FATE DEVELOPMENT (Systemic) TISSUE DIFFERENTIATION ORGAN DIFFERENTIATION CELL TYPE DIFFERENTIATION |
