Improved multi-label classifiers for predicting protein subcellular localization

1.   Introduction

Proteins, as the material basis of life, play an important role in participating in various forms of life activities. Generally, the locations where these protein molecules reside in compartments or organelles are called "subcellular locations" ^[1]. It has been found that there is a close relationship between the functions of proteins and their subcellular locations in cells. Thus, correct prediction of protein subcellular locations is helpful to uncover their functions. Determination of protein subcellular locations is one of the most important and essential problems in protein science.

The traditional methods for identifying protein subcellular location include fluorescence microscopy, electron microscopy, cell fractionation, etc. ^[2]. Although these experimental approaches can output assured results, there still exists a great gap between the number of proteins with known subcellular locations and those without determined subcellular locations ^[3,4] because many new proteins have been generated or found. Evidently, the above traditional methods cannot timely determine the subcellular locations of new proteins. In recent years, with the rapid development of computer science, computational methods are an important alternative way to determine protein subcellular locations, especially the machine learning based methods.

During the last two decades, plenty of efforts have been made to design computational methods for determining protein subcellular locations. As mentioned above, most of them are machine learning based methods. As most machine learning algorithms need numeric values as input, the main step to design machine learning based methods is to encode proteins into several features. According to the current research progress, the machine learning based methods can be roughly divided into the following four groups. The first group consists of sequence-based methods, which extract protein features from their sequences, such as amino acid composition ^[5,6], pseudo amino acid composition ^{[7,8,9,10,11]}, position specific score matrix (PSSM) ^{[12,13,14,15]}, etc. As sequence is the widely used form to represent proteins, this method always had wide applications. However, some essential properties of proteins cannot be extracted from their sequences, which affected the efficiency of this method. The second group consists of annotation-based methods. This group of methods uses annotation information of proteins for extracting essential protein features. Gene ontology (GO) ^{[16,17,18,19,20,21,22]} information is widely used in this group. Other information includes functional domain ^{[23,24,25,26]}, Swiss-Prot keywords, PubMed abstracts, etc. The efficiency of this method is quite high because the annotation information contains several essential properties of proteins. However, for a newly designed protein, this method cannot always output the result, as its annotation information is not available. The third group consists of network-based methods. Protein-protein interaction (PPI) networks have wide applications for tackling protein-related problems, including the prediction of protein subcellular locations. Such methods use the features derived from one or more PPI networks, which are fed into downstream classification algorithms ^{[27,28,29,30]}. Although such methods also provide high performance, their application to newly designed proteins is a problem, as their locations in PPI networks are unknown. The last group consists of the recently proposed image-based methods. These methods adopt the features derived from protein images ^[31,32,33] and always employ deep learning algorithms to make predictions. The performance of such methods is very high. However, their interpretability is quite poor. In this study, we focused on annotation-based methods. In previous studies ^{[16,17,18,19]}, Cheng et al. proposed a novel scheme to extract features from GO information of proteins, on which efficient multi-label classifiers were built. These features had low dimensions and further contained the label information of training samples. However, they adopted a weak prediction engine, which did not contain a strict learning procedure, thereby leaving great spaces for improvement. This study continued their work by employing a set of powerful machine learning algorithms.

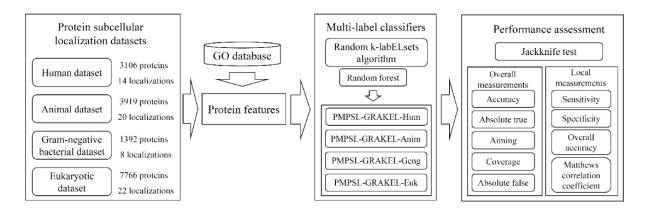
In this study, four multi-label classifiers were set up for predicting subcellular locations of human, animal, Gram-negative bacterial and eukaryotic proteins, respectively. These proteins were directly retrieved from four previous studies ^{[16,17,18,19]}. Each protein was represented by compact features derived from its GO information. To fully learn these features, a powerful multi-label algorithm, random k-labelsets (RAKEL) ^[34], with random forest (RF) ^[35] as the basic prediction engine, was adopted to construct the classifiers. The jackknife test results of the classifiers on corresponding protein datasets indicated their quite high performance to predict protein subcellular locations. The full comparisons confirmed that the proposed classifiers were superior to several previous classifiers.

2.   Materials and methods

2.1.   Benchmark datasets

In this study, four protein types and their subcellular locations were investigated, including human, animal, Gram-negative bacterial and eukaryotic proteins. This information was directly collected from four previous studies ^{[16,17,18,19]}. Accordingly, four protein datasets were obtained, each of which consisted of proteins in one above-mentioned protein type. For easy description, the four protein datasets were called human, animal, Gram-negative bacterial and eukaryotic datasets, respectively. Some information of these four datasets is listed in Table 1. Their brief descriptions are as follows.

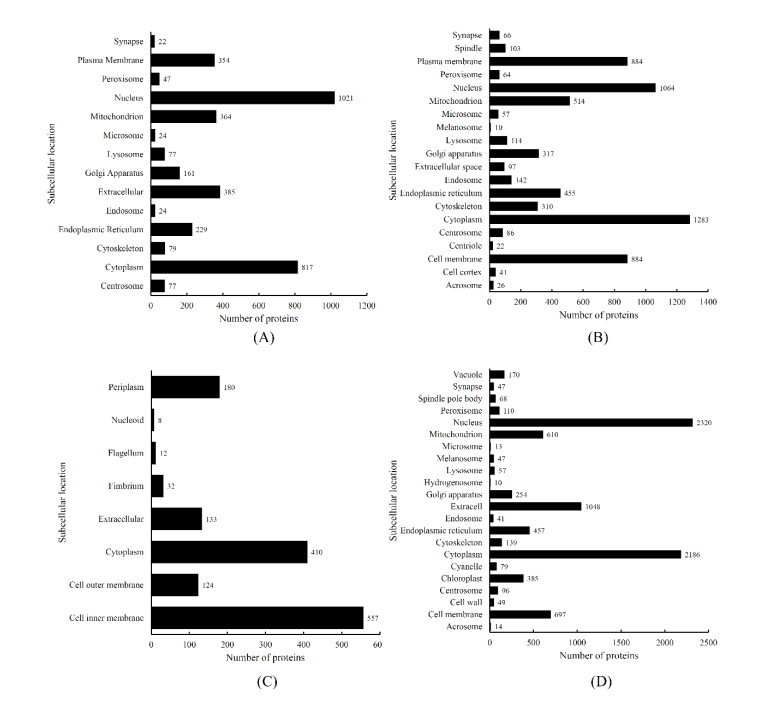
The human dataset consisted of 3106 human proteins reported in ^[16,36,37]. The sequence identity of any two proteins in this dataset was less than 25%. Fourteen subcellular locations were involved with these proteins, as shown in Figure 1(A). According to the subcellular locations of these proteins, all 3106 proteins were classified into fourteen classes. The number of proteins in each class is also shown in Figure 1(A). By simple calculation, the sum of protein numbers in all classes was 3681, which was larger than the number of different proteins (3016), indicating that some proteins belonged to more than one class. The average number of locations for proteins in this dataset was 1.185. It was a multi-label classification problem to assign the above fourteen subcellular locations to the given proteins.

In the animal dataset, 3919 proteins were contained, which were retrieved from ^[17,38]. Any protein had a sequence identity of less than 40% with any other protein in this dataset. The above proteins had 20 subcellular locations, which are listed in Figure 1(B). Accordingly, these proteins were divided into 20 classes. The number of proteins in each class is listed in Figure 1(B). Likewise, the sum of protein numbers in all classes was 6519, also larger than the number of different animal proteins. Each animal protein, on average, 1.669 subcellular locations. Thus, it was also a multi-label classification problem.

As for the third dataset, the Gram-negative bacterial dataset, 1392 proteins were included. These proteins were collected from ^[18,39,40]. The sequence identity of any two proteins in this dataset was less than 25%. Eight subcellular locations were assigned to these proteins, which are shown in Figure 1(C). Accordingly, 1392 proteins were classified into eight classes. The size of each class is also listed in Figure 1(C). Similar to the above two datasets, the sum of protein numbers in all classes (1456) was larger than the number of different Gram-negative bacterial proteins (1392), and the average number of locations that a protein was assigned in this dataset was 1.046. Assigning eight subcellular locations to the given proteins was also a multi-label classification problem.

The last dataset, the eukaryotic dataset, was sourced from ^[19,24]. Overall, 7766 proteins were contained in this dataset, which were classified into 22 subcellular locations, as shown in Figure 1(D). The number of proteins in each class is also listed in Figure 1(D). The sequence identity of any two proteins in this dataset was less than 25%. Similarly, some proteins can belong to more than one class, as the sum of protein numbers in all classes (8897) was larger than the number of different proteins (7766). The average number of locations that a protein was assigned was 1.146. A multi-label classifier should be built to assign these subcellular locations to any eukaryotic protein.

2.2.   Protein representation

It is an essential step to encode each sample into a series of numeric values, which can be processed by most computer algorithms. These numeric values should contain essential properties of samples as much as possible. For proteins, GO is an important type of annotation information, which labels the essential functions of proteins. At first, the one-hot scheme was adopted for the GO annotation information of proteins, generating a high-dimensional binary feature vector for each protein. The classification models built on such representation were always of low efficiency. It is necessary to refine such information to tackle this problem. Here, we directly adopted the scheme reported in ^{[16,17,18,19]} to encode proteins for easy comparisons. This scheme not only reduced the dimensions of the final representation but also included the label information of training samples, which was deemed to be helpful for improving the classification performance. A brief description of such scheme is as follows.

Given a training dataset S with N proteins, denoted by ${p}_{1}, {p}_{2}, \cdots , {p}_{N}$, and L labels, denoted by ${l}_{1}, {l}_{2}, \cdots , {l}_{L}$, let ${C}_{i}$ be a subset of S consisting of proteins with label ${l}_{i}$. In this case, $S = {C}_{1}\cup {C}_{2}\cup \cdots \cup {C}_{L}$. In this study, as some proteins may have more than one label, common proteins may exist for two subsets. Furthermore, the GO terms of protein ${p}_{a}$ in S constitute the set $GO\left({p}_{a}\right)$. The feature vector of each training and test protein p is finally formulated by

where L is the number of labels. Each component ${\delta }_{i}$ in this vector indicates the relationship between p and proteins in ${C}_{i}$, which can be determined in the following manner:

Step 1: Determine the GO information of p. If such information is not available, find the protein in the Swiss-Prot database with the highest pairwise sequence identity to p whose GO information is available. Use this GO information to represent p. For formulation, the GO information of p thus obtained is denoted by $GO\left(p\right) = \{{GO}_{p}^{1}, {GO}_{p}^{2}, \cdots , {GO}_{p}^{k}\}$, where k denotes the number of GO terms annotated to p or its most similar protein.

Step 2: For each GO ${GO}_{p}^{j}(1\le j\le k)$, count the number of proteins in the training dataset that are annotated by ${GO}_{p}^{j}$, denoted by ${N(GO}_{p}^{j})$, i.e., ${N(GO}_{p}^{j}) = \left|\left\{{p}_{a}|{p}_{a}\in S\;and\;{GO}_{p}^{j}\in GO({p}_{a})\right\}\right|$. In addition, count the number of proteins in ${C}_{i}$ which are also annotated by ${GO}_{p}^{j}$, indicated by ${N(GO}_{p}^{j}, i)$, i.e., ${N(GO}_{p}^{j}, i) = \left|\left\{{p}_{a}|{p}_{a}\in {C}_{i}\;and\;{GO}_{p}^{j}\in GO({p}_{a})\right\}\right|$. Then, calculate ${R(GO}_{p}^{j}, i) = \frac{{N(GO}_{p}^{j}, i)}{{N(GO}_{p}^{j})}$.

Step 3: Take the maximum value among ${R(GO}_{p}^{1}, i), {R(GO}_{p}^{2}, i), \cdots , {R(GO}_{p}^{k}, i)$ and set it as ${\delta }_{i}$, i.e., ${\delta }_{i} = \mathrm{m}\mathrm{a}\mathrm{x}\{{R(GO}_{p}^{1}, i), {R(GO}_{p}^{2}, i), \cdots , {R(GO}_{p}^{k}, i)\}$.

To understand the above procedures, an example is given. Consider a protein p annotated by three GO terms, say, GO1, GO2 and GO3. The numbers of training proteins annotated by these three GO terms are first counted (e.g., 120 for GO1,150 for GO2 and 200 for GO3). Then, the numbers of training proteins in the first category (for label ${l}_{1}$) that are also annotated by GO1, GO2 and GO3 are counted (e.g., 60 for GO1, 10 for GO2 and 20 for GO3). The maximum is picked from $\{\frac{60}{120}, \frac{10}{150}, \frac{20}{200}\}$ as ${\delta }_{1}$, that is, ${\delta }_{1} = \frac{60}{120} = 0.5$. ${\delta }_{2}, {\delta }_{3}, \cdots , {\delta }_{L}$ can be obtained in a similar way.

With the above operation, L features were generated to represent a protein. These features contained not only the GO information of the encoded protein but also the statistical information of GO terms of proteins in the training dataset. The number of features was greatly reduced compared to the one-hot scheme.

Four datasets were investigated in this study. With the above scheme, proteins in the human, animal, Gram-negative bacterial and eukaryotic datasets were represented by 14, 20, 8 and 22 features. Based on these features, efficient multi-label classifiers can be built.

2.3.   Random k-labelsets algorithm

As mentioned in the section "Benchmark datasets, " some proteins in each dataset had more than one subcellular location, suggesting we should construct a multi-label classifier for each dataset for assigning subcellular locations to proteins. Generally, there are two ways to construct multi-label classifiers ^[41]. The first one is problem transformation, which creates some single-label problems from the original multi-label problem, builds a single-label classifier for each single-label problem and integrates the results yielded by the single-label classifiers as the output. The second way is algorithm adaption, which generalizes the single-label classifiers such that they can process samples with multiple labels. To our knowledge, problem transformation methods are more popular than algorithm adaption methods when constructing multi-label classifiers. In fact, a multi-label classifier built by a certain problem transformation method is a combination of single-label classifiers. At present, lots of single-label classification algorithms have been proposed, providing abundant sources for building such multi-label classifiers. The pure multi-label classification algorithms are much fewer than single-label classification algorithms, resulting in much fewer choices to build multi-label classifiers through algorithm adaption methods. In the previous studies ^{[16,17,18,19]}, a multi-label Gaussian kernel regression (ML-GKR) classifier was built on each dataset, and it was an algorithm adaption method. Here, we employed a more powerful problem transformation method, RAKEL ^[34], to build the multi-label classifiers.

RAKEL can be deemed as an improved version of the label powerset (LP) ^[42] method. Given a training dataset containing L labels, LP uses members in the power set of the label set as new labels and assigns them to all samples. For example, if a sample has two labels, say ${l}_{1}$ and ${l}_{3}$, ${\{l}_{1}, {l}_{3}\}$ will be treated as a new label and be assigned to this sample. After this operation, all samples have exactly one label. A single-label classifier can be built on the dataset with new assigned labels based on a certain single-label classification algorithm. The LP method has an evident defect. A large number of labels results in a label disaster. So many new labels are involved, and the number of samples for some labels may small, decreasing the learning results. In view of this, RAKEL was proposed. It randomly constructs m label subsets with size k (1 ≤ k ≤ L). For each label subset, a single-label classifier is built using the LP method, called the LP classifier. RAKEL integrates m LP classifiers as the final multi-label classifier. For a test sample, each LP classifier gives its predictions (binary predictions for labels involved in this LP classifier). Then, among the LP classifiers related to one label, count the proportion of classifiers that give positive prediction on this label. If such proportion is larger than the predefined threshold, which is generally set to 0.5, RAKEL assigns this label to the test sample. In recent years, RAKEL has been used to construct lots of multi-label classifiers in bioinformatics ^{[43,44,45,46,47,48,49,50]}.

The present study directly adopted the tool "RAKEL" in Meka (http://waikato.github.io/meka/) ^[51] to implement the above RAKEL method. Various values of k were tried to build the optimal classifier.

2.4.   Random forest

When using RAKEL to construct multi-label classifiers, we need to select a base single-label classification algorithm. A proper selection may greatly improve the performance of the final classifier. In this study, the classic classification algorithm, RF ^[35], was used.

RF is an ensemble learning algorithm containing several decision trees ^[35]. When constructing a decision tree, the same number of samples in the training dataset was randomly selected with replacement (i.e., some samples may be selected more than once), and a small proportion of features are also randomly selected. Given a test sample, each decision tree generates its prediction. RF integrates these predictions with majority voting. Although decision tree is the basis of RF, and it is deemed to be a weak algorithm, RF is much more powerful. Accordingly, it has been widely used in the field of bioinformatics ^{[52,53,54,55,56,57,58,59]}.

The above RF algorithm was also implemented in Meka (http://waikato.github.io/meka/) ^[51] by a tool "RandomForest, " which was directly used in this study. Default parameters were used, where the number of decision trees was 100.

2.5.   Jackknife test

Cross-validation methods are widely used and accepted to evaluate the performance of classifiers. The jackknife test ^[60] is one of the commonly used cross-validation methods and has been used to evaluate many previous classifiers, including classifiers in pLoc and iLoc series ^{[16,17,18,19,36,38,40,61]}. To give a fair comparison with previous classifiers, we also adopted the jackknife test to examine all constructed multi-label classifiers. In such test, each sample is singled out as a test sample one by one, while the rest of the samples constitute a dataset to train the classifier. Evidently, such procedures are completely open, that is, the test and training samples are assured in each round. This makes the evaluation results more reliable and objective. Furthermore, such a test can always output a unique result in most cases. Thus, it has wide applications in testing the qualities of various classifiers ^{[43,44,62,63,64,65]}.

2.6.   Measurements for multi-label classifiers

To evaluate the performance of multi-label classifiers, several measurements have been proposed. In this study, we adopted the same measurements used in ^{[16,17,18,19]} for easy comparisons. These measurements included absolute true, absolute false, accuracy, aiming and coverage. Given a dataset with N samples and L labels, let ${D}_{i}$ denote the set of true labels for the $i$th sample and ${D}_{i}^{*}$ denote the set of predicted labels for the $i$th sample. The above five measurements can be computed as

where $\Delta$ is defined as below:

According to these definitions, the higher the values of absolute true, accuracy and aiming, coverage are, the higher the performance of the classifier. As for absolute false, the relationship is the opposite. A low absolute false value indicates high performance. Among these measurements, we selected absolute true as the key measurement as used in ^{[16,17,18,19]} for optimizing parameters.

Also, some local measurements on each class were also employed, including sensitivity (SN), specificity (SP), overall accuracy (ACC) and Matthews correlation coefficient (MCC). For the $j$-th class, these measurements can be computed by

where $TP$ denotes the total number of correctly classified samples that belong to the $j$-th class; $TN$ denotes the number of correctly classified samples that do not belong to the $j$-th class; $FP$ denotes the number of samples that do not belong to the $j$-th class but are misclassified to the $j$-th class; $FN$ denotes the number of samples that belong to the $j$-th label and are misclassified to other classes. The higher the above measurements are, the higher the performance of the classifiers.

3.   Results and discussion

In this study, a set of multi-label classifiers was proposed to identify subcellular locations of four protein types. The entire procedures are illustrated in Figure 2. This section gives the detailed evaluation results for these classifiers and compares their performance with previous classifiers. For convenience, we named the four multi-label classifiers as PMPSL-GRAKEL-Hum (on the human dataset), PMPSL-GRAKEL-Anim (on the animal dataset), PMPSL-GRAKEL-Geng (on Gram-negative bacterial dataset) and PMPSL-GRAKEL-Euk (on the eukaryotic dataset), respectively.

3.1.   Parameter optimization

RAKEL was adopted to build classifiers in this study. There are two main parameters, m and k, which can be tuned to optimize the classifier. The parameter m determines the number of LP classifiers. We used its default value (10) in Meka. As for the parameter k, it determines the number of labels for building each LP classifier. Here, we tried all possible values between two and the number of labels in each dataset. All classifiers under different k values were set up and tested by the jackknife test. In multi-label classification, accuracy and absolute true are main measurements to evaluate the quality of prediction results. Relatively, absolute true is stricter than accuracy because the sample is deemed to be correctly predicted if and only if the predicted labels are identical to true labels. If the predicted labels are partly correct, they cannot give positive contributions to absolute true, whereas they can provide this contribution to accuracy. Meanwhile, the previous studies ^{[16,17,18,19]} also selected absolute true to optimize parameters. Thus, absolute true was selected as the key measurement to optimize parameter k.

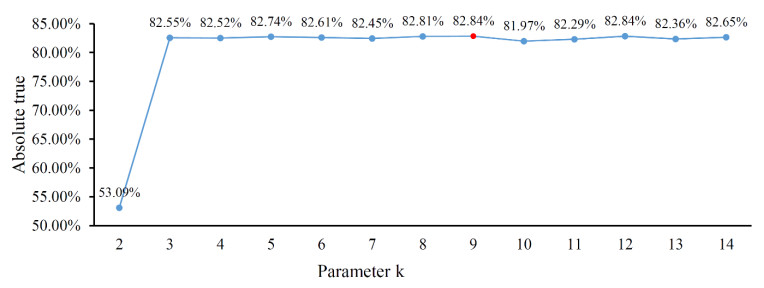
For the classifier PMPSL-GRAKEL-Hum on the human dataset, its performance on different k values is shown in Figure 3. It can be observed that when k = 2, the classifier provided quite low performance. As k determines the number of selected features for constructing LP classifiers, they may not cover all labels when k is small, inducing low performance on some labels. This fact further decreases the overall performance of classifiers. When k > 2, the performances of the classifiers were almost at the same level. Relatively speaking, when k = 9 and 12, the classifier provided the highest performance, with absolute true of 82.84%. Considering that the complexity of the classifier follows an increasing trend with the increasing of k, we finally determine k as nine for PMPSL-GRAKEL-Hum.

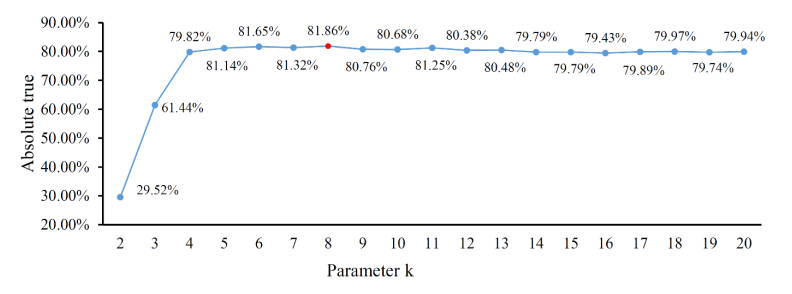
For the classifier PMPSL-GRAKEL-Anim on the animal dataset, a curve was also plotted, as shown in Figure 4, to indicate its performance under different k values. When k was small (≤3), the performance was also low, which was same as that illustrated in Figure 3. It was caused by the same reason. When k > 3, the performance was quite stable. The highest absolute true was 81.86%, when k was set to eight. Thus, PMPSL-GRAKEL-Anim was built with k = 8.

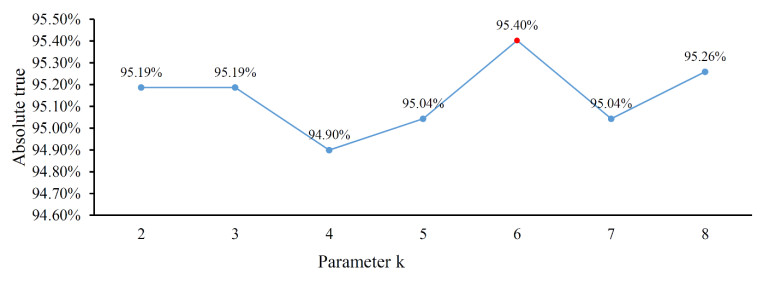
For the classifier PMPSL-GRAKEL-Geng on the Gram-negative bacterial dataset, we also plotted a curve to illustrate its performance with different k values, as shown in Figure 5. It can be observed that all classifiers with different k values provided high performance, with absolute true higher than 94%. When k = 6, the highest absolute true of 95.40% was achieved. Accordingly, the PMPSL-GRAKEL-Geng using k = 6 was set up.

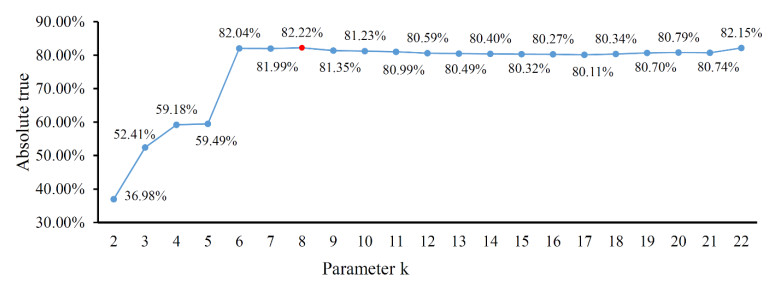
As for the last classifier, PMPSL-GRAKEL-Euk on the eukaryotic dataset, its performance under different k values is shown in Figure 6. Similar to Figures 3 and 4, the classifiers with small values still provided low performance, which was caused by the same reason elaborated above. Likewise, classifiers with large k values provided almost equal performance. When k was set to eight, the classifier yielded the highest absolute true of 82.22%. Accordingly, the PMPSL-GRAKEL-Euk with k = 8 was built.

3.2.   Performance of the multi-label classifiers

In the section "Parameter optimization, " the optimal k value was determined for each multi-label classifier. The detailed performances of these optimal classifiers are given in this section. Their overall performances, including aiming, coverage, accuracy, absolute true and absolute false, are listed in Table 2.

For PMPSL-GRAKEL-Hum, the jackknife test results indicated aiming of 90.73%, coverage of 92.36%, accuracy of 88.60%, absolute true of 82.84% and absolute false of 1.78% (Table 2). The aiming and coverage exceeded 90%, whereas accuracy and absolute true exceeded 80%, indicating the high performance of PMPSL-GRAKEL-Hum.

For PMPSL-GRAKEL-Anim on the animal dataset, it yielded the aiming of 93.00%, coverage of 95.21%, accuracy of 90.42%, absolute true of 81.86% and absolute false of 1.31% (Table 2). This classifier provided a little higher performance than PMPSL-GRAKEL-Hum, also suggesting the excellent performance of PMPSL-GRAKEL-Anim.

For PMPSL-GRAKEL-Geng on the Gram-negative bacterial dataset, its aiming, coverage, accuracy, absolute true and absolute false were 97.11%, 97.99%, 96.83%, 95.40% and 0.82% (Table 2), respectively. The first four measurements all exceeded 95%, and absolute false reduced to lower than 1%. If only considering such performance, it outperformed the above two classifiers.

As for PMPSL-GRAKEL-Euk on the eukaryotic dataset, the five measurements calculated by Eq (2) were 89.92%, 92.36%, 88.15%, 82.22% and 1.06% (Table 2). Such performance was almost equal to PMPSL-GRAKEL-Hum and PMPSL-GRAKEL-Anim and slightly lower than PMPSL-GRAKEL-Geng.

In addition to the above measurements to assess the overall performance of the four multi-label classifiers, four measurements (Eq (4)) for each subcellular location were also computed. The performances of the four classifiers for each subcellular location are listed in Tables S1–S4. It can be observed that most measurements were quite high, consistent with their overall performances mentioned above. In detail, the SP and ACC values were all higher than 90.00%. As for SN and MCC, those yielded by PMPSL-GRAKEL-Geng were also very high (Table S3), and most of them generated by the other three classifiers were also high. However, some SN and MCC values for a few locations generated by PMPSL-GRAKEL-Hum, PMPSL-GRAKEL-Anim and PMPSL-GRAKEL-Euk were quite low. For example, these include those for "Endosome" in the human dataset (12.50% for SN and 27.16% for MCC) (Table S1), "Microsome" in the animal dataset (20.00% for SN and 44.68% for MCC) (Table S2), "Endosome, " "Microsome" and "Acrosome" in the eukaryotic dataset (7.32%, 7.69%, 21.43% for SN and 20.83%, 27.71%, 46.26% for MCC) (Table S4), etc. By observing Figure 1, we can find that the sizes of these subcellular locations were quite small, inducing the low performance with them. Their performances can be improved if some techniques can be applied to the datasets for solving the imbalanced problem.

3.3.   Comparison with classifiers using other base prediction engines

This study adopted the problem transformation method RAKEL to build the multi-label classifiers. A certain base single-label classification algorithm is necessary for RAKEL. Here, we selected RF. To indicate this selection was reasonable, two other classic classification algorithms, decision tree (DT) ^[66] and support vector machine (SVM) ^[67], were attempted. Likewise, the parameter k in RAKEL was tuned for DT and SVM. The best performances, measured by absolute true on the four datasets, are listed in Table 3. For easy comparisons, the performances of our classifiers (using RF as base prediction engine) are also listed in this table. It was found that the classifiers with RF were evidently superior to those with DT and also slightly better than those with SVM. These results suggested that the selection of RF was proper.

3.4.   Comparison with previous classifiers

In this study, a multi-label classifier with high performance was constructed on each of four datasets. Some previous classifiers have also been proposed for the same datasets. Here, comparisons are conducted to show the superiority of the proposed four classifiers.

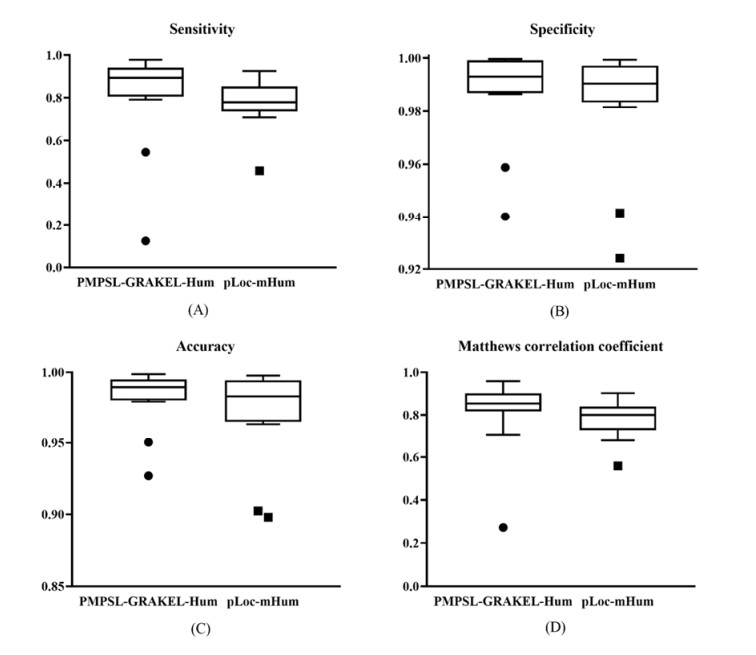
On the human dataset, pLoc-mHum ^[16] and iLoc-Hum ^[36] have been proposed to identify protein subcellular locations. Table 4 lists their overall performances, including aiming, coverage, accuracy, absolute true and absolute false. The performances of these two classifiers were also evaluated by jackknife test on the same human dataset. For pLoc-mHum, its measurements were directly retrieved from ^[16]. As for iLoc-Hum, the coverage and absolute true were reported in ^[36], which were also collected in ^[16]. The other three measurements (aiming, accuracy and absolute false) were not provided in ^[36]. For easy comparison, the overall performance of PMPSL-GRAKEL-Hum is also provided in Table 4. It can be observed that PMPSL-GRAKEL-Hum provided the best performance, followed by pLoc-mHum and iLoc-Hum. In detail, PMPSL-GRAKEL-Hum yielded the highest aiming, coverage, accuracy and absolute true, whereas the absolute false was inferior to that of pLoc-mHum. For the two most important measurements, accuracy and absolute true, PMPSL-GRAKEL-Hum improved about 4.2% and 3.7% compared with those of pLoc-mHum. As for the performance of PMPSL-GRAKEL-Hum and pLoc-mHum on 14 subcellular locations, a box plot was drawn for each of SN, SP, ACC and MCC, as shown in Figure 7, from which we can see that the main parts of the boxes for PMPSL-GRAKEL-Hum were always higher than those of pLoc-mHum on the basis of each measurement. This implied that for most subcellular locations, PMPSL-GRAKEL-Hum provided better performance than pLoc-mHum.

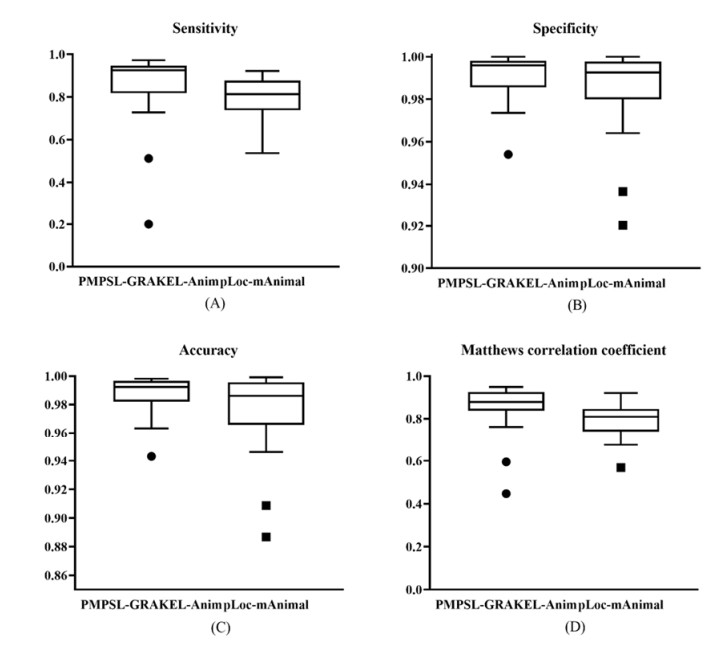
On the animal dataset, pLoc-mAnimal ^[17] and iLoc-Animal ^[38] were two previous classifiers that were also constructed on such dataset and evaluated by jackknife test. Their performances are listed in Table 4, in which the overall performance of PMPSL-GRAKEL-Anim is also provided. In this table, the measurements for pLoc-mAnimal were directly sourced from ^[17]. As for iLoc-Animal, its original performance was assessed on a similar dataset, which contained proteins with sequence identity no less than 40% in some locations. Its measurements listed in Table 4 are also obtained from ^[17], and they were produced by re-executing iLoc-Animal on the same animal dataset. It can be observed from Table 4 that PMPSL-GRAKEL-Anim provided the highest performance on the basis of all measurements, whereas pLoc-mAnimal yielded the second highest performance, and iLoc-Animal generated the lowest performance. For accuracy and absolute true, PMPSL-GRAKEL-Anim increased about 5.7% and 8.7%, which were great improvements. Likewise, a box plot was drawn for each measurement on 22 subcellular locations yielded by PMPSL-GRAKEL-Anim and pLoc-mAnimal, as shown in Figure 8. It can be concluded that PMPSL-GRAKEL-Anim outperformed pLoc-mAnimal on most locations no matter which measurements were adopted.

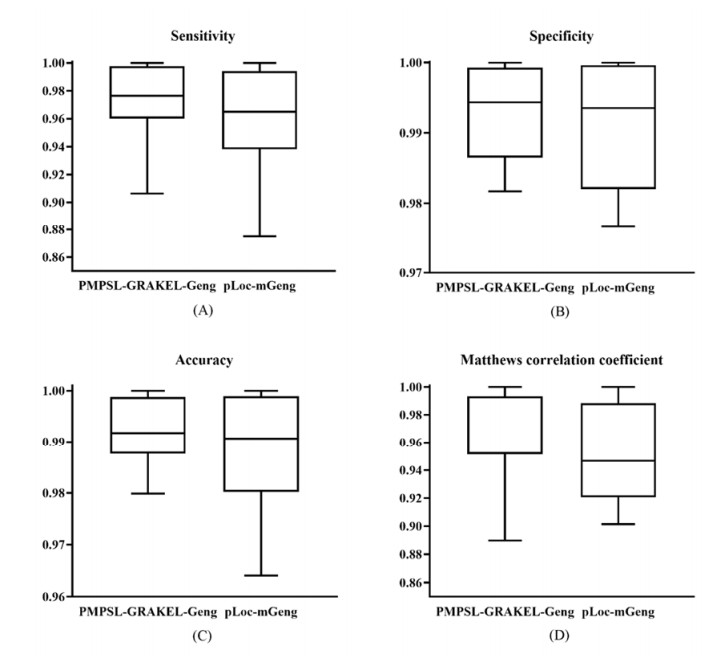
On the Gram-negative bacterial dataset, three previous classifiers have been proposed, including pLoc-mGeng ^[18], iLoc-Gneg ^[40] and Gneg-mPLoc ^[39]. Their overall performances are listed in Table 4. Such performances of three classifiers were obtained by jackknife test on the same Gram-negative bacterial dataset. The measurements for pLoc-mGeng were directly picked up from ^[18]. As for iLoc-Gneg and Gneg-mPLoc, only some measurements (coverage and absolute true for iLoc-Gneg, coverage for Gneg-mPLoc) were reported in their original studies, which were also collected in ^[18]. The overall performance of PMPSL-GRAKEL-Geng is also listed in Table 4 for easy comparisons. Again, PMPSL-GRAKEL-Geng provided highest performance on four measurements, indicating this classifier was superior to previous classifiers. The pLoc-mGeng gave the performance only inferior to PMPSL-GRAKEL-Geng. However, the superiority of PMPSL-GRAKEL-Geng was not very evident. The accuracy and absolute true were only 0.8% and 0.7% higher. According to their performances (SN, SP, ACC and MCC) on 8 subcellular locations (Figure 9), we can also conclude that PMPSL-GRAKEL-Geng was slightly better than pLoc-mGeng.

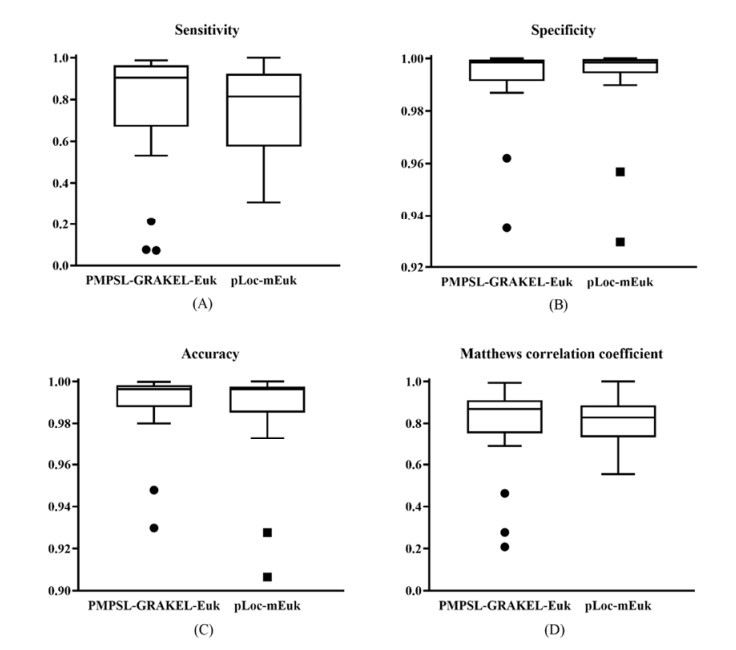
On the eukaryotic dataset, two classifiers (pLoc-mEuk ^[19] and iLoc-Euk ^[61]) have been previously reported. Their overall performances are listed in Table 4. This performance was also obtained by jackknife test on the same eukaryotic dataset. The measurements for pLoc-mEuk were directly collected from ^[19]. For iLoc-Euk, its original study only reported its coverage and absolute true ^[61], which were also used in ^[19]. By comparing the performance of PMPSL-GRAKEL-Euk, also listed in Table 4, it was easy to find that on four measurements, PMPSL-GRAKEL-Euk provided the best performance. Again, PMPSL-GRAKEL-Euk yielded a higher absolute false than pLoc-mEuk. On accuracy and absolute true, the improvement of PMPSL-GRAKEL-Euk was about 3.8% and 3.4%, respectively, which was quite similar to those on the human dataset. As for the performance of PMPSL-GRAKEL-Euk and pLoc-mEuk on 22 subcellular locations, a box plot was drawn for each measurement, as shown in Figure 10. It can be observed that for SN, ACC and MCC, the boxes of PMPSL-GRAKEL-Euk were at a higher level than those of pLoc-mEuk. For SP, the two boxes were almost at the same level. These suggested that PMPSL-GRAKEL-Euk can yield higher performance than pLoc-mEuk for most locations.

With the above arguments, the proposed classifiers (PMPSL-GRAKEL-Hum, PMPSL-GRAKEL-Anim, PMPSL-GRAKEL-Geng, and PMPSL-GRAKEL-Euk) were superior to previous classifiers (pLoc-mHum, pLoc-mAnimal, pLoc-mGen and pLoc-mEuk), respectively. These previous classifiers adopted ML-GKR as the prediction engine. As ML-GKR is not a strict machine learning algorithm, which directly makes decisions according to the distribution of data, it cannot mine hidden key patterns to identify different subcellular locations. In this study, the basic prediction engine was RF, which is one of the most classic and powerful machine learning algorithms. On basis of RF, correct patterns for different subcellular locations can be extracted, thereby improving the quality of the classifiers.

3.5.   Limitations of the classifiers

Although the proposed classifiers provided good performances to identify subcellular locations of proteins of four different types, they still had some weaknesses. The first weakness was the absolute false. The proposed classifiers yielded higher absolute false on three datasets compared with the previous classifiers. The second weakness was the low performance for some subcellular locations. The SN values for some subcellular locations were lower than 10%. Such results may be caused by the imbalanced problem. The proposed classifier was quite sensitive to the sizes of classes.

The above weaknesses may be caused by the limitations of the classifiers. First, for the base prediction engine, RF, in RAKEL, the default parameters were adopted. By tuning its main parameter, number of decision trees, the performances of the four classifiers can be improved. Second, according to Figure 1, the class sizes in the four datasets were not balanced. We did not consider this problem when constructing the classifiers. Some imbalanced data processing methods can be added to tackle this problem, thereby enhancing the performances of the four classifiers. In the future, we will continue this work to deal with these limitations and build more efficient classifiers.

4.   Conclusions

In this study, four multi-label classifiers were built to identify subcellular locations of human, animal, Gram-negative bacterial and eukaryotic proteins. These classifiers adopted the features extracted from GO information of proteins, which also included the label information in the training dataset. Furthermore, a powerful multi-label algorithm, RAKEL, with RF as the basic prediction engine was employed to construct the classifiers. These classifiers yielded quite high performance and were superior to some previous classifiers. We believe that these classifiers can be efficient tools to determine protein subcellular locations. Code and datasets are available at https://github.com/SummerXinTong/PMPSL-GRAKEL.

Use of AI tools declaration

The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare there is no conflict of interest.