Altered Sleep Mechanisms following Traumatic Brain Injury and Relation to Waking Function

Kimberly A Cote; Catherine E Milner; Tamara A Speth; Kimberly A Cote; Catherine E Milner; Tamara A Speth

doi:10.3934/Neuroscience.2015.4.203

AIMS Neuroscience

2015, Volume 2, Issue 4: 203-228. doi: 10.3934/Neuroscience.2015.4.203

Previous Article Next Article

Research article Recurring Topics

Altered Sleep Mechanisms following Traumatic Brain Injury and Relation to Waking Function

Department of Psychology, Brock University, St. Catharines, ON, Canada

Received: 27 August 2015 Accepted: 14 October 2015 Published: 22 October 2015

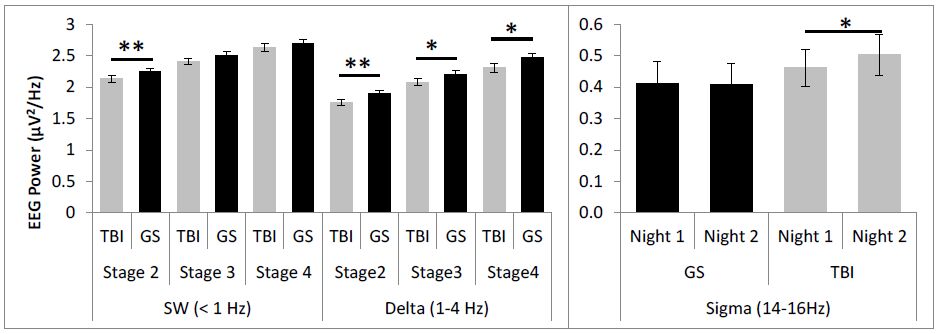
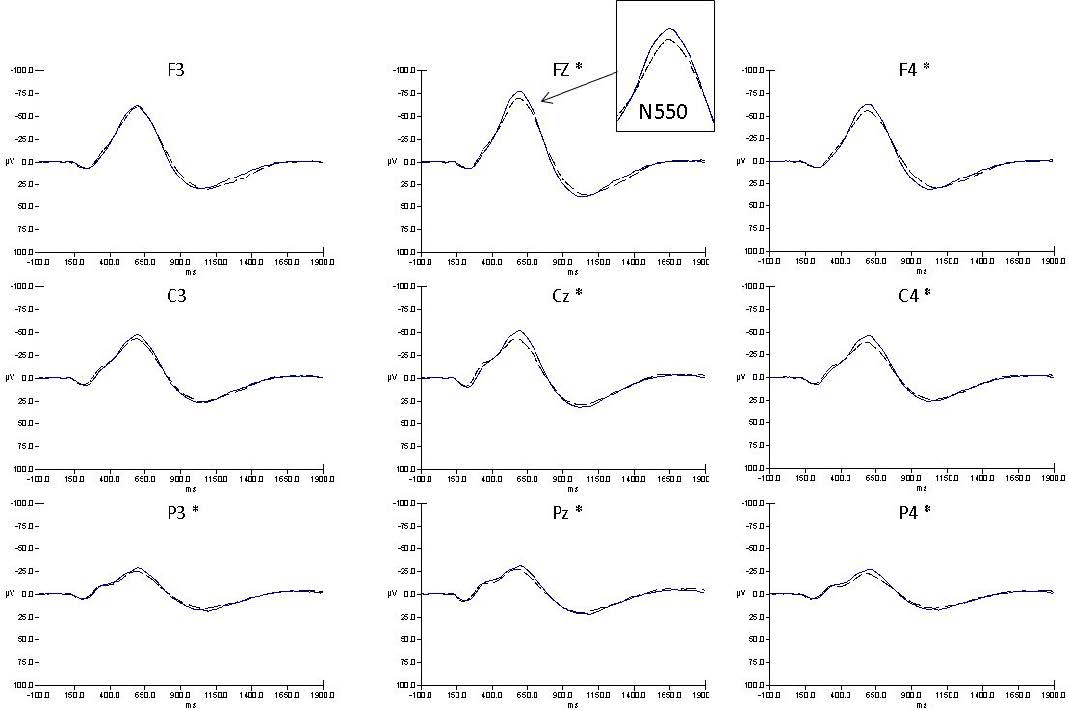
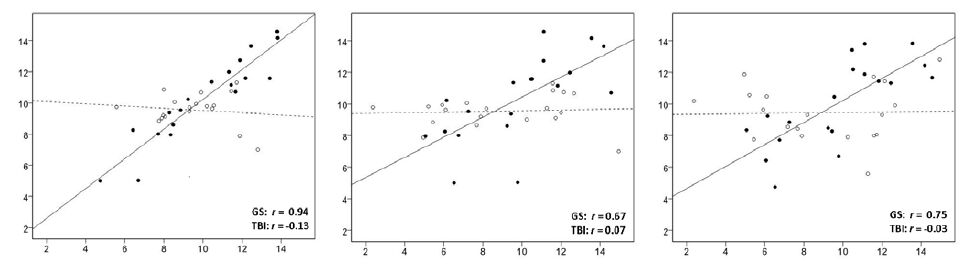
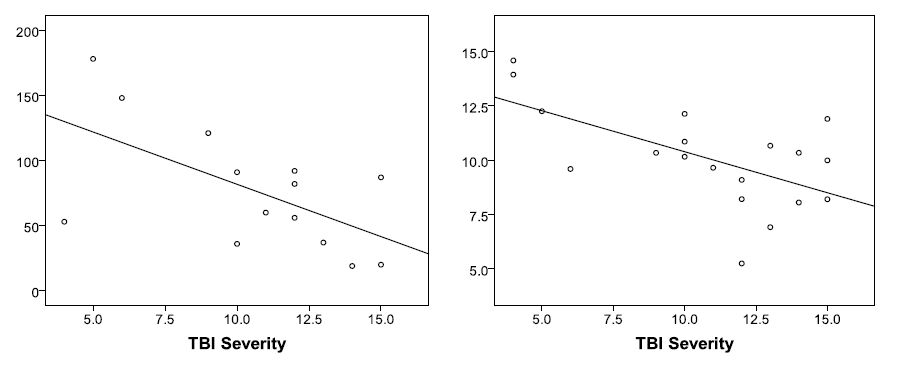
Sleep difficulties are commonly reported following traumatic brain injury (TBI), but few studies have systematically examined the neurophysiological characteristics of sleep. Sleep EEG was quantified over multiple nights to examine mechanisms underlying sleep disruption in individuals who had sustained a TBI and to explore the relationship between sleep disruption and waking function. Sleep was recorded from 20 individuals with a TBI (18-64 years) and 20 age-matched controls over two uninterrupted nights, as well as during a night where auditory stimuli were delivered. All participants underwent neuropsychological testing and waking performance assessment. Compared to controls, the TBI group had subjective complaints of falling asleep, delayed sleep onset on polysomnography (PSG), less Slow Wave (< 1 Hz) and delta (1-4 Hz) EEG power in non-REM sleep, fewer spontaneous and evoked k-complexes, reduced periodicity of spontaneous k-complexes, and lower amplitude of evoked k-complexes. While for controls, the density, duration and periodicity of sleep spindles diminished with deepening of non-REM as typically observed, this pattern was disrupted in the TBI group with peak spindle presentation occurring in Stage 3 sleep. Night-to-night-stability of Stage 2 spindles was high for controls but absent for the TBI group. Greater injury severity was related to fewer evoked k-complexes and lower spindle density. Greater spindle production predicted better waking function in the TBI group. Taken together, these data demonstrate impairment in sleep regulatory and inhibitory mechanisms as factors underlying sleep complaints following a TBI. Spindle generation may be adaptive or a marker of resiliency following TBI.

Keywords:

Citation: Kimberly A Cote, Catherine E Milner, Tamara A Speth. Altered Sleep Mechanisms following Traumatic Brain Injury and Relation to Waking Function[J]. AIMS Neuroscience, 2015, 2(4): 203-228. doi: 10.3934/Neuroscience.2015.4.203

Related Papers:

[1]	Panpan Jia, Jizhu Nan, Yongsheng Ma . Separating invariants for certain representations of the elementary Abelian $ p $-groups of rank two. AIMS Mathematics, 2024, 9(9): 25603-25618. doi: 10.3934/math.20241250
[2]	Hengbin Zhang . Automorphism group of the commuting graph of $ 2\times 2 $ matrix ring over $ \mathbb{Z}_{p^{s}} $. AIMS Mathematics, 2021, 6(11): 12650-12659. doi: 10.3934/math.2021729
[3]	Huaqing Gong, Shilin Yang . The representation ring of a non-pointed bialgebra. AIMS Mathematics, 2025, 10(3): 5110-5123. doi: 10.3934/math.2025234
[4]	Hicham Saber, Tariq Alraqad, Rashid Abu-Dawwas . On graded $ s $-prime submodules. AIMS Mathematics, 2021, 6(3): 2510-2524. doi: 10.3934/math.2021152
[5]	Fatma Zehra Uzekmek, Elif Segah Oztas, Mehmet Ozen . $ (\theta_i, \lambda) $-constacyclic codes and DNA codes over $ \mathbb{Z}_{4}+u\mathbb{Z}_{4}+u^{2}\mathbb{Z}_{4} $. AIMS Mathematics, 2024, 9(10): 27908-27929. doi: 10.3934/math.20241355
[6]	Pengcheng Ji, Jialei Chen, Fengxia Gao . Projective class ring of a restricted quantum group $ \overline{U}_{q}(\mathfrak{sl}^{}_2) $. AIMS Mathematics, 2023, 8(9): 19933-19949. doi: 10.3934/math.20231016*
[7]	Dong Su, Shilin Yang . Automorphism groups of representation rings of the weak Sweedler Hopf algebras. AIMS Mathematics, 2022, 7(2): 2318-2330. doi: 10.3934/math.2022131
[8]	Junyong Zhao . On the number of unit solutions of cubic congruence modulo $ n $. AIMS Mathematics, 2021, 6(12): 13515-13524. doi: 10.3934/math.2021784
[9]	Fareeha Jamal, Muhammad Imran . Distance spectrum of some zero divisor graphs. AIMS Mathematics, 2024, 9(9): 23979-23996. doi: 10.3934/math.20241166
[10]	Nikken Prima Puspita, Indah Emilia Wijayanti . Bi-clean and clean Hopf modules. AIMS Mathematics, 2022, 7(10): 18784-18792. doi: 10.3934/math.20221033

Abstract

1. Introduction

Tensor categories should be thought as counterparts of rings in the world of categories ^[1,2,3], i.e., the categorification of groups and rings ^[4,5,6]. They are ubiquitous in noncommutative algebra and representation theory. Tensor categories were introduced by Bénabou ^[7] in 1963 and Lane ^[8] as "categories with multiplication", and its related theories are now widely used in many fields of mathematics, including algebraic geometry ^[9], algebraic topology ^[10], number theory ^[11], operator algebraic theory ^[12], etc. The theory of tensor categories is also seen as a development following from that of Hopf algebras and their representation theory ^[13,14]. As an important invariant in the theory of tensor categories, the concept of a $ \mathbb{Z}_+ $-ring can be traced back to Lusztig's work ^[15] in 1987. Later, in ^[16,17], the notion of a $ \mathbb{Z}_+ $-module over a $ \mathbb{Z}_+ $-ring was introduced. Module categories over multitensor categories were first considered in ^[4,18], and then the notion of an indecomposable module category was introduced in ^[17]. As a categorification of irreducible $ \mathbb{Z}_+ $-modules, it is interesting to classify indecomposable exact module categories over a given tensor category. In this process, it is often necessary to first classify all irreducible $ \mathbb{Z}_+ $-modules over the Grothendieck ring of a given tensor category.

Typical examples of $ \mathbb{Z}_+ $-rings are the representation rings of Hopf algebras ^{[19,20,21,22,23,24]}. Another example is the Grothendieck rings of tensor categories ^{[25,26,27,28]}. It is natural to consider the classification of all irreducible $ \mathbb{Z}_+ $-modules over them. For example, Etingof and Khovanov classified irreducible $ \mathbb{Z}_+ $-modules over the group ring $ \mathbb ZG $, and showed that indecomposable $ \mathbb{Z}_+ $-modules over the representation ring of $ {\rm SU}(2) $, under certain conditions, correspond to affine and infinite Dynkin diagrams ^[16]. Also, there is a lot of related research in the context of near-group fusion categories. For instance, Tambara and Yamagami classified semisimple tensor categories with fusion rules of self-duality for finite abelian groups. Evans, Gannon, and Izumi have contributed to the classification of the near-group $ C^{*} $-categories ^[29,30]. Yuan et al. ^[31] studied irreducible $ \mathbb{Z}_+ $-modules of the near-group fusion ring $ K\left(\mathbb Z_3, 3\right) $ and so on.

In this paper, we explore the problem of classifying irreducible based modules of rank up to 5 over the complex representation ring $ r(S_4) $, and then discuss their categorification. Furthermore, we overcome the technical difficulty of solving a series of non-negative integer equations using MATLAB. In contrast with the representation ring of $ S_3 $, $ r(S_n) $ is no longer a near-group fusion ring when $ n > 3 $, and the classification of irreducible $ \mathbb{Z}_+ $-modules over general $ r(S_n) $ seems to be a hopeless task. Hence, our paper attempts to classify irreducible based modules for the non-near-group fusion ring $ r(S_4) $. In fact, the fusion rule of $ r(S_n) $ is already a highly nontrivial open problem in combinatorics, namely counting the multiplicities of irreducible components of the tensor product of any two irreducible complex representations of $ S_n $ (so called the Kronecker coefficients).

The paper is organized as follows. In Section 2, we recall some basic definitions and propositions. In Section 3, we discuss the irreducible based modules of rank up to 5 over $ r(S_4) $ and give the classification of all these based modules (Propositions 3.1–3.5). In Section 4, we first show that any $ \mathbb{Z}_+ $-module over the representation ring $ r(G) $ of a finite group $ G $ categorified by a module category over the representation category $ {\rm Rep}(G) $ should be a based module (Theorem 4.2), and then determine which irreducible based modules over $ r(S_4) $ can be categorified (Theorem 4.12).

2. Preliminaries

Throughout this paper, all rings are assumed to be associative with unit 1. Let $ \mathbb{Z}_+ $ denote the set of nonnegative integers. First, we recall the definitions of $ \mathbb{Z}_+ $-rings and $ \mathbb{Z}_+ $-modules. For more details about these concepts, readers can refer to ^[17,32].

2.1. $ \mathbb{Z}_+ $-rings and $ \mathbb{Z}_+ $-modules

In this section, we first recall some definitions, and then we exhibit a class of identities for transposed Poisson $ n $-Lie algebras.

Definition 2.1. Let $ A $ be a ring which is free as a $ \mathbb{Z} $-module:

(i) A $ \mathbb{Z}_+ $-basis of $ A $ is a basis

$ B = \left \{ b_{i} \right \} _{i\in I}, $

such that

$ b_{i}b_{j} = \sum\limits_{k\in I} c_{ij}^{k} b_{k}, $

where $ c_{ij}^{k}\in \mathbb{Z}_+ $.

(ii) A $ \mathbb{Z}_+ $-ring is a ring with a fixed $ \mathbb{Z}_+ $-basis and with unit 1 being a non-negative linear combination of the basis elements.

(iii) A $ \mathbb{Z}_+ $-ring is unital if the unit $ 1 $ is one of its basis elements.

Definition 2.2. Let $ A $ be a $ \mathbb{Z}_+ $-ring with basis $ \left \{ b_{i} \right \}_{i\in I} $. A $ \mathbb{Z}_+ $-module over $ A $ is an $ A $-module $ M $ with a fixed $ \mathbb{Z} $-basis $ \left \{ m_{l} \right \} _{l\in L} $ such that all the structure constants $ a_{il}^{k} $, defined by the equality

$ b_{i} m_{l} = \sum\limits_{k} a_{il}^{k} m_{k} $

are non-negative integers.

A $ \mathbb{Z}_+ $-module has the following equivalent definition referring to [32, Section 3.4].

Definition 2.3. Let $ A $ be a $ \mathbb{Z}_+ $-ring with basis $ \left \{ b_{i} \right \}_{i\in I} $. A $ \mathbb{Z}_+ $-module $ M $ over $ A $ means an assignment where each basis $ b_{i} $ in $ A $ is in one-to-one correspondence with a non-negative integer square matrix $ M_i $ such that $ M $ forms a representation of $ A $:

$ M_{i} M_{j} = \sum\limits_{k\in I} c_{ij}^{k} M_{k}, \; \; \forall \space i, j, k\in I, $

where the unit of $ A $ corresponds to the identity matrix. The rank of a $ \mathbb{Z}_+ $-module $ M $ is equal to the order of the matrix $ M_{i} $.

Definition 2.4. (i) Two $ \mathbb{Z}_+ $-modules $ M_{1}, \, M_{2} $ over $ A $ with bases $ {\left \{ m_{i}^{1} \right \} }_{i\in L_{1}}, {\left \{ m_{j}^{2} \right \} }_{j\in L_{2}} $ are equivalent if and only if there exists a bijection $ \phi $: $ L_{1}\to L_{2} $ such that the induced $ \mathbb{Z} $-linear map $ \tilde{\phi} $ of abelian groups $ M_{1}, \, M_{2} $ defined by

$ \tilde{\phi} (m_{i}^{1} ) = m_{{\phi} (i)}^{2} $

is an isomorphism of $ A $-modules. In other words, for $ a\in A $, let $ a_{M_{1} } $ and $ a_{M_{2} } $ be the matrices with respect to the bases $ {\left \{ m_{i}^{1} \right \} }_{i\in L_{1}} $ and $ {\left \{ m_{j}^{2} \right \} }_{j\in L_{2}} $, respectively. Then, two $ \mathbb{Z}_+ $-modules $ M_{1} $, $ M_{2} $ of rank $ n $ are equivalent if and only if there exists an $ n\times n $ permutation matrix $ P $ such that

$ a_{M_{2}} = Pa_{M_{1}}P^{-1}, \; \; \; \forall \space a\in A. $

(ii) The direct sum of two $ \mathbb{Z}_+ $-modules $ M_{1}, \, M_{2} $ over $ A $ is the module $ M_{1}\oplus M_{2} $ over $ A $ whose basis is the union of the bases of $ M_{1} $ and $ M_{2} $.

(iii) A $ \mathbb{Z}_+ $-module $ M $ over $ A $ is indecomposable if it is not equivalent to a nontrivial direct sum of $ \mathbb{Z}_+ $-modules.

(iv) A $ \mathbb{Z}_+ $-submodule of a $ \mathbb{Z}_+ $-module $ M $ over $ A $ with basis $ \left \{ m_{l} \right \}_{l\in L} $ is a subset $ J\subset L $ such that the abelian subgroup of $ M $ generated by $ {\left \{ m_{j} \right \} }_{j\in J} $ is an $ A $-submodule.

(v) A $ \mathbb{Z}_+ $-module $ M $ over $ A $ is irreducible if any $ \mathbb{Z}_+ $-submodule of $ M $ is 0 or $ M $. In other words, the $ \mathbb{Z} $-span of any proper subset of the basis of $ M $ is not an $ A $-submodule.

2.2. Based rings and based modules

Let $ A $ be a $ \mathbb{Z}_+ $-ring with basis $ \left \{ b_{i} \right \}_{i\in I} $, and let $ I_{0} $ be the set of $ i\in I $ such that $ b_{i} $ occurs in the decomposition of 1. Let $ \tau $: $ A\to \mathbb Z $ denote the group homomorphism defined by

$ \tau (b_{i} ) =

$\begin{cases}1, & \text{ if } \ i\in I_{0} , \\0, & \text{ if } \ i\notin I_{0} .\end{cases}$ $

Definition 2.5. A $ \mathbb{Z}_+ $-ring with basis $ \left \{ b_{i} \right \}_{i\in I} $ is called a based ring if there exists an involution $ i \mapsto i^{*} $ of $ I $ such that the induced map

$ a = \sum\limits_{i\in I} a_{i} b_{i}\mapsto {}a^{*} = \sum\limits_{i\in I} a_{i} b_{i^*}, \; \; \; a_{i}\in \mathbb{Z}, $

is an anti-involution of the ring $ A $, and

$ \tau (b_{i}b_{j} ) =

$\begin{cases}1, & { if } \ i = j^{*} , \\0, & { if } \ i\ne j^{*} .\end{cases}$ $

A fusion ring is a unital based ring of finite rank.

Definition 2.6. A based module over a based ring $ A $ with basis $ \left \{ b_{i} \right \}_{i\in I} $ is a $ \mathbb{Z}_+ $-module $ M $ with basis $ \left \{ m_{l} \right \}_{l\in L} $ over $ A $ such that

$ a_{il}^{k} = a_{i^{\ast } k}^{l} , $

where $ a_{il}^{k} $ are defined as in Definition 2.2.

Let $ A $ be a unital $ \mathbb{Z}_+ $-ring of finite rank with basis $ \left \{ b_{i} \right \}_{i\in I} $, and let $ M $ be a $ \mathbb{Z}_+ $-module over $ A $ with $ \mathbb{Z} $-basis $ \left \{ m_{l} \right \} _{l\in L} $. Take

$ b = \sum\limits_{i\in I}b_i. $

For any fixed $ m_{l_0} $, the $ \mathbb{Z}_+ $-submodule of $ M $ generated by $ m_{l_0} $ is the $ \mathbb{Z} $-span of $ \left \{m_k\right\}_{k\in Y} $, where the set $ Y $ consists of $ k\in L $ such that $ m_k $ is a summand of $ bm_{l_0} $. Also, we need the following facts.

Proposition 2.1. [32, Proposition 3.4.6] Let $ A $ be a based ring of finite rank over $ \mathbb{Z} $. Then there exist only finitely many irreducible $ \mathbb{Z}_+ $-modules over $ A $.

Proposition 2.2. [17, Lemma 2.1] Let $ M $ be a based module over a based ring $ A $. If $ M $ is decomposable as a $ \mathbb{Z}_+ $-module over $ A $, then $ M $ is irreducible as a $ \mathbb{Z}_+ $-module over $ A $.

As a result, any $ \mathbb{Z}_+ $-module of finite rank over a fusion ring is completely reducible, and then only irreducible $ \mathbb{Z}_+ $-modules need to be classified.

In general, the rank of an irreducible $ \mathbb{Z}_+ $-module over a fusion ring $ A $ may be larger than the rank of $ A $; e.g., $ A = r(D_5) $ for the dihedral group $ D_5 $ ([33, Remark 1]). In this paper, we explore which irreducible based modules over $ r(S_4) $ can be categorified by indecomposable exact module categories over the representation category $ {\rm Rep}(S_4) $. Since all these module categories are of rank not greater than 5, we only deal with based modules of rank up to 5 correspondingly.

3. Irreducible based modules over $ r(S_4) $

In this section, we will classify the irreducible based modules over the complex representation ring $ r(S_4) $ of $ S_4 $ up to equivalence. $ r(S_4) $ is a commutative fusion ring having a $ \mathbb{Z}_+ $-basis $ \left \{ 1, V_{\psi}, V_{\rho _{1}}, V_{\rho _{2}}, V_{\rho _{3}} \right \} $ with the fusion rule.

$\begin{equation} \begin{array}{c} V_{\psi}^2 = 1, \quad V_{\psi}V_{\rho _{1}} = V_{\rho _{1}}, \quad V_{\psi}V_{\rho _{2}} = V_{\rho _{3}}, \quad V_{\rho _{1}}^2 = 1+V_{\psi}+V_{\rho _{1}}, \\[.5em] V_{\rho_1 }V_{\rho_2 } = V_{\rho_2 }+V_{\rho_3}, \quad V_{\rho _{2}}^2 = 1+ V_{\rho _{1}}+ V_{\rho _{2}}+ V_{\rho _{3}}, \end{array} \end{equation}$ $

(3.1)

where $ 1 $, $ V_{\psi} $, and $ V_{\rho _{1}} $ denote the trivial representation, sign representation, and 2-dimensional irreducible representation, respectively, while $ V_{\rho_2} $ stands for the 3-dimensional standard representation and $ V_{\rho_3} $ denotes its conjugate representation. Then we have the following Table 1.

Table 1. The complex character table of $ S_4 $.

	$ (1) $	$ (12) $	$ (123) $	$ (1234) $	$ (12)(34) $
$ \chi_1 $	$ 1 $	$ 1 $	$ 1 $	$ 1 $	$ 1 $
$ \chi_\psi $	$ 1 $	$ -1 $	$ 1 $	$ -1 $	$ 1 $
$ \chi_{\rho_1} $	$ 2 $	$ 0 $	$ -1 $	$ 0 $	$ 2 $
$ \chi_{\rho_2} $	$ 3 $	$ 1 $	$ 0 $	$ -1 $	$ -1 $
$ \chi_{\rho_3} $	$ 3 $	$ -1 $	$ 0 $	$ 1 $	$ -1 $

| Show Table

DownLoad: CSV

Let $ M $ be a based module of $ r(S_4) $ with the basis $ \left \{ m_{l} \right \} _{l\in L} $. Let $ T, \, Q, \, U $, and $ W $ be the matrices representing the action of $ V_{\psi}, \, V_{\rho _{1}}, \, V_{\rho _{2}} $, and $ V_{\rho _{3}} $ on $ M $ respectively. They are all symmetric matrices with nonnegative integer entries by Definition 2.6. Let $ E $ be the identity matrix. By the fusion rule of $ r(S_4) $, we have

$\begin{align} T^2& = E, \end{align}$ $

(3.2)

$\begin{align} TQ& = QT = Q, \end{align}$ $

(3.3)

$\begin{align} TU& = UT = W, \end{align}$ $

(3.4)

$\begin{align} Q^2& = E+T+Q, \end{align}$ $

(3.5)

$\begin{align} QU& = U+TU, \end{align}$ $

(3.6)

$\begin{align} U^2& = E+Q+U+TU. \end{align}$ $

(3.7)

In particular, since $ T^2 = E $ and $ T $ has nonnegative integer entries, we know that $ T $ is a symmetric permutation matrix.

Convention 3.1. Let $ P_n $ be the group of $ n\times n $ permutation matrices. Since there is naturally a group isomorphism between $ S_n $ and $ P_n $, we will use the cycle notation of permutations to represent permutation matrices.

3.1. Irreducible based modules of rank $ \le 3 $ over $ r(S_4) $

We define a $ \mathbb{Z}_+ $-module $ M_{1, 1} $ of rank 1 over $ r(S_4) $ by letting

$\begin{equation} V_{\psi} \mapsto 1, \quad V_{\rho _{1}}\mapsto 2, \quad V_{\rho _{2}}\mapsto 3, \quad V_{\rho _{3}}\mapsto 3. \end{equation}$ $

(3.8)

Proposition 3.1. Any irreducible based module of rank $ 1 $ over $ r(S_4) $ is equivalent to $ M_{1, 1} $.

Proof. Note that any integral fusion ring $ A $ has the unique character $ {\rm FPdim} $: $ A\to \mathbb{Z} $, which takes non-negative values on the $ \mathbb{Z}_+ $-basis, so there exists a unique $ \mathbb{Z}_+ $-module $ M $ of rank 1 over it. Clearly, such $ M $ is a based module. Now this argument is available for the situation $ A = r(S_4) $. □

Next, we consider irreducible based modules of rank $ 2, 3 $. According to the fusion rule of $ r(S_4) $ given in (3.1), it is sufficient to only list the representation matrices of $ V_{\psi} $, $ V_{\rho _{1}} $, and $ V_{\rho _{2}} $ acting on them. For simplicity, we choose to present our result for the cases of small rank 2 and 3 directly, and then analyze the cases of higher rank 4 and 5 with details.

Proposition 3.2. Let $ M $ be an irreducible based module of rank $ 2 $ over $ r(S_4) $. Then $ M $ is equivalent to one of the based modules $ M_{2, i}, \, 1\leq i\leq 3 $, listed in Table 2.

Table 2. Inequivalent irreducible based modules of rank 2 over $ r(S_4) $.

	$ V_{\psi} $	$ V_{\rho _{1}} $	$ V_{\rho _{2}} $
$ M_{2, 1} $	$ $\begin{pmatrix} 1&0\\0&1\end{pmatrix}$ $	$ $\begin{pmatrix} 2&0\\0&2\end{pmatrix}$ $	$ $\begin{pmatrix} 1&2\\2&1\end{pmatrix}$ $
$ M_{2, 2} $	$ $\begin{pmatrix} 0&1\\1&0\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1\\1&1\end{pmatrix}$ $	$ $\begin{pmatrix} 2&1\\1&2\end{pmatrix}$ $
$ M_{2, 3} $	$ $\begin{pmatrix} 0&1\\1&0\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1\\1&1\end{pmatrix}$ $	$ $\begin{pmatrix} 1&2\\2&1\end{pmatrix}$ $

| Show Table

DownLoad: CSV

Proposition 3.3. Let $ M $ be an irreducible based module of rank $ 3 $ over $ r(S_4) $. Then $ M $ is equivalent to one of the based modules $ M_{3, i}, \, 1\leq i\leq 3 $, listed in Table 3.

Table 3. Inequivalent irreducible based modules of rank 3 over $ r(S_4) $.

	$ V_{\psi} $	$ V_{\rho _{1}} $	$ V_{\rho _{2}} $
$ M_{3, 1} $	$ $\begin{pmatrix} 1&0&0\\0&1&0\\0&0&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&1&1\\1&0&1\\1&1&0\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1&1\\1&1&1\\1&1&1\\\end{pmatrix}$ $
$ M_{3, 2} $	$ $\begin{pmatrix} 0&1&0\\1&0&0\\0&0&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&0&1\\0&0&1\\1&1&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&0&1\\0&1&1\\1&1&2\\\end{pmatrix}$ $
$ M_{3, 3} $	$ $\begin{pmatrix} 0&1&0\\1&0&0\\0&0&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&0&1\\0&0&1\\1&1&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&1&1\\1&0&1\\1&1&2\\\end{pmatrix}$ $

| Show Table

DownLoad: CSV

3.2. Irreducible based modules of rank $ 4, \, 5 $ over $ r(S_4) $

Proposition 3.4. Let $ M $ be an irreducible based module of rank $ 4 $ over $ r(S_4) $. Then $ M $ is equivalent to one of the based modules $ M_{4, i}, \, 1\leq i\leq 7 $, listed in Table 4.

Table 4. Inequivalent irreducible based modules of rank 4 over $ r(S_4) $.

	$ V_{\psi} $	$ V_{\rho _{1}} $	$ V_{\rho _{2}} $
$ M_{4, 1} $	$ $\begin{pmatrix} 1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&0&1&1\\0&2&0&0\\1&0&0&1\\1&0&1&0\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&1&0&0\\1&2&1&1\\0&1&0&0\\0&1&0&0\\\end{pmatrix}$ $
$ M_{4, 2} $	$ $\begin{pmatrix} 1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 2&0&0&0\\0&2&0&0\\0&0&2&0\\0&0&0&2\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&1&1&1\\1&0&1&1\\1&1&0&1\\1&1&1&0\\\end{pmatrix}$ $
$ M_{4, 3} $	$ $\begin{pmatrix} 0&1&0&0\\1&0&0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1&0&0\\1&1&0&0\\0&0&2&0\\0&0&0&2\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&0&1&1\\0&1&1&1\\1&1&0&1\\1&1&1&0\\\end{pmatrix}$ $
$ M_{4, 4} $	$ $\begin{pmatrix} 0&1&0&0\\1&0&0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1&0&0\\1&1&0&0\\0&0&2&0\\0&0&0&2\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&1&1&1\\1&0&1&1\\1&1&0&1\\1&1&1&0\\\end{pmatrix}$ $
$M_{4, 5} $	$ $\begin{pmatrix} 0&1&0&0\\1&0&0&0\\0&0&0&1\\0&0&1&0\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1&0&0\\1&1&0&0\\0&0&1&1\\0&0&1&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&1&1&1\\1&0&1&1\\1&1&0&1\\1&1&1&0\\\end{pmatrix}$ $
$ M_{4, 6} $	$ $\begin{pmatrix} 0&1&0&0\\1&0&0&0\\0&0&0&1\\0&0&1&0\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1&0&0\\1&1&0&0\\0&0&1&1\\0&0&1&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&1&1&1\\1&0&1&1\\1&1&1&0\\1&1&0&1\\\end{pmatrix}$ $
$ M_{4, 7} $	$ $\begin{pmatrix} 0&1&0&0\\1&0&0&0\\0&0&0&1\\0&0&1&0\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1&0&0\\1&1&0&0\\0&0&1&1\\0&0&1&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&0&1&1\\0&1&1&1\\1&1&1&0\\1&1&0&1\\\end{pmatrix}$ $

| Show Table

DownLoad: CSV

Proof. Before giving its detailed proof, we provide the following proof outline first.

$ ({\rm{i}}) $ The symmetric group $ S_4 $ has 3 conjugacy classes of permutations of order $ \le 2 $, so there are 3 representatives for matrix $ T $ up to conjugation as follows:

$\begin{equation*} T_1 = E_4, \quad T_2 = (12), \quad T_3 = (12)(34). \end{equation*}$ $

Consequently, we can take $ T = T_r $ for some $ r = 1, 2, 3 $ as the representation matrix of $ V_\psi $ for the based module $ M $ up to equivalence.

$ ({\rm{ii}}) $ Use MATLAB to search all solutions of the representation matrices $ Q $ and $ U $ in the group of nonnegative integer matrix Eqs (3.3)–(3.7) by constraint satisfaction.

$ ({\rm{iii}}) $ Distinguish all conjugacy classes of tuples $ (T, Q, U) $ without simultaneous block decomposition. They correspond to the equivalence classes of irreducible based modules over $ r(S_4) $.

□

Proof. Let $ M $ be a based module of rank 4 over $ r(S_4) $, with the action of $ r(S_4) $ on it given by

$\begin{equation} V_{\psi} \mapsto T, \quad V_{\rho _{1}}\mapsto Q = (a_{ij})_{1\leq i, j\leq4} , \quad V_{\rho _{2}}\mapsto U = (b_{ij})_{1\leq i, j\leq4}, \quad V_{\rho _{3}}\mapsto W = TU, \nonumber \end{equation}$ $

where $ a_{ij} = a_{ji} $, $ b_{ij} = b_{ji} $.

The symmetric group $ S_4 $ has two conjugacy classes of permutations of order 2. One conjugacy class of 6 permutations includes $ (12) $, and the other one of 3 permutations includes $ (12)(34) $. As previously seen, $ T $ is the unit or an element of order 2 in $ P_4 $, so we have 10 candidates for $ T $, and each of them is conjugate to one of the following 3 matrices:

$\begin{equation*} T_1 = E_4, \quad T_2 = (12) , \quad T_3 = (12)(34) . \end{equation*}$ $

Hence, for the based module $ M $ determined by the pair $ (T, Q, U) $, there exists a $ 4\times 4 $ permutation matrix $ P $ such that

$ T' = PTP^{-1} $

is one of the above $ T_r $'s $ (1\leq r\leq 3) $. Correspondingly, let

$ Q' = PQP^{-1} , \; \; \; U' = PUP^{-1}. $

Then we get a based module $ M' $ determined by the pair $ (T', Q', U') $ and equivalent to $ M $ as based modules by Definition 2.4 (ⅰ). So, we have reduced the proof to the situation when $ T = T_r $.

Case 1. $ T = T_1 = E_4 $.

Since $ Q $ satisfies Eq (3.5), we obtain the following system of integer equations:

$\begin{equation*} \left\{\begin{array}{l} a_{11}^2+a_{12}^2+a_{13}^2+a_{14}^2 = 2+a_{11}, \\ a_{11}a_{12}+a_{12}a_{22}+a_{13}a_{23}+a_{14}a_{24} = a_{12}, \\ a_{11}a_{13}+a_{12}a_{23}+a_{13}a_{33}+a_{14}a_{34} = a_{13}, \\ a_{11}a_{14}+a_{12}a_{24}+a_{13}a_{34}+a_{14}a_{44} = a_{14}, \\ a_{12}^2+a_{22}^2+a_{23}^2+a_{24}^2 = 2+a_{22}, \\ a_{12}a_{13}+a_{22}a_{23}+a_{23}a_{33}+a_{24}a_{34} = a_{23}, \\ a_{12}a_{14}+a_{22}a_{24}+a_{23}a_{34}+a_{24}a_{44} = a_{24}, \\ a_{13}^2+a_{23}^2+a_{33}^2+a_{34}^2 = 2+a_{33}, \\ a_{13}a_{14}+a_{23}a_{24}+a_{33}a_{34}+a_{34}a_{44} = a_{34}, \\ a_{14}^2+a_{24}^2+a_{34}^2+a_{44}^2 = 2+a_{44}. \end{array}\right. \end{equation*}$ $

We use MATLAB to figure out all the solutions of $ Q $ as follows:

$\begin{array}{l} Q_1 = \begin{pmatrix} 0&0&1&1 \\ 0&2&0&0 \\ 1&0&0&1 \\ 1&0&1&0 \end{pmatrix}, \quad Q_2 = \begin{pmatrix} 0&1&0&1 \\ 1&0&0&1 \\ 0&0&2&0 \\ 1&1&0&0 \end{pmatrix}, \quad Q_3 = \begin{pmatrix} 0&1&1&0 \\ 1&0&1&0 \\ 1&1&0&0 \\ 0&0&0&2 \end{pmatrix}, \\[2em] Q_4 = \begin{pmatrix} 2&0&0&0 \\ 0&0&1&1 \\ 0&1&0&1 \\ 0&1&1&0 \end{pmatrix}, \quad Q_5 = \begin{pmatrix} 2&0&0&0 \\ 0&2&0&0 \\ 0&0&2&0 \\ 0&0&0&2 \end{pmatrix}. \end{array}$ $

Next, we calculate $ U $ after taking $ Q $ as one $ Q_k $ $ \left (1\le k\le5 \right) $.

Case 1.1. $ Q = Q_1 $.

Since $ U $ satisfies Eq (3.6), we get

$\begin{equation*} \begin{split} b_{12}& = b_{23} = b_{24}, \\ b_{11}& = b_{13} = b_{14} = b_{33} = b_{34} = b_{44}. \end{split} \end{equation*}$ $

Then, by Eq (3.7), we have

$\begin{equation*} \left\{\begin{array}{l} 3b_{11}^2+b_{12}^2 = 2b_{11}+1, \\ 3b_{11}b_{12}+b_{12}b_{22} = 2b_{12}, \\ 3b_{12}^2+b_{22}^2 = 2b_{22}+3. \end{array}\right. \end{equation*}$ $

The solutions of $ U $ given by MATLAB are as follows:

$\begin{equation*} U_1 = \begin{pmatrix} 0&1&0&0 \\ 1&2&1&1 \\ 0&1&0&0 \\ 0&1&0&0 \end{pmatrix}, \quad U_2 = \begin{pmatrix} 1&0&1&1 \\ 0&3&0&0 \\ 1&0&1&1 \\ 1&0&1&1 \end{pmatrix}. \end{equation*}$ $

It is easy to check that the based module determined by $ \left (T_1, Q_1, U_1\right) $ is an irreducible based module denoted as $ M_{4, 1} $, while the based module determined by $ \left (T_1, Q_1, U_2\right) $ is reducible.

Note that there exists a permutation matrix $ P = (14)(23) $ such that

$ PQ_1P^{-1} = Q_2. $

Let

$ U'_1 = PU_1P^{-1}. $

There is an irreducible based module $ N' $ determined by the pair $ \big (T_1, Q_2, U'_1\big) $ and equivalent to $ M_{4, 1} $ by Definition 2.4 (ⅰ). Conversely, any irreducible based module with representation matrices $ T_1 $ and $ Q_2 $ is equivalent to $ M_{4, 1} $. The same analysis tells us that irreducible based modules with representation matrices $ T_1 $ and $ Q_3 $ (or $ Q_4 $) are also equivalent to $ M_{4, 1} $.

Case 1.2. $ Q = Q_5 $.

Since $ U $ satisfies Eqs (3.6) and (3.7), we get a system of integer equations as follows:

$\begin{equation*} \left\{\begin{array}{l} b_{11}^2+b_{12}^2+b_{13}^2+b_{14}^2 = 2b_{11}+3, \\ b_{11}b_{12}+b_{12}b_{22}+b_{13}b_{23}+b_{14}b_{24} = 2b_{12}, \\ b_{11}b_{13}+b_{12}b_{23}+b_{13}b_{33}+b_{14}b_{34} = 2b_{13}, \\ b_{11}b_{14}+b_{12}b_{24}+b_{13}b_{34}+b_{14}b_{44} = 2b_{14}, \\ b_{12}^2+b_{22}^2+b_{23}^2+b_{24}^2 = 2b_{22}+3, \\ b_{12}b_{13}+b_{22}b_{23}+b_{23}b_{33}+b_{24}b_{34} = 2b_{23}, \\ b_{12}b_{14}+b_{22}b_{24}+b_{23}b_{34}+b_{24}b_{44} = 2b_{24}, \\ b_{13}^2+b_{23}^2+b_{33}^2+b_{34}^2 = 2b_{33}+3, \\ b_{13}b_{14}+b_{23}b_{24}+b_{33}b_{34}+b_{34}b_{44} = 2b_{34}, \\ b_{14}^2+b_{24}^2+b_{34}^2+b_{44}^2 = 2b_{44}+3. \\ \end{array}\right. \end{equation*}$ $

Thus, the solutions of $ U $ by MATLAB are as follows:

$\begin{align*} &U_1 = \begin{pmatrix} 0&1&1&1 \\ 1&0&1&1 \\ 1&1&0&1 \\ 1&1&1&0\end{pmatrix}, \quad U_2 = \begin{pmatrix} 1&0&0&2 \\ 0&1&2&0 \\ 0&2&1&0 \\ 2&0&0&1\end{pmatrix}, \quad U_3 = \begin{pmatrix}1&0&2&0 \\ 0&1&0&2 \\ 2&0&1&0 \\ 0&2&0&1\end{pmatrix}, \quad U_4 = \begin{pmatrix}1&2&0&0 \\ 2&1&0&0 \\ 0&0&1&2 \\ 0&0&2&1\end{pmatrix}, \\[2em] &U_5 = \begin{pmatrix} 1&0&2&0 \\ 0&3&0&0 \\ 2&0&1&0 \\ 0&0&0&3\end{pmatrix}, \quad U_6 = \begin{pmatrix} 1&0&0&2 \\ 0&3&0&0 \\ 0&0&3&0 \\ 2&0&0&1\end{pmatrix}, \quad U_7 = \begin{pmatrix}1&2&0&0 \\ 2&1&0&0 \\ 0&0&3&0 \\ 0&0&0&3\end{pmatrix}, \quad U_8 = \begin{pmatrix}3&0&0&0 \\ 0&3&0&0 \\ 0&0&1&2 \\ 0&0&2&1\end{pmatrix}, \\ &U_9 = \begin{pmatrix} 3&0&0&0 \\ 0&1&2&0 \\ 0&2&1&0 \\ 0&0&0&3\end{pmatrix}, \quad U_{10} = \begin{pmatrix} 3&0&0&0 \\ 0&1&0&2 \\ 0&0&3&0 \\ 0&2&0&1\end{pmatrix}, \quad U_{11} = \begin{pmatrix}3&0&0&0 \\ 0&3&0&0 \\ 0&0&3&0 \\ 0&0&0&3\end{pmatrix}. \end{align*}$ $

Since $ T_1 $ and $ Q_5 $ are diagonal and the solutions $ U_t $ $ \left (2\le t\le11 \right) $ are block diagonal with at least two blocks, only the based module determined by $ (T_1, Q_5, U_1) $ is irreducible, denoted as $ M_{4, 2} $.

Case 2. $ T = T_2 = (12) $.

Since $ Q $ satisfies Eq (3.3), we get

$\begin{equation*} Q = \begin{pmatrix} a_{11}&a_{11}&a_{13}&a_{14} \\ a_{11}&a_{11}&a_{13}&a_{14}\\ a_{13}&a_{13}&a_{33}&a_{34} \\ a_{14}&a_{14}&a_{34}&a_{44} \end{pmatrix}. \end{equation*}$ $

Since $ Q $ also satisfies Eq (3.5), we have the following system of integer equations:

$\begin{equation*} \left\{\begin{array}{l} 2a_{11}^2+a_{13}^2+a_{14}^2 = a_{11}+1, \\ 2a_{11}a_{13}+a_{13}a_{33}+a_{14}a_{34} = a_{13}, \\ 2a_{11}a_{14}+a_{13}a_{34}+a_{14}a_{44} = a_{14}, \\ 2a_{13}^2+a_{33}^2+a_{34}^2 = a_{33}+2, \\ 2a_{13}a_{14}+a_{33}a_{34}+a_{34}a_{44} = a_{34}, \\ 2a_{14}^2+a_{34}^2+a_{44}^2 = a_{44}+2. \\ \end{array}\right. \end{equation*}$ $

Hence, the solutions of $ Q $ by MATLAB are as follows:

$\begin{array}{l} Q_1 = \begin{pmatrix} 0&0&0&1 \\ 0&0&0&1 \\ 0&0&2&0 \\ 1&1&0&1\end{pmatrix}, \quad Q_2 = \begin{pmatrix} 0&0&1&0 \\ 0&0&1&0 \\ 1&1&1&0 \\ 0&0&0&2\end{pmatrix}, \quad Q_3 = \begin{pmatrix}1&1&0&0 \\ 1&1&0&0 \\ 0&0&2&0 \\ 0&0&0&2\end{pmatrix}. \end{array}$ $

Since $ U $ satisfies Eq (3.4), we get

$\begin{equation*} U = \begin{pmatrix} b_{11}&b_{12}&b_{13}&b_{14}\\ b_{12}&b_{11}&b_{13}&b_{14}\\ b_{13}&b_{13}&b_{33}&b_{34} \\ b_{14}&b_{14}&b_{34}&b_{44} \end{pmatrix}. \end{equation*}$ $

Next, we calculate $ U $ after taking $ Q $ as one $ Q_k $ $ \left (1\le k\le3 \right) $.

Case 2.1. $ Q = Q_1 $.

Since $ U $ satisfies Eqs (3.6) and (3.7), the solutions of $ U $ given by MATLAB are as follows:

$\begin{array}{l} U_1 = \begin{pmatrix} 0&1&0&1 \\ 1&0&0&1 \\ 0&0&3&0 \\ 1&1&0&2\end{pmatrix}, \quad U_2 = \begin{pmatrix} 1&0&0&1 \\ 0&1&0&1 \\ 0&0&3&0 \\ 1&1&0&2\end{pmatrix}. \end{array}$ $

Since $ T_2 $, $ Q_1 $ and all the solutions $ U_t $ for $ t = 1, 2 $ are block diagonal with at least two blocks, the based modules determined by each pair $ (T_2, Q_1, U_t) $ are reducible.

Note that there exists a permutation matrix $ P = (12)(34) $ such that

$ PQ_1P^{-1} = Q_2. $

Let

$ U'_t = PU_tP^{-1}. $

Then each based module $ N_t $ determined by the pair $ \left (T_2, Q_2, U'_t\right) $ is reducible. Namely, any based module with representation matrices $ T_2 $ and $ Q_2 $ is reducible.

Case 2.2. $ Q = Q_3 $.

Since $ U $ satisfies Eqs (3.6) and (3.7), we have

$\begin{array}{l} U_1 = \begin{pmatrix} 0&1&1&1 \\ 1&0&1&1 \\ 1&1&0&1 \\ 1&1&1&0\end{pmatrix}, \quad U_2 = \begin{pmatrix} 1&0&1&1 \\ 0&1&1&1 \\ 1&1&0&1 \\ 1&1&1&0\end{pmatrix}, \quad U_3 = \begin{pmatrix}1&2&0&0 \\ 2&1&0&0 \\ 0&0&1&2 \\ 0&0&2&1\end{pmatrix}, \\[2em] U_4 = \begin{pmatrix}1&2&0&0 \\ 2&1&0&0 \\ 0&0&3&0 \\ 0&0&0&3\end{pmatrix}, \quad U_5 = \begin{pmatrix} 2&1&0&0 \\ 1&2&0&0 \\ 0&0&1&2 \\ 0&0&2&1\end{pmatrix}, \quad U_6 = \begin{pmatrix} 2&1&0&0 \\ 1&2&0&0 \\ 0&0&3&0 \\ 0&0&0&3\end{pmatrix}. \end{array}$ $

Since $ T_2 $, $ Q_3 $ and the solutions $ U_s $ $ (3\le s\le 6) $ are block diagonal with at least two blocks, only the based module determined by $ (T_2, Q_3, U_1) $ and $ (T_2, Q_3, U_2) $ are irreducible, denoted as $ M_{4, 3} $ and $ M_{4, 4} $, respectively. It is easy to check that $ M_{4, 3} $ and $ M_{4, 4} $ are inequivalent based modules.

Case 3. $ T = T_3 = (12)(34) $.

Since $ Q $ satisfies Eq (3.3), we get

$\begin{equation*} Q = \begin{pmatrix} a_{11}&a_{11}&a_{13}&a_{13} \\ a_{11}&a_{11}&a_{13}&a_{13}\\ a_{13}&a_{13}&a_{33}&a_{33} \\ a_{13}&a_{13}&a_{33}&a_{33} \end{pmatrix}. \end{equation*}$ $

Then, by Eq (3.5), we have the following system of integer equations:

$\begin{equation*} \left\{\begin{array}{l} 2a_{11}^2+2a_{13}^2 = a_{11}+1, \\ 2a_{11}a_{13}+2a_{13}a_{33} = a_{13}, \\ 2a_{13}^2+2a_{33}^2 = a_{33}+1. \end{array}\right. \end{equation*}$ $

$ Q $ has the following unique solution:

$\begin{equation*} Q_1 = \begin{pmatrix} 1&1&0&0\\ 1&1&0&0\\ 0&0&1&1\\ 0&0&1&1 \end{pmatrix}. \end{equation*}$ $

Since $ U $ satisfies Eq (3.4), we get

$\begin{equation*} U = \begin{pmatrix} b_{11}&b_{12}&b_{13}&b_{14}\\ b_{12}&b_{11}&b_{14}&b_{13}\\ b_{13}&b_{14}&b_{33}&b_{34} \\ b_{14}&b_{13}&b_{34}&b_{33} \end{pmatrix}. \end{equation*}$ $

Since $ U $ also satisfies Eqs (3.6) and (3.7), we obtain the solutions of $ U $ by MATLAB as follows:

$\begin{array}{l} U_1 = \begin{pmatrix} 0&1&1&1 \\ 1&0&1&1 \\ 1&1&0&1 \\ 1&1&1&0\end{pmatrix}, \quad U_2 = \begin{pmatrix} 0&1&1&1 \\ 1&0&1&1 \\ 1&1&1&0 \\ 1&1&0&1\end{pmatrix}, \quad U_3 = \begin{pmatrix}1&0&1&1 \\ 0&1&1&1 \\ 1&1&1&0 \\ 1&1&0&1\end{pmatrix}, \quad U_4 = \begin{pmatrix}1&0&1&1\\ 0&1&1&1 \\ 1&1&0&1 \\ 1&1&1&0\end{pmatrix}, \\[2em] U_5 = \begin{pmatrix} 1&2&0&0 \\ 2&1&0&0 \\ 0&0&1&2 \\ 0&0&2&1\end{pmatrix}, \quad U_6 = \begin{pmatrix} 1&2&0&0 \\ 2&1&0&0 \\ 0&0&2&1 \\ 0&0&1&2\end{pmatrix}, \quad U_7 = \begin{pmatrix}2&1&0&0 \\ 1&2&0&0 \\ 0&0&1&2 \\ 0&0&2&1\end{pmatrix}, \quad U_8 = \begin{pmatrix}2&1&0&0 \\ 1&2&0&0 \\ 0&0&2&1 \\ 0&0&1&2\end{pmatrix}. \end{array}$ $

Clearly, $ T_3 $, $ Q_1 $ and the solutions $ U_s $ are block diagonal with at least two blocks, but the based module determined by the pair $ \left (T_3, Q_1, U_t\right) $ is irreducible, denoted as $ M_{4, s} $, where $ 5\le s \le8, 1\le t\le4 $. Define the $ \mathbb Z $-module isomorphism $ \phi $: $ M_{4, 6}\to M_{4, 8} $ by

$\begin{equation*} \phi(v_1^1) = v_4^2, \quad \phi(v_2^1) = v_3^2, \quad \phi(v_3^1) = v_2^2, \quad\phi(v_4^1) = v_1^2. \end{equation*}$ $

It is easy to see that $ M_{4, 6} $ is equivalent to $ M_{4, 8} $ as based modules over $ r(S_4) $ under $ \phi $. Then, we can check that $ \left \{ M_{4, s} \right \} _{5\le s \le7} $ are inequivalent irreducible based modules. □

Finally, we construct two based modules $ M_{5, i}\ \left (i = 1, 2 \right) $ over $ r(S_4) $ with the actions of $ r(S_4) $ on them presented in Table 5.

Table 5. Inequivalent irreducible based modules of rank 5 over $ r(S_4) $.

	$ V_{\psi} $	$ V_{\rho _{1}} $	$ V_{\rho _{2}} $
$ M_{5, 1} $	$ $\begin{pmatrix} 0&1&0&0&0\\ 1&0&0&0&0\\ 0&0&0&1&0\\ 0&0&1&0&0\\ 0&0&0&0&1\\ \end{pmatrix}$ $	$ $\begin{pmatrix} 0&0&0&0&1\\ 0&0&0&0&1\\ 0&0&1&1&0\\ 0&0&1&1&0\\ 1&1&0&0&1\\ \end{pmatrix}$ $	$ $\begin{pmatrix} 0&0&0&1&0\\ 0&0&1&0&0\\ 0&1&1&1&1\\ 1&0&1&1&1\\ 0&0&1&1&0\\ \end{pmatrix}$ $
$ M_{5, 2} $	$ $\begin{pmatrix} 0&1&0&0&0\\ 1&0&0&0&0\\ 0&0&0&1&0\\ 0&0&1&0&0\\ 0&0&0&0&1\\ \end{pmatrix}$ $	$ $\begin{pmatrix} 1&1&0&0&0\\ 1&1&0&0&0\\ 0&0&1&1&0\\ 0&0&1&1&0\\ 0&0&0&0&2\\ \end{pmatrix}$ $	$ $\begin{pmatrix} 0&0&0&1&1\\ 0&0&1&0&1\\ 0&1&0&0&1\\ 1&0&0&0&1\\ 1&1&1&1&1\\ \end{pmatrix}$ $

| Show Table

DownLoad: CSV

Proposition 3.5. Let $ M $ be an irreducible based module of rank $ 5 $ over $ r(S_4) $. Then $ M $ is equivalent to one of the based modules $ M_{5, i}\, (i = 1, 2) $, listed in Table 5.

Proof. Let $ M $ be a based module of rank 5 over $ r(S_4) $, with the action of $ r(S_4) $ on it given by

$\begin{equation*} V_{\psi} \mapsto T, \quad V_{\rho _{1}}\mapsto Q = (a_{ij})_{1\leq i, j\leq5} , \quad V_{\rho _{2}}\mapsto U = (b_{ij})_{1\leq i, j\leq5}, \quad V_{\rho _{3}}\mapsto W = TU, \end{equation*}$ $

where $ a_{ij} = a_{ji} $, $ b_{ij} = b_{ji} $.

First, by a similar argument applied in the case of rank 4, we only need to deal with one of the following 3 cases for $ T $:

$\begin{equation*} T_1 = E_5, \quad T_2 = (12) , \quad T_3 = (12)(34) . \end{equation*}$ $

Case 1. $ T = T_1 = E_5 $.

There are 11 solutions of $ Q $ satisfying Eq (3.5), but only two conjugacy classes by permutation matrices with their representatives given as follows:

$\begin{equation*} Q_1 = \begin{pmatrix} 0&1&1&0&0 \\ 1&0&1&0&0 \\ 1&1&0&0&0 \\ 0&0&0&2&0 \\ 0&0&0&0&2 \end{pmatrix}, \quad Q_2 = \begin{pmatrix} 2&0&0&0&0 \\ 0&2&0&0&0 \\ 0&0&2&0&0 \\ 0&0&0&2&0 \\ 0&0&0&0&2 \end{pmatrix}. \end{equation*}$ $

Next, we calculate $ U $ after taking $ Q $ as one $ Q_k $ $ \left (k = 1, 2 \right) $.

Case 1.1. $ Q = Q_1 $.

There are 4 solutions of $ U $ satisfying Eqs (3.6) and (3.7) as follows:

$\begin{equation*} U_1 = \begin{pmatrix} 0&0&0&1&0 \\ 0&0&0&1&0 \\ 0&0&0&1&0 \\ 1&1&1&2&0 \\ 0&0&0&0&3 \end{pmatrix}, \ \ U_2 = \begin{pmatrix} 0&0&0&0&1 \\ 0&0&0&0&1 \\ 0&0&0&0&1 \\ 0&0&0&3&0 \\ 1&1&1&0&2 \end{pmatrix}, \ \ U_3 = \begin{pmatrix} 1&1&1&0&0 \\ 1&1&1&0&0 \\ 1&1&1&0&0 \\ 0&0&0&3&0 \\ 0&0&0&0&3 \\ \end{pmatrix}, \ \ U_4 = \begin{pmatrix} 1&1&1&0&0 \\ 1&1&1&0&0 \\ 1&1&1&0&0 \\ 0&0&0&1&2 \\ 0&0&0&2&1 \end{pmatrix}. \end{equation*}$ $

Case 1.2. $ Q = Q_2 $.

There are 31 solutions of $ U $ satisfying Eqs (3.6) and (3.7), but only 4 conjugacy classes by permutation matrices and their representatives as follows:

$\begin{equation*} U_1 = \begin{pmatrix} 0&1&1&1&0 \\ 1&0&1&1&0 \\ 1&1&0&1&0 \\ 1&1&1&0&0 \\ 0&0&0&0&3 \end{pmatrix}, \ \ U_2 = \begin{pmatrix} 1&0&0&2&0 \\ 0&1&2&0&0 \\ 0&2&1&0&0 \\ 2&0&0&1&0 \\ 0&0&0&0&3 \end{pmatrix}, \ \ U_3 = \begin{pmatrix} 1&2&0&0&0 \\ 2&1&0&0&0 \\ 0&0&3&0&0 \\ 0&0&0&3&0 \\ 0&0&0&0&3 \\ \end{pmatrix}, \ \ U_4 = \begin{pmatrix} 3&0&0&0&0 \\ 0&3&0&0&0 \\ 0&0&3&0&0 \\ 0&0&0&3&0 \\ 0&0&0&0&3 \end{pmatrix}. \end{equation*}$ $

Each pair $ (T_1, Q_k, U_r) $ above determines a based module, but is not irreducible for any $ 1\le r\le4 $.

Case 2. $ T = T_2 = (12) $.

There are 5 solutions of $ Q $ satisfying Eq (3.5), but only 3 conjugacy classes with the following representatives:

$\begin{equation*} Q_1 = \begin{pmatrix} 0&0&0&0&1 \\ 0&0&0&0&1 \\ 0&0&2&0&0 \\ 0&0&0&2&0 \\ 1&1&0&0&1 \end{pmatrix}, \quad Q_2 = \begin{pmatrix} 1&1&0&0&0 \\ 1&1&0&0&0 \\ 0&0&0&1&1 \\ 0&0&1&0&1 \\ 0&0&1&1&0 \end{pmatrix}, \quad Q_3 = \begin{pmatrix} 1&1&0&0&0 \\ 1&1&0&0&0 \\ 0&0&2&0&0 \\ 0&0&0&2&0 \\ 0&0&0&0&2 \end{pmatrix}. \end{equation*}$ $

Next, we calculate $ U $ after choosing $ Q $.

Case 2.1. $ Q = Q_1 $.

There are 4 solutions of $ U $ satisfying Eqs (3.6) and (3.7) as follows:

$\begin{equation*} U_1 = \begin{pmatrix} 0&1&0&0&1 \\ 1&0&0&0&1 \\ 0&0&1&2&0 \\ 0&0&2&1&0 \\ 1&1&0&0&2 \end{pmatrix}, \ \ U_2 = \begin{pmatrix} 0&1&0&0&1 \\ 1&0&0&0&1 \\ 0&0&3&0&0 \\ 0&0&0&3&0 \\ 1&1&0&0&2 \end{pmatrix}, \ \ U_3 = \begin{pmatrix} 1&0&0&0&1 \\ 0&1&0&0&1 \\ 0&0&1&2&0 \\ 0&0&2&1&0 \\ 1&1&0&0&2 \\ \end{pmatrix}, \ \ U_4 = \begin{pmatrix} 1&0&0&0&1 \\ 0&1&0&0&1 \\ 0&0&3&0&0 \\ 0&0&0&3&0 \\ 1&1&0&0&2 \end{pmatrix}. \end{equation*}$ $

Case 2.2. $ Q = Q_2 $.

There are 2 solutions of $ U $ satisfying Eqs (3.6) and (3.7) as follows:

$\begin{equation*} U_1 = \begin{pmatrix} 1&2&0&0&0 \\ 2&1&0&0&0 \\ 0&0&1&1&1 \\ 0&0&1&1&1 \\ 0&0&1&1&1 \end{pmatrix}, \ \ U_2 = \begin{pmatrix} 2&1&0&0&0 \\ 1&2&0&0&0 \\ 0&0&1&1&1 \\ 0&0&1&1&1 \\ 0&0&1&1&1 \end{pmatrix}. \end{equation*}$ $

Case 2.3. $ Q = Q_3 $.

There are 14 solutions of $ U $ satisfying Eqs (3.6) and (3.7), but only 6 conjugacy classes by permutation matrices with their representatives given as follows:

$\begin{array}{l} U_1 = \begin{pmatrix} 0&1&1&1&0 \\ 1&0&1&1&0 \\ 1&1&0&1&0 \\ 1&1&1&0&0 \\ 0&0&0&0&3 \end{pmatrix}, \quad U_2 = \begin{pmatrix} 1&0&1&1&0 \\ 0&1&1&1&0 \\ 1&1&0&1&0 \\ 1&1&1&0&0 \\ 0&0&0&0&3 \end{pmatrix}, \quad U_3 = \begin{pmatrix} 1&2&0&0&0 \\ 2&1&0&0&0 \\ 0&0&1&2&0 \\ 0&0&2&1&0 \\ 0&0&0&0&3 \end{pmatrix}, \\[3em] U_4 = \begin{pmatrix} 2&1&0&0&0 \\ 1&2&0&0&0 \\ 0&0&1&2&0 \\ 0&0&2&1&0 \\ 0&0&0&0&3 \end{pmatrix}, \quad U_5 = \begin{pmatrix} 1&2&0&0&0 \\ 2&1&0&0&0 \\ 0&0&3&0&0 \\ 0&0&0&3&0 \\ 0&0&0&0&3 \\ \end{pmatrix}, \quad U_6 = \begin{pmatrix} 2&1&0&0&0 \\ 1&2&0&0&0 \\ 0&0&3&0&0 \\ 0&0&0&3&0 \\ 0&0&0&0&3 \end{pmatrix}. \end{array}$ $

Through analysis, all based modules derived from Case 2 are reducible.

Case 3. $ T = T_3 = (12)(34) $.

There are 3 solutions of $ Q $ satisfying Eq (3.5) as follows:

$\begin{equation*} Q_1 = \begin{pmatrix} 0&0&0&0&1 \\ 0&0&0&0&1 \\ 0&0&1&1&0 \\ 0&0&1&1&0 \\ 1&1&0&0&1 \end{pmatrix}, \quad Q_2 = \begin{pmatrix} 1&1&0&0&0 \\ 1&1&0&0&0 \\ 0&0&1&1&0 \\ 0&0&1&1&0 \\ 0&0&0&0&2 \end{pmatrix}, \quad Q_3 = \begin{pmatrix} 1&1&0&0&0 \\ 1&1&0&0&0 \\ 0&0&0&0&1 \\ 0&0&0&0&1 \\ 0&0&1&1&1 \end{pmatrix}. \end{equation*}$ $

Next, we calculate $ U $ after fixing $ Q $.

Case 3.1. $ Q = Q_1 $.

There are 6 solutions of $ U $ satisfying Eqs (3.6) and (3.7) as follows:

$\begin{array}{l} U_1 = \begin{pmatrix} 0&0&0&1&0 \\ 0&0&1&0&0 \\ 0&1&1&1&1 \\ 1&0&1&1&1 \\ 0&0&1&1&0 \end{pmatrix}, \quad U_2 = \begin{pmatrix} 0&0&1&0&0 \\ 0&0&0&1&0 \\ 1&0&1&1&1 \\ 0&1&1&1&1 \\ 0&0&1&1&0 \end{pmatrix}, \quad U_3 = \begin{pmatrix} 0&1&0&0&1 \\ 1&0&0&0&1 \\ 0&0&1&2&0 \\ 0&0&2&1&0 \\ 1&1&0&0&2 \end{pmatrix}, \\[3em] U_4 = \begin{pmatrix} 0&1&0&0&1 \\ 1&0&0&0&1 \\ 0&0&2&1&0 \\ 0&0&1&2&0 \\ 1&1&0&0&2 \end{pmatrix}, \quad U_5 = \begin{pmatrix} 1&0&0&0&1 \\ 0&1&0&0&1 \\ 0&0&1&2&0 \\ 0&0&2&1&0 \\ 1&1&0&0&2 \\ \end{pmatrix}, \quad U_6 = \begin{pmatrix} 1&0&0&0&1 \\ 0&1&0&0&1 \\ 0&0&2&1&0 \\ 0&0&1&2&0 \\ 1&1&0&0&2 \end{pmatrix}. \end{array}$ $

Each pair $ (T_3, Q_1, U_r) $ $ \left (1\le r\le6 \right) $ above determines a based module, but only the based modules with representation matrices $ U_1 $ and $ U_2 $ are irreducible. Such two irreducible based modules are denoted by $ M_{5, 1} $ and $ M'_{5, 1} $, with the corresponding $ \mathbb Z $-basis $ \left \{ v_1^k, v_2^k, v_3^k, v_4^k, v_5^k\right \} $ for $ k = 1, 2 $, respectively. Define the $ \mathbb Z $-module isomorphism $ \phi $: $ M_{5, 1}\to M'_{5, 1} $ by

$\begin{equation*} \phi(v_s^1) = v_s^2, \quad \phi(v_3^1) = v_4^2, \quad \phi(v_4^1) = v_3^2, \quad s = 1, 2, 5. \end{equation*}$ $

Then it is easy to see that $ M_{5, 1} $ is equivalent to $ M'_{5, 1} $ as based modules over $ r(S_4) $ under $ \phi $.

Case 3.2. $ Q = Q_2 $.

There are 10 solutions of $ U $ satisfying Eqs (3.6) and (3.7), but only 7 conjugacy classes with their representatives given as follows:

$\begin{array}{l} U_1 = \begin{pmatrix} 0&0&0&1&1 \\ 0&0&1&0&1 \\ 0&1&0&0&1 \\ 1&0&0&0&1 \\ 1&1&1&1&1 \end{pmatrix}, \ \ U_2 = \begin{pmatrix} 0&1&1&1&0 \\ 1&0&1&1&0 \\ 1&1&0&1&0 \\ 1&1&1&0&0 \\ 0&0&0&0&3 \\ \end{pmatrix}, \ \ U_3 = \begin{pmatrix} 0&1&1&1&0 \\ 1&0&1&1&0 \\ 1&1&1&0&0 \\ 1&1&0&1&0 \\ 0&0&0&0&3 \\ \end{pmatrix}, \ \ U_4 = \begin{pmatrix} 1&0&1&1&0 \\ 0&1&1&1&0 \\ 1&1&1&0&0 \\ 1&1&0&1&0 \\ 0&0&0&0&3 \\ \end{pmatrix}, \end{array}$ $

$\begin{array}{l} U_5 = \begin{pmatrix} 1&2&0&0&0 \\ 2&1&0&0&0 \\ 0&0&1&2&0 \\ 0&0&2&1&0 \\ 0&0&0&0&3 \end{pmatrix}, \ \ U_6 = \begin{pmatrix} 1&2&0&0&0 \\ 2&1&0&0&0 \\ 0&0&2&1&0 \\ 0&0&1&2&0 \\ 0&0&0&0&3 \end{pmatrix}, \ \ U_7 = \begin{pmatrix} 2&1&0&0&0 \\ 1&2&0&0&0 \\ 0&0&2&1&0 \\ 0&0&1&2&0 \\ 0&0&0&0&3 \end{pmatrix}. \end{array}$ $

Each pair $ (T_3, Q_2, U_t) $ $ \left (2\le t\le7 \right) $ above determines a based module, but only the based module with representation matrix $ U_1 $ is irreducible. We denote it by $ M_{5, 2} $.

Also, the based modules obtained by taking $ Q = Q_3 $ are equivalent to the based module $ M_{5, 1} $ found in Case 3.1. □

4. Categorified based modules by module categories over $ { Rep}(S_4) $

In this section, we will apply the knowledge of module categories over the complex representation category of a finite group to find which based modules over $ r(S_4) $ can be categorified by module categories over the representation category $ {\rm Rep}(S_4) $ of $ S_4 $. For the details about module categories over tensor categories, see, e.g., [32, Section 7].

First, we recall the required result for the upcoming discussion. For any finite group $ G $, the second cohomology group $ H^2(G, {{\mathbb C}}^*) $ is known to be a finite abelian group called the Schur multiplier and classifies central extensions of $ G $. The notion of a universal central extension of a finite group was first investigated by Schur in ^[34].

Let $ {\rm Rep}(G, \alpha) $ denote the semisimple abelian category of projective representations of $ G $ with the multiplier $ \alpha\in Z^2(G, {{\mathbb C}}^*) $. Equivalently, $ {\rm Rep}(G, \alpha) $ is the representation category of the twisted group algebra $ {{\mathbb C}} G_\alpha $ of $ G $ with multiplication

$ g\cdot_\alpha h = \alpha(g, h)gh, \quad g, h\in G. $

In particular,

$ {\rm Rep}(G, \alpha) = {\rm Rep}(G), $

when taking $ \alpha = 1 $.

Let $ \alpha \in Z^2(G, {{\mathbb C}}^*) $ represent an element of order $ d $ in $ H^2(G, {{\mathbb C}}^*) $. Define

$ {\rm Rep}^\alpha(G) = \bigoplus \limits_{j = 0}^{d-1}{\rm Rep}(G, \alpha^j). $

According to the result in ^[35], we know that $ {\rm Rep}^\alpha(G) $ becomes a fusion category with the tensor product of two projective representations in $ {\rm Rep}(G, \alpha^i) $ and $ {\rm Rep}(G, \alpha^j) $ respectively lying in $ {\rm Rep}(G, \alpha^{i+j}) $, and the dual object in $ {\rm Rep}(G, \alpha^i) $ lying in $ {\rm Rep}(G, \alpha^{d-i}) $. Correspondingly, we have the fusion ring

$\begin{equation} r^\alpha(G) = \bigoplus \limits_{j = 0}^{d-1}r(G, \alpha^j). \end{equation}$ $

(4.1)

Now let $ H $ be a subgroup of $ G $ and $ \alpha \in Z^2(H, {{\mathbb C}}^*) $. The category $ {\rm Rep}(H, \alpha) $ is a module category over $ {\rm Rep}(G) $ by applying the restriction functor $ {\rm Res}_H^{G} $: $ {\rm Rep}(G)\to {\rm Rep}(H) $.

Theorem 4.1. [17, Theorem 3.2] The indecomposable exact module categories over the representation category $ {\rm Rep}(G) $ are of the form $ {\rm Rep}(H, \alpha) $ and are classified by conjugacy classes of pairs $ (H, [\alpha]) $.

Consequently, by [32, Proposition 7.7.2], we know the following:

Proposition 4.1. The Grothendieck group

$ r(H, \alpha) = {\rm Gr}({\rm Rep}(H, \alpha)) $

is an irreducible $ \mathbb{Z}_+ $-module over $ r(G) $.

Next, we show that any $ \mathbb{Z}_+ $-module over the complex representation ring $ r(G) $ of a finite group $ G $ categorified in this way is a based module.

Theorem 4.2. Let $ G $ be a finite group, $ H $ a subgroup of $ G $, and $ \alpha \in Z^2(H, {{\mathbb C}}^*) $. The $ \mathbb{Z}_+ $-module $ r(H, \alpha) $ over $ r(G) $ is a based module.

Proof. Let $ \left \{ {\psi}_i \right \} _{i\in I} $ be the $ \mathbb{Z}_+ $-basis of $ r(G) $. Take $ r^\alpha(H) $ defined in Eq (4.1) as a $ \mathbb{Z}_+ $-module over $ r(G) $ with the $ \mathbb{Z} $-basis $ \left \{ {\chi}_k \right \} _{k\in J} $ such that

$ \psi_i.\chi_k = \sum\limits_l a_{ik}^l \chi_l, \quad a_{ik}^l\in \mathbb{Z}_+. $

On the other hand, we write the fusion rule of the fusion ring $ r^\alpha(H) $ as follows:

$\begin{equation*} \chi_i\chi_j = \sum\limits_{k = 1}^{s} n_{ij}^k\chi_k, \quad n_{ij}^k\in \mathbb{Z}_+. \end{equation*}$ $

Since the number $ n_{ij}^{k^*} $ is invariant under cyclic permutations of $ i, j, k $, we have

$ n_{ij}^k = n_{k^*i}^{j^*} = n_{i^*k}^{j}. $

By the restriction rule, we interpret $ r(G) $ as a subring of $ r^\alpha(H) $ and write down

$ \psi_i = \sum\limits_j r_{ij} \chi_j, \quad r_{ij}\in \mathbb{Z}_+. $

Then

$ \psi_i.\chi_k = \sum\limits_j r_{ij} \chi_j\chi_k = \sum\limits_{j, \, l} r_{ij}n_{jk}^l \chi_l. $

By comparing the coefficients, we see that

$ a_{ik}^l = \sum\limits_{j} r_{ij}n_{jk}^l = \sum\limits_{j} r_{ij}n_{j^*l}^k = \sum\limits_{j} r_{i^*j^*}n_{j^*l}^k = \sum\limits_{j} r_{i^*j}n_{jl}^k = a_{i^*l}^k, $

so $ r^\alpha(H) $ is a based module over $ r(G) $, and $ r(H, \alpha) $ is clearly a based submodule of $ r^\alpha(H) $. Equivalently, any $ \mathbb{Z}_+ $-module over $ r(G) $ categorified by a module category $ {\rm Rep}(H, \alpha) $ over $ {\rm Rep}(G) $ must be a based module. □

By Theorem 4.2, we only need to focus on those inequivalent irreducible based modules $ M_{i, j} $ over $ r(S_4) $ collected in Section 3, each of which is possibly categorified by a module category $ {\rm Rep}(H, \alpha) $ for some $ H < S_4 $ and $ \alpha \in Z^2(H, {{\mathbb C}}^*) $.

All the non-isomorphic subgroups of the symmetric group $ S_4 $ are as follows:

$ ({\rm{i}}) $ The symmetric group $ S_3 $;

$ ({\rm{ii}}) $ The cyclic groups $ \mathbb Z_i, \, 1\leq i\leq 4 $;

$ ({\rm{iii}}) $ The Klein 4-group $ K_4 $;

$ ({\rm{iv}}) $ The alternating group $ A_4 $;

$ ({\rm{v}}) $ The dihedral group $ D_4 $;

$ ({\rm{vi}}) $ The symmetric group $ S_4 $ itself.

Correspondingly, the Schur multipliers we consider here are given as follows (see e.g., ^[36]):

$ H^2(\mathbb Z_n, {{\mathbb C}}^*)\cong H^2(S_3, {{\mathbb C}}^*)\cong 0, \ n\geq 1, \quad \ H^2(K_4, {{\mathbb C}}^*)\cong H^2(D_4, {{\mathbb C}}^*)\cong H^2(A_4, {{\mathbb C}}^*)\cong H^2(S_4, {{\mathbb C}}^*)\cong\mathbb Z_2. $

As a result, we only need to consider the following two situations:

(1) Module category $ {\rm Rep}(H) $ for any subgroup $ H < S_4 $;

(2) Module category $ {\rm Rep}(H, \alpha) $ for any subgroup $ H < S_4 $ and nontrivial twist $ \alpha \in Z^2(H, {{\mathbb C}}^*) $.

4.1. The module categories over $ { Rep}(S_4) $ with trivial twists

(ⅰ) First, we consider the representation category $ {\rm Rep}(S_3) $ as a module category over $ {\rm Rep}(S_4) $.

Theorem 4.3. $ r(S_3) = {\rm Gr}({\rm Rep}(S_3)) $ is an irreducible based module over $ r(S_4) = {\rm Gr}({\rm Rep}(S_4)) $ equivalent to the based module $ M_{3, 2} $ in Table 3.

Proof. According to the branching rule of symmetric groups (see e.g., [37, Theorem 2.8.3]), we have the following restriction rules:

$\begin{align*} {\rm Res}_{S_3}^{S_4} \left ( 1 \right ) = 1, \; \; \; {\rm Res}_{S_3}^{S_4} \left ( V_{\psi} \right ) = \chi, \; \; \; {\rm Res}_{S_3}^{S_4} \left ( V_{\rho_{1}} \right ) = V, \; \; \; {\rm Res}_{S_3}^{S_4} \left ( V_{\rho_{2}} \right ) = 1+V, \; \; \; {\rm Res}_{S_3}^{S_4} \left ( V_{\rho_{3}} \right ) = \chi+V, \end{align*}$ $

where $ \chi $ and $ V $ denote the sign representation and the standard representation in $ {\rm Rep}({S_3}) $, respectively. Hence, we get the representation matrices of basis elements of $ r(S_4) $ acting on $ r({S_3}) $ as follows:

$\begin{align*} 1 \mapsto E_3, \quad V_{\psi} \mapsto \begin{pmatrix}0& 1 &0 \\1&0 &0 \\0&0 &1\end{pmatrix}, \quad V_{\rho _{1}}\mapsto \begin{pmatrix}0& 0 &1 \\0& 0 &1 \\1& 1&1 \end{pmatrix}, \quad V_{\rho _{2}}\mapsto \begin{pmatrix}1& 0 &1 \\0& 1 &1 \\1& 1&2 \end{pmatrix}, \quad V_{\rho _{3}}\mapsto \begin{pmatrix}0& 1 &1 \\1& 0 &1 \\1& 1&2 \end{pmatrix}. \end{align*}$ $

We see that $ r(S_3) $ is an irreducible based module $ M_{3, 2} $ according to Table 3. In other words, the based module $ M_{3, 2} $ can be categorified by the module category $ {\rm Rep}({S_3}) $ over $ {\rm Rep}(S_4) $. □

Remark 4.1. Since the roles of the standard representation and its dual in $ r(S_4) $ are symmetric, we can exchange the notations $ V_{\rho_{2}} $ and $ V_{\rho_{3}} $ for them to get the following restriction rules instead:

$\begin{equation*} {\rm Res}_{S_3}^{S_4} \left ( V_{\rho_{2}} \right ) = \chi+V, \quad {\rm Res}_{S_3}^{S_4} \left ( V_{\rho_{3}} \right ) = 1+V. \end{equation*}$ $

Therefore, we get another action of $ r(S_4) $ on $ r({S_3}) $ such that $ r(S_3) $ is an irreducible based module over $ r(S_4) $ equivalent to the based module $ M_{3, 3} $ according to Table 3. In other words, the based module $ M_{3, 3} $ can also be categorified by the module category $ {\rm Rep}({S_3}) $ over $ {\rm Rep}(S_4) $.

(ⅱ) Second, we consider $ {\rm Rep}(\mathbb{Z}_4) $ as a module category over $ {\rm Rep}(S_4) $.

Theorem 4.4. $ r(\mathbb{Z}_4) = {\rm Gr}({\rm Rep}(\mathbb{Z}_4)) $ is an irreducible based module over $ r(S_4) $ equivalent to the based module $ M_{4, 5} $ in Table 4.

Proof. Let

$ \mathbb{Z}_4 = \left \{ 1, g, g^2, g^3 \right \} $

be the cyclic group of order $ 4 $, with four non-isomorphic 1-dimensional irreducible representations denoted by $ U_i, \, i = 0, 1, 2, 3 $. Let $ U_0 = 1 $ represent the trivial representation, and

$\begin{equation*} \chi_{U_1}(g) = \sqrt{-1} , \quad \chi_{U_2}(g) = -1, \quad\chi_{U_3}(g) = -\sqrt{-1}. \end{equation*}$ $

On the other hand, we consider $ \mathbb{Z}_4 $ as the subgroup of $ S_4 $ generated by $ g = (1234) $. Then, by the character table of $ S_4 $ (Table 1), we have

$\begin{align*} \chi_\psi(g^i)& = (-1)^i, \quad \chi_{\rho_1}(g^i) = 1+(-1)^i, \\ \chi_{\rho_2}(g^i)& = (-1)^i+(\sqrt{-1})^i+(-\sqrt{-1})^i, \\ \chi_{\rho_3}(g^i)& = 1+(\sqrt{-1})^i+(-\sqrt{-1})^i. \end{align*}$ $

So, the restriction rule of $ r(S_4) $ on $ r(\mathbb{Z}_4) $ is given as follows:

$\begin{align*} {\rm Res}_{\mathbb{Z}_4}^{S_4} \left ( 1 \right )& = 1, \quad {\rm Res}_{\mathbb{Z}_4}^{S_4} \left ( V_{\psi} \right ) = U_2, \quad {\rm Res}_{\mathbb{Z}_4}^{S_4} \left ( V_{\rho_{1}} \right ) = 1+U_2, \\ {\rm Res}_{\mathbb{Z}_4}^{S_4} \left ( V_{\rho_{2}} \right )& = U_1+U_2+U_3, \quad\quad{\rm Res}_{\mathbb{Z}_4}^{S_4} \left ( V_{\rho_{3}} \right ) = 1+U_1+U_3. \end{align*}$ $

Then, we get the representation matrices of basis elements of $ r(S_4) $ acting on $ r(\mathbb{Z}_4) $ as follows:

$\begin{align*} &1 \mapsto E_4, \space V_{\psi} \mapsto \begin{pmatrix}0& 0 &1 &0\\0& 0 &0&1\\1& 0&0&0\\0&1&0&0\end{pmatrix}, \space V_{\rho _{1}}\mapsto \begin{pmatrix}1&0&1&0\\0&1&0&1\\1&0&1&0\\0&1&0&1\end{pmatrix}, \space &V_{\rho _{2}}\mapsto \begin{pmatrix}0&1&1&1\\1&0&1&1\\1&1&0&1\\1&1&1&0 \end{pmatrix}, \space V_{\rho_{3}}\mapsto \begin{pmatrix}1&1&0&1\\1&1&1&0\\0&1&1&1\\1&0&1&1\end{pmatrix}. \end{align*}$ $

Let $ \left \{ w_i\right \}_{1\leq i\leq 4} $ be the stated $ \mathbb{Z} $-basis of $ M_{4, 5} $, and define a $ \mathbb{Z} $-linear map $ \varphi $: $ M_{4, 5}\to r(\mathbb{Z}_4) $ by

$\begin{equation*} \varphi (w_1) = U_3, \quad \varphi (w_2) = U_1, \quad \varphi (w_3) = U_2, \quad\varphi (w_4) = 1. \end{equation*}$ $

Then, it is easy to check that $ \varphi $ is an isomorphism of $ r(S_{4}) $-modules, so $ M_{4, 5} $ is equivalent to $ r(\mathbb{Z}_4) $ as based modules by Definition 2.4 (ⅰ). In other words, the based module $ M_{4, 5} $ can be categorified by the module category $ {\rm Rep}(\mathbb{Z}_4) $ over $ {\rm Rep}(S_4) $. □

Remark 4.2. By the same argument as in Remark 4.1, $ V_{\rho _{2}} $ and $ V_{\rho _{3}} $ can be required to satisfy the following restriction rules instead:

$\begin{equation*} {\rm Res}_{\mathbb{Z}_4}^{S_4} \left ( V_{\rho_{2}} \right ) = 1+U_1+U_3, \quad{\rm Res}_{\mathbb{Z}_4}^{S_4} \left ( V_{\rho_{3}} \right ) = U_1+U_2+U_3. \end{equation*}$ $

Therefore, we get another action of $ r(S_4) $ on $ r({\mathbb{Z}_4}) $ such that $ r(\mathbb{Z}_4) $ is an irreducible based module over $ r(S_4) $ equivalent to the based module $ M_{4, 7} $ according to Table 4. In other words, the based module $ M_{4, 7} $ can also be categorified by the module category $ {\rm Rep}(\mathbb{Z}_4) $ over $ {\rm Rep}(S_4) $.

Also, one can similarly check that the module category $ {\rm Rep}(\mathbb{Z}_2) $ over $ {\rm Rep}(S_4) $ categorifies the based modules $ M_{2, 2} $ and $ M_{2, 3} $, while $ {\rm Rep}(\mathbb{Z}_3) $ over $ {\rm Rep}(S_4) $ categorifies the based module $ M_{3, 1} $.

(ⅲ) Now we consider $ {\rm Rep}(K_4) $ as a module category over $ {\rm Rep}(S_4) $.

Theorem 4.5. $ r(K_4) = {\rm Gr}({\rm Rep}(K_4)) $ is an irreducible based module over $ r(S_4) $ equivalent to the based module $ M_{4, 7} $ in Table 4.

Proof. We consider $ K_4 $ as the subgroup of $ S_4 $ generated by $ (12) $ and $ (34) $, and it has four non-isomorphic 1-dimensional irreducible representations $ Y_0 = 1 $ and $ Y_1, Y_2, Y_3 $ such that

$\begin{align*} &\chi_{Y_1}((12)) = -1, \quad \chi_{Y_1}((34)) = 1;\quad\; \; \chi_{Y_2}((12)) = 1, \\ &\chi_{Y_2}((34)) = -1;\quad \chi_{Y_3}((12)) = -1, \quad \chi_{Y_3}((34)) = -1. \end{align*}$ $

On the other hand, by the character table of $ S_4 $ (Table 1), we have

$\begin{align*} &\chi_\psi((12)) = \chi_\psi((34)) = -1, \quad \chi_\psi((12)(34)) = 1;\\ &\chi_{\rho_1}((12)) = \chi_{\rho_1}((34)) = 0, \quad \chi_{\rho_1}((12)(34)) = 2;\\ &\chi_{\rho_2}((12)) = \chi_{\rho_2}((34)) = 1, \quad \chi_{\rho_2}((12)(34)) = -1;\\ &\chi_{\rho_3}((12)) = \chi_{\rho_3}((34)) = -1, \quad \chi_{\rho_3}((12)(34)) = -1. \end{align*}$ $

So, we have the following restriction rules:

$\begin{align*} {\rm Res}_{K_4}^{S_4} \left ( 1 \right )& = 1, \quad {\rm Res}_{K_4}^{S_4} \left ( V_{\psi} \right ) = Y_3, \quad {\rm Res}_{K_4}^{S_4} \left ( V_{\rho_{1}} \right ) = 1+Y_3, \\ {\rm Res}_{K_4}^{S_4} \left ( V_{\rho_{2}} \right )& = 1+Y_1+Y_2, \quad\quad {\rm Res}_{K_4}^{S_4} \left ( V_{\rho_{3}} \right ) = Y_1+Y_2+Y_3. \end{align*}$ $

Then we get the representation matrices of basis elements of $ r(S_4) $ acting on $ r(K_4) $ as follows:

$\begin{align*} &1 \mapsto E_4, \quad V_{\psi} \mapsto \begin{pmatrix}0& 0 &0 &1\\0& 0 &1&0 \\0&1&0&0\\1&0&0&0\end{pmatrix}, \quad V_{\rho _{1}}\mapsto \begin{pmatrix}1&0&0&1\\0&1&1&0\\0&1&1&0\\1&0&0&1 \end{pmatrix}, \\ &V_{\rho _{2}}\mapsto \begin{pmatrix}1&1&1&0\\1&1&0&1\\1&0&1&1\\0&1&1&1\end{pmatrix}, \quad\quad V_{\rho_{3}}\mapsto \begin{pmatrix}0&1&1&1\\1&0&1&1\\1&1&0&1\\1&1&1&0 \end{pmatrix}. \end{align*}$ $

Let $ \left \{ w_i\right \}_{1\leq i\leq 4} $ be the stated $ \mathbb{Z} $-basis of $ M_{4, 7} $ listed in Table 4. Then

$\begin{equation*} w_1\mapsto Y_2, \quad w_2\mapsto Y_1, \quad w_3\mapsto 1, \quad w_4\mapsto Y_3, \end{equation*}$ $

defines an equivalence of $ \mathbb{Z}_+ $-modules between $ M_{4, 7} $ and $ r(K_4) $. In other words, the irreducible based module $ M_{4, 7} $ can be categorified by the module category $ {\rm Rep}(K_4) $ over $ {\rm Rep}(S_4) $. □

Remark 4.3. In a manner analogous to the argument in Remark 4.1, it follows that the irreducible based module $ M_{4, 5} $ can also be categorified by the module category $ {\rm Rep}(K_4) $ over $ {\rm Rep}(S_4) $.

(ⅳ) We consider $ {\rm Rep}(A_4) $ as a module category over $ {\rm Rep}(S_4) $.

Theorem 4.6. $ r(A_4) = {\rm Gr}({\rm Rep}(A_4)) $ is an irreducible based module over $ r(S_4) $ equivalent to the based module $ M_{4, 1} $ in Table 4.

Proof. We know that $ A_4 $ has three non-isomorphic 1-dimensional irreducible representations and one 3-dimensional irreducible representation, denoted by $ N_0, N_1, N_2 $, and $ N_3 $, respectively, where $ N_0 = 1 $ represents the trivial representation, and

$\begin{align*} &\chi_{N_1}((123)) = \omega , \quad \chi_{N_1}((12)(34)) = 1;\quad \chi_{N_2}((123)) = \omega^2, \quad \chi_{N_2}((12)(34)) = 1;\\ &\chi_{N_3}((123)) = \chi_{N_3}((132)) = 0, \quad\ \chi_{N_3}((12)(34)) = -1, \quad\ \omega = \frac{-1+\sqrt{-3} }{2}. \end{align*}$ $

On the other hand, the character table of $ S_4 $ (Table 1) tells us that

$\begin{align*} &\chi_\psi((123)) = 1, \quad\; \; \chi_\psi((12)(34)) = 1;\quad \chi_{\rho_1}((123)) = -1, \quad \chi_{\rho_1}((12)(34)) = 2;\\ &\chi_{\rho_2}((123)) = 0, \quad \chi_{\rho_2}((12)(34)) = -1;\quad \chi_{\rho_3}((123)) = 0, \quad \chi_{\rho_3}((12)(34)) = -1. \end{align*}$ $

So, we have the following restriction rules:

$\begin{align*} {\rm Res}_{A_4}^{S_4} \left ( 1 \right ) = {\rm Res}_{A_4}^{S_4} \left ( V_{\psi} \right ) = 1, \quad {\rm Res}_{A_4}^{S_4} \left ( V_{\rho_{1}} \right ) = N_1+N_2, \quad {\rm Res}_{A_4}^{S_4} \left ( V_{\rho_{2}} \right ) = {\rm Res}_{A_4}^{S_4} \left ( V_{\rho_{3}} \right ) = N_3. \end{align*}$ $

Hence, we get the representation matrices of basis elements of $ r(S_4) $ acting on $ r(A_4) $ as follows:

$\begin{align*} 1 \mapsto E_4, \quad V_{\psi} \mapsto E_4, \quad V_{\rho _{1}}\mapsto \begin{pmatrix}0& 1 &1 &0\\1& 0 &1&0 \\1& 1&0&0\\0&0&0&2 \end{pmatrix}, \quad V_{\rho _{2}}, V_{\rho_{3}}\mapsto \begin{pmatrix}0& 0 &0 &1\\0& 0 &0 &1\\0& 0 &0 &1\\1&1&1&2 \end{pmatrix}. \end{align*}$ $

Then, $ r(A_4) $ is an irreducible based module over $ r(S_4) $ equivalent to $ M_{4, 1} $ listed in Table 4. In other words, the irreducible based module $ M_{4, 1} $ can be categorified by the module category $ {\rm Rep}(A_4) $ over $ {\rm Rep}(S_4) $. □

(ⅴ) Next, we consider $ {\rm Rep}(D_4) $ as a module category over $ {\rm Rep}(S_4) $.

Theorem 4.7. $ r(D_4) = {\rm Gr}({\rm Rep}(D_4)) $ is an irreducible based module over $ r(S_4) $ equivalent to the based module $ M_{5, 2} $ in Table 5.

Proof. The dihedral group

$ D_4 = \langle r, s\, |\, r^4 = s^2 = (rs)^2 = 1\rangle $

has four 1-dimensional irreducible representations and one 2-dimensional irreducible representation up to isomorphism, denoted by $ W_0, W_1, W_2, W_3 $, and $ W_4 $, respectively. Let $ W_0 = 1 $ stand for the trivial representation, and

$\begin{align*} &\chi_{W_1}(r) = 1 , \quad\; \; \chi_{W_1}(s) = -1; \quad\chi_{W_2}(r) = -1, \quad \chi_{W_2}(s) = 1;\\ &\chi_{W_3}(r) = -1, \quad\chi_{W_3}(s) = -1; \quad \chi_{W_4}(r) = \chi_{W_4}(s) = \chi_{W_4}(rs) = 0. \end{align*}$ $

On the other hand, we consider $ D_4 $ as the subgroup of $ S_4 $ by taking $ r = (1234) $ and $ s = (12)(34) $. Then $ rs = (13) $. By the character table of $ S_4 $ (Table 1), we have

$\begin{align*} &\chi_\psi((1234)) = -1, \quad \chi_\psi((12)(34)) = 1, \quad \chi_\psi((13)) = -1;\\ &\chi_{\rho_1}((1234)) = 0, \quad \chi_{\rho_1}((12)(34)) = 2, \quad \chi_{\rho_1}((13)) = 0;\\ &\chi_{\rho_2}((1234)) = -1, \quad \chi_{\rho_2}((12)(34)) = -1, \quad \chi_{\rho_2}((13)) = 1;\\ &\chi_{\rho_3}((1234)) = 1, \quad \chi_{\rho_3}((12)(34)) = -1, \quad \chi_{\rho_3}((13)) = -1. \end{align*}$ $

So, we have the following restriction rules:

$\begin{align*} {\rm Res}_{D_4}^{S_4} \left ( 1 \right )& = 1, \quad {\rm Res}_{D_4}^{S_4} \left ( V_{\psi} \right ) = W_2, \quad {\rm Res}_{D_4}^{S_4} \left ( V_{\rho_{1}} \right ) = 1+W_2, \\ {\rm Res}_{D_4}^{S_4} \left ( V_{\rho_{2}} \right )& = W_3+W_4, \quad\quad {\rm Res}_{D_4}^{S_4} \left ( V_{\rho_{3}} \right ) = W_1+W_4. \end{align*}$ $

Then we get the representation matrices of basis elements of $ r(S_4) $ acting on $ r(D_4) $ as follows:

$\begin{align*} &1 \mapsto E_5, \quad V_{\psi} \mapsto \begin{pmatrix}0& 0 &1 &0&0\\0& 0 &0&1&0 \\1& 0&0&0&0\\0&1&0&0&0\\0&0&0&0&1 \end{pmatrix}, \quad V_{\rho _{1}}\mapsto \begin{pmatrix}1&0&1&0&0\\0&1&0&1&0\\1&0&1&0&0\\0&1&0&1&0\\0&0&0&0&2 \end{pmatrix}, \\ &\; \; \; \; \; \; V_{\rho _{2}}\mapsto \begin{pmatrix}0&0&0&1&1\\0&0&1&0&1\\0&1&0&0&1\\1&0&0&0&1\\1&1&1&1&1 \end{pmatrix}, \quad V_{\rho_{3}}\mapsto \begin{pmatrix}0&1&0&0&1\\1&0&0&0&1\\0&0&0&1&1\\0&0&1&0&1\\1&1&1&1&1 \end{pmatrix}. \end{align*}$ $

Then $ r(D_4) $ is an irreducible based module over $ r(S_4) $ equivalent to $ M_{5, 2} $ listed in Table 5. In other words, the irreducible based module $ M_{5, 2} $ can be categorified by the module category $ {\rm Rep}(D_4) $ over $ {\rm Rep}(S_4) $. □

(ⅵ) Finally, we consider $ {\rm Rep}(S_4) $ as a module category over itself.

Theorem 4.8. The regular $ \mathbb{Z}_+ $-module $ r(S_4) $ over itself is equivalent to the irreducible based module $ M_{5, 1} $ in Table 5.

Proof. Let $ r(S_4) $ be the regular $ \mathbb{Z}_+ $-module over itself with the $ \mathbb{Z} $-basis $ \left \{ 1, V_{\psi}, V_{\rho_{1}}, V_{\rho_{2}}, V_{\rho_{3}} \right \} $, and the action of $ r(S_4) $ on it is given as follows:

$\begin{align*} &1 \mapsto E_5, \quad V_{\psi} \mapsto \begin{pmatrix} 0&1&0&0&0 \\ 1&0&0&0&0 \\ 0&0&1&0&0 \\ 0&0&0&0&1 \\ 0&0&0&1&0 \end{pmatrix}, \quad V_{\rho _{1}}\mapsto \begin{pmatrix} 0&0&1&0&0 \\ 0&0&1&0&0 \\ 1&1&1&0&0 \\ 0&0&0&1&1 \\ 0&0&0&1&1 \end{pmatrix}, \\ &\; \; \; \; \; \; \; V_{\rho _{2}}\mapsto \begin{pmatrix} 0&0&0&1&0 \\ 0&0&0&0&1 \\ 0&0&0&1&1 \\ 1&0&1&1&1 \\ 0&1&1&1&1 \end{pmatrix}, \quad V_{\rho _{3}}\mapsto \begin{pmatrix} 0&0&0&0&1 \\ 0&0&0&1&0 \\ 0&0&0&1&1 \\ 0&1&1&1&1 \\ 1&0&1&1&1 \end{pmatrix}. \end{align*}$ $

Then, the regular $ \mathbb{Z}_+ $-module $ r(S_4) $ over itself is equivalent to $ M_{5, 1} $ listed in Table 5. In other words, the irreducible based module $ M_{5, 1} $ over $ r(S_4) $ can be categorified by the module category $ {\rm Rep}(S_4) $ over itself. □

Remark 4.4. Following the argument presented in Remark 4.1, if we exchange the notations $ V_{\rho _{2}} $ and $ V_{\rho _{3}} $ with their restriction rules given in the proof of Theorems 4.7 and 4.8, we see that $ r(D_4) $ and $ r(S_4) $ are still equivalent to $ M_{5, 2} $ and $ M_{5, 1} $, respectively.

4.2. The module categories over $ { Rep}(S_4) $ with nontrivial twists

Lastly, we consider the module category $ {\rm Rep}(H, \alpha) $ over $ {\rm Rep}(S_4) $, where $ H $ is a subgroup of $ S_4 $ with $ \alpha $ representing the unique nontrivial cohomological class in $ H^2(H, {{\mathbb C}}^*) $. All non-isomorphic irreducible projective representations of $ H $ with the multiplier $ \alpha $ form a $ \mathbb Z $-basis of $ r(H, \alpha) $, whose cardinality is the number of $ \alpha $-regular conjugacy classes by [38, Theorem 6.1.1].

First, we consider the twisted group algebra of $ K_4 $. There is only one irreducible projective representation with respect to $ \alpha $ up to isomorphism, see, e.g., [39, Appendix D.1]. Hence, $ r(K_4, \alpha) $ is a based module of rank $ 1 $ over $ r(S_4) $ equivalent to $ M_{1, 1} $ defined in (3.8). Namely, the based module $ M_{1, 1} $ can also be categorified by $ {\rm Rep}(K_4, \alpha) $.

Second, we consider the twisted group algebra of $ D_4 $.

Theorem 4.9. $ r(D_4, \alpha) = {\rm Gr}({\rm Rep}(D_4, \alpha)) $ is an irreducible based module over $ r(S_4) $ equivalent to the based module $ M_{2, 3} $ in Table 2.

Proof. Let

$ D_4 = \langle r, s\, |\, r^4 = s^2 = (rs)^2 = 1\rangle . $

Let $ \alpha\in Z^2(D_4, {{\mathbb C}}^*) $ be the 2-cocycle defined by

$\begin{equation} \alpha (r^is^j, r^{i'}s^{j'}) = (\sqrt{-1})^{ji'}.\nonumber \end{equation}$ $

Here, $ i, i'\in {\left \{ 0, 1, 2, 3 \right \} }, \, j, j'\in\left \{ {0, 1} \right \} $. As shown in [40, Section 3.7], this is a unitary 2-cocycle representing the unique non-trivial cohomological class in $ H^2(D_4, {{\mathbb C}}^*) $. According to [35, Section 3], there exist two (2-dimensional) non-isomorphic irreducible projective representations of $ D_4 $ with respect to $ \alpha $, which are given by

$\begin{equation} \begin{aligned} \pi_{l}: D_4 & \rightarrow \mathrm{GL}_{2}(\mathbb{C}), \\ r^{i} s^{j} & \mapsto A_{l}^{i} B^{j}, \end{aligned}\nonumber \end{equation}$ $

where

$ A_l =

$\begin{pmatrix}(\sqrt{-1})^l &0 \\ 0&(\sqrt{-1})^{1-l}\end{pmatrix}$ , \; \; \; B =

$\begin{pmatrix}0 &1 \\1 &0\end{pmatrix}$ , \; \; \; l = 1, 2. $

Also, for irreducible representations $ W_0 $–$ W_4 $ of $ D_4 $ mentioned in the proof of Theorem 4.7, we have

$\begin{equation} W_0\otimes \pi_l = W_1\otimes\pi_l = \pi_l, \quad W_2\otimes \pi_l = W_3\otimes \pi_l = \pi_{3-l}, \quad W_4\otimes \pi_l = \pi_1+\pi_2.\nonumber \end{equation}$ $

Next, using the previous restriction rule of $ r(S_4) $ on $ r(D_4) $, we get the representation matrices of basis elements of $ r(S_4) $ acting on $ r(D_4, \alpha) $ as follows:

$\begin{equation} \begin{aligned} 1 \mapsto E_2, \quad V_{\psi} \mapsto \begin{pmatrix} 0 &1 \\ 1&0 \end{pmatrix}, \quad V_{\rho_1} \mapsto \begin{pmatrix} 1 &1 \\ 1&1 \end{pmatrix}, \quad V_{\rho_2} \mapsto \begin{pmatrix} 1&2 \\ 2&1 \end{pmatrix}, \quad V_{\rho_3} \mapsto \begin{pmatrix} 2&1 \\ 1&2 \end{pmatrix}.\nonumber \end{aligned} \end{equation}$ $

Then, $ r(D_4, \alpha) $ is an irreducible based module over $ r(S_4) $ equivalent to $ M_{2, 3} $ listed in Table 2. In other words, the irreducible based module $ M_{2, 3} $ can be categorified by the module category $ {\rm Rep}(D_4, \alpha) $ over $ {\rm Rep}(S_4) $. □

Remark 4.5. As discussed in Remark 4.1, it follows that the irreducible based module $ M_{2, 2} $ can also be categorified by the module category $ {\rm Rep}(D_4, \alpha) $ over $ {\rm Rep}(S_4) $.

Next, we consider the twisted group algebras of $ A_4 $ and $ S_4 $. By [38, Theorem 6.1.1], $ A_4 $ has three (2-dimensional) non-isomorphic irreducible projective representations, denoted as $ V_{\gamma _{1}}, V_{\gamma _{2}} $, and $ V_{\gamma _{3}} $, respectively. Similarly, $ S_4 $ has two (2-dimensional) non-isomorphic irreducible projective representations $ V_{\xi_1}, V_{\xi_2} $, and one (4-dimensional) irreducible projective representation $ V_{\xi_3} $. We give the character table for projective representations of $ A_4 $ and $ S_4 $ in Tables 6 and 7, respectively, where primes are used to differentiate between the two classes splitting from a single conjugacy class of $ A_4 $ in its double cover $ \tilde A_4 $, and the same applies to $ S_4 $; subscripts distinguish between the two classes splitting from the conjugacy classes $ (31)^{'} $ and $ (31)^{''} $ in the double cover $ \tilde S_4 $ of $ S_4 $, respectively. For more details, see [41, Section 4].

Table 6. The character table for irreducible projective representations of $ A_4 $.

	$ (1^4)^{'} $	$ (1^4)^{''} $	$ (2^2) $	$ (31)^{'}_1 $	$ (31)^{''}_1 $	$ (31)^{'}_2 $	$ (31)^{''}_2 $
$ \chi_{\gamma _{1}} $	$ 2 $	$ -2 $	$ 0 $	$ 1 $	$ -1 $	$ 1 $	$ -1 $
$ \chi_{\gamma _{2}} $	$ 2 $	$ -2 $	$ 0 $	$ \omega $	$ -\omega $	$ \omega^2 $	$ -\omega^2 $
$ \chi_{\gamma _{3}} $	$ 2 $	$ -2 $	$ 0 $	$ \omega^2 $	$ -\omega^2 $	$ \omega $	$ -\omega $

| Show Table

DownLoad: CSV

Table 7. The character table for irreducible projective representations of $ S_4 $.

	$ (1^4)^{'} $	$ (1^4)^{''} $	$ (2 1^2) $	$ (2^2) $	$ (3 1)^{'} $	$ (31)^{''} $	$ (4)^{'} $	$ (4)^{''} $
$ \chi_{\xi_1} $	$ 2 $	$ -2 $	$ 0 $	$ 0 $	$ 1 $	$ -1 $	$ \sqrt{2} $	$ -\sqrt{2} $
$ \chi_{\xi_2} $	$ 2 $	$ -2 $	$ 0 $	$ 0 $	$ 1 $	$ -1 $	$ -\sqrt{2} $	$ \sqrt{2} $
$ \chi_{\xi_3} $	$ 4 $	$ -4 $	$ 0 $	$ 0 $	$ -1 $	$ 1 $	$ 0 $	$ 0 $

| Show Table

DownLoad: CSV

In Table 6, we denote

$ \omega = e^{2\pi\sqrt{-1}/3} = \frac{-1+\sqrt{-3}}{2}. $

Then we have the following theorems.

Theorem 4.10. $ r(A_4, \alpha) = {\rm Gr}({\rm Rep}(A_4, \alpha)) $ is an irreducible based module over $ r(S_4) $ equivalent to the based module $ M_{3, 1} $ in Table 3.

Proof. For the irreducible representations $ N_0, N_1, N_2 $, and $ N_3 $ of $ A_4 $ mentioned in the proof of Theorem 4.6, we obtain the following tensor product rule in $ r^\alpha(A_4) $ by computing the values of products of characters:

$\begin{align*} &N_0 \otimes V_{\gamma_i } = V_{\gamma_{i} }, \quad N_1 \otimes V_{\gamma_j } = V_{\gamma_{j+1} }, \quad N_1 \otimes V_{\gamma_3 } = V_{\gamma_{1} };\quad N_2 \otimes V_{\gamma_1 } = V_{\gamma_{3} }, \\ & N_2 \otimes V_{\gamma_2 } = V_{\gamma_{1} }, \quad\ N_2 \otimes V_{\gamma_3 } = V_{\gamma_{2} };\quad\ N_3 \otimes V_{\gamma_i } = V_{\gamma_{1} }+V_{\gamma_{2} }+V_{\gamma_{3} }, \end{align*}$ $

where $ i = 1, 2, 3 $, $ j = 1, 2 $. Next, by combining this with the previous restriction rule of $ r(S_4) $ on $ r(A_4) $, we obtain

$ 1, V_{\psi} \mapsto E_3, \quad V_{\rho_1} \mapsto

$\begin{pmatrix} 0 &1 &1\\ 1 &0 &1\\ 1 &1 &0 \end{pmatrix}$ , \quad V_{\rho_2}, V_{\rho_3} \mapsto

$\begin{pmatrix} 1 &1 &1\\ 1 &1 &1\\ 1 &1 &1 \end{pmatrix}$ . $

Then $ r(A_4, \alpha) $ is an irreducible based module over $ r(S_4) $ equivalent to $ M_{3, 1} $ listed in Table 3. In other words, the irreducible based module $ M_{3, 1} $ can be categorified by $ {\rm Rep}(A_4, \alpha) $. □

Theorem 4.11. $ r(S_4, \alpha) = {\rm Gr}({\rm Rep}(S_4, \alpha)) $ is an irreducible based module over $ r(S_4) $ equivalent to the based module $ M_{3, 3} $ in Table 3.

Proof. Let $ \alpha $ be a nontrivial 2-cocycle in $ Z^2(S_4, {{\mathbb C}}^*) $ (see e.g., [42, Section 3.2.4]). By checking products of characters, we get the following tensor product rule in $ r^\alpha(S_4) $:

$\begin{align*} 1 \otimes V_{\xi_i } = V_{\xi_{i} };\; \; \; V_\psi \otimes V_{\xi_j } = V_{\xi_{3-j} }, \; \; \; V_\psi \otimes V_{\xi_3 } = V_{\xi_{3} };\; \; \; V_{\rho_1} \otimes V_{\xi_j } = V_{\xi_{3} }, \; \; \; V_{\rho_1} \otimes V_{\xi_3 } = V_{\xi_{1} }+ V_{\xi_{2} }+V_{\xi_{3} };\\ V_{\rho_2} \otimes V_{\xi_j } = V_{\xi_{3-j} }+ V_{\xi_{3} }, \; \; \; V_{\rho_2} \otimes V_{\xi_3 } = V_{\rho_3} \otimes V_{\xi_3 } = V_{\xi_{1} }+ V_{\xi_{2} }+2V_{\xi_{3} };\; \; \; V_{\rho_3} \otimes V_{\xi_j } = V_{\xi_{j} }+ V_{\xi_{3} };\; \; \; \; \; \end{align*}$ $

where $ i = 1, 2, 3 $, $ j = 1, 2 $. Thus, we get

$ 1 \mapsto E_3, \quad V_{\psi} \mapsto

$\begin{pmatrix} 0 &1 &0\\ 1 &0 &0\\ 0 &0 &1 \end{pmatrix}$ , \quad V_{\rho_1} \mapsto

$\begin{pmatrix} 0 &0 &1\\ 0 &0 &1\\ 1 &1 &1 \end{pmatrix}$ , \quad V_{\rho_2} \mapsto

$\begin{pmatrix} 0 &1 &1\\ 1 &0 &1\\ 1 &1 &2 \end{pmatrix}$ , \quad V_{\rho_3} \mapsto

$\begin{pmatrix} 1 &0 &1\\ 0 &1 &1\\ 1 &1 &2 \end{pmatrix}$ . $

Then $ r(S_4, \alpha) $ is an irreducible based module over $ r(S_4) $ equivalent to $ M_{3, 3} $ listed in Table 3. In other words, the irreducible based module $ M_{3, 3} $ over $ r(S_4) $ can be categorified by $ {\rm Rep}(S_4, \alpha) $. □

In summary, we have the following classification theorem.

Theorem 4.12. The inequivalent irreducible based modules over $ r(S_4) $ are

$ M_{1, 1}, \; \; \; {\left \{ M_{2, i}\right \} } _{i = 1, 2, 3} , \; \; \; {\left \{ M_{3, j}\right \} } _{j = 1, 2, 3} , \; \; \; {\left \{ M_{4, s}\right \} } _{1\le s\le 7} \; \; \; \mathit{\text{and}}\; \; \; {\left \{ M_{5, t}\right \} } _{t = 1, 2}, $

among which

$ M_{1, 1} , \; \; \; {\left \{ M_{2, i}\right \} } _{i = 2, 3} , \; \; \; {\left \{ M_{3, j}\right \} } _{j = 1, 2, 3}, \; \; \; {\left \{ M_{4, s}\right \} } _{s = 1, 5, 7} \; \; \; \mathit{\text{and}}\; \; \; {\left \{ M_{5, t}\right \} } _{t = 1, 2} $

can be categorified by module categories over $ {\rm Rep}(S_4) $; see Table 8.

Table 8. Inequivalent irreducible based modules over $ r(S_4) $.

		$ V_{\psi} $	$ V_{\rho _{1}} $	$ V_{\rho _{2}} $	Categorification
Rank 1	$ M_{1, 1} $	$ 1 $	$ 2 $	$ 3 $	$ {\rm Rep}(\mathbb Z_1) $, $ {\rm Rep}(K_4, \alpha) $
Rank 2	$ M_{2, 1} $	$ $\begin{pmatrix} 1&0\\0&1\end{pmatrix}$ $	$ $\begin{pmatrix} 2&0\\0&2\end{pmatrix}$ $	$ $\begin{pmatrix} 1&2\\2&1\end{pmatrix}$ $	No
	$ M_{2, 2} $	$ $\begin{pmatrix} 0&1\\1&0\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1\\1&1\end{pmatrix}$ $	$ $\begin{pmatrix} 2&1\\1&2\end{pmatrix}$ $	$ {\rm Rep}(\mathbb Z_2) $, $ {\rm Rep}(D_4, \alpha) $
	$ M_{2, 3} $	$ $\begin{pmatrix} 0&1\\1&0\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1\\1&1\end{pmatrix}$ $	$ $\begin{pmatrix} 1&2\\2&1\end{pmatrix}$ $	$ {\rm Rep}(\mathbb Z_2) $, $ {\rm Rep}(D_4, \alpha) $
Rank 3	$ M_{3, 1} $	$ $\begin{pmatrix} 1&0&0\\0&1&0\\0&0&1\end{pmatrix}$ $	$ $\begin{pmatrix} 0&1&1\\1&0&1\\1&1&0\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1&1\\1&1&1\\1&1&1\end{pmatrix}$ $	$ {\rm Rep}(\mathbb Z_3) $, $ {\rm Rep}(A_4, \alpha) $
	$ M_{3, 2} $	$ $\begin{pmatrix} 0&1&0\\1&0&0\\0&0&1\end{pmatrix}$ $	$ $\begin{pmatrix} 0&0&1\\0&0&1\\1&1&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&0&1\\0&1&1\\1&1&2\\\end{pmatrix}$ $	$ {\rm Rep}(S_3) $
	$ M_{3, 3} $	$ $\begin{pmatrix} 0&1&0\\1&0&0\\0&0&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&0&1\\0&0&1\\1&1&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&1&1\\1&0&1\\1&1&2\\\end{pmatrix}$ $	$ {\rm Rep}(S_3) $, $ {\rm Rep}(S_4, \alpha) $
Rank 4	$ M_{4, 1} $	$ $\begin{pmatrix} 1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&0&1&1\\0&2&0&0\\1&0&0&1\\1&0&1&0\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&1&0&0\\1&2&1&1\\0&1&0&0\\0&1&0&0\\\end{pmatrix}$ $	$ {\rm Rep}(A_4) $
	$ M_{4, 2} $	$ $\begin{pmatrix} 1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 2&0&0&0\\0&2&0&0\\0&0&2&0\\0&0&0&2\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&1&1&1\\1&0&1&1\\1&1&0&1\\1&1&1&0\\\end{pmatrix}$ $	No
	$ M_{4, 3} $	$ $\begin{pmatrix} 1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1&0&0\\1&1&0&0\\0&0&2&0\\0&0&0&2\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&1&1&1\\1&0&1&1\\1&1&0&1\\1&1&1&0\\\end{pmatrix}$ $	No
	$ M_{4, 4} $	$ $\begin{pmatrix} 0&1&0&0\\1&0&0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1&0&0\\1&1&0&0\\0&0&2&0\\0&0&0&2\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&0&1&1\\0&1&1&1\\1&1&0&1\\1&1&1&0\\\end{pmatrix}$ $	No
	$ M_{4, 5} $	$ $\begin{pmatrix} 0&1&0&0\\1&0&0&0\\0&0&0&1\\0&0&1&0\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1&0&0\\1&1&0&0\\0&0&1&1\\0&0&1&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&1&1&1\\1&0&1&1\\1&1&0&1\\1&1&1&0\\\end{pmatrix}$ $	$ {\rm Rep}(\mathbb Z_4), \, {\rm Rep}(K_4) $
	$ M_{4, 6} $	$ $\begin{pmatrix} 0&1&0&0\\1&0&0&0\\0&0&0&1\\0&0&1&0\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1&0&0\\1&1&0&0\\0&0&1&1\\0&0&1&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&1&1&1\\1&0&1&1\\1&1&1&0\\1&1&0&1\\\end{pmatrix}$ $	No
	$ M_{4, 7} $	$ $\begin{pmatrix} 0&1&0&0\\1&0&0&0\\0&0&0&1\\0&0&1&0\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1&0&0\\1&1&0&0\\0&0&1&1\\0&0&1&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&0&1&1\\0&1&1&1\\1&1&1&0\\1&1&0&1\\\end{pmatrix}$ $	$ {\rm Rep}(\mathbb Z_4), \, {\rm Rep}(K_4) $
Rank 5	$ M_{5, 1} $	$ $\begin{pmatrix} 0&1&0&0&0\\1&0&0&0&0\\0&0&0&1&0\\0&0&1&0&0\\0&0&0&0&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&0&0&0&1\\0&0&0&0&1\\0&0&1&1&0\\0&0&1&1&0\\1&1&0&0&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&0&0&1&0\\0&0&1&0&0\\0&1&1&1&1\\1&0&1&1&1\\0&0&1&1&0\\\end{pmatrix}$ $	$ {\rm Rep}(S_4) $
	$ M_{5, 2} $	$ $\begin{pmatrix} 0&1&0&0&0\\1&0&0&0&0\\0&0&0&1&0\\0&0&1&0&0\\0&0&0&0&1\\\end{pmatrix}$ $	$ $\begin{pmatrix} 1&1&0&0&0\\1&1&0&0&0\\0&0&1&1&0\\0&0&1&1&0\\0&0&0&0&2\\\end{pmatrix}$ $	$ $\begin{pmatrix} 0&0&0&1&1\\0&0&1&0&1\\0&1&0&0&1\\1&0&0&0&1\\1&1&1&1&1\\\end{pmatrix}$ $	$ {\rm Rep}(D_4) $

| Show Table

DownLoad: CSV

5. Conclusions

The analysis in this paper shows that the classification of the irreducible based modules of rank up to 5 over the complex representation ring $ r(S_4) $. We also showed that any $ \mathbb{Z}_+ $-modules over the representation ring $ r(G) $ categorified by a module category over the representation category $ {\rm Rep}(G) $ must be a based module. At the end, we present the categorification of based modules over $ r(S_4) $ by module categories over the complex representation category $ {\rm Rep}(S_4) $ of $ S_4 $, using projective representations of specific subgroups of $ S_4 $. We expect that the studies developed here will be helpful in investigations of the structures of module categories over fusion categories. Our future study will focus on the existence of any irreducible based module of rank $ \geq 6 $ over $ r(S_4) $ and classifying irreducible $ \mathbb Z_+ $-modules over $ r(S_4) $, especially for high-rank cases. Also, some other small finite groups may be interesting to consider, e.g., the dihedral group $ D_5 $.

Author contributions

Wenxia Wu: Writing-original draft and editing, conceptualization, software, methodology; Yunnan Li: Topic selection, writing-review and editing, funding acquisition, methodology, supervision. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

We would like to thank Zhiqiang Yu for helpful discussion. This work is supported by Guangdong Basic and Applied Basic Research Foundation (2022A1515010357).

Conflict of interest

The authors declare that there are no conflicts of interest.

References

[1]	Orff HJ, Ayalon L, Drummond SP (2009) Traumatic brain injury and sleep disturbance: A review of current research. J Head Trauma Rehabil 24: 155-165. doi: 10.1097/HTR.0b013e3181a0b281
[2]	Wiseman-Hakes C, Colantonio A, Gargaro J (2009) Sleep and wake disorders following traumatic brain injury: A systematic review of the literature. Critical Rev Phys Rehab Med 21: 317-374. doi: 10.1615/CritRevPhysRehabilMed.v21.i3-4.70
[3]	Ouellet MC, Beaulieu-Bonneau S, Morin CM (2015) Sleep-wake disturbances after traumatic brain injury. Lancet Neurol 14: 746-757. doi: 10.1016/S1474-4422(15)00068-X
[4]	Grossman C (1949) Sensory stimulation during sleep. observations on the EEG responses to auditory stimulation during sleep in patients with brain pathology (preliminary report). Electroencephalogr Clin Neurophysiol 1: 487-490.
[5]	Harada M, Minami R, Hattori E, et al. (1976). Sleep in brain-damaged patients an all night sleep study of 105 cases. Kumamoto Med J 29: 110-127.
[6]	Schreiber S, Barkai G, Gur-Hartman T, et al. (2008) Long-lasting sleep patterns of adult patients with minor traumatic brain injury (mTBI) and non-mTBI subjects. Sleep Med 9: 481-487. doi: 10.1016/j.sleep.2007.04.014
[7]	Ouellet MC, Morin CM (2006) Subjective and objective measures of insomnia in the context of traumatic brain injury: a preliminary study. Sleep Med 7: 486-497. doi: 10.1016/j.sleep.2006.03.017
[8]	Ponsford JL, Ziino C, Parcell DL, et al. (2012) Fatigue and sleep disturbance following traumatic brain injury--their nature, causes, and potential treatments. J Head Trauma Rehabil 27: 224-233. doi: 10.1097/HTR.0b013e31824ee1a8
[9]	Lu W, Cantor JB, Aurora RN, et al. (2015) The relationship between self-reported sleep disturbance and polysomnography in individuals with traumatic brain injury. Brain Inj 19: 1-9.
[10]	Parcell DL, Ponsford JL, Redman JR, et al. (2008) Poor sleep quality and changes in objectively recorded sleep after traumatic brain injury: a preliminary study. Arch Phys Med Rehabil 89: 843-850. doi: 10.1016/j.apmr.2007.09.057
[11]	Shekleton JA, Parcell DL, Redman JR, et al. (2010) Sleep disturbance and melatonin levels following traumatic brain injury. Neurology 74: 1732-1738. doi: 10.1212/WNL.0b013e3181e0438b
[12]	Sommerauer M, Valko PO, Werth E, et al. (2013) Excessive sleep need following traumatic brain injury: a case-control study of 36 patients. J Sleep Res 22: 634-639. doi: 10.1111/jsr.12068
[13]	Mantua J, Mahan KM, Henry OS, et al. (2015) Altered sleep composition after traumatic brain injury does not affect declarative sleep-dependent memory consolidation. Front Hum Neurosci 9: 328.
[14]	Imbach LL, Valko PO, Li T, et al. (2015) Increased sleep need and daytime sleepiness 6 months after traumatic brain injury: a prospective controlled clinical trial. Brain 138: 726-735. doi: 10.1093/brain/awu391
[15]	Parsons LC, Crosby LJ, Perlis M, et al. (1976) Longitudinal sleep EEG power spectral analysis studies in adolescents with minor head injury. J Neurotrauma 14: 549-559.
[16]	Williams BR, Lazic SE, Ogilvie RD (2008) Polysomnographic and quantitative EEG analysis of subjects with long-term insomnia complaints associated with mild traumatic brain injury. Clin Neurophysiol 119: 429-438. doi: 10.1016/j.clinph.2007.11.003
[17]	Gosselin N, Lassonde M, Petit D, et al. (2009) Sleep following sport-related concussions. Sleep Med 10: 35-46. doi: 10.1016/j.sleep.2007.11.023
[18]	Khoury S, Chouchou F, Amzica F, et al. (2013) Rapid EEG activity during sleep dominates in mild traumatic brain injury patients with acute pain. J Neurotrauma 30: 633-641. doi: 10.1089/neu.2012.2519
[19]	Arbour C, Khoury S, Lavigne GJ, et al. (2015) Are NREM sleep characteristics associated to subjective sleep complaints after mild traumatic brain injury? Sleep Med 16: 534-539.
[20]	Levin H, Kraus MF (1994) The frontal lobes and traumatic brain injury. J Neuropsychiatry Clin Neurosci 6: 443-454. doi: 10.1176/jnp.6.4.443
[21]	Lezak MD, Howieson DB, Loring DW (2004) Neuropsychological assessment (4th ed.). New York, NY: Oxford University Press, Inc.
[22]	Giza CC, Hovda DA (2001) The neurometabolic cascade of concussion. J Athl Train 36: 228-235.
[23]	Williamson DJG, Scott JG, Adams RL (1996) Traumatic brain injury. In: Adams RL, Parsons OA, Culbertson JL, Nixon SJ, eds. Neuropsychology for clinical practice. Washington, D.C.: American Psychological Association: 9-64.
[24]	Levenstein S, Prantera C, Varvo V, et al. (1993). Development of the perceived stress questionnaire: A new tool for psychosomatic research. J Psychosom Res 37: 19-32.
[25]	Horne J, Ostberg O (1976) A self-assessment questionnaire to determine morningness-eveningness. Int J Chronobiol 4: 97-110.
[26]	Yositake H (1978) Three characteristics patterns of subjective fatigue symptoms. Ergonomics 21: 231-233. doi: 10.1080/00140137808931718
[27]	Beck AT, Ward CH, Mendelson M, et al. (1961) An inventory for measuring depression. Arch Gen Psychiatry 4: 561-571. doi: 10.1001/archpsyc.1961.01710120031004
[28]	Beck AT, Epstein N, Brown G, et al. (1988) An inventory for measuring clinical anxiety: Psychometric properties. J Consult Clin Psychol 56: 893-897. doi: 10.1037/0022-006X.56.6.893
[29]	Wechsler D (1997) Wechsler Adult Intelligence Scale - Third Edition (WAIS-III). San Antonio, TX: Pearson.
[30]	Stuss DT, Benson DF (1986) The frontal lobes. New York, NY: Raven Press.
[31]	Delis DC, Kramer JH, Kaplan E, et al. (2000) California Verbal Learning Test-Second Edition (CVLT-II). San Antonio, TX: Pearson.
[32]	Delis DC, Kaplan E, Kramer JH (2001) Delis-Kaplan Executive Function System (D-KEFS). San Antonio, TX: Pearson.
[33]	Hammill DD, Pearson NA, Widerholdt JL (1996) Comprehensive Test of Nonverbal Intelligence (CTONI). Austin, TX: Pro-Ed.
[34]	Baddeley A, Emslie H, Nimmo-Smith I (1993) Speed and Capacity of Language Processing Test (SCOLP). San Antonio, TX: Pearson.
[35]	Watson D, Clark AC, Tellegen A (1988) Development and validation of brief measures of positive and negative affect: the PANAS scales. J Person Soc Psyc 54: 1063-1070. doi: 10.1037/0022-3514.54.6.1063
[36]	Pivik RT, Broughton RJ, Coppola R, et al. (1993) Guidelines for the recording and quantitative analysis of electroencephalographic activity in research contexts. Psychophysiol 30: 547-558. doi: 10.1111/j.1469-8986.1993.tb02081.x
[37]	Rechtschaffen A, Kales A (1968) A manual of standardized terminology, techniques, and scoring system for sleep stages of human subjects. Washington, D.C.:N. I. H. Publishing 204, U. S. Government Printing Office.
[38]	Cote KA, Epps T, Campbell KB (2000) The role of the spindle in human information processing of high intensity stimuli during sleep. J Sleep Res 9: 19-26. doi: 10.1046/j.1365-2869.2000.00188.x
[39]	Cote KA, de Lugt DR, Langley SD, et al. (1999) Scalp topography of the auditory evoked K-complex in stage 2 and slow wave sleep. J Sleep Res 8: 263-274.
[40]	Bastien C, Campbell K (1992) The evoked K-complex: All-or-none phenomenon? Sleep 15: 236-245.
[41]	Bastien C, Campbell K (1994) Effects of rate of tone-pip stimulation on the evoked K-complex. J Sleep Res 3: 65-72. doi: 10.1111/j.1365-2869.1994.tb00109.x
[42]	Howell DC. Statistical methods for psychology. Boston, MA: PWS-Kent Publishing, 1992.
[43]	Dien J, Santuzzi AM (2005) Application of repeated measures ANOVA to high-density ERP datasets :a review and tutorial. In: Handy TC, ed., Event-related potentials: A methods handbook. Cambridge, MA: The MIT Press: 57-84.
[44]	Dijk DJ, Hayes B, Czeisler CA (1993) Dynamics of electroencephalographic sleep spindles and slow wave activity in men: Effect of sleep deprivation. Brain Res 626: 190-199.
[45]	McGinty D, Szymusiak R (2011) Neural control of sleep in mammals. In: Kryger MH, Roth T, Dement WC (Eds.), Principles and Practice of Sleep Medicine, 5^th ed., W.C. Elsevier: 54-66.
[46]	Riemann D, Spiegelhalder K, Feige B, et al. (2010) The hyperarousal model of insomnia: a review of the concept and its evidence. Sleep Med Rev 14: 19-31. doi: 10.1016/j.smrv.2009.04.002
[47]	Colrain IM (2005) The K-complex: A 7-decade history. Sleep 28: 255-273.
[48]	Liotti M, Tucker DM (1992) Right hemisphere sensitivity to arousal and depression. Brain Cog 18: 138-151. doi: 10.1016/0278-2626(92)90075-W
[49]	De Gennaro L, Ferrara M, Bertini M (2000) The spontaneous K-complex during stage 2 sleep: is it the 'forerunner' of delta waves? Neurosci Lett 291: 41-43. doi: 10.1016/S0304-3940(00)01366-5
[50]	Amzica F, Steriade M (2000) Integration of low-frequency sleep oscillations in corticothalamic networks. Acta Neurobiologiae Experimentalis 60: 229-245.
[51]	Fogel SM, Smith CT, Cote KA (2007) Dissociable learning-dependent changes in REM and non-REM sleep in declarative and procedural memory systems. Behav Brain Res 180: 48-61. doi: 10.1016/j.bbr.2007.02.037
[52]	Mölle M, Bergmann TO, Marshall L, et al. (2011) Fast and slow spindles during the sleep slow oscillation: disparate coalescence and engagement in memory processing. Sleep 34: 1411-1421.
[53]	Fogel SM, Nader R, Cote KA, et al. (2007) Sleep spindles and learning potential. Behav Neurosci 121: 1-10. doi: 10.1037/0735-7044.121.1.1
[54]	Bastien CH, St-Jean G, Turcotte I, et al. (2009) Spontaneous K-complexes in chronic psychophysiological insomnia. J Psychosom Res 67: 117-125.
[55]	Bastien CH, St-Jean G, Turcotte I, et al. (2009) Sleep spindles in chronic psychophysiological insomnia. J Psychosom Res 66: 59-65. doi: 10.1016/j.jpsychores.2008.05.013
[56]	Moldofsky H (2001) Sleep and pain. Sleep Med Rev 5: 385-396. doi: 10.1053/smrv.2001.0179
[57]	Armitage R (2007) Sleep and circadian rhythms in mood disorders. Acta Psychiatrica Scandinavica 115: 104-115. doi: 10.1111/j.1600-0447.2007.00968.x
[58]	Ramsawh H, Stein MB, Mellman TA (2011) Anxiety disorders. In: Kryger MH, Roth T, Dement WC (Eds.), Principles and Practice of Sleep Medicine, 5th ed., W.C. Elsevier: 1473-1487.
[59]	Baumann CR, Werth E, Stocker R, et al. (2007) Sleep-wake disturbances 6 months after traumatic brain injury: a prospective study. Brain 130: 1873-1883. doi: 10.1093/brain/awm109
[60]	Kempf J, Werth E, Kaiser PR, et al. (2010) Sleep-wake disturbances 3 years after traumatic brain injury. J Neurol Neurosurg Psychiatry 81: 1402-1405. doi: 10.1136/jnnp.2009.201913
[61]	Mahmood O, Rapport LJ, Hanks Robin A, et al. (2004) Neuropsychological performance and sleep disturbance following traumatic brain injury. J Head Trauma Rehab 19: 378-390. doi: 10.1097/00001199-200409000-00003

Reader Comments

Your name:*

Email:*
© 2015 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)