Role of PTH in the Renal Handling of Phosphate

1.   Introduction

The Lyapunov exponent (LE), as introduced by Oseledets ^[1] in the context of his multiplicative ergodic theorem, serves as a quantifier of the divergence between two proximal trajectories over time within a dynamical system. In an $ n $-dimensional dynamical system, there are $ n $ LEs available, with their quantity corresponding to the dimensionality of the system's phase space. Each LE characterizes the rate of convergence or divergence of the system's attractor in a specific direction. The spectrum of LEs offers a metric for assessing the local sensitivity of a system to initial conditions, as well as for providing crucial insights into the system's global dynamics. This spectrum facilitates the effective description and classification of system attractors based on their LEs. For stable equilibrium points, all LEs are real and negative; in the case of stable limit cycles, one LE is zero while the remainders are real and negative. An attractor is identified as a $ k $-torus if the first $ k $ LEs are zero and the others are negative. The presence of positive values within the LEs spectrum signifies a chaotic attractor, which is further classified as hyperchaotic if two or more LEs are positive ^[2].

The calculation or estimation of LEs constitutes a core aspect of research into nonlinear dynamical systems. Notably, the largest LE (LLE) holds particular significance as it directly influences the predictability of the system in question. Over the past several decades, a diverse array of studies focusing on the calculation schemes for LEs, especially the LLE, have been published. These studies have predominantly categorized them into two main methodologies: the determination of LEs from governing equations ^[3,4,5,6,7] and the estimation of LEs from time series data ^[8,9,10,11]. Benettin et al. ^[3] first introduced the method for calculating all LEs of dynamical systems, grounded in Oseledets's theory ^[1]. This methodology was later refined by Wolf et al. ^[8]. Additionally, Briggs ^[12] explored the calculation of LEs by using experimental data, proposing that the optimal estimation of Jacobian matrices in the presence of noisy data is attained through least-squares polynomial fitting. The QR decomposition (short for "QR factorization" is a process that decomposes a matrix into the product of an orthogonal matrix (Q) and an upper triangular matrix (R)) and the singular value decomposition (SVD) methods for determining all LEs of dynamical systems were developed by Von Bremen et al. ^[13] and Dieci and Elia ^[14], respectively. Dabrowski ^[15] numerically derived the LLE by calculating the LE in the direction of a disturbance, as based on the perturbation vector and its derivative's dot product. Liao ^[16] investigated the sensitivity gradients of the LLE in dynamical systems to address the deficiency of previous approaches, which were prohibitively time-consuming and resource-intensive for most optimization problems of reasonable size. Certain methods described above embody the direct approach, which quantifies the divergence growth rate between two trajectories that have an infinitesimal discrepancy in their initial conditions. Conversely, other methods aim to estimate the Jacobian matrices of systems, addressing the limitations inherent to direct approaches, especially in the context of noise ^[17]. However, approaches that rely on linear approximation often fall short of capturing nonlinear growth and typically necessitate laborious computations. In some instances, they may even result in erroneous LEs due to ill-conditioned Jacobian matrices ^[18]. Additionally, if the number of iterations is insufficient, the outcomes are likely to be imprecise ^[19]. Zhou et al. ^[20] introduced a groundbreaking method to derive the LLE by using two nearby pseudo-orbits, eliminating the need for phase space reconstruction and Jacobian matrix computation. Utilizing machine learning to forecast LEs from data was an approach adopted by Pathak et al. ^[21] and McAllister et al. ^[22]. The perturbation vectors method ^[23], the cloned dynamics approach ^[24], and the synchronization technique ^[25,26,27] have been developed as strategies to circumvent the direct calculation of Jacobian matrices or the need to solve variational equations. Recent advancements and applications of LLEs are documented in references ^[28].

The analytical estimation of LEs within a dynamical system represents a compelling and significant topic. According to the definition of LEs, their analytical formulas are readily derivable only for steady-state solutions, including fixed points in nonlinear systems with a limited number of degrees of freedom and steady-state, spatially homogeneous solutions in spatially extended systems. Analytical expressions for LEs have been derived for neural oscillator models ^[29,30,31], as well as for certain simple models of nonlinear oscillators applied for synchronization problems triggered by common external noise ^[32,33,34]. Caponetto and Fazzino ^[7] introduced a semi-analytical approach, utilizing the differential transform method, to compute LEs in fractional order systems. Hramov et al. ^[35] first presented the analytical formula for the zero LE. A zero LE exists within the spectrum of LEs for flow systems, characterizing the perturbation evolution along the phase trajectory ^[36]. To derive the analytical expression for the zero LE, Hramov et al. analyzed a model system that describes the behavior of a driven periodic oscillator with noise near the synchronization onset. In chaotic systems, analytical approximations of LEs typically retain validity within a very narrow range of control parameter values, despite their derivability ^[37]. The analytical characterization of LEs for chaotic oscillators remains to be a formidable challenge.

In this paper, we aim to derive an analytical expression for the LLE of a Rössler chaotic system ^[38] by utilizing the synchronization method ^{[25,26,27,39]}. It is established that synchronization between two diffusively coupled identical chaotic systems is invariably achievable with a sufficiently large coupling parameter ^[40]. A linear relationship exists between the synchronization threshold of the coupling parameter in two identical systems and the value of the LLE of the coupled systems. Consequently, the LLE can be estimated based on the critical coupling required for synchronization ^[39]. This paper focuses on the analytical criteria for synchronization between two identical Rössler chaotic systems from the perspective of the linear coupling of state variables. Unlike previous studies ^[41,42,43], we initially transform the synchronization error system between two identical Rössler chaotic systems into a set of Volterra integral equations, utilizing the Laplace transform and the convolution theorem. The critical coupling required for synchronization can be derived by applying the successive approximation method ^[44] within the framework of integral equation theory to resolve the error system's solution. Numerical simulations have been conducted to confirm the efficacy of our analytical estimation of the LLE for the Rössler chaotic system. Furthermore, this analytical estimation remains valid across a broad range of parameter variations.

The remainder of the paper is structured as follows. Section 2 introduces the theoretical foundation of the estimation procedure for the LLE based on the synchronization method. Section 3 details the analytical estimation of the LLE for a Rössler system. Section 4 validates the analytical findings through numerical simulations. Finally, Section 5 provides the conclusions.

2.   Theoretical background of estimation procedure for LLE based on the synchronization method

2.1.   The definition of LEs

Consider a set of ordinary differential equations

where $ x\in R^n $ represents the state variables and $ f:R^n\rightarrow R^n $ is a smooth vector function. Assume that $ s_t(x_0) $ is the solution of Eq (2.1) with the initial condition $ x = x_0 $ which has the components ($ x_{10}, x_{20}, \cdots, x_{n0} $); one has

Taking the variation with respect to $ x_0 $ on both sides of Eq (2.2) yields

where $ \frac{\partial f[s_t(x_0)]}{\partial x} = \frac{\partial f(x)}{\partial x}\bigg|_{x = s_t(x_0)} $, $ J_t(x_0) = \frac{\partial s_t(x_0)}{\partial x_0} $. Clearly, $ J_t(x_0) $ can be obtained by solving Eq (2.3), which describes the influence of infinitesimal disturbance $ \Delta x_0 $ to the initial condition $ x_0 $ on the trajectory $ s_t(x_0) $, that is,

Thus, the length of vector $ \Delta s(t) $ can be given as

where the notation $ T $ denotes the transpose of vectors. Since $ J_t(x_0) $ is a real matrix, $ J_t(x_0)^TJ_t(x_0) $ is real symmetric and positive semi-definite. Assume that $ \xi_i(t) $, $ i = 1, 2, \cdots, n $, denotes the eigenvalues of the matrix $ J_t(x_0)^TJ_t(x_0) $. Obviously, $ \xi_i(t)\geq0 $. Assume that $ v_i(t) $ is the corresponding eigenvector of $ \xi_i(t) $. If $ \Delta x_0 $ has the same direction as $ v_i(t) $, Eq (2.5) becomes

The definition of LEs denoted by $ \lambda_i $, $ i = 1, 2, \cdots, n $, in system (2.1) is given as

From Eq (2.7), after long enough one has

Substituting Eq (2.8) into Eq (2.6), leads to

The LEs are related to the expanding or contracting nature of different directions in phase space.

2.2.   The relation between chaos synchronization and the LLE

Consider a chaotic system in the following form ^[25]

where $ x\in R^n $ and $ f:R^n\rightarrow R^n $ is a smooth functional vector. Two such identical oscillators couple to undergo unidirectional coupling, as follows:

where $ x, y\in R^n $ and $ k\in R $ is the coupling parameter. If $ k = 0 $, two separate dynamical systems are obtained

Assume that each system in Eq (2.12) evolves on an asymptotically stable chaotic attractor $ X $. The solutions of Eq (2.12) starting from different initial conditions represent two independent trajectories on the atrractor $ X $. If the two initial conditions are the same the two subsystems will exhibit identical behaviors ($ x = y $). If the initial conditions for the two subsystems in Eq (2.12) have a small difference, then a state difference exists between the two subsystems during the time evolution, which is defined by the expression

where $ z\in R^n $.

Theorem 1. Assume that $ k_{min} > 0 $ is the boundary value of the coupling parameter $ k $ that is required to cause synchronization in system (2.11), and that $ \lambda_{max} $ is the LLE of system (2.10) such that $ \lambda_{max}\approx k_{min} $ holds.

Proof. To make further considerations easier, the following notations are first introduced:

$ * $ $ \lambda_j $ denotes the LEs in system (2.10) excluding $ \lambda_{max} $, $ j = 1, 2, \cdots, n-1 $,

$ * $ $ \Delta\lambda_{j} = \lambda_{max}-\lambda_j $ denotes the difference between $ \lambda_{max} $ and other LEs $ \lambda_{j} $, $ j = 1, 2, \cdots, n-1 $,

$ * $ $ \delta_0 $ is initial distance in the $ \lambda_{max} $ direction,

$ * $ $ \delta_{j0} = m_j\delta_0 $ denotes the initial distances in the $ \lambda_j $ direction, where $ m_j $ denotes constant values, $ j = 1, 2, \cdots, n-1 $.

The norm of vector $ z $ is given by

Assume that $ z_0 = x_0-y_0 $ is an initial distance between two trajectories of subsystems in system (2.12), where $ z_0 $ has the components ($ z_{10}, z_{20}, \cdots, z_{n0} $). Obviously, $ z_0 $ is the total $ \lambda- $distance vector, which is a sum of $ \delta_0 $ and $ \delta_{j0} $, $ j = 1, 2, \cdots, n-1 $. From Eq (2.9), $ ||z|| $ can be written as

Since $ \Delta\lambda_{j} < 0 $ holds for $ j = 1, 2, \cdots, n-1 $, the sum in Eq (2.15) finally decreases to zero during the time evolution; the norm of state difference $ z $ between two subsystems in Eq (2.12) approaches the following:

This implies that the distance associated with the $ \lambda_{max} $ direction becomes dominant after enough time.

Next, we consider the case of $ k\neq0 $ in Eq (2.11). For clarity, redefine the norm of the state difference between two subsystems in Eq (2.11) by $ Q $. Clearly, $ Q\geq0 $ for any values of $ x, y $ and $ k $. From Eq (2.16), if $ k > 0 $ one has

For $ k < 0 $,

Solving Eqs (2.17) and (2.18) yields

where $ Q_0 $ is a constant determined by the initial conditions given in Eq (2.11). If $ k > 0 $ and the synchronization between two subsystems in Eq (2.11) is achieved, then $ Q\rightarrow0 $. From the first relation in Eq (2.19), it must follow that $ \lambda_{max} < k $. Assume that $ k_{min} > 0 $ is the boundary value of the coupling parameter $ k $ that is required to cause synchronization in system (2.11); then, the following inequality should be held: $ \lambda_{max} < k_{min} $.

On the contrary, if $ \lambda_{max}\geq k_{min} $, from the first inequality in Eq (2.19), the synchronization cannot be achieved. Therefore, one can have the following approximation

From Eq (2.18) and the second inequality in Eq (2.19), $ Q\rightarrow0 $ is impossible when $ \lambda_{max} > 0 $ and $ k < 0 $. It implies that two identical chaotic systems in Eq (2.11) cannot synchronize with each other when $ k < 0 $.

3.   The analytical estimation for the LLE of a Rössler chaotic system

The Rössler oscillator ^[38] is described as follows:

where $ u $, $ v $, $ w $ are state variables, and $ a $, $ b $, $ c $ are parameters. For convenience, by moving the equilibrium ($ u_0, v_0, w_0 $) of system (3.1) to the origin, system (3.1) can be rewritten as follows:

where $ x = u-u_0 $, $ y = v-v_0 $, $ z = w-w_0 $. Consider two unidirectionally coupled Rössler systems as follows:

where $ k $ is a coupling parameter. Synchronization is said to occur in system (3.3) if

By introducing

to system (3.3), the dynamical behavior of errors denoted by $ e_i $, $ i = 1, 2, 3 $, can be described as follows:

Then the synchronization condition given by Eq (3.4) becomes $ \lim_{t\rightarrow \infty}{||e_i|| = 0}, \; i = 1, 2, 3. $ Consider the Laplace transform defined as follows:

By taking the Laplace transform on both sides of system (3.5), we obtain

where $ e_{0i} $, $ i = 1, 2, 3 $, denotes the given initial values of system (3.5), $ I_{3} $ is the $ 3\times3 $ real identity matrix, and

$ W $ is the Laplace transform of the nonlinear parts in the third equation in system (3.5)

Solving Eq (3.7) by using the Cramer's rule, one has

where $ D(s) = s^3+\beta_1s^2+\beta_2s+\beta_3 $ is the characteristic polynomial of the matrix of Eq (3.8), and

To investigate whether $ ||e_i||\rightarrow0 $, $ i = 1, 2, 3 $, when $ t\rightarrow \infty $, we take the inverse Laplace transform on both sides of three equations in system (3.9) and consider the convolution theorem in the Laplace transform, which yields

where $ \gamma_1 = L^{-1}[\frac{s+k-a}{D(s)}] $, $ \gamma_2 = L^{-1}[\frac{s+k+c+u_0}{D(s)}] $, $ \gamma_3 = L^{-1}[\frac{(s+k)(s+k-a)}{D(s)}] $, $ \gamma_4 = L^{-1}[\frac{(s+k)(s+k+c+u_0)}{D(s)}] $, $ \gamma_5 = L^{-1}[\frac{(s+k-a)(s+k+c+u_0)}{D(s)}] $, $ \gamma_6 = L^{-1}[\frac{1}{D(s)}] $.

Theorem 2. The necessary condition for $ e_{1, 2, 3}\rightarrow0 $ with $ t\rightarrow \infty $ in Eq (3.10) is that all eigenvalues of the matrix of Eq (3.8) have negative real parts.

Proof. Without loss of generality, consider the inverse Laplace transform of the following true fraction

where $ D(s) $ is the characteristic polynomial of the matrix of Eq (3.8) and $ A_i $, $ i = 1, 2, 3 $, denotes constants. There exist the following four cases:

● $ D(s) $ has $ 3 $ single real roots: $ s_1, s_2, s_3 $

$ \frac{A_1s^2+A_2s+A_3}{D(s)} = \frac{B_1}{s-s_1}+\frac{B_2}{s-s_2}+\frac{B_3}{s-s_3} $,

where $ B_i = \frac{A_1s^2+A_2s+A_3}{D(s)}(s-s_i)\bigg|_{s = s_i} $, $\quad i = 1, 2, 3 $.

$ L^{-1}[\frac{A_1s^2+A_2s+A_3}{D(s)}] = B_1e^{s_1t}+B_2e^{s_2t}+B_{3}e^{s_{3}t} $

● $ D(s) $ has a pair of conjugate complex roots $ s_{1, 2} = \omega_1\pm j\omega_2 $ and a real root $ s_3 = \omega_3 $

$ \frac{A_1s^2+A_2s+A_3}{D(s)} = \frac{A_1s^2+A_2s+A_3}{(s-\omega_1-j\omega_2)(s-\omega_1+j\omega_2)(s-\omega_3)} = \frac{B_1}{s-\omega_1-j\omega_2}+\frac{B_2}{s-\omega_1+j\omega_2}+\frac{B_3}{s-\omega_3} $,

where $ B_{1, 2} = \frac{A_1s^2+A_2s+A_3}{D'(s)}\bigg|_{s = \omega_1\pm j\omega_2}, \quad B_3 = \frac{A_1s^2+A_2s+A_3}{D(s)}(s-\omega_3)\bigg|_{s = \omega_3} $,

$ L^{-1}[\frac{A_1s^2+A_2s+A_3}{D(s)}] = B_1e^{(\omega_1+j\omega_2)t}+B_2e^{(\omega_1-j\omega_2)t}+B_3e^{\omega_3t} $

● $ D(s) $ has $ 2 $ repeated real roots $ s = s_0 $ and a single real root $ s = s_k $

$ \frac{A_1s^2+A_2s+A_3}{D(s)} = \frac{B_1}{s-s_0}+\frac{B_2}{(s-s_0)^2}+\frac{B_3}{s-s_k} $,

where $ B_{1} = \frac{1}{2}\frac{d^2}{ds^2}[\frac{A_1s^2+A_2s+A_3}{D(s)}(s-s_0)^2]\bigg|_{s = s_0} $, $ B_{2} = \frac{A_1s^2+A_2s+A_3}{D(s)}(s-s_0)^{2}\bigg|_{s = s_0} $,

$ B_3 = \frac{A_1s^2+A_2s+A_3}{D(s)}(s-s_k)\bigg|_{s = s_k} $,

$ L^{-1}[\frac{A_1s^2+A_2s+A_3}{D(s)}] = (B_1+B_2t)e^{s_{0}t}+B_3e^{s_kt} $

● $ D(s) $ has $ 3 $ repeated real roots: $ s = s_0 $

$ \frac{A_1s^2+A_2s+A_3}{D(s)} = \frac{B_1}{s-s_0}+\frac{B_2}{(s-s_0)^2}+\frac{B_3}{(s-s_0)^{3}} $,

where $ B_{(3-i)} = \frac{1}{i!}\frac{d^i}{ds^i}[\frac{A_1s^2+A_2s+A_3}{D(s)}(s-s_0)^{3}]\bigg|_{s = s_0} $, $\quad i = 1, 2 $,

$ B_{3} = [\frac{A_1s^2+A_2s+A_3}{D(s)}(s-s_0)^{3}]\bigg|_{s = s_0} $,

$ L^{-1}[\frac{A_1s^2+A_2s+A_3}{D(s)}] = (B_1+B_2t+B_{3}t^{2})e^{s_{0}t} $

It is evident that for $ ||e_i|| $ to approach zero ($ i = 1, 2, 3 $) in system (3.10), a necessary condition is that $ \gamma_{j} $ tends toward zero as time approaches infinity ($ j = 1, 2, 3, 4, 5, 6 $). This condition is satisfied if all roots of the equation $ D(s) = 0 $ possess negative real parts, implying that all eigenvalues of the matrix of Eq (3.8) also have negative real parts.

Under the condition given in Theorem 2, when $ t\rightarrow \infty $ system (3.10) becomes as follows:

Theorem 3.2. $ e_{1, 2, 3} = 0 $ represents the unique continuous solutions to Eq (3.11).

Proof. System (3.11) is a set of Volterra integral equations that can be solved by using the successive approximation method ^[44]. Consider the integral equation of the following form

where $ g $ is an $ n\times n $ matrix and $ \Psi(t) $ and $ H(t, h(t)) $ are vectors with $ n $ components. If the following conditions are satisfied

● $ |h| < \infty $;

● $ \Psi $ and $ h $ are continuous for $ 0 < t < t_0 $, where $ 0 < t_0 < +\infty $;

● $ |g|\in L[0, \epsilon] $ holds for any $ 0 < \epsilon < t_0 $;

● For any $ \eta > 0 $, if $ |h_1-h_2| < \eta $ there must exist a constant $ \kappa > 0 $ such that $ |H(t, h_1)-H(t, h_2)| < \kappa $,

from the successive approximation method ^[44], Eq (3.12) has a unique continuous solution. Moreover the successive approximations given by

will uniformly converge to the unique continuous solution of Eq (3.12).

Comparing Eq (3.11) with Eq (3.12), it is easy to verify that $ e_1 = e_2 = e_3 = 0 $ constitutes the unique continuous solution of Eq (3.11).

From Theorems 2 and 3, we have the following result:

Theorem 4. The necessary condition for $ e_{1, 2, 3}\to 0 $ in Eq (3.5) is that all eigenvalues of the matrix of Eq (3.8) have negative real parts.

From the Routh-Hurwitz stability criterion, the necessary condition in {Theorem 4} is equivalent to the following condition:

where $ \beta_{1, 2, 3} $ has been defined in Eq (3.9). Since $ \beta_i $, $ i = 1, 2, 3 $, denotes functions of $ k $, from Eq (3.14) one can determine the boundary value of $ k $.

Theorem 5. The boundary value of $ k $ for synchronization in system (3.3) can be given as

where $ \max\{\cdot\} $ represents taking the maximum value of elements in the set,

and $ m_{2, 3} $ are the maximum real roots of the equations

respectively.

Proof. $ \beta_{i} $, $ i = 1, 2, 3 $, denotes functions of $ k $; it is easy to check that

Therefore, one has

If $ \beta_{1, 2} > 0 $, then $ \beta_{3} $ and $ \beta_1\beta_2-\beta_3 $ are always monotonically increasing functions of $ k $. $ \beta_1 > 0 $ leads to

Solving $ \beta_2 > 0 $ yields the following:

Denote

If $ k > m_1 $, $ \beta_{3} $ and $ \beta_1\beta_2-\beta_3 $ are always monotonically increasing with an increase of $ k $. Assume that $ k = m_{2, 3} $ denotes the maximum real roots of equations $ \beta_{3} $ and $ \beta_1\beta_2-\beta_3 $, respectively, and that Eq (3.14) holds if and only if $ k > \max\{m_1, m_2, m_3\} $.

Remark. Suppose that system (3.1) has more than one equilibrium point $ (u_{01}, v_{01}, w_{01}) $, $ (u_{02}, v_{02}, w_{02}) $, $ \cdots $, $ (u_{0n}, v_{0n}, w_{0n}) $. For each equilibrium point $ (u_{0i}, v_{0i}, w_{0i}) $, one from Eq (3.15) has one $ k_{c}^{i} $, $ i = 1, 2, \cdots, n $. Then the boundary value of $ k $ for synchronization in system (3.3) is given by

where $ \min\{\cdot\} $ denotes the minimum value of elements in the set.

4.   Numerical verification

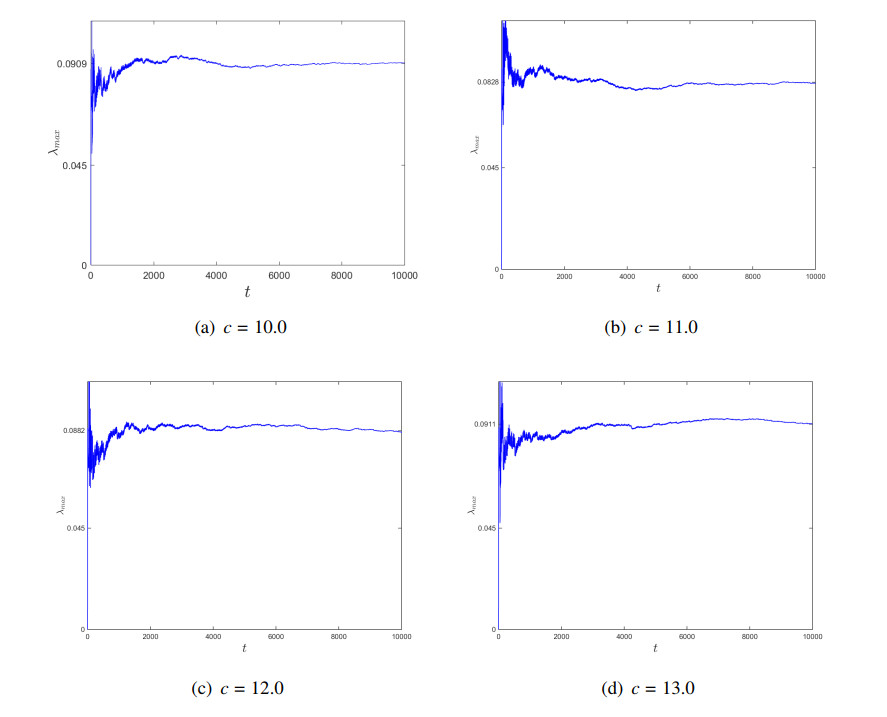
In this section, numerical simulations are presented to illustrate the correctness of the result given by Eq (3.18). If $ a = 0.15 $, $ b = 0.2 $, and $ c = 10.0 $, system (3.1) is chaotic ^[38]. Under such parameter conditions, the numerical result for the LLE of system (3.1) is $ \lambda_{max} = 0.092 $ ^[8,45], where the initial conditions are taken as $ u(0) = -1 $, $ v(0) = 1 $, and $ w(0) = 1 $.

4.1.   $ a=0.15 $ and $ b=0.2 $ are fixed

Consider that the value of $ c $ is allowed to vary between $ 10.0 $ and $ 13.0 $. Using the numerical method proposed in ^[8], the LLEs of system (3.1) for different values of $ c $ can be obtained as shown in Figure 1, where the initial conditions are retained as $ u(0) = -1 $, $ v(0) = 1 $, and $ w(0) = 1 $.

From Theorem 5, under the certain limitation of the parameters, the LLE of system (3.1) is just the maximum real root of the following equation (obtained from the second equation in Eq (3.17))

where

$ a = 0.15 $, $ b = 0.2 $ and $ c $ varies in the range of $ 10 $ to $ 13 $.

From Appendix, the analytic expression of the LLE of system (3.1) can be given as

where

Figure 2 illustrates the comparisons between the analytical results from Eq (4.2) and the numerical results obtained by using the method described in ^[8]. The numerical results exhibit minor differences relative to the analytical results as the value of $ c $ increases. Figure 3 displays the time series for $ x_{1, 2} $, $ y_{1, 2} $, and $ z_{1, 2} $ in system (3.3) with varying $ c $ values to identify the critical synchronization conditions for $ k $. The analytical estimation based on Eq (4.2) for the LLE of system (3.1) is confirmed to be valid and highly accurate, as evidenced by the data in Figures 2 and 3.

4.2.   $ b=0.2 $ and $ c=10.0 $ are fixed

Consider that the value of $ a $ changes in the range of $ 0.15 $ to $ 0.2 $. Applying the numerical method in ^[8], one can obtain the LLEs of system (3.1) for different values of $ a $, as depicted in Figure 4. The initial conditions were applied as $ u(0) = -1 $, $ v(0) = 1 $, and $ w(0) = 1 $.

For the parameter values considered in this section, the analytical expression of the LLE of system (3.1) is still given by Eq (4.2). The comparisons between the analytical results obtained based on Eq (4.2) and the numerical results derived by using the method in ^[8] are depicted in Figure 5.

Figure 5 demonstrates that the analytical results linearly increase as the value of $ a $ rises. The numerical results, however, display slight fluctuations before reaching their peak. Figure 6 depicts the time series for $ x_{1, 2} $, $ y_{1, 2} $ and $ z_{1, 2} $ in system (3.3) for various values of $ a $ and $ k $. A comparison of Figures 5 and 6 reveals that the analytic approach outlined in Eq (4.2) is both effective and highly accurate as a tool to determine the LLE of system (3.1), especially when the value of $ a $ varies within the range of $ 0.15 $ to $ 0.2 $.

4.3.   $ b=0.2 $ is fixed

Considering that the values of $ a $ and $ c $ vary within the ranges of $ 0.15 $ to $ 0.2 $ and $ 10 $ to $ 13 $, respectively, Figure 7 was constructed based on the calculated results of Eq (4.2) to illustrate the variation in the LLE of system (3.1) as $ a $ and $ c $ change. Equation (4.2) facilitates the examination of how wide-ranging parameter values influence the LLE in system (3.1).

5.   Conclusions

Although a linear relationship exists between the synchronization threshold of the coupling coefficient in two identical chaotic systems and their LLE, previous studies have primarily derived the boundary value of the coupling parameter by employing numerical methods to estimate the LLE, to the best of our knowledge. This paper has presented an approach to analytically estimate the LLE of the Rössler chaotic system by using the synchronization method. Unlike previous studies, this approach transforms the synchronization error system into a set of Volterra integral equations. The stability of these equations was then examined through the application of the successive approximation method in accordance with the theory of integral equations. Compared to the numerical results for the LLEs of Rössler chaotic systems, our analytical estimates demonstrate high accuracy. Moreover, these analytical estimates remain valid across a wide range of parameter variations.

Our findings reveal that the value of the LLE for the Rössler chaotic system corresponds to the maximum real root of a cubic algebraic equation. This insight simplifies the challenge associated with analytically determining the LLE to solve such an equation. Our research introduces a novel approach for the analysis and management of the impact of parameter variations on the LLE value in the Rössler chaotic system.

Use of AI tools declaration

The authors declare that they have not used artificial intelligence tools in the creation of this article.

Acknowledgments

The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China grant numbers 11672185 and 11972327.

Conflict of interest

The authors declare that there is no conflict of interest.

Appendix

In the Appendix, expressions of real roots of a cubic equation are provided according to the Cardano formula. Consider the following cubic equation:

where $ a, b, c, d $ are real constants and $ a\neq0 $. Denote

● If $ \Delta > 0 $, there is only one real root:

$ x = \frac{\sqrt[3]{Y_1}+\sqrt[3]{Y_2}-b}{3a}. $

● If $ \Delta = 0 $ and $ A = 0 $, there are three equal real roots:

$ x_1 = x_2 = x_3 = -\frac{b}{3a} $.

● If $ \Delta = 0 $ and $ A > 0 $, there are three real roots, where two roots are equal:

$ x_1 = \frac{B}{A}-\frac{b}{a} $, $\quad x_2 = x_3 = -\frac{B}{2A}. $

● If $ \Delta < 0 $ and $ A > 0 $, there are three different real roots:

$ x_i = \frac{2\sqrt{A}\cos(\frac{\phi+2(i-1)\pi}{3})-b}{3a} $, $\quad \phi = \arccos(\frac{3aB-2Ab}{2A\sqrt{A}}), \quad i = 1, 2, 3. $