Citation: Lin Dong, Michael Grissom, Frank T. Fisher. Resonant frequency of mass-loaded membranes for vibration energy harvesting applications[J]. AIMS Energy, 2015, 3(3): 344-359. doi: 10.3934/energy.2015.3.344
| [1] | Amine Ben Alaya, Charfeddine Mrad, Férid Kourda . Piezoelectric energy harvesting under free and forced vibrations for different operating conditions. AIMS Energy, 2024, 12(6): 1334-1365. doi: 10.3934/energy.2024060 |
| [2] | Wan Nabila Mohd Fairuz, Illani Mohd Nawi, Mohamad Radzi Ahmad, Ramani Kannan . Design analysis and simulation of serpentine-shaped piezoelectric cantilever beam for pipeline vibration-based energy harvester. AIMS Energy, 2024, 12(3): 561-599. doi: 10.3934/energy.2024027 |
| [3] | Azevedo Joaquim, Mendonça Fábio . Small scale wind energy harvesting with maximum power tracking. AIMS Energy, 2015, 2(3): 297-315. doi: 10.3934/energy.2015.3.297 |
| [4] | Antwi Nimo, Tobias Beckedahl, Thomas Ostertag, Leonhard Reindl . Analysis of Passive RF-DC Power Rectification and Harvesting Wireless RF Energy for Micro-watt Sensors. AIMS Energy, 2015, 3(2): 184-200. doi: 10.3934/energy.2015.2.184 |
| [5] | Lawrence Moura, Mario González, Jéssica Silva, Lara Silva, Izaac Braga, Paula Ferreira, Priscila Sampaio . Evaluation of technological development of hydrogen fuel cells based on patent analysis. AIMS Energy, 2024, 12(1): 190-213. doi: 10.3934/energy.2024009 |
| [6] | Joaquim Azevedo, Jorge Lopes . Energy harvesting from hydroelectric systems for remote sensors. AIMS Energy, 2016, 4(6): 876-893. doi: 10.3934/energy.2016.6.876 |
| [7] | Stefano Farnesi, Mario Marchesoni, Massimiliano Passalacqua, Luis Vaccaro . Soft-switching cells for Modular Multilevel Converters for efficient grid integration of renewable sources. AIMS Energy, 2019, 7(3): 246-263. doi: 10.3934/energy.2019.3.246 |
| [8] | Nan Liu, Thomas G. Habetler . Design of a parallel-LC-compensated on-board charger for universal inductive charging in electric vehicles. AIMS Energy, 2016, 4(5): 658-674. doi: 10.3934/energy.2016.5.658 |
| [9] | Mark P. McHenry, P. V. Brady, M. M. Hightower . PV-Li-ion-micropump membrane systems for portable personal desalination. AIMS Energy, 2016, 4(3): 444-460. doi: 10.3934/energy.2016.3.444 |
| [10] | Zhaolong Wang, Guihui Duan, Huigao Duan . Optimization of the perfect absorber for solar energy harvesting based on the cone-like nanostructures. AIMS Energy, 2021, 9(4): 714-726. doi: 10.3934/energy.2021033 |
Energy harvesting is a rapidly expanding field which seeks to generate small but useful levels of electrical energy from mechanical vibrations omnipresent in most environments. Several recent reviews discuss in detail the mechanisms, technologies, and potential applications of energy harvesting. For example, Beeby et al. [1] reviewed a variety of energy harvesting sources for microsystem applications, while Cook-Chennault et al. [2] covered the applications of piezoelectric energy harvesting systems and Dutoit et al. [3] presented the design considerations to be examined for the application of energy harvesting technology at the microscale. In addition, a recent study has summarized the energy harvesting market and identified potential applications including healthcare, e-books, electronics, and automotive applications [4]. Among the proposed energy harvesting applications, the (self) powering of wireless micro sensors is particularly attractive due to the potential of small size, flexibility, ease of implementation, and the ability to facilitate the placement of sensors in inaccessible locations. In addition, a comparison of the output power density suggests that mechanical vibration provides great potential as a high power density and long lifetime energy source [5] among the variety of ambient source candidates for energy harvesting sources. It is this vibration-based energy source that is the focus of the work described within.
Normally, it is desired to ensure that the resonant frequencies of the energy harvesting device match the ambient vibration frequencies to maximize the energy harvested, and several frequency tuning approaches have been proposed. For example, Scheibner et al. [6] reported a vibration detector consisting of an array of eight comb resonators with eight different base resonant frequencies, while Peters et al. [7] designed a tunable resonator by applying an electrical potential to change the shape of the structure in order to alter mechanical stiffening. Leland et al. [8] designed a tunable-resonance vibration energy scavenger by using an axial compressive preload on a piezoelectric bimorph with a tuning rage from 200 Hz to 250 Hz. Challa et al. [9] presented a resonance frequency tunable energy harvesting device by applying a magnetic force perpendicular to the cantilever beam. The vertical tuning mechanism employs magnetic force/stiffness to increase or decrease the frequencies based on the mode (attractive, repulsive) of the magnetic force. In addition, Zhu et al. [10] designed a horizontal tunable electromagnetic vibration-based micro-generator, where an effective resonant frequency range from 67.6 Hz to 98 Hz was obtained using an axial tensile force. Here the distance between the fixed and tuned magnets is adjusted by the actuator, and the horizontal magnetic force induces variable axial loads on the cantilever beam.
In addition to the cantilever-based energy harvesting approaches described above, a membrane-based energy harvester could be implemented. For example, Rezaeisaray et al. [11] designed and analyzed an SU-8 membrane and a frequency bandwidth of 146 Hz was obtained, which they suggested could be used to design polymer membrane based micro-structures with large deflections and small size energy harvesters with low resonant frequencies. Mo et al. [12] presented a theoretical model of a piezoelectric circular membrane subjected to pressure fluctuations for predicting the energy harvested, and they concluded that the optimization of energy generating performance is highly dependent on the ratio between the thickness and radius of the membrane. In addition, a piezoelectric circular membrane array for energy harvesting was analyzed by Wang et al. [13], with series and parallel connections investigated.
In this work we focus on pursuing both analytical and computational (finite element) approaches to determine the vibration response of a membrane-with-added-mass structure, with the proof mass added to further decrease the resonant frequency of the membrane. A generic model of vibration based energy harvesting is presented in Section 2. Section 3.1 describes the free vibration of the circular membrane, with the vibration response for a centrally-loaded circular membrane is discussed in Section 3.2. The analytical solution for the resonant frequency of a square membrane and its relationship to a finite element analysis of a centrally-loaded square mass on a square membrane is presented in Section 3.3. Experimental verification of the resonant frequency of a circular centrally-loaded mass membrane is discussed in Section 3.4. The manuscript concludes with some thoughts regarding the use of membrane tension and applied mass for the resonant frequency tuning of membranes for energy harvesting applications.
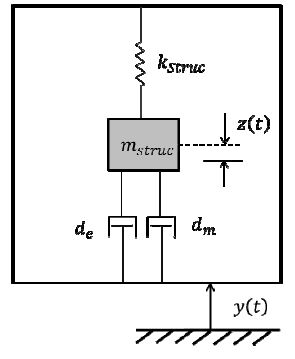
In this section the theoretical modeling and analysis of a generic (geometry and structure independent) energy harvesting device are discussed. In general, an energy harvesting device can be modeled as a spring-mass-damper system as shown in Figure 1,which consists of a spring of stiffness kstruc, a mass of mstruc, and dampers denoted as mechanical dashpot dm and electrical dashpot de. Here the mechanical dashpot accounts for the energy losses due to structural and viscous damping, while the electrical damping corresponds to the energy harvested through the energy conversion mechanism [14].
Figure 1. Schematic model of generic vibration energy harvesting.
Given a sinusoidal excitation vibration y(t) = Ysin ωst (where Y and ωs are the source vibration amplitude and frequency, respectively) the net electrical power generated can be written [14] as
|
P=mstrucζtY2(ωsωstruc)3ωs3[1−(ωsωstruc)2]2+[2ζtωsωstruc]2 |
(1) |
where ζt is the total damping ratio (ζt = ζm + ζe) which is the sum of mechanical damping ratio ζm and electrical damping ratio ζe and ωstruc is the undamped natural frequency of the vibrating structure, which can be written as
|
ωstruc=√kstrucωstruc |
(2) |
When the energy harvesting device is in resonance such that ωs = ωstruc, the power output at resonance Pres can be simplified as
|
Pres=ζe4ζ2tmstrucY2ωs3 |
(3) |
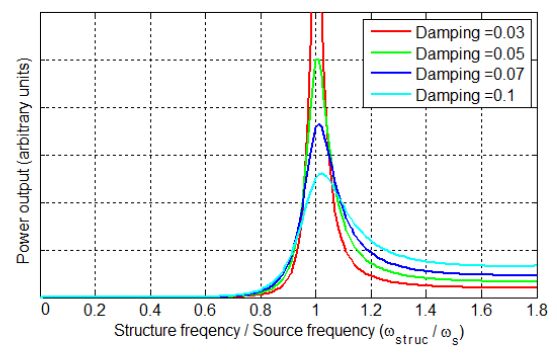
According to equation (3), when the device is vibrating in resonance, the power output is dependent on the mass of structure, the amplitude and frequency of the source vibration, and the damping characteristics of the system. As the vibration amplitude and frequency are a function of the environmental vibration source and thus not design variables, the vibrating structure and damping parameters can be optimized to maximize the power output of the energy harvesting device. Figure 2 gives the power output of the energy harvesting device with respect to the ratio of structure frequency to source frequency at various damping values for the case where the electrical damping ζe matches the mechanical damping ζm of the system (ζe = ζm). It is clear that the maximum power output can be archived when the structure frequency matches the source frequency (ωstruc = ωs). For this reason there is in general a desire for an energy harvesting device to have an adjustable resonant frequency that can be tuned to match a varying vibration source frequency to maximize the power output of the device. For a membrane-based geometry, changes in both the membrane tension and the addition of a mass on the membrane can adjust the resonant frequency of the membrane as described below.
Figure 2. Generic power output as a function of the ratio of structure frequency to source frequency for the case where the electrical damping matches the mechanical damping of the system.
In this section, the free vibration of circular membrane is discussed. Theoretical calculations performed by MATLAB and finite element simulations based on ANSYS are conducted to study the impact of the initial tension of the membrane and the geometric properties (thickness and radius) of the membrane on the fundamental frequencies of vibration of circular membrane.
By definition, membranes are always stretched in tension. In addition, here only the first fundamental mode, with maximum amplitude at the center, is considered. For a perfectly clamped homogeneous circular membrane, the resonant frequency can be written as [15]
|
fij=αij2πR√Tρtfori,j=0,1,2,3,⋯ |
(4) |
where αij is a dimensionless parameter,R is the radius of the membrane, and T,ρ, and t are the tension, density, and thickness of the membrane, respectively. Here we are most interested in the first fundamental frequency, which we assume is the target frequency for the device. For this first fundamental (0,1) mode, α01 = 2.405 [15].
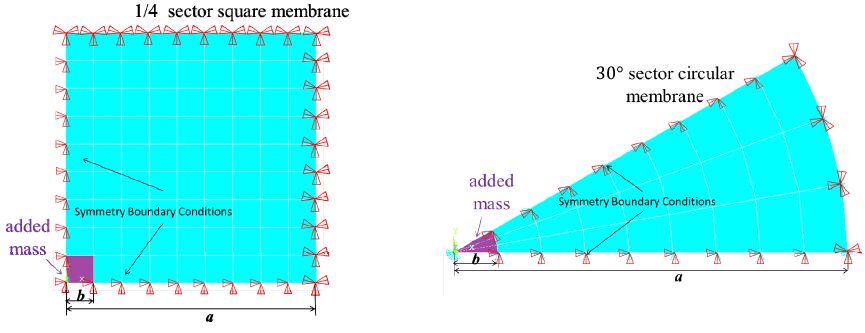
For the finite element simulation, modal analysis of the clamped circular membrane (without mass) is performed using ANSYS with Shell 41 elements. An axisymmetric model with a 30° sector with cyclic symmetry in cylinder coordinates is used (see Figure 3(right)). A static analysis is first performed to apply a desired initial tension (pre-stress) to the membrane. Specifically, the pre-stress of the membrane is induced by the method of uniform cooling, where the temperature difference ΔTtemp is calculated from ΔTtemp = T/(Eαt) [16], where T is membrane initial tension, E is the Young’s modulus of membrane, and α is the thermal expansion coefficient of membrane. Details of the parameters used in the ANSYS study are given in Table 1,where a membrane radius of 19.05 mm is used to correspond to the experimental data discussed in Section 3.4. Once the static analysis for the pre-stress has been completed in ANSYS, this result is then used as the basis for the modal analysis simulation to determine the resonant frequencies of the membrane.
Figure 3. A schematic model of membrane with central loaded mass in ANSYS: (left) square membrane, (right) circular membrane.
| Symbol | Description | Value | |
| Membrane | |||
| R | Diameter (circular) | 38.1 | mm |
| L | Side length (square) | 38.1 | mm |
| t | Thickness | 10 | μm |
| ρ | Density | 960 | kg/m3 |
| E | Young’s modulus | 1 | MPa |
| T | Initial tension | 10 | N/m |
| α | Thermal expansion coefficient | 1.8×10-4 | m/m-℃ |
| Added-mass | |||
| r | Radius | 2.1167 | mm |
| ρ | Density | 2330 | kg/m3 |
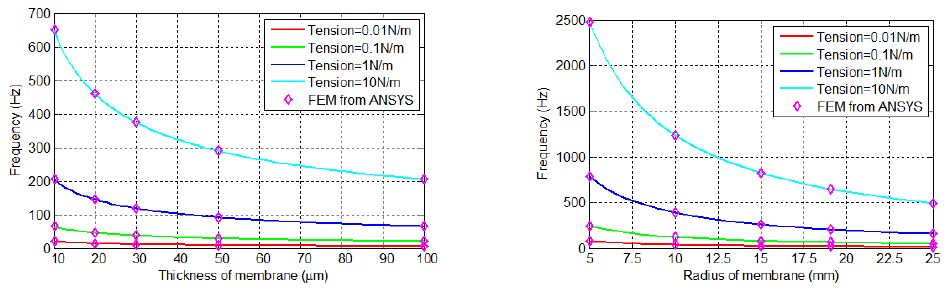
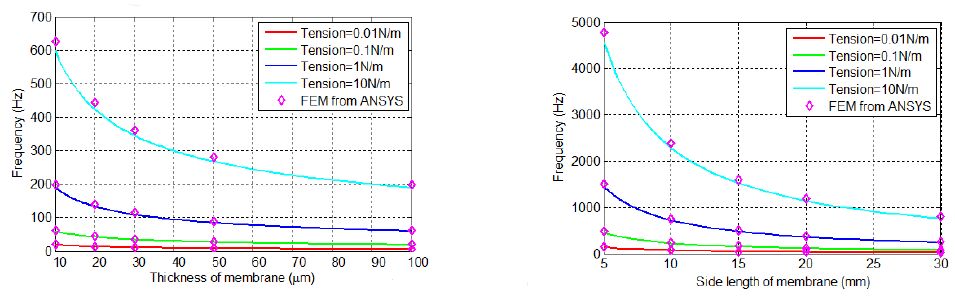
DownLoad: CSVThe theoretical calculations for the first fundamental resonant frequency of a circular membrane from Equation (4) are compared with the FEM simulation results from ANSYS in Figure 4,where the natural frequency of the membrane as a function of thickness and radius for different initial membrane tensions are shown. According to the analytical expressions in Equation (4), there are three factors that affect the resonance frequency including the initial (unloaded) membrane tension, the membrane thickness, and the radius of the membrane. Figure 4 (left) shows that the fundamental frequency of the membrane decreases with increasing thickness of membrane, while Figure 4 (right) confirms that increasing the radius of the membrane can significantly decrease the effective fundamental frequency of the membrane. Also clear from Figure 4 is that the FEM results from ANSYS (symbol) agree with the theoretical results (solid line) very well. In addition, the results from Figure 4 also indicate that a decrease in membrane tension could significantly decrease the resonant frequency of the membrane.
Figure 4. Natural frequency of membrane (without mass) for different initial membrane tension: (left) Natural frequency as a function of membrane thickness (constant membrane radius of 19.05 mm); (right) Natural frequency as a function of membrane radius (constant thickness of 10 μm).
Here the frequency response of a central mass-loaded membrane is further discussed. When an additional mass is added to the membrane, the natural frequencies of membrane could be lowered in order to target ambient vibration sources. Both theoretical calculations and simulations results from ANSYS give very similar solutions for the frequencies of the central mass-loaded membrane.
In order to lower the frequencies for the membrane geometry, it is possible to add an additional mass to the membrane. Here we assume that the added mass m is spread over a contact circle of radius b at the center of the membrane with a radius of a. Compared to the circular membrane without mass, this mechanical load (added mass) to the membrane will significantly affect its vibration behavior. The frequency of the first fundamental frequency for the membrane with central mass-loaded is given [15] as
|
f=√T2πmln(ab) |
(5) |
where the mass of the membrane M is assumed small compared to the added mass m and hence neglected. Note that in the derivation of Equation (5) b must not be significantly smaller than a, as this concentrated “point load” would result in significant stretch in the center of the membrane [15]. Based on Equation (5), three factors that affect the mass-loaded circular membrane frequency include the initial (unloaded) membrane tension, the mass of the added mass, and the radius ratio of the membrane and the added mass. Because the mass of the membrane is much smaller than the mass of the additional added mass, the added mass can have a large effect on the frequency of the mass-loaded membrane.
A finite element model using ANSYS was developed to verify the theoretical calculations shown in Equation (5). As shown in Figure 3 (right), the membrane with central loaded mass is modeled asymmetrically with an opening angle of thirty degrees and symmetric boundary conditions. The modal analysis of the clamped membrane with the additional added central mass is performed using ANSYS with Shell 41 elements. In this ANSYS model, the added mass attached to the central section of the membrane is modeled as two sets of overlapping elements. The first set of elements representing the membrane (lower layer) has its nodal plane located on the ‘top’ face, whereas the set of elements corresponding to the added mass (top layer) has its nodal plane located on the ‘bottom’ face. The combination of overlapping elements thus defines the attachment of this layered membrane with its nodal plane at the interface between the layers. The parameters of the membrane with added mass used in the model are given in Table 1. In addition, the initial tension of membrane is induced by the uniform cooling method in ANSYS as discussed in Section 3.1.
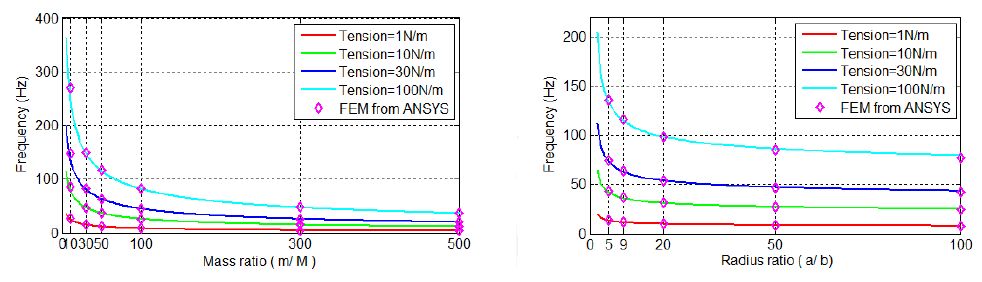
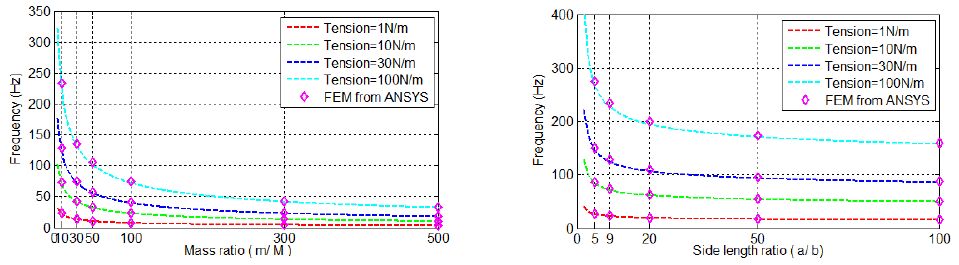
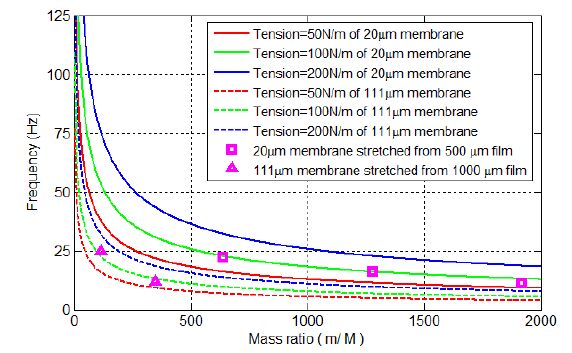
Given that the mass of the membrane is a very small compared to the added mass, the mass ratio between the membrane and the added mass will the focus in the following analysis. Figure 5 (left) shows that increasing the mass ratio (i.e. a larger centrally-loaded mass in comparison to the mass of the membrane) can significantly decrease the first natural frequency of the loaded membrane, with FEM results from ANSYS (denoted as symbols) agreeing with the theoretical results very well. This lowering of the resonant frequency is dramatic and could be potentially leveraged in the future design of energy harvesters seeking to target the lower source excitations commonly found in ambient environments. Figure 5 (right) shows that the first natural frequency of the loaded membrane decreases with the increasing of the radius ratio (i.e. a larger radius of membrane in comparison to the radius of the central load). Again, the results shown in Figure 5 indicate that lowering the membrane tension could significantly decrease the frequency of the membrane.
Figure 5. Natural frequency of membrane with centrally added mass for different initial membrane tensions: (left) Natural frequency as a function of mass ratio (constant radius ratio (a/b) of 9); (right) Natural frequency as a function of radius ratio (constant mass ratio (m/M) of 50).
Expanding upon the analysis of a circular membrane discussed above, the first fundamental frequency for a mass-loaded square membrane is further presented in this section. Similar to Equation (4), an analytical expression for the first fundamental frequency for a square membrane without added mass is shown in Equation (6) [15]. Here the first fundamental frequency of the square membrane is also a function of the square root of the tension T, membrane thickness t and density ρ, and is inversely proportional to the side length L of the square membrane. The parameters used in the model for calculations and simulations of the square membrane and its additional added mass (as will be discussed below) are shown in Table 1.
|
fsquare=√22L√Tρt |
(6) |
Two separate FEM simulations from ANSYS were performed for the cases of a square membrane with and without additional added mass, respectively, using a one-fourth model with symmetrical boundary conditions and Shell 41 elements as shown in Figure 3 (left). A comparison of the analytical frequency predictions based on Equation (6) and the ANSYS FEM simulations for the free vibration of a square membrane (with no added mass) are shown in Figure 6. It is clear that ANSYS results (symbol) agree well with theoretical results (solid line). Compared to the plot of the free vibration of the circular membrane respectively in Figure 4,the frequency of the square membrane follows the same general trend of curves as circular membrane.
Figure 6. Natural frequency of square membrane (without added mass) for different initial membrane tensions: (left) Natural frequency as a function of membrane thickness (constant membrane side length of 19.05 mm); (right) Natural frequency as a function of membrane side length (constant thickness of 10 μm).
For a square membrane subjected to a centrally loaded cubic mass, an ANSYS finite element model is developed using the same approach of two sets of overlapping elements as discussed in Section 3.2.2. The ANSYS simulation results are plotted as symbols in Figure 7,and of interest here is the fact that are very well approximated by the analytical expression for a centrally-loaded circular membrane based on Equation (5) (shown using dashed lines in the Figure 7).
Figure 7. Natural frequency of square membrane with centrally added mass for different initial membrane tension: (left) Natural frequency as a function of mass ratio (constant side length ratio (a/b) = 9); (right) Natural frequency as a function of side length ratio (constant mass ratio (m/M) of 10). Predicated calculations based on Equation 5 are shown as dashed lines.
Recall that for a centrally loaded circular membrane, according to Equation (5), only the initial (unloaded) membrane tension, the mass of added mass, and the radius ratio of the membrane can affect the frequencies. While a complete derivation of the analytical expression for a centrally-loaded square membrane is outside the scope of the current work, it appears that the factors corresponding to the effective frequency of the mass-loaded square membrane are similar to those for the circular membrane. As shown in Figure7,these results indicate that increasing the mass ratio and side length ratio (i.e. a larger centrally-loaded mass in comparison to the mass of the membrane, and a larger side length of membrane in comparison to the side length of the central load, respectively) can significantly decrease frequency of the loaded square membrane. The membrane frequency can also be decreased by lowering the membrane tension.
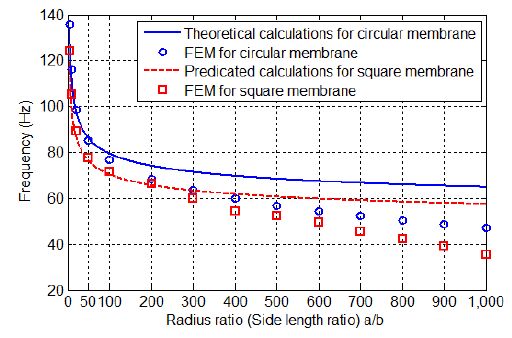
Furthermore, the effects of radius ratio for a circular membrane and side length ratio for a square membrane on the first fundamental frequency are compared in Figure 8. It shows that the first fundamental frequency of the loaded membrane (circular and square) decreases with increasing of the radius (side) ratio the membrane. When the radius (side) ratio is less than 100 (a/b ＜ 100),Figure 8 shows that the FEM simulations closely match the theoretical calculations based on Equation 5 for both the circular and the square membrane (even though Equation 5 is derived for the specific case of a circular membrane). While the derivation of the expression for the mass-loaded square membrane is outside the scope of the current work,Figure 8 suggests that ultimately the derivation will simplify to Equation 5 due to the thin-membrane assumptions that would be shared with both derivations. However, as shown in Figure 8,for values of a/b > 100, the simplified theoretical expression in Equation 5 does not capture the results from the FEM simulation for either the circular or square mass-loaded membrane and a more detailed theoretical derivation would be required.
Figure 8. Comparison of theoretical calculations and FEM simulations for the first fundamental frequencies of circular and square membranes with centrally added mass. The membrane is stretched at a constant tension of 100 N/m.
A preliminary experimental study measuring the resonant frequency of a mass-loaded circular membrane was conducted to confirm the results from the analytical and computational models described above. The membrane material used was a high performance electroactive polymer (3M VHB 4910 acrylic) [17]. Parameters described the properties of the EAP material are shown in Table 1. For the two sets of data for the experimental membranes, initial films with thicknesses of 500 µm and 1000 µm, respectively, where stretched to membrane thicknesses of 20 µm and 111 µm, respectively, via the application of an unknown initial tension.
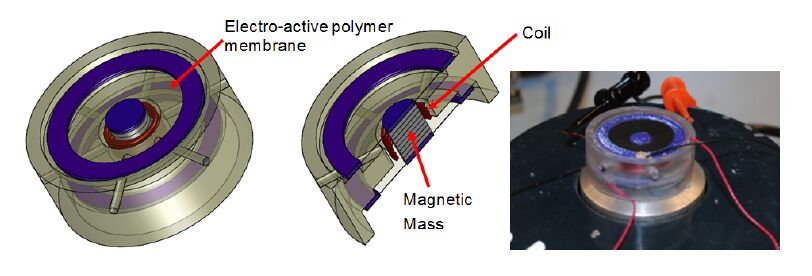
The tests to determine the resonant frequencies of the membranes were performed by mounting a prototype on a small shaker to evaluate the frequency of the mechanism as shown in Figure 9. The prototype consisted of a membrane, a central magnet/mass, and a coil fixed to the frame which is mounted on a shaker to provide a given vibration of known amplitude and frequency. The mass at the center of the membrane was varied by adding 14 gram ferrous masses to the central magnet. The resonance for the mass-membrane system was evaluated by measuring the frequency response function of the voltage induced in the coil relative to the input force measured by a dynamic load cell (PCB 208A02) mounted between the shaker and the prototype using a high impedance measurement device (NI-9215). The peak of the frequency response functions is recorded as an estimate of the resonance of the system.
Figure 9. Schematic of the resonant frequency test for a circular EAP membrane with a centrally-loaded (magnetic) mass.
Figure 10 compares the analytical predictions for the effective resonant frequency of a mass-loaded circular membrane as a function of different mass ratios using the expression provided in Equation (5) with two small sets of experimental data for an EAP membrane. For the mass loaded membranes, masses of 14,28 (only for the thinner film), and 42 g, respectively, were applied to the center of the film. A radius ratio of a/b = 9 was used for the analytical predictions. Because the applied initial tensions used to generate the membranes of the stated thickness are unknown, three representative values of membrane tension ranging from 50 to 200 N/m were used in the analytical model. As can be observed in Figure 10,the experimental data points appear to indicate that the experimental data sets are both well described using an initial (unloaded) membrane tension of 100 N/m for each sample. However, we note that previous work for EAP films has found that experimental factors such as temperature during measurement, time of purchase, storage time, and preparation and history of test samples, method of extraction of data can greatly influence the effective properties, and hence the resulting membrane tension [18,19]. In addition, the (somewhat) complicated hyperelastic constitutive models necessary to describe the EAP material behavior, particularly at these large values of stretch [20], suggest that a necessary component of future work in this area is to experimentally determine the effective membrane tension of the samples as a function of material and processing parameters.
Figure 10. Comparison of analytical predictions and experimental data for the effective first mode natural frequency of a circular mass-loaded membrane. The membrane diameters were 1.5 inches, and the membrane thicknesses were 20 µm (stretched from 500 µm film) and 111 µm (stretched from 1000 µm), respectively.
As discussed in Section 2, a typical vibration-based energy harvester achieves optimal power output only when it is vibrating at resonance. Therefore, it is desirable to tune the resonant frequency of the device to match the source environmental frequency. A comprehensive review of different strategies for tuning the frequency range of vibration-based energy harvesters to match the ambient vibration frequency or to widen the operation bandwidth of the generator has been described previously [21]. Here, an approach of resonant frequencies tuning by lowering the membrane tensions is presented.
For a membrane-based energy harvesting device (with/without added mass), the tension of the membrane could be used to tune the resonant frequency of vibrating membrane structure in order to target a particular ambient vibration source frequency. According to Equations (4) and (5), the frequencies of the unloaded and centrally-loaded membrane are proportional to the square root of the tension, which means that the square of the new effective frequency f2 is simply proportional to the membrane tension T such that
|
T0f20=Tf2=C | (7) |
where T0 and f0 are the initial membrane tension and resonant frequency, respectively, and C is a constant. For a circular membrane without an added mass, the constant C=ρt(2πR/αij ), while the constant is C=4π2m ln(a/b) for a mass-loaded circular membrane (which appears to also fit the ANSYS FEM results for a centrally-loaded square membrane as shown in Figure7). The change in membrane tension can be written as
|
ΔT=T−T0 | (8) |
Substituting Equation (8) into Equation (7), one can show that
|
ff0=√1+ΔTT0 | (9) |
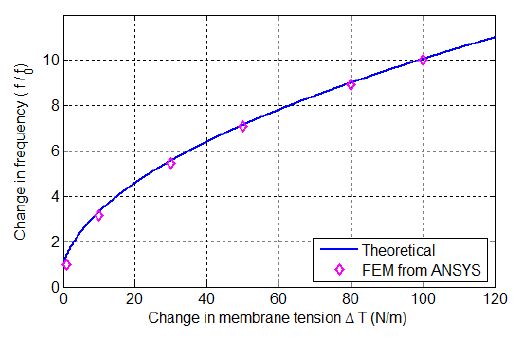
Thus from Equation (9) the ratio of the effective membrane frequency to the original frequency is a function of the change in membrane tension. This relationship is shown in Figure 11,where the theoretical calculations (Equation (9)) agree well with the FEM simulation results in ANSYS. Therefore, tuning the membrane tension could significantly alter the resonant frequency of the device, which would be useful in the development of small footprint energy harvesting devices which are able to target lower environmental source frequencies.
Figure 11. Example of membrane resonance frequency as a function of change in applied tension.
In this paper, the vibration responses of circular and square membranes with and without a centrally-loaded mass are theoretically and computationally determined. The FEM simulation is performed in ANSYS by modeling added mass and membrane as two sets of overlapping elements. The results show that the FEM results well agree with the theoretical results under the assumption that mass of the membrane is small compared to the added mass. The results indicate that increasing the mass ratio or the radius ratio can significantly decrease the effective first fundamental frequency of centrally loaded membrane. In addition, the results also show that lowering the membrane tension can effectively decrease the first resonant frequency of the loaded membrane. We note that a limitation of the proposed tuning approach is that such a technique may be difficult to practically implement while the device is in operation (i.e. adaptive, real-time tuning of the membrane resonant frequency [22]). Nonetheless, such results may find use as a means of tuning the resonant frequency of membrane-based energy harvesting devices.
The work was funded in part by the Defense Threat Reduction Agency contract # HDTRA1-11-P-0023. L.D. and F.T.F. acknowledge the fruitful conversations with Professor M.G. Prasad at Stevens Institute of Technology. The authors also acknowledge the financial support of the Innovation and Entrepreneurship Doctoral Fellowship program at Stevens.
All authors declare no conflicts of interest in this paper.
| [1] |
Beeby SP, Tudor MJ, White NM (2006) Energy harvesting vibration sources for microsystems applications. Meas Sci Technol 17: R175-R195. doi: 10.1088/0957-0233/17/12/R01
|
| [2] |
Cook-Chennault KA, Thambi N, Sastry AM (2008) Powering MEMS portable devices—a review of non-regenerative and regenerative power supply systems with special emphasis on piezoelectric energy harvesting systems. Smart Mater Struct 17: 043001. doi: 10.1088/0964-1726/17/4/043001
|
| [3] |
Dutoit NE, Wardle BL, Kim SG (2005) Design considerations for MEMS-scale piezoelectric mechanical vibration energy harvesters. Integr Ferroelectr 71: 121-160. doi: 10.1080/10584580590964574
|
| [4] | Harrop P, Das R (2010) IDTechEx Report: Energy harvesting and storage for electronic devices 2010-2020. IDTechEx. Ltda. |
| [5] |
Roundy S, Wright PK, Rabaey J (2003) A study of low level vibrations as a power source for wireless sensor nodes. Comput Commun 26: 1131-1144. doi: 10.1016/S0140-3664(02)00248-7
|
| [6] |
Scheibner D, Mehner J, Reuter D, et al. (2005) A spectral vibration detection system based on tunable micromechanical resonators. Sensor Actuat A-Phys 123-124: 63-72. doi: 10.1016/j.sna.2005.03.034
|
| [7] | Peters C, Maurath D, Schock W, et al. (2008) Novel electrically tunable mechanical resonator for energy harvesting. Proceedings of Power MEMS 2008 November 9-12, Sendai, Japan, 253-256. |
| [8] |
Leland ES, Wright PK (2006) Resonance tuning of piezoelectric vibration energy scavenging generators using compressive axial preload. Smart Mater Struct 15: 1413-1420. doi: 10.1088/0964-1726/15/5/030
|
| [9] |
Challa VR, Prasad MG, Shi Y, et al. (2008) A vibration energy harvesting device with bidirectional resonance frequency tunability. Smart Mater Struct 17: 015035. doi: 10.1088/0964-1726/17/01/015035
|
| [10] |
Zhu D, Roberts S, Tudor MJ, et al. (2010) Design and experimental characterization of a tunable vibration-based electromagnetic micro-generator. Sensor Actuat A-Phys 158: 284-293. doi: 10.1016/j.sna.2010.01.002
|
| [11] |
Rezaeisaray M, Gowini MEI, Sameoto D, et al. (2015) Wide-bandwidth piezoelectric energy harvester with polymeric structure. J Micromech Microeng 25: 015018. doi: 10.1088/0960-1317/25/1/015018
|
| [12] |
Mo C, Davidson J, Clark WW (2014) Energy harvesting with piezoelectric circular membrane under pressure loading. Smart Mater Struct 23: 045005. doi: 10.1088/0964-1726/23/4/045005
|
| [13] |
Wang W, Yang T (2012) Vibration energy harvesting using a piezoelectric circular diaphragm array. IEEE T Ultrason Ferr 59: 2022-2026. doi: 10.1109/TUFFC.2012.2422
|
| [14] |
Williams CB, Yates RB (1996) Analysis of a micro-electric generator for microsystems. Sensor Actuat A-Phys 52: 8-11. doi: 10.1016/0924-4247(96)80118-X
|
| [15] | Fletcher NH (1992) Acoustic Systems in Biology. New York: Oxford University Press, Inc, 73-82. |
| [16] | Timoshenko S, Young DH (1955) Vibration Problems in Engineering, ed. 3rd., New York, NY: D. Van Nostrand Co., Inc, 439-440. |
| [17] |
Pelrine R, Kornbluh R, Pei Q, et al. (2000) High-speed electrically actuated elastomers with strain greater than 100%. Science 287: 836-839. doi: 10.1126/science.287.5454.836
|
| [18] | Kofod G (2001) Dielectric elastomer actuators [Ph.D. Thesis] [Kongens Lyngby, Denmark]: The Technical University of Denmark. |
| [19] |
Kofod G (2008) The static actuation of dielectric elastomer actuators: How does pre-stretch improve actuation? Journal Phys D Appl Phys 41: 215405. doi: 10.1088/0022-3727/41/21/215405
|
| [20] |
Wissler M, Mazza E (2005) Modeling and simulation of dielectric elastomer actuators. Smart Mater Struct 14: 1396. doi: 10.1088/0964-1726/14/6/032
|
| [21] |
Zhu D, Tudor M J, Beeby SP (2010) Strategies for increasing the operating frequency range of vibration energy harvesters: A review. Meas Sci Technol 21: 022001. doi: 10.1088/0957-0233/21/2/022001
|
| [22] |
Challa VR, Prasad MG, Fisher FT (2011) Towards an autonomous self-tuning vibration energy harvesting device for wireless sensor network applications. Smart Mater Struct 20: 025004. doi: 10.1088/0964-1726/20/2/025004
|
| 1. | Cong Gao, Dunant Halim, Xiaosu Yi, Study of bandgap property of a bilayer membrane-type metamaterial applied on a thin plate, 2020, 184, 00207403, 105708, 10.1016/j.ijmecsci.2020.105708 | |
| 2. | Kathryn L. Dallon, Jing Yao, Dean R. Wheeler, Brian A. Mazzeo, Characterization of mechanical properties of battery electrode films from acoustic resonance measurements, 2018, 123, 0021-8979, 135102, 10.1063/1.5021809 | |
| 3. | Lin Dong, Andrew B. Closson, Congran Jin, Ian Trase, Zi Chen, John X. J. Zhang, Vibration‐Energy‐Harvesting System: Transduction Mechanisms, Frequency Tuning Techniques, and Biomechanical Applications, 2019, 4, 2365-709X, 1900177, 10.1002/admt.201900177 | |
| 4. | Lin Dong, Andrew B. Closson, Congran Jin, Yuan Nie, Andrew Cabe, Danny Escobedo, Shicheng Huang, Ian Trase, Zhe Xu, Zi Chen, Marc D. Feldman, John X. J. Zhang, Multifunctional Pacemaker Lead for Cardiac Energy Harvesting and Pressure Sensing, 2020, 9, 2192-2640, 2000053, 10.1002/adhm.202000053 | |
| 5. | Lin Dong, Michael D Grissom, Tahzib Safwat, M G Prasad, Frank T Fisher, Resonant frequency tuning of electroactive polymer membranes via an applied bias voltage, 2018, 27, 0964-1726, 114005, 10.1088/1361-665X/aacdc0 | |
| 6. | Kathryn L. Dallon, Jing Yao, Dean R. Wheeler, Brian A. Mazzeo, 2018, 1949, 0094-243X, 140009, 10.1063/1.5031614 | |
| 7. | Nibir K. Dhar, Achyut K. Dutta, Lin Dong, Michael Grissom, Frank T. Fisher, 2016, 9865, 0277786X, 98650J, 10.1117/12.2229294 | |
| 8. | Andrei L. Kholkin, Andrei D. Ushakov, Maria A. Chuvakova, Mikhail S. Kosobokov, Andrey R. Akhmatkhanov, Andrei V. Turutin, Maxim V. Chichkov, Ivan I. Kravchenko, Yakov Kopelevich, Vladimir Ya. Shur, Piezoelectric Actuation of Graphene-Coated Polar Structures, 2020, 67, 0885-3010, 2142, 10.1109/TUFFC.2020.2998976 | |
| 9. | Lin Dong, Michael D. Grissom, M.G. Prasad, Frank T. Fisher, Application of mechanical stretch to tune the resonance frequency of hyperelastic membrane-based energy harvesters, 2016, 252, 09244247, 165, 10.1016/j.sna.2016.10.034 | |
| 10. | Lin Dong, Congran Jin, Andrew B. Closson, Ian Trase, Haley C. Richards, Zi Chen, John X.J. Zhang, Cardiac energy harvesting and sensing based on piezoelectric and triboelectric designs, 2020, 76, 22112855, 105076, 10.1016/j.nanoen.2020.105076 | |
| 11. | Sun Hwa Kwon, Lin Dong, Flexible sensors and machine learning for heart monitoring, 2022, 102, 22112855, 107632, 10.1016/j.nanoen.2022.107632 | |
| 12. | Lucas Y.M. Sampaio, Pedro C.M. Cerântola, Leopoldo P.R. de Oliveira, Lightweight decorated membranes as an aesthetic solution for sound insulation panels, 2022, 532, 0022460X, 116971, 10.1016/j.jsv.2022.116971 | |
| 13. | Linshi Guo, Wei Zhao, Jingchao Guan, Nobuyuki Gomi, Xilu Zhao, Horizontal Bi-Stable Vibration Energy Harvesting Using Electromagnetic Induction and Power Generation Efficiency Improvement via Stochastic Resonance, 2022, 10, 2075-1702, 899, 10.3390/machines10100899 | |
| 14. | Jin Soo Park, Keun Young Huh, Min-Seok Kim, Soo Young Jung, Jung Ho Park, Soo Jin Kim, Ho Won Jang, Kyeong Seob Hwang, Hong Nam Kim, Tae Geun Kim, Seung-Hyub Baek, Byung Chul Lee, A relaxor-ferroelectric PMN-PZT thin-film-based drop-on-demand printhead for bioprinting applications with high piezoelectricity and low heat dissipation, 2024, 417, 09254005, 136194, 10.1016/j.snb.2024.136194 | |
| 15. | Dajun Zhang, Akhil Polamarasetty, Muhammad Osama Shahid, Bhuvana Krishnaswamy, Chu Ma, Metamaterial-based passive analog processor for wireless vibration sensing, 2024, 3, 2731-3395, 10.1038/s44172-024-00190-8 | |
| 16. | Yuxiao Wang, Mengdie Sun, Sun Hwa Kwon, Lin Dong, Advancements in flexible biomechanical energy harvesting for smart health applications, 2025, 1359-7345, 10.1039/D4CC05917D |
Figures(11)
Lin Dong, Michael Grissom, Frank T. Fisher. Resonant frequency of mass-loaded membranes for vibration energy harvesting applications[J]. AIMS Energy, 2015, 3(3): 344-359. doi: 10.3934/energy.2015.3.344
| Symbol | Description | Value | |
| Membrane | |||
| R | Diameter (circular) | 38.1 | mm |
| L | Side length (square) | 38.1 | mm |
| t | Thickness | 10 | μm |
| ρ | Density | 960 | kg/m3 |
| E | Young’s modulus | 1 | MPa |
| T | Initial tension | 10 | N/m |
| α | Thermal expansion coefficient | 1.8×10-4 | m/m-℃ |
| Added-mass | |||
| r | Radius | 2.1167 | mm |
| ρ | Density | 2330 | kg/m3 |
DownLoad: CSV
