Oil extraction from plant seeds for biodiesel production

1.   Introduction

Wentzell boundary conditions arise in applications in which diffusion or thermal/electrical energy transfer processes on boundaries or interfaces have to be taken into account. This is the case, for example, in coupled bulk-surface problems ^[2,12,15], in the scattering of electromagnetic waves by conductors coated with a thin layer of dielectric material ^[7,13] or in the modeling of heat transfer within a conducting solid whose boundary has the capacity to store heat ^[16,30]. Unlike the common boundary conditions, such as the Dirichlet, Neumann or Robin conditions, which involve only first-order spatial derivatives, Wentzell boundary conditions can involve higher-order derivatives ^{[9,15,20,30,32]}. The present paper deals with the heat equation

with the initial value

Dirichlet boundary condition

and nonlocal Wentzell-Neumann boundary condition

with $T > 0$, $\Omega = (0, 1)$ and $\Omega_T = \Omega \times (0, T]$, and given functions $f$ and $\phi$ in $\overline\Omega_{T}.$ Wentzell boundary conditions appear in heat transfer and multidimensional diffusion processes ^[1,31], and in multidimensional wave dissipative equations ^[26]. Also, they appear in the form of generalized impedance boundary conditions in electromagnetic scattering problems ^[7,13]. We note in passing that, since Eq (1.4) involves distinct points in the domain, the boundary condition is nonlocal in nature. This contrast with the existing literature on Wentzell boundary conditions, which mainly deals with a local version of Eq (1.4) and is often related to unidirectional "heat waves" traveling to the region ^[16,29,30]; of course, however, the physics involved there is not always simple to interpret. Nevertheless, as pointed out in [11, pp. 79], in the diffusion of chemicals, the term $u_x(0, t)/\alpha$ represents the diffusive transport of materials to the boundary, so Eq (1.4) can be regarded as a nonlocal boundary reaction. The boundary conditions given by Eqs (1.3) and (1.4) are also considered in ^[21], where the reconstruction problem of the lowest term of a parabolic equation is studied. Similar problems with standard nonlocal boundary conditions can be found in ^[9,24,25,33].

It is worth noting that, if Eq (1.1) holds at $x = 1$, the boundary condition Eq (1.4) can be rewritten as

When the functions $r(t)$ and $f(x, t)$ are given, the problem of finding $u(x, t)$ satisfying the heat equation given by Eq (1.1), initial condition given by Eq (1.2) and boundary conditions given by Eqs (1.3) and (1.4) is referred to as the direct (or forward) problem. The existence and uniqueness of classical solutions of this direct problem have been established in ^[23] by using the generalized Fourier method. On the other hand, when the function $r(t)$ for $t\in[0, T]$ is unknown, we face an inverse problem which looks for a pair of functions $\{r(t), u(x, t)\}$ satisfying Eqs (1.1)–(1.4) and the overdetermination condition

where $E(t)$ is a given function that represents the mass or energy measurement; in diffusion problems, for instance, $E(t)$ specifies the mass of the entire diffusion domain ^[5,11].

Under smoothness and suitable compatibility conditions for function $f$, initial condition $\varphi$ and energy $E$, the existence and uniqueness of classical solutions for this inverse problem follow from [23, Theorem 1]. However, because in practice, $E(t)$ is often contaminated by noise, the identification of $r(t)$ demands regularization ^[14,19,23]. Physical motivations for finding a source in the heat equation, as subject to condition (1.6) can be found in ^{[10,11,23,28]}; for example, assume that an external energy is supplied to a target at a controlled level via microwave-generating equipment; however, the dielectric constant of the target material varies in space and time, resulting in the spatially heterogeneous conversion of electromagnetic energy to heat. This can correspond to a source term $r(t)f (x, t)$, where $r(t)$ is proportional to the power of the external energy source and $f(x, t)$ is the local conversion rate of microwave energy. If $u(x, t)$ denotes the concentration of absorbed energy, then its integral $E(t)$ over the entire volume of material determines the time dependent absorbed energy.

The source recovering problem for parabolic equations subject to condition (1.6) has attracted the attention of several authors in recent years. The case of local nonlinear Wentzell boundary conditions is addressed in ^[31], where the authors deal with the identification of a time-dependent function $h(t)$ in a source term modeled in the form $h(t)f(x)$; in this case, the well-posedness of the problem is established by means of variational techniques and a numerical scheme based on Rothe's method for the noise free data is designed. In ^[22], a one-dimensional heat equation subject to standard nonlocal boundary conditions is considered, and a numerical method is proposed based on the Crank-Nicolson finite-difference scheme combined with an iterative method. A similar problem under local Wentzell boundary conditions is addressed in ^[19], where the well-posedness of the identification problem is based on a spectral analysis of eigenvalue problems in which spectral parameter is also in the boundary conditions; the problem is numerically addressed by using the boundary element method combined with Tikhonov regularization. Regarding the Dirichlet boundary conditions, the well-posedness of the problem is discussed in ^[10,28] by considering spatial or time-dependent source terms.

In this work, we revisit and improve previous results on the existence and uniqueness of the solution of the inverse source problem reported in ^[23]; then, we introduce a numerical method for recovering the pair $\{r(t), u(x, t)\}$ by using as input data the model parameters $f$, $\varphi$ and $\alpha$, together with energy values satisfying the overdetermination condition given by Eq (1.6) and Eqs (1.1)–(1.4). So, in a sense, this paper fulfills what was promised in ^[23]. For this, we first introduce a semi-discrete model obtained via the spatial semi-discretization of the continuous model; then, we show that the source term solves a Volterra integral equation of the first kind involving the time variable only. In addition, unlike the discretization schemes and matrices used by all methods mentioned above, a reconstruction method that regularizes a triangular linear system is proposed, where a time-marching implicit midpoint method is used as a solver of the semi-discrete model. More specifically, to build stable reconstructions of the source term, we use the generalized singular value decomposition (GSVD) of an appropriate matrix pair, along with proper truncation regularization techniques. Precisely, we consider three truncation parameter selection criteria, namely, the Morozov's discrepancy principle (DP) ^[17], the minimum product rule (MPR) ^[4] and the generalized cross-validation (GCV) ^[17]. The proposed method is illustrated through some numerical examples.

The paper is organized as follows. Section 2 is devoted to the theoretical foundations of the problem, and we briefly discuss the well-posedness of classical solutions for the aforementioned inverse source reconstruction problem. Section 3 describes a semi-discrete model for the problem given by Eqs (1.1)–(1.4), together with a spectral analysis that shows the connection between eigenpairs of the semi-discrete model and eigenpairs of the continuous model. A surrogate model for source reconstruction, as well as our practical reconstruction method, is derived and stated in Section 4. In Section 5, we present some numerical experiments to illustrate the efficiency of the method. Finally, Section 6 ends the paper with concluding remarks and future work plans.

2.   Theoretical foundation

Model problems involving a time-dependent source function and homogeneous linear boundary conditions can be solved by employing the method of separation of variables using the eigenpairs of a proper spectral problem. The auxiliary spectral problem for Eqs (1.1)–(1.4) is given by ^[23]

Clearly, as this is a non self-adjoint spectral problem, which results from requiring the solution $u(x, t)$ to satisfy the the non-standard boundary conditions given by Eqs (1.3) and (1.4), the standard Fourier expansion method cannot be used to solve Eqs (1.1)–(1.4). In fact, in this case, the key tool is a more general concept of basis, i.e., the so-called Riesz basis, which allows us to employ the generalized Fourier expansion method, where the solution is expressed in terms of eigenvalues and eigenfunctions of the auxiliary spectral problem. It is readily seen that the eigenvalues $\lambda$ of Eq (2.1) are roots of the nonlinear equation

Regarding the roots, it is known that there are infinitely many positive real roots, and that there can also be a finite number of complex solutions, the number of which depends on $\alpha$ ^[23,27]. Furthermore, although not mentioned explicitly in ^[23,27], we emphasize that, if $\alpha\ne \dfrac{1}{x_j\sin(x_j)}$, where $x_j$ is any positive root of $\sin(x)+x\cos(x) = 0$, then all eigenvalues $\lambda$ are simple; this is because, if $\alpha = 1/x_j\sin(x_j)$ for some $j$, both equations, $\alpha x\sin(x) = 1$ and $\sin(x)+x\cos(x) = 0$, will share the same root $x_j$, in which case $\lambda$ is at least a double eigenvalue.

Assign a zero index to any of the complex eigenvalues and list the remaining eigenvalues in ascending order of $Re(\sqrt{\lambda})$, that is, let $\lambda_n$ be numbered so that $\lambda_n$ is complex for $n = 0, 1, \dots, n_\alpha$, while, for $n > n_{\alpha}$, $\lambda_n$ is real. The asymptotic estimate for the eigenvalues given by

is valid for large $n$ ^[27]. It is straightforward to see that the eigenfunction associated with eigenvalue $\lambda_n$, $n = 0, 1, 2, \ldots$, is given by

In addition, as shown in ^[27], the system of eigenfunctions $X_{n}(x),$ $n = 1, 2, ..$, that is, the system of eigenfunctions of problem (2.1), with one of them deleted, is a Riesz basis in $L_2[0, 1]$, and the system

is bi-orthogonal to the system $X_{n}(x),$ $n = 1, 2, ...$.

Definition 2.1. The class of functions denoted by

is called a class of admissible data.

Note that, in the present paper, the class of admissible data requires less stringent conditions than the class of admissible data introduced in ^[23], and it includes a wide class of functions. Indeed, all $C_0^\infty (\Omega)$-functions that belong to the orthogonal complement of the subspace

in $L_2[0, 1]$ are members of $\mathcal{F}^{3}\left[ 0, 1\right]$. Of course, for any given $w\in C_0^\infty (\Omega)$ such that

it is clear that $w\in S_0^{\perp}$ and $w\in \mathcal{F}^{3}\left[ 0, 1\right]$. On the other hand, if $w\in C_0^\infty (\Omega)$ but $w\notin S_0^{\perp}$, let $g = w(c-w)$, where $c = \dfrac{\left(w^2, \sin \left(\sqrt{\lambda _{0}}(x-1)\right)\right)}{\left(w, \sin \left(\sqrt{\lambda _{0}}(x-1)\right)\right)}$. It is readily seen that $g$ and all of its derivatives vanish at $x = 0$ and $x = 1$; thus, $g\in S_0^\perp$, that is, $g\in \mathcal{F}^{3}\left[ 0, 1\right]$.

The pair $\{r(t), u(x, t)\}$ from the class $C[0, T]\times (C^{2, 1}(\Omega_{T})\cap C^{2, 0}(\overline{\Omega}_{T}))$, for which the conditions given by Eqs (1.1)–(1.4) and (1.6) are satisfied, is called a classical solution of the inverse problem defined by Eqs (1.1)–(1.4), (1.6).

The lemma below establishes conditions under which a Fourier series expansion of a continuous function on $[0, 1]$ in terms of the system $X_n$, $n = 1, 2, \dots,$ is uniformly convergent.

Lemma 2.1. ^[23] Suppose that $\varphi\in C[0, 1]$ has a uniformly convergent Fourier series expansion in the system $\sin(\pi nx), n = 1, 2, \dots,$ on the interval $[0, 1]$. Then, this function can be expanded in a Fourier series in the system $X_n(x), \; n = 0, 1, 2, \dots$ and this expansion is uniformly convergent on $[0, 1]$ if $(\varphi, \sin(\lambda_0(1-x)) = 0$. Moreover, if $\varphi \in \mathcal{F}^{3}\left[ 0, 1\right]$, then the inequality

holds, where $\varphi _{n} = \left(\varphi, Y_{n}\right)$.

The matter about the existence and uniqueness of the solution of the inverse problem under study is established in the following theorem.

Theorem 2.1. (Existence and uniqueness) Let the following conditions be satisfied:

1. $E(t)\in C^{1}\left[ 0, T\right]$;

2. $\varphi (x)\in \mathcal{F} ^{3}\left[ 0, 1\right]$ and $E(0) = \int\limits_{0}^{1}\varphi (x)dx;$

3. $f(x, t)\in C\left(\overline{\Omega}_{T}\right)$ and $f(x, t)\in \mathcal{F} ^{3}\left[ 0, 1\right]$, $\int\limits_{0}^{1}f(x, t)dx\neq 0,$ $\forall t\in \left[ 0, T\right].$

Then, the inverse source problem defined by Eqs (1.1)–(1.4) and (1.6) has a unique classical solution $\{r(t), u(x, t)\}\in C[0, T]\times (C^{2, 1}(\Omega_{T})\cap C^{2, 0}(\overline{\Omega} _{T}))$. Moreover, $u(x, t)\in C^{2, 1}(\overline{\Omega}_{T})$.

Analogous results were established in ^[23] under the stronger assumption that

In essence, such an assumption ensures that the contribution of complex valued eigenfunctions to the solution is neglected. Here, in view of definition of $\mathcal{F}^3 [0, 1]$ and conditions 1, 2 and 3 from Theorem 2.1 above, the only orthogonality condition we require is that $(\varphi(x), \sin{(\sqrt{\lambda_0}(1-x))}) = (f(x, t), \sin{(\sqrt{\lambda_0}(1-x))}) = 0$. This is explained as follows. From ^[23], the solution $u(x, t)$ of the forward problem defined by Eqs (1.1)–(1.4) can be expressed as

where $n_{\alpha }$ is the number of complex eigenvalues, and $u_{n}(t) = \varphi _{n}e^{-\lambda _{n}t}+\int_{0}^{t}r(\tau)f_{n}(\tau)e^{-\lambda _{n}(t-\tau)}d\tau$, with

and

Now because the majorizing series

and

are convergent (by Lemma 2.1), the series given by Eq (2.5), their $t$-partial derivative and the $xx$-second-order partial derivative are uniformly convergent. Then, $u(x, t)\in C^{2, 1}(\Omega_{T})\cap C^{1, 0}(\overline{\Omega}_{T})$, and it satisfies the conditions given by Eqs (1.1)–(1.4). In ^[23], the assumption given Eq (2.4) was used to ensure that $u(x, t)$ is a real-valued function. However, such an assumption is not needed. Indeed, as $\alpha$ is supposed to be real, if $\lambda\in \mathbb{C}$ is an eigenvalue of Eq (2.1), then $\overline{\lambda}$ is also an eigenvalue with a corresponding eigenfunction given by $\sqrt{2}\sin({\overline{\sqrt{\lambda}}x})$. This means that $n_\alpha$ is odd and the complex eigenvalues are ordered as follows:

The corresponding eigenfunctions that are members of the Riesz basis are given by $X_1(x) = \sqrt{2}\sin(\overline{\sqrt{\lambda_0}} x)$, $X_2(x) = \sqrt{2}\sin(\sqrt{\lambda_2} x)$, $X_3(x) = \sqrt{2}\sin(\overline{\sqrt{\lambda_2}} x) , \ldots, X_{n_\alpha-1}(x) = \sqrt{2}\sin(\sqrt{\lambda_{n_\alpha-1}}\; x)$ and $X_{n_\alpha}(x) = \sqrt{2}\sin(\overline{\sqrt{\lambda_{n_\alpha-1}}}\; x)$ (recall that $X_0$ was deleted). Because $\varphi$ is real-valued and belongs to $\mathcal{F}^3[0, 1]$, it is clear that $(\varphi, \sin{(\overline{\sqrt{\lambda_0}}(1-x))}) = 0$ so that, taking into account Eq (2.3), it holds that $\varphi_1 = (\varphi, Y_1) = 0$; also, as it is readily seen, we have that $(\varphi, Y_{n+1}) = (\varphi, \overline{Y_n})$, $n = 2, \ldots, n_\alpha-1$. Consequently, the term $\sum\limits_{n = 1}^{n_{\alpha }}\varphi _{n}e^{-\lambda _{n}t}X_{n}(x)$ in Eq (2.5) comprises $(n_\alpha-1)/2$ sums of the form

which, clearly, is a real-valued expression. Since $r(t)$ and $f(x, t)$ are also supposed to be real-valued, we can argue analogously to conclude that the sum

is also real-valued. Hence, $u(x, t)$ is a real-valued function.

Equations (1.6) and (2.5) yield the following Volterra integral equation with respect to $r(t)$:

where

Alternatively, upon time differentiation of Eq (2.6) we have

By using Lemma 2.1, the functions $F^{\prime }(t)$ and $E^{\prime }(t)$ and kernel $K_{t}(t, \tau)$ are continuous functions in $[0, T]$ and $[0, T]\times \lbrack 0, T]$, respectively. We therefore obtain a unique function $r(t)$, continuous on $[0, T]$, which, together with the solution of the problem defined by Eqs (1.1)–(1.4) given by the Fourier series expressed as Eq (2.5), form the unique solution of the inverse problem. Evidently, because $(u(x, t), r(t))$ satisfies Eq (1.1) and $u(x, t)$ and $f(x, t)$ are real-valued, the resulting $r(t)$ is real-valued.

We emphasize that finding examples where the solution of the inverse problem, $(u(x, t), r(t))$, is given explicitly, with $\varphi(x)$, $f(x, t)$ and $E(t)$ satisfying the assumptions of Theorem 2.1, is a difficult task. However, since conditions 1, 2 and 3 of Theorem 2.1 are just enough to guarantee the existence of a solution to the inverse problem, there are cases in which such a solution exists, even for data that do not meet these conditions, as we will see later.

The following result on the continuous dependence on the data of the solution of the inverse problem holds.

Theorem 2.2. ^[23] (Continuous dependence upon the data) Let $\digamma$ be the class of triples in the form of $\{f,$ $\varphi,$ $E\}$ which satisfy the assumptions of Theorem 2.1 and

for some positive constants $M_{i},$ $i=0,$ $1,$ $2,$ $3$. Then, the solution pair $\left(u, r\right)$ of the inverse problem defined by Eqs (1.1)–(1.4) and (1.6) depends continuously upon the data in $\digamma$.

3.   Semi-discrete model

For simplicity, let us derive a semi-discrete heat model, which we obtain by discretizing the spatial derivative at equally spaced points $x_k = kh, \; k = 0, \dots, m,$ with $h = 1/m$. We are going to build approximations for the solution of the problem defined by Eqs (1.1)–(1.4) at the points $x_k$, $k = 1, \ldots, m-1$, based on finite differences and a collocation method. In fact, the key observation here is that, if $u(x, t)$ denotes the exact solution of the continuous model, then the relation

holds at the grid points $x_k, \; k = 1, \dots, m-1$. In addition, it is clear that, if the spatial derivative is approximated by centered finite differences, the approximate relation

is still valid. This leads to a search for an approximation $v_k(t)$ of $u(x_k, t)$ by neglecting the approximation errors associated with Eq (3.2) in such a way that $v_k(t)$ is enforced to solve the following system of ordinary differential equations:

where $v_0$ is taken to be identically zero because of the boundary condition given by Eq (1.3), and where we have taken into account the boundary condition given by Eq (1.5) to derive the last equation. More precisely, the last equation is obtained by using a forward finite difference to approximate $u_x(0, t)$. Further, for the approximate solution to satisfy the initial condition given by Eq (1.2) we take

The system defined by Eqs (3.3) and (3.4), together with the initial condition given by Eq (3.5), can now be written as follows:

where

and

It is known that the numerical stability of numerical solutions of the initial value problem given by Eq (3.6) depends on the eigenvalues of the system matrix $A$. This encourages the eigenvalue analysis described below.

If $\{\lambda, {\boldsymbol{v}}\}$ is an eigenpair of $A$, we look for eigenvectors in the form

where $a$ is a constant to be determined and constrained to $ah\ne \pi$ (otherwise, ${\boldsymbol{v}} = {\boldsymbol{0}}$). For this, we first note that the matrix-eigenvector product $A{\boldsymbol{v}}$,

has entries given by

where the first $m-1$ entries can be obtained by using trigonometric identities. The last equation, together with the fact that $A{\boldsymbol{v}} = \lambda {\boldsymbol{v}}$, show that all eigenvalues of $A$ are of the form

with $a$ satisfying

Note that

results in the equation

the roots of which are shown to provide the eigenvalues of the continuous eigenvalue problem given by Eq (2.2).

The main conclusions of the above analysis are summarized in the following theorem.

Theorem 3.1. The eigenpairs $\{\lambda, {\boldsymbol{v}}\}$ of the system matrix of the semi-discrete model expressed as Eq (3.6) are given by

where $a$ is a root of the nonlinear equation

Further, as $h\rightarrow 0$, we have that $\lambda\rightarrow -a^2.$

Proof. It is enough to say that the last assertion of the theorem follows from taking the limit as $h\rightarrow 0$ to $\lambda$ in Eq (3.11). ■

To understand more about the eigenvalues $\lambda$, for ease of analysis, we will allow the value $a$ to vary continuously and replace it for $x$. With this notation, if

then the nonlinear equation given as Eq (3.10) can be rewritten in a more convenient form:

It is apparent that, depending on the constant $\alpha$, all roots of this equation can be complex, all roots can be real or there can even be just a few complex conjugate roots. The main result of the section provides conditions under which all roots of Eq (3.14) are distinct and real.

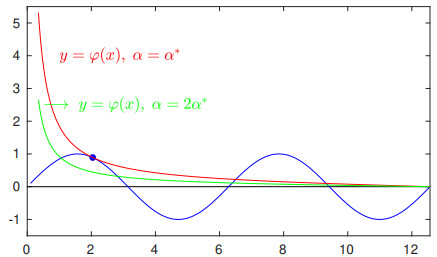
Theorem 3.2. Suppose that the curves defined by $y = \varphi_{\alpha}(x)$ and $y = sin(x)$ are denoted by $C_1$ and $C_2$, respectively; there exists a pair of positive numbers $\{x^*, \alpha^*\}$ such that $C_1$ and $C_2$ have the same tangent line at $x = x^*$ when $\alpha = \alpha^*$. In addition, provided that $\alpha > \alpha^*$, all eigenvalues of the system matrix $A$ are real and distinct.

Proof. First, we note that

Also, from elementary properties of limits, it is not difficult to see that

Consequently, $\varphi_\alpha$ is positive, decreasing, convex and bounded above. In order to proceed, if $C_1$ and $C_2$ share the same tangent line at some point $x$, then $\varphi'(x) = \cos(x)$, which implies that

But, since both curves contain the point of tangency, then we must have

and a simple manipulation of Eqs (3.17) and (3.18) gives

Now, to simplify the exposition, we restrict ourselves to $0 < x < \pi$. In fact, as it is apparent that the left-hand side of the above equation changes sign in the interval $[\dfrac {\pi}{2}, \pi]$, there will be at least one real root. Therefore, if $C_1$ and $C_2$ share the same tangent line at $(x^*, y^*)$, then $x^*$ has to be a root of the nonlinear equation given as Eq (3.19) and, consequently, of Eqs (3.17) and (3.18). From this fact, by substituting $x = x^*$ in Eq (3.18) and isolating the $\alpha$ parameter, we obtain

With this choice of $\alpha$, it is immediate to check that $\varphi_{\alpha^*}(x^*) = \sin(x^*)$ and $\varphi_{\alpha^*}'(x^*) = \cos(x^*)$. Therefore, $x^*$ is actually a root of both Eqs (3.17) and (3.18); that is, $x^*$ is a double root of Eq (3.14). Moreover, if $\xi(x) = \varphi_{\alpha^*}(x)-\sin(x),$ based on Eq (3.15), because $\xi''(x^*) > 0$, we conclude that $x^*$ cannot be a triple root. This ends the proof of the first part of our theorem.

To end the proof, now suppose that the parameter $\alpha$ is chosen such that $\alpha = \rho \alpha^*$ with $\rho > 1$. In this case, we have

Hence, if we restrict ourselves to the interval $[0, 2\pi]$, because $\varphi_{\alpha}(x)$ is decreasing, $C_1$ passes below the point of tangency $(x^*, y^*)$ with $y^* = \sin(x^*)$, producing two intersection points, as seen in Figure 1. The abscissas of the intersection points are obviously roots of Eq (3.13). As in $[0, m\pi]$, the same event occurs $m-1$ times if $m$ is even; we conclude that the nonlinear equation given as Eq (3.18) admits $m$ distinct roots, which give $m$ distinct eigenvalues of the system matrix $A$. A similar conclusion can be drawn if $m$ is odd. This ends the proof. ■

Remark 3.1. In practice, the root $x^*$ is not known in advance and the condition $\alpha > \alpha^*$ may not be simple to achieve. In that case, the simplest choice of $\alpha$ to guarantee that all eigenvalues of $A$ are distinct may be $\alpha > 2/\pi$. This conclusion follows from Eq (3.16).

4.   Surrogate model for source reconstruction

From elementary theory of ordinary differential equations it follows that the unique solution of the initial value problem given by Eq (3.6) can be expressed as

In our case, this is easy to calculate because, thanks to Theorem 3.2, with a proper $\alpha$, the system matrix $A$ is diagonalizable. Let $\alpha$ be chosen as in Theorem 3.2, and let $A = {\boldsymbol{V}}{\boldsymbol{\Lambda}}{\boldsymbol{V}}^{-1}$ with

Based on the eigenpairs of $A$, the solution can be expressed as

or, even with the left eigenvectors of $A$ being denoted by ${\boldsymbol{y}}_j$, that is,

where $e_j$ stands for the $j$-th canonical vector in $\mathbb{R}^m$, with ${\boldsymbol{g}}(t) = {\boldsymbol{V}}^{-1}\sf{f}(\tau)$ and

the solution can be rewritten as

which looks essentially the same as Eq (2.5). Now, proceeding in the same way as we did for the infinite series expression of $u(x, t)$, if the energy $E(t)$ is approximated by using a quadrature rule with weights ${\boldsymbol{\omega}}_k$ and points $x_k$, i.e.,

where ${\boldsymbol{\omega}}$ is the vector of weights, neglecting approximation errors the energy function can be expressed as

or even as a Volterra integral equation:

where

In a sense, Eq (4.5) can be thought of as a discrete version of the Volterra equation given by Eq (2.6) for the unknown continuous function $r(t)$; hence, it can be used as a surrogate model for source reconstruction. In fact, through the numerical integration of Eq (4.5) with time spacing $\Delta t$, it is easy to show that the above equation can be transformed into a triangular system of linear equations with unknowns $r_i$.

4.1.   Implicit midpoint rule

As an alternative to the use of the above surrogate model for source reconstruction, we propose the numerical integration of the semi-discrete model given by Eq (3.6) so as to avoid eigenvalue computations followed by the construction of another linear system from which the source term is recovered. To this end, notice that, among a number of possibilities for the numerical solution of the general evolution initial value problem

on the mesh points $t_j$, $j\ge 0$, with timestep $\Delta t$ such that $t_{j+1} = t_j+\Delta t$, $t_{j+1/2} = t_j+\dfrac{1}{2}\Delta t$, we consider the midpoint method

This method is an implicit second-order, absolutely stable, time stepping method that is frequently used to solve evolutive conservative systems of partial differential equations ^[8].

Applying Eq (4.7) to the semi-discrete problem given by Eq (3.6), after a rearrangement, successive approximation ${\sf v}_{j}$ and ${\sf v}_{j+1}$ satisfy

where

Obviously, as all eigenvalues of matrix $A$ are negative, matrix $B$ is nonsingular. Then, an expression for ${\sf v}_{j+1}$ reads as

We now build up an expression for ${\sf v}_{m}$ iteratively:

${\sf v}_{1} \;\;\;\;\; = \;\;\;\;\; G {\sf v}_0 + \Delta t\, {\widehat r}_0 B^{-1}\, \widehat{\sf f}_{0},$

${\sf v}_{2} \;\;\;\;\; = \;\;\;\;\; G {\sf v}_1 + \Delta t\, {\widehat r}_1 B^{-1}\, \widehat{\sf f}_{1}, = G^2{\sf v}_0+\Delta t\, {\widehat r}_0 G B^{-1}\, \widehat{\sf f}_{0} + \Delta t\, {\widehat r}_1 B^{-1}\, \widehat{\sf f}_{1},$

${\sf v}_{3} \;\;\;\;\; = \;\;\;\;\; G {\sf v}_2 + \Delta t\, {\widehat r}_2 B^{-1}\, \widehat{\sf f}_2 = G^3{\sf v}_0+\Delta t\, {\widehat r}_0 G^2 B^{-1}\, \widehat{\sf f}_{0} + \Delta t\, {\widehat r}_1 GB^{-1}\, \widehat{\sf f}_{1} + \Delta t\, {\widehat r}_2 B^{-1}\, \widehat{\sf f}_2,$

$\;\;\;\;\; \vdots \;\;\;\;\;$

${\sf v}_m \;\;\;\;\; = \;\;\;\;\; G^m{\sf v}_0+ \Delta t\, {\widehat r}_0 G^{m-1} B^{-1}\, \widehat{\sf f}_{0} + \Delta t\, {\widehat r}_1 G^{m-2}B^{-1}\widehat{\sf f}_{1} + \cdots+ \Delta t\, {\widehat r}_{m-1} B^{-1}\, \widehat{\sf f}_{m-1}$.

If we use Eq (4.3) to compute approximations of energy values $E(t_k)$, neglecting the approximation errors, the set of above relationships respectively yields

$E_{1} = {\boldsymbol{\omega}}^T G {\sf v}_0 + \Delta t\, {\widehat r}_0 {\boldsymbol{\omega}}^TB^{-1}\, \widehat{\sf f}_{0},$

$E_{2} = {\boldsymbol{\omega}}^TG^2{\sf v}_0+\Delta t\, {\widehat r}_0 {\boldsymbol{\omega}}^TG B^{-1}\, \widehat{\sf f}_{0} + \Delta t\, {\widehat r}_1 {\boldsymbol{\omega}}^T B^{-1}\, \widehat{\sf f}_{1},$

$E_{3} = {\boldsymbol{\omega}}^TG^3{\sf v}_0+\Delta t\, {\widehat r}_0 {\boldsymbol{\omega}}^TG^2 B^{-1}\, \widehat{\sf f}_{0} + \Delta t\, {\widehat r}_1 {\boldsymbol{\omega}}^TGB^{-1}\, \widehat{\sf f}_{1} + \Delta t\, {\widehat r}_2{\boldsymbol{\omega}}^T B^{-1}\, \widehat{\sf f}_2,$

$\quad \quad\vdots$

$E_m = {\boldsymbol{\omega}}^TG^m{\sf v}_0+ \Delta t\, {\widehat r}_0{\boldsymbol{\omega}}^TG^{m-1} B^{-1}\, \widehat{\sf f}_{0} + \Delta t\, {\widehat r}_1{\boldsymbol{\omega}}^T G^{m-2}B^{-1}\widehat{\sf f}_{1} + \cdots+ \Delta t\, {\widehat r}_{m-1}{\boldsymbol{\omega}}^T B^{-1}\, \widehat{\sf f}_{m-1}$.

The above set of linear equations can be rewritten in matrix form as

where

Thus, provided that we are given a set of energy values $E_j$, $j = 1, \dots, m$, the unknowns $\widehat{r}_j$ can be obtained by solving the linear system given by Eq (4.10) in conjunction with some regularization method to mitigate any possible effects of bad conditioning.

Regarding the practical details of the matrix calculation for Eq (4.11), we note that the matrix $G = B^{-1}C$ is never explicitly calculated. Instead, based on the fact that $B$ and $C$ share the same eigenvectors, which implies that $B^{-1}$ and $C$ commute, the quantities $\omega^TG^pB^{-1}\widehat f_i$ can be efficiently calculated by solving linear systems of the type $Bx = f_i$ and $B^T y = \omega$. To do so, we take advantage of the sparseness of matrix $A$ and calculate an LU factorization of $B$ only once.

5.   Numerical experiments

This section includes three numerical examples devoted to illustrating the effectiveness of the numerical method proposed in the work. In all cases, we consider test problems with a known explicit solution, using input data that do not satisfy the hypotheses of Theorem 2.1. It is worth emphasizing that this does not cause any problem here, because, on the one hand, such hypotheses are just sufficient, not necessary, and, on the other hand, the purpose of the section is to test the reconstruction method proposed in the work. Effectiveness is assessed by computing relative errors in the reconstructions of the source function,

where $r$ and $\widetilde r$ denote the exact and recovered sources, respectively, the latter being obtained from noisy data of the form

where $\epsilon$ denotes a zero mean random vector $\epsilon$ scaled such that $\|\widetilde E-E\|_2 = {\text{NL}}\|E\|_2$, with ${\text{NL}}$ representing normwise relative noise level in the data. In all computations, the noise vector $\epsilon$ is generated by the Matlab routine randn.

Before proceeding, it is worth mentioning that, despite the apparent simplicity in determining the source estimates by solving the linear triangular system given as Eq (4.10), due to potential ill-conditioning coming from the discretization of the Volterra integral equation of the first kind, the reconstructions obtained with a perturbed data vector become unstable and some regularization method is needed to filter the noise contribution in the solution.

5.1.   Regularization by truncation

Perhaps one of the most well-known methods to deal with ill-conditioned problems of the form

is the truncated singular value decomposition (TSVD), based on the singular value decomposition of $A$,

where $\textsf{U} = [\textsf{u}_1, \ldots, \textsf{u}_M]\in \mathbb{R}^{M\times M}$ and $\textsf{V} = [\textsf{v}_1, \ldots, \textsf{v}_N]\in \mathbb{R}^{N\times N}$ are orthogonal matrices and $\Sigma_0 = \rm{diag}(\sigma_1, \ldots, \sigma_N)$, with the singular values ${\sf \sigma}_j$ ordered such that $\sigma_1\geq \cdots \geq \sigma_N \ge 0$. The naive least squares solution to Eq (5.2) is thus given by

The main problem with $\widetilde{x}$ is that noise components in $\widetilde b$ can be greatly amplified because of the division by small singular values; in this event, the computed estimate can differ enormously from $x^+$, the solution of Eq (5.2) with $\epsilon = 0$. To filter out the contribution of noise to the computed solution, the TSVD method determines regularized solutions by truncating the summation Eq (5.4) to $k\leq N$ terms; see, e.g., ^[17]. Hence, the $k$-th TSVD solution is defined as

The point here is that, if $k$ is poorly chosen, the TSVD solution $x_k$ either captures an insufficient amount of information about the problem, or the noise in the data dominates the approximate solution. The challenge in connection with TSVD is thus how to choose a proper truncation parameter. Truncated GSVD solutions are defined similarly based on the GSVD of the matrix pair $(A, L)$, where $L$ is introduced to incorporate a priori information of the solution. Explicitly, for $A\in \mathbb{R}^{M\times N}$ and $L\in \mathbb{R}^{p\times N}$, with $M\ge N\ge p$, which always occurs in discrete ill-posed problems, the GSVD of the pair $(A, L)$ reads as

where $U = [u_1, \dots, u_N]\in \mathbb{R}^{M\times N}$ and $V = [{\sf v}_1, \dots, {\sf v}_p]\in \mathbb{R}^{p\times p}$ have orthonormal columns, $X = [{\bf x}_1, \dots, {\bf x}_N]\in \mathbb{R}^{N\times N}$ is nonsingular and $S_1 = {\rm diag}(\sigma_1, \dots, \sigma_p)$ (with $\sigma_i$ ordered in non increasing form) and $S_2 = {\rm diag}(\mu_1, \dots, \mu_p)$ (with $\mu_i$ ordered in nondecreasing form) are $p\times p$ diagonal matrices whose entries are positive and normalized so that

The generalized singular values values of $(A, L)$ are defined as the ratios

Obviously, the $\sigma_i$ here has nothing to do with the "ordinary" singular value $\sigma_i$ of A, as described in Eq (5.3). The same observation holds for the vectors $u_i$ and ${\sf v}_i$. Turning to the estimation of $x^+$ based on the GSVD of the matrix pair $(A, L)$, a truncated GSVD (TGSVD) solution is defined as

It is well known that there exists a close relationship between TGSVD solutions and general form Tikhonov-based solutions ^[17,18]:

where $\lambda > 0$ is the regularization parameter. General-form Tikhonov-based solutions have been used in inverse heat transfer problems elsewhere; see, e.g., ^[3,19]. In this work, we will concentrate on regularization by truncation or filtering. The challenge associated with TGSVD is the same as that of TSVD: how to choose a proper truncation parameter.

In this work, stable estimates of the source function $r(t)$ are computed by using TGSVD, equipped with three parameter selection criteria, namely, the DP by Morozov ^[17], which requires noise estimates of $\|\widetilde E-E\|_2$, a criterion introduced recently by Bazán et al. ^[4] and referred to as MPR and GCV. While the former enjoys strong theoretical support with regard to the convergence of estimates to the exact solution as the noise level decreases to zero, the others are heuristics, so they may fail; but, they do not require any information on the noise level in the data. However, heuristic methods have become popular in many areas and are frequently used in practical problems.

The truncation parameter chosen by applying the DP in connection with TSVD is defined as the first $k$ such that

where $1\lessapprox\tau$ is a user specified parameter. As for the MPR, it chooses as a truncation parameter the integer defined as

The MPR appeared for the first time in connection with LSQR in ^[4], and, more recently, in connection with TSVD in ^[6]. Finally, the truncation parameter chosen by applying GCV in connection with TSVD is defined by

The DP, MPR and GCV are implemented similarly by considering the residual $R_{k, L}$ and corresponding TGSVD solutions $x_{k, L}$. Matlab m-files that implement TGSVD are available in ^[18].

5.2.   Numerical examples

We now consider three numerical examples devoted to illustrating the effectiveness of the truncation regularization methods described above in recovering the source function from noisy data. All computations were carried out in Matlab for several choices of $m$, with $dt = h = 1/m$, $T_f = 1$ and $\alpha$ chosen in such a way that all eigenvalues of matrix $A$ are real.

Example 1.

In this case, we consider a test problem with the analytical solution given by

input data $u(x, 0) = 0$,

and energy function

Note that $\varphi(x) = 0, \; x\in[0, 1]$ simplifies the calculation of the right-hand side vector ${\sf g}$ in Eq (4.10) as ${\sf v}_0 = {\sf 0}$. For the numerical experiment, we set $\Upsilon = 3/2$ and, in order to ensure that all eigenvalues of the system matrix $A$ are real, we chose $\alpha = 1$.

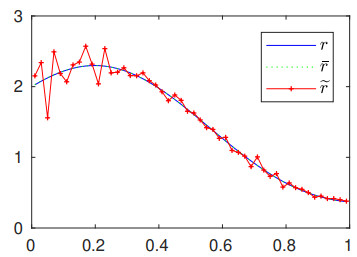
First, to illustrate the need to use regularization methods to obtain the inverse problem solution from noisy data, the linear system given by Eq (4.10) was solved by forward substitution using noiseless and noisy data; the discrete sources obtained in this way are denoted by $\bar r$ and $\widetilde r$, respectively. Recovered discrete sources for $m = 50$ and data with 1% noise are displayed in Figure 2.

The fact that the reconstructed source becomes unstable when using noisy data is apparent and reinforces the need for some regularization to overcome instability. Relative errors of the reconstructed sources presented in Table 1 show that, while, for noiseless data, the reconstruction error decreases as $m$ increases, for noisy data, the error increases.

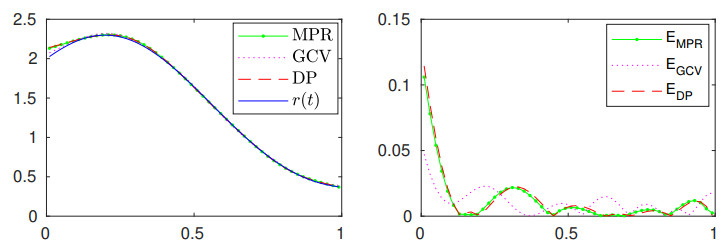
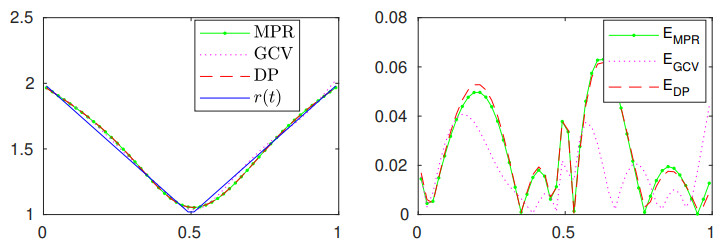
We now proceed to describe the results obtained from noisy data with three noise levels: 0.25%, 1% and 2.5%, under the conditions of the DP, MPR and GCV. Reconstructions, as well as the corresponding absolute errors, ${\text{E}}_{(\cdot)} = |r-\widetilde r_{(\cdot)}|$, for data with 1% noise, are displayed in Figure 3. From this figure, it can be seen that the sources obtained by the three regularization strategies are stably recovered, and with good accuracy.

For completeness, relative errors for the three noise levels, including the corresponding regularization parameters, are all concentrated in Table 2. The results not only show that all of the regularization strategies tested here work well, but they also confirm what is known from regularization theory regarding the DP: the error decreases as the noise level approaches zero, contrary to the regularization parameters that increase in this case. It is worth noting that the MPR and GCV follow this behavior, despite being heuristics.

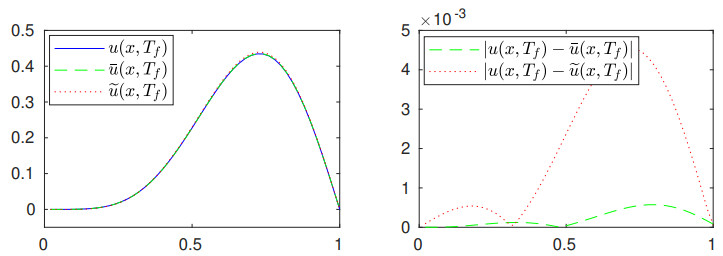
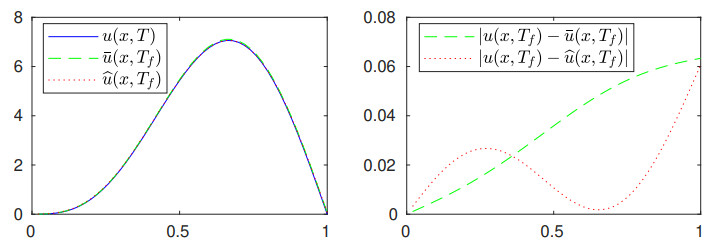
Finally, to illustrate the accuracy of the proposed method regarding the recovery of $u(x, t)$ by using the estimated source, $\widetilde r$, and the input data, $u(x, 0)$, $f (x, t)$, the implicit midpoint method has been used to calculate the approximate solutions that match these data; the results are displayed in Figure 4. As before, the bar symbol is used to denote the numerical solution obtained with the exact discrete source, while the tilde symbol is reserved to denote the results obtained for the retrieved source under the condition of noisy data. The discrete source used in this illustration is the one obtained by applying the DP for $m = 50$, data with 1% noise and $t = T_f$. Approximate solutions obtained for the other source reconstructions were very similar and are omitted here.

Example 2

For this example, the exact solution of the inverse problem, $\{r(t), u(x, t)\}$, is given by

Contrary to the previous example, here, the input data involves a nonzero initial condition:

$\varphi(x) = 2\sin(\pi x)-\sin(2\pi x), \; x\in[0, 1]$ and

$f(x, t) = 2(1+\pi^2)\sin(\pi x)-(1+4\pi^2)\sin(2\pi x)$.

In this case, the energy function is $E(t) = \dfrac{4}{\pi}e^{t}, \; t\in [0, 1]$, and the numerical results correspond to $\alpha = 2$.

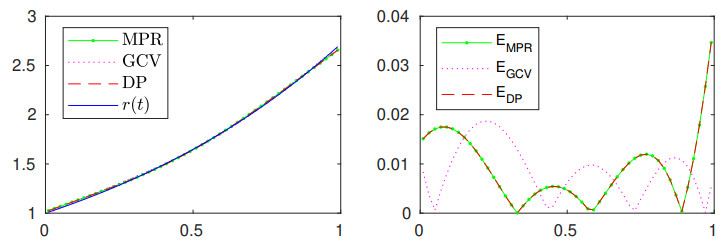
Analogous to the previous example, the numerical reconstruction of the source function was performed by using data with the same noise levels and the same $m$ values as before. The quality of the reconstructions is very similar to what we saw in the previous example, and there is not much to comment here. For illustration, Figure 5 presents the recovered sources and the corresponding absolute errors obtained for data with $1%$ noise.

Also, for completeness, the reconstructed approximate solutions $\bar u(x, t)$, $\widetilde u(x, t)$, as obtained by applying the DP to data with 1% noise, and the corresponding absolute errors are presented in Figure 6.

Example 3

This example differs from the previous ones in that the source function to be recovered is non-smooth. We want to retrieve the pair $(r(t, u(x, t))$,

$r(t) = 1+|2t-1|$,

$u(x, t) = 100e^{-t/2}(2+\cos(4\pi t))\left(-\dfrac{4}{7}x^8+\dfrac{29}{14}x^7-\dfrac{5}{2}x^6+x^5\right)$ from the input data

$\varphi(x) = 300\left(-\dfrac{4}{7}x^8+\dfrac{29}{14}x^7-\dfrac{5}{2}x^6+x^5\right),$

and energy function

$E(t) = \dfrac{125}{252}e^{-t/2}(2+\cos(4\pi t)).$

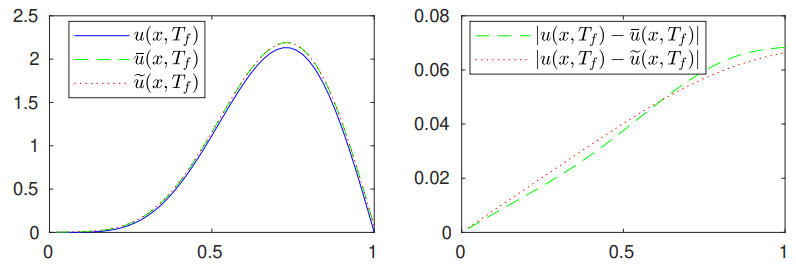
In this case, for the numerical experiment, we set $\alpha = 2$, and to challenge the proposed method, in addition to considering noise-free data, the retrieved source functions were obtained by using noisy data with noise levels of ${\rm NL} = 1%$, ${\rm NL} = 2.5%$ and ${\rm NL} = 5%$. The results obtained by using noise-free data behaved as in Example 1, and thus are not presented here. Retrieved source functions obtained with regularization for ${\rm NL} = 1%$ and $m = 50$, as well as the the respective absolute errors, are presented in Figure 7. As we can see, despite the source function not being smooth, good quality results are again evident.

Similar to the first example, all information regarding the relative errors and regularization parameters for the three noise levels are presented in Table 3. Once again, we see that the quality of recovered quantities is excellent and is associated with relative errors that were nearly equal to the noisy level of the input data, regardless of whether the number of data points used was $m = 50$ or $m = 100$.

Lastly, we also used the recovered source $\widetilde r$, obtained by applying the DP to calculate the approximate solution $\widetilde u(x, t)$. Numerical results presented in Figure 8 confirm, again, that the recovered solution is stable and accurate.

6.   Conclusion

In this work, an inverse source reconstruction method for the heat equation subject to a nonlocal Wentzell-Neumann boundary conditions and the specification of energy/mass data has been investigated. As a first contribution, we have improved the results on the existence and uniqueness of classical solutions of the inverse problem presented in ^[23], noting that the annihilation assumption of complex terms of the Fourier series expansion can be relaxed. From a numerical point of view, another major contribution of the work describes a GSVD expansion for the unknown source term $r(t)$ together with a regularization procedure to calculate stable solutions in the case of noisy data. Regularization has been achieved by truncating the GSVD expansion with the truncation parameter selected based on three criteria, namely, Morozov's DP, MPR and GCV. The method is quite simple to implement and computationally fast. Three numerical experiments using noisy synthetic data showed that the proposed method is capable of producing numerical reconstructions of the source term with the reconstruction error of the same order as the error in the input data, regardless of the parameter selection criteria and the number of data points used. Extensions of the proposed method to 2D problems will be the subject of future research.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. The authors declare that no funds, grants, or other support were received during the preparation of this manuscript.

Conflict of interest

The authors declare that there is no conflicts of interest.